Comparison of Bayesian Clustering and Edge Detection Methods for Inferring Boundaries in Landscape Genetics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Methods
2.2. Simulation Data
2.2.1. Simulation of Equilibrium Global Spatial Evolutionary Processes
2.2.2. Imposing Barriers to Gene Flow
2.2.3. Simulation Parameters
2.2.4. Boundary Detection and Performance Evaluation of Each Method
- For each data set, we performed 10 independent runs for values of Kmax ranging from 1 to 6 (Table 3). In the case of TESS, values of K corresponding to the highest average likelihood score across runs were identified. Outputs from TESS analyses using the identified value of K were averaged over the 10 runs using the computer program CLUMPP [50]. BAPS5 provides its own internal approach for inferring the most likely number of clusters in a data set, presenting only the result with the highest average likelihood score and the corresponding cluster membership coefficients of each individual across the 10 runs.
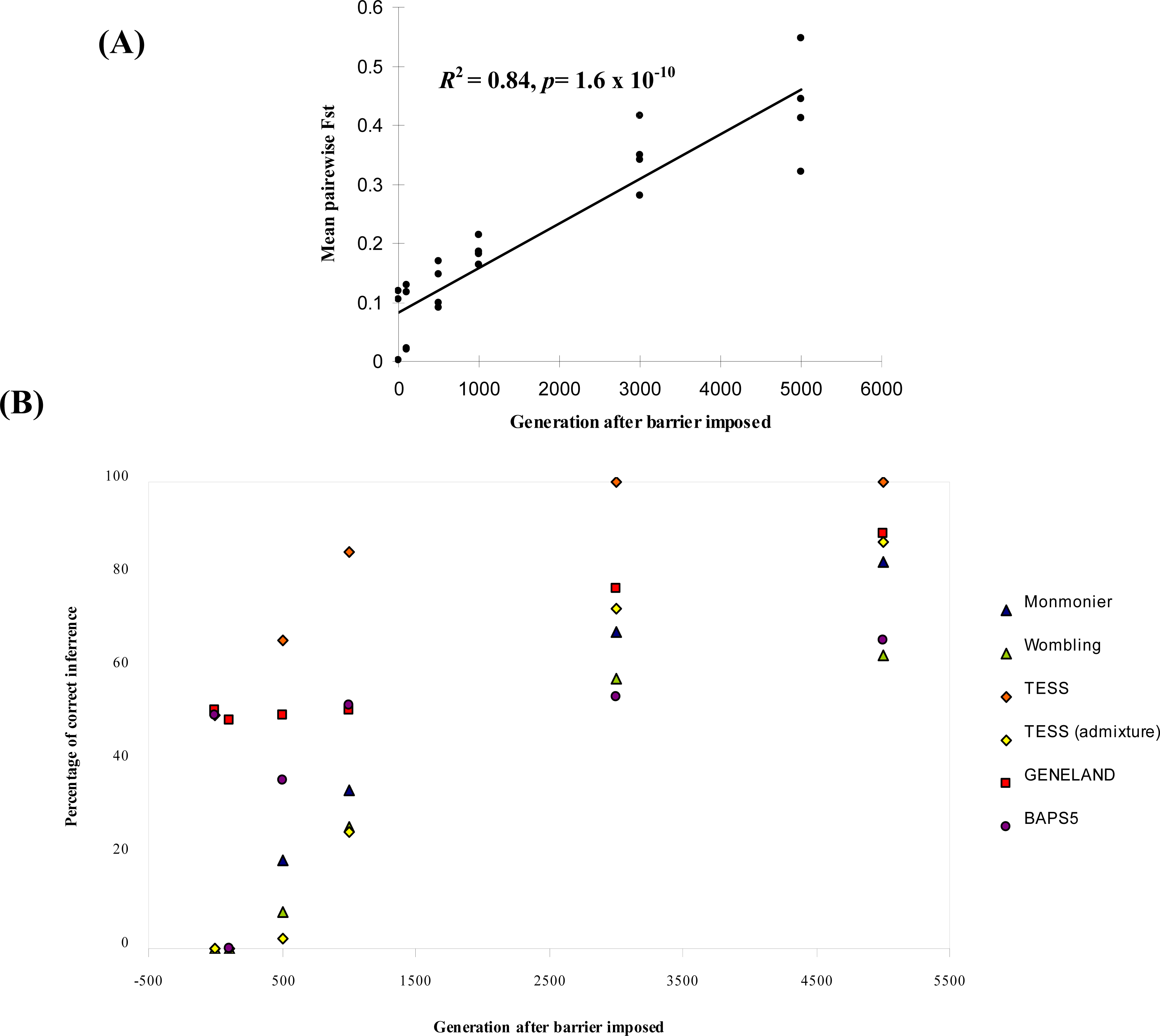
- For Bayesian clustering methods, we considered boundaries to be correctly inferred if the number of spatial clusters estimated was four and if individuals were all correctly assigned to the clusters from their respective landscape region, except for generation time 0. At generation 0, we expected no detectable boundary and for all individuals to be assigned to the same cluster (K = 1).
- For each parameter combination and at each time point, we calculated the percentage (out of the 25 repetitions) of cases where the boundaries (or no boundary at generation 0) had been correctly detected.
2.3. Empirical Data
2.3.1. Puma (Puma Concolor)
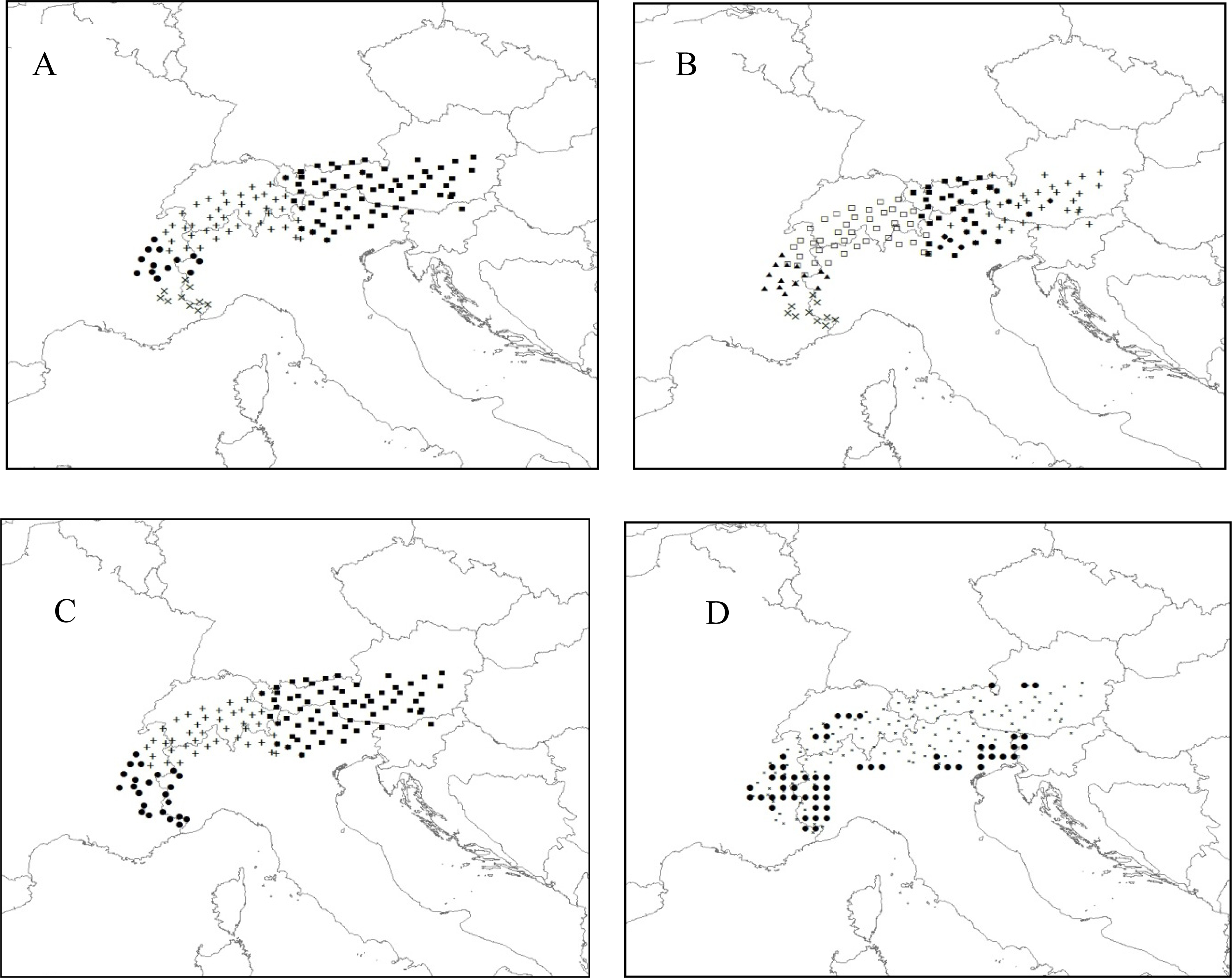
2.3.2. Rhododendron (Rhododendron Ferrugineum)
3. Results
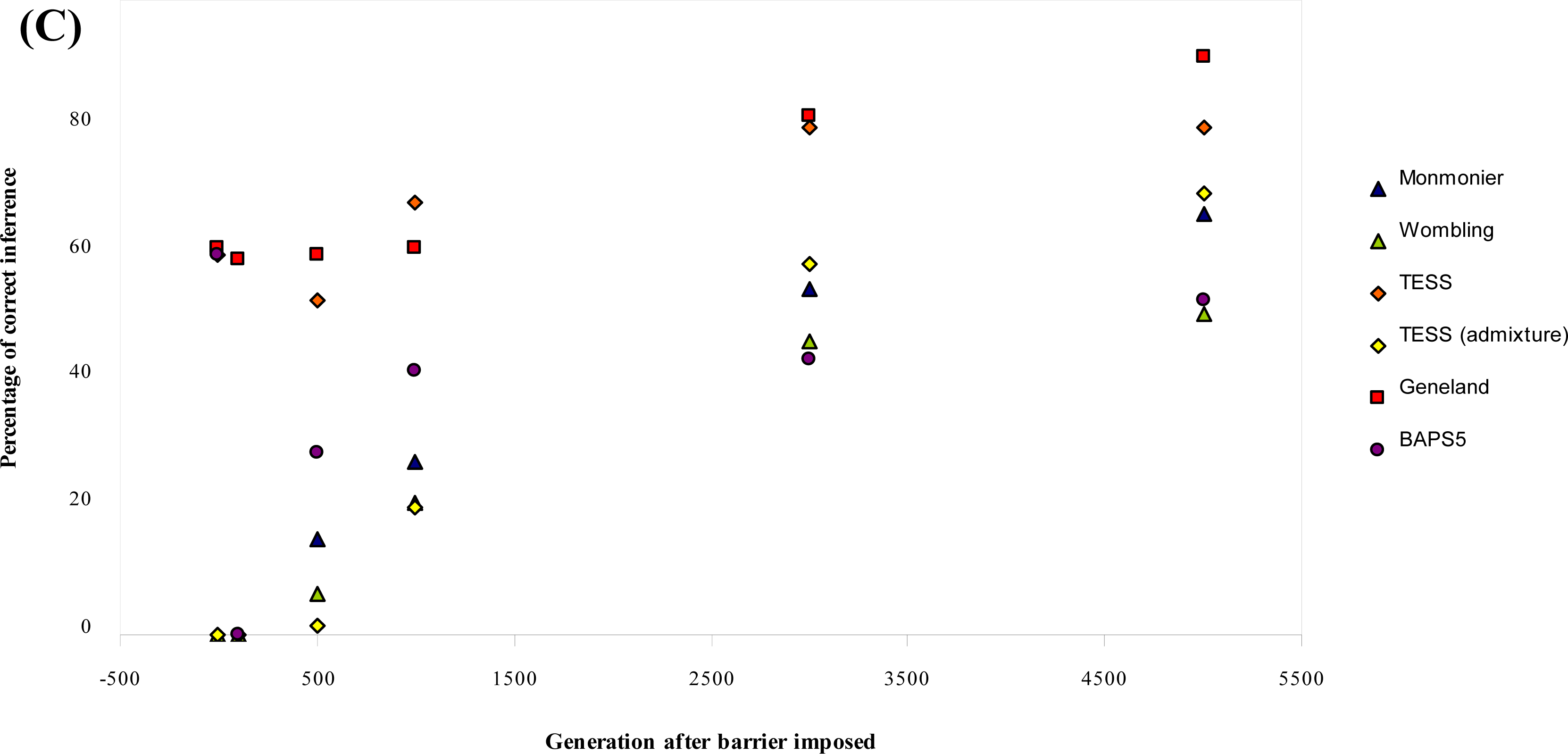
3.1. Simulated Data
3.2. Empirical Data
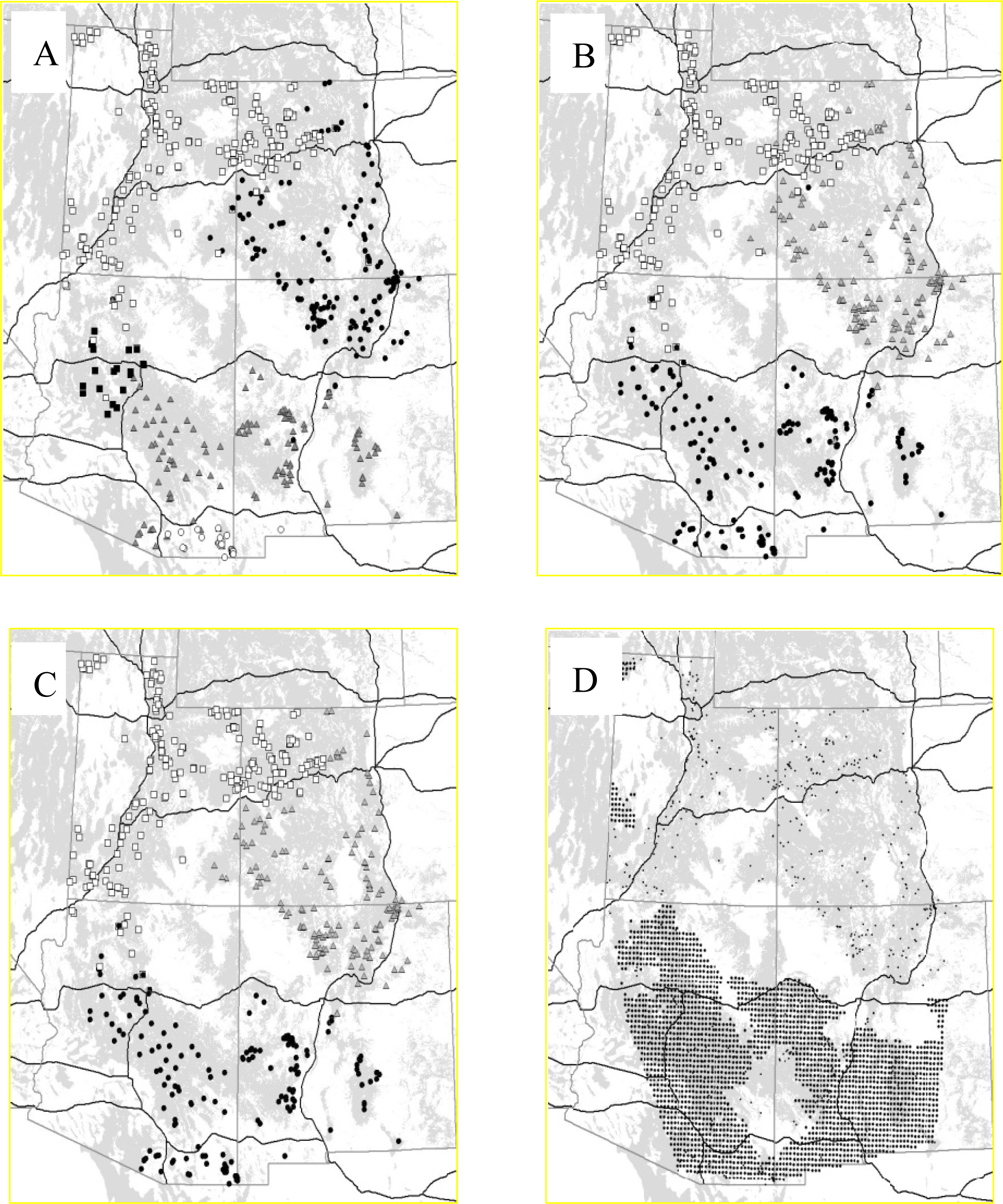
3.2.1. Puma
3.2.2. Rhododendron
4. Discussion
5. Conclusions and Recommendations
Acknowledgments
References
- Jacquez, GM. The map comparison problem: Tests for the overlap of geographic boundaries. Stat. Med 1995, 14, 2343–2361. [Google Scholar]
- Miller, MP; Bellinger, MR; Forsman, ED; Haig, SM. Effects of historical climate change, habitat connectivity, and vicariance on genetic structure and diversity across the range of the red tree vole (Phenacomys longicaudus) in the Pacific Northwestern United States. Mol. Ecol 2006, 15, 145–159. [Google Scholar]
- Coulon, A; Guillot, G; Cosson, J-F; Angibault, JMA; Aulagnier, S; Cargnelutti, B; Galan, M; Hewison, AJM. Genetic structure is influenced by landscape features: Empirical evidence from a roe deer population. Mol. Ecol 2006, 15, 1669–1679. [Google Scholar]
- Cushman, SA; McKelvey, KS; Hayden, J; Schwartz, MK. Gene flow in complex landscapes: Testing multiple hypotheses with causal modeling. Am. Naturalist 2006, 168, 486–499. [Google Scholar]
- Safner, T; Miaud, C; Gaggiotti, O; Decout, S; Rioux, D; Zundel, S; Manel, S. Combining demography and genetic analysis to assess the population structure of an amphibian in a human-dominated landscape. Conserv. Genet 2010, 12, 161–173. [Google Scholar]
- DeSalle, R; Amato, G. The expansion of conservation genetics. Nat. Rev. Genet 2004, 5, 702–712. [Google Scholar]
- Musiani, M; Leonard, JA; Cluff, HD; Gates, CC; Mariani, S; Paquet, PC; Vilà, C; Wayne, RK. Differentiation of tundra/taiga and boreal coniferous forest wolves: Genetics, coat colour and association with migratory caribou. Mol. Ecol 2007, 16, 4149–4170. [Google Scholar]
- Guillot, G; Leblois, R; Coulon, A; Frantz, AC. Statistical methods in spatial genetics. Mol. Ecol 2009, 18, 4734–4756. [Google Scholar]
- Pritchard, JK; Stephens, M; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar]
- Dawson, KJ; Belkhir, K. A Bayesian approach to the identification of panmictic populations and the assignment of individuals. Genet. Res 2001, 78, 59–77. [Google Scholar]
- Corander, J; Waldmann, P; Sillanpaa, MJ. Bayesian analysis of genetic differentiation between populations. Genetics 2003, 163, 367–374. [Google Scholar]
- Manel, S; Bellemain, E; Swenson, JE; Francois, O. Assumed and inferred spatial structure of populations: The Scandinavian brown bears revisited. Mol. Ecol 2004, 13, 1327–1331. [Google Scholar]
- McRae, BH; Beier, P; Dewald, LE; Huynh, LY; Keim, P. Habitat barriers limit gene flow and illuminate historical events in a wide-ranging carnivore, the American puma. Mol. Ecol 2005, 14, 1965–1977. [Google Scholar]
- Guillot, G; Estoup, A; Mortier, F; Cosson, JF. A Spatial statistical model for landscape genetics. Genetics 2005, 170, 1261–1280. [Google Scholar]
- Guillot, G; Mortier, F; Estoup, A. Geneland: A computer package for landscape genetics. Mol. Ecol. Notes 2005, 5, 712–715. [Google Scholar]
- Francois, O; Ancelet, S; Guillot, G. Bayesian clustering using hidden markov random fields in spatial population genetics. Genetics 2006, 174, 805–816. [Google Scholar]
- Chen, C; Durand, E; Forbes, F; Francois, O. Bayesian clustering algorithms ascertaining spatial population structure: A new computer program and a comparison study. Mol. Ecol. Notes 2007, 7, 747–756. [Google Scholar]
- Corander, J; Sirén, J; Arjas, E. Bayesian spatial modeling of genetic population structure. Comput Stat 2008, 23, 111–129. [Google Scholar]
- Fortin, M-J; Drapeau, P. Delineation of ecological boundaries: Comparison of approaches and significance tests. Oikos 1995, 72, 323–332. [Google Scholar]
- Monmonier, MS. Maximum-difference barriers: An alternative numerical regionalization method. Geogr. Anal 2010, 5, 245–261. [Google Scholar]
- Womble, WH. Differential Systematics. Science 1951, 114, 315–322. [Google Scholar]
- Barbujani, G; Oden, NL; Sokal, RR. Detecting regions of abrupt change in maps of biological variables. Syst Zool 1989, 38, 376–389. [Google Scholar]
- Jacquez, GM; Maruca, S; Fortin, M-J. From fields to objects: A review of geographic boundary analysis. J. Geogr. Syst 2000, 2, 221–241. [Google Scholar]
- Manni, F; Guerard, E; Heyer, E. Geographic patterns of (genetic, morphologic, linguistic) variation: How barriers can be detected by using monmonier’s algorithm. Hum. Biol 2004, 76, 173–190. [Google Scholar]
- Miller, MP. Alleles in space (AIS): Computer software for the joint analysis of interindividual spatial and genetic information. J. Hered 2005, 96, 722–724. [Google Scholar]
- Cercueil, A; Francois, O; Manel, S. The Genetical Bandwidth Mapping: A spatial and graphical representation of population genetic structure based on the Wombling method. Theor. Popul. Biol 2007, 71, 332–341. [Google Scholar]
- Crida, A; Manel, S. wombsoft: An r package that implements the Wombling method to identify genetic boundary. Mol. Ecol. Notes 2007, 7, 588–591. [Google Scholar]
- Dupanloup, I; Schneider, S; Excoffier, L. A simulated annealing approach to define the genetic structure of populations. Mol. Ecol 2002, 11, 2571–2581. [Google Scholar]
- Kuehn, R; Hindenlang, KE; Holzgang, O; Senn, J; Stoeckle, B; Sperisen, C. Genetic effect of transportation infrastructure on roe deer populations (Capreolus capreolus). J. Hered 2007, 98, 13–22. [Google Scholar]
- Segelbacher, G; Manel, S; Tomiuk, J. Temporal and spatial analyses disclose consequences of habitat fragmentation on the genetic diversity in capercaillie (Tetrao urogallus). Mol. Ecol 2008, 17, 2356–2367. [Google Scholar]
- Latch, EK; Dharmarajan, G; Glaubitz, JC; Rhodes, OE. Relative performance of Bayesian clustering software for inferring population substructure and individual assignment at low levels of population differentiation. Conserv. Genet 2006, 7, 295–302. [Google Scholar]
- Frantz, AC; Cellina, S; Krier, A; Schley, L; Burke, T. Using spatial Bayesian methods to determine the genetic structure of a continuously distributed population: Clusters or isolation by distance? J. Appl. Ecol 2009, 46, 493–505. [Google Scholar]
- Francois, O; Durand, E. Spatially explicit Bayesian clustering models in population genetics. Mol Ecol Resour 2010, 10, 773–784. [Google Scholar]
- Corander, J; Waldmann, P; Marttinen, P; Sillanpää, MJ. BAPS 2: Enhanced possibilities for the analysis of genetic population structure. Bioinformatics 2004, 20, 2363–2369. [Google Scholar]
- Corander, J; Tang, J. Bayesian analysis of population structure based on linked molecular information. Math. Biosci 2007, 205, 19–31. [Google Scholar]
- Durand, E; Jay, F; Gaggiotti, OE; Francois, O. Spatial inference of admixture proportions and secondary contact zones. Mol. Biol. Evol 2009, 26, 1963–1973. [Google Scholar]
- Guillot, G. On the inference of spatial structure from population genetics data. Bioinformatics 2009, 25, 1796–1801. [Google Scholar]
- Durand, E; Chen, C; Francois, O. Comment on “On the inference of spatial structure from population genetics data”. Bioinformatics 2009, 25, 1796–1801. [Google Scholar]
- Guillot, G; Santos, F; Estoup, A. Analysing georeferenced population genetics data with Geneland: A new algorithm to deal with null alleles and a friendly graphical user interface. Bioinformatics 2008, 24, 1406–1407. [Google Scholar]
- Guillot, G. Inference of structure in subdivided populations at low levels of genetic differentiation—the correlated allele frequencies model revisited. Bioinformatics 2008, 24, 2222–2228. [Google Scholar]
- Guillot, G; Santos, F. A computer program to simulate multilocus genotype data with spatially autocorrelated allele frequencies. Mol. Ecol. Resour 2009, 9, 1112–1120. [Google Scholar]
- Manel, S; Schwartz, MK; Luikart, G; Taberlet, P. Landscape genetics: Combining landscape ecology and population genetics. Trends Ecol. Evol 2003, 18, 189–197. [Google Scholar]
- Jombart, T; Devillard, S; Dufour, A-B; Pontier, D. Revealing cryptic spatial patterns in genetic variability by a new multivariate method. Heredity 2008, 101, 92–103. [Google Scholar]
- Slatkin, M; Barton, NH. A comparison of three indirect methods for estimating average levels of gene flow. Evolution 1989, 43, 1349–1368. [Google Scholar]
- Miller, MP; Haig, SM. Identifying shared genetic structure patterns among pacific northwest forest taxa: Insights from use of visualization tools and computer simulations. PLoS ONE 2010, 5, e13683. [Google Scholar]
- Austerlitz, F; Smouse, PE. Two-generation analysis of pollen flow across a landscape. III. Impact of adult population structure. Genet. Res 2001, 78, 271–280. [Google Scholar]
- Hartl, DL; Clark, AG. Principles of Population Genetics, Fourth Edition, 4th ed; Sinauer Associates, Inc: Sunderland, MA, USA, 2006. [Google Scholar]
- Excoffier, L; Laval, G; Schneider, S. Arlequin (version 3.0): An integrated software package for population genetics data analysis. Evol. Bioinform. Online 2005, 1, 47–50. [Google Scholar]
- Rousset, F. Genetic differentiation between individuals. J. Evol. Biol 2000, 13, 58–62. [Google Scholar]
- Jakobsson, M; Rosenberg, NA. CLUMPP: A cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics 2007, 23, 1801–1806. [Google Scholar]
- Manel, S; Berthoud, F; Bellemain, E; Gaudeul, M; Luikart, G; Swenson, JE; Waits, LP; Taberlet, P. A new individual-based spatial approach for identifying genetic discontinuities in natural populations. Mol. Ecol 2007, 16, 2031–2043. [Google Scholar]
- Vos, P; Hogers, R; Bleeker, M; Reijans, M; Lee, T; van de Hornes, M; Frijters, A; Pot, J; Peleman, J; Kuiper, M. AFLP: A new technique for DNA fingerprinting. Nucleic Acids Res 1995, 23, 4407–4414. [Google Scholar]
- Bonin, A; Ehrich, D; Manel, S. Statistical analysis of amplified fragment length polymorphism data: A toolbox for molecular ecologists and evolutionists. Mol. Ecol 2007, 16, 3737–3758. [Google Scholar]
- Evanno, G; Regnaut, S; Goudet, J. Detecting the number of clusters of individuals using the software STRUCTURE: A simulation study. Mol. Ecol 2005, 14, 2611–2620. [Google Scholar]
- Landguth, EL; Cushman, SA; Schwartz, MK; McKelvey, KS; Murphy, M; Luikart, G. Quantifying the lag time to detect barriers in landscape genetics. Mol. Ecol 2010, 19, 4179–4191. [Google Scholar]
- Schwartz, MK; McKelvey, KS. Why sampling scheme matters: The effect of sampling scheme on landscape genetic results. Conserv. Genet 2010, 10, 441–452. [Google Scholar]
- Fortin, M-J; Keitt, TH; Maurer, BA; Taper, ML; Kaufman, DM; Blackburn, TM. Species’ geographic ranges and distributional limits: Pattern analysis and statistical issues. Oikos 2005, 108, 7–17. [Google Scholar]
- Barbujani, G; Sokal, RR. Zones of sharp genetic change in Europe are also linguistic boundaries. Proc. Natl. Acad. Sci. USA 1990, 87, 1816–1819. [Google Scholar]
- Fortin, M-J; Dale, MRT. Spatial Analysis; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
| BAPS5 | TESS | GENELAND | WOMBSOFT | AIS (Monmonier) | |
|---|---|---|---|---|---|
| Model | Spatial Bayesian clustering | Spatial Bayesian clustering | Spatial Bayesian clustering | Non parametric | Non parametric |
| Analytical and Stochastic methods | Markov chain Monte Carlo | Markov chain Monte Carlo | |||
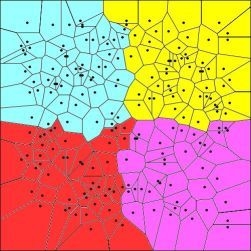
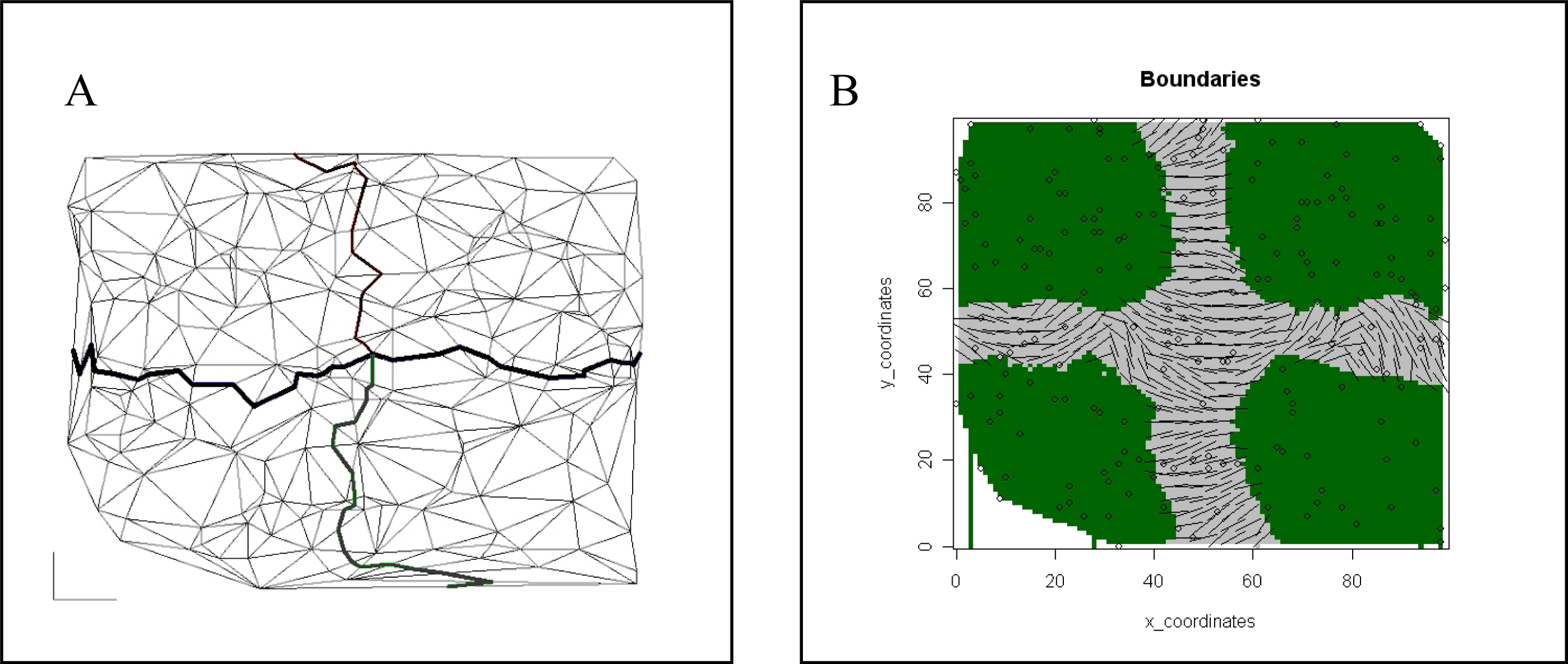
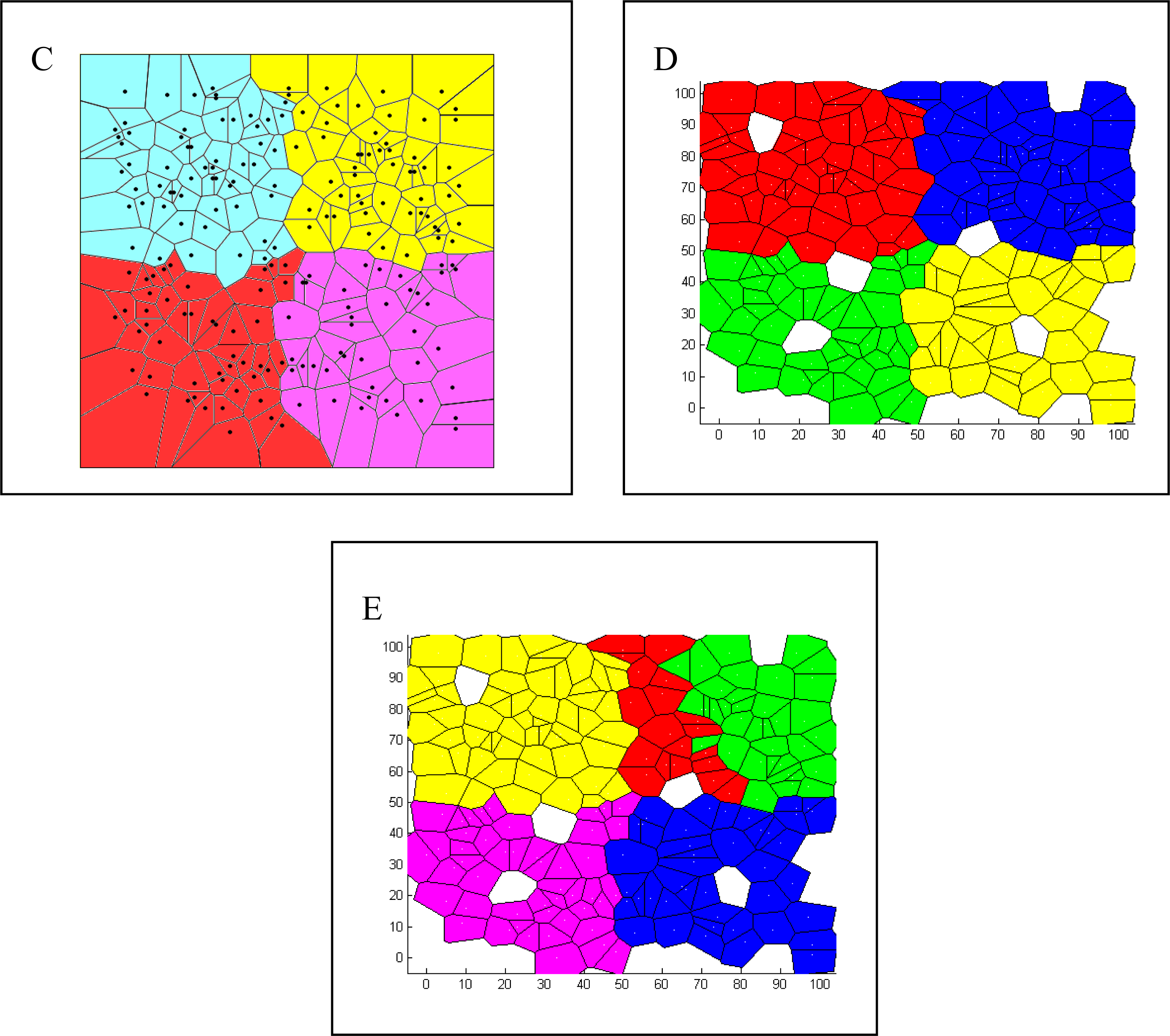
| Spatial | Colored Voronoi tessellation based on discrete sampling site | Hidden Markov random field | Free colored Voronoi tessellation based on continuous Poisson point process | Geographic coordinates are included in the local weighted regression | Delaunay triangulation (Table 5) |
| Clustering criteria | *HWE and **LE between loci | *HWE and **LE between loci | *HWE and **LE between loci | None | None |
| Local edge detection criteria | None | None | None | Average rate of change based on individuals located within a kernel of a given bandwidth size | High rate of change between paired individuals based on Delaunay link |
| Data | Co-dominant and Dominant | Codominant | Co-dominant and Dominant | Co-dominant, Dominant and categorical data | Co-dominant, Dominant, and Sequence Data |
| Platforms | Windows, Unix/Linux Mac OS X | Windows, Unix/Linux | R package Windows, Unix/Linux Mac OS X | R package Windows, Unix/Linux Mac OS X | Windows |
| Reference | [35] | [16,17] | [15] | [27] | [25] |
| URL | http://web.abo.fi/fak/mnf//mate/jc/software/baps.html | http://www-timc.imag.fr/Olivier.Francois/tess.html | http://www2.imm.dtu.dk/~gigu/Geneland/ | http://cran.r-project.org/web/packages/wombsoft/index.html | http://www.marksgeneticsoftware.net/AISInfo.htm |
| Hidden Markov Random Field | A hidden Markov random field model is a special case of Hidden Markov Models (HMM). A HMM is a statistical model in which the system being modeled is assumed to be a Markov process with unknown parameters, and the challenge is to determine the hidden parameters from the observable parameters. |
| Markov chain Monte Carlo | Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. |
| Neighborhood graphs | Neighborhood graphs capture proximity between points by connecting nearby points with a graph edge. Many possible ways to determine nearby points lead to a variety of neighborhood graph types such as Voronoi tesselation and Delaunay triangulation. |
| Voronoi tesselation | Given a set of N points in a plane, Voronoi tessellation divides the domain in a set of polygonal regions, the boundaries of which are the perpendicular bisectors of the lines joining the points. |
| Delaunay triangulation | The Delaunay triangulation graph connects the adjacent geographical positions of the samples on a map, resulting in a network that connects all the samples. None of the points is inside the circumcircle of any triangle. |
| Input parameter | Simulations | Puma | Rhododendron | |
|---|---|---|---|---|
| BAPS5 | *K | 1–6 | 1–8 | 1–10 |
| Number of replications | 10 | 10 | 10 | |
| TESS | *K | 1–6 | 1–7 | 1–7 |
| **Psi: | 0–0.6 | 0.6–1 | 0.6–1 | |
| Number of Sweeps | 10,000 | 100,000 | 100,000 | |
| Number of burnin period | 2000 | 10,000 | 10,000 | |
| Number of runs | 10 | 10 | 10 | |
| Admixture parameter | †Yes and no | Yes and no | Yes and no | |
| GENELAND | *K | 1–6 | 1–7 | 1–7 |
| Number of iterations | 50,000 | 100,000 | 100,000 | |
| Thinning | 10 | 10 | 10 | |
| Number of replications | 10 | 10 | 10 | |
| Allele frequencies | Correlated | Correlated | Correlated | |
| WOMBSOFT | Resolution of the grid | 100 × 100 | 100 × 100 | 34 × 16 |
| Bandwidth | 7 | 70 km | 30 km | |
| Binomial threshold | 0.3 | 0.3 | 0.3 | |
| Statistical significance of the binomial test | 0.05 | 0.01 | 0.05 | |
| Monmonier’s algorithm | Genetic distances were specified | Residual | Raw and residuals | Raw and residuals |
| Number of barriers to be identified. | 4 | 1–7 | 1–7 | |
| Parameter combination | Mean Number of alleles* | Mean gene diversity (H)* | Mean IBD Slope† |
|---|---|---|---|
| μ = 0.0001 − δ = 1 | 24.9 [0.59] | 0.86 [0.0088] | 0.265 [0.02] (100%) |
| μ = 0.000025 − δ = 1 | 9.5 [0.68] | 0.62 [0.0073] | 0.202 [0.03] (100%) |
| μ = 0.0001 − δ = 11 | 17.8 [1.28] | 0.79 [0.0182] | 0.004 [0.003] (12%) |
| μ = 0.000025 - δ = 11 | 6.32 [0.36] | 0.49 [0.0098] | 0.002 [0.002] (24%) |
| Parameter combination | Generation after barrier imposed | Monmonier | WOMBSOFT | TESS | TESS admixture | GENELAND | BAPS5 |
|---|---|---|---|---|---|---|---|
| μ = 0.0001 | 0 | 0 | 0 | 0 [5.4] | 0 [5.2] | 0 [2.0] | 0 [6.0] |
| δ = 1 | 100 | 0 | 0 | 0 [5.2] | 0 [4.8] | 0 [5.2] | 0 [6.0] |
| b = 0 | 500 | 36 | 0 | 72 [4.3] | 4 [4.6] | 0 [5.2] | 0 [6.0] |
| 1000 | 68 | 8 | 84 [4.2] | 52 [4.1] | 4 [5.1] | 0 [6.0] | |
| 3000 | 96 | 20 | 100 [4.0] | 100 [4.0] | 60 [4.5] | 0 [5.9] | |
| 5000 | 100 | 24 | 100 [4.0] | 92 [4.0] | 88 [4.1] | 0 [5.9] | |
| μ = 0.000025 | 0 | 0 | 0 | 0 [5.4] | 0 [4.9] | 4 [5.0] | 0 [6.0] |
| δ = 1 | 100 | 0 | 0 | 0 [5.5] | 0 [4.6] | 0 [5.0] | 0 [6.0] |
| b = 0 | 500 | 4 | 0 | 36 [4.7] | 0 [4.6] | 0 [5.2] | 0 [5.9] |
| 1000 | 8 | 0 | 68 [4.3] | 12 [4.3] | 0 [5.6] | 12 [5.6] | |
| 3000 | 40 | 28 | 100 [4.0] | 60 [4.1] | 48 [4.7] | 16 [5.2] | |
| 5000 | 68 | 40 | 100 [4.0] | 80 [4.0] | 68 [4.4] | 64 [4.5] | |
| μ = 0.0001 | 0 | 0 | 0 | 100 [1.0] | 0 [3.5] | 100 [1.0] | 100 [1.0] |
| δ = 11 | 100 | 0 | 0 | 0 [2.6] | 0 [3.9] | 100 [4.0] | 0 [1.0] |
| b = 0 | 500 | 36 | 32 | 100 [4.0] | 4 [4.0] | 100 [4.0] | 100 [4.0] |
| 1000 | 60 | 72 | 100 [4.0] | 32 [4.0] | 100 [4.0] | 100 [4.0] | |
| 3000 | 96 | 92 | 100 [4.0] | 92 [4.0] | 100 [4.0] | 100 [4.0] | |
| 5000 | 100 | 88 | 100 [4.0] | 96 [4.0] | 100 [4.0] | 100 [4.0] | |
| μ = 0.000025 | 0 | 0 | 0 | 100 [1.0] | 0 [3.6] | 100 [1.0] | 100 [1.0] |
| δ = 11 | 100 | 0 | 0 | 0 [1.4] | 0 [3.8] | 96 [4.0] | 0 [1.0] |
| b = 0 | 500 | 0 | 0 | 56 [4.0] | 0 [4.0] | 100 [4.0] | 44 [4.0] |
| 1000 | 0 | 24 | 88 [4.0] | 4 [4.0] | 100 [4.0] | 96 [4.0] | |
| 3000 | 40 | 92 | 100 [4.0] | 40 [4.1] | 100 [4.0] | 100 [4.0] | |
| 5000 | 64 | 100 | 100 [4.0] | 80 [4.0] | 100 [4.0] | 100 [4.0] | |
| Mean % (b = 0) | 27.20 | 20.67 | 56.80 | 24.93 | 68.93 | 37.73 | |
| μ= 0.0001 | 0 | 0 | 0 | 100 [1.0] | 0 [2.4] | 100 [1.0] | 100 [1.0] |
| δ = 11 | 100 | 0 | 0 | 0 [1.0] | 0 [2.3] | 100 [4.0] | 0 [1.0] |
| b = 0.03 | 500 | 0 | 0 | 0 [1.9] | 0 [2.3] | 100 [4.0] | 0 [1.0] |
| 1000 | 0 | 0 | 0 [1.9] | 0 [2.4] | 100 [4.0] | 0 [1.0] | |
| 3000 | 0 | 0 | 0 [2.0] | 0 [2.6] | 100 [4.0] | 0 [1.0] | |
| 5000 | 0 | 0 | 0 [2.0] | 0 [2.9] | 100 [4.0] | 0 [1.0] | |
| Overall Mean % | 34.00 | 25.83 | 66.83 | 31.16 | 61.17 | 43.00 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Safner, T.; Miller, M.P.; McRae, B.H.; Fortin, M.-J.; Manel, S. Comparison of Bayesian Clustering and Edge Detection Methods for Inferring Boundaries in Landscape Genetics. Int. J. Mol. Sci. 2011, 12, 865-889. https://doi.org/10.3390/ijms12020865
Safner T, Miller MP, McRae BH, Fortin M-J, Manel S. Comparison of Bayesian Clustering and Edge Detection Methods for Inferring Boundaries in Landscape Genetics. International Journal of Molecular Sciences. 2011; 12(2):865-889. https://doi.org/10.3390/ijms12020865
Chicago/Turabian StyleSafner, Toni, Mark P. Miller, Brad H. McRae, Marie-Josée Fortin, and Stéphanie Manel. 2011. "Comparison of Bayesian Clustering and Edge Detection Methods for Inferring Boundaries in Landscape Genetics" International Journal of Molecular Sciences 12, no. 2: 865-889. https://doi.org/10.3390/ijms12020865