Correlation of the Rates of Solvolysis of Neopentyl Chloroformate—A Recommended Protecting Agent
Abstract
:1. Introduction
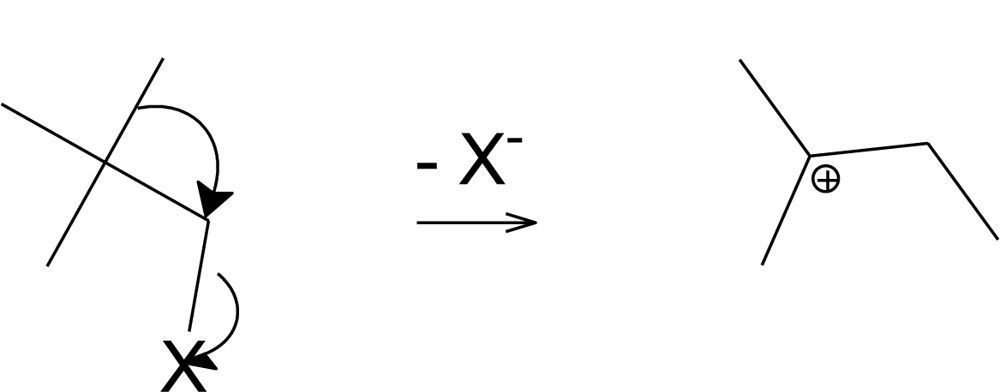
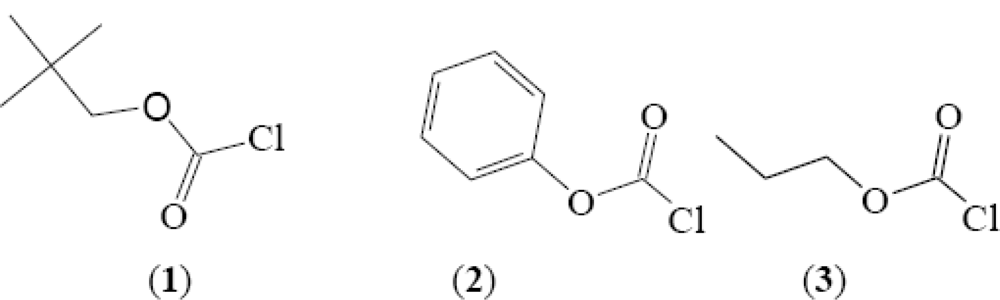
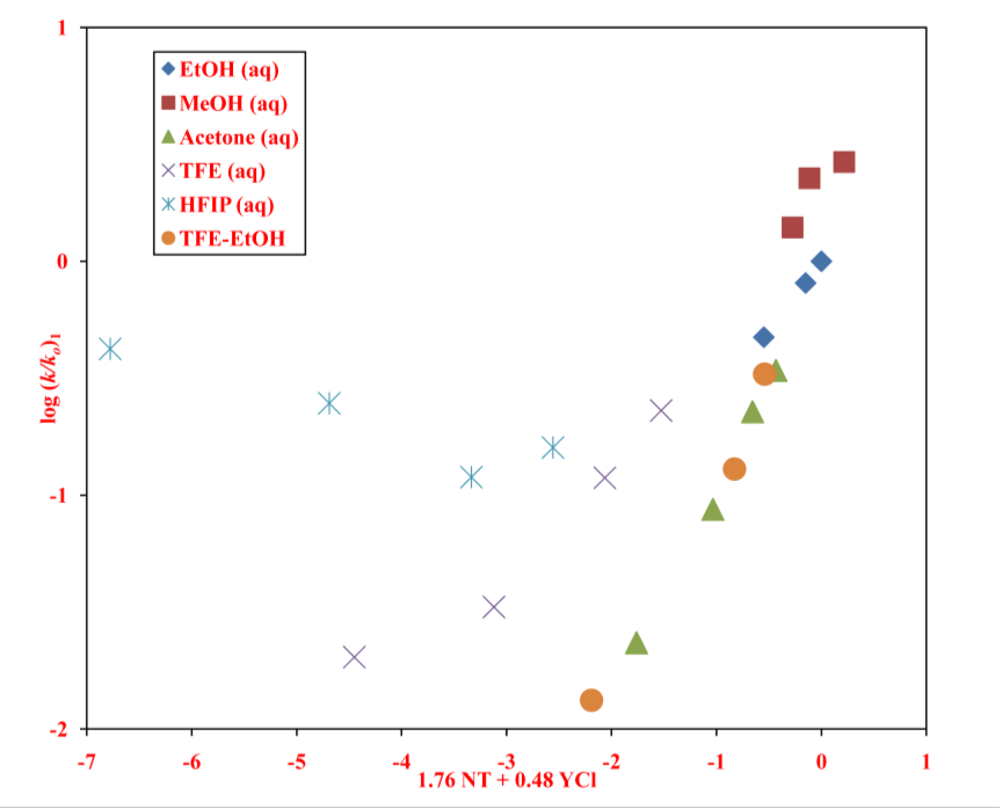
2. Results and Discussion
3. Experimental Section
4. Conclusions
Acknowledgments
References
- Kevill, DN. Chloroformate Esters and Related Compounds. In The Chemistry of the Functional Groups: The Chemistry of Acyl Halides; Patai, S, Ed.; Wiley: New York, NY, USA, 1972; Chapter 12; pp. 381–453. [Google Scholar]
- Matzner, M; Kurkjy, RP; Cotter, RJ. The Chemistry of Chloroformates. Chem. Rev 1964, 64, 645–687. [Google Scholar]
- Jones, J. The Chemical Synthesis of Peptides; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Hashiguchi, S; Natsugari, H; Ochiai, M. Synthesis of γ-Lactam Analogues of Carbapenems with Substituted-thio Groups at the C-3 Position. J. Chem. Soc. Perkin Trans 1 1988, 8, 2345–2352. [Google Scholar]
- Shields, JE; Carpenter, FH. Synthesis of a Heptapeptide Sequence from Bovine Insulin. J. Am. Chem. Soc 1961, 83, 3066–3070. [Google Scholar]
- Haas, WL; Krumkalns, EV; Gerzon, K. Adamantyloxycarbonyl, a New Blocking Group. Preparation of 1-Adamantyl Chloroformate. J. Am. Chem. Soc 1966, 88, 1988–1992. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolysis of Phenyl Chloroformate. J. Chem. Soc., Perkin Trans. 2 1997, 9, 1721–1724. [Google Scholar]
- D’Souza, MJ; Reed, D; Koyoshi, F; Kevill, DN. Consideration of the Factors Influencing the Specific Rates of Solvolysis of p-Methoxyphenyl Chloroformate. Int. J. Mol. Sci 2007, 8, 788–796. [Google Scholar]
- D’Souza, MJ; Shuman, KE; Carter, SE; Kevill, DN. Extended Grunwald-Winstein Analysis—LFER Used to Gauge Solvent Effects in p-Nitrophenyl Chloroformate Solvolysis. Int. J. Mol. Sci 2008, 9, 2231–2242. [Google Scholar]
- Kevill, DN; Kim, JC; Kyong, JB. Correlation of the Rates of Methyl Chloroformate with Solvent Properties. J. Chem. Res. Synop 1999, 2, 150–151. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Concerning the Two Reaction Channels for the Solvolyses of Ethyl Chloroformate and Ethyl Chlorothioformate. J. Org. Chem 1998, 63, 2120–2124. [Google Scholar]
- Kyong, JB; Won, H; Kevill, DN. Application of the Extended Grunwald-Winstein Equation to Solvolyses of n-Propyl Chloroformate. Int. J. Mol. Sci 2005, 6, 87–96. [Google Scholar]
- Kyong, JB; Kim, YG; Kim, DK; Kevill, DN. Dual Pathways in the Solvolyses of Isopropyl Chloroformate. Bull. Korean Chem. Soc 2000, 21, 662–664. [Google Scholar]
- D’Souza, MJ; Reed, DN; Erdman, KJ; Kevill, DN. Grunwald-Winstein Analysis–Isopropyl Chloroformate Solvolysis Revisited. Int. J. Mol. Sci 2009, 10, 862–879. [Google Scholar]
- Park, KH; Kyong, JB; Kevill, DN. Nucleophilic Substitution Reactions of p-Nitrobenzyl Chloroformate. Bull. Korean Chem. Soc 2000, 21, 1267–1270. [Google Scholar]
- Kyong, JB; Park, B-C; Kim, C-B; Kevill, DN. Rate and Product Studies with Benzyl and p-Nitrobenzyl Chloroformates Under Solvolytic Conditions. J. Org. Chem 2000, 65, 8051–8058. [Google Scholar]
- Kyong, JB; Suk, YJ; Kevill, DN. Solvolysis-Decomposition of 2-Adamantyl Chloroformate: Evidence for Two Reaction Pathways. J. Org. Chem 2003, 68, 3425–3432. [Google Scholar]
- Kevill, DN; Kyong, JB; Weitl, FL. Solvolysis-Decomposition of 1-Adamantyl Chloroformate: Evidence for Ion Pair Return in 1-Adamantyl Chloride Solvolysis. J. Org. Chem 1990, 55, 4304–4311. [Google Scholar]
- Koh, HJ; Kang, SJ; Kevill, DN. Kinetic Studies of the Solvolyses of 2,2,2-Trichloro-1,1-dimethylethyl Chloroformate. Bull. Korean Chem. Soc 2010, 31, 835–839. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Sixty Years of the Grunwald-Winstein Equation: Development and Recent Applications. J. Chem. Res 2008, 2, 61–66. [Google Scholar]
- Grunwald, E; Winstein, S. The Correlation of Solvolysis Rates. J. Am. Chem. Soc 1948, 70, 846–854. [Google Scholar]
- Wells, PR. Linear Free Energy Relationships; Academic Press: New York, NY, USA, 1968; pp. 8–35. [Google Scholar]
- Bentley, TW; Carter, GE. The SN2-SN1 Spectrum. 4. Mechanism for Solvolyses of tert-Butyl Chloride: A Revised Y Scale of Solvent Ionizing Power based on Solvolyses of 1-Adamantyl Chloride. J. Am. Chem. Soc 1982, 104, 5741–5747. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Additional YCl Values and Correlation of the Specific Rates of Solvolysis of tert-Butyl Chloride in Terms of NT and YCl Scales. J. Chem. Res. Synop 1993, 5, 174–175. [Google Scholar]
- Schadt, FL; Bentley, TW; Schleyer, PvR. The SN2-SN1 Spectrum. 2. Quantitative Treatments of Nucleophilic Solvent Assistance. A Scale of Solvent Nucleophilicities. J. Am. Chem. Soc 1976, 98, 7667–7674. [Google Scholar]
- Bentley, TW; Llewellyn, G. YX Scales of Solvent Ionizing Power. Prog. Phys. Org. Chem 1990, 17, 121–158. [Google Scholar]
- Winstein, S; Grunwald, E; Jones, HW. The Correlation of Solvolyses Rates and the Classification of Solvolysis Reactions into Mechanistic Categories. J. Am. Chem. Soc 1951, 73, 2700–2707. [Google Scholar]
- Kevill, DN; Anderson, SW. An Improved Scale of Solvent Nucleophilicity Based on the Solvolysis of the S-Methyldibenzothiophenium Ion. J. Org. Chem 1991, 56, 1845–1850. [Google Scholar]
- Kevill, DN. Development and Uses of Scales of Solvent Nucleophilicity. In Advances in Quantitative Structure-Property Relationships; Charton, M, Ed.; JAI Press: Greenwich, CT, USA, 1996; Volume 1, pp. 81–115. [Google Scholar]
- D’Souza, MJ; Ryu, ZH; Park, B-C; Kevill, DN. Correlation of the Rates of Solvolysis of Acetyl Chloride and α-Substituted Derivatives. Can. J. Chem 2008, 86, 359–367. [Google Scholar]
- Kevill, DN; Koyoshi, F; D’Souza, MJ. Correlation of the Specific Rates of Solvolysis of Aromatic Carbamoyl Chlorides, Chloroformates, Chlorothionoformates, and Chlorodithioformates Revisited. Int. J. Mol. Sci 2007, 8, 346–352. [Google Scholar]
- Queen, A; Nour, TA. Kinetics and Mechanism of the Acetate Catalyzed Hydrolysis of 4-Methoxyphenyl Chloroformate and 4-Methoxyphenyl Fluoroformate in Aqueous Dioxane. Evidence for Rate-Determining Attack of Acetate Ions on an Intermediate Mixed Anhydride. J. Chem. Soc. Perkin Trans 2 1976, 8, 935–939. [Google Scholar]
- Koo, IS; Yang, K; Kang, K; Lee, I. Transition-State Variation in the Solvolyses of para-Substituted Phenyl Chloroformates in Alcohol-Water Mixtures. Bull. Korean Chem. Soc 1998, 19, 968–973. [Google Scholar]
- Koo, IS; Yang, K; Kang, K; Oh, HK; Lee, I. Stoichiometric Solvation Effects. Product-Rate Correlation for the Solvolyses of Phenyl Chloroformate in Alcohol-Water Mixtures. Bull. Korean Chem. Soc 1996, 17, 520–524. [Google Scholar]
- Song, BD; Jencks, WP. Mechanism of Solvolysis of Substituted Benzoyl Halides. J. Am. Chem. Soc 1989, 111, 8470–8479. [Google Scholar]
- Bentley, TW; Harris, HC. Separation of Mass Law and Solvent Effects in Kinetics of Solvolyses of p-Nitrobenzoyl Chloride in Aqueous Binary Mixtures. J. Org. Chem 1988, 53, 724–728. [Google Scholar]
- Bentley, TW; Jones, RO. Stiochiometric Solvent Effects. Part I. New Equations Relating Product Selectivities to Alcohol-Water Solvent Compositions for Hydrolyses of p-Nitrobenzoyl Chloride. J. Chem. Soc. Perkin Trans 2 1993, 9, 2351–2357. [Google Scholar]
- Stewart, MD; Tran, HV; Schmid, GM; Stachowiak, TB; Becker, DJ; Willson, CG. Acid Catalyst Mobility in Resist Resins. J. Vac. Sci. Technol. B 2002, 20, 2946–2952. [Google Scholar]
- Kanai, M; Kato, N; Ichikawa, E; Shibasaki, M. Power of Cooperativity: Lewis Acid-Lewis Base Bifunctional Asymmetric Catalysis. Chem. Inform 2005, 41, 1491–1508. [Google Scholar]
- Dostrovsky, I; Hughes, ED; Ingold, CK. Mechanism of Substitution as a Saturated Carbon Atom. XXXII. The Role of Hindrance. G. Magnitude of Steric Effects, Range of Occurrence of Steric and Polar Effects, and Place of Wagner Rearrangement in Nucleophilic Substitution and Elimination. J. Chem. Soc 1946, 1, 173–194. [Google Scholar]
- Karabatsos, GJ; Orzech, CE; Meyerson, S. Carbonium Ion Rearrangements. VI. Mechanism of the Rearrangement of Neopentyl Compounds. J. Am. Chem. Soc 1964, 86, 1994–1997. [Google Scholar]
- Bentley, TW; Koo, IS. Trends in Selectivity. Evidence from Rates and Products for Simultaneous Reaction Channels in Solvolyses of Benzoyl Chloride and Substituted Derivatives. J. Chem. Soc. Perkin Trans 2 1989, 10, 1385–1392. [Google Scholar]
- Abraham, MH; Grellier, PL; Abboud, J-LM; Doherty, RM; Taft, RW. Solvent Effects in Organic Chemistry—Recent Developments. Can. J. Chem 1998, 66, 2673–2686. [Google Scholar]
- Fry, JL; Lancelot, CJ; Lam, LKM; Harris, JM; Bingham, RC; Raber, DJ; Hall, RE; Schleyer, PVR. Solvent Assistance of Secondary Substrates. I. The 2-Adamantyl System, a Standard for Limiting Solvolysis in a Secondary Substrate. J. Am. Chem. Soc 1970, 92, 2538–2540. [Google Scholar]
- Frost, AA; Pearson, RG. Kinetics and Mechanism-a Study of Homogeneous Chemical Reactions, 2nd ed; Wiley: New York, NY, USA, 1961; pp. 49–50. [Google Scholar]
- Kevill, DN; Abduljaber, MH. Correlation of the Rates of Solvolysis of Cyclopropylcarbinyl and Cyclobutyl Bromides Using the Extended Grunwald-Winstein Equation. J. Org. Chem 2000, 65, 2548–2554. [Google Scholar]




| Solvent (%) a | 1 at 45.0 °C; 105 k, s−1 b | NT c | YCl d |
|---|---|---|---|
| 100% MeOH | 47.9 ± 0.3 | 0.17 | −1.2 |
| 90% MeOH | 77.6 ± 0.6 | −0.01 | −0.20 |
| 80% MeOH | 91.3 ± 0.6 | −0.06 | 0.67 |
| 100% EtOH | 16.3 ± 0.3 | 0.37 | −2.50 |
| 90% EtOH | 27.7 ± 0.1 | 0.16 | −0.90 |
| 80% EtOH | 34.3 ± 0.1 | 0.00 | 0.00 |
| 90% Acetone | 0.804 ± 0.005 | −0.35 | −2.39 |
| 80% Acetone | 2.99 ± 0.04 | −0.37 | −0.80 |
| 70% Acetone | 7.81 ± 0.01 | −0.42 | 0.17 |
| 60% Acetone | 11.7 ± 0.1 | −0.52 | 1.00 |
| 97% TFE (w/w) | 0.697 ± 0.002 | −3.30 | 2.83 |
| 90% TFE (w/w) | 1.14 ± 0.01 | −2.55 | 2.85 |
| 70% TFE (w/w) | 4.07 ± 0.02 | −1.98 | 2.96 |
| 50% TFE (w/w) | 7.89 ± 0.07 | −1.73 | 3.16 |
| 80T-20E | 0.455 ± 0.002 | −1.76 | 1.89 |
| 40T-60E | 4.44 ± 0.08 | −0.34 | −0.48 |
| 20T-80E | 11.3 ± 0.1 | 0.08 | −1.42 |
| 97% HFIP (w/w) | 14.5 ± 0.1 | −5.26 | 5.17 |
| 90% HFIP (w/w) | 8.48 ± 0.01 | −3.84 | 4.41 |
| 70% HFIP (w/w) | 4.09 ± 0.01 | −2.94 | 3.83 |
| 50% HFIP (w/w) | 5.48 ± 0.02 | −2.49 | 3.80 |
| Substrate | n a | l b | m b | c b | l/m | R c | F d | Mechanism |
|---|---|---|---|---|---|---|---|---|
| neoPOCOCl | 13 | 1.76 ± 0.14 | 0.48 ± 0.06 | 0.14 ± 0.08 | 3.67 | 0.977 | 226 | A-E e |
| 8 | 0.36 ± 0.10 | 0.81 ± 0.14 | −2.79 ± 0.33 | 0.44 | 0.938 | 18 | I f | |
| n-PrOCOCl g | 22 | 1.57 ± 0.12 | 0.56 ± 0.06 | 0.15 ± 0.08 | 2.79 | 0.947 | 83 | A-E |
| 6 | 0.40 ± 0.12 | 0.64 ± 0.13 | −2.45 ± 0.27 | 0.63 | 0.942 | 11 | I | |
| 8 h | 0.66 ± 0.14 | 0.91 ± 0.19 | −2.61 ± 0.44 | 0.73 | 0.912 | 12 | I | |
| EtOCOCl g | 28 | 1.56 ± 0.09 | 0.55 ± 0.03 | 0.19 ± 0.24 | 2.84 | 0.967 | 179 | A-E |
| 7 | 0.69 ± 0.13 | 0.82 ± 0.16 | −2.40 ± 0.27 | 0.84 | 0.946 | 17 | I | |
| MeOCOCl g | 19 | 1.59 ± 0.09 | 0.58 ± 0.05 | 0.16 ± 0.07 | 2.74 | 0.977 | 171 | A-E |
| PhOCOCl g | 49 | 1.66 ± 0.05 | 0.56 ± 0.03 | 0.15 ± 0.07 | 2.95 | 0.980 | 568 | A-E |
| BzOCOCl g | 11 | 0.25 ± 0.05 | 0.66 ± 0.06 | −2.05± 0.11 | 0.38 | 0.976 | 80 | I |
| i-PrOCOCl g | 9 | 1.35 ± 0.22 | 0.40 ± 0.05 | 0.18 ± 0.07 | 3.38 | 0.960 | 35 | A-E |
| 16 | 0.28 ± 0.04 | 0.59 ± 0.04 | −0.32 ± 0.06 | 0.47 | 0.982 | 176 | I | |
| 2-AdOCOCl g | 19 | 0.03 ± 0.07 | 0.48 ± 0.04 | −0.10 ± 0.09 | 0.06 | 0.971 | 130 | I |
| 1-AdOCOCl g | 11 | 0.08 ± 0.20 | 0.59 ± 0.05 | 0.06 ± 0.08 | 0.14 | 0.985 | 133 | I |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
D’Souza, M.J.; Carter, S.E.; Kevill, D.N. Correlation of the Rates of Solvolysis of Neopentyl Chloroformate—A Recommended Protecting Agent. Int. J. Mol. Sci. 2011, 12, 1161-1174. https://doi.org/10.3390/ijms12021161
D’Souza MJ, Carter SE, Kevill DN. Correlation of the Rates of Solvolysis of Neopentyl Chloroformate—A Recommended Protecting Agent. International Journal of Molecular Sciences. 2011; 12(2):1161-1174. https://doi.org/10.3390/ijms12021161
Chicago/Turabian StyleD’Souza, Malcolm J., Shannon E. Carter, and Dennis N. Kevill. 2011. "Correlation of the Rates of Solvolysis of Neopentyl Chloroformate—A Recommended Protecting Agent" International Journal of Molecular Sciences 12, no. 2: 1161-1174. https://doi.org/10.3390/ijms12021161
APA StyleD’Souza, M. J., Carter, S. E., & Kevill, D. N. (2011). Correlation of the Rates of Solvolysis of Neopentyl Chloroformate—A Recommended Protecting Agent. International Journal of Molecular Sciences, 12(2), 1161-1174. https://doi.org/10.3390/ijms12021161




