Chiral Vibrational Structures of Proteins at Interfaces Probed by Sum Frequency Generation Spectroscopy
Abstract
:1. Introduction
2. General Principles of Chiral Sum Frequency Generation Spectroscopy
2.1. SFG Method
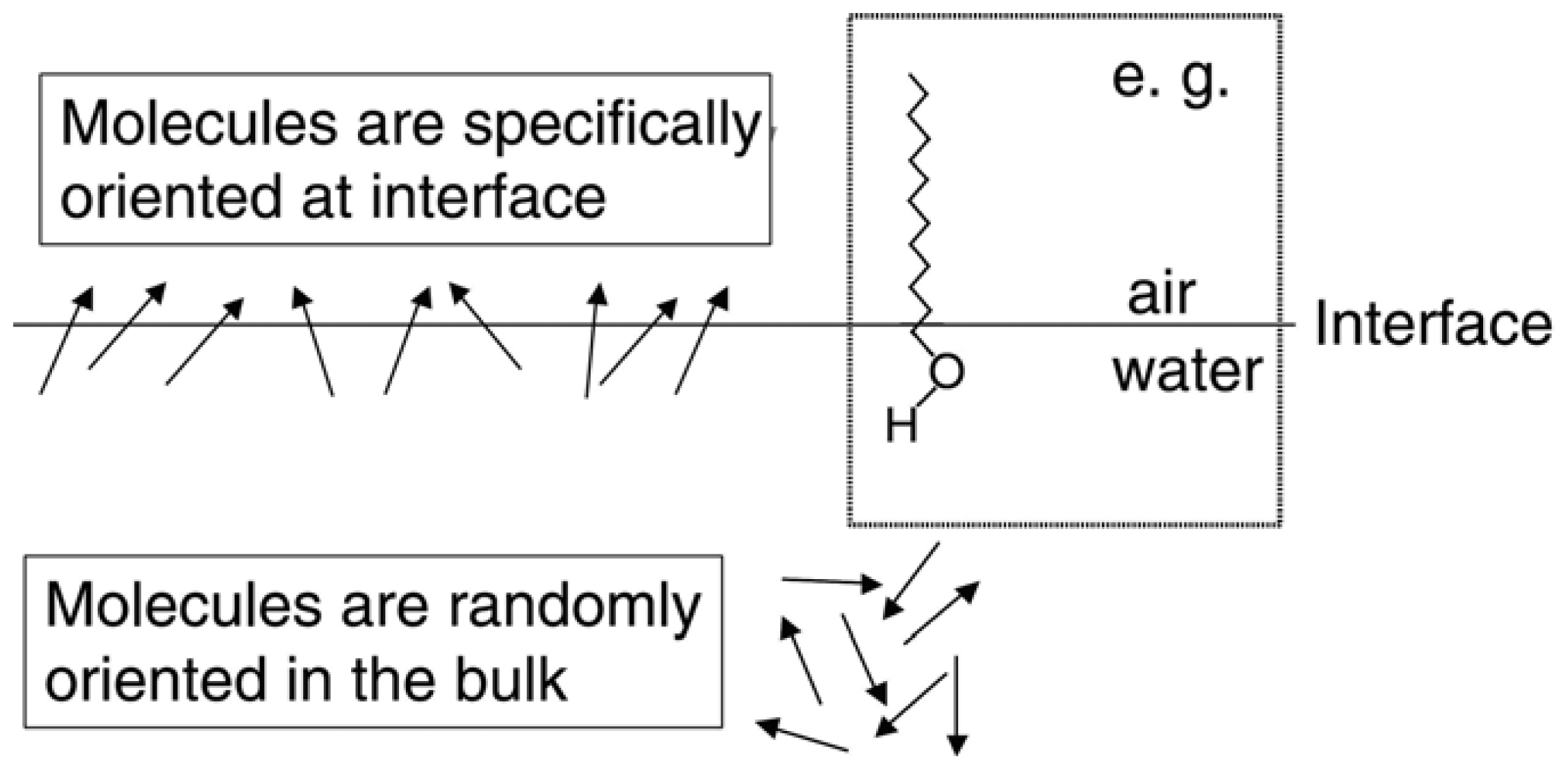
2.2. Chiral SFG
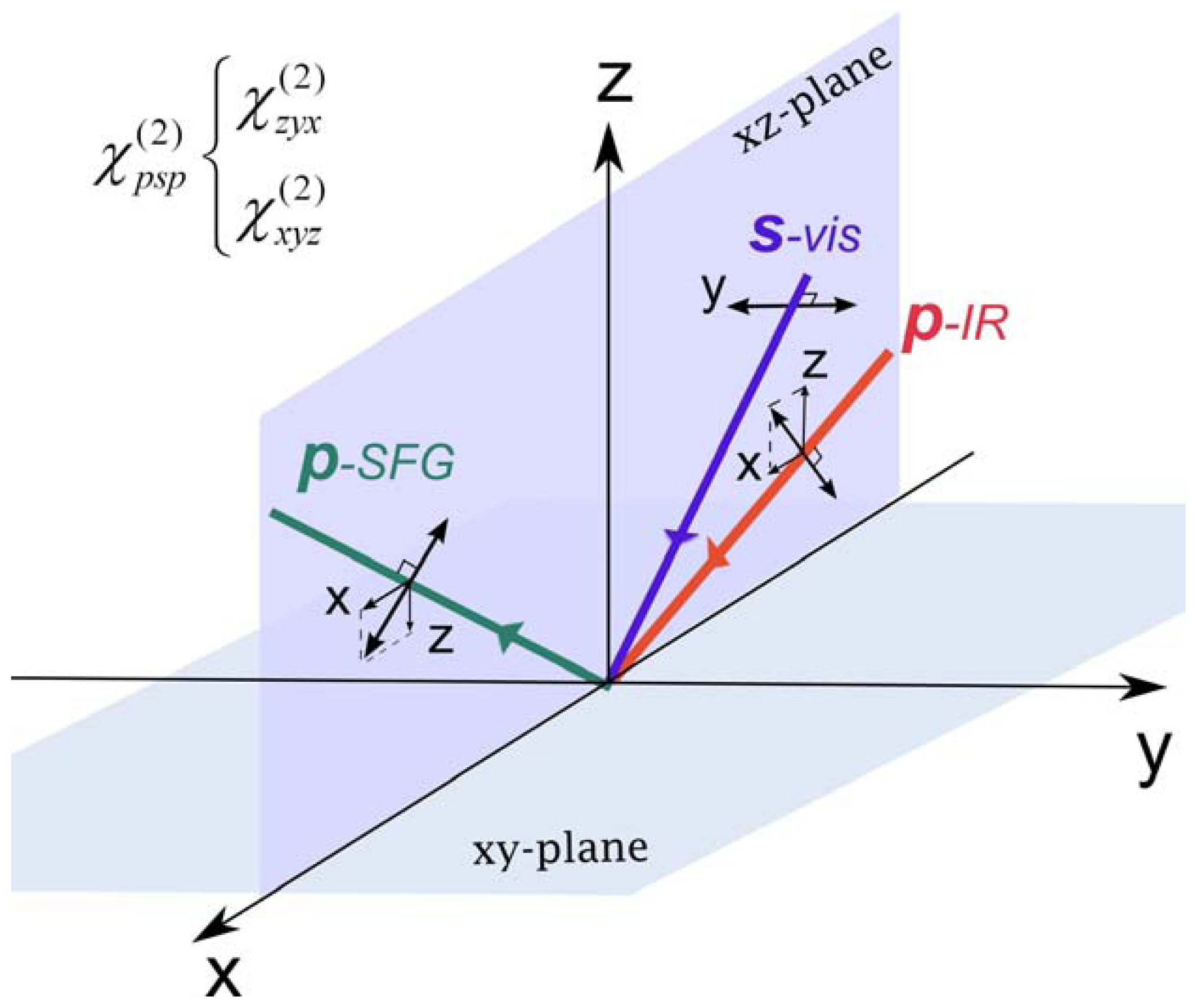
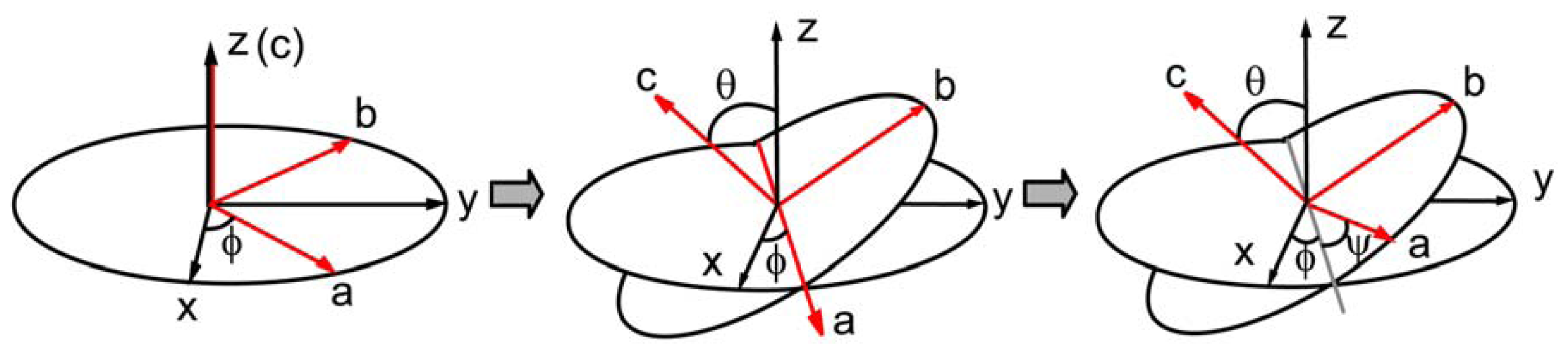
2.3. Hyperpolarizability and Molecular Orientation
2.4. The Origin of Chiral SFG Response
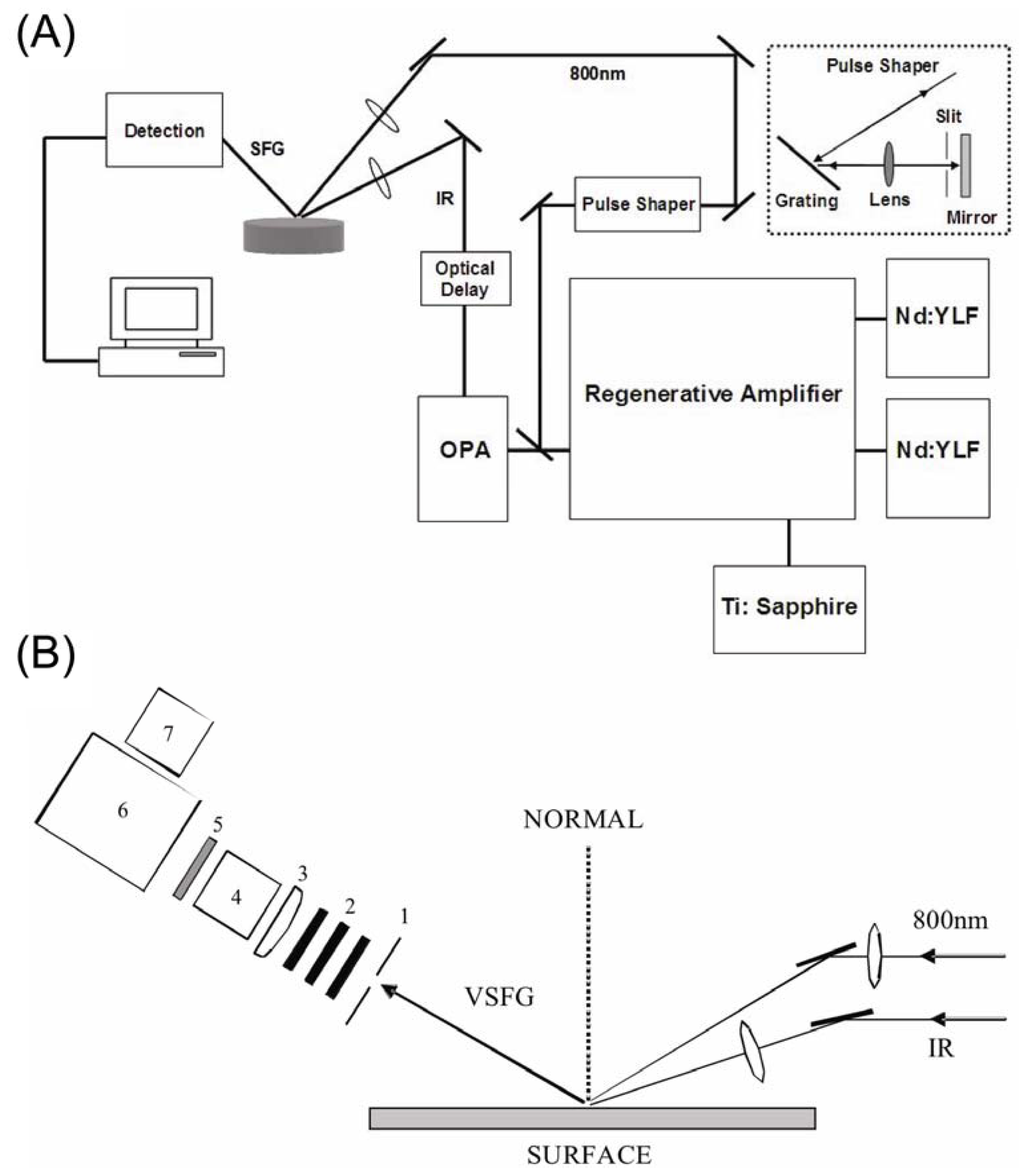
3. Experimental Setup
4. Experimental Observations and Biological Applications of Chiral SFG
4.1. Chiral SFG with Electronic Resonance
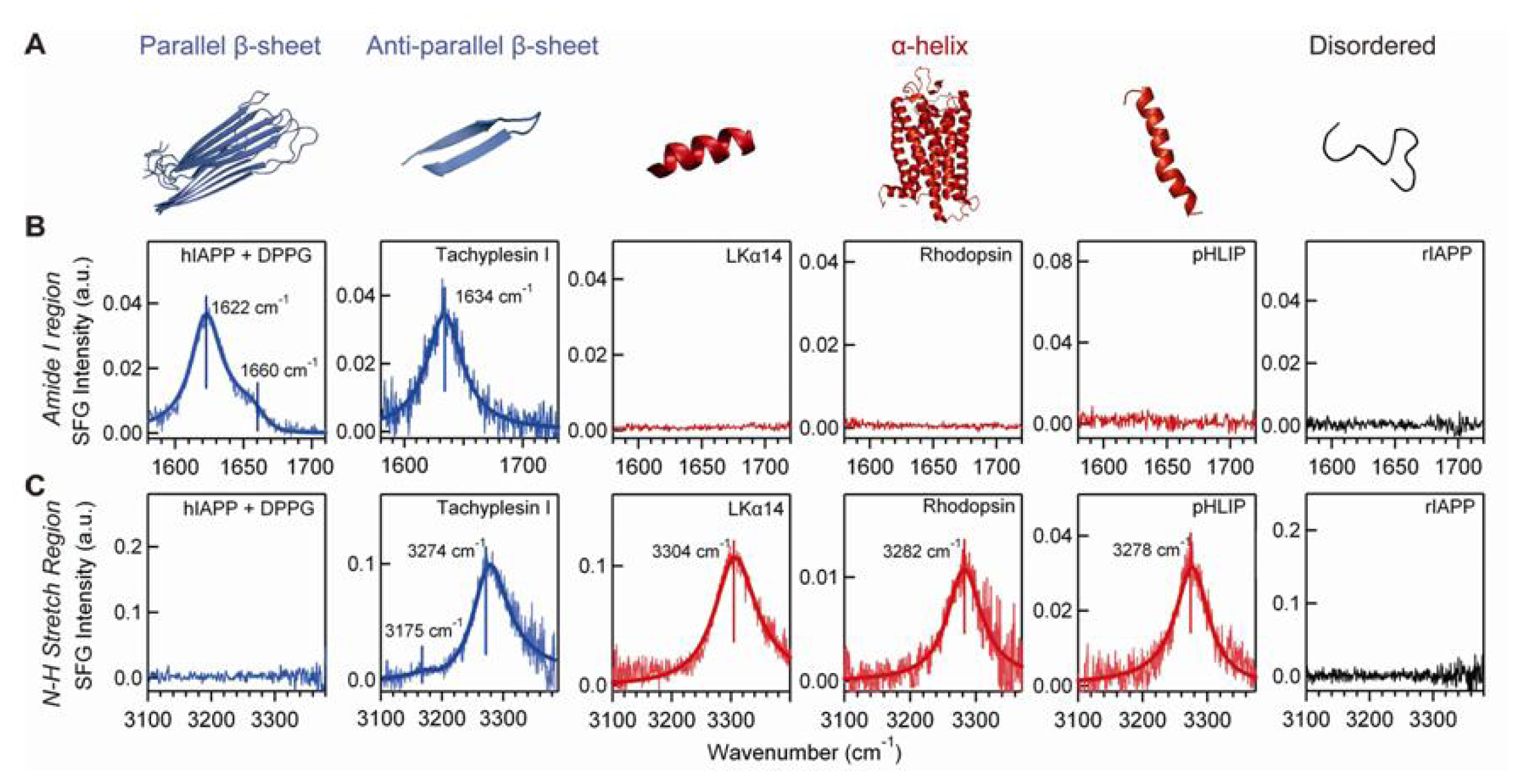
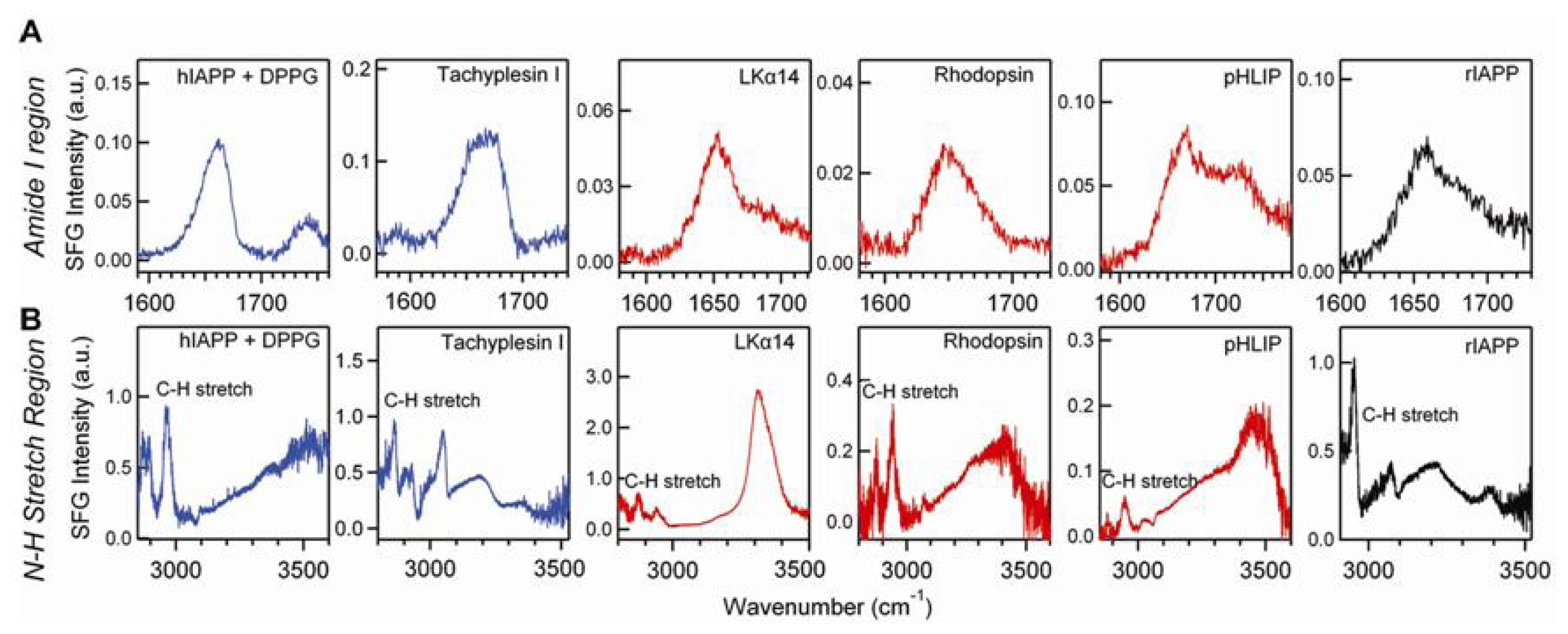
4.2. Chiral SFG for Probing Biomolecules at Interfaces
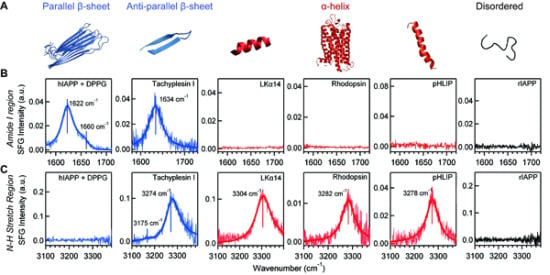
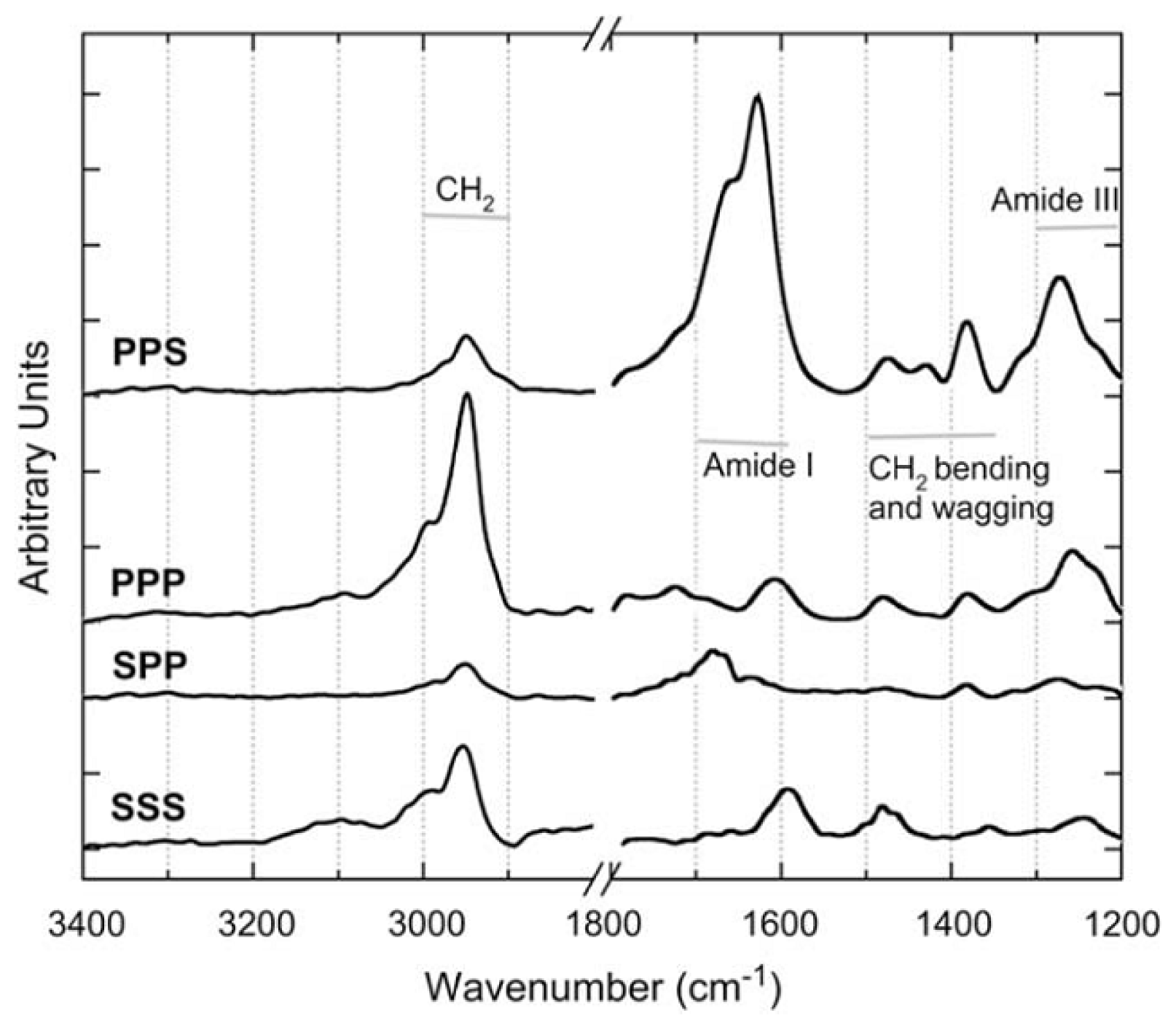
4.3. Chiral SFG for Characterization Protein Secondary Structures
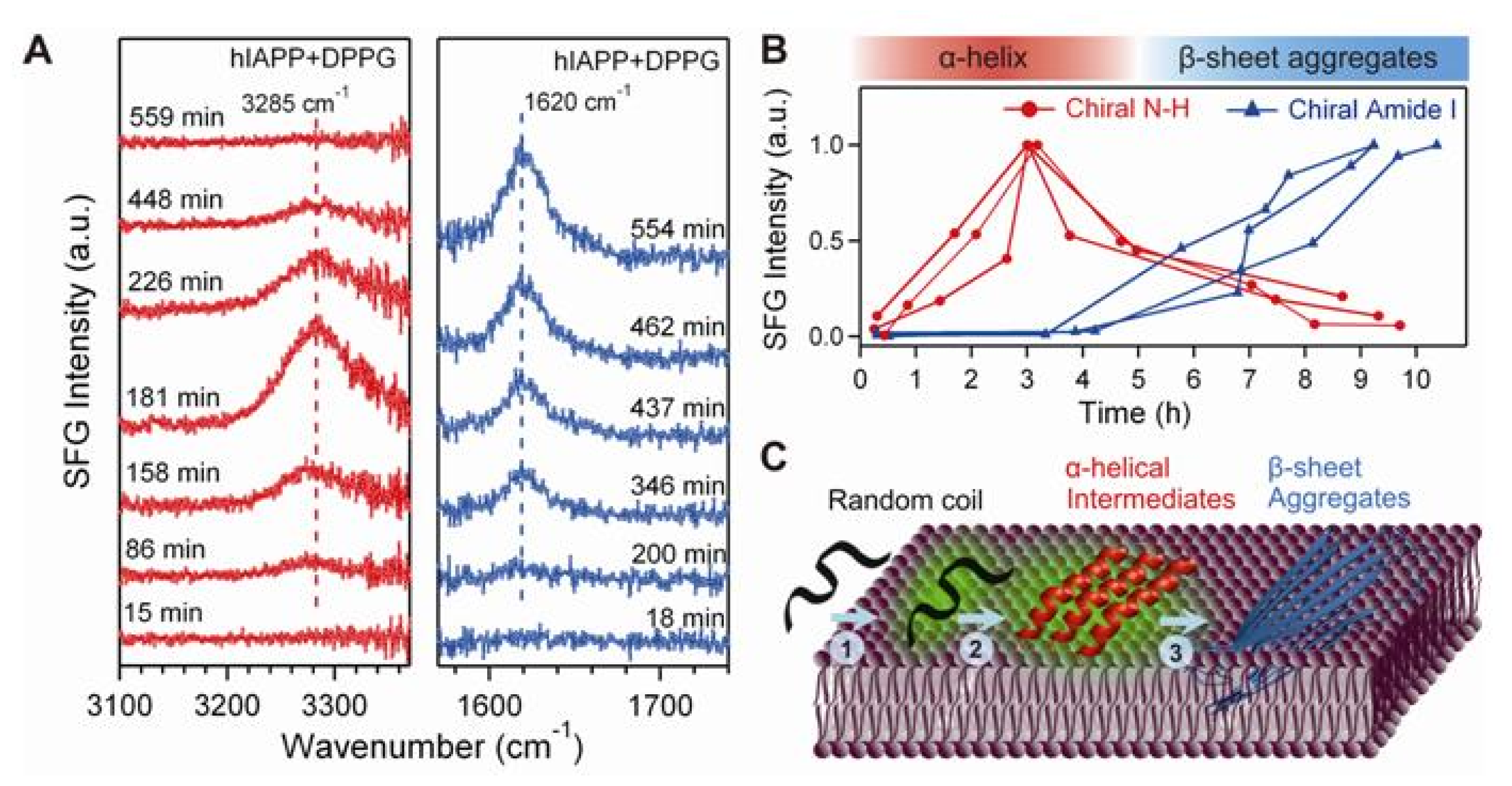
4.4. Chiral SFG for Monitoring Protein Folding at Interfaces
5. Advantages and Prospective of Chiral SFG
6. Conclusions
Acknowledgments
References
- Greenfie, N.; Fasman, G.D. Computed circular dichroism spectra for the evaluation of protein conformation. Biochemistry 1969, 8, 4108–4116. [Google Scholar]
- Chen, Y.H.; Yang, J.T.; Chau, K.H. Determination of the helix and beta form of proteins in aqueous solution by circular dichroism. Biochemistry 1974, 13, 3350–3359. [Google Scholar]
- Garnier, J.; Osguthorpe, D.J.; Robson, B. Analysis of the accuracy and implications of simple methods for predicting the secondary structure of globular proteins. J. Mol. Biol 1978, 120, 97–120. [Google Scholar]
- Chen, Y.H.; Yang, J.T.; Martinez, H.M. Determination of the secondary structures of proteins by circular dichroism and optical rotatory dispersion. Biochemistry 1972, 11, 4120–4131. [Google Scholar]
- Urry, D.W. Protein conformation in biomembranes: Optical rotation and absorption of membrane suspensions. Biochim. Biophys. Acta 1972, 265, 115–168. [Google Scholar]
- Polavarapu, P.L. Optical rotation: Recent advances in determining the absolute configuration. Chirality 2002, 14, 768–781. [Google Scholar]
- Nafie, L.A. Infrared and Raman vibrational optical activity: Theoretical and experimental aspects. Annu. Rev. Phys. Chem 1997, 48, 357–386. [Google Scholar]
- Barron, L.D.; Hecht, L.; Blanch, E.W.; Bell, A.F. Solution structure and dynamics of biomolecules from Raman optical activity. Prog. Biophys. Mol. Biol 2000, 73, 1–49. [Google Scholar]
- Barron, L.D.; Hecht, L.; Bell, A.F. Raman optical activity: An incisive new probe of the structure and dynamics of biomolecules. Sci. Prog 1998, 81, 17–34. [Google Scholar]
- Bjorling, S.C.; Zhang, C.F.; Farrens, D.L.; Song, P.S.; Kliger, D.S. Time-resolved circulardichroism of native oat phytochrome photointermediates. J. Am. Chem. Soc 1992, 114, 4581–4588. [Google Scholar]
- Goldbeck, R.A.; Kliger, D.S. Nanosecond time-resolved absorption and polarization dichroism spectroscopies. Metallobiochemistry Part C 1993, 226, 147–177. [Google Scholar]
- Chen, E.F.; Wood, M.J.; Fink, A.L.; Kliger, D.S. Time-resolved circular dichroism studies of protein folding intermediates of cytochrome c. Biochemistry 1998, 37, 5589–5598. [Google Scholar]
- Goldbeck, R.A.; Thomas, Y.G.; Chen, E.F.; Esquerra, R.M.; Kliger, D.S. Multiple pathways on a protein-folding energy landscape: Kinetic evidence. Proc. Natl. Acad. Sci. USA 1999, 96, 2782–2787. [Google Scholar]
- Nafie, L.A.; Keiderling, T.A.; Stephens, P.J. Vibrational circular dichroism. J. Am. Chem. Soc 1976, 98, 2715–2723. [Google Scholar]
- Diem, M.; Polavarapu, P.L.; Oboodi, M.; Nafie, L.A. Vibrational circular dichroism in amino acids and peptides. 4. Vibrational analysis, assignments, and solution-phase Raman spectra of deuterated isotopomers of alanine. J. Am. Chem. Soc 1982, 104, 3329–3336. [Google Scholar]
- Stephens, P.J.; Lowe, M.A. Vibrational circular dichroism. Annu. Rev. Phys. Chem 1985, 36, 213–241. [Google Scholar]
- Toro, C.; De Boni, L.; Lin, N.; Santoro, F.; Rizzo, A.; Hernandez, F.E. Two-photon absorption circular dichroism: A new twist in nonlinear spectroscopy. Chemistry 2010, 16, 3504–3509. [Google Scholar]
- Hernandez, F.E.; Rizzo, A. Two-photon polarization dependent spectroscopy in chirality: A novel experimental-Theoretical approach to study optically active systems. Molecules 2011, 16, 3315–3337. [Google Scholar]
- Jansik, B.; Rizzo, A.; Agren, H. Ab initio study of the two-photon circular dichroism in chiral natural amino acids. J. Phys. Chem. B 2007, 111, 446–460. [Google Scholar]
- Petralli-Mallow, T.; Wong, T.M.; Byers, J.D.; Yee, H.I.; Hicks, J.M. Circular dichroism spectroscopy at interfaces: A surface second harmonic generation study. J. Phys. Chem 1993, 97, 1383–1388. [Google Scholar]
- Byers, J.D.; Yee, H.I.; Hicks, J.M. A 2nd-harmonic generation analog of optical-rotatory dispersion for the study of chiral monolayers. J. Chem. Phys 1994, 101, 6233–6241. [Google Scholar]
- Byers, J.D.; Hicks, J.M. Electronic spectral effects on chiral surface second harmonic generation. Chem. Phys. Lett 1994, 231, 216–224. [Google Scholar]
- Kauranen, M. Second-harmonic generation from chiral surfaces. J. Chem. Phys 1994, 101. [Google Scholar] [CrossRef]
- Maki, J.J.; Kauranen, M.; Persoons, A. Surface second-harmonic generation from chiral materials. Phys. Rev. B 1995, 51. [Google Scholar] [CrossRef]
- Verbiest, T.; Kauranen, M.; Persoons, A.; Ikonen, M.; Kurkela, J.; Lemmetyinen, H. Nonlinear optical activity and biomolecular chirality. J. Am. Chem. Soc 1994, 116, 9203–9205. [Google Scholar]
- Xu, Y.-Y.; Rao, Y.; Zheng, D.-S.; Guo, Y.; Liu, M.-H.; Wang, H.-F. Inhomogeneous and spontaneous formation of chirality in the Langmuir monolayer of achiral molecules at the air/water interface probed by in situ surface second harmonic generation linear dichroism. J. Phys. Chem. C 2009, 113, 4088–4098. [Google Scholar]
- Burke, B.J.; Moad, A.J.; Polizzi, M.A.; Simpson, G.J. Experimental confirmation of the importance of orientation in the anomalous chiral sensitivity of second harmonic generation. J. Am. Chem. Soc 2003, 125, 9111–9115. [Google Scholar]
- Simpson, G.J. Structural origins of circular dichroism in surface second harmonic generation. J. Chem. Phys 2002, 117, 3398–3410. [Google Scholar]
- Huttunen, M.J.; Virkki, M.; Erkintalo, M.; Vuorimaa, E.; Efimov, A.; Lemmetyinen, H.; Kauranen, M. Absolute probe of surface chirality based on focused circularly polarized light. J. Phys. Chem. Lett 2010, 1, 1826–1829. [Google Scholar]
- Fujiwara, K.; Monjushiro, H.; Watarai, H. Non-linear optical activity of porphyrin aggregate at the liquid/liquid interface. Chem. Phys. Lett 2004, 394, 349–353. [Google Scholar]
- Mitchell, S.A.; McAloney, R.A.; Moffatt, D.; Mora-Diez, N.; Zgierski, M.Z. Second-harmonic generation optical activity of a polypeptide alpha-helix at the air/water interface. J. Chem. Phys 2005, 122. [Google Scholar] [CrossRef]
- Belkin, M.A.; Kulakov, T.A.; Ernst, K.H.; Yan, L.; Shen, Y.R. Sum-frequency vibrational spectroscopy on chiral liquids: A novel technique to probe molecular chirality. Phys. Rev. Lett 2000, 85, 4474–4477. [Google Scholar]
- Wang, J.; Chen, X.Y.; Clarke, M.L.; Chen, Z. Detection of chiral sum frequency generation vibrational spectra of proteins and peptides at interfaces in situ. Proc. Natl. Acad. Sci. USA 2005, 102, 4978–4983. [Google Scholar]
- Wei, F.; Xu, Y.Y.; Guo, Y.; Liu, S.L.; Wang, H.F. Quantitative surface chirality detection with sum frequency generation vibrational spectroscopy: Twin polarization angle approach. Chin. J. Chem. Phys 2009, 22, 592–600. [Google Scholar]
- Fu, L.; Liu, J.; Yan, E.C.Y. Chiral sum frequency generation spectroscopy for characterizing protein secondary structures at interfaces. J. Am. Chem. Soc 2011, 133, 8094–8097. [Google Scholar]
- Stokes, G.Y.; Gibbs-Davis, J.M.; Boman, F.C.; Stepp, B.R.; Condie, A.G.; Nguyen, S.T.; Geiger, F.M. Making “ Sense” of DNA. J. Am. Chem. Soc 2007, 129, 7492–7493. [Google Scholar]
- Fu, L.; Ma, G.; Yan, E.C.Y. In situ misfolding of human islet amyloid polypeptide at interfaces probed by vibrational sum frequency generation. J. Am. Chem. Soc 2010, 132, 5405–5412. [Google Scholar]
- Nguyen, K.T.; King, J.T.; Chen, Z. Orientation determination of interfacial beta-sheet structures in situ. J. Phys. Chem. B 2010, 114, 8291–8300. [Google Scholar]
- Ostroverkhov, V.; Singer, K.D.; Petschek, R.G. Second-harmonic generation in nonpolar chiral materials: Relationship between molecular and macroscopic properties. J. Opt. Soc. Am. B 2001, 18, 1858–1865. [Google Scholar]
- Ostroverkhov, V.; Ostroverkhova, O.; Petschek, R.G.; Singer, K.D.; Sukhomlinova, L.; Twieg, R.J. Prospects for chiral nonlinear optical media. IEEE J. Sel. Top. Quant 2001, 7, 781–792. [Google Scholar]
- Campagnola, P.J.; Wei, M.-D.; Lewis, A.; Loew, L.M. High-resolution nonlinear optical imaging of live cells by second harmonic generation. Biophys. J 1999, 77, 3341–3349. [Google Scholar]
- Kriech, M.A.; Conboy, J.C. Imaging chirality with surface second harmonic generation microscopy. J. Am. Chem. Soc 2005, 127, 2834–2835. [Google Scholar]
- Yan, P.; Millard, A.C.; Wei, M.; Loew, L.M. Unique contrast patterns from resonance-enhanced chiral SHG of cell membranes. J. Am. Chem. Soc 2006, 128, 11030–11031. [Google Scholar]
- Shen, Y.R. Surface-properties probed by 2nd-harmonic and sum-frequency generation. Nature 1989, 337, 519–525. [Google Scholar]
- Eisenthal, K.B. Liquid interfaces probed by second-harmonic and sum-frequency spectroscopy. Chem. Rev 1996, 96, 1343–1360. [Google Scholar]
- Richmond, G.L. Molecular bonding and interactions at aqueous surfaces as probed by vibrational sum frequency spectroscopy. Chem. Rev 2002, 102, 2693–2724. [Google Scholar]
- Boyed, R.W. Nolinear Optics; Academic Press: New York, NY, USA, 2003. [Google Scholar]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Wang, H.-F.; Gan, W.; Lu, R.; Rao, Y.; Wu, B.-H. Quantitative spectral and orientational analysis in surface sum frequency generation vibrational spectroscopy (SFG-VS). Int. Rev. Phys. Chem 2005, 24, 191–256. [Google Scholar]
- Moad, A.J.; Simpson, G.J. A unified treatment of selection rules and symmetry relations for sum-frequency and second harmonic spectroscopies. J. Phys. Chem. B 2004, 108, 3548–3562. [Google Scholar]
- Marsh, D. Dichroic ratios in polarized Fourier transform infrared for nonaxial symmetry of beta-sheet structures. Biophys. J 1997, 72, 2710–2718. [Google Scholar]
- Tsuboi, M.; Ikeda, T.; Ueda, T. Raman microscopy of a small uniaxial crystal: Tetragonal aspartame. J. Raman Spectrosc 1991, 22, 619–626. [Google Scholar]
- Perry, J.M.; Moad, A.J.; Begue, N.J.; Wampler, R.D.; Simpson, G.J. Electronic and vibrational second-order nonlinear optical properties of protein secondary structural motifs. J. Phys. Chem. B 2005, 109, 20009–20026. [Google Scholar]
- Belkin, M.A.; Shen, Y.R. Non-linear optical spectroscopy as a novel probe for molecular chirality. Int. Rev. Phys. Chem 2005, 24, 257–299. [Google Scholar]
- Zheng, R.-H.; Chen, D.-M.; Wei, W.-M.; He, T.-J.; Liu, F.-C. Theoretical investigation of doubly resonant IR-UV sum-frequency vibrational spectroscopy of binaphthol chiral solution. J. Phys. Chem. B 2006, 110, 4480–4486. [Google Scholar]
- Haupert, L.M.; Simpson, G.J. Chirality in nonlinear optics. Annu. Rev. Phys. Chem 2009, 60, 345–365. [Google Scholar]
- Simpson, G.J.; Perry, J.M.; Ashmore-Good, C.L. Molecular and surface hyperpolarizability of oriented chromophores of low symmetry. Phys. Rev. B 2002, 66, 165437. [Google Scholar]
- Simpson, G.J. Molecular origins of the remarkable chiral sensitivity of second-order nonlinear optics. Chemphyschem 2004, 5, 1301–1310. [Google Scholar]
- Hore, D.K.; King, J.L.; Moore, F.G.; Alavi, D.S.; Hamamoto, M.Y.; Richmond, G.L. Ti: Sapphire-based picosecond visible-infrared sum-frequency spectroscopy from 9003100 cm−1. Appl. Spectrosc 2004, 58, 1377–1384. [Google Scholar]
- Schrödle, S.; Richmond, G.L. Sequential wavelength tuning: Dynamics at interfaces investigated by vibrational sum-frequency spectroscopy. Appl. Spectrosc 2008, 62, 389–393. [Google Scholar]
- Richter, L.J.; Petralli-Mallow, T.P.; Stephenson, J.C. Vibrationally resolved sum-frequency generation with broad-bandwidth infrared pulses. Opt. Lett 1998, 23, 1594–1596. [Google Scholar]
- Hommel, E.L.; Ma, G.; Alle, H.C. Broadband vibrational sum frequency generation spectroscopy of a liquid surface. Anal. Sci 2001, 17, 1325–1329. [Google Scholar]
- Ma, G.; Allen, H.C. Surface studies of aqueous methanol solutions by vibrational broad bandwidth sum frequency generation spectroscopy. J. Phys. Chem. B 2003, 107, 6343–6349. [Google Scholar]
- Verreault, D.; Kurz, V.; Howell, C.; Koelsch, P. Sample cells for probing solid/liquid interfaces with broadband sum-frequency-generation spectroscopy. Rev. Sci. Instrum 2010, 81, 063111. [Google Scholar]
- Ma, G.; Liu, J.; Fu, L.; Yan, E.C.Y. Probing water and biomolecules at the air-water interface with a broad bandwidth vibrational sum frequency generation spectrometer from 3800 to 900 cm−1. Appl. Spectrosc 2009, 63, 528–537. [Google Scholar]
- Lagutchev, A.; Hambir, S.A.; Dlott, D.D. Nonresonant background suppression in broadband vibrational sum-frequency generation spectroscopy. J. Phys. Chem. C 2007, 111, 13645–13647. [Google Scholar]
- Stiopkin, I.V.; Jayathilake, H.D.; Bordenyuk, A.N.; Benderskii, A.V. Heterodyne-detected vibrational sum frequency generation spectroscopy. J. Am. Chem. Soc 2008, 130, 2271–2275. [Google Scholar]
- Stiopkin, I.V.; Weeraman, C.; Pieniazek, P.A.; Shalhout, F.Y.; Skinner, J.L.; Benderskii, A.V. Hydrogen bonding at the water surface revealed by isotopic dilution spectroscopy. Nature 2011, 474, 192–195. [Google Scholar]
- Eftekhari-Bafrooei, A.; Borguet, E. Effect of hydrogen-bond strength on the vibrational relaxation of interfacial water. J. Am. Chem. Soc 2010, 132, 3756–3761. [Google Scholar]
- Laaser, J.E.; Xiong, W.; Zanni, M.T. Time-Domain SFG spectroscopy using mid-IR pulse shaping: Practical and intrinsic advantages. J. Phys. Chem. B 2011, 115, 2536–2546. [Google Scholar]
- Ji, N.; Shen, Y.R. A novel spectroscopic probe for molecular chirality. Chirality 2006, 18, 146–158. [Google Scholar]
- Ji, N.; Ostroverkhov, V.; Belkin, M.; Shiu, Y.-J.; Shen, Y.-R. Toward chiral sum-frequency spectroscopy. J. Am. Chem. Soc 2006, 128, 8845–8848. [Google Scholar]
- Belkin, M.A.; Han, S.H.; Wei, X.; Shen, Y.R. Sum-frequency generation in chiral liquids near electronic resonance. Phys. Rev. Lett 2001, 87, 113001. [Google Scholar]
- Nagahara, T.; Kisoda, K.; Harima, H.; Aida, M.; Ishibashi, T.-A. Chiral sum frequency spectroscopy of thin films of porphyrin J-aggregates. J. Phys. Chem. B 2009, 113, 5098–5103. [Google Scholar]
- Busson, B.; Tadjeddine, A. Chiral specificity of doubly resonant sum-frequency generation in an anisotropic thin film. J. Phys. Chem. C 2008, 112, 11813–11821. [Google Scholar]
- Rocha-Mendoza, I.; Yankelevich, D.R.; Wang, M.; Reiser, K.M.; Frank, C.W.; Knoesen, A. Sum frequency vibrational spectroscopy: The molecular origins of the optical second-order nonlinearity of collagen. Biophys. J 2007, 93, 4433–4444. [Google Scholar]
- Walter, S.R.; Geiger, F.M. DNA on stage: Showcasing oligonucleotides at surfaces and interfaces with second harmonic and vibrational sum frequency generation. J. Phys. Chem. Lett 2009, 1, 9–15. [Google Scholar]
- Lopes, D.H.J.; Meister, A.; Gohlke, A.; Hauser, A.; Blume, A.; Winter, R. Mechanism of islet amyloid polypeptide fibrillation at lipid interfaces studied by infrared reflection absorption spectroscopy. Biophys. J 2007, 93, 3132–3141. [Google Scholar]
- Jayasinghe, S.A.; Langen, R. Membrane interaction of islet amyloid polypeptide. BBA-Biomembranes 2007, 1768, 2002–2009. [Google Scholar]
- Knight, J.D.; Miranker, A.D. Phospholipid catalysis of diabetic amyloid assembly. J. Mol. Chem 2004, 341, 1175–1187. [Google Scholar]
- Matsuzaki, K.; Nakayama, M.; Fukui, M.; Otaka, A.; Funakoshi, S.; Fujii, N.; Bessho, K.; Miyajima, K. Role of disulfide linkages in tachyplesin-lipid interactions. Biochemistry 1993, 32, 11704–11710. [Google Scholar]
- Chen, X.Y.; Chen, Z. SFG studies on interactions between antimicrobial peptides and supported lipid bilayers. BBA-Biomembranes 2006, 1758, 1257–1273. [Google Scholar]
- Laederach, A.; Andreotti, A.H.; Fulton, D.B. Solution and micelle-bound structures of tachyplesin I and its active aromatic linear derivatives. Biochemistry 2002, 41, 12359–12368. [Google Scholar]
- Palczewski, K. G protein-coupled receptor rhodopsin. Annu. Rev. Biochem 2006, 75, 743–767. [Google Scholar]
- Palczewski, K.; Kumasaka, T.; Hori, T.; Behnke, C.A.; Motoshima, H.; Fox, B.A.; Le Trong, I.; Teller, D.C.; Okada, T.; Stenkamp, R.E.; Yamamoto, M.; Miyano, M. Crystal structure of rhodopsin: A G protein-coupled receptor. Science 2000, 289, 739–745. [Google Scholar]
- Andreev, O.A.; Karabadzhak, A.G.; Weerakkody, D.; Andreev, G.O.; Engelman, D.M.; Reshetnyak, Y.K. pH (low) insertion peptide (pHLIP) inserts across a lipid bilayer as a helix and exits by a different path. Proc. Natl. Acad. Sci. USA 2010, 107, 4081–4086. [Google Scholar]
- An, M.; Wijesinghe, D.; Andreev, O.A.; Reshetnyak, Y.K.; Engelman, D.M. pH-(low)-insertionpeptide (pHLIP) translocation of membrane impermeable phalloidin toxin inhibits cancer cell proliferation. Proc. Natl. Acad. Sci. USA 2010, 107, 20246–20250. [Google Scholar]
- DeGrado, W.F.; Lear, J.D. Induction of peptide conformation at apolar water interfaces. 1. A study with model peptides of defined hydrophobic periodicity. J. Am. Chem. Soc 1985, 107, 7684–7689. [Google Scholar]
- Weidner, T.; Apte, J.S.; Gamble, L.J.; Castner, D.G. Probing the orientation and conformation of alpha-helix and beta-strand model peptides on self-assembled monolayers using sum frequency generation and NEXAFS spectroscopy. Langmuir 2009, 26, 3433–3440. [Google Scholar]
- Weidner, T.; Breen, N.F.; Li, K.; Drobny, G.P.; Castner, D.G. Sum frequency generation and solid-state NMR study of the structure, orientation, and dynamics of polystyrene-adsorbed peptides. Proc. Natl. Acad. Sci. USA 2010, 107, 13288–13293. [Google Scholar]
- Westermark, P.; Engstrom, U.; Johnson, K.H.; Westermark, G.T.; Betsholtz, C. Islet amyloid polypeptide - pinpointing amino-acid-residues linked to amyloid fibril formation. Proc. Natl. Acad. Sci. USA 1990, 87, 5036–5040. [Google Scholar]
- Korenbrot, J.I.; Jones, O. Linear dichroism of rhodopsin in air-water interface films. J. Membr. Biol 1979, 46, 239–254. [Google Scholar]
- Lavoie, H.; Desbat, B.; Vaknin, D.; Salesse, C. Structure of rhodopsin in monolayers at the airwater interface: A PM-IRRAS and X-Ray reflectivity study. Biochemistry 2002, 41, 13424–13434. [Google Scholar]
- Dobson, C.M. Protein folding and misfolding. Nature 2003, 426, 884–890. [Google Scholar]
- Chiti, F.; Dobson, C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem 2006, 75, 333–366. [Google Scholar]
- Höppener, J.W.M.; Ahren, B.; Lips, C.J.M. Islet amyloid and type 2 diabetes mellitus. N. Engl. J. Med 2000, 343, 411–419. [Google Scholar]
- Höppener, J.W.M.; Lips, C.J.M. Role of islet amyloid in type 2 diabetes mellitus. Int. J. Biochem. Cell Biol 2006, 38, 726–736. [Google Scholar]


© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fu, L.; Wang, Z.; Yan, E.C.Y. Chiral Vibrational Structures of Proteins at Interfaces Probed by Sum Frequency Generation Spectroscopy. Int. J. Mol. Sci. 2011, 12, 9404-9425. https://doi.org/10.3390/ijms12129404
Fu L, Wang Z, Yan ECY. Chiral Vibrational Structures of Proteins at Interfaces Probed by Sum Frequency Generation Spectroscopy. International Journal of Molecular Sciences. 2011; 12(12):9404-9425. https://doi.org/10.3390/ijms12129404
Chicago/Turabian StyleFu, Li, Zhuguang Wang, and Elsa C.Y. Yan. 2011. "Chiral Vibrational Structures of Proteins at Interfaces Probed by Sum Frequency Generation Spectroscopy" International Journal of Molecular Sciences 12, no. 12: 9404-9425. https://doi.org/10.3390/ijms12129404