Prediction of PKCθ Inhibitory Activity Using the Random Forest Algorithm
Abstract
:1. Introduction
2. Results and Discussion
2.1. Performance of RF, PLS and SVM
2.2. Comparison of Different Statistical Approaches
2.3. Focus on the RF Model
3. Material and Experimental Methods
3.1. Data Sets and Descriptors
3.2. Statistical Methods
3.3. Evaluation of the Prediction Performance
4. Conclusions
Acknowledgements
References
- Boschelli, D. Small molecule inhibitors of PKCθ as potential antiinflammatory therapeutics. Curr. Top. Med. Chem 2009, 9, 640–654. [Google Scholar]
- Salek-Ardakani, S; So, T; Halteman, BS; Altman, A; Croft, M. Protein kinase Cθ controls Th1 cells in experimental autoimmune encephalomyelitis. J. Immunol 2005, 175, 7635–7641. [Google Scholar]
- Tan, SL; Zhao, J; Bi, C; Chen, XC; Hepburn, DL; Wang, J; Sedgwick, JD; Chintalacharuvu, SR; Na, S. Resistance to experimental autoimmune encephalomyelitis and impaired IL-17 production in protein kinase Cθ-deficient mice. J. Immunol 2006, 176, 2872–2879. [Google Scholar]
- Healy, AM; Izmailova, E; Fitzgerald, M; Walker, R; Hattersley, M; Silva, M; Siebert, E; Terkelsen, J; Picarella, D; Pickard, MD; LeClair, B; Chandra, S; Jaffee, B. PKC-θ-deficient mice are protected from Th1-dependent antigen-induced arthritis. J. Immunol 2006, 177, 1886–1893. [Google Scholar]
- Wang, L; Xiang, Z; Ma, LL; Chen, Z; Gao, X; Sun, Z; Williams, P; Chari, RS; Yin, DP. Deficiency of protein kinase C-θ facilitates tolerance induction. Transplantation 2009, 87, 507–516. [Google Scholar]
- Berg-Brown, NN; Gronski, MA; Jones, RG; Elford, AR; Deenick, EK; Odermatt, B; Littman, DR; Ohashi, PS. PKCθ signals activation versus tolerance in vivo. J. Exp. Med 2004, 199, 743–752. [Google Scholar]
- Chaudhary, D; Kasaian, M. PKCθ: A potential therapeutic target for T-cell-mediated diseases. Curr. Opin. Investig. Drugs 2006, 7, 432–437. [Google Scholar]
- Cole, D; Asselin, M; Brennan, A; Czerwinski, R; Ellingboe, J; Fitz, L; Greco, R; Huang, X; Joseph-McCarthy, D; Kelly, M; Kirisits, M; Lee, J; Li, Y; Morgan, P; Stock, J; Tsao, D; Wissner, A; Yang, X; Chaudhary, D. Identification, characterization and initial hit-to-lead optimization of a series of 4-arylamino-3-pyridinecarbonitrile as protein kinase C theta (PKCθ) inhibitors. J. Med. Chem 2008, 51, 5958–5963. [Google Scholar]
- Tumey, L; Boschelli, D; Lee, J; Chaudhary, D. 2-Alkenylthieno [2, 3-b] pyridine-5-carbonitriles: Potent and selective inhibitors of PKCθ. Bioorg. Med. Chem. Lett 2008, 18, 4420–4423. [Google Scholar]
- Tumey, L; Bhagirath, N; Brennan, A; Brooijmans, N; Lee, J; Yang, X; Boschelli, D. 5-Vinyl-3-pyridinecarbonitrile inhibitors of PKCθ: Optimization of enzymatic and functional activity. Bioorg. Med. Chem 2009, 17, 7933–7948. [Google Scholar]
- Wu, B; Boschelli, D; Lee, J; Yang, X; Chaudhary, D. Second generation 4-(4-methyl-1H-indol- 5-ylamino)-2-phenylthieno [2,3-b] pyridine-5-carbonitrile PKCθ inhibitors. Bioorg. Med. Chem. Lett 2009, 19, 766–769. [Google Scholar]
- Dushin, R; Nittoli, T; Ingalls, C; Boschelli, D; Cole, D; Wissner, A; Lee, J; Yang, X; Morgan, P; Brennan, A; Chaudhary, D. Synthesis and PKCθ inhibitory activity of a series of 4-indolylamino-5-phenyl-3-pyridinecarbonitriles. Bioorg. Med. Chem. Lett 2009, 19, 2461–2463. [Google Scholar]
- Boschelli, D; Wang, D; Prashad, A; Subrath, J; Wu, B; Niu, C; Lee, J; Yang, X; Brennan, A; Chaudhary, D. Optimization of 5-phenyl-3-pyridinecarbonitriles as PKCθ inhibitors. Bioorg. Med. Chem. Lett 2009, 19, 3623–3626. [Google Scholar]
- Subrath, J; Wang, D; Wu, B; Niu, C; Boschelli, D; Lee, J; Yang, X; Brennan, A; Chaudhary, D. C-5 Substituted heteroaryl 3-pyridinecarbonitriles as PKCθ inhibitors: Part I. Bioorg. Med. Chem. Lett 2009, 19, 5423–5425. [Google Scholar]
- Prashad, A; Wang, D; Subrath, J; Wu, B; Lin, M; Zhang, M; Kagan, N; Lee, J; Yang, X; Brennan, A; Chaudhary, D; Xu, X; Leung, L; Wang, J; Boschelli, D. C-5 substituted heteroaryl-3-pyridinecarbonitriles as PKCθ inhibitors: Part II. Bioorg. Med. Chem. Lett 2009, 19, 5799–5802. [Google Scholar]
- Niu, C; Boschelli, D; Tumey, L; Bhagirath, N; Subrath, J; Shim, J; Wang, Y; Wu, B; Eid, C; Lee, J; Yang, X; Brennan, A; Chaudhary, D. First generation 5-vinyl-3-pyridinecarbonitrile PKCθ inhibitors. Bioorg. Med. Chem. Lett 2009, 19, 5829–5832. [Google Scholar]
- Shim, J; Eid, C; Lee, J; Liu, E; Chaudhary, D; Boschelli, D. Synthesis and PKCθ inhibitory activity of a series of 5-vinyl phenyl sulfonamide-3-pyridinecarbonitriles. Bioorg. Med. Chem. Lett 2009, 19, 6575–6577. [Google Scholar]
- Li, Y; Wang, Y; Ding, J; Chang, Y; Zhang, S. In silico prediction of androgenic and nonandrogenic compounds using random forest. QSAR Comb. Sci 2009, 28, 396–405. [Google Scholar]
- Hong, H; Xie, Q; Ge, W; Qian, F; Fang, H; Shi, L; Su, Z; Perkins, R; Tong, W. Mold2, molecular descriptors from 2D structures for chemoinformatics and toxicoinformatics. J. Chem. Inf. Model 2008, 48, 1337–1344. [Google Scholar]
- Svetnik, V; Liaw, A; Tong, C; Culberson, J; Sheridan, R; Feuston, B. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci 2003, 43, 1947–1958. [Google Scholar]
- Bakken, G; Jurs, P. Classification of multidrug-resistance reversal agents using structure-based descriptors and linear discriminant analysis. J. Med. Chem 2000, 43, 4534–4541. [Google Scholar]
- Pontes, M; Galvao, R; Araujo, M; Moreira, P; Neto, O; Jose, G; Saldanha, T. The successive projections algorithm for spectral variable selection in classification problems. Chemom. Intell. Lab. Syst 2005, 78, 11–18. [Google Scholar]
- Pourbasheer, E; Riahi, S; Ganjali, M; Norouzi, P. QSAR study on melanocortin-4 receptors by support vector machine. Eur. J. Med. Chem 2010, 45, 1087–1093. [Google Scholar]
- Wang, Y; Li, Y; Wang, B. An in silico method for screening nicotine derivatives as cytochrome P450 2A6 selective inhibitors based on kernel partial least squares. Int. J. Mol. Sci 2007, 8, 166–179. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
- Polishchuk, P; Muratov, E; Artemenko, A; Kolumbin, O; Muratov, N; Kuz’min, V. Application of random forest approach to QSAR prediction of aquatic toxicity. J. Chem. Inf. Model 2009, 49, 2481–2488. [Google Scholar]
- Caret: Classification and Regression Training. http://cran.r-project.org/web/packages/caret/index.html (accessed on 06 September 2010).
- RandomForest: Breiman and Cutler’s random forests for classification and regression. http://cran.rproject.org/web/packages/randomForest/index.html (accessed on 06 September 2010).
- Kernlab: Kernel-based Machine Learning Lab. http://cran.r-project.org/web/packages/kernlab/index.html (accessed on 06 September 2010).
- PLS: Partial Least Squares Regression (PLSR) and Principal Component Regression (PCR). http://cran.r-project.org/web/packages/pls/index.html (accessed on 06 September 2010).
- Palmer, D; O’Boyle, N; Glen, R; Mitchell, J. Random forest models to predict aqueous solubility. J. Chem. Inf. Model 2007, 47, 150–158. [Google Scholar]
- Si, H; Wang, T; Zhang, K; Duan, Y; Yuan, S; Fu, A; Hu, Z. Quantitative structure activity relationship model for predicting the depletion percentage of skin allergic chemical substances of glutathione. Anal. Chim. Acta 2007, 591, 255–264. [Google Scholar]
- Si, H; Yuan, S; Zhang, K; Fu, A; Duan, Y; Hu, Z. Quantitative structure activity relationship study on EC50 of anti-HIV drugs. Chemom. Intell. Lab. Syst 2008, 90, 15–24. [Google Scholar]
- Tropsha, A; Gramatica, P; Gombar, V. The importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci 2003, 22, 69–77. [Google Scholar]
- Takaoka, Y; Endo, Y; Yamanobe, S; Kakinuma, H; Okubo, T; Shimazaki, Y; Ota, T; Sumiya, S; Yoshikawa, K. Development of a method for evaluating drug-likeness and ease of synthesis using a data set in which compounds are assigned scores based on chemists’ intuition. J. Chem. Inf. Comput. Sci 2003, 43, 1269–1275. [Google Scholar]
- Crivori, P; Cruciani, G; Carrupt, P; Testa, B. Predicting blood-brain barrier permeation from three-dimensional molecular structure. J. Med. Chem 2000, 43, 2204–2216. [Google Scholar]
- Zamora, I; Oprea, T; Cruciani, G; Pastor, M; Ungell, A. Surface descriptors for protein-ligand affinity prediction. J. Med. Chem 2003, 46, 25–33. [Google Scholar]
- Liu, H; Hu, R; Zhang, R; Yao, X; Liu, M; Hu, Z; Fan, B. The prediction of human oral absorption for diffusion rate-limited drugs based on heuristic method and support vector machine. J. Comput. Aided Mol. Des 2005, 19, 33–46. [Google Scholar]
- Yao, X; Panaye, A; Doucet, J; Zhang, R; Chen, H; Liu, M; Hu, Z; Fan, B. Comparative study of QSAR/QSPR correlations using support vector machines, radial basis function neural networks and multiple linear regression. J. Chem. Inf. Comput. Sci 2004, 44, 1257–1266. [Google Scholar]
- Pourbasheer, E; Riahi, S; Ganjali, M; Norouzi, P. Application of genetic algorithm-support vector machine (GA-SVM) for prediction of BK-channels activity. Eur. J. Med. Chem 2009, 44, 5023–5028. [Google Scholar]
- Wang, Y; Li, Y; Yang, S; Yang, L. An in silico approach for screening flavonoids as p-glycoprotein inhibitors based on a bayesian-regularized neural network. J. Comput. Aided Mol. Des 2005, 19, 137–147. [Google Scholar]
- Golbraikh, A; Shen, M; Xiao, Z; Xiao, Y; Lee, K; Tropsha, A. Rational selection of training and test sets for the development of validated QSAR models. J. Comput. Aided Mol. Des 2003, 17, 241–253. [Google Scholar]
- Golbraikh, A; Tropsha, A. Predictive QSAR modeling based on diversity sampling of experimental datasets for the training and test set selection. J. Comput. Aided Mol. Des 2002, 16, 357–369. [Google Scholar]
- Uddin, R; Yuan, H; Petukhov, P; Choudhary, M; Madura, J. Receptor-based modeling and 3D-QSAR for a quantitative production of the butyrylcholinesterase inhibitors based on genetic algorithm. J. Chem. Inf. Model 2008, 48, 1092–1103. [Google Scholar]
- Roy, K; Leonard, J. QSAR analyses of 3-(4-benzylpiperidin-1-yl)-N-phenylpropylamine derivatives as potent CCR5 antagonists. J. Chem. Inf. Model 2005, 45, 1352–1368. [Google Scholar]
- Egan, WJ; Morgan, SL. Outlier detection in multivariate analytical chemical data. Anal. Chem 1998, 70, 2372–2379. [Google Scholar]
- Burden, F. Molecular identification number for substructure searches. J. Chem. Inf. Comput. Sci 1989, 29, 225–227. [Google Scholar]
- Burden, F; Polley, M; Winkler, D. Toward novel universal descriptors: Charge fingerprints. J. Chem. Inf. Model 2009, 49, 710–715. [Google Scholar]
- Zhu, Y; Lei, M; Lu, A; Zhao, X; Yin, X; Gao, Q. 3D-QSAR studies of boron-containing dipeptides as proteasome inhibitors with CoMFA and CoMSIA methods. Eur. J. Med. Chem 2009, 44, 1486–1499. [Google Scholar]
- Song, M; Breneman, CM; Sukumar, N. Three-dimensional quantitative structure-activity relationship analyses of piperidine-based CCR5 receptor antagonists. Bioorg. Med. Chem 2004, 12, 489–499. [Google Scholar]
- Leonard, J; Roy, K. On selection of training and test sets for the development of predictive QSAR models. QSAR Comb. Sci 2006, 25, 235–251. [Google Scholar]
- MDL® ISIS Draw, version 2.3; MDL Information Systems, Inc: San Diego, CA, USA, 2010.
- Geladi, P; Kowalski, B. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar]
- Cortes, C; Vapnik, V. Support-vector networks. Mach. Learn 1995, 20, 273–297. [Google Scholar]
- Wold, S. Cross-validatory estimation of the number of components in factor and principal components models. Technometrics 1978, 20, 397–405. [Google Scholar]
- Karchin, R; Karplus, K; Haussler, D. Classifying G-protein coupled receptors with support vector machines. Bioinformatics 2002, 18, 147. [Google Scholar]
- Cai, Y; Liu, X; Xu, X; Chou, K. Support vector machines for predicting HIV protease cleavage sites in protein. J. Comput. Chem 2002, 23, 267–274. [Google Scholar]
- Tay, F; Cao, L. Modified support vector machines in financial time series forecasting. Neurocomputing 2003, 48, 847–862. [Google Scholar]
- Brown, RD; Martin, YC. Use of structure-activity data to compare structure-based clustering methods and descriptors for use in compound selection. J. Chem. Inf. Comput. Sci 1996, 36, 572–584. [Google Scholar]
- Afantitis, A; Melagraki, G; Sarimveis, H; Koutentis, P; Igglessi-Markopoulou, O; Kollias, G. A combined LS-SVM & MLR QSAR workflow for predicting the inhibition of CXCR3 receptor by quinazolinone analogs. Mol. Divers 2010, 14, 1–11. [Google Scholar]
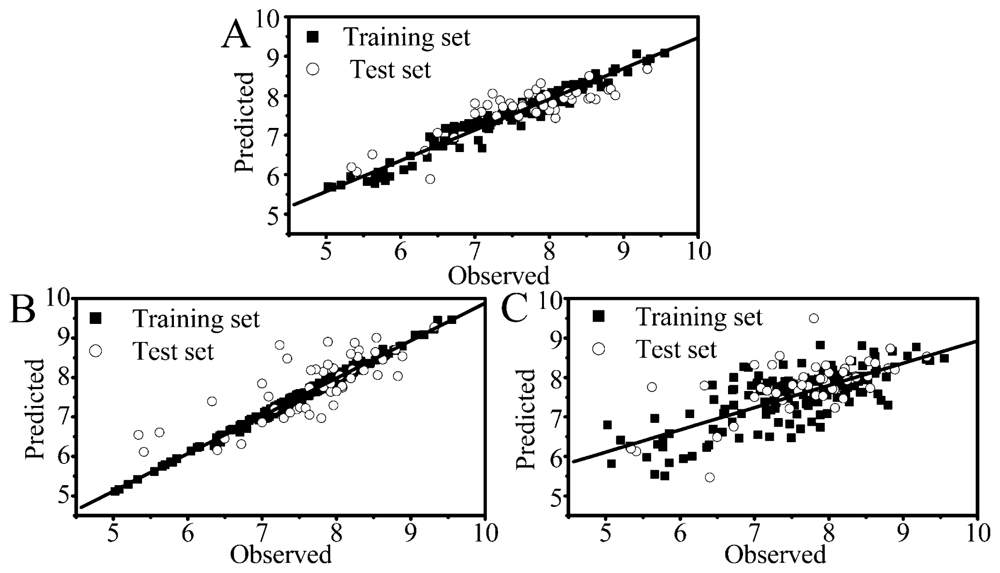


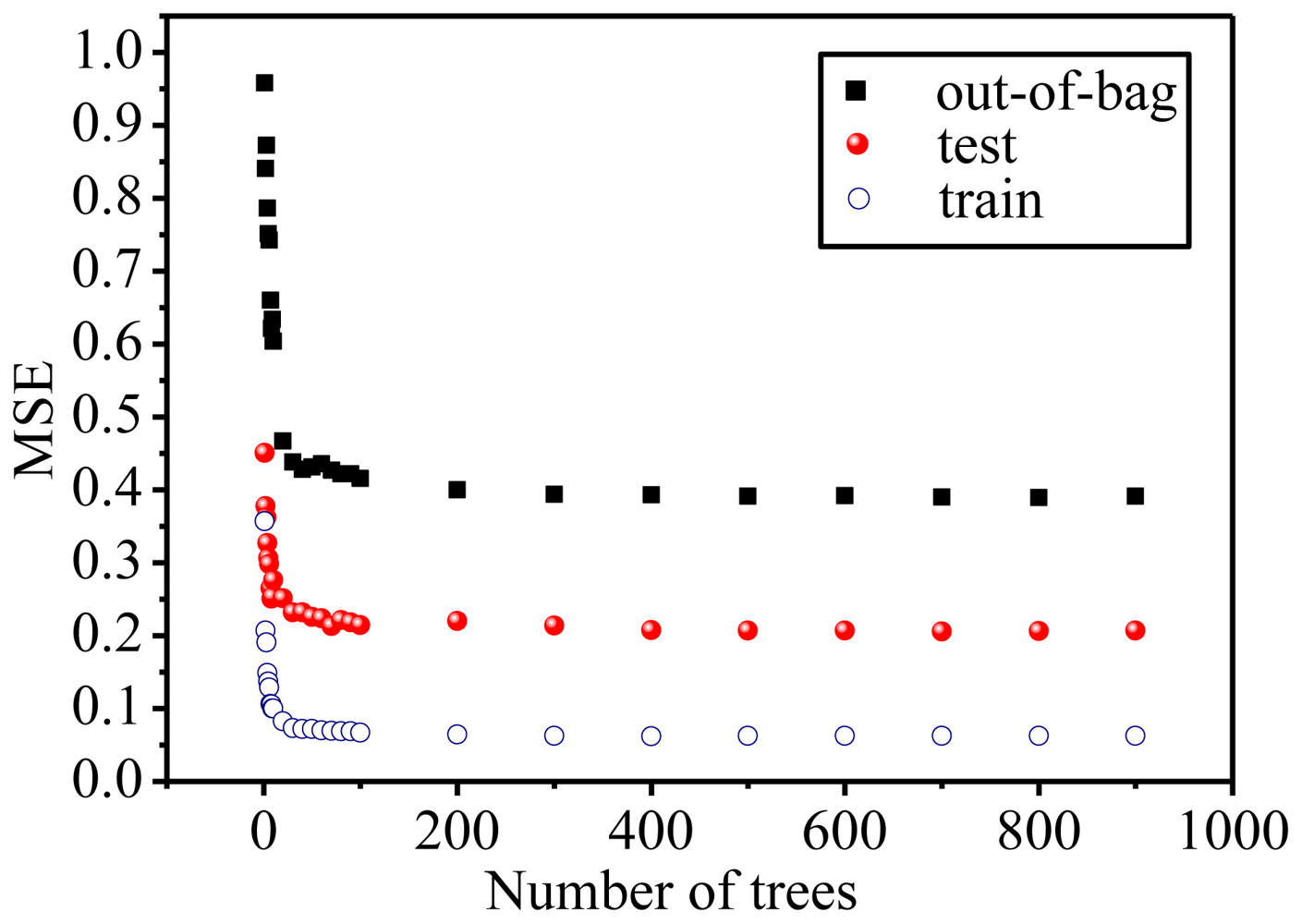
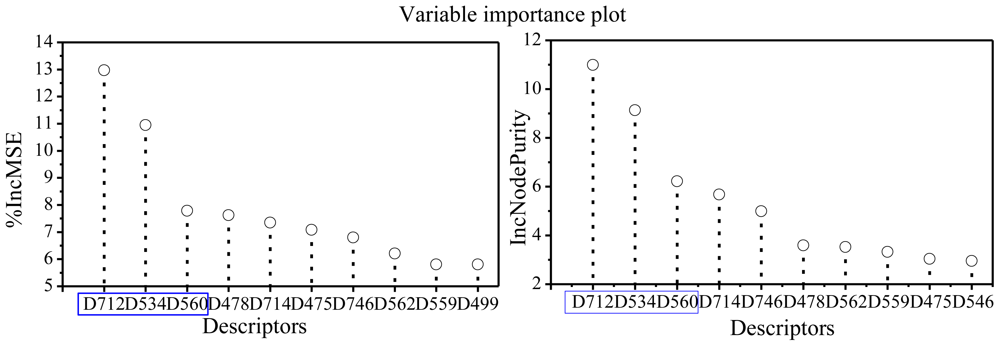
| Para.a | RF | SVM | PLS | |||
|---|---|---|---|---|---|---|
| Training | Test | Training | Test | Training | Test | |
| Size | 157 | 51 | 157 | 51 | 157 | 51 |
| R2 | 0.96 | 0.76 | 0.99 | 0.61 | 0.57 | 0.42 |
| Q2 | 0.54 | - | 0.57 | - | 0.36 | - |
| R2pred | - | 0.72 | - | 0.59 | - | 0.39 |
| SEE | 0.25 | - | 0.08 | - | 0.59 | - |
| SEP | - | 0.45 | - | 0.55 | - | 0.67 |
| Paraa | RF | SVM | PLS | |||
|---|---|---|---|---|---|---|
| Training | Test | Training | Test | Training | Test | |
| Size | 157 | 51 | 157 | 51 | 157 | 51 |
| R2 | 0.95 ± 0.003 | 0.58 ± 0.09 | 0.82 ± 0.01 | 0.49 ± 0.10 | 0.64 ± 0.13 | 0.41 ± 0.13 |
| Q2 | 0.57 ± 0.03 | - | 0.59 ± 0.02 | - | 0.39 ± 0.11 | - |
| R2pred | - | 0.56 ± 0.09 | - | 0.45 ± 0.10 | - | 0.10 ± 0.84 |
| SEE | 0.24 ± 0.01 | - | 0.39 ± 0.01 | - | 0.53 ± 0.09 | - |
| SEP | - | 0.59 ± 0.06 | - | 0.63 ± 0.05 | - | 0.79 ± 0.25 |
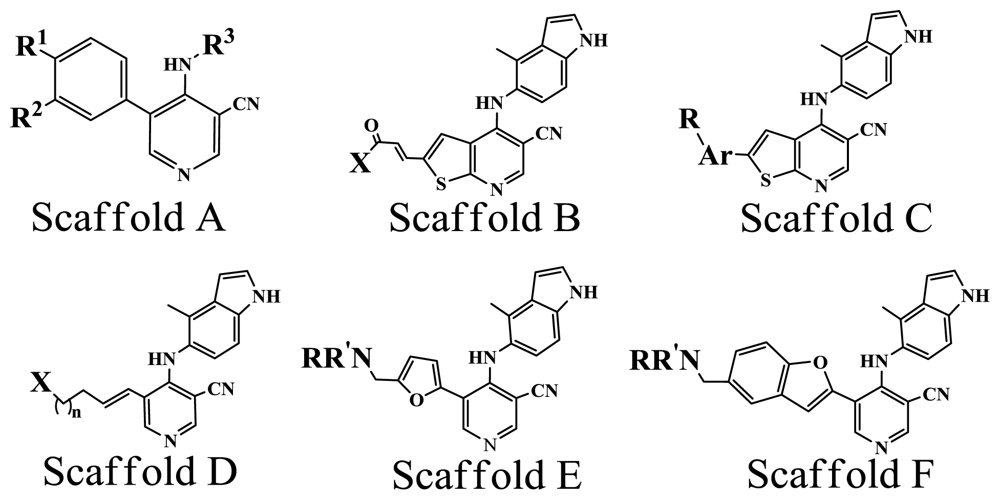 | ||||||
|---|---|---|---|---|---|---|
| No. | Scaffold | Substituent | pIC50 | Refa | ||
| R1 | R2 | R3 | ||||
| 1* | A | OMe | OMe | 3-Bromophenyl | 5.337 | [8] |
| 2 | A | OMe | OMe | Phenyl | 5.796 | [8] |
| 3* | A | OMe | OMe | 3-Chlorophenyl | 5.409 | [8] |
| X | ||||||
| 17 | B | Pyrrolidine | 8.420 | [9] | ||
| 23 | B | H2N | 7.921 | [9] | ||
| 27 | B | PhNH | 6.959 | [9] | ||
| Ar | R | |||||
| 77 | C | Phenyl | 4-CH2-NMe2 | 7.854 | [11] | |
| 80 | C | 3-Pyridine | 5-CH2-NMe2 | 7.076 | [11] | |
| 85* | C | Phenyl | 2-OMe,3-CH2-NMe2 | 7.921 | [11] | |
| X | n | |||||
| 37 | D | 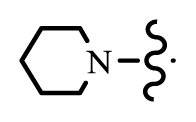 | 1 | 7.456 | [10] | |
| 41* | D |  | 2 | 7.469 | [10] | |
| NR’R | ||||||
| 137 | E | Morpholine | 8.108 | [14] | ||
| 140 | E | Pyrrolidine | 7.456 | [14] | ||
| NR’R | ||||||
| 153* | F | Morpholine | 7.886 | [15] | ||
| 157* | F | NHCH2CH(OH)CH2OH | 8.824 | [15] | ||
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hao, M.; Li, Y.; Wang, Y.; Zhang, S. Prediction of PKCθ Inhibitory Activity Using the Random Forest Algorithm. Int. J. Mol. Sci. 2010, 11, 3413-3433. https://doi.org/10.3390/ijms11093413
Hao M, Li Y, Wang Y, Zhang S. Prediction of PKCθ Inhibitory Activity Using the Random Forest Algorithm. International Journal of Molecular Sciences. 2010; 11(9):3413-3433. https://doi.org/10.3390/ijms11093413
Chicago/Turabian StyleHao, Ming, Yan Li, Yonghua Wang, and Shuwei Zhang. 2010. "Prediction of PKCθ Inhibitory Activity Using the Random Forest Algorithm" International Journal of Molecular Sciences 11, no. 9: 3413-3433. https://doi.org/10.3390/ijms11093413




