Excited-State Dynamics of Overlapped Optically-Allowed 1Bu+ and Optically-Forbidden 1Bu- or 3Ag- Vibronic Levels of Carotenoids: Possible Roles in the Light-Harvesting Function
Abstract
:1. Introduction
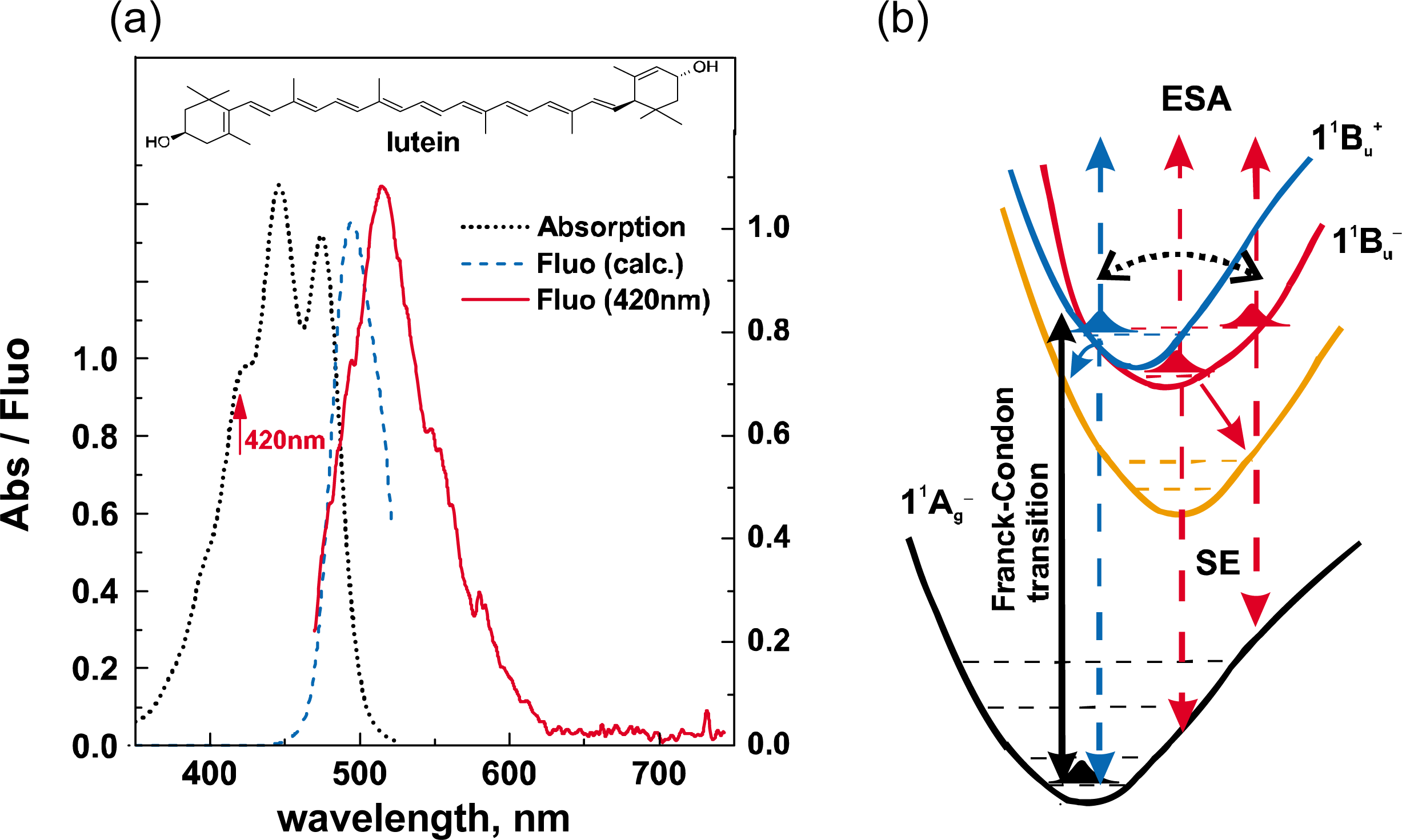
1.1. Low-Lying Singlet-Excited States and Their Light-Harvesting Function
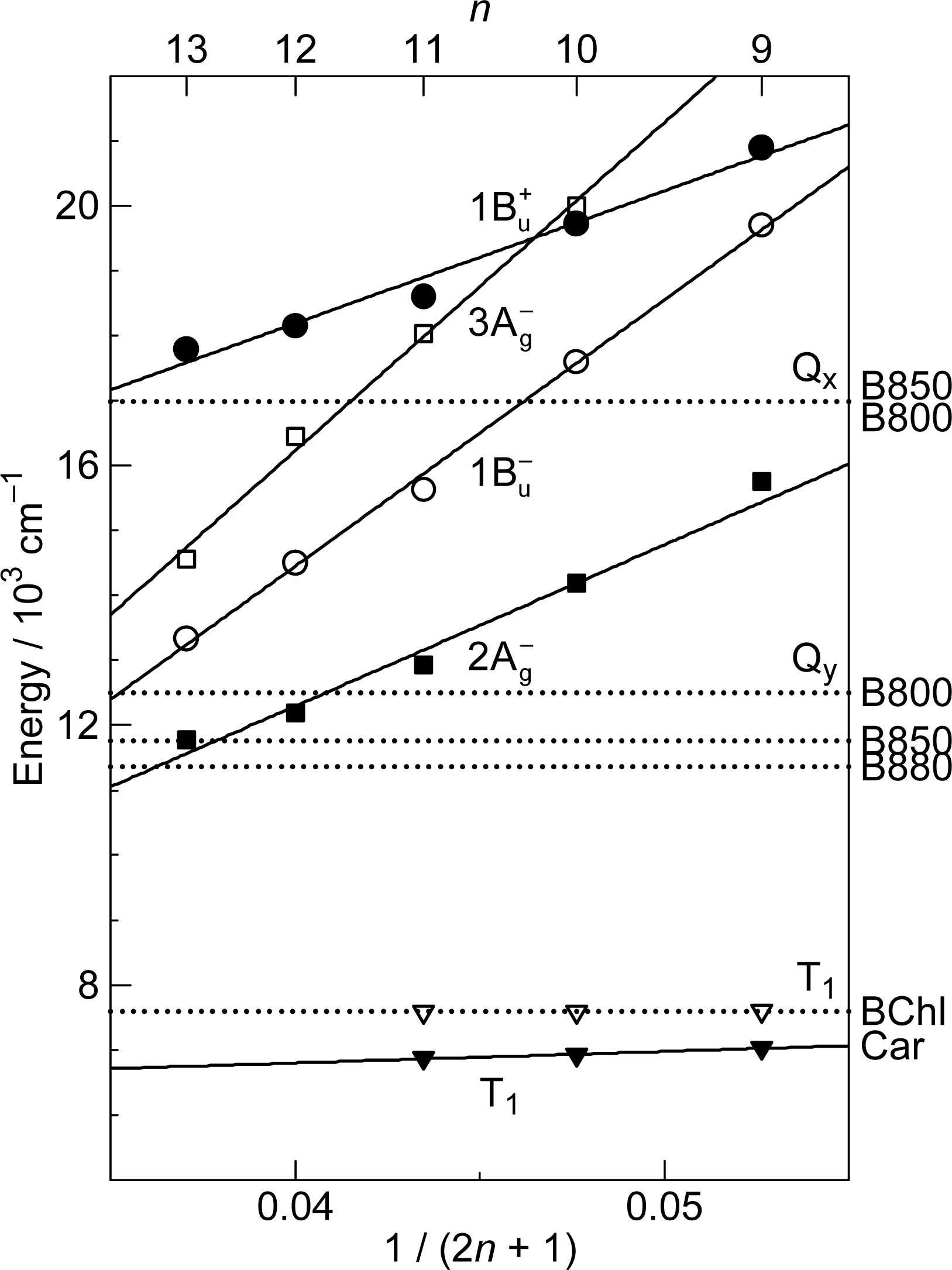
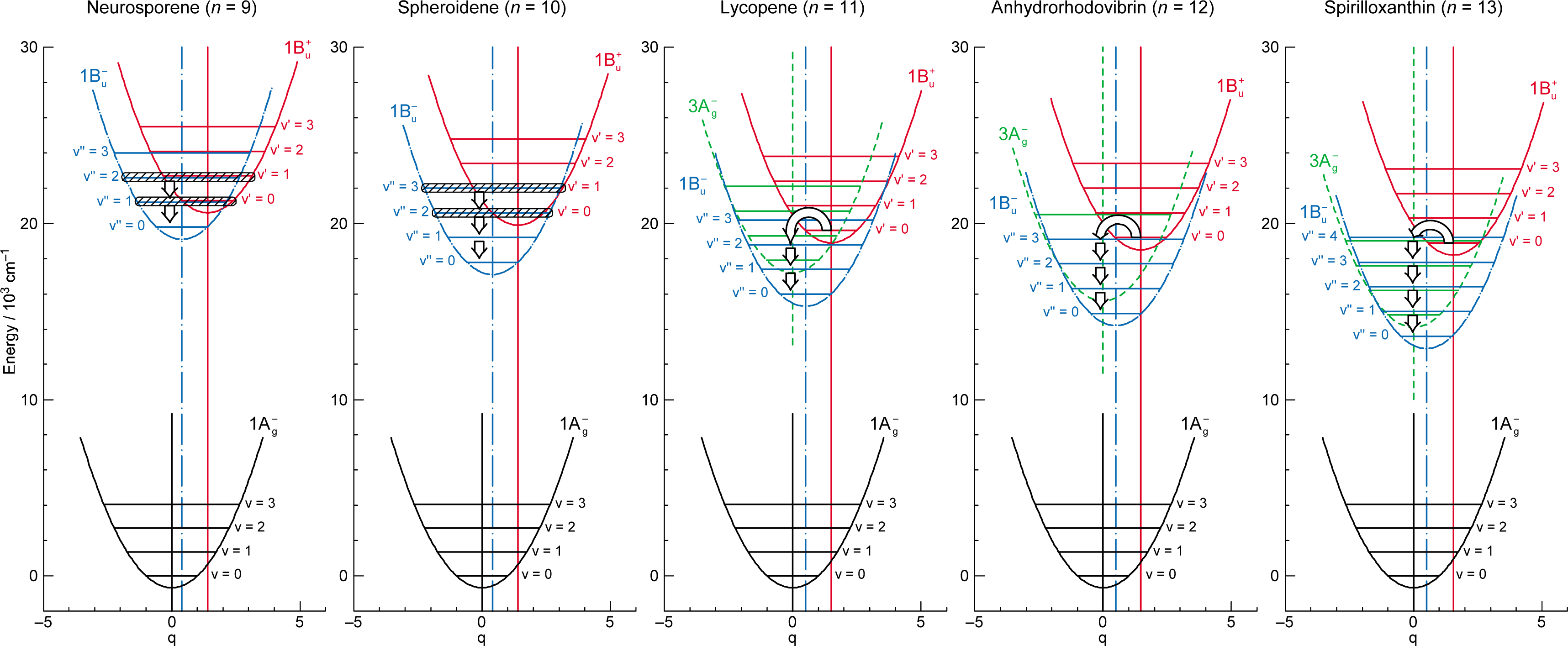
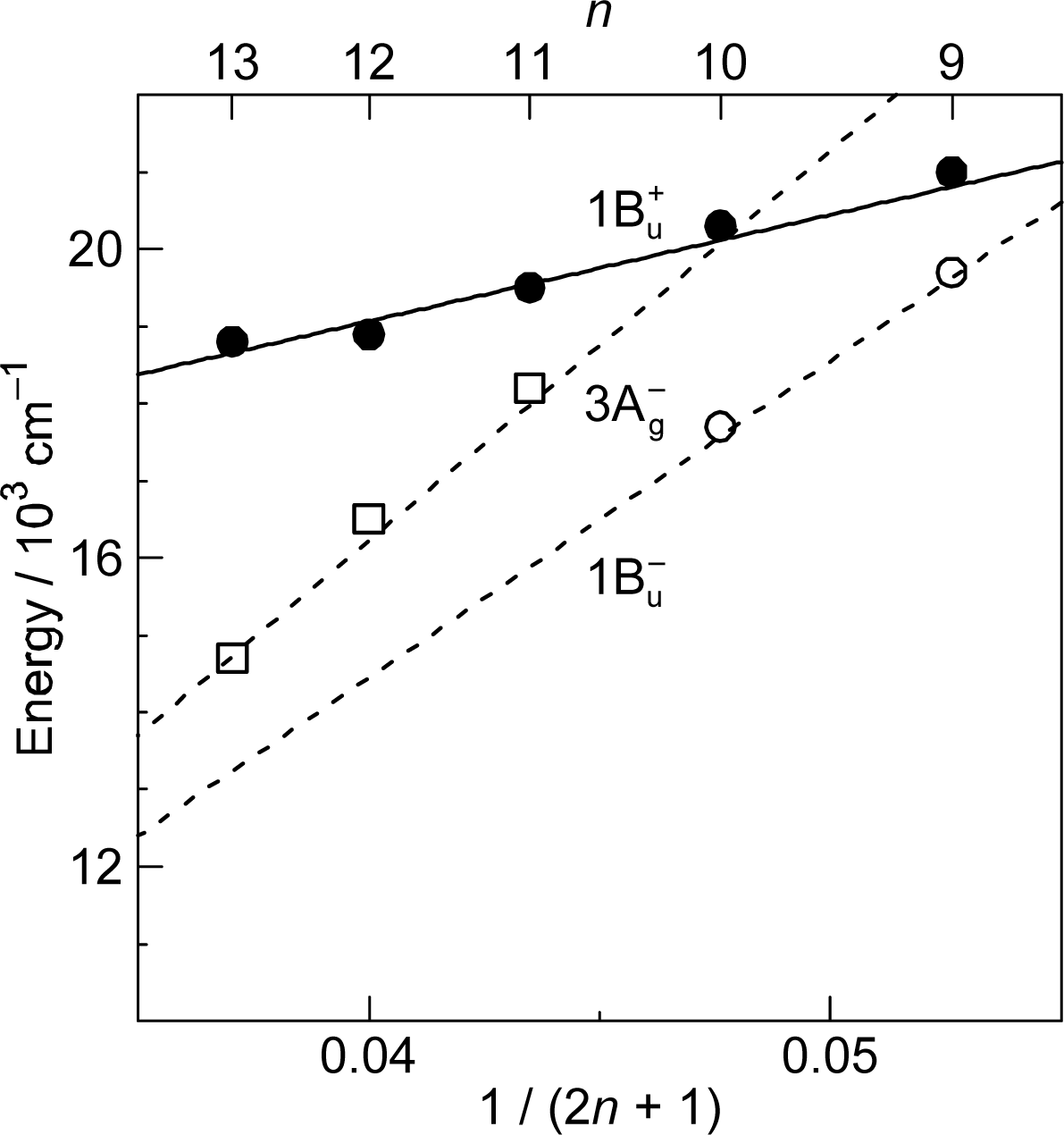
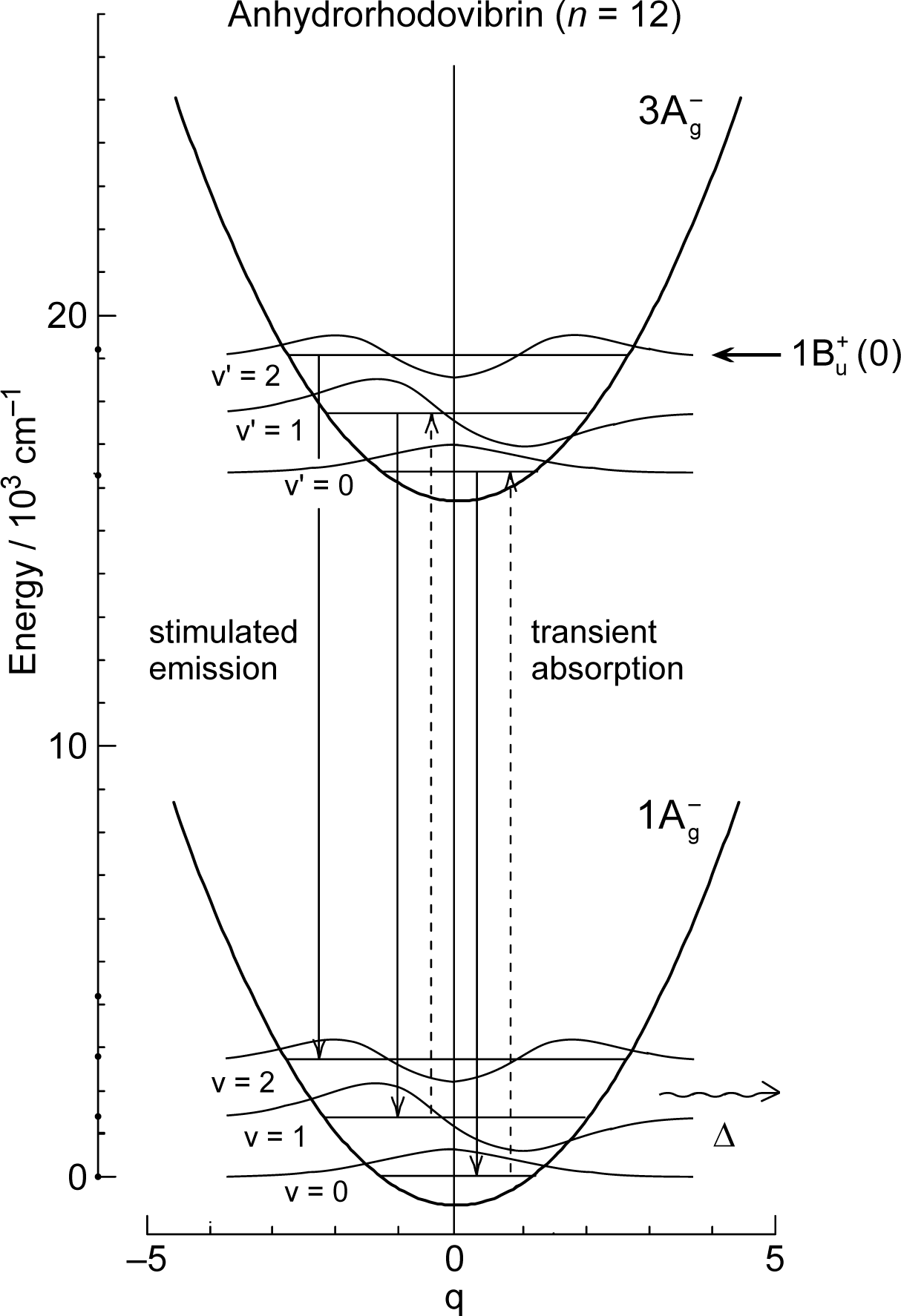
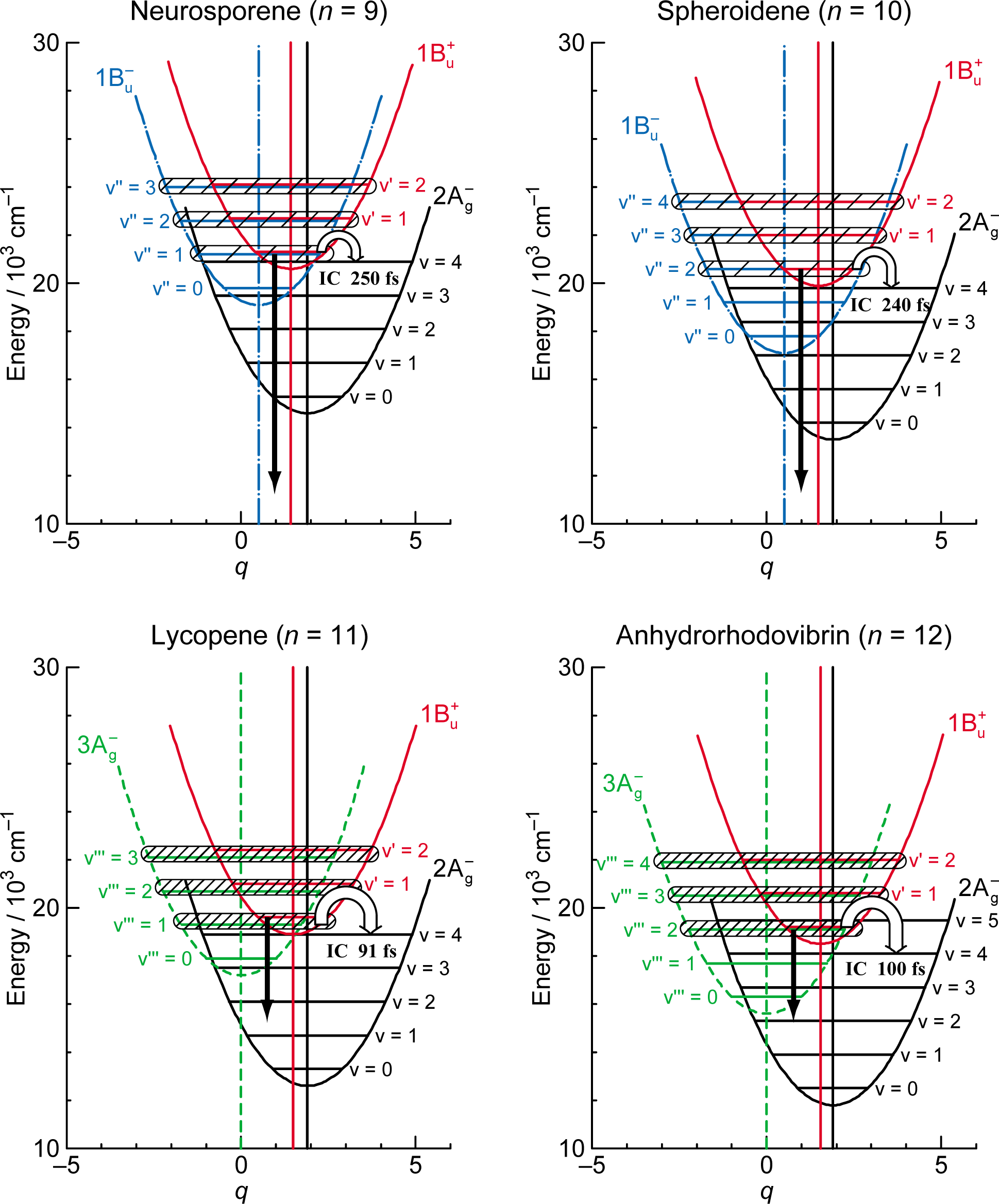
1.2. Diabatic Vibronic Levels
1.3. Conical Intersection and Conservation of Symmetries in Singlet-Excited States
1.4. Time-Resolved Spectroscopies Used
1.5. Contents of This Review
2. Pump-Probe Spectroscopy: Selective excitation
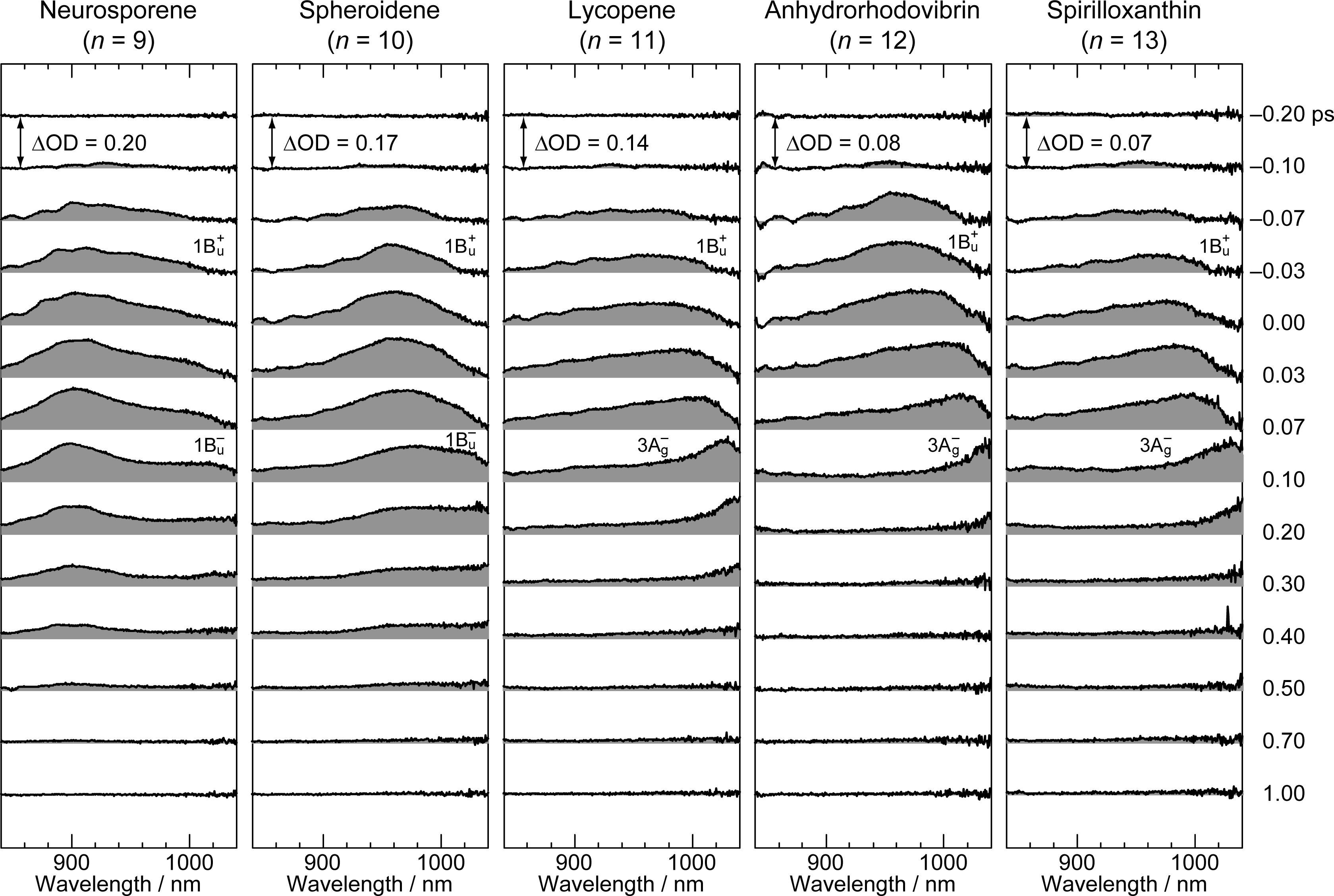
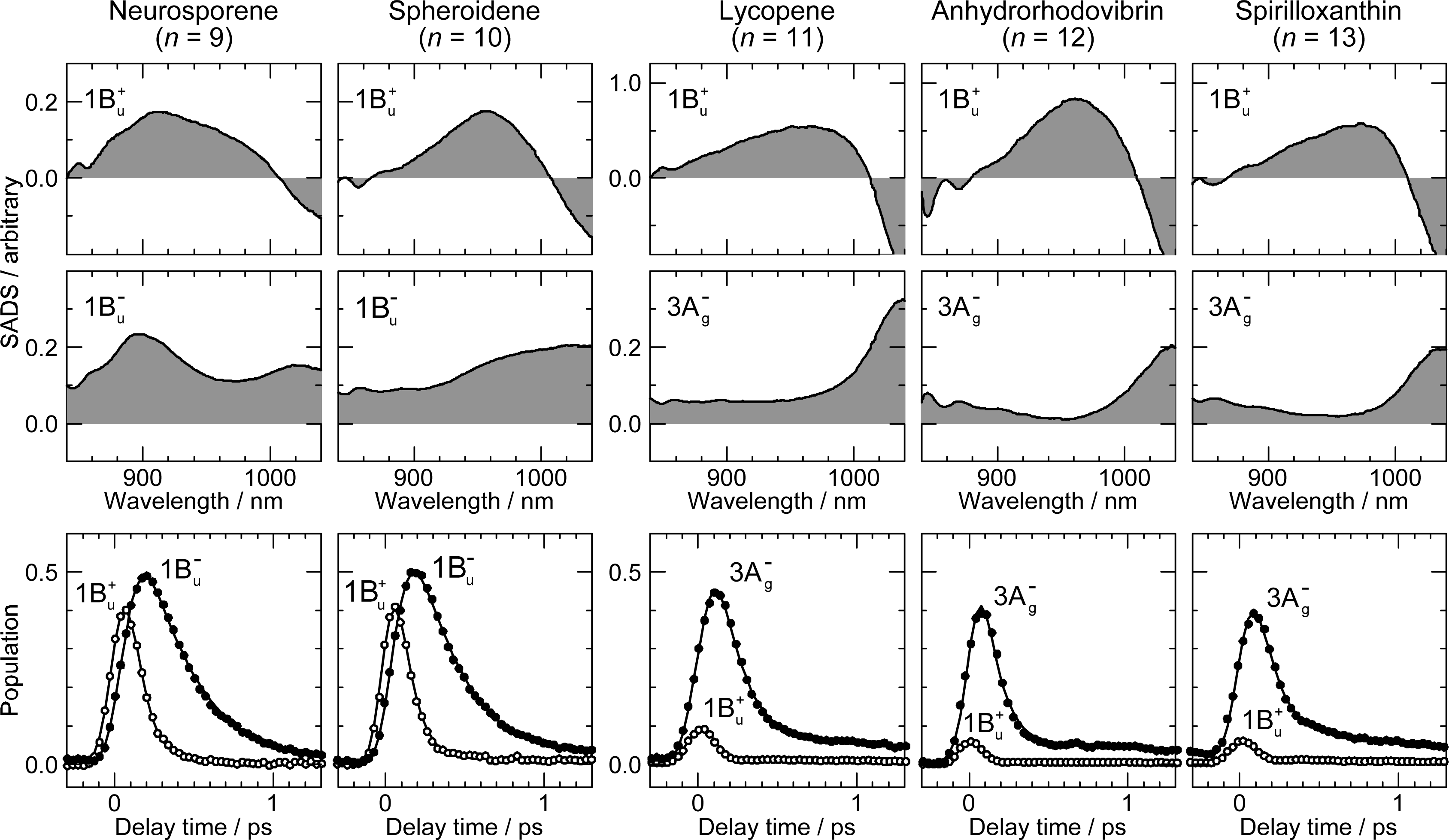
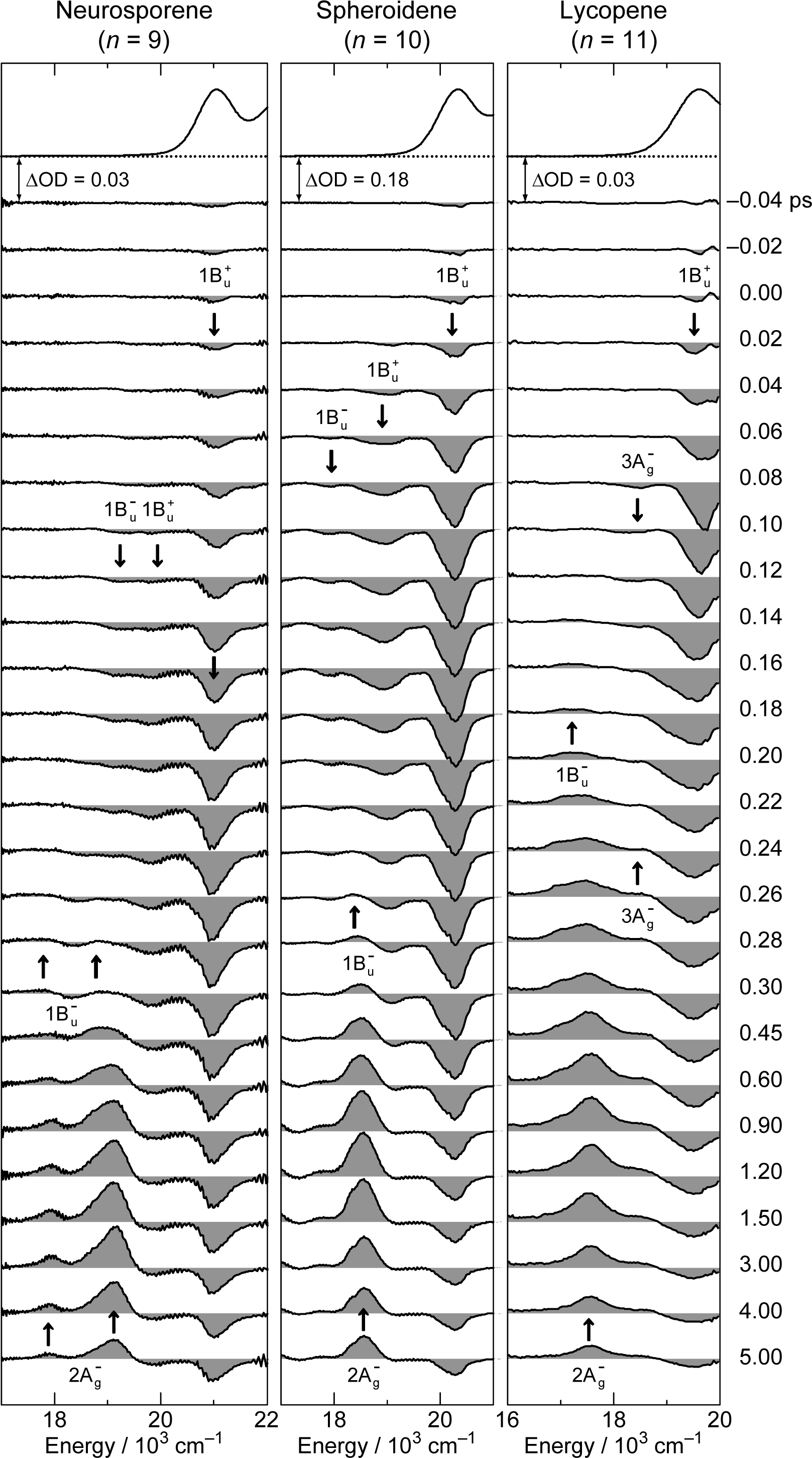
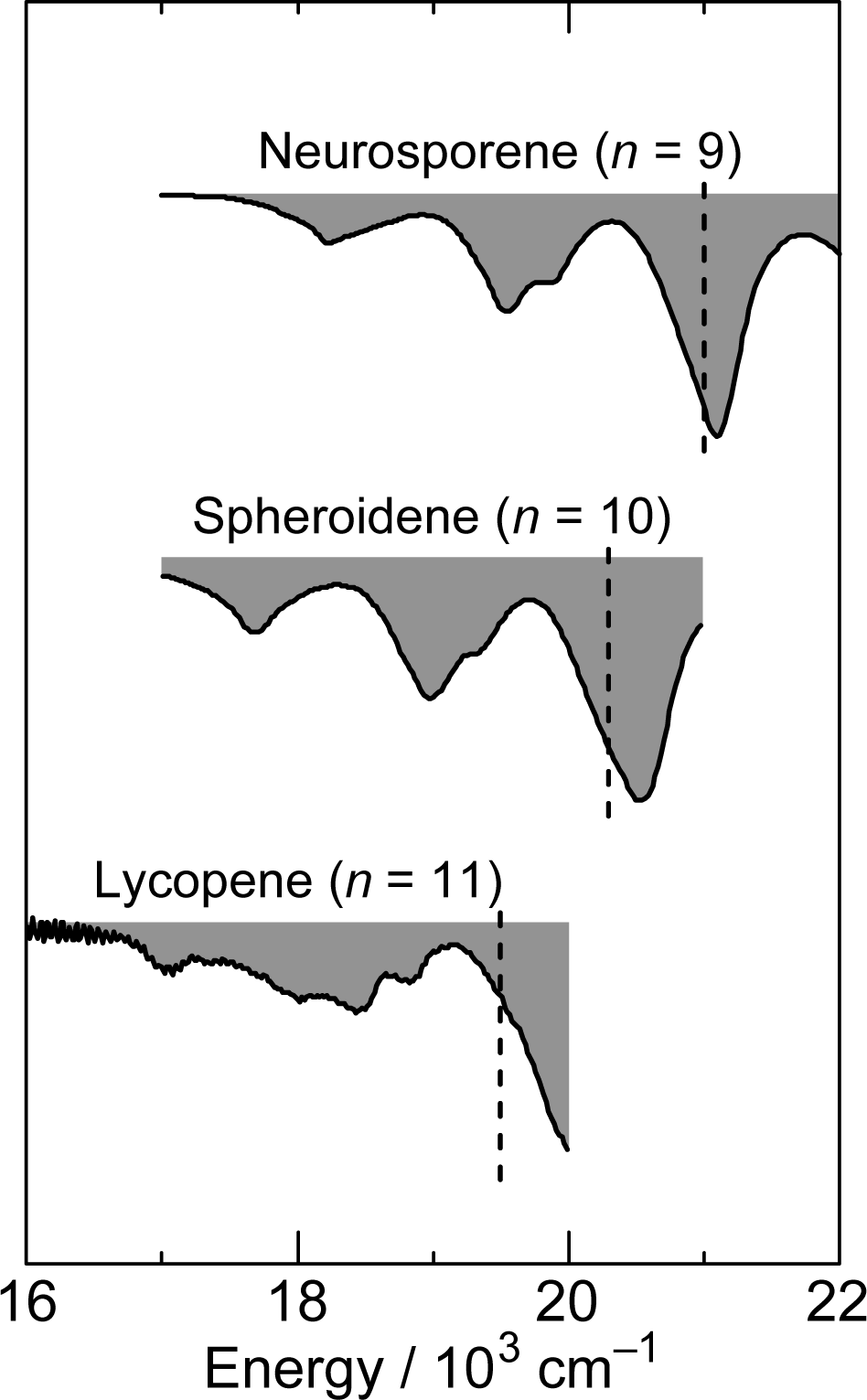
2.1. Excitation to the 1Bu+(0) Level of Cars (n = 9–13) in Nonpolar Solvent and Probing in the NIR Region [12]
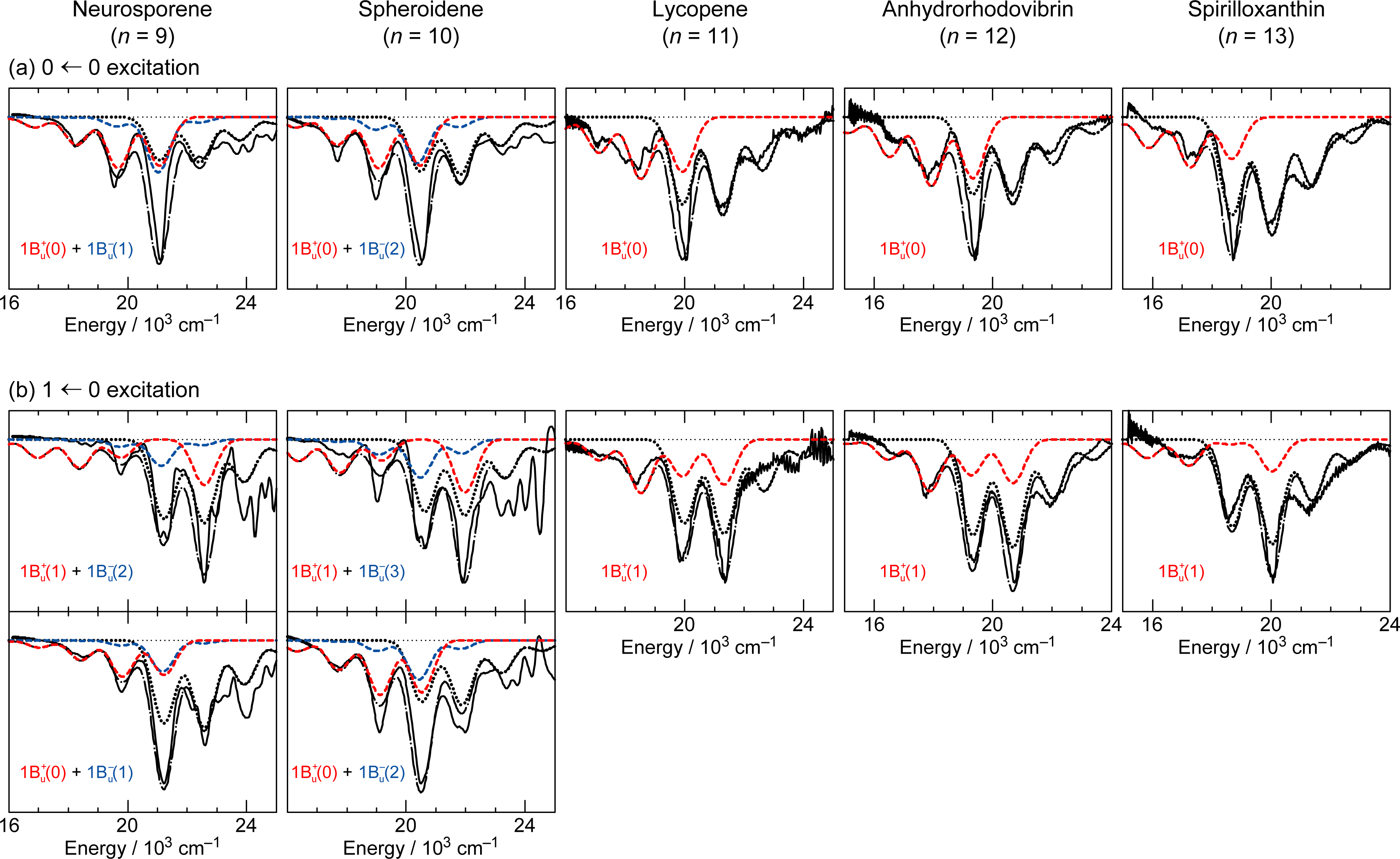
2.2. Excitation to the 1Bu+(0) and 1Bu+(1) Levels of Cars (n = 9–13) in Nonpolar Solvent and Probing in the VIS Region [10]
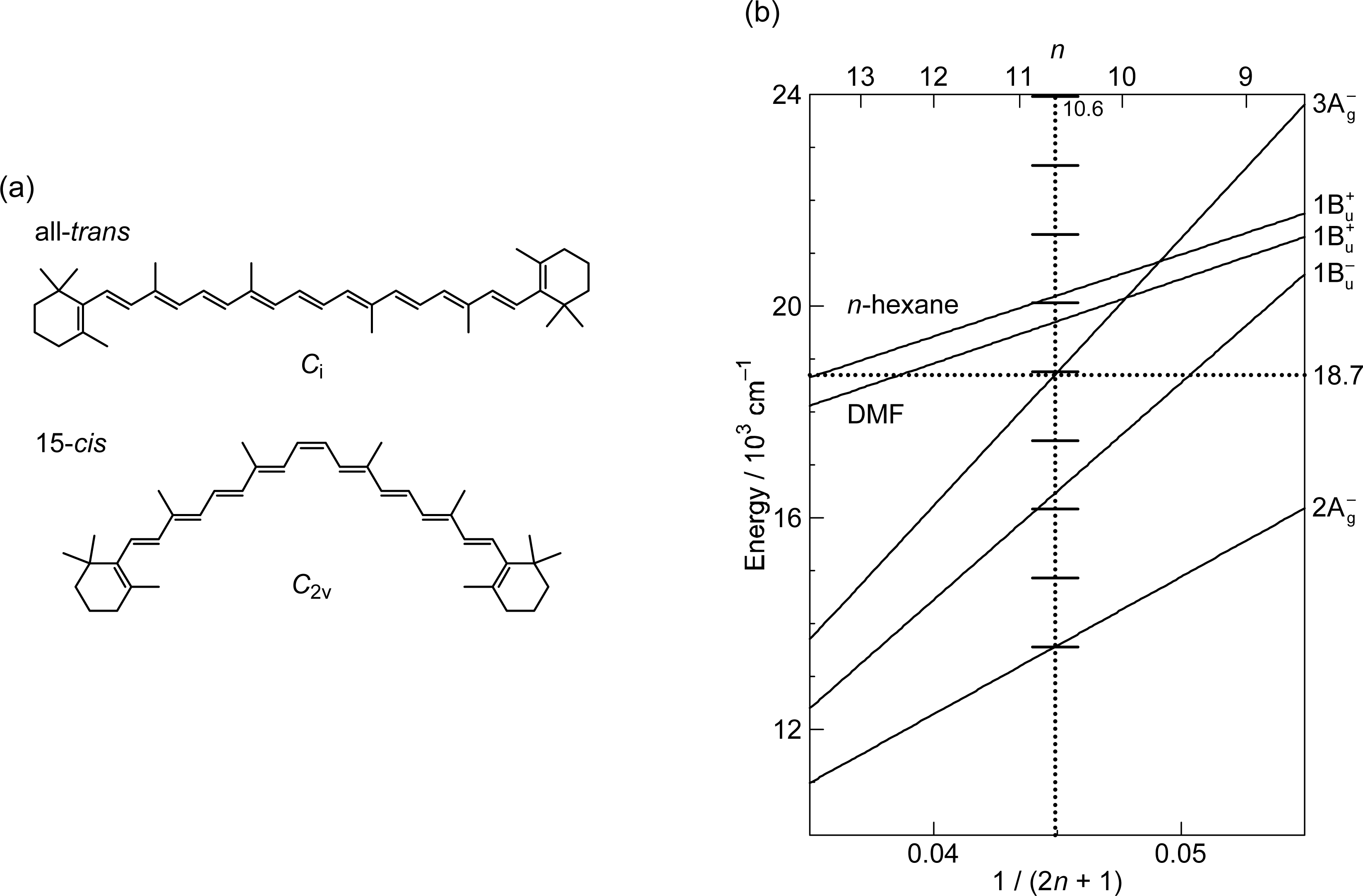
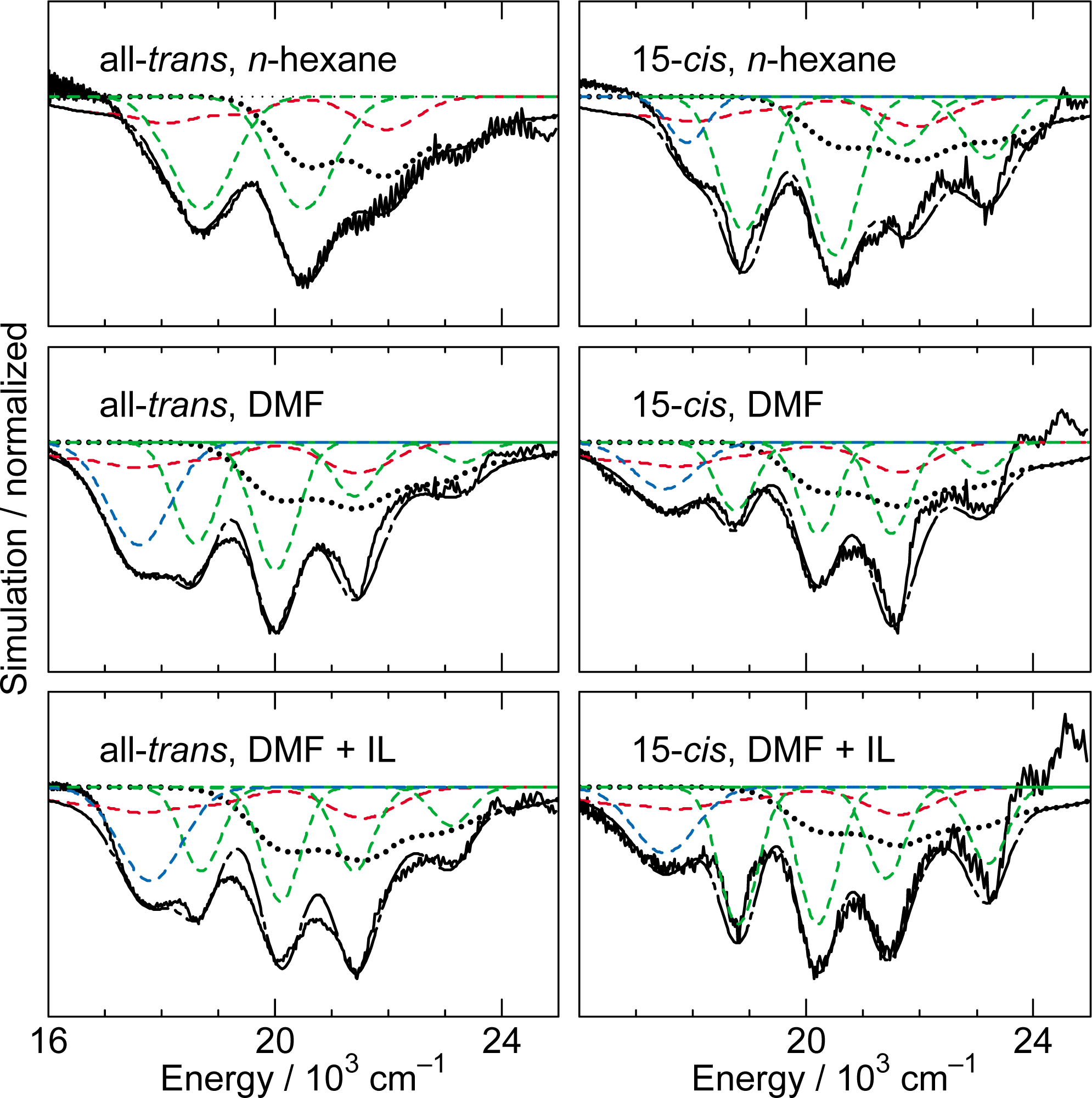
2.3. Excitation to the 1Bu+(1) Level of All-Trans- and 15-Cis-β-Carotenes in Nonpolar and Polar Solvents [14]
3. Pump-Probe Spectroscopy: Coherent Excitation
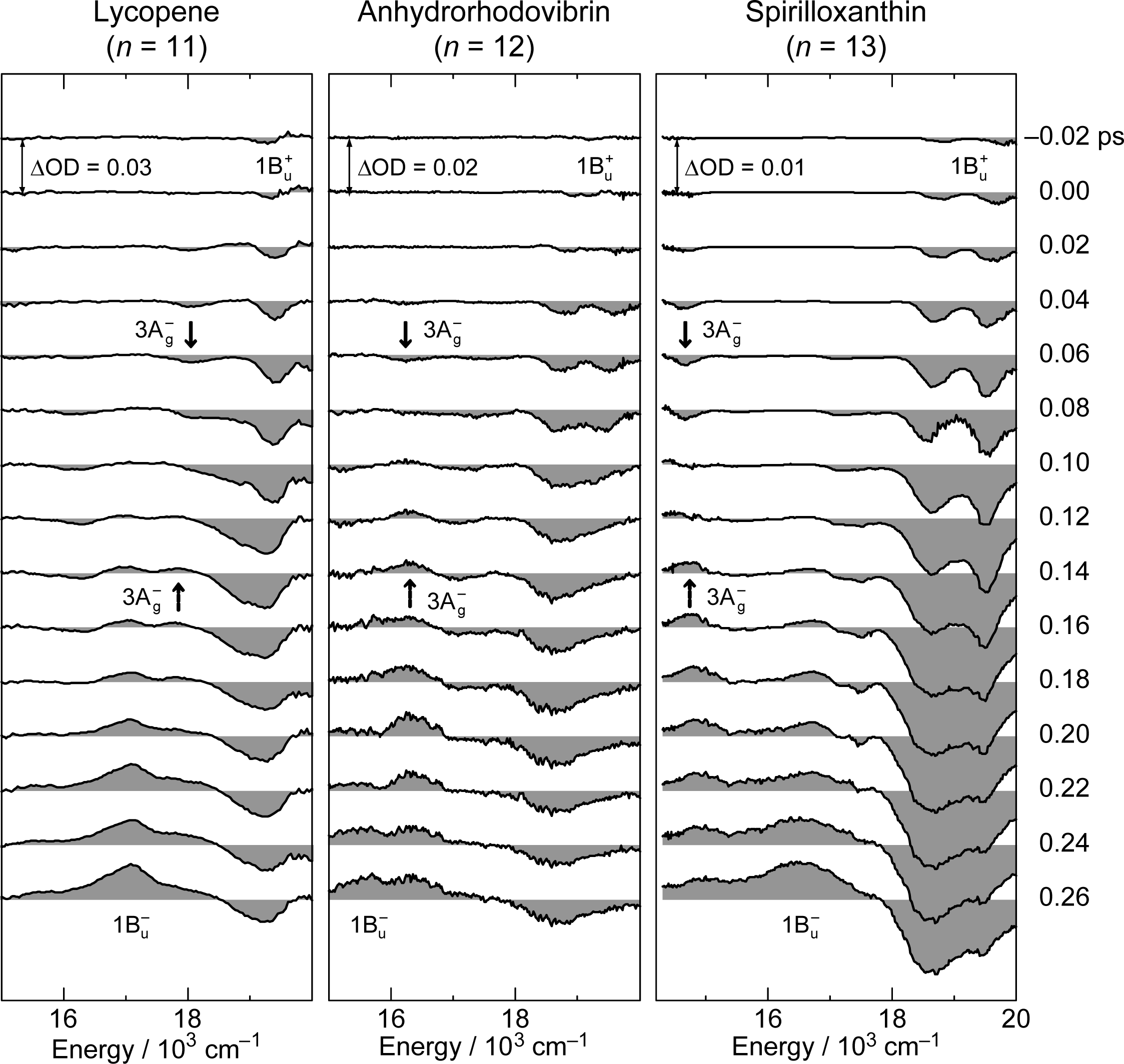
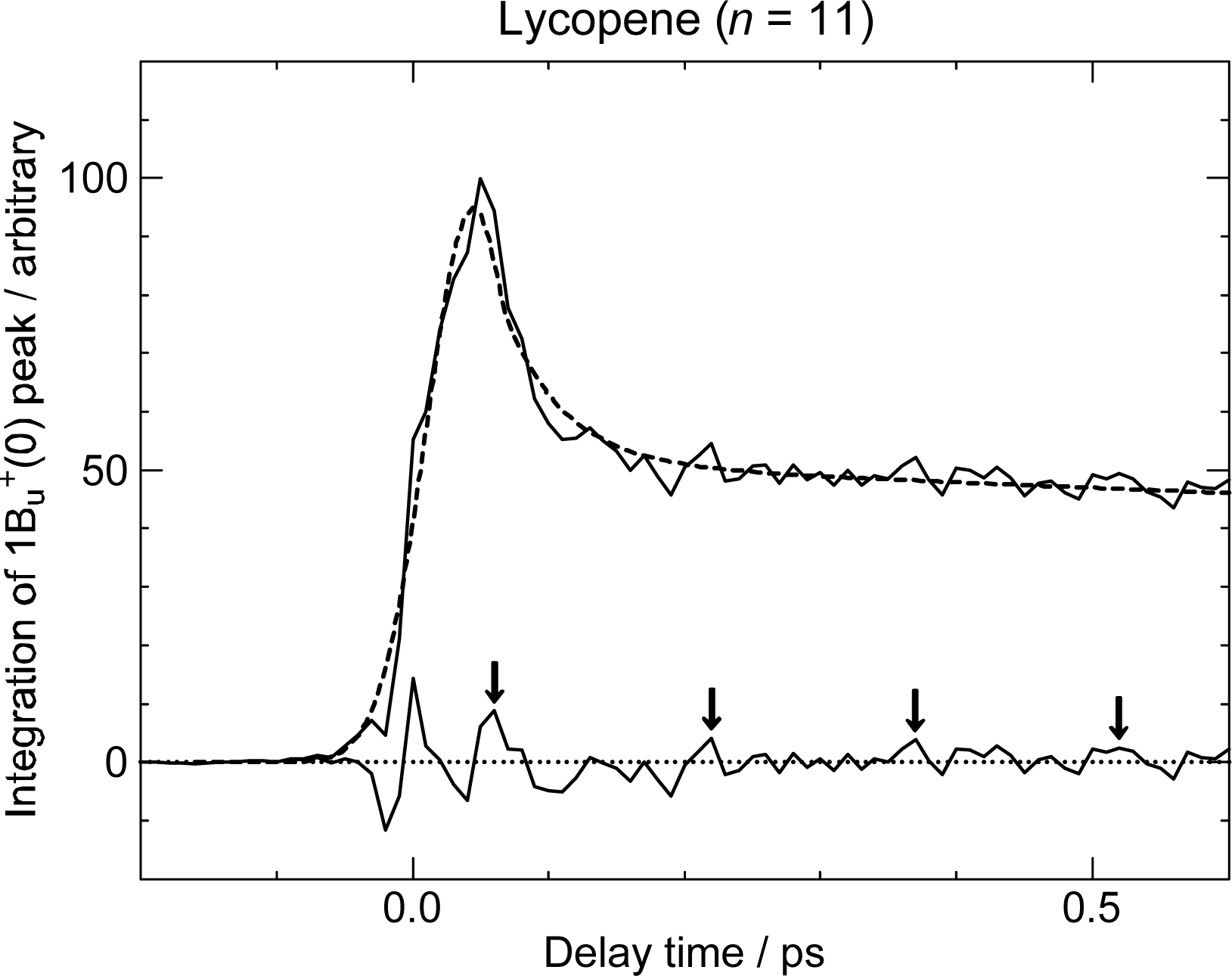
3.1. Excitation to the 1Bu+(0) Level of Car (n = 11–13) in THF: Negligible Shift of the 3Ag− Potential [11]
3.2. Excitation to the 1Bu+(0) Level of Cars (n = 9–13) in THF: Quantum Beat Mechanism [16]
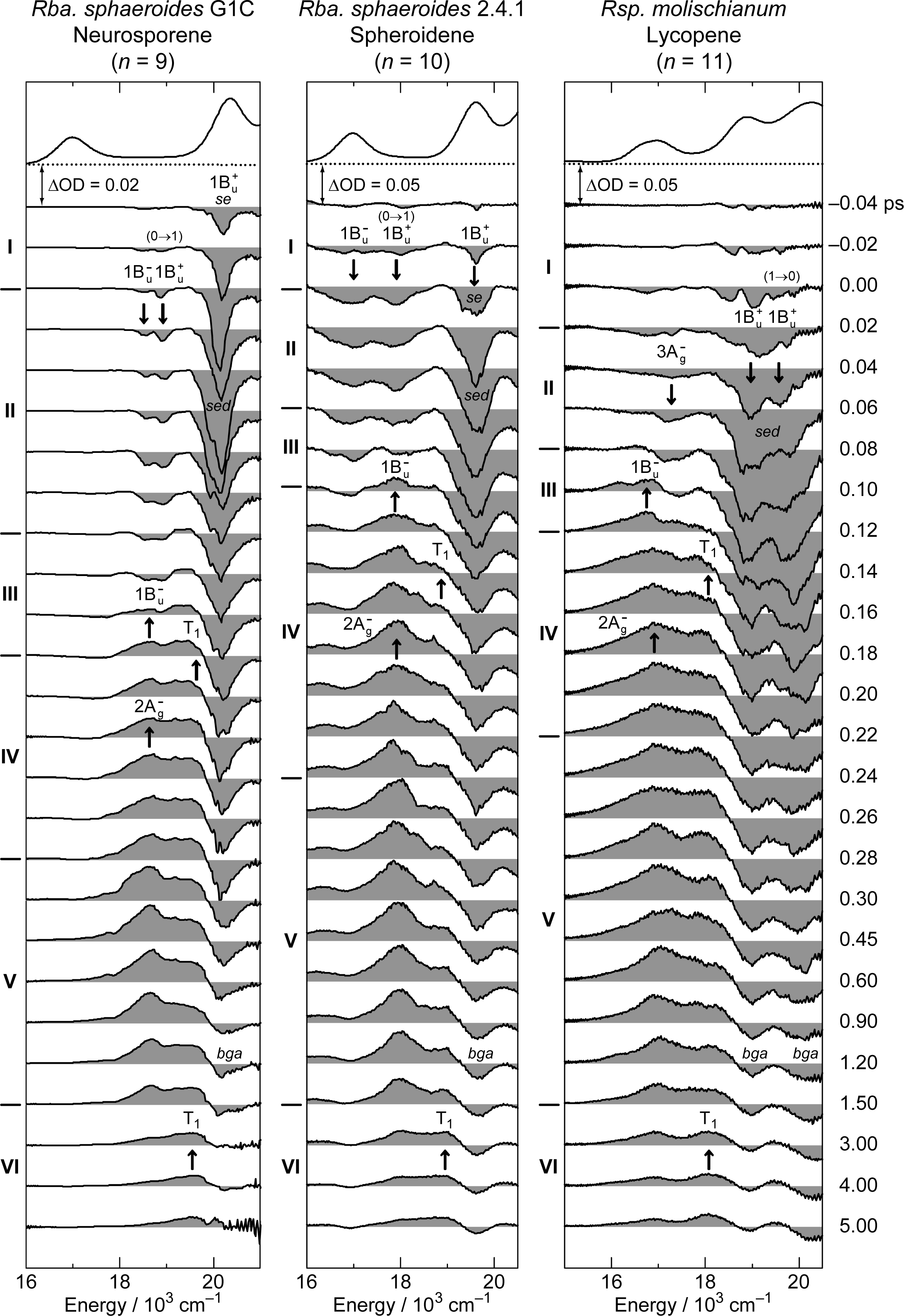
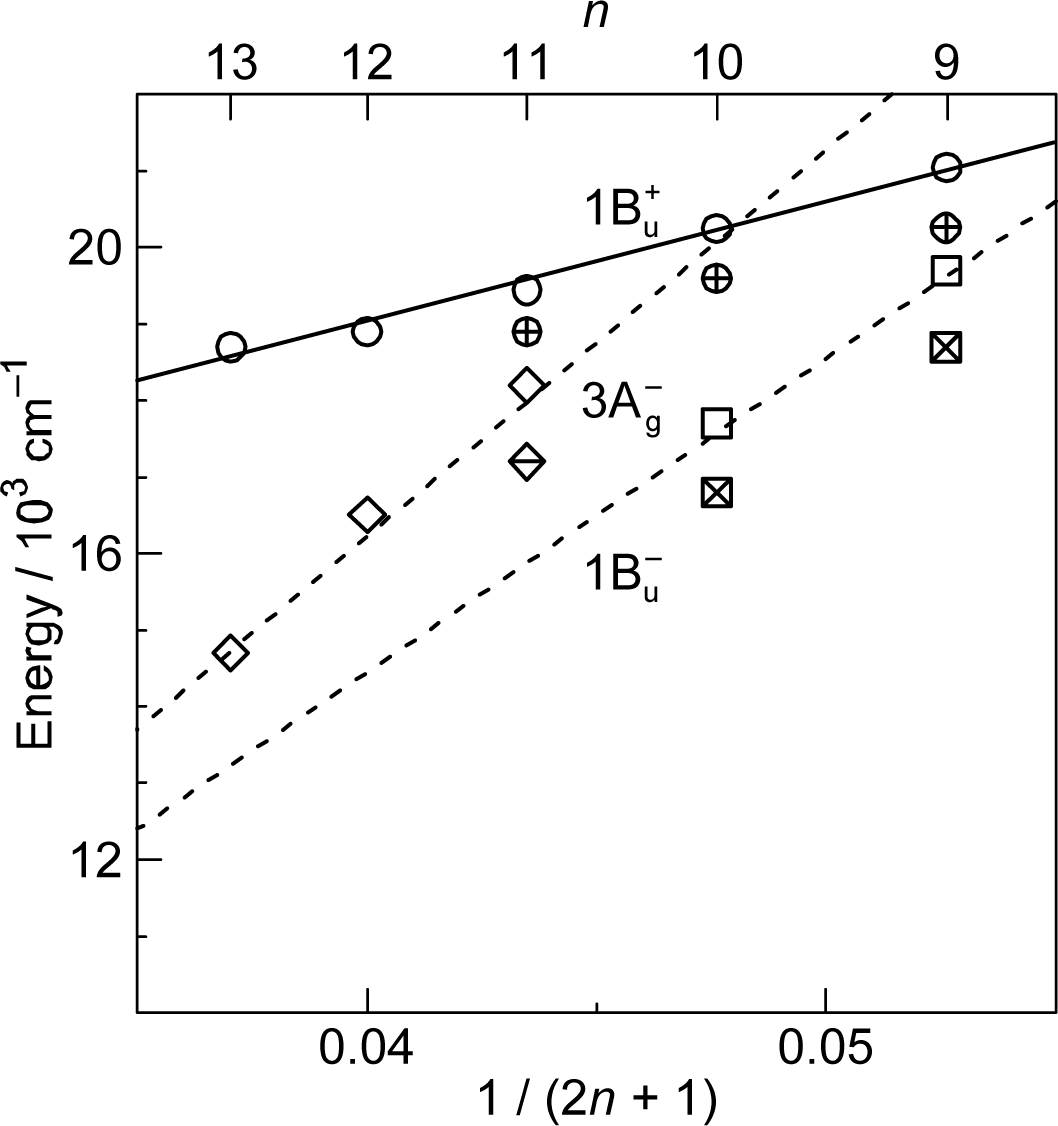
3.3. Excitation to the 1Bu+(0) Level of Cars (n = 9–11) Bound to LH2 Antenna Complexes [17]
4. Kerr-Gate Fluorescence Spectroscopy
Excitation to the 1Bu+(υ = 3 or 4) Vibronic Level of Cars (n = 9–12) in Nonpolar Solvent and Probing the 1Bu+(2) → 1Bu+(1) → 1Bu+(0) Vibrational Relaxation [9]
5. Summary and Future Trend
6. Conclusions
7. Relevant Works by Other Investigators
7.1. Ab Initio Calculation of the π → π* Excited States of Linear Polyenes [32]
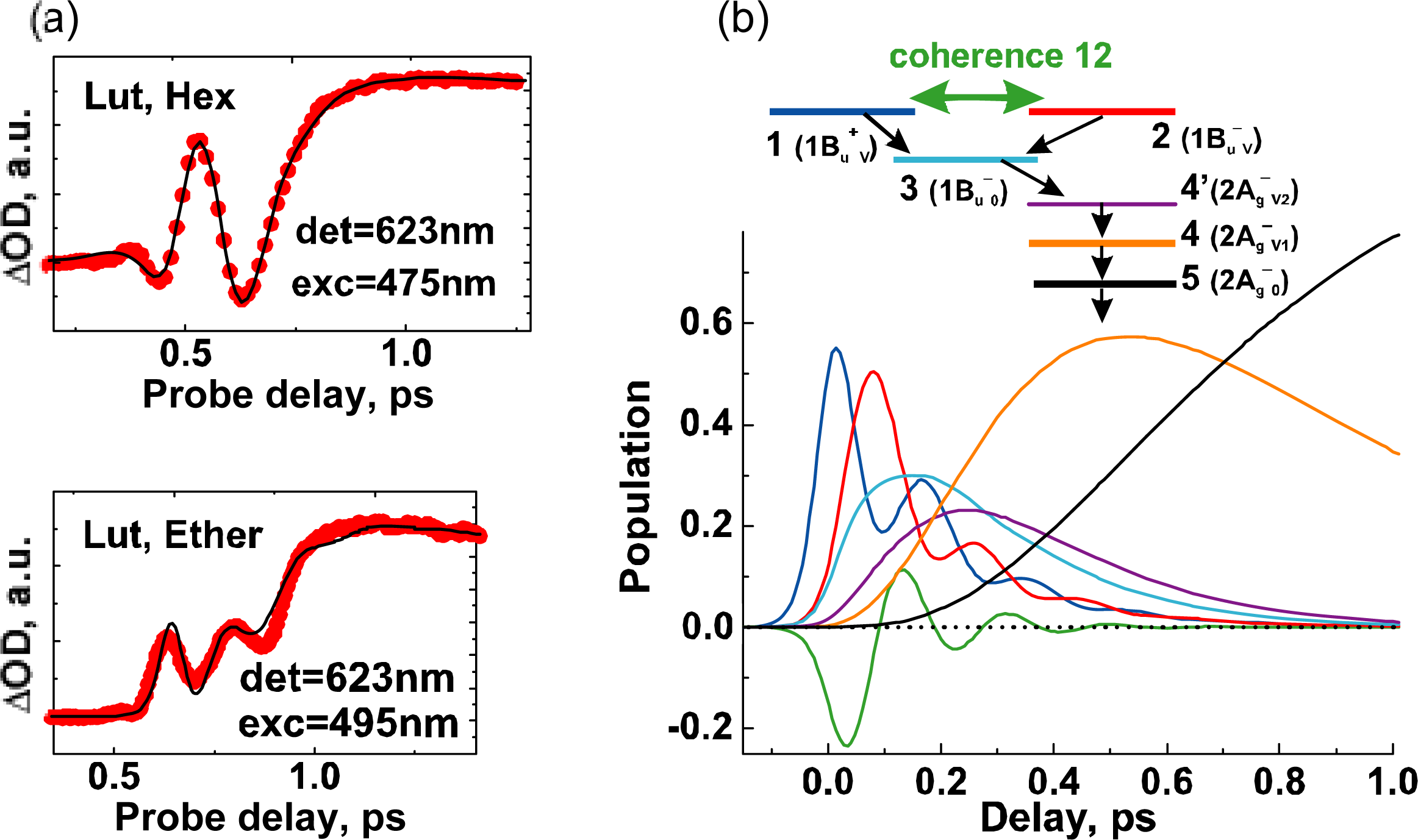
7.2. Oscillatory Intensity Changes in Electronic Absorption Immediately after Pulsed Excitation of Lutein [33,34]
Acknowledgments
References and Notes
- Koyama, Y; Kakitani, Y; Watanabe, Y. Primary Processes of Photosynthesis, Part I: Principles and Apparatus (Comprehensive Series in Photochemical and Photobiology); Renger, G, Ed.; RSC Publishing: Cambridge, UK, 2008; pp. 151–201. [Google Scholar]
- Pariser, R. Theory of the Electronic Spectra and Structure of the Polyacenes and of Alternant Hydrocarbons. J. Chem. Phys 1956, 24, 250–268. [Google Scholar]
- Callis, PR; Scott, TW; Albrecht, AC. Perturbation selection rules for multiphoton electronic spectroscopy of neutral alternant hydrocarbons. J. Chem. Phys 1983, 78, 16–22. [Google Scholar]
- Tavan, P; Schulten, K. The low-lying electronic excitations in long polyenes: A PPP-MRD-CI study. J. Chem. Phys 1986, 85, 6602–6609. [Google Scholar]
- Ikuta, M; Yabushita, A; Rondonuwu, FS; Akahane, J; Koyama, Y; Kobayashi, T. The 1Bu+ → 3Ag− → 1Bu− → 2Ag− internal conversion in carotenoids following the energy-gap law identified by 5 fs spectroscopy. Chem. Phys. Lett 2006, 422, 95–99. [Google Scholar]
- Rondonuwu, FS; Kakitani, Y; Tamura, H; Koyama, Y. Singlet internal conversion processes in the order of 1Bu+ → 3Ag− → 1Bu− → 2Ag− → 1Ag− in all-trans-spheroidene and lycopene as revealed by subpicosecond time-resolved Raman spectroscopy. Chem. Phys. Lett 2006, 429, 234–238. [Google Scholar]
- Rondonuwu, FS; Yokoyama, K; Fujii, R; Koyama, Y; Cogdell, RJ; Watanabe, Y. The role of the 11Bu− state in carotenoid-to-bacteriochlorophyll singlet-energy transfer in the LH2 antenna complexes from Rhodobacter sphaeroides G1C, Rhodobacter sphaeroides 2.4.1, Rhodospirillum molischianum and Rhodopseudomonas acidophila. Chem. Phys. Lett 2004, 390, 314–322. [Google Scholar]
- Koyama, Y; Kakitani, Y. Mechanisms of carotenoid-to-bacteriochlorophyll energy transfer in the light harvesting antenna complexes 1 and 2: Dependence on the conjugation length of carotenoids. In Chlorophylls and Bacteriochlorophylls: Biochemistry, Biophysics, Functions and Applications; Grimm, B, Porra, RJ, Rüdiger, W, Scheer, H, Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 431–443. [Google Scholar]
- Kakitani, Y; Miki, T; Koyama, Y; Nagae, H; Nakamura, R; Kanematsu, Y. Vibrational relaxation and internal conversion in the overlapped optically-allowed 1Bu+ and optically-forbidden 1Bu− or 3Ag− vibronic levels of carotenoids: Effects of diabatic mixing as determined by Kerr-gate fluorescence spectroscopy. Chem. Phys. Lett 2009, 477, 194–201. [Google Scholar]
- Nagae, H; Kakitani, Y; Koyama, Y. Theoretical description of diabatic mixing and coherent excitation in singlet-excited states of carotenoids. Chem. Phys. Lett 2009, 474, 342–351. [Google Scholar]
- Li, C; Miki, T; Kakitani, Y; Koyama, Y; Nagae, H. Negligible shift of 3Ag− potential in longer-chain carotenoids as revealed by a single persistent peak of 3Ag− → 1Ag− stimulated emission followed by 3Ag− ← 1Ag− transient-absorption. Chem. Phys. Lett 2007, 450, 112–118. [Google Scholar]
- Fujii, R; Inaba, T; Watanabe, Y; Koyama, Y; Zhang, J-P. Two different pathways of internal conversion in carotenoids depending on the length of the conjugated chain. Chem. Phys. Lett 2003, 369, 165–172. [Google Scholar]
- Sutresno, A; Kakitani, Y; Zuo, P; Li, C; Koyama, Y; Nagae, H. Presence and absence of electronic mixing in shorter-chain and longer-chain carotenoids: Assignment of the symmetries of 1Bu− and 3Ag− states located just below the 1Bu+ state. Chem. Phys. Lett 2007, 447, 127–133. [Google Scholar]
- Bialek-Bylka, GE; Kakitani, Y; Li, C; Koyama, Y; Kuki, M; Yamano, Y; Nagae, H. Excitation followed by stimulated-emission from diabatic levels in all-trans-and 15-cis-β-carotenes: Effects of molecular symmetry and solvent polarity. Chem. Phys. Lett 2008, 454, 367–373. [Google Scholar]
- Onaka, K; Fujii, R; Nagae, H; Kuki, M; Koyama, Y; Watanabe, Y. The state energy and the displacements of the potential minima of the 2Ag− state in all-trans-β-carotene as determined by fluorescence spectroscopy. Chem. Phys. Lett 1999, 315, 75–81. [Google Scholar]
- Miki, T; Kakitani, Y; Koyama, Y; Nagae, H. Stimulated emission from the 1Bu− (0) level and the 1Bu+ (0) + 1Bu− (1 and 2) diabatic levels upon excitation to the 1Bu+ (0) level in neurosporene and spheroidene. Chem. Phys. Lett 2008, 457, 222–226. [Google Scholar]
- Christiana, R; Miki, T; Kakitani, Y; Aoyagi, S; Koyama, Y; Limantara, L. Energies and excited-state dynamics of 1Bu+, 1Bu− and 3Ag− states of carotenoids bound to LH2 antenna complexes from purple photosynthetic bacteria. Chem. Phys. Lett 2009, 480, 289–295. [Google Scholar]
- Zhang, J-P; Inaba, T; Watanabe, Y; Koyama, Y. Excited-state dynamics among the 1Bu+, 1Bu− and 2Ag− states of all-trans-neurosporene as revealed by near-infrared time-resolved absorption spectroscopy. Chem. Phys. Lett 2000, 332, 351–358. [Google Scholar]
- Rondonuwu, FS; Watanabe, Y; Zhang, J-P; Furuichi, K; Koyama, Y. Internal-conversion and radiative-transition processes among the 1Bu+, 1Bu− and 2Ag− states of all-trans-neurosporene as revealed by subpicosecond time-resolved Raman spectroscopy. Chem. Phys. Lett 2002, 357, 376–384. [Google Scholar]
- Fujii, R; Fujino, T; Inaba, T; Nagae, H; Koyama, Y. Internal conversion of 1Bu+ → 1Bu− → 2Ag− and fluorescence from the 1Bu− state in all-trans-neurosporene as probed by up-conversion spectroscopy. Chem. Phys. Lett 2004, 384, 9–15. [Google Scholar]
- Nakamura, R; Fujii, R; Nagae, H; Koyama, Y; Kanematsu, Y. Vibrational relaxation in the 1Bu+ state of carotenoids as determined by Kerr-gate fluorescence spectroscopy. Chem. Phys. Lett 2004, 400, 7–14. [Google Scholar]
- Fourkas, JT; Kawashima, H; Nelson, KA. Theory of nonlinear optical experiments with harmonic oscillators. J. Chem. Phys 1995, 103, 4393–4407. [Google Scholar]
- Gradinaru, CC; Kennis, JTM; Papagiannakis, E; van Stokkum, IHM; Cogdell, RJ; Fleming, GR; Niederman, RA; van Grondelle, R. An usual pathway of excitation energy deactivation in carotenoids: Singlet-to-triplet conversion on an ultrafast timescale in a photosynthetic antenna. Proc. Natl. Acad. Sci. USA 2001, 98, 2364–2369. [Google Scholar]
- Papagiannakis, E; Kennis, JTM; van Stokkum, IHM; Cogdell, RJ; van Grondelle, R. An alternative carotenoid-to-bacteriochlorophyll energy transfer pathway in photosynthetic light harvesting. Proc. Natl. Acad. Sci. USA 2002, 99, 6017–6022. [Google Scholar]
- Papagiannakis, E; Das, SK; Gall, A; van Stokkum, IHM; Robert, B; van Grondelle, R; Frank, HA; Kennis, JTM. Light harvesting by carotenoids incorporated into the B850 light-harvesting complex from Rhodobacter sphaeroides R-26.1: Excited-state relaxation, ultrafast triplet formation, and energy transfer to bacteriochlorophyll. J. Phys. Chem. B 2003, 107, 5642–5649. [Google Scholar]
- Cerullo, G; Polli, D; Lanzani, G; De Silvestri, S; Hashimoto, H; Cogdell, RJ. Photosynthetic light harvesting by carotenoids: Detection of an intermediate excited state. Science 2002, 298, 2395–2398. [Google Scholar]
- Larsen, DS; Papagiannakis, E; van Stokkum, IHM; Vengris, M; Kennis, JTM; van Grondelle, R. Excited state dynamics of β-carotene explored with dispersed multi-pulse transient absorption. Chem. Phys. Lett 2003, 381, 733–742. [Google Scholar]
- Polivka, T; Sundström, V. Ultrafast dynamics of carotenoid excited states-from solution to natural and artificial systems. Chem. Rev 2004, 104, 2021–2071. [Google Scholar]
- Polivka, T; Sundström, V. Dark excited states of carotenoids: Concensus and controversy. Chem. Phys. Lett 2009, 477, 1–11. [Google Scholar]
- Hashimoto, H; Yanagi, K; Yoshizawa, M; Polli, D; Cerullo, G; Lanzani, G; De Silvestri, S; Gardiner, AT; Cogdell, RJ. The very early events following photoexcitation of carotenoids. Arch. Biochem. Biophys 2004, 430, 61–69. [Google Scholar]
- Hashimoto, H; Kosumi, D; Sugisaki, M; Fujiwara, M; Fujii, R; Cogdell, R. The possible involvement of multiple ‘dark’ states in carotenoid photophysics. Carotenoid Sci 2009, 14, 14–20. [Google Scholar]
- Kurashige, Y; Nakano, H; Nakao, Y; Hirao, K. The π → π* excited states of long linear polyenes studied by the CASCI-MRMP method. Chem. Phys. Lett 2004, 400, 425–429. [Google Scholar]
- Lustres, JLP; Dobryakov, AL; Holzwarth, A; Veiga, M. S2→S1 internal conversion in β-Carotene: Strong vibronic coupling from amplitude oscillations of transient absorption bands. Angew. Chem. Int. Ed 2007, 46, 3758–3761. [Google Scholar]
- Ostroumov, E; Müller, MG; Marian, CM; Kleinschmidt, M; Holzwarth, AR. Electronic coherence provides a direct proof for energy-level crossing in photoexcited lutein and β-carotene. Phys Rev Lett 2009, 103, 108302:1–108302:4. [Google Scholar]















| Neurosporene (n = 9) | Spheroidene (n = 10) | Lycopene (n = 11) | Anhydrorhodovibrin (n = 12) | Spirilloxanthin (n = 13) | |
|---|---|---|---|---|---|
| 1Bu+ | 0.10 | 0.10 | 0.02 | 0.01 | 0.01 |
| 1Bu− | 0.24 | 0.23 | – | – | – |
| 3Ag− | – | – | 0.15 | 0.10 | 0.10 |
| 2Ag− | 24.0 | 8.9 | 3.9 | 2.2 | 1.4 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Koyama, Y.; Kakitani, Y.; Miki, T.; Christiana, R.; Nagae, H. Excited-State Dynamics of Overlapped Optically-Allowed 1Bu+ and Optically-Forbidden 1Bu- or 3Ag- Vibronic Levels of Carotenoids: Possible Roles in the Light-Harvesting Function. Int. J. Mol. Sci. 2010, 11, 1888-1929. https://doi.org/10.3390/ijms11041888
Koyama Y, Kakitani Y, Miki T, Christiana R, Nagae H. Excited-State Dynamics of Overlapped Optically-Allowed 1Bu+ and Optically-Forbidden 1Bu- or 3Ag- Vibronic Levels of Carotenoids: Possible Roles in the Light-Harvesting Function. International Journal of Molecular Sciences. 2010; 11(4):1888-1929. https://doi.org/10.3390/ijms11041888
Chicago/Turabian StyleKoyama, Yasushi, Yoshinori Kakitani, Takeshi Miki, Rebecca Christiana, and Hiroyoshi Nagae. 2010. "Excited-State Dynamics of Overlapped Optically-Allowed 1Bu+ and Optically-Forbidden 1Bu- or 3Ag- Vibronic Levels of Carotenoids: Possible Roles in the Light-Harvesting Function" International Journal of Molecular Sciences 11, no. 4: 1888-1929. https://doi.org/10.3390/ijms11041888





