Intrinsically Disordered Proteins in a Physics-Based World
Abstract
:1. Introduction
2. Challenges in Detailed Experimental Characterization of IDPs
3. Opportunities and Challenges for de Novo Simulations
4. Key Lessons from Recent de Novo Simulations of Regulatory IDPs
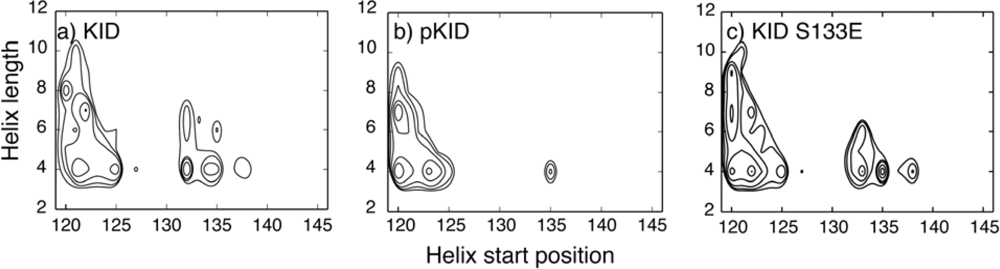
4.1. Unbound IDPs: Nascent Structures and Dependence on Post-Translational Modifications
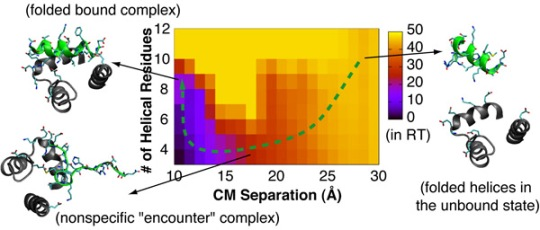
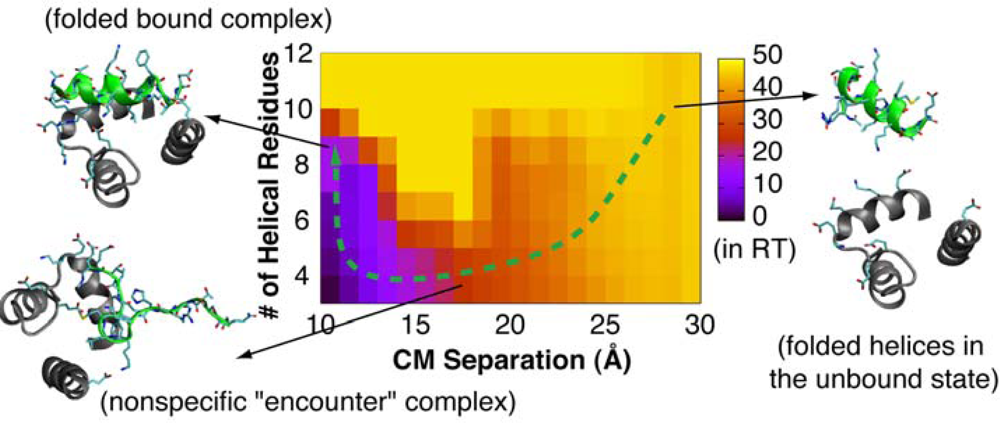
4.2. Mechanism of Coupled Binding and Folding: Intrinsic Flexibility vs. Preformed Structures
5. Conclusions
Acknowledgments
References
- Kriwacki, RW; Hengst, L; Tennant, L; Reed, SI; Wright, PE. Structural studies of p21(Waf1/Cip1/Sdi1) in the free and Cdk2-bound state: Conformational disorder mediates binding diversity. Proc. Natl. Acad. Sci. USA 1996, 93, 11504–11509. [Google Scholar]
- Wright, PE; Dyson, HJ. Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. J. Mol. Biol 1999, 293, 321–331. [Google Scholar]
- Tompa, P. Intrinsically unstructured proteins. Trends Biochem. Sci 2002, 27, 527–533. [Google Scholar]
- Fink, AL. Natively unfolded proteins. Curr. Opin. Struct. Biol 2005, 15, 35–41. [Google Scholar]
- Dunker, AK; Brown, CJ; Lawson, JD; Iakoucheva, LM; Obradovic, Z. Intrinsic disorder and protein function. Biochemistry 2002, 41, 6573–6582. [Google Scholar]
- Dunker, AK; Lawson, JD; Brown, CJ; Williams, RM; Romero, P; Oh, JS; Oldfield, CJ; Campen, AM; Ratliff, CR; Hipps, KW; Ausio, J; Nissen, MS; Reeves, R; Kang, CH; Kissinger, CR; Bailey, RW; Griswold, MD; Chiu, M; Garner, EC; Obradovic, Z. Intrinsically disordered protein. J. Mol. Graph. Model 2001, 19, 26–59. [Google Scholar]
- Dyson, HJ; Wright, PE. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol 2005, 6, 197–208. [Google Scholar]
- Uversky, VN; Oldfield, CJ; Dunker, AK. Showing your ID: Intrinsic disorder as an ID for recognition, regulation and cell signaling. J. Mol. Recognit 2005, 18, 343–384. [Google Scholar]
- Smock, RG; Gierasch, LM. Sending signals dynamically. Science 2009, 324, 198–203. [Google Scholar]
- Iakoucheva, LM; Brown, CJ; Lawson, JD; Obradovic, Z; Dunker, AK. Intrinsic disorder in cell-signaling and cancer-associated proteins. J. Mol. Biol 2002, 323, 573–584. [Google Scholar]
- Uversky, VN; Oldfield, CJ; Dunker, AK. Intrinsically disordered proteins in human diseases: Introducing the D-2 concept. Annu. Rev. Biophys 2008, 37, 215–246. [Google Scholar]
- Wright, PE; Dyson, HJ. Linking folding and binding. Curr. Opin. Struct. Biol 2009, 19, 31–38. [Google Scholar]
- Mittag, T; Orlicky, S; Choy, WY; Tang, XJ; Lin, H; Sicheri, F; Kay, LE; Tyers, M; Forman-Kay, JD. Dynamic equilibrium engagement of a polyvalent ligand with a single-site receptor. Proc. Natl. Acad. Sci. USA 2008, 105, 17772–17777. [Google Scholar]
- Mittag, T; Marsh, J; Grishaev, A; Orlicky, S; Lin, H; Sicheri, F; Tyers, M; Forman-Kay, JD. Structure/function implications in a dynamic complex of the intrinsically disordered Sic1 with the Cdc4 subunit of an SCF ubiquitin lLigase. Structure 2010, 18, 494–506. [Google Scholar]
- Meekin, TJ. Milk Proteins. J. Food Protect 1952, 15, 57–63. [Google Scholar]
- Jirgensons, B. Classification of proteins according to conformation. Macromol. Chem. Phys 1966, 91, 74–86. [Google Scholar]
- Doolittle, RF. Structural aspects of the fibrinogen to fibrin conversion. Adv. Protein Chem 1973, 27, 1–109. [Google Scholar]
- Doolittle, RF; Kollman, JM. Natively unfolded regions of the vertebrate fibrinogen molecule. Proteins 2006, 63, 391–397. [Google Scholar]
- Oldfield, CJ; Meng, J; Yang, JY; Yang, MQ; Uversky, VN; Dunker, AK. Flexible nets: disorder and induced fit in the associations of p53 and 14-3-3 with their partners. BMC Genomics 2008, 9, S1. [Google Scholar]
- Dunker, AK; Cortese, MS; Romero, P; Iakoucheva, LM; Uversky, VN. Flexible nets - The roles of intrinsic disorder in protein interaction networks. FEBS J 2005, 272, 5129–5148. [Google Scholar]
- Hilser, VJ; Thompson, EB. Intrinsic disorder as a mechanism to optimize allosteric coupling in proteins. Proc. Natl. Acad. Sci. USA 2007, 104, 8311–8315. [Google Scholar]
- Sugase, K; Dyson, HJ; Wright, PE. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature 2007, 447, 1021–1025. [Google Scholar]
- Narayanan, R; Ganesh, OK; Edison, AS; Hagen, SJ. Kinetics of folding and binding of an intrinsically disordered protein: The inhibitor of yeast aspartic proteinase YPrA. J. Am. Chem. Soc 2008, 130, 11477–11485. [Google Scholar]
- Lu, Q; Lu, HP; Wang, J. Exploring the mechanism of flexible biomolecular recognition with single molecule dynamics. Phys. Rev. Lett 2007, 98, 128105. [Google Scholar]
- Keskin, O; Gursoy, A; Ma, B; Nussinov, R. Principles of protein-protein interactions: What are the preferred ways for proteins to interact? Chem. Rev 2008, 108, 1225–1244. [Google Scholar]
- Receveur-Brechot, V; Bourhis, JM; Uversky, VN; Canard, B; Longhi, S. Assessing protein disorder and induced folding. Proteins 2006, 62, 24–45. [Google Scholar]
- Fuxreiter, M; Simon, I; Friedrich, P; Tompa, P. Preformed structural elements feature in partner recognition by intrinsically unstructured proteins. J. Mol. Biol 2004, 338, 1015–1026. [Google Scholar]
- Zor, T; Mayr, BM; Dyson, HJ; Montminy, MR; Wright, PE. Roles of phosphorylation and helix propensity in the binding of the KIX domain of CREB-binding protein by constitutive (c-Myb) and inducible (CREB) activators. J. Biol. Chem 2002, 277, 42241–42248. [Google Scholar]
- Bienkiewicz, EA; Adkins, JN; Lumb, KJ. Functional consequences of preorganized helical structure in the intrinsically disordered cell-cycle inhibitor p27(Kip1). Biochemistry 2002, 41, 752–759. [Google Scholar]
- Dunker, AK; Silman, I; Uversky, VN; Sussman, JL. Function and structure of inherently disordered proteins. Curr. Opin. Struct. Biol 2008, 18, 756–764. [Google Scholar]
- Bourhis, JM; Canard, B; Longhi, S. Predicting protein disorder and induced folding: From theoretical principles to practical applications. Curr. Protein Pept. Sci 2007, 8, 135–149. [Google Scholar]
- Bracken, C; Iakoucheva, LM; Rorner, PR; Dunker, AK. Combining prediction, computation and experiment for the characterization of protein disorder. Curr. Opin. Struct. Biol 2004, 14, 570–576. [Google Scholar]
- Bartlett, AI; Radford, SE. An expanding arsenal of experimental methods yields an explosion of insights into protein folding mechanisms. Nat. Struct. Mol. Biol 2009, 16, 582–588. [Google Scholar]
- Eliezer, D. Biophysical characterization of intrinsically disordered proteins. Curr. Opin. Struct. Biol 2009, 19, 23–30. [Google Scholar]
- Noivirt-Brik, O; Prilusky, J; Sussman, JL. Assessment of disorder predictions in CASP8. Proteins 2009, 77, S210–S216. [Google Scholar]
- Meszaros, B; Tompa, P; Simon, I; Dosztanyi, Z. Molecular principles of the interactions of disordered proteins. J. Mol. Biol 2007, 372, 549–561. [Google Scholar]
- Keskin, O; Gursoy, A; Ma, B; Nussinov, R. Towards drugs targeting multiple proteins in a systems biology approach. Curr. Top Med. Chem 2007, 7, 943–951. [Google Scholar]
- Dyson, HJ; Wright, PE. Unfolded proteins and protein folding studied by NMR. Chem. Rev 2004, 104, 3607–3622. [Google Scholar]
- Wishart, DS; Sykes, BD. The C-13 Chemical-Shift Index—a simple method for the identification of protein secondary structure using C-13 chemical-shift data. J. Biomol. NMR 1994, 4, 171–180. [Google Scholar]
- Wang, AC; Bax, A. Determination of the backbone dihedral angles phi in human ubiquitin from reparametrized empirical Karplus equations. J. Am. Chem. Soc 1996, 118, 2483–2494. [Google Scholar]
- Cornilescu, G; Delaglio, F; Bax, A. Protein backbone angle restraints from searching a database for chemical shift and sequence homology. J. Biomol. NMR 1999, 13, 289–302. [Google Scholar]
- Marsh, JA; Singh, VK; Jia, ZC; Forman-Kay, JD. Sensitivity of secondary structure propensities to sequence differences between alpha- and gamma-synuclein: Implications for fibrillation. Protein Sci 2006, 15, 2795–2804. [Google Scholar]
- Gillespie, JR; Shortle, D. Characterization of long-range structure in the denatured state of staphylococcal nuclease. 1. Paramagnetic relaxation enhancement by nitroxide spin labels. J. Mol. Biol 1997, 268, 158–169. [Google Scholar]
- Gillespie, JR; Shortle, D. Characterization of long-range structure in the denatured state of staphylococcal nuclease. 2. Distance restraints from paramagnetic relaxation and calculation of an ensemble of structures. J. Mol. Biol 1997, 268, 170–184. [Google Scholar]
- Shortle, D; Ackerman, MS. Persistence of native-like topology in a denatured protein in 8 M urea. Science 2001, 293, 487–489. [Google Scholar]
- Mittag, T; Forman-Kay, JD. Atomic-level characterization of disordered protein ensembles. Curr. Opin. Struct. Biol 2007, 17, 3–14. [Google Scholar]
- Vendruscolo, M. Determination of conformationally heterogeneous states of proteins. Curr. Opin. Struct. Biol 2007, 17, 15–20. [Google Scholar]
- Bloembergen, N; Morgan, LO. Proton relaxation times in paramagnetic solutions effecs of electron spin relaxation. J. Chem. Phys 1961, 34, 842–850. [Google Scholar]
- Lindorff-Larsen, K; Kristjansdottir, S; Teilum, K; Fieber, W; Dobson, CM; Poulsen, FM; Vendruscolo, M. Determination of an ensemble of structures representing the denatured state of the bovine acyl-coenzyme A binding protein. J. Am. Chem. Soc 2004, 126, 3291–3299. [Google Scholar]
- Vise, P; Baral, B; Stancik, A; Lowry, DF; Daughdrill, GW. Identifying long-range structure in the intrinsically unstructured transactivation domain of p53. Proteins 2007, 67, 526–530. [Google Scholar]
- Ganguly, D; Chen, J. Structural interpretation of paramagnetic relaxation enhancement-derived distances for disordered protein states. J. Mol. Biol 2009, 390, 467–477. [Google Scholar]
- Delaglio, F; Kontaxis, G; Bax, A. Protein structure determination using molecular fragment replacement and NMR dipolar couplings. J. Am. Chem. Soc 2000, 122, 2142–2143. [Google Scholar]
- Hus, JC; Marion, D; Blackledge, M. Determination of protein backbone structure using only residual dipolar couplings. J. Am. Chem. Soc 2001, 123, 1541–1542. [Google Scholar]
- Rathinavelan, T; Im, W. A novel strategy to determine protein structures using exclusively residual dipolar coupling. J. Comput. Chem 2008, 29, 1640–1649. [Google Scholar]
- Jha, AK; Colubri, A; Freed, KF; Sosnick, TR. Statistical coil model of the unfolded state: Resolving the reconciliation problem. Proc. Natl. Acad. Sci. USA 2005, 102, 13099–13104. [Google Scholar]
- Bernado, P; Blanchard, L; Timmins, P; Marion, D; Ruigrok, RWH; Blackledge, M. A structural model for unfolded proteins from residual dipolar couplings and small-angle x-ray scattering. Proc. Natl. Acad. Sci. USA 2005, 102, 17002–17007. [Google Scholar]
- Marsh, JA; Baker, JMR; Tollinger, M; Forman-Kay, JD. Calculation of residual dipolar couplings from disordered state ensembles using local alignment. J. Am. Chem. Soc 2008, 130, 7804–7805. [Google Scholar]
- Jensen, MR; Salmon, L; Nodet, G; Blackledge, M. Defining conformational ensembles of intrinsically disordered and partially folded proteins directly from chemical shifts. J. Am. Chem. Soc 2010, 132, 1270–1272. [Google Scholar]
- Felitsky, DJ; Lietzow, MA; Dyson, HJ; Wright, PE. Modeling transient collapsed states of an unfolded protein to provide insights into early folding events. Proc. Natl. Acad. Sci. USA 2008, 105, 6278–6283. [Google Scholar]
- Jensen, MR; Houben, K; Lescop, E; Blanchard, L; Ruigrok, RW; Blackledge, M. Quantitative conformational analysis of partially folded proteins from residual dipolar couplings: application to the molecular recognition element of Sendai virus nucleoprotein. J. Am. Chem. Soc 2008, 130, 55–61. [Google Scholar]
- Marsh, JA; Neale, C; Jack, FE; Choy, WY; Lee, AY; Crowhurst, KA; Forman-Kay, JD. Improved structural characterizations of the drkN SH3 domain unfolded state suggest a compact ensemble with native-like and non-native structure. J. Mol. Biol 2007, 367, 1494–1510. [Google Scholar]
- Mackerell, AD. Empirical force fields for biological macromolecules: Overview and issues. J. Comput. Chem 2004, 25, 1584–1604. [Google Scholar]
- Ponder, JW; Case, DA. Force fields for protein simulations. Adv. Protein Chem 2003, 66, 27–85. [Google Scholar]
- Yoda, T; Sugita, Y; Okamoto, Y. Secondary-structure preferences of force fields for proteins evaluated by generalized-ensemble simulations. Chem. Phys 2004, 307, 269–283. [Google Scholar]
- Best, RB; Buchete, NV; Hummer, G. Are current molecular dynamics force fields too helical? Biophys. J 2008, 95, L07–L09. [Google Scholar]
- Kang, M; Smith, PE. A Kirkwood-Buff derived force field for amides. J. Comput. Chem 2006, 27, 1477–1485. [Google Scholar]
- Lindorff-Larsen, K; Piana, S; Palmo, K; Maragakis, P; Klepeis, JL; Dror, RO; Shaw, DE. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins 2010, 78, 1950–1958. [Google Scholar]
- Best, RB; Mittal, J. Balance between alpha and beta structures in ab initio protein folding. J. Phys. Chem. B 2010, 114, 8790–8798. [Google Scholar]
- Mittal, J; Best, RB. Tackling force-field bias in protein folding simulations: folding of Villin HP35 and Pin WW domains in explicit water. Biophys. J 2010, 99, L26–L28. [Google Scholar]
- Chen, JH; Brooks, CL; Khandogin, J. Recent advances in implicit solvent based methods for biomolecular simulations. Curr. Opin. Struct. Biol 2008, 18, 140–148. [Google Scholar]
- Roux, B; Simonson, T. Implicit solvent models. Biophys. Chem 1999, 78, 1–20. [Google Scholar]
- Im, WP; Lee, MS; Brooks, CL. Generalized born model with a simple smoothing function. J. Comput. Chem 2003, 24, 1691–1702. [Google Scholar]
- Chen, JH; Im, WP; Brooks, CL. Balancing solvation and intramolecular interactions: Toward a consistent generalized born force field. J. Am. Chem. Soc 2006, 128, 3728–3736. [Google Scholar]
- Khandogin, J; Brooks, CL. Toward the accurate first-principles prediction of ionization equilibria in proteins. Biochemistry 2006, 45, 9363–9373. [Google Scholar]
- Khandogin, J; Chen, JH; Brooks, CL. Exploring atomistic details of pH-dependent peptide folding. Proc. Natl. Acad. Sci. USA 2006, 103, 18546–18550. [Google Scholar]
- Khandogin, J; Brooks, CL. Linking folding with aggregation in Alzheimer’s beta-amyloid peptides. Proc. Natl. Acad. Sci. USA 2007, 104, 16880–16885. [Google Scholar]
- Khandogin, J; Raleigh, DP; Brooks, CL. Folding intermediate in the villin headpiece domain arises from disruption of a N-terminal hydrogen-bonded network. J. Am. Chem. Soc 2007, 129, 3056–3057. [Google Scholar]
- Chen, JH; Brooks, CL. Can molecular dynamics simulations provide high-resolution refinement of protein structure? Proteins 2007, 67, 922–930. [Google Scholar]
- Ganguly, D; Chen, J. Atomistic details of the disordered states of KID and pKID. implications in coupled binding and folding. J. Am. Chem. Soc 2009, 131, 5214–5223. [Google Scholar]
- Chen, JH. Intrinsically disordered p53 extreme C-terminus binds to S100B(betabeta) through “fly-casting”. J. Am. Chem. Soc 2009, 131, 2088–2089. [Google Scholar]
- Okur, A; Strockbine, B; Hornak, V; Simmerling, C. Using PC clusters to evaluate the transferability of molecular mechanics force fields for proteins. J. Comput. Chem 2003, 24, 21–31. [Google Scholar]
- Jang, S; Kim, E; Pak, Y. Direct folding simulation of alpha-helices and beta-hairpins based on a single all-atom force field with an implicit solvation model. Proteins 2007, 66, 53–60. [Google Scholar]
- Vitalis, A; Pappu, RV. ABSINTH: A New Continuum Solvation Model for Simulations of Polypeptides in Aqueous Solutions. J. Comput. Chem 2009, 30, 673–699. [Google Scholar]
- Masunov, A; Lazaridis, T. Potentials of mean force between ionizable amino acid side chains in water. J. Am. Chem. Soc 2003, 125, 1722–1730. [Google Scholar]
- Chen, JH; Brooks, CL. Critical importance of length-scale dependence in implicit modeling of hydrophobic interactions. J. Am. Chem. Soc 2007, 129, 2444–2445. [Google Scholar]
- Chen, JH; Brooks, CL. Implicit modeling of nonpolar solvation for simulating protein folding and conformational transitions. Phys. Chem. Chem. Phys 2008, 10, 471–481. [Google Scholar]
- Scheraga, HA; Khalili, M; Liwo, A. Protein-folding dynamics: Overview of molecular simulation techniques. Annu. Rev. Phys. Chem 2007, 58, 57–83. [Google Scholar]
- Lei, H; Duan, Y. Improved sampling methods for molecular simulation. Curr. Opin. Struct. Biol 2007, 17, 187–191. [Google Scholar]
- Sugita, Y; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett 1999, 314, 141–151. [Google Scholar]
- Zuckerman, DM; Lyman, E. A second look at canonical sampling of biomolecules using replica exchange simulation. J. Chem. Theor. Comput 2006, 2, 1200–1202. [Google Scholar]
- Zheng, W; Andrec, M; Gallicchio, E; Levy, RM. Simulating replica exchange simulations of protein folding with a kinetic network model. Proc. Natl. Acad. Sci. USA 2007, 104, 15340–15345. [Google Scholar]
- Nymeyer, H. How efficient is replica exchange molecular dynamics? An analytic approach. J. Chem. Theor. Comput 2008, 4, 626–636. [Google Scholar]
- Zhang, W; Wu, C; Duan, Y. Convergence of replica exchange molecular dynamics. J Chem Phys 2005, 123, 154105:1–154105:9. [Google Scholar]
- Periole, X; Mark, AE. Convergence and sampling efficiency in replica exchange simulations of peptide folding in explicit solvent. J Chem Phys 2007, 126, 014903:1–014903:11. [Google Scholar]
- Sindhikara, D; Meng, YL; Roitberg, AE. Exchange frequency in replica exchange molecular dynamics. J Chem Phys 2008, 128, 024103:1–024103:10. [Google Scholar]
- Rao, F; Caflisch, A. Replica exchange molecular dynamics simulations of reversible folding. J. Chem. Phys 2003, 119, 4035–4042. [Google Scholar]
- Rico, F; Moy, VT. Energy landscape roughness of the streptavidin-biotin interaction. J. Mol. Recognit 2007, 20, 495–501. [Google Scholar]
- Janovjak, H; Sapra, KT; Kedrov, A; Muller, DJ. From valleys to ridges: Exploring the dynamic energy landscape of single membrane proteins. ChemPhysChem 2008, 9, 954–966. [Google Scholar]
- Kapon, R; Nevo, R; Reich, Z. Protein energy landscape roughness. Biochem. Soc. Trans 2008, 36, 1404–1408. [Google Scholar]
- Zwanzig, R. Diffusion in a rough potential. Proc. Natl. Acad. Sci. USA 1988, 85, 2029–2030. [Google Scholar]
- Shirts, M; Pande, VS. Computing-Screen savers of the world unite! Science 2000, 290, 1903–1904. [Google Scholar]
- Bowman, GR; Beauchamp, KA; Boxer, G; Pande, VS. Progress and challenges in the automated construction of Markov state models for full protein systems. J Chem Phys 2009, 131, 124101:1–124101:11. [Google Scholar]
- Bowman, GR; Huang, XH; Pande, VS. Using generalized ensemble simulations and Markov state models to identify conformational states. Methods 2009, 49, 197–201. [Google Scholar]
- Bowman, GR; Ensign, DL; Pande, VS. Enhanced modeling via network theory: Adaptive sampling of markov state models. J. Chem. Theor. Comput 2010, 6, 787–794. [Google Scholar]
- Bowman, GR; Pande, VS. Protein folded states are kinetic hubs. Proc. Natl. Acad. Sci. USA 2010, 107, 10890–10895. [Google Scholar]
- Voelz, VA; Bowman, GR; Beauchamp, K; Pande, VS. Molecular Simulation of ab Initio Protein Folding for a Millisecond Folder NTL9(1-39). J. Am. Chem. Soc 2010, 132, 1526–1528. [Google Scholar]
- Voelz, VA; Singh, VR; Wedemeyer, WJ; Lapidus, LJ; Pande, VS. Unfolded-state dynamics and structure of protein L characterized by simulation and experiment. J. Am. Chem. Soc 2010, 132, 4702–4709. [Google Scholar]
- Schaeffer, RD; Fersht, A; Daggett, V. Combining experiment and simulation in protein folding: closing the gap for small model systems. Curr. Opin. Struct. Biol 2008, 18, 4–9. [Google Scholar]
- Daggett, V. Protein folding-simulation. Chem. Rev 2006, 106, 1898–1916. [Google Scholar]
- Chen, HF; Luo, R. Binding induced folding in p53-MDM2 complex. J. Am. Chem. Soc 2007, 129, 2930–2937. [Google Scholar]
- Verkhivker, GM; Bouzida, D; Gehlhaar, DK; Rejto, PA; Freer, ST; Rose, PW. Simulating disorder-order transitions in molecular recognition of unstructured proteins: Where folding meets binding. Proc. Natl. Acad. Sci. USA 2003, 100, 5148–5153. [Google Scholar]
- Joerger, AC; Fersht, AR. Structure-function-rescue: the diverse nature of common p53 cancer mutants. Oncogene 2007, 26, 2226–2242. [Google Scholar]
- Lane, DP; Hupp, TR. Drug discovery and p53. Drug. Discov. Today 2003, 8, 347–355. [Google Scholar]
- Wells, M; Tidow, H; Rutherford, TJ; Markwick, P; Jensen, MR; Mylonas, E; Svergun, DI; Blackledge, M; Fersht, AR. Structure of tumor suppressor p53 and its intrinsically disordered N-terminal transactivation domain. Proc. Natl. Acad. Sci. USA 2008, 105, 5762–5767. [Google Scholar]
- Demarest, SJ; Martinez-Yamout, M; Chung, J; Chen, HW; Xu, W; Dyson, HJ; Evans, RM; Wright, PE. Mutual synergistic folding in recruitment of CBP/p300 by p160 nuclear receptor coactivators. Nature 2002, 415, 549–553. [Google Scholar]
- Bertoncini, CW; Rasia, RM; Lamberto, GR; Binolfi, A; Zweckstetter, M; Griesinger, C; Fernandez, CO. Structural characterization of the intrinsically unfolded protein beta-synuclein, a natural negative regulator of alpha-synuclein aggregation. J. Mol. Biol 2007, 372, 708–722. [Google Scholar]
- Sung, YH; Eliezer, D. Residual structure, backbone dynamics, and interactions within the synuclein family. J. Mol. Biol 2007, 372, 689–707. [Google Scholar]
- Sivakolundu, SG; Bashford, D; Kriwacki, RW. Disordered p27(Kip1) exhibits intrinsic structure resembling the Cdk2/cyclin A-bound conformation. J. Mol. Biol 2005, 353, 1118–1128. [Google Scholar]
- Yoon, MK; Venkatachalam, V; Huang, A; Choi, BS; Stultz, CM; Chou, JJ. Residual structure within the disordered C-terminal segment of p21(Waf1/Cip1/Sdi1) and its implications for molecular recognition. Protein Sci 2009, 18, 337–347. [Google Scholar]
- Tran, HT; Mao, A; Pappu, RV. Role of backbone-solvent interactions in determining conformational equilibria of intrinsically disordered proteins. J. Am. Chem. Soc 2008, 130, 7380–7392. [Google Scholar]
- Mao, AH; Crick, SL; Vitalis, A; Chicoine, CL; Pappu, RV. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 8183–8188. [Google Scholar]
- Marsh, JA; Forman-Kay, JD. Sequence determinants of compaction in intrinsically disordered proteins. Biophys. J 2010, 98, 2383–2390. [Google Scholar]
- Vuzman, D; Azia, A; Levy, Y. Searching DNA via a “Monkey Bar” mechanism: The Significance of disordered tails. J. Mol. Biol 2010, 396, 674–684. [Google Scholar]
- Sugase, K; Dyson, HJ; Wright, PE. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature 2007, 447, 1021–1025. [Google Scholar]
- Parker, D; Ferreri, K; Nakajima, T; Morte, VJL; Evans, R; Koerber, SC; Hoeger, C; Montminy, MR. Phosphorylation of CREB at Ser-133 induces complex formation with CREB-binding protein via a direct mechanism. Mol. Cell. Biol 1996, 16, 694–703. [Google Scholar]
- Chrivia, JC; Kwok, RPS; Lamb, N; Hagiwara, M; Montminy, MR; Goodman, RH. Phosphorylated creb binds specifically to the nuclear-protein Cbp. Nature 1993, 365, 855–859. [Google Scholar]
- Radhakrishnan, I; PerezAlvarado, GC; Parker, D; Dyson, HJ; Montminy, MR; Wright, PE. Solution structure of the KIX domain of CBP bound to the transactivation domain of CREB: A model for activator: Coactivator interactions. Cell 1997, 91, 741–752. [Google Scholar]
- Radhakrishnan, I; Perez-Alvarado, GC; Dyson, HJ; Wright, PE. Conformational preferences in the Ser(133)-phosphorylated and non-phosphorylated forms of the kinase inducible transactivation domain of CREB. FEBS Lett 1998, 430, 317–322. [Google Scholar]
- Solt, I; Simon, I; Tompa, P; Fuxreiter, M. Phosphorylation induced preformed structural element in KID contributes to recognition by KIX. FEBS J 2005, 272, 391–392. [Google Scholar]
- Parker, D; Jhala, US; Radhakrishnan, I; Yaffe, MB; Reyes, C; Shulman, AI; Cantley, LC; Wright, PE; Montminy, M. Analysis of an activator : coactivator complex reveals an essential role for secondary structure in transcriptional activation. Mol. Cell 1998, 2, 353–359. [Google Scholar]
- Mandell, DJ; Chorny, I; Groban, ES; Wong, SE; Levine, E; Rapp, CS; Jacobson, MP. Strengths of hydrogen bonds involving phosphorylated amino acid side chains. J. Am. Chem. Soc 2007, 129, 820–827. [Google Scholar]
- Verkhivker, GM; Bouzida, D; Gehlhaar, DK; Rejto, PA; Freer, ST; Rose, PW. Simulating disorder-order transitions in molecular recognition of unstructured proteins: where folding meets binding. Proc. Natl. Acad. Sci. USA 2003, 100, 5148–5153. [Google Scholar]
- Shoemaker, BA; Portman, JJ; Wolynes, PG. Speeding molecular recognition by using the folding funnel: The fly-casting mechanism. Proc. Natl. Acad. Sci. USA 2000, 97, 8868–8873. [Google Scholar]
- Trizac, E; Levy, Y; Wolynes, PG. Capillarity theory for the fly-casting mechanism. Proc. Natl. Acad. Sci. USA 2010, 107, 2746–2750. [Google Scholar]
- Chen, HF. Molecular dynamics simulation of phosphorylated KID post-translational modification. PLoS ONE 2009, 4, e6516. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Click, T.H.; Ganguly, D.; Chen, J. Intrinsically Disordered Proteins in a Physics-Based World. Int. J. Mol. Sci. 2010, 11, 5292-5309. https://doi.org/10.3390/ijms11125292
Click TH, Ganguly D, Chen J. Intrinsically Disordered Proteins in a Physics-Based World. International Journal of Molecular Sciences. 2010; 11(12):5292-5309. https://doi.org/10.3390/ijms11125292
Chicago/Turabian StyleClick, Timothy H., Debabani Ganguly, and Jianhan Chen. 2010. "Intrinsically Disordered Proteins in a Physics-Based World" International Journal of Molecular Sciences 11, no. 12: 5292-5309. https://doi.org/10.3390/ijms11125292