Exploring Kinetics of Phenol Biodegradation by Cupriavidus taiwanesis 187
Abstract
:1. Introduction
2. Model description
2.1. Microbial Growth
2.2. Substrate Inhibition Model
3. Results and Discussions
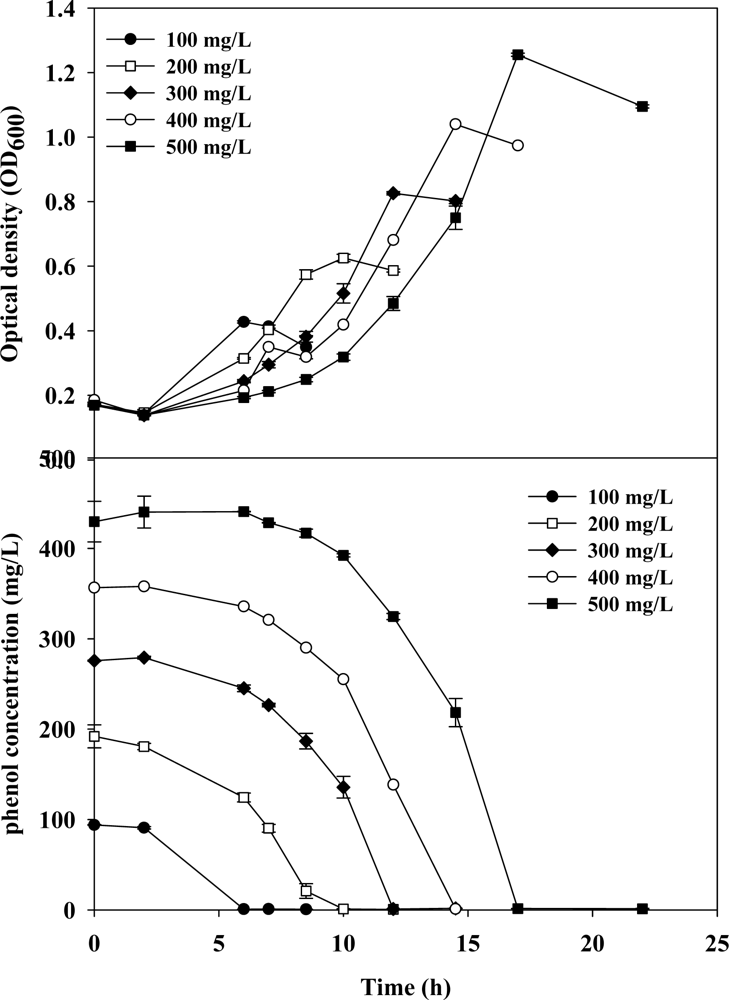
3.1. Cell Growth and Phenol Degradation in Batch Culture
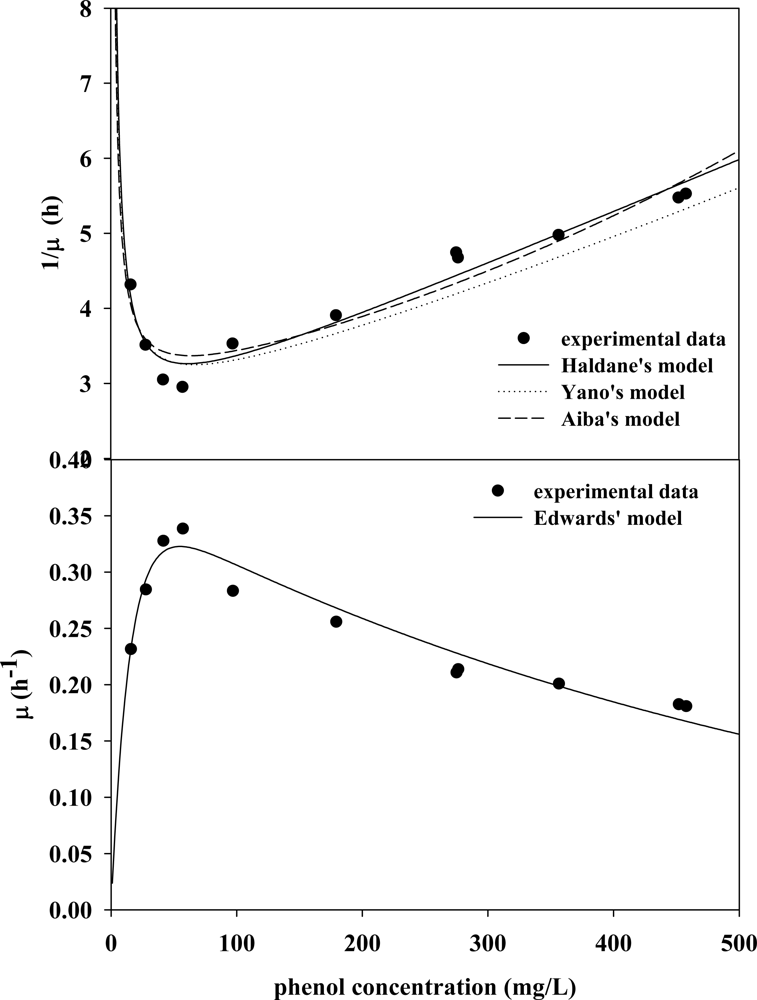
3.2. Evaluation of Kinetic Parameters
3.3. Verifying Feasible Kinetic Models
4. Experimental Section
4.1. Bacterial Strain and Culture Medium
4.2. Culture Conditions
4.3. Analytical Methods
4.4. Data Analysis
5. Conclusion
Nomenclature
| K: | substrate-inhibition constant (mg/L) |
| KS: | substrate-affinity constant (mg/L) |
| KI: | substrate-inhibition constant (mg/L) |
| m: | specific maintenance coefficient (g substrate/g cell-h) |
| S: | substrate concentration (mg/L) |
| S0: | initial substrate concentration (mg/L) |
| t: | time (h) |
| X: | cell concentration (g/L) |
| YXIS: | cell yield (g cell/ g substrate) |
| μ: | specific growth rate (h−1) |
| μmax: | maximum specific growth rate (h−1) |
Acknowledgments
References
- Hill, GA; Robinson, CW. Substrate inhibition kinetics: Phenol degradation by Pseudomonas putida. Biotechnol. Bioeng 1975, 17, 1599–1615. [Google Scholar]
- Juang, RS; Tsai, SY. Growth kinetics of Pseudomonas putida in the biodegradation of single and mixed phenol and sodium salicylate. Biochem. Eng. J 2006, 31, 133–140. [Google Scholar]
- Agency for Toxic Substances and Disease Registry (ATSDR). Toxicological Profile for Phenol; US Public Health Service, U.S. Department of Health and Human Services: Atlanta, GA, USA, 1989. [Google Scholar]
- Monteiro, AAMG; Boaventura, RAR; Rodrigues, AE. Phenol biodegradation by Pseudomonas putida DSM 548 in a batch reactor. Biochem. Eng. J 2000, 6, 45–49. [Google Scholar]
- Tomei, MC; Annesini, MC; Luberti, R; Cento, G; Senia, A. Kinetics of 4-nitrophenol biodegradation in a sequencing batch reactor. Wat. Res 2003, 37, 3803–3814. [Google Scholar]
- Khleifat, KM. Biodegradation of phenol by Ewingella americana: Effect of carbon starvation and some growth conditions. Proc. Biochem 2006, 41, 2010–2016. [Google Scholar]
- Cai, W; Li, J; Zhang, Z. The characteristics and mechanisms of phenol biodegradation by Fusarium sp. J. Hazard. Mater 2007, 148, 38–42. [Google Scholar]
- Enroth, C; Neujahr, H; Schneider, G; Lindqvist, Y. The crystal structure of phenol hydroxylase in complex with FAD and phenol provides evidence for a concerted conformational change in the enzyme and its cofactor during catalysis. Structure 1998, 6, 605–617. [Google Scholar]
- Der Yang, R; Humphrey, AE. Dynamic and steady state studies of phenol biodegradation in pure and mixed cultures. Biotechnol. Bioeng 1975, 17, 1211–1235. [Google Scholar]
- Chen, BY; Chang, JS. Phenol degradation and toxicity assessment upon biostimulation to an indigenous rhizobium Ralstonia taiwanensis. Biotechnol. Prog 2005, 21, 1085–1092. [Google Scholar]
- Permutter, DD. Chapter 2 steady sstates of CSTR models. In Stability of Chemical Reactors, 8th ed; Permutter, DD, Ed.; Prentice-Hall International Series: Englewood Cliffs, NJ, USA, 1972; pp. 19–50. [Google Scholar]
- Reardon, KF; Mosteller, DC; Rogers, JDB. Biodegradation kinetics of benzene, toluene, and phenol as single and mixed substrates for Pseudomonas putida F1. Biotechnol. Bioeng 2000, 69, 385–400. [Google Scholar]
- Allsop, PJ; Chisti, Y; Young, MM; Sullivan, GR. Dynamics of phenol degradation by Pseudomonas putida. Biotechnol. Bioeng 1993, 41, 572–580. [Google Scholar]
- Onysko, KA; Budman, HM; Robinson, CW. Effect of temperature on the inhibition kinetics of phenol biodegradation by Pseudomonas putida Q5. Biotechnol. Bioeng 2000, 70, 291–299. [Google Scholar]
- Chen, BY; Liu, HL; Chen, YW; Cheng, YC. Dose-response assessment of metal toxicity upon indigenous Thiobacillus thiooxidans BC1. Proc. Biochem 2004, 39, 735–745. [Google Scholar]
- Bailey, JE; Ollis, DF. Design and Analysis of Biological Reactors, 2nd ed; Chemical Engineering Series; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Chen, BY; Chen, WM; Chang, JS. Optimal biostimulation strategy for phenol degradation with indigenous rhizobium Ralstonia taiwanensis. J. Hazard. Mater 2007, B139, 232–237. [Google Scholar]
Appendix A: Rolle Theorem ensures uniqueness condition(s) for phenol degradation
- = (substrate inlet) − (substrate output) − (substrate consumption)
Appendix B: Sufficient conditions to guarantee the uniqueness condition(s) of solutions

| Source | Model | Reference |
|---|---|---|
| Yano et al. | [14] | |
| Aiba et al. | [14] | |
| Edwards | [15] |
| Model | Rearranged equation |
|---|---|
| Haldane model | |
| Yano’s model | |
| Aiba’s model | |
| Edwards model |
| Model | Estimates | r2 | |||
|---|---|---|---|---|---|
| μmax (h−1) | KS (mg/L) | KI (mg/L) | K (mg/L) | ||
| Haldane’s model | 0.4160 | 10.87 | 341 | 0.9249 | |
| Yano’s model | 0.3972 | 9.70 | 467 | 1561.47 | 0.9237 |
| Aiba’s model | 0.3640 | 6.99 | 638 | 0.9028 | |
| Edwards’ model | 0.3630 | 14.41 | 592 | 0.9527 | |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wei, Y.-H.; Chen, W.-C.; Chang, S.-M.; Chen, B.-Y. Exploring Kinetics of Phenol Biodegradation by Cupriavidus taiwanesis 187. Int. J. Mol. Sci. 2010, 11, 5065-5076. https://doi.org/10.3390/ijms11125065
Wei Y-H, Chen W-C, Chang S-M, Chen B-Y. Exploring Kinetics of Phenol Biodegradation by Cupriavidus taiwanesis 187. International Journal of Molecular Sciences. 2010; 11(12):5065-5076. https://doi.org/10.3390/ijms11125065
Chicago/Turabian StyleWei, Yu-Hong, Wei-Chuan Chen, Shan-Ming Chang, and Bor-Yann Chen. 2010. "Exploring Kinetics of Phenol Biodegradation by Cupriavidus taiwanesis 187" International Journal of Molecular Sciences 11, no. 12: 5065-5076. https://doi.org/10.3390/ijms11125065





