Ionocovalency and Applications 1. Ionocovalency Model and Orbital Hybrid Scales

Abstract

Ionocovalency (IC), a quantitative dual nature of the atom, is defined and correlated with quantum-mechanical potential to describe quantitatively the dual properties of the bond. Orbiotal hybrid IC model scale, IC, and IC electronegativity scale, X_IC, are proposed, wherein the ionicity and the covalent radius are determined by spectroscopy. Being composed of the ionic function I and the covalent function C, the model describes quantitatively the dual properties of bond strengths, charge density and ionic potential. Based on the atomic electron configuration and the various quantum-mechanical built-up dual parameters, the model formed a Dual Method of the multiple-functional prediction, which has much more versatile and exceptional applications than traditional electronegativity scales and molecular properties. Hydrogen has unconventional values of IC and X_IC, lower than that of boron. The IC model can agree fairly well with the data of bond properties and satisfactorily explain chemical observations of elements throughout the Periodic Table.

1. Introduction

In the valence-bond (VB) approach, the molecular wave function is written as a product of the state functions of the constituent atoms. This makes models based on the VB approximation intuitively appealing, as exemplified by the extreme usefulness of Lewis structures of “The Atom and the Molecule” [1] and by the wide acceptance of Pauling’s “Nature of the Chemical Bond” [2]. Before Lewis proposed his theory of the shared electron pair bond, bonding in some compounds could be satisfactorily explained on the basis of simple electrostatic forces between the positive and negative ions which are assumed to be the basic molecular units. The shared electron pair bond is known as the covalent bond, while the other type is the ionic bond.

Over the years, the description of the properties of the covalent and ionic bond remains largely qualitative and Pauling’s scale [3] due to not based on the electron configuration data, left a wide front for arguments and has lead to many different suggestions for the bond strengths [4–24].

In the present work, we defined and correlated ionocovalency (IC), a quantitative atomic dual nature of ionicity and σ- and spatial-covalency with the quantum-mechanical potential to describe quantitatively the dual properties of bonds. Orbital hybrid IC scale and IC electronegativity X_IC scale are proposed wherein the ionicity and the covalent radius are determined by spectroscopy. Being composed of the ionic function I and the covalent function C, the model exhibits quantitatively the dual properties of bond strengths, charge density and ionic potential. Based on the atomic electron configuration, the quantum-mechanical built-up dual parameters and sub-models, which in turn exhibit various specific bond properties, the model formed a Dual Method of the multiple-functional prediction which has much more versatile and exceptional applications than traditional electronegativity scales and molecular properties. Hydrogen has its unconventional values lower than that of boron, residing on the borderline between the weak ionic and the weak covalent ions. The IC model can agree fairly well with the data of bond properties and satisfactorily explain chemical observations of elements throughout the Periodic Table.

2. Methodology

2.1. IC Model

Based on the VB approximation, the bond strengths can be considered mainly about the potential energy: the nuclear charge Z felt by valence electrons at the covalent boundary. And the term of Schrödinger’s Wave Equation incorporating bond strength is the potential energy Ze²ψ/r.

$$-h^2{\nabla }^2\psi /8{\pi }^{2}m-Z{e}^2\psi /4\pi {\varepsilon }_{0}r=E\psi$$

(2.1.1)

Ionic bonds are omnidirectional. The nuclear charge Z possesses the power of ionizing radiation and radiates positive charge in all directions. Therefore, the nuclear charge Z is directly proportional to the bond strengths but has the delocalized ionic nature.

The covalent radius, r_c is the other important part of the potential here. It is a distance from nucleus to a charge density wherein the bonding atoms are aligned and localized at very specific bond lengths, and it is inversely proportional to the bond strengths. In the case of the hydrogen atom, as Equation (2.1.1) shows, as the electron approaches the nucleus, the potential energy dives down toward minus-infinity, in order for the total energy E to remain constant, and its kinetic energy shoots up toward positive-infinity. So a compromise is reached in which theory tells us that the fall potential energy is just twice the kinetic energy, and the electron dances at an average distance that corresponds to the Bohr radius [25]. The calculation of the H₂ molecule by Heitler and London showed that as the inter-nuclear distance decreased, the potential energy associated with interactions between nucleus and electrons dropped very markedly until a minimum was reached, and then (owing to the greater effect of internuclear repulsion at much smaller internuclear distances) to rise sharply [26]. The minimum corresponded fairly closely to the experimentally determined value of R, 0.74 Å (covalent radius = 0.37 Å, see below 4.2). Therefore, the covalent radius has the harmoniously localized covalent nature.

As atoms and molecules have the dual nature, ionocovalency, the bond strengths can be considered as a combination of the ionic and the covalent functions [10]. So the ionic function I can be considered as a function of the nuclear charge Z: I(Z); and the covalent function C can be considered as a function of the covalent radius r_c: C(r_c⁻¹), wherein the reciprocal of r_c can be defined as atomic covalency.

Ionocovalently, the bond strengths and electronegativity, therefore, can be accounted for on the basis of the dual nature of bonds, and functionally defined as ionocovalency, a product of the ionic and the covalent functions:

$$IC=I(Z*)C(r_c^{-1})$$

(2.1.2)

And so the bond strengths, the potential energy and electronegativity have the IC framework of ionocovalency, which shows an effective ionocovalent potential, the attraction power that should be Pauling postulated.

According to the Bohr energy model

$$E=-Z^{2}m{e}^4/8n^2{h}^2{\varepsilon }_0^2=-R{Z}^2/n^2$$

(2.1.3)

we have derived the effective nuclear charge Z* from ionization energy and the effective principal quantum number n* [8,9]:

$$Z*=n*{(I_z/R)}^{½}$$

(2.1.4)

where I_z is the ultimate IE. R is the Rydberg constant, R = 2π²μ⁴2e⁴/h² = 13.6 eV, h is Planck’s constant. Substituting Equation (2.1.4) into (2.1.2), we can naturally correlate the bond properties to the quantum-mechanics, and get the IC model:

$$I(I_z)C(n*r_c^{-1})=n*{(I_{av}/R)}^{½}{r}_c^{-1}$$

(2.1.5)

where the effective principal quantum number n* is related to the electron energy, distribution and the distance from the nucleus. Hence, n* can be considered as an energy of ionic function and also as a spatial distance of covalent function. The n*r_c⁻¹, which is related to the spatial overlap, can be defined as spatial-covalency of covalent function (r_c⁻¹ is a linear- or σ-covalency).

2.2. IC Electronegativity X_IC

As an application of ionocovalency, by Plotting Pauling values of X_p against n*(I_av/R)^½r_c⁻¹, we obtain a new IC-potential electronegativity

$$X_{IC}=0.412n*{(I_{av}/R)}^{½}{r}_c^{-1}+0.387$$

(2.1.6)

Based on the above IC model, our previous electronegativity scale X_z [8,9] can be accounted for IC-force:

$$IC=I(V)C(r^{-1})=I(Z*)C(r^{-2})=n*{(I_z/R)}^{½}{r}_c^{-2}$$

(2.1.7)

$$X_z=0.241n*{(I_z/R)}^{½}{r}_c^{-2}+0.775$$

(2.1.8)

In Equation 2.1.5 and 2.1.6, I_av is ionicity (the average IE of valence shell electrons) determined by the following IC orbital hybrid bonding procedures. The diagrams are adapted from those in the excellent article by Blaber [27].

2.3. IC Orbital Hybrid Bonding Procedures

(1) Ionization promotion: As a valence shell fills, the successive increased ionization energy of an electron would provide the promotion energy for hybrid orbital formation e.g., consider gaseous molecules of BeF₂. The fluorine atom has the electron configuration: 1s²2s²2p⁵. The beryllium atom has the electron configuration: 1s²2s².

In the ground state, there are no unpaired electrons. However, the beryllium atom could obtain an unpaired electron by promoting an electron from the 2s orbital to the 2p orbital by its lower first IE (9.32 eV). The beryllium atom can now forms two covalent bonds with fluorine atoms:

(2) Ionicity hybridization: We can combine functions for the 2s and 2p electrons to produce a “hybrid” orbital for both electrons. The charge transfer and charge distribution would occur from the higher energy level of the 2p orbital to the lower energy level of the 2s orbital to form an energy-lower and identical 2sp hybrid orbital. The ideas developed are adequate for calculation of the charge density identically distributed. The IEs of the 2s and 2p electrons can be averaged to result in a hybridizing ionicity, I_av:

$$I_{av}=n^{-1}{\Sigma }_{i=1}^n{I}_i$$

(2.1.9)

where I_i is the IE of single electron of valence shell, n is number of valence shell electrons.

By Equation (2.1.9), we get an average IE: I_av = 13.76 eV from the first IE (9.32 eV) and second IE (18.2 eV):

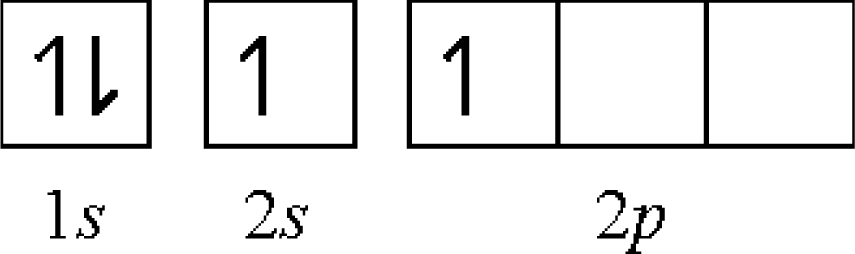
• first: Be[He](2s)² → Be⁺[He] (2s)¹ − 9.32 eV
• second: Be⁺[He](2s)¹ → Be²⁺[He] − 18.20 eV

of 2s electrons for 2sp electrons:

(3) Ionocovalency: by localizing the hybridized ionicity at the covalent boundary r_c to form an ionocovalent bond of 2sp hybrid orbitals:

Hence, for beryllium, IC = I(I_av)C(n*r_c⁻¹) = n*(I_av/R)^½r_c⁻¹ = 1.99(13.76/13.6)^½ (0.970)⁻¹ = 2.064 And X_IC = 0.412 n*(I_av/R)^½ r_c⁻¹ + 0.387 = 0.412*1.99(13.76/13.6)^½(0.970) ⁻¹ + 0.387 = 1.237.

Similarly, an s orbital can also mix with all three p orbitals in the same subshell. For CH₄ by Equation (2.1.9), we get ionicity: I_av = 37.015 eV from the first IE (11.26 eV), second IE (24.40 eV), third IE (47.90 eV) and fourth IE (64.50 eV)

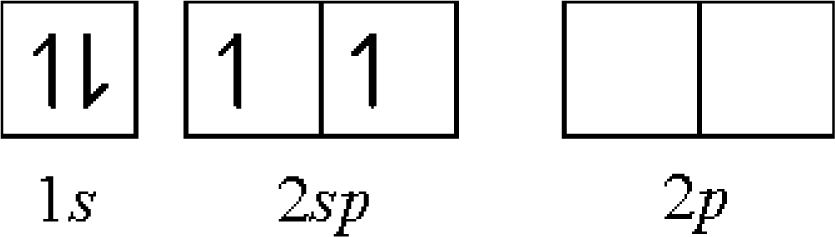
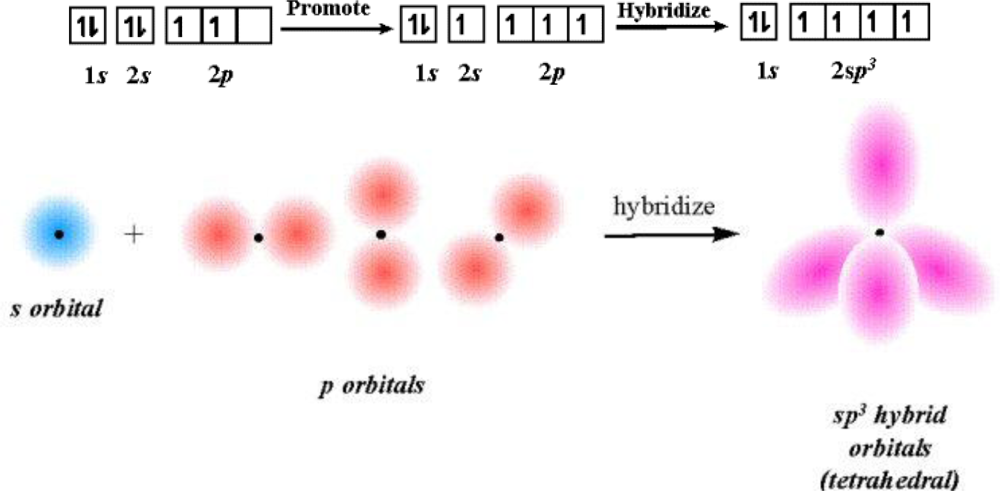
• first: C[He](2s)²(2p)² → C⁺[He](2s)²(2p)¹ − 11.26 eV
• second: C⁺[He](2s)²(2p)¹ → C²⁺[He](2s)² − 24.40 eV
• third: C²⁺[He](2s)² → C³⁺[He](2s)¹ − 47.90 eV
• fourth: C³⁺[He](2s)¹ → C⁴⁺[He] − 64.50 eV

of the all 2s and 2p electrons and form 2sp³ hybrid orbitals:

The IE is taken from Mackay et al. [28], the covalent radius r_c, is taken from Pauling [29], Batsanov [30], Cordero et al. [31], Rappe et al. [32] and the effective principal quantum number n* is from our previous work [8,9]. The ionocovalency scale, IC, calculated from Equation (2.1.5) is listed in Chart 1 and the electronegativity scale, X_IC calculated from Equation (2.1.6) are listed in

Table 1. Atomic parameters.

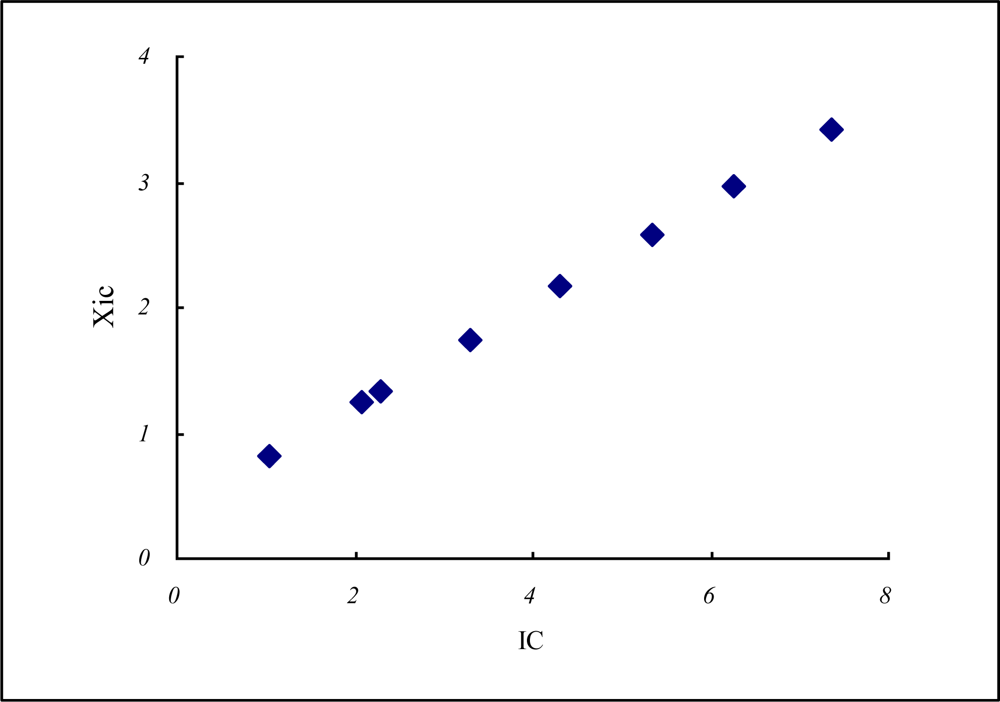
Atm.No	Cations		n*	Iz	Iav	rc−1	n*rc−1	Z*	rc	Xz	XIC	IC
1	H+		0.85	13.600	13.600	2.703	2.297	0.850	0.370	2.271	1.333	2.297
2	He2+		0.85	54.400	39.500	3.571	3.036	1.449	0.280	6.001	2.518	5.173
3	Li+		1.99	5.3900	5.3900	0.816	1.624	1.253	1.225	0.976	0.808	1.023
4	Be2+		1.99	18.200	13.760	1.031	2.052	2.002	0.970	1.365	1.237	2.064
5	B3+		1.99	37.900	23.800	1.250	2.488	2.633	0.800	2.026	1.743	3.291
6	C4+		1.99	64.500	37.015	1.316	2.618	3.283	0.760	2.583	2.167	4.320
6	C3+		1.99	47.900	27.853	1.316	2.618	2.848	0.760	2.333	1.931	3.747
6	C2+		1.99	24.400	17.830	1.316	2.618	2.279	0.760	1.887	1.622	2.998
7	N5+		1.99	97.900	53.406	1.351	2.689	3.943	0.740	3.125	2.583	5.329
7	N4+		1.99	77.500	42.283	1.351	2.689	3.509	0.740	2.866	2.341	4.742
7	N3+		1.99	47.500	30.543	1.351	2.689	2.982	0.740	2.412	2.047	4.030
7	N2+		1.99	29.600	22.065	1.351	2.689	2.535	0.740	2.067	1.798	3.425
7	N+		1.99	14.530	14.530	1.351	2.689	2.057	0.740	1.680	1.532	2.780
8	O6+		1.99	138.00	72.020	1.370	2.726	4.579	0.730	3.642	2.972	6.273
8	O2+		1.99	35.100	24.360	1.370	2.726	2.663	0.730	2.221	1.890	3.648
9	F7+		1.99	185.00	94.030	1.408	2.803	5.233	0.710	4.284	3.423	7.370
10	Ne4+		1.99	97.100	55.785	1.724	3.431	4.030	0.580	4.584	3.250	6.949
10	Ne2+		1.99	41.000	31.270	1.724	3.431	3.018	0.580	3.250	2.530	5.203
11	Na+		2.89	5.1400	5.1400	0.636	1.838	1.777	1.572	0.948	0.853	1.130
12	Mg2+		2.89	15.000	11.325	0.733	2.119	2.637	1.364	1.168	1.184	1.933
13	Al3+		2.89	28.500	17.763	0.826	2.388	3.303	1.210	1.464	1.512	2.730
13	Al+		2.89	5.9900	5.9900	0.826	2.388	1.918	1.210	1.091	1.040	1.585
14	Si4+		2.89	45.100	25.763	0.847	2.449	3.978	1.180	1.686	1.776	3.371
14	Si2+		2.89	16.300	12.225	0.847	2.449	2.740	1.180	1.323	1.344	2.322
15	P5+		2.89	65.000	35.358	0.935	2.701	4.660	1.070	2.105	2.181	4.355
15	P4+		2.89	51.400	27.948	0.935	2.701	4.143	1.070	1.958	1.982	3.872
15	P3+		2.89	30.200	20.130	0.935	2.701	3.516	1.070	1.682	1.741	3.286
15	P+		2.89	10.490	10.490	0.935	2.701	2.538	1.070	1.309	1.364	2.372
16	S6+		2.89	88.000	46.077	0.971	2.806	5.319	1.030	2.445	2.515	5.165
16	S4+		2.89	47.300	28.940	0.971	2.806	4.216	1.030	1.999	2.073	4.093
16	S2+		2.89	23.300	16.830	0.971	2.806	3.215	1.030	1.634	1.673	3.121
17	Cl7+		2.89	114.00	58.381	1.010	2.919	5.988	0.990	2.832	2.879	6.048
17	Cl5+		2.89	67.800	39.534	1.010	2.919	4.927	0.990	2.362	2.438	4.977
17	Cl3+		2.89	39.600	25.457	1.010	2.919	3.954	0.990	1.988	2.032	3.994
17	Cl+		2.89	12.970	12.970	1.010	2.919	2.822	0.990	1.469	1.562	2.851
18	Ar4+		2.89	59.800	35.965	1.031	2.979	4.700	0.970	2.327	2.383	4.845
18	Ar2+		2.89	27.600	21.680	1.031	2.979	3.649	0.970	1.830	1.937	3.762
19	K+		3.45	4.3400	4.3400	0.513	1.769	1.949	1.950	0.899	0.799	0.999
20	Ca2+		3.45	11.900	9.0050	0.576	1.987	2.807	1.736	1.033	1.053	1.617
21	Sc3+		3.45	24.800	14.713	0.695	2.397	3.588	1.439	1.317	1.414	2.494
22	Ti4+		3.45	43.300	22.805	0.755	2.606	4.468	1.324	1.621	1.777	3.374
22	Ti3+		3.45	27.500	15.973	0.755	2.606	3.739	1.324	1.449	1.550	2.824
22	Ti2+		3.45	13.600	10.210	0.755	2.606	2.989	1.324	1.249	1.317	2.258
23	V5+		3.45	65.200	32.528	0.817	2.819	5.336	1.224	1.990	2.183	4.359
23	V4+		3.45	46.700	24.360	0.817	2.819	4.617	1.224	1.803	1.941	3.772
23	V3+		3.45	29.300	16.913	0.817	2.819	3.847	1.224	1.590	1.682	3.143
23	V2+		3.45	14.700	10.720	0.817	2.819	3.063	1.224	1.352	1.418	2.502
23	V+		3.45	6.7400	6.7400	0.817	2.819	2.429	1.224	1.166	1.205	1.984
24	Cr6+		3.45	90.600	43.878	0.853	2.944	6.197	1.172	2.337	2.565	5.287
24	Cr5+		3.45	69.300	34.534	0.853	2.944	5.498	1.172	2.141	2.320	4.691
24	Cr4+		3.45	49.100	25.843	0.853	2.944	4.756	1.172	1.925	2.059	4.058
24	Cr3+		3.45	31.000	18.090	0.853	2.944	3.979	1.172	1.689	1.786	3.395
24	Cr2+		3.45	16.500	11.635	0.853	2.944	3.191	1.172	1.442	1.509	2.723
24	Cr+		3.45	6.7700	6.7700	0.853	2.944	2.434	1.172	1.202	1.243	2.077
25	Mn7+		3.45	119.00	56.334	0.856	2.954	7.022	1.168	2.578	2.864	6.012
25	Mn6+		3.45	95.000	45.890	0.856	2.954	6.337	1.168	2.386	2.622	5.426
25	Mn5+		3.45	72.400	36.068	0.856	2.954	5.618	1.168	2.181	2.369	4.810
25	Mn4+		3.45	51.200	26.985	0.856	2.954	4.860	1.168	1.958	2.101	4.161
25	Mn3+		3.45	33.700	18.913	0.856	2.954	4.068	1.168	1.734	1.822	3.483
25	Mn2+		3.45	15.600	11.520	0.856	2.954	3.175	1.168	1.428	1.507	2.719
25	Mn+	3.45		7.4400	7.4400	0.856	2.954	2.552	1.168	1.226	1.287	2.185
26	Fe6+	3.45		99.000	47.262	0.858	2.961	6.431	1.165	2.428	2.661	5.520
26	Fe5+	3.45		75.000	36.914	0.858	2.961	5.684	1.165	2.214	2.397	4.879
26	Fe4+	3.45		54.800	27.393	0.858	2.961	4.896	1.165	2.005	2.119	4.203
26	Fe3+	3.45		30.700	18.257	0.858	2.961	3.997	1.165	1.695	1.801	3.431
26	Fe2+	3.45		16.200	12.035	0.858	2.961	3.245	1.165	1.444	1.535	2.786
26	Fe+	3.45		7.8700	7.8700	0.858	2.961	2.624	1.165	1.241	1.315	2.253
27	Co4+	3.45		51.300	27.440	0.870	3.000	4.901	1.150	1.996	2.143	4.261
27	Co3+	3.45		33.500	19.487	0.870	3.000	4.130	1.150	1.762	1.867	3.591
27	Co2+	3.45		17.100	12.480	0.870	3.000	3.305	1.150	1.480	1.571	2.874
27	Co+	3.45		7.8600	7.8600	0.870	3.000	2.623	1.150	1.253	1.327	2.281
28	Ni4+	3.45		54.900	28.985	0.901	3.108	5.037	1.110	2.131	2.256	4.537
28	Ni3+	3.45		35.200	20.347	0.901	3.108	4.220	1.110	1.861	1.953	3.802
28	Ni2+	3.45		18.200	12.920	0.901	3.108	3.363	1.110	1.556	1.635	3.029
28	Ni+	3.45		7.6400	7.6400	0.901	3.108	2.586	1.110	1.281	1.347	2.330
29	Cu3+	3.45		36.800	21.610	0.901	3.108	4.349	1.110	1.885	2.001	3.918
29	Cu2+	3.45		20.300	14.015	0.901	3.108	3.502	1.110	1.599	1.687	3.155
29	Cu+	3.45		7.7300	7.7300	0.901	3.108	2.601	1.110	1.284	1.352	2.343
30	Zn2+	3.45		18.000	13.695	0.801	2.762	3.462	1.249	1.388	1.529	2.772
30	Zn+	3.45		9.3900	9.3900	0.801	2.762	2.867	1.249	1.218	1.333	2.295
31	Ga3+	3.45		30.700	19.067	0.803	2.771	4.085	1.245	1.581	1.739	3.281
31	Ga+	3.45		6.0000	6.0000	0.803	2.771	2.292	1.245	1.131	1.145	1.841
32	Ge4+	3.45		45.700	25.925	0.818	2.821	4.763	1.223	1.794	1.992	3.895
32	Ge2+	3.45		15.900	11.900	0.818	2.821	3.227	1.223	1.376	1.474	2.639
33	As5+	3.45		62.600	33.902	0.826	2.851	5.447	1.210	1.993	2.242	4.502
33	As3+	3.45		28.400	18.937	0.826	2.851	4.071	1.210	1.596	1.773	3.364
33	As+	3.45		9.810	9.8100	0.826	2.851	2.930	1.210	1.257	1.385	2.422
34	Se6+	3.45		81.700	42.442	0.855	2.949	6.095	1.170	2.264	2.533	5.209
34	Se4+	3.45		42.900	26.163	0.855	2.949	4.785	1.170	1.854	2.072	4.090
34	Se2+	3.45		21.200	15.480	0.855	2.949	3.681	1.170	1.533	1.683	3.146
35	Br7+	3.45		103.00	52.601	0.876	3.021	6.785	1.142	2.529	2.835	5.941
35	Br5+	3.45		59.700	35.322	0.876	3.021	5.560	1.142	2.111	2.393	4.869
35	Br+	3.45		11.810	11.810	0.876	3.021	3.215	1.142	1.369	1.547	2.815
36	Kr6+	3.45		78.500	45.200	0.862	2.974	6.290	1.160	2.260	2.621	5.422
36	Kr4+	3.45		52.500	32.000	0.862	2.974	5.292	1.160	1.989	2.267	4.562
36	Kr2+	3.45		24.500	19.250	0.862	2.974	4.105	1.160	1.604	1.845	3.538
37	Rb+	3.85		4.1800	4.1800	0.463	1.782	2.134	2.160	0.885	0.794	0.988
38	Sr2+	3.85		11.000	8.3500	0.522	2.011	3.017	1.914	1.003	1.036	1.576
39	Y3+	3.85		20.500	13.027	0.619	2.382	3.768	1.616	1.211	1.348	2.332
40	Zr4+	3.85		34.300	19.310	0.688	2.648	4.588	1.454	1.472	1.687	3.155
40	Zr3+	3.85		23.000	14.313	0.688	2.648	3.950	1.454	1.346	1.506	2.716
40	Zr2+	3.85		13.100	9.9700	0.688	2.648	3.296	1.454	1.206	1.321	2.267
41	Nb5+	3.85		50.600	27.016	0.745	2.869	5.426	1.342	1.769	2.053	4.043
41	Nb4+	3.85		38.300	21.120	0.745	2.869	4.798	1.342	1.640	1.860	3.575
41	Nb3+	3.85		25.000	15.393	0.745	2.869	4.096	1.342	1.474	1.644	3.052
41	Nb2+	3.85		14.300	10.590	0.745	2.869	3.397	1.342	1.303	1.430	2.532
41	Nb+	3.85		6.8800	6.8800	0.745	2.869	2.738	1.342	1.141	1.228	2.040
42	Mo6+	3.85		68.000	37.683	0.775	2.982	6.409	1.291	2.020	2.432	4.964
42	Mo5+	3.85		61.200	31.620	0.775	2.982	5.870	1.291	1.956	2.260	4.547
42	Mo+4	3.85		46.400	24.225	0.775	2.982	5.138	1.291	1.803	2.027	3.980
42	Mo+3	3.85		27.200	16.833	0.775	2.982	4.283	1.291	1.562	1.754	3.318
42	Mo+2	3.85		16.200	11.650	0.775	2.982	3.563	1.291	1.383	1.524	2.760
42	Mo+	3.85		7.1000	7.1000	0.775	2.982	2.782	1.291	1.177	1.275	2.155
43	Tc7+	3.85		94.000	46.297	0.787	3.031	7.103	1.270	2.287	2.691	5.593
43	Tc6+	3.85		76.000	38.347	0.787	3.031	6.465	1.270	2.135	2.484	5.090
43	Tc5+	3.85		59.000	30.816	0.787	3.031	5.795	1.270	1.973	2.267	4.563
43	Tc4+	3.85		43.000	23.770	0.787	3.031	5.090	1.270	1.798	2.038	4.008
43	Tc3+	3.85		29.500	17.360	0.787	3.031	4.350	1.270	1.622	1.798	3.425
43	Tc2+	3.85		15.300	11.290	0.787	3.031	3.508	1.270	1.385	1.525	2.762
43	Tc+	3.85		7.2800	7.2800	0.787	3.031	2.817	1.270	1.196	1.301	2.218
44	Ru8+	3.85		119.00	57.771	0.806	3.102	7.935	1.241	2.557	3.021	6.394
44	Ru7+	3.85		100.00	49.024	0.806	3.102	7.310	1.241	2.409	2.814	5.890
44	Ru6+	3.85		81.000	40.528	0.806	3.102	6.646	1.241	2.245	2.593	5.355
44	Ru5+	3.85		63.000	32.434	0.806	3.102	5.946	1.241	2.072	2.361	4.791
44	Ru4+	3.85		46.500	24.793	0.806	3.102	5.198	1.241	1.889	2.113	4.189
44	Ru3+	3.85		28.500	17.557	0.806	3.102	4.374	1.241	1.647	1.839	3.525
44	Ru2+	3.85		16.800	12.085	0.806	3.102	3.629	1.241	1.445	1.592	2.924
45	Rh6+	3.85		85.000	42.377	0.802	3.087	6.796	1.247	2.267	2.632	5.450
45	Rh4+	3.85		45.600	25.565	0.802	3.087	5.279	1.247	1.868	2.131	4.233
45	Rh3+	3.85		31.100	18.887	0.802	3.087	4.537	1.247	1.677	1.886	3.638
45	Rh2+	3.85		18.100	12.780	0.802	3.087	3.732	1.247	1.463	1.620	2.993
45	Rh+	3.85		7.4600	7.4600	0.802	3.087	2.851	1.247	1.217	1.329	2.287
46	Pd6+	3.85		90.000	44.273	0.782	3.013	6.946	1.278	2.236	2.626	5.435
46	Pd5+	3.85		66.000	35.128	0.782	3.013	6.188	1.278	2.026	2.382	4.842
46	Pd4+	3.85		49.000	27.410	0.782	3.013	5.466	1.278	1.853	2.149	4.277
46	Pd3+	3.85		32.900	20.210	0.782	3.013	4.693	1.278	1.659	1.900	3.672
46	Pd2+	3.85		19.400	13.870	0.782	3.013	3.888	1.278	1.453	1.640	3.042
47	Ag3+	3.85		34.600	21.227	0.747	2.875	4.810	1.339	1.600	1.867	3.592
47	Ag2+	3.85		21.500	14.540	0.747	2.875	3.981	1.339	1.426	1.612	2.973
47	Ag+	3.85		7.5800	7.5800	0.747	2.875	2.874	1.339	1.161	1.271	2.147
48	Cd2+	3.85		16.900	12.945	0.708	2.725	3.756	1.413	1.293	1.482	2.658
48	Cd+	3.85		8.9900	8.9900	0.694	2.674	3.130	1.440	1.139	1.283	2.174
49	In3+	3.85		28.000	17.563	0.668	2.572	4.375	1.497	1.369	1.591	2.923
49	In+	3.85		5.7900	5.7900	0.668	2.572	2.512	1.497	1.045	1.078	1.678
50	Sn4+	3.85		40.700	23.285	0.715	2.752	5.038	1.399	1.595	1.871	3.601
50	Sn2+	3.85		14.600	10.970	0.715	2.752	3.458	1.399	1.266	1.405	2.472
51	Sb5+	3.85		55.500	30.028	0.709	2.730	5.721	1.410	1.718	2.059	4.057
51	Sb3+	3.85		25.300	16.813	0.709	2.730	4.281	1.410	1.412	1.638	3.036
52	Te6+	3.85		70.700	37.085	0.730	2.810	6.358	1.370	1.902	2.299	4.641
52	Te4+	3.85		37.400	23.253	0.730	2.810	5.034	1.370	1.595	1.901	3.675
52	Te2+	3.85		18.600	13.810	0.730	2.810	3.880	1.370	1.353	1.554	2.832
53	I7+	3.85		92.344	46.535	0.750	2.886	7.122	1.334	2.134	2.587	5.339
53	I5+	3.85		52.395	23.794	0.750	2.886	5.092	1.334	1.798	1.960	3.817
53	I+	3.85		10.450	10.450	0.750	2.886	3.375	1.334	1.232	1.429	2.530
54	Xe8+	3.85		112.91	55.46	0.714	2.750	7.775	1.400	2.139	2.675	5.553
54	Xe6+	3.85		68.718	39.18	0.714	2.750	6.534	1.400	1.839	2.310	4.667
54	Xe4+	3.85		43.956	27.35	0.714	2.750	5.459	1.400	1.626	1.994	3.900
54	Xe2+	3.85		21.200	16.670	0.714	2.750	4.262	1.400	1.366	1.641	3.044
55	Cs+	4.36		3.8900	3.8900	0.426	1.855	2.332	2.350	0.877	0.796	0.992
56	Ba2+	4.36		10.000	7.6050	0.505	2.201	3.260	1.981	1.005	1.065	1.646
57	La3+	4.36		19.200	11.960	0.534	2.330	4.089	1.871	1.132	1.287	2.185
58	Ce4+	4.36		36.720	18.311	0.608	2.649	5.059	1.646	1.412	1.653	3.074
58	Ce3+	4.36		20.199	12.174	0.608	2.649	4.125	1.646	1.248	1.420	2.506
59	Pr4+	4.36		38.979	17.918	0.607	2.646	5.005	1.648	1.430	1.638	3.037
59	Pr3+	4.36		21.619	10.898	0.607	2.646	3.903	1.648	1.263	1.363	2.368
60	Nd4+	4.36		40.420	19.676	0.609	2.655	5.244	1.642	1.447	1.703	3.194
60	Nd3+	4.36		22.075	12.762	0.609	2.655	4.223	1.642	1.272	1.447	2.572
60	Nd2+	4.36		10.716	8.105	0.609	2.655	3.366	1.642	1.121	1.232	2.050
61	Pm3+	4.36		22.283	12.914	0.613	2.675	4.249	1.630	1.281	1.461	2.606
62	Sm3+	4.36		23.423	13.373	0.602	2.627	4.323	1.660	1.275	1.460	2.604
63	Eu3+	4.36		24.874	13.929	0.541	2.357	4.412	1.850	1.190	1.370	2.385
63	Eu2+	4.36		11.245	8.4570	0.541	2.357	3.438	1.850	1.054	1.153	1.858
64	Gd3+	4.36		20.624	12.962	0.620	2.701	4.256	1.614	1.272	1.474	2.637
64	Gd2+	4.36		12.126	9.1310	0.620	2.701	3.572	1.614	1.156	1.299	2.213
65	Tb4+	4.36		39.798	19.759	0.628	2.739	5.255	1.592	1.484	1.747	3.301
65	Tb3+	4.36		21.868	13.079	0.628	2.739	4.276	1.592	1.301	1.494	2.686
66	Dy3+	4.36		22.801	13.466	0.629	2.744	4.339	1.589	1.314	1.512	2.730
67	Ho3+	4.36		22.801	13.542	0.633	2.759	4.351	1.580	1.320	1.521	2.754
68	Er3+	4.36		22.697	13.577	0.638	2.782	4.356	1.567	1.328	1.532	2.780
69	Tm3+	4.36		23.671	13.970	0.640	2.791	4.419	1.562	1.343	1.553	2.829
69	Tm2+	4.36		12.053	9.1190	0.640	2.791	3.570	1.562	1.180	1.329	2.286
70	Yb3+	4.36		25.029	14.487	0.589	2.566	4.500	1.699	1.269	1.478	2.649
70	Yb2+	4.36		12.178	9.2160	0.589	2.566	3.589	1.699	1.119	1.257	2.112
71	Lu3+	4.36		20.956	13.423	0.598	2.609	4.332	1.671	1.242	1.455	2.592
72	Hf4+	4.36		33.300	19.538	0.693	3.024	5.226	1.442	1.566	1.880	3.624
72	Hf3+	4.36		23.300	14.950	0.693	2.024	4.571	1.442	1.436	1.693	3.170
72	Hf2+	4.36		14.900	10.775	0.693	2.024	3.881	1.442	1.304	1.496	2.691
73	Ta5+	4.36		45.000	24.898	0.745	3.246	5.899	1.343	1.835	2.197	4.393
73	Ta4+	4.36		33.100	19.873	0.745	3.246	5.270	1.343	1.684	2.004	3.924
73	Ta3+	4.36		22.300	15.463	0.745	3.246	4.649	1.343	1.521	1.813	3.462
73	Ta2+	4.36		16.200	12.050	0.745	3.246	4.104	1.343	1.411	1.646	3.056
73	Ta+	4.36		7.8900	7.8900	0.745	3.246	3.321	1.343	1.219	1.406	2.473
74	W6+	4.36		61.000	32.363	0.770	3.356	6.726	1.299	2.094	2.520	5.178
74	W5+	4.36		48.000	26.636	0.770	3.356	6.102	1.299	1.945	2.322	4.697
74	W4+	4.36		35.400	21.295	0.770	3.356	5.456	1.299	1.780	2.117	4.200
74	W3+	4.36		24.100	16.593	0.770	3.356	4.816	1.299	1.604	1.914	3.707
74	W2+	4.36		17.700	12.840	0.770	3.356	4.236	1.299	1.485	1.731	3.261
75	Re7+	4.36		79.000	40.311	0.782	3.412	7.506	1.278	2.326	2.807	5.874
75	Re6+	4.36		64.000	33.863	0.782	3.412	6.880	1.278	2.171	2.605	5.383
75	Re5+	4.36		51.000	27.836	0.782	3.412	6.238	1.278	2.021	2.398	4.881
75	Re4+	4.36		37.700	22.045	0.782	3.412	5.551	1.278	1.846	2.177	4.344
75	Re3+	4.36		26.000	16.827	0.782	3.412	4.850	1.278	1.665	1.950	3.795
75	Re2+	4.36		16.600	12.240	0.782	3.412	4.136	1.278	1.486	1.720	3.237
75	Re+	4.36		7.8800	7.8800	0.782	3.412	3.319	1.278	1.265	1.457	2.597
76	Os8+	4.36		99.000	49.325	0.797	3.474	8.303	1.255	2.575	3.113	6.616
76	Os7+	4.36		83.000	42.230	0.797	3.474	7.683	1.255	2.423	2.909	6.122
76	Os6+	4.36		68.000	35.433	0.797	3.474	7.038	1.255	2.267	2.697	5.608
76	Os5+	4.36		54.000	28.920	0.797	3.474	6.358	1.255	2.104	2.474	5.066
76	Os4+	4.36		40.000	22.650	0.797	3.474	5.627	1.255	1.919	2.234	4.483
76	Os3+	4.36		25.000	16.867	0.797	3.474	4.855	1.255	1.680	1.981	3.869
76	Os2+	4.36		16.900	12.800	0.797	3.474	4.230	1.255	1.519	1.776	3.370
76	Os+	4.36		8.7000	8.7000	0.797	3.474	3.487	1.255	1.309	1.532	2.779
77	Ir6+	4.36		72.000	36.683	0.794	3.460	7.161	1.260	2.298	2.728	5.683
77	Ir5+	4.36		57.000	29.620	0.794	3.460	6.434	1.260	2.130	2.491	5.107
77	Ir4+	4.36		39.000	22.775	0.794	3.460	5.642	1.260	1.896	2.232	4.478
77	Ir3+	4.36		27.000	17.367	0.794	3.460	4.927	1.260	1.708	1.998	3.910
77	Ir2+	4.36		16.000	12.550	0.794	3.460	4.188	1.260	1.493	1.757	3.324
77	Ir+	4.36		9.1000	9.1000	0.794	3.460	3.566	1.260	1.316	1.553	2.831
78	Pt6+	4.36		75.000	37.867	0.775	3.380	7.275	1.290	2.258	2.711	5.640
78	Pt5+	4.36		55.000	30.440	0.775	3.380	6.523	1.290	2.045	2.470	5.056
78	Pt4+	4.36		41.100	24.300	0.775	3.380	5.828	1.290	1.873	2.248	4.518
78	Pt3+	4.36		28.500	18.700	0.775	3.380	5.113	1.290	1.689	2.020	3.963
78	Pt2+	4.36		18.600	13.800	0.775	3.380	4.392	1.290	1.513	1.790	3.405
78	Pt+	4.36		9.0000	9.0000	0.775	3.380	3.547	1.290	1.289	1.520	2.749
79	Au5+	4.36		58.000	32.346	0.749	3.263	6.724	1.336	1.991	2.461	5.033
79	Au3+	4.36		30.500	20.077	0.749	3.263	5.297	1.336	1.657	2.021	3.965
79	Au2+	4.36		20.500	14.865	0.749	3.263	4.558	1.336	1.498	1.793	3.412
79	Au+	4.36		9.2300	9.2300	0.749	3.263	3.592	1.336	1.260	1.495	2.689
80	Hg2+	4.33		18.800	14.620	0.694	3.008	4.490	1.440	1.367	1.672	3.118
80	Hg+	4.36		10.440	10.440	0.694	3.028	3.820	1.440	1.219	1.480	2.653
81	Tl+3	4.36		29.800	18.770	0.646	2.815	5.122	1.549	1.423	1.749	3.307
81	Tl+	4.36		6.1100	6.1100	0.646	2.815	2.922	1.549	1.069	1.164	1.887
82	Pb4+	4.36		42.300	24.180	0.650	2.835	5.814	1.538	1.558	1.944	3.780
82	Pb2+	4.36		15.000	11.210	0.650	2.835	3.958	1.538	1.242	1.447	2.574
83	Bi5+	4.36		56.000	30.178	0.658	2.868	6.495	1.520	1.698	2.147	4.273
83	Bi+3	4.36		25.600	16.530	0.658	2.868	4.807	1.520	1.399	1.690	3.162
84	Po6+	4.36		71.488	37.111	0.654	2.850	7.202	1.530	1.804	2.326	4.707
84	Po4+	4.36		37.448	22.922	0.654	2.850	5.660	1.530	0.775	1.911	3.700
84	Po3+	4.36		27.745	18.072	0.654	2.850	5.026	1.530	1.416	1.740	3.285
84	Po2+	4.36		18.051	13.235	0.654	2.850	4.301	1.530	1.292	1.545	2.811
85	At7+	4.36		88.291	44.345	0.690	3.007	7.873	1.450	2.048	2.624	5.430
85	At5+	4.36		88.291	29.370	0.690	3.007	6.407	1.450	2.048	2.208	4.419
85	At3+	4.36		29.262	18.660	0.690	3.007	5.107	1.450	1.508	1.838	3.522
85	At+	4.36		9.2000	9.2000	0.690	3.007	3.586	1.450	1.186	1.406	2.473
86	Rn8+	4.36		106.54	44.700	0.704	3.070	7.904	1.420	2.234	2.680	5.567
86	Rn6+	4.36		65.490	36.730	0.704	3.070	7.165	1.420	1.919	2.466	5.046
86	Rn4+	4.36		41.900	25.250	0.704	3.070	5.941	1.420	1.690	2.111	4.183
87	Fr+	4.36		3.9800	3.9800	0.407	1.772	2.359	2.460	0.869	0.782	0.959
88	Ra2+	4.36		10.200	7.740	0.426	1.855	3.289	2.350	0.940	0.964	1.400
89	Ac3+	4.36		19.692	12.321	0.504	2.199	4.150	1.983	1.097	1.249	2.093
90	Th4+	4.36		28.800	16.595	0.581	2.533	4.816	1.721	1.291	1.540	2.798
90	Th3+	4.36		20.000	12.527	0.581	2.533	4.184	1.721	1.205	1.389	2.431
91	Pa4+	4.36				0.584	2.548	3.900	1.711	1.096	1.326	2.279
92	U4+	4.36				0.594	2.589	3.900	1.684	1.106	1.341	2.316
93	Np4+	4.36				0.600	2.617	3.900	1.666	1.114	1.351	2.341
94	Pu4+	4.36				0.604	2.631	3.900	1.657	1.117	1.357	2.354
95	Am4+	4.36				0.602	2.627	3.900	1.660	1.116	1.355	2.349
96	Cm3+	4.36				0.555	2.421	3.900	1.801	1.065	1.279	2.165
97	Bk3+	4.36				0.568	2.476	3.900	1.761	1.078	1.299	2.215
98	Cf3+	4.36				0.571	2.491	3.900	1.750	1.082	1.305	2.229
99	Es3+	4.36				0.580	2.529	3.900	1.724	1.091	1.319	2.262
100	Fm3+	4.36				0.584	2.547	3.900	1.712	1.096	1.326	2.278
101	Md3+	4.36				0.592	2.581	3.900	1.689	1.104	1.338	2.309
102	No3+	4.36				0.596	2.597	3.900	1.679	1.108	1.344	2.323
103	Lw3+	4.36				1.000	4.360	3.900	1.000	1.715	1.994	3.900

.

Based on the IC model, ionocovalency can be finally defined as “the effective potential caused by the ionicity on a bonding pair of electrons at the localized covalent boundary in different valence hybrid orbital states, forming an ionocovalent charge density”.

3. Results

3.1. General Trend of Periodic Table

Natural Values: Chart 1 shows that IC has a same value range as that of its atomic core charge. This phenomenon is particularly noticeable for the top period elements which have not yet experienced much shielding effects. The atomic core charge is an effective nuclear charge and is always markedly less than the actual nuclear charge Z, but, as the shielding is not perfect, the core charge increases as Z increases, but more slowly. In the IC model, the effective nuclear charge is determined by natural IE, not from the calculation by shielding constants.

Ionocovalent Continuum: Chart 1 and Table 1 show that the ionocovalency IC and the electronegativity X_IC exhibit evidently the ionocovalency character. The greater the IC and the X_IC, the more covalent and the less ionic the cation is, and vice versa. Generally, across the period, the more right-hand-side an element is, the more covalent it is. And the more down-ward an element is, the more ionic it is. The IC and X_IC increase from the lower left to the upper right of the Periodic Table across the s and p blocks, and decrease down most columns. Trends parallel periodic trends in IE.

The ionocovalency is a continuum which is certainly an improvement over the old ionic-versus-covalent dichotomy. In so-called ‘pure’ ionic bonding, an electron is transferred completely from one atom to another, once this transfer is complete, the IC potential will act to try to pull this electron back to its parent ion. If IC partially succeeds then there will be some electron density, n*(I_av/R)^½r_c⁻¹, in the region in between the ions, which is the situation in a covalent bond. Thus ‘pure’ ionic and ‘pure’ covalent bonds could be seen as two extremes of an IC continuum. And so a covalent scale has the ionic degree.

Energy-lowered Hybrid Bonding: The ionocovalent bonding procedures runs a charge promotion, charge distribution and energy-lowered hybrid sequence. Using Equation 2.1.5. and 2.1.6., we get the energy-lowered hybrid IC and X_IC values which are evidently lower than that of unhybridized values. For example, for carbon we have the energy-lowered 2sp³ hybrid IC = 4.320 and X_IC = 2.167. In the unhybridized situation, IC would be as higher as 5.702 and all unhybridized conventional electronegativities are as higher as than 2.5 for carbon.

3.2. Hydrogen

Pauling’s scale is estimated from the bond dissociation energies of two atoms, hydrogen and chlorine, and then arbitrarily extended to all elements not based on the quantitative configuration energy data [3].

Hydrogen has the lowest energy, E = −13.6 eV. Batsanov has an experimental covalent radius of 0.37 Å [30] equal to the Heitler-London’s half H-H value R (R = 0.74 Å) [26]. Based on these spectroscopic data and the IC model (Equation 2.1.5), we reach its IC value of 2.297 eV and its electronegativity, X_IC of 1.333 (

Table 2. IC and X_IC for hydrogen and the top elements.

Elements	Li	Be	H	B	C	N	O	F
IC	1.023	2.064	2.297	3.291	4.302	5.329	6.273	7.37
XIC	0.808	1.237	1.333	1.743	2.167	2.583	2.972	3.423

and Figure 1) that is not that conventionally high as 2.2.

The result is strongly supported by the point-charge distribution in hydrides (

Table 3. Point-charge distribution q_A and dipole moment.

Hydrides	LiH	BeH	BH	CH	NH	OH	FH
Bond Length (expr)	1.595	1.343	1.233	1.12	1.038	0.971	0.917
Dipole Moment (expr)	5.88	-	-	1.46	-	1.66	1.82
Dipole Moment (calc)	5.999	0.281	−1.689	−1.647	−1.743	−1.864	−2.02
qA	0.783	0.044	−0.285	−0.306	−0.350	−0.400	−0.459

) proposed by Mo [33], which shows that in the typical ionic LiH (lithium monohydride) hydrogen gains point charge of 0.783, in the weak ionic BeH (beryllium monohydride) gains only 0.044, but in the covalent BH (boron monohydride) starts to loss point charge. That means that the ionocovalency and the electronegativity of hydrogen are smaller than that of boron. And moreover, the data of electric dipole moments for AlH (aluminum monohydride) (

Table 4. Bond length and dipole moment

Bond	H-Na	H-Mg	H-Al	H-Si	H-Se	H-P	H-S	H-Cl
Bond Length (expr)	1.887	1.73	1.648	1.52	1.475	1.422	1.341	1.275
Dipole Moment (cal)	5.966	1.231	−0.169	−0.332	−0.634	−0.651	−1.06	−1.468

), proposed by the National Institute of Standards and Technology [34], shows that the aluminum end of the dipole is negative. That means that the ionocovalency and the electronegativity of hydrogen are smaller than that of aluminum.

Hydrogen has one valency orbital and a single electron. It can be an anion to form an ionic bond by gaining another electron and it can be a cation to form a covalent bond by sharing another electron. Therefore, the IC and the X_IC values of hydrogen happen to lie on the border between the weaker ionic beryllium and the weaker covalent boron (Chart 1 and Table 1). We can assign the IC value of hydrogen (2.297) as a standard to estimate the ionocovalent character of the cations. The cations with IC values smaller than that of hydrogen we call the ionic cations and those with IC values greater than that of hydrogen we call the covalent cations. The cations with IC values greater than that of beryllium (2.064) and smaller than that of boron (3.291) we might call borderline cations. The greater the IC than that of hydrogen, the more covalent and the less ionic the caton is, and vice versa.

3.3. Diagonal Relationship (Top Periods)

Chart 2 and Chart 3 show that the IC and the X_IC scales of the top period rationalize an interesting empirical observation of a similar situation that exists for the pairs of elements. The first element in a given family of the periodic chart tends to resemble the second element in the family to the right as indicated below:

Chart 1. Ionocovalency.

H																	He
(1)2.297																	(2)5.173
Li	Be											B	C	N	O	F	Ne
(1)1.023	(2)2.064											(3)3.291	(4)4.302	(5)5.329	(6)6.273	(7)7.370	(4)6.949
													(2)2.998	(3)4.030	(2)3.648		(2)5.203
Na	Mg											Al	Si	P	S	Cl	Ar
1.130	(2)1.933											(3)2.730	(4)3.371	(5)4.355	(6)5.165	(7)6.048	(4)4.845
												(1)1.585	(2)2.322	(4)3.872	(4)4.093	(5)4.977	(2)3.762
														(3)3.286	(2)2.121	(1)2.851
K	Ca	Sc	Ti	V	Cr	Mn	Fe	Co	Ni	Cu	Zn	Ga	Ge	As	Se	Br	Kr
(1)0.999	(2)1.617	(3)2.494	(4)3.374	(5)4.359	(6)5.287	(7)6.012	(6)5.520	(4)4.261	(4)4.537	(3)3.918	(2)2.772	(3)3.281	(4)3.895	(5)4.502	(6)5.209	(7)5.941	(6)5.422
			(3)2.824	(4)3.772	(5)4.691	(6)5.426	(5)4.879	(3)3.591	(3)3.802	(2)3.155	(1)2.331	(1)1.841	(2)2.639	(3)3.364	(4)4.090	(5)4.869	(4)4.562
			(2)2.258	(3)3.143	(4)4.058	(5)4.810	(4)4.203	(2)2.874	(2)3.029	(1)2.343				(1)2.422	(2)3.146	(1)2.815	(2)3.538
				(2)2.502	(3)3.395	(4)4.161	(3)3.431	(1)2.113	(1)2.330
					(1)2.077	(2)2.719	(1)2.253
						(1)2.185
Rb	Sr	Y	Zr	Nb	Mo	Tc	Ru	Rh	Pd	Ag	Cd	In	Sn	Sb	Te	I	Xe
(1)0.988	(2)1.576	(3)2.332	(4)3.716	(5)4.043	(6)4.964	(7)5.593	(8)6.394	(6)5.450	(5)4.842	(3)3.592	(2)2.658	(3)2.923	(4)3.601	(5)4.057	(6)4.641	(7)5.339	(8)5.553
			(3)2.267	(4)3.575	(5)4.547	(6)5.090	(7)5.890	(4)4.233	(4)4.277	(2)2.973	(1)2.174	(1)1.678	(2)2.472	(3)3.036	(4)3.675	(5)3.817	(6)4.667
			(2)1.884	(3)3.052	(4)3.980	(5)4.563	(6)5.355	(3)3.638	(3)3.672	(1)2.147					(2)2.832	(1)2.530	(4)3.900
				(2)2.532	(3)3.318	(4)4.008	(5)4.791	(2)2.993	(2)3.042								(2)3.044
				(1)2.040	(2)2.760	(3)3.425	(4)4.189	(1)2.287
					(1)2.155	(2)2.762	(3)3.525
		Δ				(1)2.218	(2)2.924
Cs	Ba	La	Hf	Ta	W	Re	Os	Ir	Pt	Au	Hg	Tl	Pb	Bi	Po	At	Rn
(1)0.992	(2)1.646	(3)2.185	(4)3.624	(5)4.393	(6)5.178	(7)5.874	(8)6.616	(6)5.683	(6)5.640	(5)5.033	(2)3.118	(3)3.307	(4)3.780	(5)4.273	(6)4.707	(7)5.430	(8)5.567
			(3)3.170	(4)3.924	(5)4.697	(6)5.383	(7)6.122	(5)5.107	(5)5.056	(3)3.965	(1)2.653	(1)1.887	(2)2.574	(3)3.162	(4)3.700	(5)4.419	(6)5.046
			(2)2.691	(3)3.462	(4)4.200	(5)4.881	(6)5.608	(4)4.478	(4)4.518	(2)3.412					(3)3.285	(3)3.522	(4)4.183
				(2)3.056	(3)3.707	(4)4.344	(5)5.066	(3)3.910	(3)3.963	(1)2.689					(2)2.811	(1)2.473
				(1)2.473	(2)3.261	(3)3.795	(4)4.483	(2)3.324	(2)3.405
						(2)3.237	(3)3.869	(1)2.831	(1)2.749
						(1)2.597	(2)3.370
		ΔΔ					(1)2.779
Fr	Ra	Ac	Δ	Ce	Pr	Nd	Pm	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm	Yb	Lu
(1)0.959	(2)1.400	(3)2.093		(4)3.074	(4)3.037	(3)2.572	(3)2.606	(3)2.604	(3)2.385	(3)2.637	(4)3.301	(3)2.730	(3)2.754	(3)2.780	(3)2.829	(3)2.649	(3)2.592
				(3)2.506	(3)2.368	(2)2.050			(2)1.858	(2)2.213	(3)2.686				(2)2.286	(2)2.112
			ΔΔ	Th	Pa	U	Np	Pu	Am	Cm	Bk	Cf	Es	Fm	Md	No	Lw
				(4)2.789	(3)2.279	(3)2.316	(4)2.341	(4)2.354	(4)2.349	(3)2.165	(3)2.215	(3)2.229	(3)2.262	(3)2.278	(3)2.309	(3)2.323	(3)3.900
				(3)2.431

Note: Some ions which might not actually exist are included here just for research reference.

Chart 1. Ionocovalency.

H																	He
(1)2.297																	(2)5.173
Li	Be											B	C	N	O	F	Ne
(1)1.023	(2)2.064											(3)3.291	(4)4.302	(5)5.329	(6)6.273	(7)7.370	(4)6.949
													(2)2.998	(3)4.030	(2)3.648		(2)5.203
Na	Mg											Al	Si	P	S	Cl	Ar
1.130	(2)1.933											(3)2.730	(4)3.371	(5)4.355	(6)5.165	(7)6.048	(4)4.845
												(1)1.585	(2)2.322	(4)3.872	(4)4.093	(5)4.977	(2)3.762
														(3)3.286	(2)2.121	(1)2.851
K	Ca	Sc	Ti	V	Cr	Mn	Fe	Co	Ni	Cu	Zn	Ga	Ge	As	Se	Br	Kr
(1)0.999	(2)1.617	(3)2.494	(4)3.374	(5)4.359	(6)5.287	(7)6.012	(6)5.520	(4)4.261	(4)4.537	(3)3.918	(2)2.772	(3)3.281	(4)3.895	(5)4.502	(6)5.209	(7)5.941	(6)5.422
			(3)2.824	(4)3.772	(5)4.691	(6)5.426	(5)4.879	(3)3.591	(3)3.802	(2)3.155	(1)2.331	(1)1.841	(2)2.639	(3)3.364	(4)4.090	(5)4.869	(4)4.562
			(2)2.258	(3)3.143	(4)4.058	(5)4.810	(4)4.203	(2)2.874	(2)3.029	(1)2.343				(1)2.422	(2)3.146	(1)2.815	(2)3.538
				(2)2.502	(3)3.395	(4)4.161	(3)3.431	(1)2.113	(1)2.330
					(1)2.077	(2)2.719	(1)2.253
						(1)2.185
Rb	Sr	Y	Zr	Nb	Mo	Tc	Ru	Rh	Pd	Ag	Cd	In	Sn	Sb	Te	I	Xe
(1)0.988	(2)1.576	(3)2.332	(4)3.716	(5)4.043	(6)4.964	(7)5.593	(8)6.394	(6)5.450	(5)4.842	(3)3.592	(2)2.658	(3)2.923	(4)3.601	(5)4.057	(6)4.641	(7)5.339	(8)5.553
			(3)2.267	(4)3.575	(5)4.547	(6)5.090	(7)5.890	(4)4.233	(4)4.277	(2)2.973	(1)2.174	(1)1.678	(2)2.472	(3)3.036	(4)3.675	(5)3.817	(6)4.667
			(2)1.884	(3)3.052	(4)3.980	(5)4.563	(6)5.355	(3)3.638	(3)3.672	(1)2.147					(2)2.832	(1)2.530	(4)3.900
				(2)2.532	(3)3.318	(4)4.008	(5)4.791	(2)2.993	(2)3.042								(2)3.044
				(1)2.040	(2)2.760	(3)3.425	(4)4.189	(1)2.287
					(1)2.155	(2)2.762	(3)3.525
		Δ				(1)2.218	(2)2.924
Cs	Ba	La	Hf	Ta	W	Re	Os	Ir	Pt	Au	Hg	Tl	Pb	Bi	Po	At	Rn
(1)0.992	(2)1.646	(3)2.185	(4)3.624	(5)4.393	(6)5.178	(7)5.874	(8)6.616	(6)5.683	(6)5.640	(5)5.033	(2)3.118	(3)3.307	(4)3.780	(5)4.273	(6)4.707	(7)5.430	(8)5.567
			(3)3.170	(4)3.924	(5)4.697	(6)5.383	(7)6.122	(5)5.107	(5)5.056	(3)3.965	(1)2.653	(1)1.887	(2)2.574	(3)3.162	(4)3.700	(5)4.419	(6)5.046
			(2)2.691	(3)3.462	(4)4.200	(5)4.881	(6)5.608	(4)4.478	(4)4.518	(2)3.412					(3)3.285	(3)3.522	(4)4.183
				(2)3.056	(3)3.707	(4)4.344	(5)5.066	(3)3.910	(3)3.963	(1)2.689					(2)2.811	(1)2.473
				(1)2.473	(2)3.261	(3)3.795	(4)4.483	(2)3.324	(2)3.405
						(2)3.237	(3)3.869	(1)2.831	(1)2.749
						(1)2.597	(2)3.370
		ΔΔ					(1)2.779
Fr	Ra	Ac	Δ	Ce	Pr	Nd	Pm	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm	Yb	Lu
(1)0.959	(2)1.400	(3)2.093		(4)3.074	(4)3.037	(3)2.572	(3)2.606	(3)2.604	(3)2.385	(3)2.637	(4)3.301	(3)2.730	(3)2.754	(3)2.780	(3)2.829	(3)2.649	(3)2.592
				(3)2.506	(3)2.368	(2)2.050			(2)1.858	(2)2.213	(3)2.686				(2)2.286	(2)2.112
			ΔΔ	Th	Pa	U	Np	Pu	Am	Cm	Bk	Cf	Es	Fm	Md	No	Lw
				(4)2.789	(3)2.279	(3)2.316	(4)2.341	(4)2.354	(4)2.349	(3)2.165	(3)2.215	(3)2.229	(3)2.262	(3)2.278	(3)2.309	(3)2.323	(3)3.900
				(3)2.431

Note: Some ions which might not actually exist are included here just for research reference.

Chart 2. IC-diagonal relationship.

Be2+ (2.252)	B3+ (3.291)	C4+ (4.320)	N5+ (5.554)	O6+ (6.939)
Mg2+ (1.933)	Al3+ (2.730)	Si4+ (3.371)	P5+ (4.355)	S6+ (5.165)

Chart 2. IC-diagonal relationship.

Be2+ (2.252)	B3+ (3.291)	C4+ (4.320)	N5+ (5.554)	O6+ (6.939)
Mg2+ (1.933)	Al3+ (2.730)	Si4+ (3.371)	P5+ (4.355)	S6+ (5.165)

Chart 3. X_IC-diagonal relationship.

Be2+ (1.315)	B3+ (1.743)	C4+ (2.167)	N5+ (2.675)	O6+ (3.246)
Mg2+ (1.184)	Al3+ (1.418)	Si4+ (1.776)	P5+ (2.181)	S6+ (2.515)

Chart 3. X_IC-diagonal relationship.

Be2+ (1.315)	B3+ (1.743)	C4+ (2.167)	N5+ (2.675)	O6+ (3.246)
Mg2+ (1.184)	Al3+ (1.418)	Si4+ (1.776)	P5+ (2.181)	S6+ (2.515)

Chart 4. I_av-diagonal relationship.

Be2+ (13.76)	B3+ (23.800)	C4+ (37.015)	N5+ (53.406)	O6+ (72.020)
Mg2+ (11.325)	Al3+ (17.763)	Si4+ (25.763)	P5+ (35.358)	S6+ (46.077)

Chart 4. I_av-diagonal relationship.

Be2+ (13.76)	B3+ (23.800)	C4+ (37.015)	N5+ (53.406)	O6+ (72.020)
Mg2+ (11.325)	Al3+ (17.763)	Si4+ (25.763)	P5+ (35.358)	S6+ (46.077)

Chart 5. n*/r_c-diagonal telationship.

Be2+ (2.238)	B3+ (2.488)	C4+ (2.618)	N5+ (2.803)	O6+ (3.015)
Mg2+ (2.119)	Al3+ (2.189)	Si4+ (2.449)	P5+ (2.701)	S6+ (2.806)

Chart 5. n*/r_c-diagonal telationship.

Be2+ (2.238)	B3+ (2.488)	C4+ (2.618)	N5+ (2.803)	O6+ (3.015)
Mg2+ (2.119)	Al3+ (2.189)	Si4+ (2.449)	P5+ (2.701)	S6+ (2.806)

The reason for this relationship is that the pairs of element have approximately similar ionocovalency, IC = I(I_av)C(n*r_c⁻¹), due to the approximately similar ionic function I(I_av) (Chart 4) and covalent function C(n*r_c⁻¹) (Chart 5). Because of the electron configuration nature of the elements, the downwards vertical trend in decreasing covalency r_c⁻¹ is the opposite of the downwards vertical trend in increasing principal quantum number n*, and in this section of the Periodic Table the two opposing trends in C(n*r_c⁻¹) approximately cancel each other, resulting in similar values of ionicity, I(I_av).

3.4. Carbon, Sulfur, P-elements and Hydrogen

There are some arguments about the values of electronegativities of carbon, sulfur, selenium, tellurium, iodine and hydrogen [22]. Chart 1 shows IC values in the order:

$$S{e}^{2+}(3.146)>S^{2+}(3.121)>C^{2+}(2.998)>T{e}^{2+}(2.832)>I^{+}(2.530)>H^{+}(2.297)$$

The results are consistent with the observations that hydrides H₂Se, H₂S, H₂C, H₂Te and HI form H₃O⁺ ions in water [35].

As Thomas reviewed, the electronegativity of carbon and sulfur in most of the scale are almost identical. The key point, however, so far as their role as poisons is concerned, is that they differ markedly in the distance at which they sit on the nickel overlayers [36]. The calculations for these locations show that sulfur is very much stronger than carbon as a poison.

The results are also consistent with the experiment data of the dipole moment, which indicates that the electron clouds on the C-S and C-I bond in the molecules CS₂ and CI₄ are close to the sulfur end and the iodine end, respectively [37]. From IC model data (Chart 4), we can see that S⁶⁺ has a greater ionicity than that of C⁴⁺: I_av (S⁶⁺ = 46.077, C⁴⁺ = 37.015), although they have the close spatial covalency, n*r_c⁻¹ (C⁴⁺ = 2.618, S⁶⁺ = 2.805) (Chart 5).

3.5. 3d and 4f Electron Inefficient Screening (p-Block)

As Chart 1 and Table 1 show, the IC and X_IC run the same uneven trend that is expected to decrease down a group with the features in terms of As³⁺(IC = 3.364, X_IC = 1.773) and Bi³⁺(IC = 3.162, X_IC = 1.690) both having higher than expected values, comparing those of P³⁺(IC = 3.286, X_IC = 1.741) and Sb³⁺(IC = 3.036, X_IC = 1.638). This apparent anomaly derives from the filling of the 3d row prior to gallium and the 4f row prior to thallium, both of which lead to higher effective nuclear charges (Table 1) than the previous periods as a result of inefficient screening of the nuclear charge by the 3d and 4f electrons, respectively.

3.6. Standard Potential Redox E⁰ (Transition Elements)

The IC values with a trend of decreasing at d⁵ and d¹⁰ agree well with the variation in values of E⁰ (M²⁺/M) [38] as a function of dⁿ configuration for the first row of transition metals; the d⁰ corresponds to M = Ca (

Table 5. Correlation of IC with the standard redox potential E⁰ (M²⁺/M).

dn	0	2	3	4	5	6	7	8	9	10
E0/V	−2.87	−1.63	−1.18	−0.971	−1.19	−0.44	−0.28	−0.25	0.34	−0.76
IC	1.617	2.258	2.502	2.723	2.719	2.786	2.874	3.029	3.155	2.772

).

3.7. Inert Pair Effect (6s² Elements)

The IC model, based on the VB approximation’s intuitive appeal and determined by covalent radius and ionization energy, is in accord with the relativistic effects with which contributions to the unusual chemistry of the heavier elements are two principal consequences. First, the s orbitals become more stable. Second, d and f orbitals expand and their energies are less.

For the inert pair effect in Tl(I), Pb(II), and Bi(III), the relativistic effects can give a qualitative verbalization: “The s orbitals of the heavier elements become more stable than otherwise expected” [39]. In the IC model, as

Table 6. Atomic parameters of Tl, Pb and Bi.

Cations	Tl+	Tl2+	Tl3+	Pb2+	Pb3+	Pb4+	Bi3+	Bi4+	Bi5+
Iz	6.11	20.4	29.8	15	32	42.3	25.6	45.3	56
Iav	6.11	13.26	18.77	11.21	18.14	24.18	16.63	23.72	30.18
XIC	1.16	1.59	1.75	1.45	1.74	1.94	1.69	1.95	2.15
IC	1.89	2.92	3.31	2.58	3.44	3.78	3.16	3.81	4.27

shows, the effect is attributable to the fact that the bond property in this case is controlled by the ionic function I(I_z, I_av). They are more stable in ionic compounds than in the entirely covalent form. Their IEs for forming higher covalent bonds are too much higher to form a stable hybridizing ionicity I_av:

3.8. Color of Copper, Silver and Gold

According to the relativistic effects: “The s orbitals of the heavier elements become more stable than otherwise expected” [39], we can only give a qualitative overview on the color of gold and silver, but this has nothing to do with the color of copper.

In the IC model, the phenomenon of “the Color of Copper, Silver and Gold” is attributable to the fact that their bond structure is controlled by their ionocovalency dual properties and we can get a satisfactory explanation by the Dual method.

As

Table 7. Atomic parameters of Cu, Ag and Au.

Cations	Cu3+	Ag3+	Au3+
n*	3.45	3.85	4.36
Z*	4.349	4.81	5.297
rc	1.11	1.339	1.336
rc−1	0.901	0.747	0.749
n*rc−1	3.108	2.875	3.263
Iav	21.610	21.227	18.77
XIC	1.885	1.867	2.021
IC	3.918	3.592	3.965

shows, with the increase of the contraction of the s orbital, the outer d orbitals expand and their ionicities I_av are decreased from Cu³⁺ via Ag³⁺ to Au³⁺, however, with the increase of their effective principle quantum number n* the covalency r_c⁻¹ decreases from Cu³⁺ to Ag³⁺ but increases from Ag³⁺ to Au³⁺, which causes the spatial covalency n*r_c⁻¹ of Cu³⁺ higher than that of Ag³⁺ but close to Au³⁺, leading to same trend in ionocovalency.

This quantitative trend in their structure and energy nicely reflect their character of color. Copper and gold are the only two elemental metals with a natural color other than gray or silver, which depends on their ionic delocalizing property of “electron sea” that is capable of absorbing and re-emitting photons over a wide range of frequencies. Copper in its liquefied state, a pure copper surface without ambient light, appears somewhat greenish, a characteristic shared with gold.

4. Applications

4.1. Covalency Result Is Retrieved

Villesuzanne et al. proposed the study: “New considerations on the role of covalency in ferroelectric niobates and tantalites” [23]. Here, covalency means the amount of mixing of oxygen 2p and metal d orbitals to form valence bands; it is evaluated quantitatively through the computation of the crystal orbital overlap population (COOP). The energies of Ta 5d and Nb 4d atomic orbitals are the same in EHTB parameters. The bond lengths are equal too, as found experimentally. The difference in COOP’s occurs because of larger radial extension of Ta 5d compared to Nb 4d orbitals, leading to a greater overlap with oxygen 2p orbitals. The fact that Ta⁵⁺-O bonds are more covalent than Nb⁵⁺-O bonds is due to a larger radial expansion of Ta 5d orbitals. This effect is not accounted for in Pauling electronegativity scales [3], which give information on the energy difference between valence orbitals, not on their spatial overlap. The arguments led to the opposite assumption of reference [24] concerning the covalency of Ta⁵⁺-O and Nb⁵⁺-O bonds from Pauling electronegativity X_p: Ta(1.5) < Nb(1.6).

In their later paper, they proposed that the explicit calculation of the electronic structure—COOP’s in particular—gives a larger covalency for Ta⁵⁺-O bonds than for Nb⁵⁺-O bonds. This result is retrieved in the Allred and Rochow scale [7] and in Zhang electronegativity scales for ions [9]. The results can be fairly well accounted in IC model: the energies of Ta 5d and Nb 4d atomic orbitals are the same in EHTB parameters due to having similar atomic ionicity I_av of 24.89 and 27.02, respectively. The bond lengths are equal due to having similar linear covalency r_c⁻¹ of 0.745 and 0.745, respectively. The big difference is the spatial covalency, n*r_c⁻¹, in I(I_av)C(n*r_c⁻¹) = n*(I_av/R)^½r_c⁻¹. The Ta 5d orbitals, compared to Nb 4d orbitals, involve greater spatial covalency, n*r_c⁻¹, (Ta⁵⁺ = 3.246, Nb⁵⁺ = 2.869), leading to a greater overlap with oxygen 2p orbitals and a greater IC: Ta⁵⁺ (4.393) > Nb⁵⁺ (4.043) and X_IC: Ta⁵⁺(2.197) > Nb⁵⁺(2.053).

4.2. Mössbauer Parameters δ and Δ

As the IC model, n*(I_av/R)^½r_c⁻¹, is defined as ionocovalent density of the effective nuclear charges at covalent boundary, it is strongly related with the Mössbauer parameters δ and Δ [40,41]. The value of the isomer shift, δ, depends particularly on the density of s electrons at the nucleus. Therefore, in iron-57 an increase in electron density causes a negative isomer shift; since d electrons tend to shield the nucleus slightly from the s electrons, the value of δ falls as the number of d electrons in the iron atom falls. Mean values of δ [42], Z* and IC for some oxidation states of iron are shown in

Table 8. IC, Z* and δ for Iron-57.

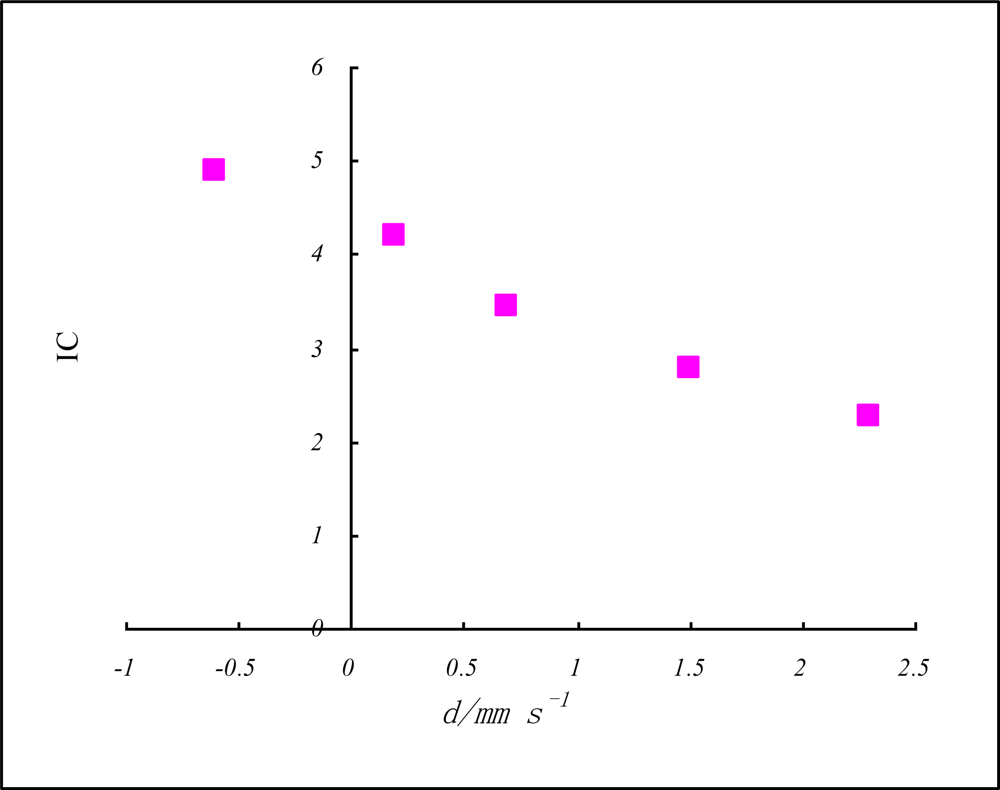
Iron-57	FeI	FeII	FeIII	FeIV	FeV
δ/mm s−1	2.3	1.5	0.7	0.2	−0.6
Z* = n*(Iav/R)½	2.624	3.245	3.997	4.896	5.684
IC = n*(Iav/R)½rc−1	2.253	2.786	3.431	4.203	4.879

and Figure 2.

4.3. Effective Polarizing Power and Fajans Rules

Fajans suggested the rules to estimate the extent to which a cation could polarize an anion and thus induce covalent character. This Fajans phenomenon happens to be the IC-potential, the ionocovalency, the effective ionic potential (or the effective polarizing power), n*(I_av/R)^½r_c⁻¹.

The simple form of the ionic potential considered the valence charge of the ion with respect to its size. The valence charge is numerically equal to the number of valence electrons of the ion. In some cases we may consider the effective nuclear charge Z*. For two ions of the same actual nuclear charge, Hg²⁺ and Ca²⁺, the Hg²⁺ has the higher effective nuclear charge Z* (4.490) and the IC (3.118), it is considerably more polarizing and its compounds are considerably more covalent than those of Ca²⁺ which has the smaller effective nuclear charge Z* (2.807) and the IC (1.617). So we have their related melting points HgCl₂ = 276 and CaCl₂ = 772. Comparisons of more compounds are listed in

Table 9. Parameters and melting points.

Compound	Cation	Z*	Iav	rc−1	n*rc−1	XIC	IC	Melt.pt (°C) [43]
KF	K+	1.949	4.34	0.513	1.769	0.799	0.999	880⋄
AgF	Ag+	2.874	7.58	0.747	2.875	1.271	2.147	435⋄
CaCl2	Ca+2	2.807	9.005	0.576	1.987	1.053	1.617	772⋄
HgCl2	Hg+2	4.49	14.82	0.694	3.008	1.672	3.118	276⋄
CaCl2	Ca+2	2.807	9.005	0.576	1.987	1.053	1.617	772⋄
BeCl2	Be+2	2.002	13.76	1.125	2.238	1.315	2.252	405⋄
NaBr	Na+	1.777	5.14	0.636	1.838	0.853	1.13	755⋄
MgBr2	Mg+2	2.637	11.33	0.733	2.119	1.184	1.933	700⋄
AlBr3	Al+3	3.303	17.76	0.826	2.388	1.512	2.73	97.5⋄
KBr	K+	1.949	4.34	0.513	1.769	0.799	0.999	730⋄
CaBr2	Ca+2	2.807	9.005	0.576	1.987	1.053	1.617	765⋄
CsF	Cs+	2.332	3.89	0.41	1.787	0.781	0.956	684⋄
BaF2	Ba+2	3.26	7.605	0.505	2.201	1.065	1.646	1280⋄

(below).

4.4. Melting Points and Bond Properties

Table 9 shows that for the covalent bonding, the increased covalent bonding resulting from increasing the ionicity I_av, the σ⁻ covalency r_c⁻¹ or the spatial covalency n*r_c⁻¹ can lower the transition temperatures. The melting points decrease with increasing the covalency r_c⁻¹ and the spatial covalency n*r_c⁻¹.

However, for ionic bonding (see 4.5.), the ionic compounds are characterized by very strong IC potentials holding the ions together. Increasing the ionic function I(Z*, I_av) tends to increase the lattice energy of a crystal. For compounds which are predominantly ionic, increased ionic function I(Z*, I_av) or covalent function C(r_c⁻¹, n*r_c⁻¹) will result in increased melting points.

4.5. Lattice Energy

The IC model Equation 2.1.5 is correlated with the electrostatic energy of a cation in Born-Landé equation of the lattice energy

$$U=-Z^2{e}^{2}AN/4\pi {\varepsilon }_{0}r(1-n^{-1})$$

(4.5.1)

The both equations reveal how ionic bond strengths vary with the cation ionic charges and inversely with the distance between ions in the lattice. The IC gives a reasonable correlation to the lattice energy as shown in Table 10 and

Table 11. Lattice energies U (kJmol⁻¹) for MCl₂ correlate with IC.

dn	0	2	3	4	5	6	7	8	9	10
U	2260	2500	2580	2580	2550	2650	2700	2790	2840	2760
IC	1.617	2.258	2.502	2.723	2.719	2.786	2.874	3.029	3.155	2.772

.

4.6. Lowis Acid Strengths

As we have described [8–10], the stability of a metal complex (the strength of metal-ligand bond) should be a function of the electron-attraction power of the metal. The IC value agrees fairly well with the lattice energy and the crystal field stabilization energy (CFES):

Table 10. Parameters and lattice energies, −U.

Compound	Cation	Z*	Iav	rc−1	n*rc−1	XIC	IC	U(kJmol 1) [44]
LiH	Li+	1.253	5.39	0.816	2.238	0.808	1.023	905.4
NaH	Na+	1.777	5.14	0.636	1.838	0.853	1.13	810.9
KH	K+	1.949	4.34	0.513	1.769	0.799	0.999	714.2
AgF	Ag+	2.874	7.58	0.747	2.875	1.271	2.147	954
NaF	Na+	1.777	5.14	0.636	1.838	0.853	1.13	903.9
KF	K+	1.949	4.34	0.513	1.769	0.799	0.999	801.2
AgCl	Ag+	2.874	7.58	0.747	2.875	1.271	2.147	904
TlCl	Tl+	2.922	6.11	0.646	2.815	1.164	1.887	732
KCl	K+	1.949	4.34	0.513	1.769	0.799	0.999	697.9
RbCl	Rb+	2.134	4.18	0.455	1.75	0.787	0.97	677.8

Table 10. Parameters and lattice energies, −U.

Compound	Cation	Z*	Iav	rc−1	n*rc−1	XIC	IC	U(kJmol 1) [44]
LiH	Li+	1.253	5.39	0.816	2.238	0.808	1.023	905.4
NaH	Na+	1.777	5.14	0.636	1.838	0.853	1.13	810.9
KH	K+	1.949	4.34	0.513	1.769	0.799	0.999	714.2
AgF	Ag+	2.874	7.58	0.747	2.875	1.271	2.147	954
NaF	Na+	1.777	5.14	0.636	1.838	0.853	1.13	903.9
KF	K+	1.949	4.34	0.513	1.769	0.799	0.999	801.2
AgCl	Ag+	2.874	7.58	0.747	2.875	1.271	2.147	904
TlCl	Tl+	2.922	6.11	0.646	2.815	1.164	1.887	732
KCl	K+	1.949	4.34	0.513	1.769	0.799	0.999	697.9
RbCl	Rb+	2.134	4.18	0.455	1.75	0.787	0.97	677.8

Table 11 shows that the IC values correlate with the lattice energies derived from Born-Haber cycle data for MCl₂ where M is a first row d-block metal; the point for d⁰ corresponds to CaCl₂. (Data are not available for scandium where the stable oxidation state is +3) [38].

Crystal field stabilization energy (CFES) causes to d level an effect upon thermodynamic stability of complex ions. Owing to the overall contraction in size on traversing a period from left to right, there is an increase in CFES from Ca²⁺ to Zn²⁺ and same trend occurred in IC and X_IC, For weak-field ligands (

Table 12. Values of log β for complexes of 1st row metal ions.

	Mn2+	Fe2+	Co2+	Ni2+	Cu2+	Zn2+
IC	2.719	2.786	2.874	3.029	3.155	2.772
Xic	1.507	1.535	1.571	1.635	1.687	1.529
Log β for [M(en)3]2−	5.7	9.5	13.8	18.6	18.7	12.1
Log β for [M(EDTA)]2−	13.8	14.3	16.3	18.6	18.7	16.1

This order is some time called Irving-Williams series, and is often used in discussing metalloenzyme stabilities (e.g., bioinorganic chemistry).

), the formation constants log β [38] follow the uneven trend and the IC and X_IC run in same way: Mn²⁺ < Fe²⁺< Co²⁺ < Ni²⁺ < Cu²⁺ < Zn²⁺.

5. Dual Method

We couldn’t expect “verbum sat sapienti”, but we have a dual parameter group that can dialectically serve many purposes. When IC and X_IC correlate with some properties, their dual component parameters and sub-models would give some reason to an observation or find some clue to a new idea. See above all parameters, sub-models and observations to which we have applied the Dual Method. Further examples are as follows:

5.1. An Interesting Comparison

In

Table 13. Parameters and melting points.

Compound	Cation	Z*	Iav	rc−1	n*rc−1	XIC	IC	Melt.pt (°C) [43]
KBr	K+	1.949	4.34	0.513	1.769	0.799	0.999	730
CaBr2	Ca+2	2.807	9.005	0.576	1.987	1.053	1.617	765
CsF	Cs+	2.332	3.89	0.41	1.787	0.781	0.956	684
BaF2	Ba+2	3.26	7.605	0.505	2.201	1.065	1.646	1280

an interpretation for an interesting comparison can be made between the predominantly ionic species CsF and BaF₂ and the more covalent species KBr and CaBr₂. For ionic species, the bond strengths are controlled by the ionic function I(I_av). Doubling the I_av from 3.890 to 7.605 in the highly ionic fluorides produces the expected increase in lattice energy and correspondingly doubles the transition temperatures (from 684 °C to 1,28 °C). For covalent bonding, the covalent function C(n*r_c⁻¹) is controlling factor. The little change in covalency r_c⁻¹: 0.513, 0.576 and spatial covalency n*r_c⁻¹: 1.769, 1.987 produces the expected little change in transition temperatures (from 730 °C to 765 °C), despite the doubling of I_av from 4.340 to 9.345.

5.2. “Inverted” Sodium-Lithium Electronegativity

Table 14. Parameters and lattice energies, −U.

Compound	Cation	Z*	Iav	rc−1	n*rc−1	XIC	IC	U (kJmol−1) [44]
LiH	Li+	1.253	5.39	0.816	2.238	0.808	1.023	905.4
NaH	Na+	1.777	5.14	0.636	1.838	0.853	1.13	810.9
KH	K+	1.949	4.34	0.513	1.769	0.799	0.999	714.2

shows why electronegativity of sodium is higher than that of lithium. When we correlate IC or X_IC with lattice energies, there is the “inverted” sodium-lithium electronegativity [8,9,45]; that Li⁺ has unexpectedly low values of IC and X_IC. However, we can ask I(I_av, Z*) and C(n*, r_c⁻¹) to dialectically explain it: after 1st filling of p orbitals, Na⁺ reaches a much higher effective nuclear charge Z*(1.777) than that of Li⁺(1.253). The spatial covalency n*r_c⁻¹(Na⁺ = 1.838, Li⁺ = 1.624) does not cancel the higher effective nuclear charge Z* anymore. Dialectically, however, Li⁺ still has higher ionicity, I_av(5.390) and covalency r_c⁻¹(0.816) than that of Na⁺(I_av = 5.140, r_c⁻¹ = 0.636) although covalency is not so important in lattice energy.

5.3. Predicting Raw Material for InN Nanocrystals

Changzheng et al. [46] presented an effective synthetic protocol to produce high quality InN nanocrystals using indium iodide (InI₃). There has been a question: “Is it possible for high-quality InN to be synthesized from indium halides?” The positive answer has been found in their work using InI₃. Concerning the four kinds of indium halides, InF₃, InCl₃, InBr₃, and InI₃, InI₃ has the strongest covalent ability. As is known, when two atoms form a chemical bond, the greater the difference between the electronegativity values for the two atoms, the more ionic the chemical bond between them [8–10].

According to the IC model, in the effective polarizing power, n*(I_av/R)^½r_c⁻¹, both the effective principle quantum number, n*, and the covalent radius, r_c, for halogens are increased in the order: F < Cl < Br < I (Table 1). The polarizability of the anion will be related to its “softness”; that is, to the deformability of its electron cloud. Both increasing n* and r_c will cause this cloud to be less under the influence of the nuclear charge of the anion and more easily influenced by the charge on the cation. So concerning the four kinds of indium halides, InI₃ is more covalent than the other three. And it is possible for high-quality InN to be synthesized from indium iodide (InI₃).

Comparison of melting points for the anion pairs KF/KBr and CaCl₂/CaBr₂ from Table 9 can be treated in same way. KBr and CaBr₂ are more covalent and have lower melting points than KF and CaCl₂ respectively (see 4.4.).

6. Conclusions

Bond properties can be described quantitatively by an atomic dual nature, Ionocovalency (IC), which is defined and correlated with quantum-mechanical potential.

Ionocovalency, n*(I_av/R)^½r_c⁻¹, which is a dual ionocovalent function of bond strength, charge distribution, charge density, effective ionic potential, or effective polarizing power, is composed of quantum parameters or sub-models, which in turn exhibit versatile specific bond properties and applications, forming a multiple functional Dual Method.

The Dual Method of multiple-functional prediction of that the dual properties of ionocovalency, which is a bridge of the chemical bond and the potential, should be able to explain fairly well the chemical observations of elements throughout the Periodic Table because they are based on the electron configuration and spectroscopy from 1s to nf.

Ionocovalency will be further tested against accurate experimental results and in our later papers we shall apply ionocovalency to discuss the types of chemical bonds, the Lewis acid strengths and the glass crosslink density with the Dual Method. And we believe more new applications will be followed by our colleagues.