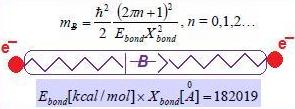The Bondons: The Quantum Particles of the Chemical Bond
Abstract
:1. Introduction
2. Method: Identification of Bondons (B̶)
- Considering the de Broglie-Bohm electronic wave-function/spinor Ψ0 formulation of the associated quantum Schrödinger/Dirac equation of motion.
- Checking for recovering the charge current conservation lawthat assures for the circulation nature of the electronic fields under study.
- Recognizing the quantum potential Vqua and its equation, if it eventually appears.
- Reloading the electronic wave-function/spinor under the augmented U(1) or SU(2) group formwith the standard abbreviation in terms of the chemical field ℵ considered as the inverse of the fine-structure order:since upper bounded, in principle, by the atomic number of the ultimate chemical stable element (Z = 137). Although apparently small enough to be neglected in the quantum range, the quantity (6) plays a crucial role for chemical bonding where the energies involved are around the order of 10–19 Joules (electron-volts)! Nevertheless, for establishing the physical significance of such chemical bonding quanta, one can proceed with the chain equivalencesrevealing that the chemical bonding field caries bondons with unit quanta ħc/e along the distance of bonding within the potential gap of stability or by tunneling the potential barrier of encountered bonding attractors.
- Rewriting the quantum wave-function/spinor equation with the group object ΨG, while separating the terms containing the real and imaginary ℵ chemical field contributions.
- Identifying the chemical field charge current and term within the actual group transformation context.
- Establishing the global/local gauge transformations that resemble the de Broglie-Bohm wave-function/spinor ansatz Ψ0 of steps (i)–(iii).
- Imposing invariant conditions for ΨG wave function on pattern quantum equation respecting the Ψ0 wave-function/spinor action of steps (i)–(iii).
- Establishing the chemical field ℵ specific equations.
- Solving the system of chemical field ℵ equations.
- Assessing the stationary chemical fieldthat is the case in chemical bonds at equilibrium (ground state condition) to simplify the quest for the solution of chemical field ℵ.
- The manifested bondonic chemical field ℵbondon is eventually identified along the bonding distance (or space).
- Checking the eventual charge flux condition of Bader within the vanishing chemical bonding field [26]
- Employing the Heisenberg time-energy relaxation-saturation relationship through the kinetic energy of electrons in bonding
- Equate the bondonic chemical bond field with the chemical field quanta (6) to get the bondons’ mass
3. Type of Bondons
3.1. Non-Relativistic Bondons
3.2. Relativistic Bondons
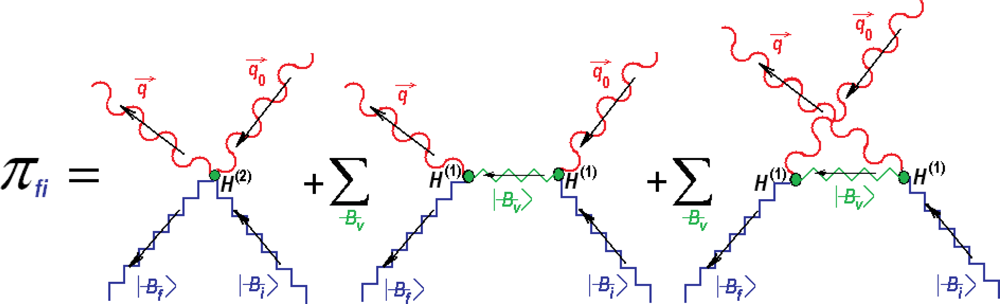
4. Discussion
5. Conclusion
Acknowledgments
References
- Thomson, JJ. On the structure of the molecule and chemical combination. Philos. Mag 1921, 41, 510–538. [Google Scholar]
- Hückel, E. Quantentheoretische beiträge zum benzolproblem. Z. Physik 1931, 70, 204–286. [Google Scholar]
- Doering, WV; Detert, F. Cycloheptatrienylium oxide. J. Am. Chem. Soc 1951, 73, 876–877. [Google Scholar]
- Lewis, GN. The atom and the molecule. J. Am. Chem. Soc 1916, 38, 762–785. [Google Scholar]
- Langmuir, I. The arrangement of electrons in atoms and molecules. J. Am. Chem. Soc 1919, 41, 868–934. [Google Scholar]
- Pauling, L. Quantum mechanics and the chemical bond. Phys. Rev 1931, 37, 1185–1186. [Google Scholar]
- Pauling, L. The nature of the chemical bond. I. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules. J. Am. Chem. Soc 1931, 53, 1367–1400. [Google Scholar]
- Pauling, L. The nature of the chemical bond II. The one-electron bond and the three-electron bond. J. Am. Chem. Soc 1931, 53, 3225–3237. [Google Scholar]
- Heitler, W; London, F. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik. Z. Phys 1927, 44, 455–472. [Google Scholar]
- Slater, JC. The self consistent field and the structure of atoms. Phys. Rev 1928, 32, 339–348. [Google Scholar]
- Slater, JC. The theory of complex spectra. Phys. Rev 1929, 34, 1293–1322. [Google Scholar]
- Hartree, DR. The Calculation of Atomic Structures; Wiley & Sons: New York, NY, USA, 1957. [Google Scholar]
- Löwdin, PO. Quantum theory of many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals, and convergence problems in the method of configurational interaction. Phys. Rev 1955, 97, 1474–1489. [Google Scholar]
- Löwdin, PO. Quantum theory of many-particle systems. II. Study of the ordinary Hartree-Fock approximation. Phys. Rev 1955, 97, 1474–1489. [Google Scholar]
- Löwdin, PO. Quantum theory of many-particle systems. III. Extension of the Hartree-Fock scheme to include degenerate systems and correlation effects. Phys. Rev 1955, 97, 1509–1520. [Google Scholar]
- Roothaan, CCJ. New developments in molecular orbital theory. Rev. Mod. Phys 1951, 23, 69–89. [Google Scholar]
- Pariser, R; Parr, R. A semi - empirical theory of the electronic spectra and electronic structure of complex unsaturated molecules. I. J. Chem. Phys 1953, 21, 466–471. [Google Scholar]
- Pariser, R; Parr, R. A semi-empirical theory of the electronic spectra and electronic structure of complex unsaturated molecules. II. J. Chem. Phys 1953, 21, 767–776. [Google Scholar]
- Pople, JA. Electron interaction in unsaturated hydrocarbons. Trans. Faraday Soc 1953, 49, 1375–1385. [Google Scholar]
- Hohenberg, P; Kohn, W. Inhomogeneous electron gas. Phys. Rev 1964, 136, B864–B871. [Google Scholar]
- Kohn, W; Sham, LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev 1965, 140, A1133–A1138. [Google Scholar]
- Pople, JA; Binkley, JS; Seeger, R. Theoretical models incorporating electron correlation. Int. J. Quantum Chem 1976, 10, 1–19. [Google Scholar]
- Head-Gordon, M; Pople, JA; Frisch, MJ. Quadratically convergent simultaneous optimization of wavefunction and geometry. Int. J. Quantum Chem 1989, 36, 291–303. [Google Scholar]
- Putz, MV. Density functionals of chemical bonding. Int. J. Mol. Sci 2008, 9, 1050–1095. [Google Scholar]
- Putz, MV. Path integrals for electronic densities, reactivity indices, and localization functions in quantum systems. Int. J. Mol. Sci 2009, 10, 4816–4940. [Google Scholar]
- Bader, RFW. Atoms in Molecules-A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Bader, RFW. A bond path: A universal indicator of bonded interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar]
- Bader, RFW. Principle of stationary action and the definition of a proper open system. Phys. Rev. B 1994, 49, 13348–13356. [Google Scholar]
- Mezey, PG. Shape in Chemistry: An Introduction to Molecular Shape and Topology; VCH Publishers: New York, NY, USA, 1993. [Google Scholar]
- Maggiora, GM; Mezey, PG. A fuzzy-set approach to functional-group comparisons based on an asymmetric similarity measure. Int. J. Quantum Chem 1999, 74, 503–514. [Google Scholar]
- Szekeres, Z; Exner, T; Mezey, PG. Fuzzy fragment selection strategies, basis set dependence and HF–DFT comparisons in the applications of the ADMA method of macromolecular quantum chemistry. Int. J. Quantum Chem 2005, 104, 847–860. [Google Scholar]
- Parr, RG; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Putz, MV. Contributions within Density Functional Theory with Applications in Chemical Reactivity Theory and Electronegativity. Ph.D. dissertation, West University of Timisoara, Romania,. 2003. [Google Scholar]
- Sanderson, RT. Principles of electronegativity Part I. General nature. J. Chem. Educ 1988, 65, 112–119. [Google Scholar]
- Mortier, WJ; Genechten, Kv; Gasteiger, J. Electronegativity equalization: Application and parametrization. J. Am. Chem. Soc 1985, 107, 829–835. [Google Scholar]
- Parr, RG; Donnelly, RA; Levy, M; Palke, WE. Electronegativity: The density functional viewpoint. J. Chem. Phys 1978, 68, 3801–3808. [Google Scholar]
- Sen, KD; Jørgenson, CD. Structure and Bonding; Springer: Berlin, Germany, 1987; Volume 66. [Google Scholar]
- Pearson, RG. Hard and Soft Acids and Bases; Dowden, Hutchinson & Ross: Stroudsberg, PA, USA, 1973. [Google Scholar]
- Pearson, RG. Hard and soft acids and bases—the evolution of a chemical concept. Coord. Chem. Rev 1990, 100, 403–425. [Google Scholar]
- Putz, MV; Russo, N; Sicilia, E. On the applicability of the HSAB principle through the use of improved computational schemes for chemical hardness evaluation. J. Comp. Chem 2004, 25, 994–1003. [Google Scholar]
- Chattaraj, PK; Lee, H; Parr, RG. Principle of maximum hardness. J. Am. Chem. Soc 1991, 113, 1854–1855. [Google Scholar]
- Chattaraj, PK; Schleyer, PvR. An ab initio study resulting in a greater understanding of the HSAB principle. J. Am. Chem. Soc 1994, 116, 1067–1071. [Google Scholar]
- Chattaraj, PK; Maiti, B. HSAB principle applied to the time evolution of chemical reactions. J Am Chem Soc 2003, 125, 2705–2710. [Google Scholar]
- Putz, MV. Maximum hardness index of quantum acid-base bonding. MATCH Commun. Math. Comput. Chem 2008, 60, 845–868. [Google Scholar]
- Putz, MV. Systematic formulation for electronegativity and hardness and their atomic scales within densitiy functional softness theory. Int. J. Quantum Chem 2006, 106, 361–386. [Google Scholar]
- Putz, MV. Absolute and Chemical Electronegativity and Hardness; Nova Science Publishers: New York, NY, USA, 2008. [Google Scholar]
- Dirac, PAM. Quantum mechanics of many-electron systems. Proc. Roy. Soc. (London) 1929, A123, 714–733. [Google Scholar]
- Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev 1926, 28, 1049–1070. [Google Scholar]
- Dirac, PAM. The quantum theory of the electron. Proc. Roy. Soc. (London) 1928, A117, 610–624. [Google Scholar]
- Einstein, A; Podolsky, B; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev 1935, 47, 777–780. [Google Scholar]
- Bohr, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev 1935, 48, 696–702. [Google Scholar]
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev 1952, 85, 166–179. [Google Scholar]
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. II. Phys. Rev 1952, 85, 180–193. [Google Scholar]
- de Broglie, L. Ondes et quanta. Compt. Rend. Acad. Sci. (Paris) 1923, 177, 507–510. [Google Scholar]
- de Broglie, L. Sur la fréquence propre de l'électron. Compt. Rend. Acad. Sci. (Paris) 1925, 180, 498–500. [Google Scholar]
- de Broglie, L; Vigier, MJP. La Physique Quantique Restera-t-elle Indéterministe? Gauthier-Villars: Paris, France, 1953. [Google Scholar]
- Bohm, D; Vigier, JP. Model of the causal interpretation of quantum theory in terms of a fluid with irregular fluctuations. Phys. Rev 1954, 96, 208–216. [Google Scholar]
- Pyykkö, P; Zhao, L-B. Search for effective local model potentials for simulation of QED effects in relativistic calculations. J. Phys. B 2003, 36, 1469–1478. [Google Scholar]
- Pyykkö, P. Relativistic theory of atoms and molecules. III A Bibliography 1993–1999, Lecture Notes in Chemistry. Springer-Verlag: Berlin, Germany, 2000; Volume 76. [Google Scholar]
- Snijders, JG; Pyykkö, P. Is the relativistic contraction of bond lengths an orbital contraction effect? Chem. Phys. Lett 1980, 75, 5–8. [Google Scholar]
- Lohr, LL, Jr; Pyykkö, P. Relativistically parameterized extended Hückel theory. Chem. Phys. Lett 1979, 62, 333–338. [Google Scholar]
- Pyykkö, P. Relativistic quantum chemistry. Adv. Quantum Chem 1978, 11, 353–409. [Google Scholar]
- Einstein, A. On the electrodynamics of moving bodies. Ann. Physik (Leipzig) 1905, 17, 891–921. [Google Scholar]
- Einstein, A. Does the inertia of a body depend upon its energy content? Ann. Physik (Leipzig) 1905, 18, 639–641. [Google Scholar]
- Whitney, CK. Closing in on chemical bonds by opening up relativity theory. Int. J. Mol. Sci 2008, 9, 272–298. [Google Scholar]
- Whitney, CK. Single-electron state filling order across the elements. Int. J. Chem. Model 2008, 1, 105–135. [Google Scholar]
- Whitney, CK. Visualizing electron populations in atoms. Int. J. Chem. Model 2009, 1, 245–297. [Google Scholar]
- Boeyens, JCA. New Theories for Chemistry; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Berlin, T. Binding regions in diatomic molecules. J. Chem. Phys 1951, 19, 208–213. [Google Scholar]
- Einstein, A. On a Heuristic viewpoint concerning the production and transformation of light. Ann. Physik (Leipzig) 1905, 17, 132–148. [Google Scholar]
- Oelke, WC. Laboratory Physical Chemistry; Van Nostrand Reinhold Company: New York, NY, USA, 1969. [Google Scholar]
- Findlay, A. Practical Physical Chemistry; Longmans: London, UK, 1955. [Google Scholar]
- Hiberty, PC; Megret, C; Song, L; Wu, W; Shaik, S. Barriers of hydrogen abstraction vs halogen exchange: An experimental manifestation of charge-shift bonding. J. Am. Chem. Soc 2006, 128, 2836–2843. [Google Scholar]
- Freeman, S. Applications of Laser Raman Spectroscopy; John Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Heitler, W. The Quantum Theory of Radiation, 3rd ed; Cambridge University Press: New York, NY, USA, 1954. [Google Scholar]
- Gillespie, RJ. The electron-pair repulsion model for molecular geometry. J. Chem. Educ 1970, 47, 18–23. [Google Scholar]
- Daudel, R. Electron and Magnetization Densities in Molecules and Crystals; Becker, P, Ed.; NATO ASI, Series B-Physics, Plenum Press: New York, NY, USA, 1980; Volume 40. [Google Scholar]
- Putz, MV. Chemical action and chemical bonding. J. Mol. Struct. (THEOCHEM) 2009, 900, 64–70. [Google Scholar]
- Putz, MV. Levels of a unified theory of chemical interaction. Int. J. Chem. Model 2009, 1, 141–147. [Google Scholar]
- Putz, MV. The chemical bond: Spontaneous symmetry–breaking approach. Symmetr. Cult. Sci 2008, 19, 249–262. [Google Scholar]
- Putz, MV. Hidden side of chemical bond: The bosonic condensate. In Chemical Bonding; NOVA Science Publishers: New York, NY, USA, 2011; to be published. [Google Scholar]
- Putz, MV. Conceptual density functional theory: From inhomogeneous electronic gas to Bose-Einstein condensates. In Chemical Information and Computational Challenges in 21st A Celebration of 2011 International Year of Chemistry; Putz, MV, Ed.; NOVA Science Publishers Inc: New York, NY, USA, 2011; to be published. [Google Scholar]
- Kaplan, IG. Is the Pauli exclusive principle an independent quantum mechanical postulate? Int. J. Quantum Chem 2002, 89, 268–276. [Google Scholar]
- Whitney, CK. Relativistic dynamics in basic chemistry. Found. Phys 2007, 37, 788–812. [Google Scholar]
| Bond Type | Xbond (Å) | Ebond (kcal/mol) | tB̶[×1015] (seconds) | |||
|---|---|---|---|---|---|---|
| H–H | 0.60 | 104.2 | 2.34219 | 3.451 | 0.3435 | 9.236 |
| C–C | 1.54 | 81.2 | 0.45624 | 6.890 | 0.687 | 11.894 |
| C–C (in diamond) | 1.54 | 170.9 | 0.21678 | 14.385 | 1.446 | 5.743 |
| C=C | 1.34 | 147 | 0.33286 | 10.816 | 1.082 | 6.616 |
| C≡C | 1.20 | 194 | 0.31451 | 12.753 | 1.279 | 5.037 |
| N≡N | 1.10 | 225 | 0.32272 | 13.544 | 1.36 | 4.352 |
| O=O | 1.10 | 118.4 | 0.61327 | 7.175 | 0.716 | 8.160 |
| F–F | 1.28 | 37.6 | 1.42621 | 2.657 | 0.264 | 25.582 |
| Cl–Cl | 1.98 | 58 | 0.3864 | 6.330 | 0.631 | 16.639 |
| I–I | 2.66 | 36.1 | 0.3440 | 5.296 | 0.528 | 26.701 |
| C–H | 1.09 | 99.2 | 0.7455 | 5.961 | 0.594 | 9.724 |
| N–H | 1.02 | 93.4 | 0.9042 | 5.254 | 0.523 | 10.32 |
| O–H | 0.96 | 110.6 | 0.8620 | 5.854 | 0.583 | 8.721 |
| C–O | 1.42 | 82 | 0.5314 | 6.418 | 0.64 | 11.771 |
| C=O (in CH2O) | 1.21 | 166 | 0.3615 | 11.026 | 1.104 | 5.862 |
| C=O (in O=C=O) | 1.15 | 191.6 | 0.3467 | 12.081 | 1.211 | 5.091 |
| C–Cl | 1.76 | 78 | 0.3636 | 7.560 | 0.754 | 12.394 |
| C–Br | 1.91 | 68 | 0.3542 | 7.155 | 0.714 | 14.208 |
| C–I | 2.10 | 51 | 0.3906 | 5.905 | 0.588 | 18.9131 |
| Ebond [(kcal/mol)] | tB̶[×1015] (seconds) | ||||
|---|---|---|---|---|---|
| 1 | 87.86 | 10.966 | 4.84691 | 1 | 0.4827 × 10−3 |
| 1 | 182019 | 53.376 | 99.9951 | 4.82699 × 10−4 | 1 |
| 10 | 18201.9 | 533.76 | 99.9951 | 4.82699 × 10−5 | 1 |
| 100 | 1820.19 | 5337.56 | 99.9951 | 4.82699 × 10−6 | 1 |
| Property | ςm | ςv | ςe | tB̶ | |
|---|---|---|---|---|---|
| Chemical bond | |||||
| Covalence | >> | << | << | >> | |
| Multiple bonds | < | > | > | < | |
| Metallic | << | > | > | < | |
| Ionic | ∼> | ∼ | ∼ | ∼> | |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Putz, M.V. The Bondons: The Quantum Particles of the Chemical Bond. Int. J. Mol. Sci. 2010, 11, 4227-4256. https://doi.org/10.3390/ijms11114227
Putz MV. The Bondons: The Quantum Particles of the Chemical Bond. International Journal of Molecular Sciences. 2010; 11(11):4227-4256. https://doi.org/10.3390/ijms11114227
Chicago/Turabian StylePutz, Mihai V. 2010. "The Bondons: The Quantum Particles of the Chemical Bond" International Journal of Molecular Sciences 11, no. 11: 4227-4256. https://doi.org/10.3390/ijms11114227