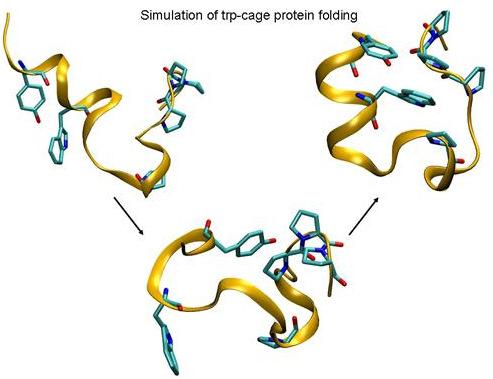
Folding of Trp-cage Mini Protein Using Temperature and Biasing Potential Replica—Exchange Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
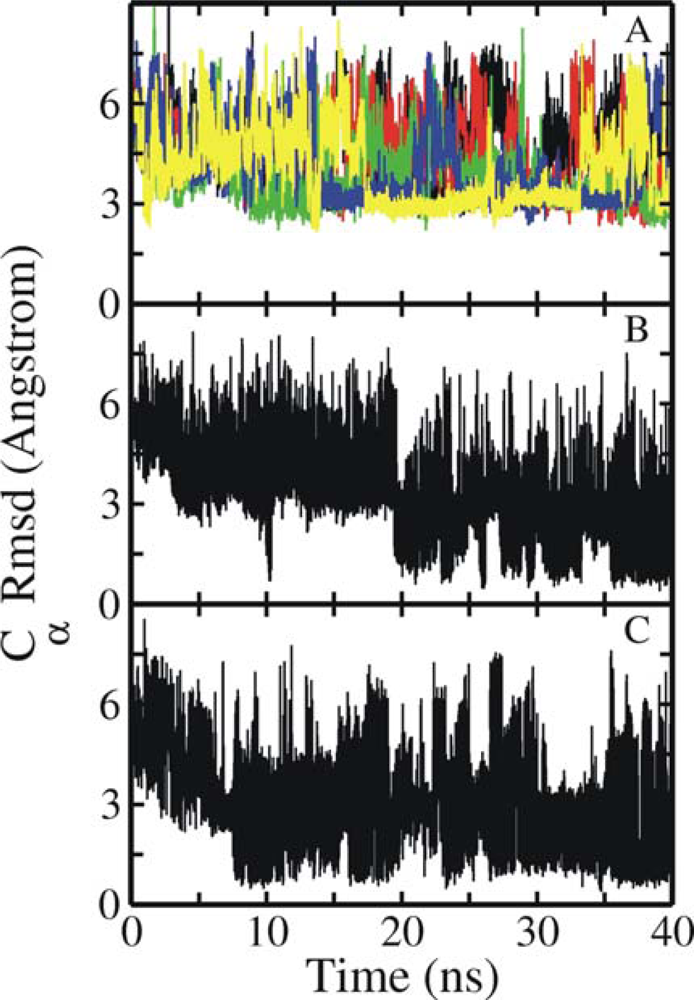
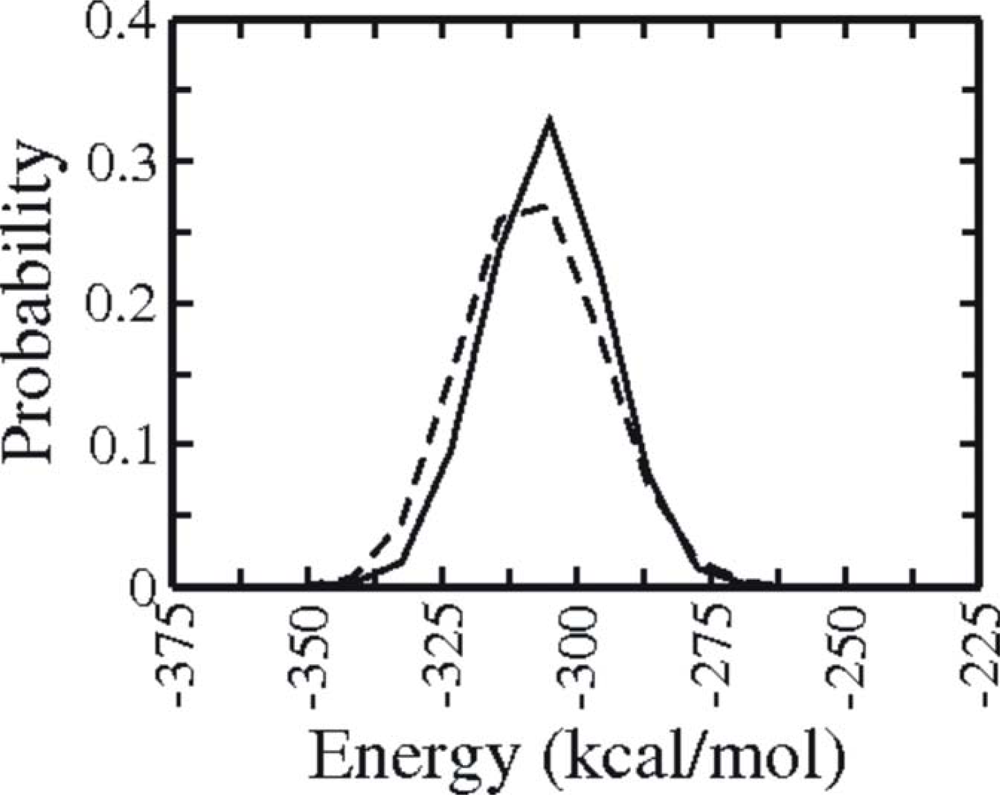
3.1. Comparison of continuous and Replica Exchange MD simulations
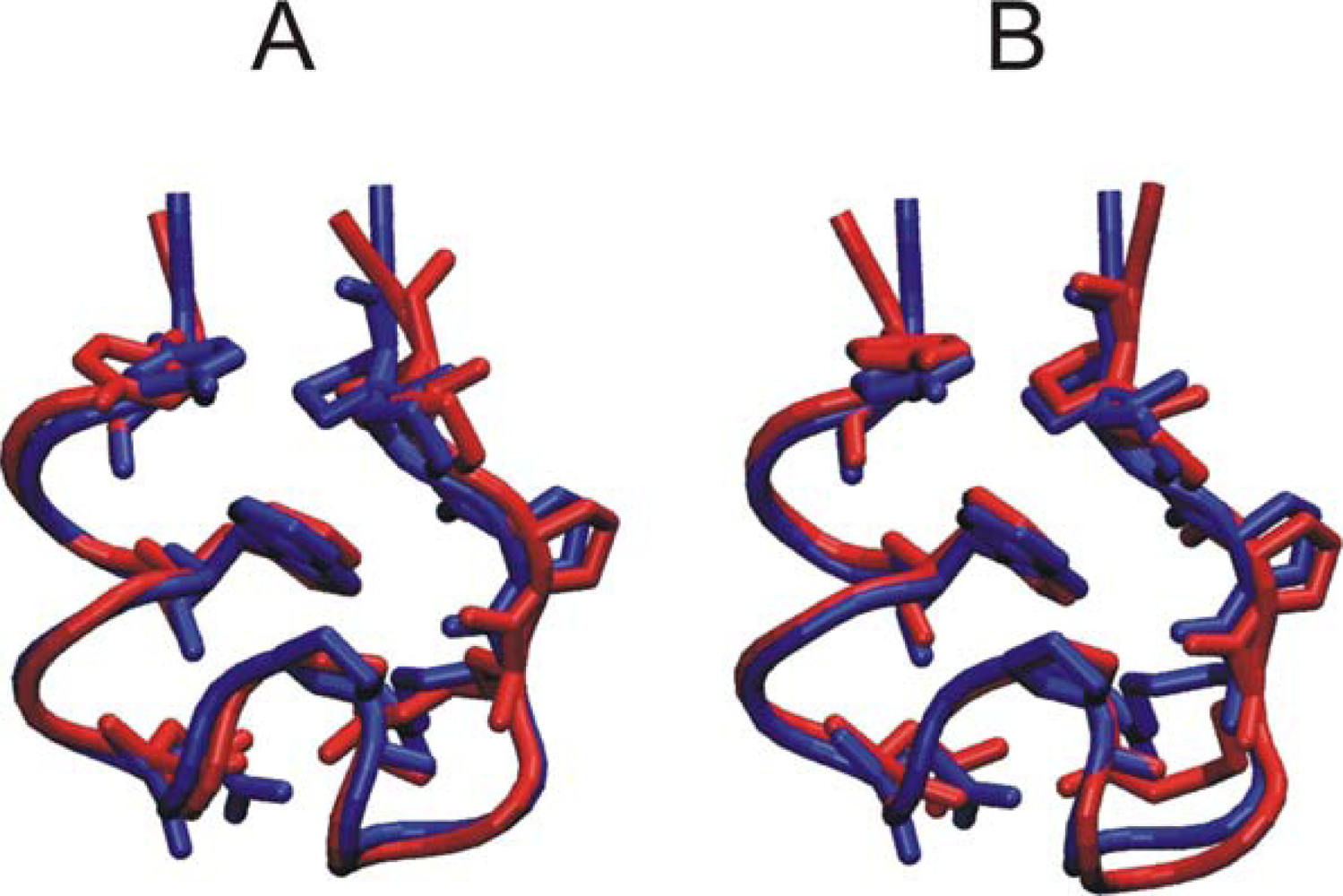
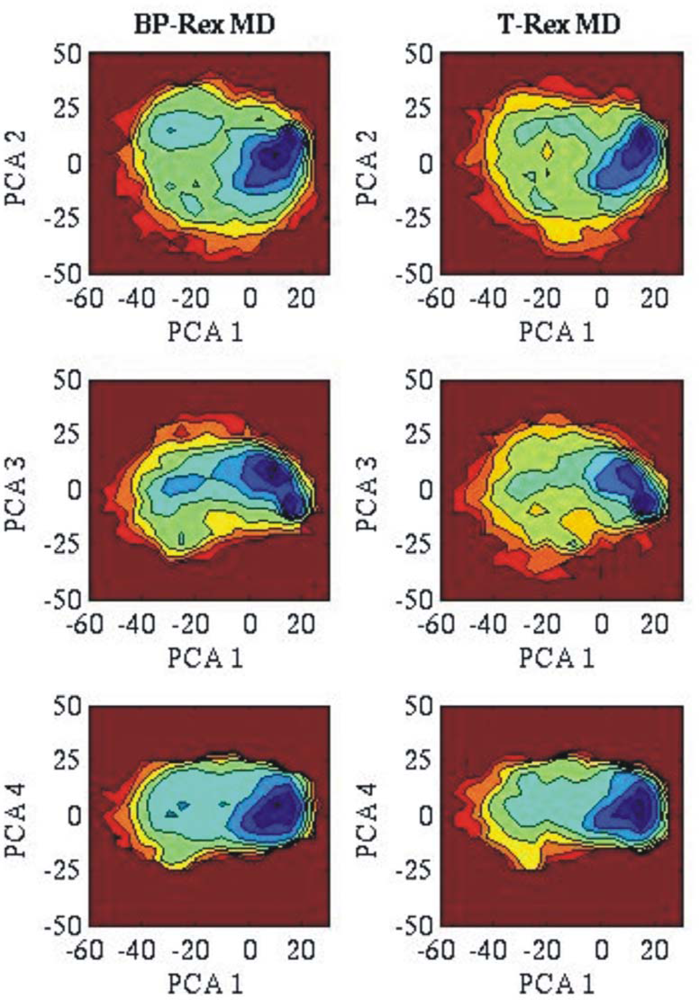
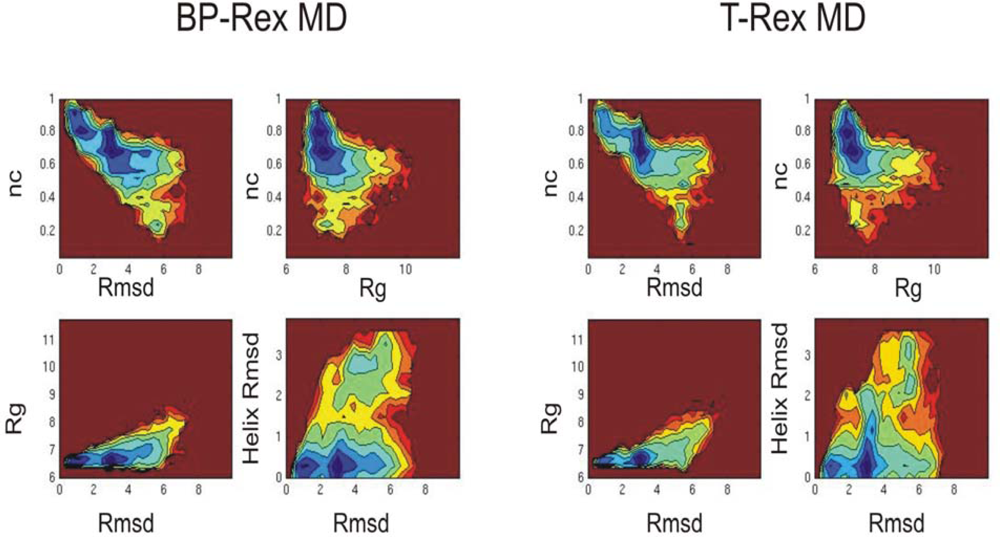
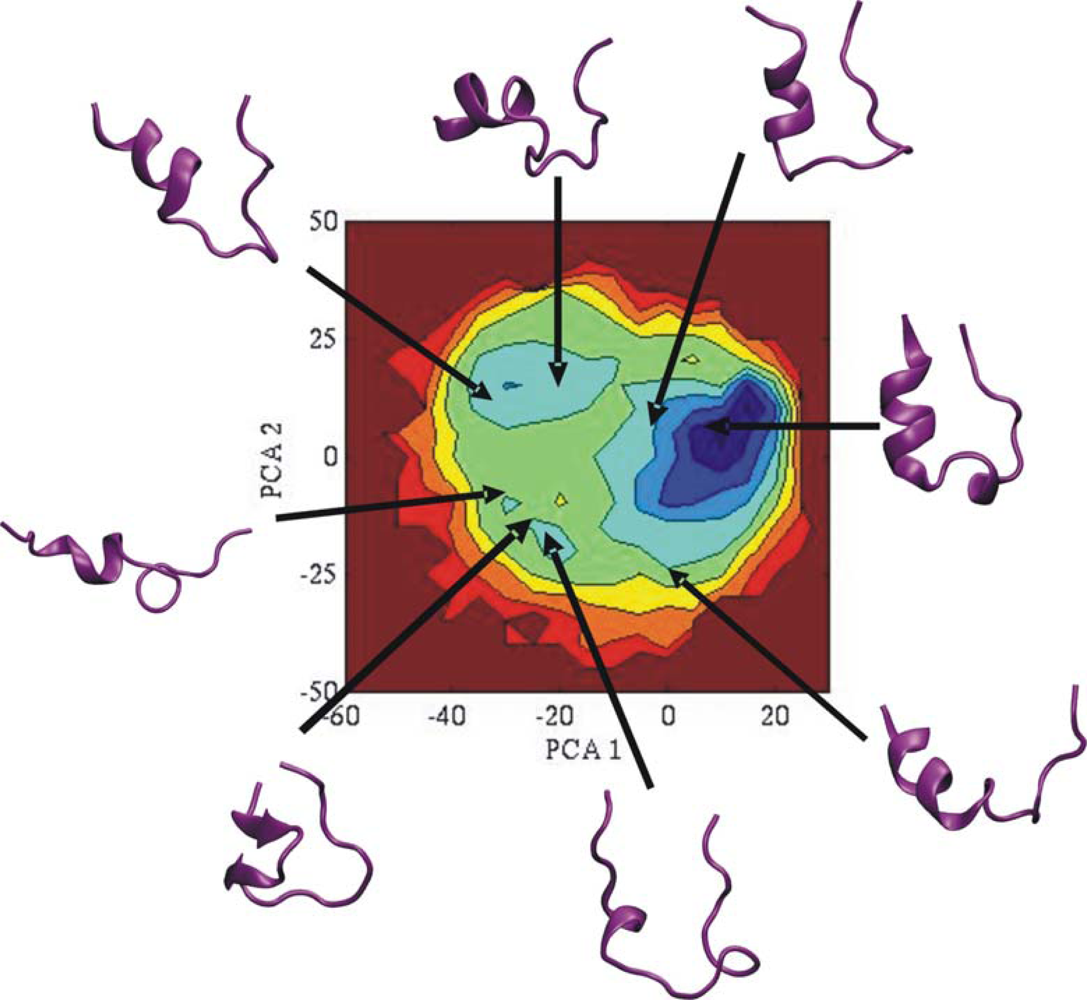
3.2. Comparison of conformational sampling during T-RexMD and BP-RexMD
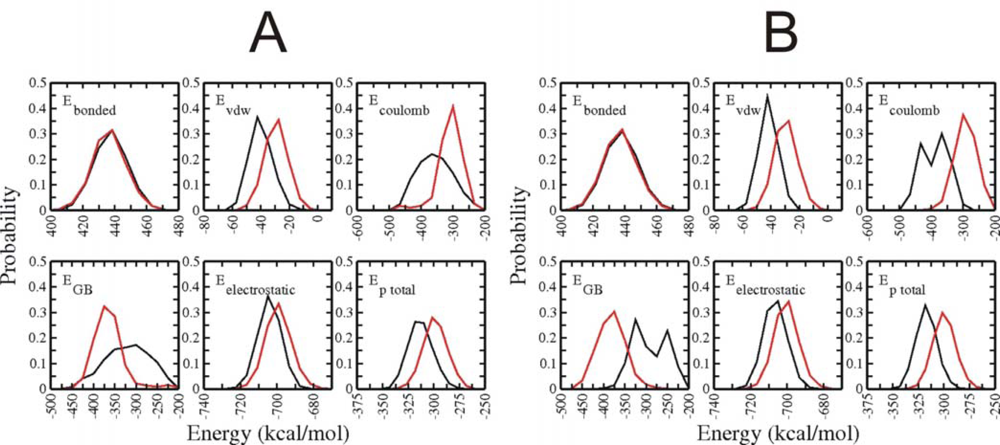
3.3. Analysis of potential energy contributions to folding of Trp-cage protein
4. Conclusions
Acknowledgments
References
- Daura, X; Jaun, B; Seebach, D; van Gunsteren, WF; Mark, AE. Reversible peptide folding in solution by molecular dynamics simulation. J. Mol. Biol 1998, 280, 925–932. [Google Scholar]
- Duan, Y; Kollman, PA. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science 1998, 282, 740–744. [Google Scholar]
- Roccatano, D; Nau, WM; Zacharias, M. Structural and dynamic properties of the CAGQW peptide in water: A molecular dynamics simulation study using different force fields. J. Phys. Chem 2004, 108, 18734–18742. [Google Scholar]
- Seibert, MM; Patriksson, A; Hess, B; van der Spoel, D. Reproducible polypeptide folding and structure prediction using molecular dynamics simulations. J. Mol. Biol 2005, 354, 173–183. [Google Scholar]
- Gnanakaran, S; Nymeyer, H; Portman, J; Sanbonmatsu, KY; Garcia, AE. Peptide folding simulations. Curr. Opin. Struct. Biol 2003, 15, 168–174. [Google Scholar]
- Kaihsu, T. Conformational sampling for the impatient. Biophys. Chem 2004, 107, 213–220. [Google Scholar]
- Brunger, AT; Adams, PD; Rice, LM. New applications of simulated annealing in X-ray crystallography and solution NMR. Structure 1997, 5, 325–336. [Google Scholar]
- Kostrowicki, J; Scheraga, HA. Application of the diffusion equation method for global optimization to oligopeptides. J. Chem. Phys 1992, 96, 7442–7449. [Google Scholar]
- Straatsma, TP; McCammon, JA. Treatment of rotational isomers III. The use of biasing potentials. J. Chem. Phys 1994, 101, 5032–5039. [Google Scholar]
- Huber, T; Torda, AE; van Gunsteren, WF. Structure optimization combining soft-core interaction functions, the diffusion equation method and molecular dynamics. J. Phys. Chem. A 1997, 10, 5926–5930. [Google Scholar]
- Tappura, K; Lahtela-Kakkonen, M; Teleman, O. A new soft-core potential function for molecular dynamics applied to the prediction of protein loop conformations. J. Comput. Chem 2000, 21, 388–397. [Google Scholar]
- Tappura, K. Influence of rotational energy barriers to the conformational search of protein loops in molecular dynamics and ranking the conformations. Proteins. Struct. Funct. Genet 2001, 44, 167–179. [Google Scholar]
- Riemann, RN; Zacharias, M. Reversible scaling of dihedral angle barriers during molecular dynamics to improve structure prediction of cyclic peptides. J. Pept. Res 2004, 63, 354–364. [Google Scholar]
- Riemann, RN; Zacharias, M. Refinement of protein cores and protein-peptide interfaces using a potential scaling approach. Prot. Eng. Des. Select 2005, 18, 465–476. [Google Scholar]
- Hornak, V; Simmerling, C. Generation of accurate protein loop conformations through low-barrier molecular dynamics. Proteins. Struct. Funct. Bioinf 2003, 51, 577–590. [Google Scholar]
- Simmerling, C; Miller, JL; Kollman, PA. Combined locally enhanced sampling and particle mesh ewald as a strategy to locate the experimental structure of a nonhelical nucleic acid. J. Am. Chem. Soc 1998, 120, 7149–7158. [Google Scholar]
- Swendsen, RH; Wang, JS. Replica Monte Carlo simulations of spin glasses. Phys. Rev. Lett 1986, 57, 2607–2609. [Google Scholar]
- Okamoto, Y. Generalized-ensemble algorithms: Enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. J. Mol. Graph. Model 2004, 22, 425–439. [Google Scholar]
- Predescu, C; Predescu, M; Ciobanu, CVJ. On the efficiency of exchange in parallel tempering Monte Carlo simulations. J. Phys. Chem. B 2005, 109, 4189–4196. [Google Scholar]
- Kirkpatrick, S; Gelatt, CD; Vecchi, MP, Jr. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar]
- Simulated Annealing: Theory and Applications; Larrhoven, PJM; Aarts, EHL (Eds.) Reidel: Dordrecht, 1987; p. 187.
- Sugita, Y; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett 1999, 314, 141–151. [Google Scholar]
- Mitsutake, A; Sugita, Y; Okamoto, Y. Generalized-ensemble algorithms for molecular simulations of biopolymers. Biopolymers 2001, 60, 96–123. [Google Scholar]
- Sanbonmatsu, KY; Garcia, AE. Structure of Met-enkephalin in explicit aqueous solution using replica exchange molecular dynamics. Proteins. Struct. Funct. Bioinf 2002, 46, 225–234. [Google Scholar]
- Zhou, R; Berne, BJ. Can a continuum solvent model reproduce the free energy landscape of a β-hairpin folding in water? Proc. Natl. Acad. Sci. USA 2002, 99, 12777–12782. [Google Scholar]
- Zhou, R. Free energy landscape of protein folding in water: explicit vs. implicit solvent. Proteins Struct. Funct. Bioinf 2003, 53, 148–161. [Google Scholar]
- Nymeyer, H; Garcia, AE. Simulation of the folding equilibrium of α-helical peptides: A comparison of the generalized Born approximation with explicit solvent. Proc. Natl. Acad. Sci. USA 2003, 100, 13934–13939. [Google Scholar]
- Yoshida, K; Yamaguchi, T; Okamoto, Y. Replica-exchange molecular dynamics simulation of small peptide in water and in ethanol. Chem. Phys. Lett 2005, 41, 2280–2284. [Google Scholar]
- Rao, F; Caflisch, A. Replica exchange molecular dynamics simulations of reversible folding. J. Chem. Phys 2003, 119, 4035–4042. [Google Scholar]
- Nguyen, P; Stock, G; Mittag, E; Hu, C-K; Li, MS. Free energy landscape and folding mechanism of a β-hairpin in explicit water: A replica exchange molecular dynamics study. Proteins 2006, 61, 795–808. [Google Scholar]
- Rathore, N; Chopra, M; de Pablo, JJ. Optimal allocation of replicas in parallel tempering simulations. J. Chem. Phys 2005, 122, 24111–24118. [Google Scholar]
- Cheng, X; Cui, G; Hornak, V; Simmerling, C. Modified replica exchange simulation methods for local structure refinement. J. Phys. Chem. B 2005, 109, 8220–8230. [Google Scholar]
- Jang, S; Shin, S; Pak, Y. Replica-exchange method using the generalized effective potential. Phys. Rev. Lett 2003, 91, 58305–58309. [Google Scholar]
- Zhu, Z; Tuckerman, ME; Samuelson, SO; Martyna, GJ. Using Novel variable transformations to enhance conformational sampling in molecular dynamics. Phys. Rev. Lett 2002, 88, 100201–100205. [Google Scholar]
- Liu, P; Kim, B; Friesner, RA; Berne, BA. Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. USA 2005, 102, 13749–13754. [Google Scholar]
- Affentranger, R; Tavernelli, I; Di Iorio, EE. A novel Hamiltonian replica exchange MD protocol to enhance protein conformational space sampling. J. Chem. Theory. Comput 2006, 2, 217–228. [Google Scholar]
- Kannan, S; Zacharias, M. Enhanced sampling of peptide and protein conformations using replica exchange simulations with a peptide backbone biasing-potential. Proteins 2007, 66, 697–706. [Google Scholar]
- Neidigh, JW; Fesinmeyer, MR; Andersen, NH. Designing a 20-residue protein. Nat. Struct. Biol 2002, 9, 425–430. [Google Scholar]
- Qiu, L; Pabit, SA; Roitberg, AE; Hagen, SJ. Smaller and faster: the 20-residue Trp-cage protein folds in 4 micros. J. Am. Chem. Soc 2002, 124, 12952–12953. [Google Scholar]
- Ahmed, Z; Beta, IA; Mikhonin, AV; Asher, SA. UV-resonance Raman thermal unfolding study of Trp-cage shows that it is not a simple two-state miniprotein. J. Am. Chem. Soc 2005, 127, 10943–10950. [Google Scholar]
- Mok, KH; Kuhn, LT; Goez, M; Day, IJ; Lin, JC; Andersen, NH; Hore, PJ. Pre-existing hydrophobic collapse in the unfolded state of an ultrafast folding protein. Nature 2007, 447, 106–109. [Google Scholar]
- Simmerling, C; Strockbine, B; Roitberg, AE. All-atom structure prediction and folding simulations of a stable protein. J. Am. Chem. Soc 2002, 124, 11258–11259. [Google Scholar]
- Snow, CD; Zagrovic, B; Pande, VS. The Trp cage: Folding kinetics and unfolded state topology via molecular dynamics simulations. J. Am. Chem. Soc 2002, 124, 14548–14549. [Google Scholar]
- Chowdhury, S; Lee, MC; Xiong, G; Duan, Y. Ab initio folding simulation of the Trp-cage mini-protein approaches NMR resolution. J. Mol. Biol 2003, 327, 711–717. [Google Scholar]
- Chowdhury, S; Lee, MC; Duan, Y. Characterizing the rate-limiting step of Trp-cage folding by All-Atom molecular dynamics simulations. J. Phys. Chem. B 2004, 108, 13855–13865. [Google Scholar]
- Pitera, JW; Swope, W. Understanding folding and design: replica-exchange simulations of “Trp-cage” miniproteins. Proc. Natl. Acad. Sci. USA 2003, 100, 7587–7592. [Google Scholar]
- Case, D; Pearlman, DA; Caldwell, JW; Cheatham, TE, III; Ross, WS; Simmerling, CL; Darden, TA; Merz, KM; Stanton, RV; Cheng, AL; Vincent, JJ; Crowley, M; Tsui, V; Radmer, RJ; Duan, Y; Pitera, J; Massova, I; Seibel, GL; Singh, UC; Weiner, PK; Kollman, PA. Amber 8; University of California: San Francisco, 2003. [Google Scholar]
- Duan, Y; Wu, A; Chowdhury, CS; Lee, MC; Xiong, G; Zhang, W; Yang, R; Cieplak, P; Luo, R; Lee, T; Caldwell, J; Wang, J; Kollman, P. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem 2003, 24, 1999–2012. [Google Scholar]
- Onufriev, A; Bashford, D. Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized Born model. Proteins 2004, 55, 383–394. [Google Scholar]
- Feig, M; Karanicolas, J; Brooks, CL. MMTSB tool set: Enhanced sampling and multiscale modeling methods for applications in structural biology. J. Mol. Graph. Model 2004, 22, 377–395. [Google Scholar]
- Humphrey, W; Dalke, A; Schulten, K. VMD - Visual Molecular Dynamics. J. Molec. Graphics 1996, 14, 33–38. [Google Scholar]
- Paschek, D; Nymeyer, H; Garcia, AE. Replica exchange simulation of reversible folding/unfolding of the Trp-cage miniprotein in explicit solvent: On the structure and possible role of internal water. J. Struct. Biol 2007, 157, 524–533. [Google Scholar]
- Paschek, D; Hempel, S; Garcia, AE. Computing the stability diagram of the Trp-cage miniprotein. Proc. Natl. Acad. Sci. USA 2008, 105, 17754–17759. [Google Scholar]
- Streicher, WW; Makhatadze, GI. Unfolding thermodynamics of trp-cage, a 20 residue miniprotein, studied by differential scanning calorimetry and circular dichroism spectroscopy. Biochemistry 2007, 46, 2876–2880. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kannan, S.; Zacharias, M. Folding of Trp-cage Mini Protein Using Temperature and Biasing Potential Replica—Exchange Molecular Dynamics Simulations. Int. J. Mol. Sci. 2009, 10, 1121-1137. https://doi.org/10.3390/ijms10031121
Kannan S, Zacharias M. Folding of Trp-cage Mini Protein Using Temperature and Biasing Potential Replica—Exchange Molecular Dynamics Simulations. International Journal of Molecular Sciences. 2009; 10(3):1121-1137. https://doi.org/10.3390/ijms10031121
Chicago/Turabian StyleKannan, Srinivasaraghavan, and Martin Zacharias. 2009. "Folding of Trp-cage Mini Protein Using Temperature and Biasing Potential Replica—Exchange Molecular Dynamics Simulations" International Journal of Molecular Sciences 10, no. 3: 1121-1137. https://doi.org/10.3390/ijms10031121