First-Principles Molecular Dynamics Calculations of the Equation of State for Tantalum
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
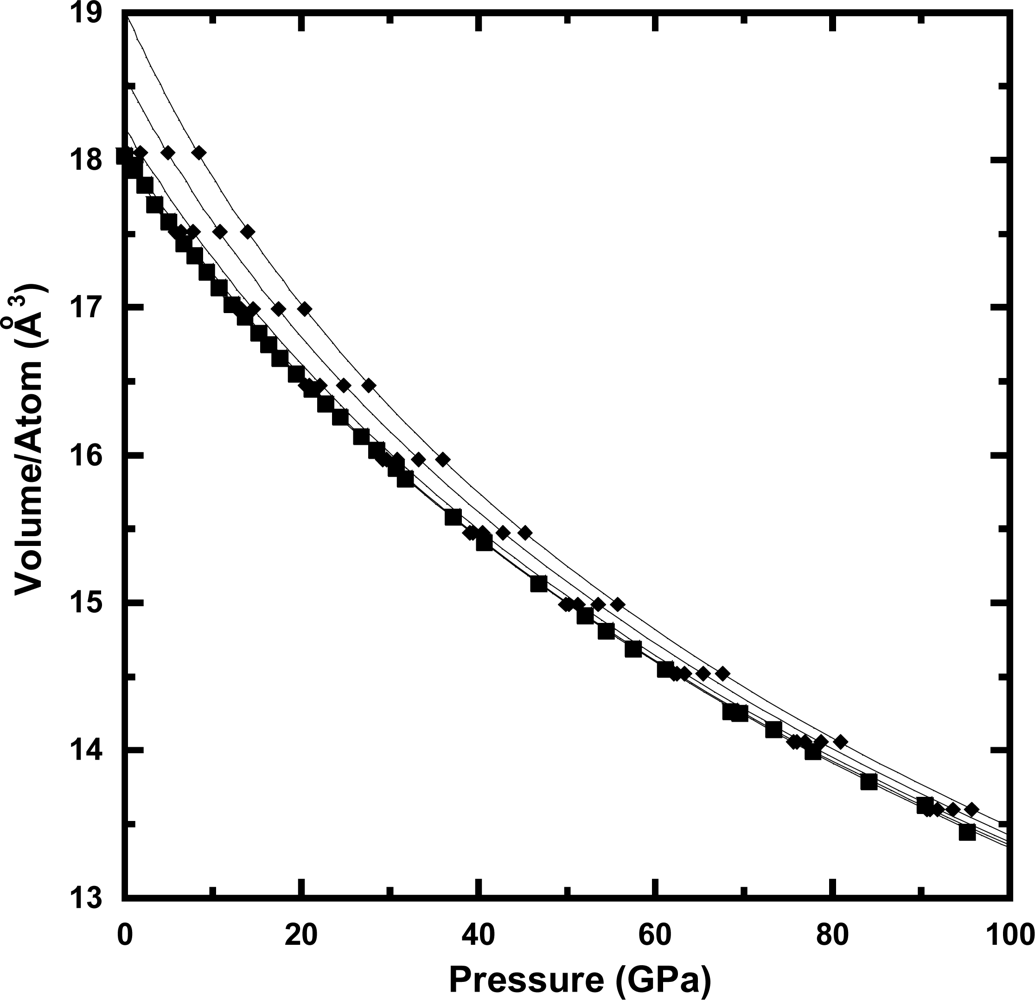
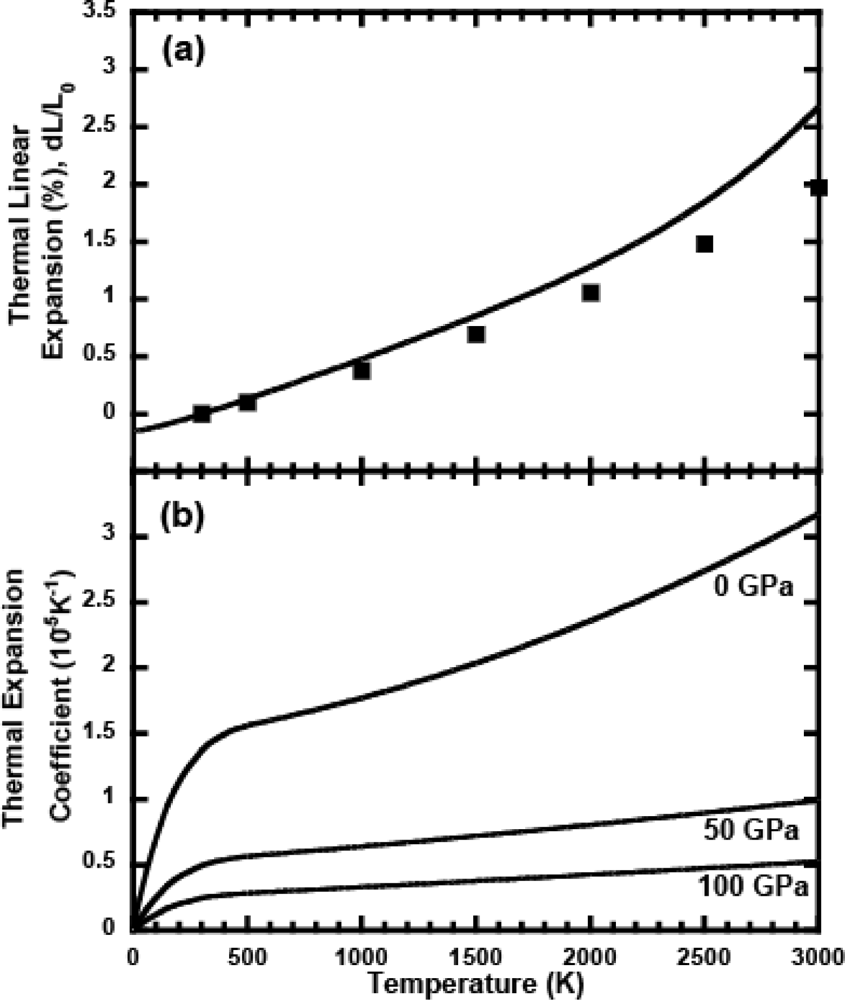
3.1. Thermal Equation of State
3.2. Equation of State at Ambient Temperature
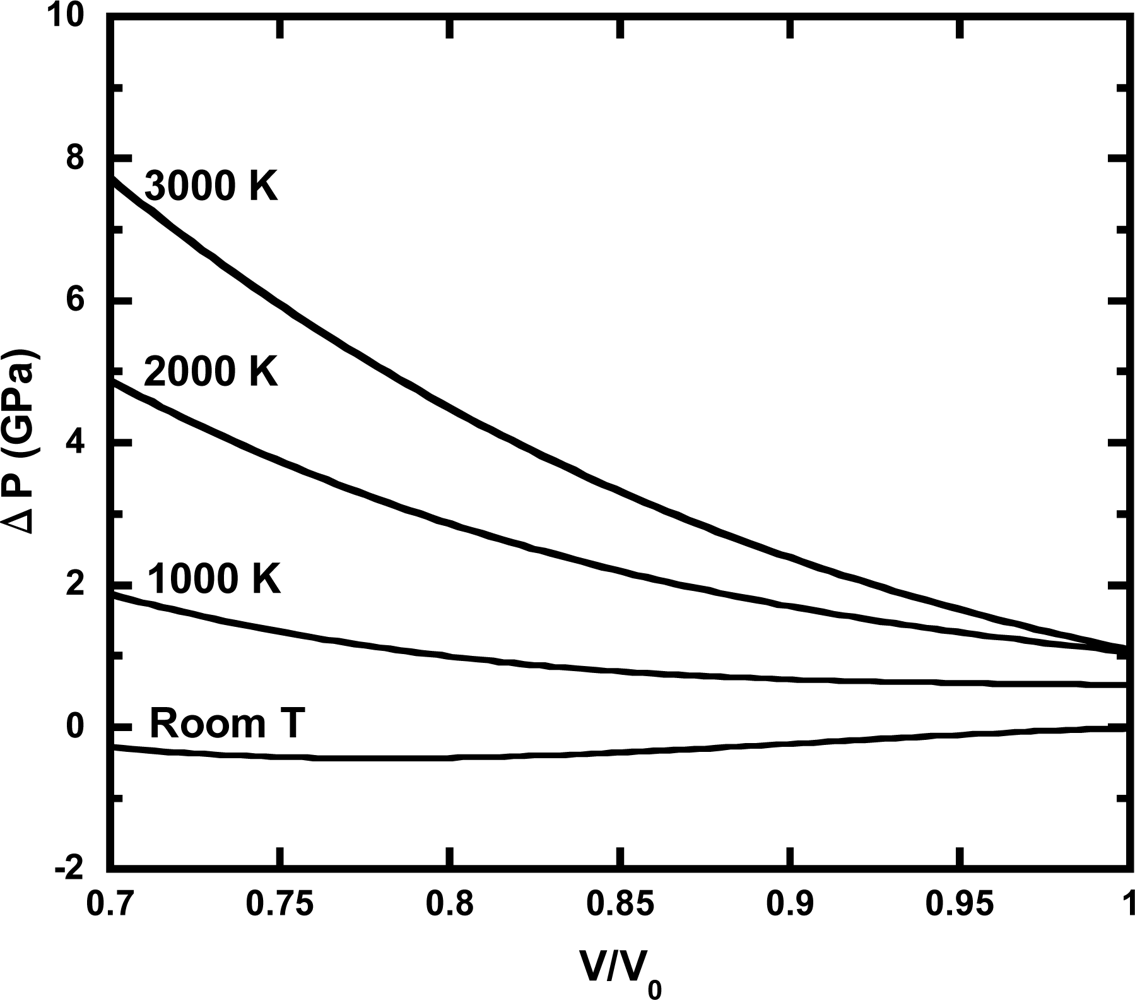
3.3. Thermal Pressure at High Pressure Conditions
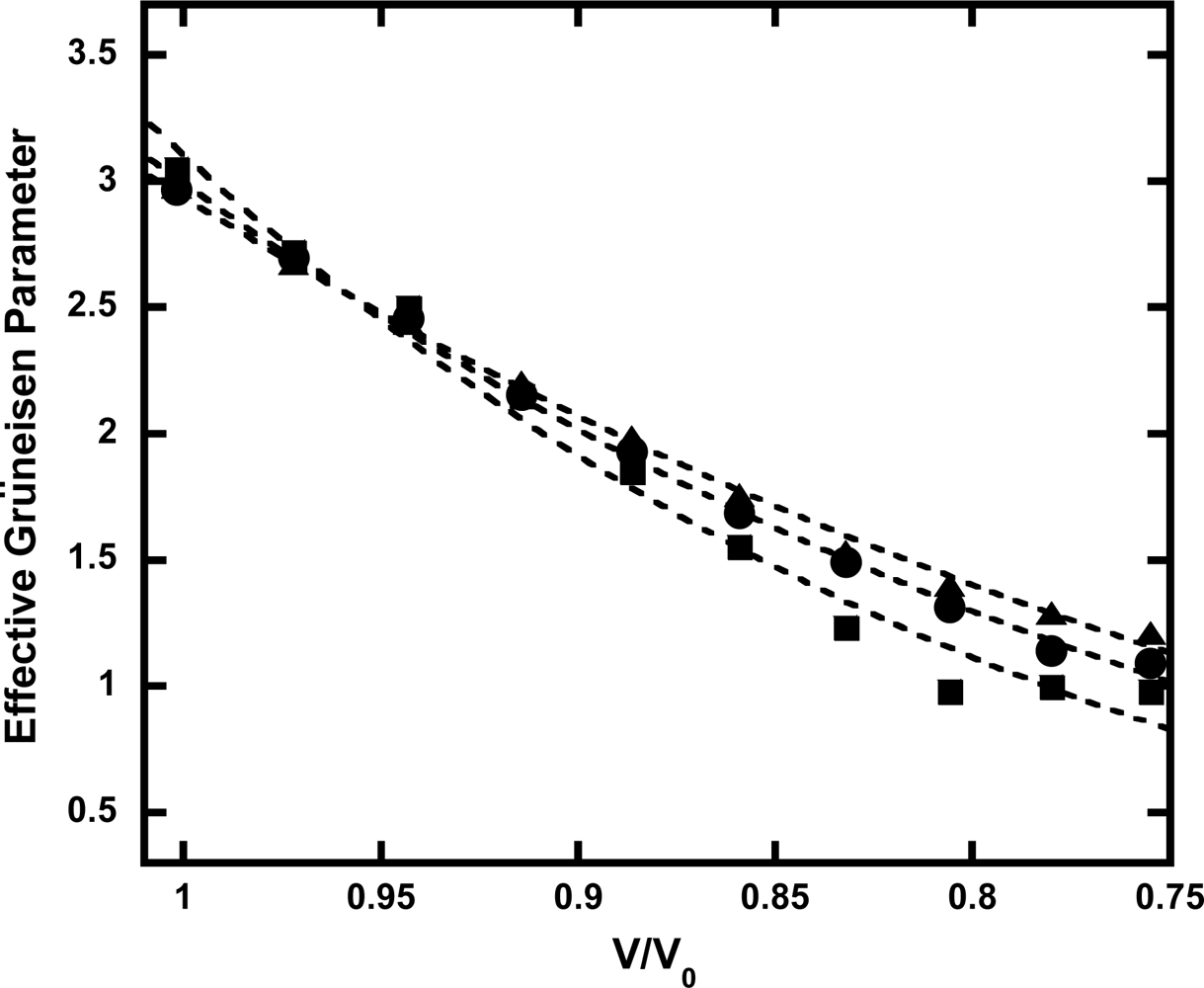
3.4. Anharmonic Effects
4. Conclusions
Acknowledgments
References and Notes
- Fei, Y; Mao, HK. Static compresson of Mg(OH)2 to 78 GPa at high temperature and constraints on the equation of state of fluid H2O. J .Geophys. Res 1993, 98, 11875–11884. [Google Scholar]
- Andrault, D; Fiquet, G; Guyot, F; Hanfland, M. Pressure-induced Landau-type transition in stishovite. Science 1998, 282, 720–772. [Google Scholar]
- Ono, S; Hirose, K; Kikegawa, T; Saito, Y. The compressibility of a natural composition calcium ferrite-type aluminous phase to 70 GPa. Phys. Earth Planet. Inter 2002, 131, 311–318. [Google Scholar]
- Irifune, T; Nishiyama, N; Kuroda, K; Inoue, T; Isshiki, M; Utsumi, W; Funakoshi, K; Urakawa, S; Uchida, T; Katsura, T; Ohtaka, O. The postspinel phase boundary in Mg2SiO4 determined by in situ X-ray diffraction. Science 1998, 279, 1698–1700. [Google Scholar]
- Ono, S; Ito, E; Katsura, T; Yoneda, A; Walter, MJ; Urakawa, S; Utsumi, W; Funakoshi, K. Thermoelastic properties of the high-pressure phase of SnO2 determined by in situ X-ray observations up to 30 GPa and 1400 K. Phys. Chem. Minerals 2000, 27, 618–622. [Google Scholar]
- Wang, Y; Uchida, T; Zhang, J; Rivers, ML; Sutton, SR. Thermal equation of state of akimotoite MgSiO3 and effects of the akimotoite–garnet transformation on seismic structure near the 660 km discontinuity. Phys Earth Planet Inter 2004, 143–144, 57–80. [Google Scholar]
- Cynn, H; Yoo, CS. Equation of state of tantalum to 174 GPa. Phys. Rev. B 1999, 59, 8526–8529. [Google Scholar]
- Ross, M; Errandonea, D; Boehler, R. Melting of transition metals at high pressure and the influence of liquid frustration: The early metals Ta and Mo. Phys. Rev. B 2007, 76, 184118. [Google Scholar]
- Katahara, KW; Manghnani, MH; Fisher, ES. Pressure derivatives of the elastic moduli of niobium and tantalum. J. Appl. Phys 1976, 47, 434–439. [Google Scholar]
- Ming, L; Manghnani, MH. Isothermal compression of bcc transition metals to 100 kbar. J. Appl. Phys 1978, 49, 208–212. [Google Scholar]
- Mitchell, AC; Nellis, WJ. Shock compression of aluminum, copper, and tantalum. J. Appl. Phys 1981, 52, 3363–3374. [Google Scholar]
- Dewaele, A; Loubeyre, P; Mezouar, M. Equations of state of six metals above 94 GPa. Phys. Rev. B 2004, 70, 094112. [Google Scholar]
- Bercegeay, C; Bernard, S. First-principles equations of states and elastic properties of seven metals. Phys. Rev. B 2005, 72, 214101. [Google Scholar]
- Chijioke, AD; Nelis, WJ; Silvera, IF. High-pressure equations of states of Al, Cu, Ta, and W. J. Appl. Phys 2005, 98, 073526. [Google Scholar]
- Orlikowski, D; Söderlind, P; Moriarty, JA. First-principles thermoelasticity of transition metals at high pressure: Tantalum prototype in the quasiharmonic limit. Phys Rev B 2006, 74, 054109.1–054109.10. [Google Scholar]
- Foata-Prestavoine, M; Robert, G; Nadal, M; Bernard, S. First-principles study of the relations between the elastic constants, phonon dispersion curves, and melting temperatures ob bcc Ta at pressures up to 1000 GPa. Phys. Rev. B 2007, 76, 104104. [Google Scholar]
- Taioli, S; Cazorla, C; Gillan, MJ; Alfè, D. Melting curve of tantalum from principles. Phys. Rev. B 2007, 75, 214103. [Google Scholar]
- Kresse, G; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar]
- Perdew, JP; Burke, K; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett 1996, 77, 3865–3868. [Google Scholar]
- Blöchl, PE. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar]
- Kresse, G; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Molec. Phys 1984, 52, 255–268. [Google Scholar]
- Ono, S; Brodholt, JP; Alfè, D; Alfredsson, M; Price, GD. Ab initio molecular dynamics simulations for thermal equation of state of B2-type NaCl. J. Appl. Phys 2008, 103, 023510. [Google Scholar]
- Vinet, P; Ferrante, J; Rose, J; Smith, J. Compressibility of solids. J. Geophys. Res 1987, 92, 9319–9325. [Google Scholar]
- Jackson, I; Rigden, SM. Analysis of P-V-T data: Constraints on the thermoelastic properties of high-pressure minerals. Phys. Earth Planet. Inter 1996, 96, 85–112. [Google Scholar]
- Holzapfel, WB. Refinement of the ruby luminescence pressure scale. J. Appl. Phys 2003, 93, 1813–1818. [Google Scholar]
- Kunc, K; Loa, I; Syassen, K. Diamond under pressure: ab initio calculations of the equation of state and optical phonon frequency revisited. High Press. Res 2004, 24, 101–110. [Google Scholar]
- Dorogokupets, PI; Oganov, AR. Ruby, metals, and MgO as alternative pressure scales: A semienprical description of shock-wave, ultrasonic, X-ray, and thermochemical data at high temperatures and pressures. Phys. Rev. B 2007, 75, 024115. [Google Scholar]
- Liu, ZL; Cai, LC; Chen, XR; Wu, Q; Jing, FQ. Ab initio refinement of the thermal equation of state for bcc tantalum: The effect of bonding on anharmonicity. J Phys Condens Matter 2009, 21, 095408.1–095408.10. [Google Scholar]
- Touloukian, TS; Kirby, RK; Taylar, RE; Desai, PD. Thermophysical Properties of Matter; IFI/Plenum: New York, NY, USA, 1977; p. 317. [Google Scholar]

| Parameter | |
|---|---|
| V0 (Å3) | 18.016 |
| BT0 (GPa) | 194 |
| BT0′ | 3.740(11) |
| α0 (10−5 K−1) | 1.47(2) |
| (δBT/δT)V (GPaK−1) | −0.0050(1) |
| (δ2P/δT2)V (10−7GPa2K−2) | 2.11(31) |
| 1-V/V0 | 300 K | 500 K | 1000 K | 1500 K | 2000 K | 2500 K | 3000 K |
|---|---|---|---|---|---|---|---|
| 0.00 | 0.00 | 0.58 | 2.10 | 3.73 | 5.46 | 7.30 | 9.24 |
| 0.02 | 4.07 | 4.63 | 6.10 | 7.67 | 9.36 | 11.14 | 13.04 |
| 0.04 | 8.54 | 9.08 | 10.50 | 12.03 | 13.66 | 15.39 | 17.23 |
| 0.06 | 13.46 | 13.98 | 15.35 | 16.82 | 18.40 | 20.08 | 21.87 |
| 0.08 | 18.88 | 19.37 | 20.68 | 22.10 | 23.63 | 25.25 | 26.99 |
| 0.10 | 24.84 | 25.30 | 26.56 | 27.92 | 29.39 | 30.97 | 32.65 |
| 0.12 | 31.38 | 31.83 | 33.04 | 34.34 | 35.75 | 37.27 | 38.90 |
| 0.14 | 38.60 | 39.03 | 40.17 | 41.42 | 42.78 | 44.24 | 45.80 |
| 0.16 | 46.55 | 46.96 | 48.04 | 49.23 | 50.53 | 51.93 | 53.44 |
| 0.18 | 55.32 | 55.70 | 56.72 | 57.86 | 59.09 | 60.43 | 61.88 |
| 0.20 | 65.00 | 65.35 | 66.32 | 67.38 | 68.56 | 69.84 | 71.22 |
| 0.22 | 75.69 | 76.02 | 76.92 | 77.92 | 79.03 | 80.25 | 81.57 |
| 0.24 | 87.50 | 87.81 | 88.64 | 89.58 | 90.63 | 91.78 | 93.04 |
| 0.26 | 100.59 | 100.86 | 101.63 | 102.51 | 103.49 | 104.57 | 105.76 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ono, S. First-Principles Molecular Dynamics Calculations of the Equation of State for Tantalum. Int. J. Mol. Sci. 2009, 10, 4342-4351. https://doi.org/10.3390/ijms10104342
Ono S. First-Principles Molecular Dynamics Calculations of the Equation of State for Tantalum. International Journal of Molecular Sciences. 2009; 10(10):4342-4351. https://doi.org/10.3390/ijms10104342
Chicago/Turabian StyleOno, Shigeaki. 2009. "First-Principles Molecular Dynamics Calculations of the Equation of State for Tantalum" International Journal of Molecular Sciences 10, no. 10: 4342-4351. https://doi.org/10.3390/ijms10104342




