Nonlocal Buckling Analysis of Composite Curved Beams Reinforced with Functionally Graded Carbon Nanotubes
Abstract
1. Introduction
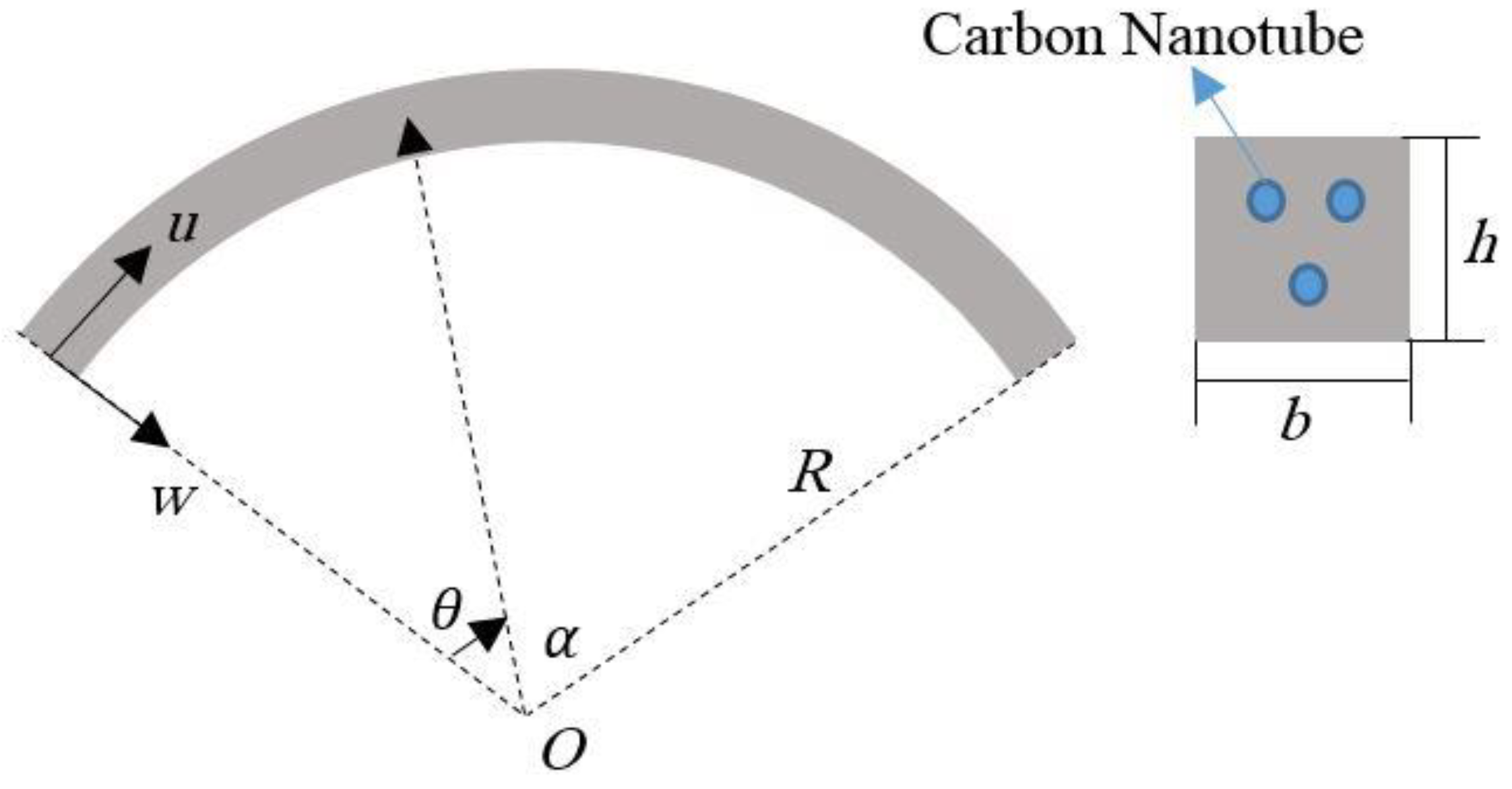
2. Size-Dependent Problem
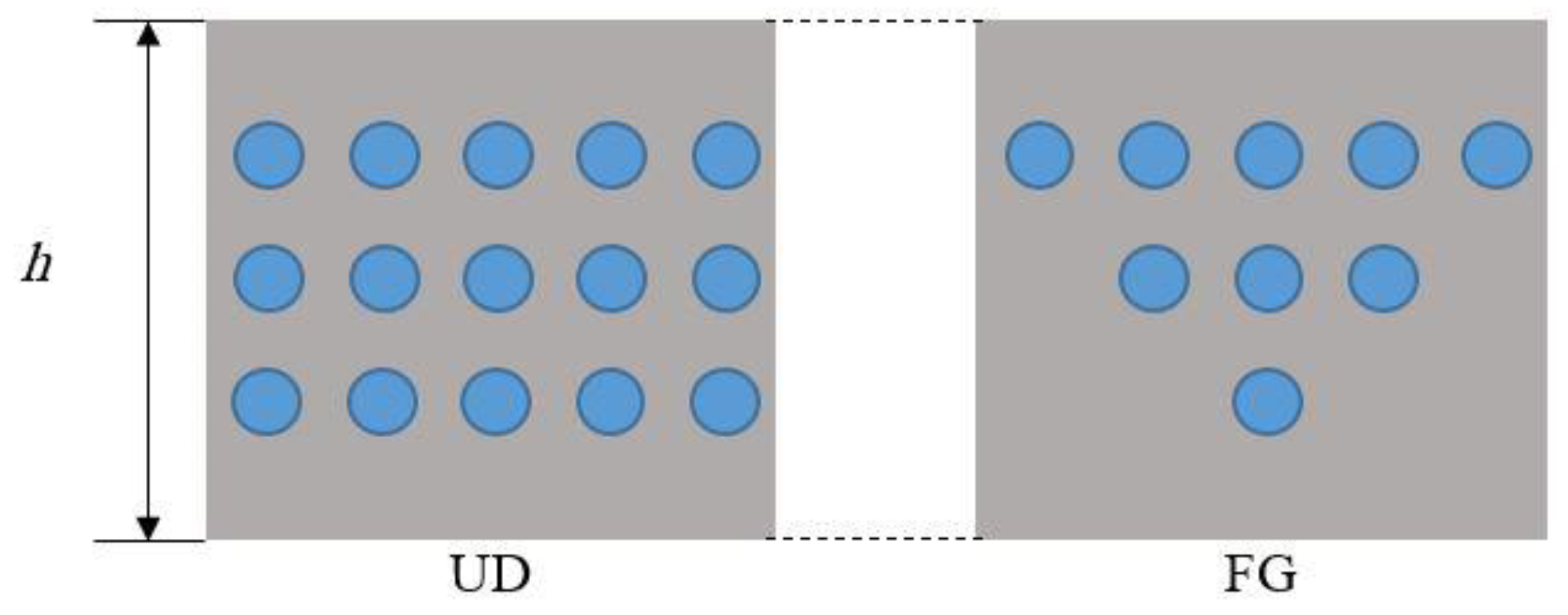
2.1. Basic Fundamentals
2.2. Displacement Field and Strain
2.3. Governing Equations
3. Solution Methodology
- S-S:
- C-S:
- C-C:
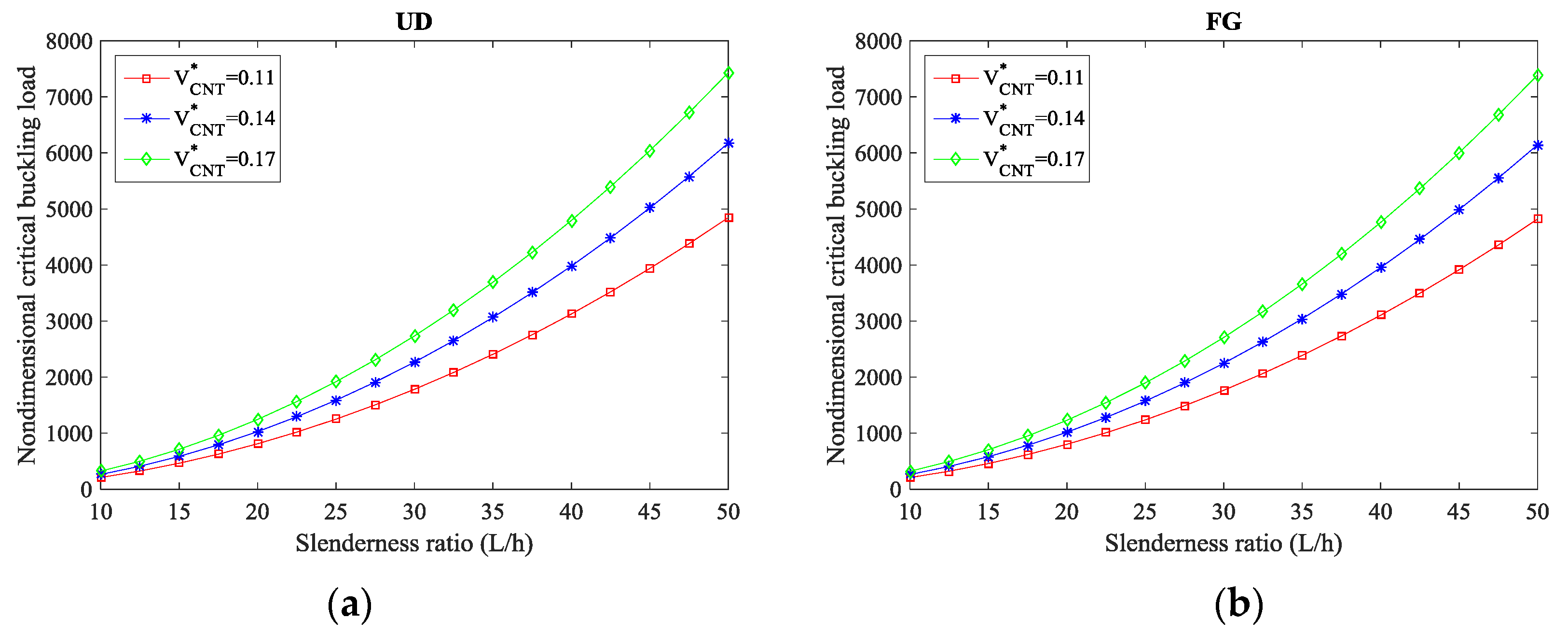
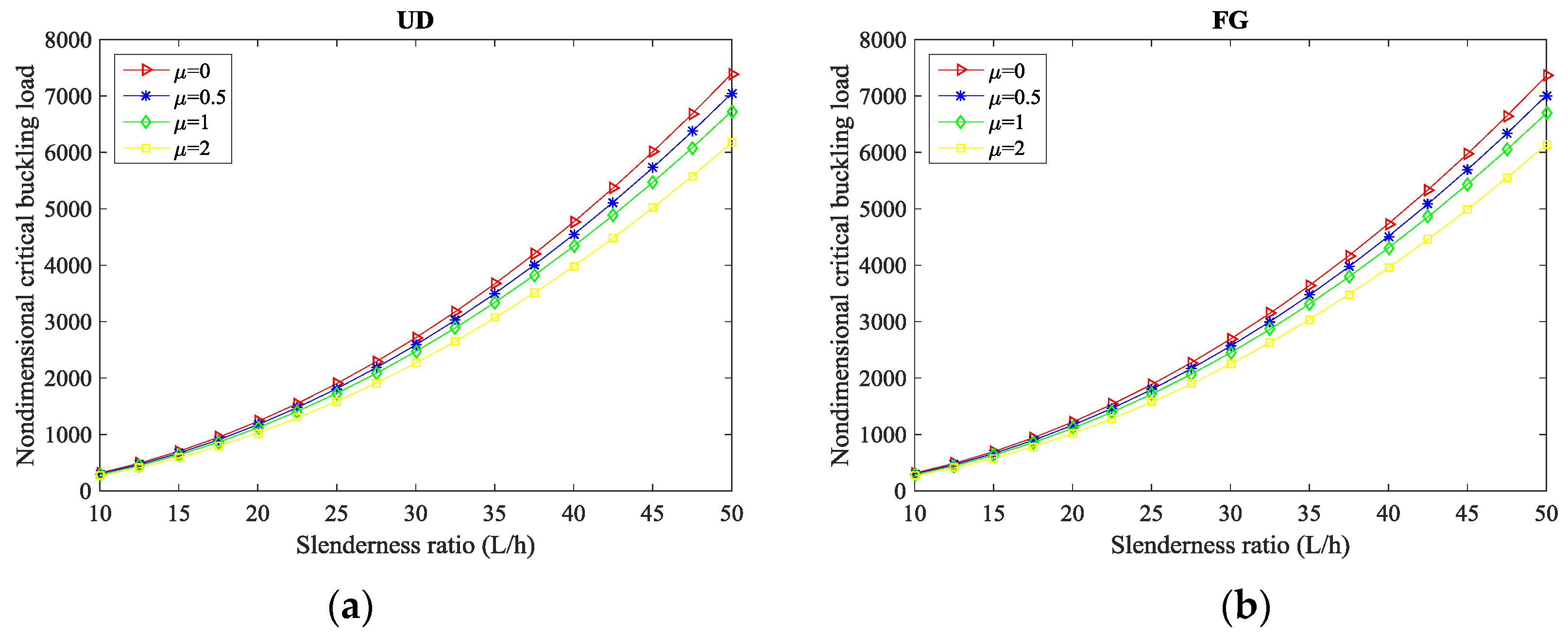
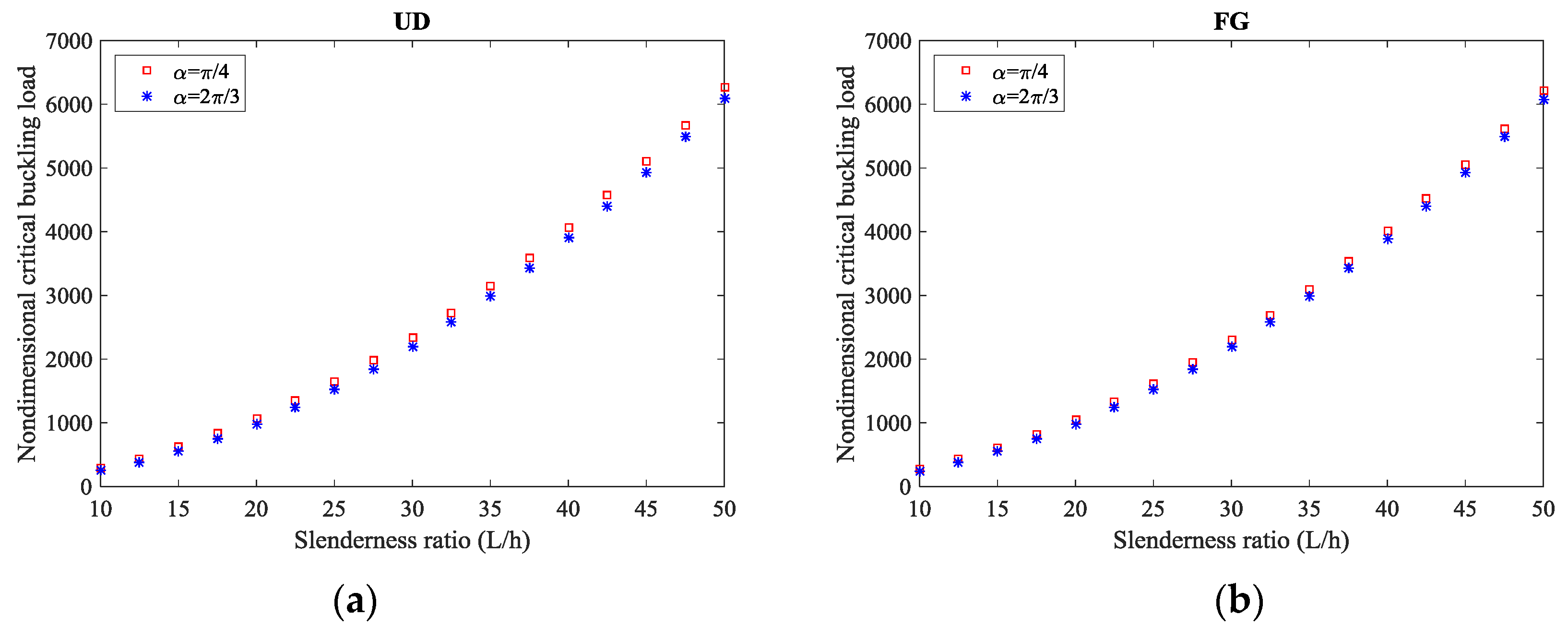
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qian, D.; Dickey, E.C.; Andrews, R.; Rantell, T. Load transfer and deformation mechanisms in carbon nanotube-polystyrene composites. Appl. Phys. Lett. 2000, 76, 2868–2870. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B-Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free vibration analysis of arbitrarily shaped Functionally Graded Carbon Nanotube-reinforced plates. Compos. Part B-Eng. 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear static response of nanocomposite plates and shells reinforced by agglomerated carbon nanotubes. Compos. Part B-Eng. 2017, 115, 449–476. [Google Scholar] [CrossRef]
- Banić, D.; Bacciocchi, M.; Tornabene, F.; Ferreira, A.J.M. Influence of Winkler-Pasternak foundation on the vibrational behavior of plates and shells reinforced by agglomerated carbon nanotubes. Appl. Sci. 2017, 7, 1228. [Google Scholar] [CrossRef]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration of FG-CNT reinforced composite skew cylindrical shells using the Chebyshev-Ritz formulation. Compos. Part B-Eng. 2018, 147, 169–177. [Google Scholar] [CrossRef]
- Bisheh, H.K.; Wu, N. Wave propagation in smart laminated composite cylindrical shells reinforced with carbon nanotubes in hygrothermal environments. Compos. Part B-Eng. 2019, 162, 219–241. [Google Scholar] [CrossRef]
- Khoshnevisa, H.; Tran, T.Q.; Mint, S.M.; Zadhoush, A.; Duong, H.M.; Youssefi, M. Effect of alignment and packing density on the stress relaxation process of carbon nanotube fibers spun from floating catalyst chemical vapor deposition method. Colloids Surf. A 2018, 558, 570–578. [Google Scholar] [CrossRef]
- Duong, H.M.; Tran, T.Q.; Kopp, R.; Mint, S.M.; Peng, L. Direct spinning of horizontally aligned carbon nanotube fibers and films from the floating catalyst method. Nanotube Superfiber Mater. 2019, 3–29. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, H.; Sahmani, S. Calibration of the analytical nonlocal shell model for vibrations of double-walled carbon nanotubes with arbitrary boundary conditions using molecular dynamics. Int. J. Mech. Sci. 2011, 53, 786–792. [Google Scholar] [CrossRef]
- Lau, D.; Jian, W.; Yu, Z.; Hui, D. Nano-engineering of construction materials using molecular dynamics simulations: Prospects and challenges. Compos. Part B-Eng. 2018, 143, 282–291. [Google Scholar] [CrossRef]
- Rahman, R.; Foster, J. A molecular dynamics-based investigation of thermally vibrating graphene under different boundary conditions. Physica E 2015, 72, 25–47. [Google Scholar] [CrossRef]
- Xiang, Y.; Shen, H.S. Shear buckling of rippled graphene by molecular dynamics simulation. Mater. Today Comm. 2015, 3, 149–155. [Google Scholar] [CrossRef]
- Rouhi, S.; Shahnazari, A.; Ansari, R. Vibrational analysis of armchair phosphorene nanotubes by a DFT-based finite element model. Arch. Civ. Mech. Eng. 2018, 18, 611–621. [Google Scholar] [CrossRef]
- Soleimani, I.; Beni, Y.T. Vibration analysis of nanotubes based on two-node size dependent axisymmetric shell element. Arch. Civ. Mech. Eng. 2018, 18, 1345–1358. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Tounsi, A. Nonlocal strain gradient 3D elasticity theory for anisotropic spherical nanoparticles. Steel Comp. Struct. 2018, 27, 201–216. [Google Scholar]
- Shahsavari, D.; Karami, B.; Mansouri, S. Shear buckling of single layer graphene sheets in hygrothermal environment resting on elastic foundation based on different nonlocal strain gradient theories. Eur. J. Mech.-A/Solids 2018, 67, 200–214. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Mohandes, M.; Dimitri, R.; Tornabene, F. Agglomeration Effects on the Vibrations of CNTS/Fiber/Polymer/Metal Hybrid Laminates Cylindrical Shell. Compos. Part B-Eng. 2019, 167, 700–716. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.; Dimitri, R.; Tornabene, F. Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp. Sci. Technol. 2018, 81, 108–117. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Bouafia, K.; Kaci, A.; Houari, M.S.A.; Benzair, A.; Tounsi, A. A nonlocal quasi-3D theory for bending and free flexural vibration behaviors of functionally graded nanobeams. Smart Struct. Syst. 2017, 19, 115–126. [Google Scholar] [CrossRef]
- Shahsavari, D.; Karami, B.; Janghorban, M.; Li, L. Dynamic characteristics of viscoelastic nanoplates under moving load embedded within visco-Pasternak substrate and hygrothermal environment. Mater. Res Express 2017, 4, 085013. [Google Scholar] [CrossRef]
- Ganapathi, M.; Merzouki, T.; Polit, O. Vibration study of curved nanobeams based on nonlocal higher-order shear deformation theory using finite element approach. Compos. Struct. 2018, 184, 821–838. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Li, L. On guided wave propagation in fully clamped porous functionally graded nanoplates. Acta Astronaut. 2018, 143, 380–390. [Google Scholar] [CrossRef]
- Polit, O.; Merzouki, T.; Ganapathi, M. Elastic stability of curved nanobeam based on higher-order shear deformation theory and nonlocal analysis by finite element approach. Finite Elem. Anal Des. 2018, 146, 1–15. [Google Scholar] [CrossRef]
- Ganapathi, M.; Polit, O. A nonlocal higher-order model including thickness stretching effect for bending and buckling of curved nanobeams. Appl Math. Model. 2018, 57, 121–141. [Google Scholar] [CrossRef]
- Shahsavari, D.; Karami, B.; Fahham, H.R.; Li, L. On the shear buckling of porous nanoplates using a new size-dependent quasi-3D shear deformation theory. Acta Mech. 2018, 229, 4549–4573. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Shetty, R.A.; Guha, A. A single variable shear deformable nonlocal theory for transversely loaded micro-and nano-scale rectangular beams. Sādhanā 2018, 43, 73. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M. A comprehensive analytical study on functionally graded carbon nanotube-reinforced composite plates. Aerosp. Sci. Technol. 2018, 82, 499–512. [Google Scholar] [CrossRef]
- Hong, C.C. Rapid heating induced vibration of circular cylindrical shells with magnetostrictive functionally graded material. Arch. Civ. Mech. Eng. 2014, 14, 710–720. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Buckling and bending analyses of a novel functionally graded porous plate using Chebyshev-Ritz method. Arch. Civ. Mech. Eng. 2019, 19, 157–170. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B-Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Nonlocal bending analysis of curved nanobeams reinforced by graphene nanoplatelets. Compos. Part B-Eng. 2019, 166, 1–12. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M.; Dimitri, R.; Tornabene, F. Wave propagation of porous nanoshells. Nanomaterials 2019, 9, 22. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater. Res. Express 2018, 5, 095006. [Google Scholar] [CrossRef]
- Polit, O.; Anant, C.; Anirudh, B.; Ganapathi, M. Functionally graded graphene reinforced porous nanocomposite curved beams: Bending and elastic stability using a higher-order model with thickness stretch effect. Compos. Part B-Eng. 2018, 166, 310–327. [Google Scholar] [CrossRef]
- Malikan, M.; Dimitri, R.; Tornabene, F. Transient response of oscillated carbon nanotubes with an internal and external damping. Compos. Part B-Eng. 2019, 158, 198–205. [Google Scholar] [CrossRef]
- Mohammadi, M.; Arefi, M.; Dimitri, R.; Tornabene, F. Higher-order thermo-elastic analysis of FG-CNTRC cylindrical vessels surrounded by a Pasternak foundation. Nanomaterials 2019, 9, 79. [Google Scholar] [CrossRef]
- She, G.L.; Yuan, F.G.; Karami, B.; Ren, Y.R.; Xiao, W.S. On nonlinear bending behavior of FG porous curved nanotubes. Int. J. Eng. Sci. 2019, 135, 58–74. [Google Scholar] [CrossRef]
- Zhao, J.; Choe, K.; Shuai, C.; Wang, A.; Wang, Q. Free vibration analysis of functionally graded carbon nanotube reinforced composite truncated conical panels with general boundary conditions. Compos. Part B-Eng. 2019, 160, 225–240. [Google Scholar] [CrossRef]
- Shen, H.S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comp. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. A nonlocal strain gradient refined beam model for buckling analysis of size-dependent shear-deformable curved FG nanobeams. Compos. Struct. 2017, 159, 174–182. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Aydogdu, M. A general nonlocal beam theory: Its application to nanobeam bending, buckling and vibration. Physica E 2009, 41, 1651–1655. [Google Scholar] [CrossRef]
- Eltaher, M.; Emam, S.A.; Mahmoud, F. Static and stability analysis of nonlocal functionally graded nanobeams. Compos. Struct. 2013, 96, 82–88. [Google Scholar] [CrossRef]
| MD [43] | Rule of Mixture | |||||
|---|---|---|---|---|---|---|
| E11 (GPa) | E22 (GPa) | E11 (GPa) | η1 | E22 (GPa) | η2 | |
| 0.11 | 94.8 | 2.2 | 94.42 | 0.149 | 2.20 | 0.934 |
| 0.14 | 120.2 | 2.3 | 120.38 | 0.150 | 2.30 | 0.941 |
| 0.17 | 145.6 | 3.5 | 144.77 | 0.140 | 3.49 | 1.381 |
| µ | Reddy [45] | Aydogdu [46] | Eltaher [47] | Present |
|---|---|---|---|---|
| 0 | 9.8696 | 9.8696 | 9.86973 | 9.80601 |
| 1 | 8.9830 | 9.6319 | 8.98312 | 8.92692 |
| 2 | 8.2426 | 9.4055 | 8.24267 | 8.19176 |
| 3 | 7.6149 | 9.1894 | 7.61499 | 7.56846 |
| 4 | 7.0761 | 8.9830 | 7.07614 | 7.03246 |
| µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | ||
|---|---|---|---|---|---|---|---|
| UD-CNTRC | 0.11 | 12.5642 | 12.4111 | 12.2617 | 12.1158 | 11.9734 | 11.6983 |
| 0.14 | 14.3533 | 14.1784 | 14.0077 | 13.8411 | 13.6783 | 13.3641 | |
| 0.17 | 19.6015 | 19.3626 | 19.1295 | 18.9019 | 18.6797 | 18.2505 | |
| FG-CNTRC | 0.11 | 10.1067 | 9.9835 | 9.8633 | 9.7459 | 9.6314 | 9.4101 |
| 0.14 | 11.7678 | 11.6244 | 11.4844 | 11.3478 | 11.2144 | 10.9567 | |
| 0.17 | 15.6689 | 15.4780 | 15.2916 | 15.1097 | 14.9321 | 14.5890 |
| µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | ||
|---|---|---|---|---|---|---|---|
| UD-CNTRC | 0.11 | 123.0005 | 119.3204 | 115.8541 | 112.5835 | 109.4924 | 103.7931 |
| 0.14 | 153.2617 | 148.6762 | 144.3571 | 140.2818 | 136.4303 | 129.3288 | |
| 0.17 | 189.3549 | 183.6894 | 178.3532 | 173.3182 | 168.5597 | 159.7857 | |
| FG-CNTRC | 0.11 | 120.5401 | 116.9336 | 113.5366 | 110.3314 | 107.3022 | 101.7169 |
| 0.14 | 150.8821 | 146.3677 | 142.1157 | 138.1037 | 134.3120 | 127.3207 | |
| 0.17 | 185.4017 | 179.8545 | 174.6296 | 169.6998 | 165.0406 | 156.4498 |
| µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | ||
|---|---|---|---|---|---|---|---|
| UD-CNTRC | 0.11 | 251.6676 | 239.8324 | 229.0603 | 219.2143 | 210.1798 | 194.1748 |
| 0.14 | 316.4206 | 301.5402 | 287.9965 | 275.6171 | 264.2581 | 244.1351 | |
| 0.17 | 386.8498 | 368.6573 | 352.0990 | 336.9642 | 323.0770 | 298.4749 | |
| FG-CNTRC | 0.11 | 249.5883 | 237.8509 | 227.1678 | 217.4031 | 208.4433 | 192.5705 |
| 0.14 | 314.4762 | 299.6872 | 286.2267 | 273.9234 | 262.6343 | 242.6349 | |
| 0.17 | 383.5269 | 365.4907 | 349.0746 | 334.0698 | 320.3018 | 295.9111 |
| L/h | µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | |
|---|---|---|---|---|---|---|---|
| UD-CNTRC | 10 | 14.3533 | 14.1784 | 14.0077 | 13.8411 | 13.6783 | 13.3641 |
| 20 | 25.2537 | 24.9459 | 24.6456 | 24.3524 | 24.0660 | 23.5132 | |
| 30 | 29.4450 | 29.0862 | 28.7360 | 28.3941 | 28.0603 | 27.4156 | |
| 50 | 32.1881 | 31.7958 | 31.4130 | 31.0393 | 30.6744 | 29.9697 | |
| FG-CNTRC | 10 | 11.7678 | 11.6244 | 11.4844 | 11.3478 | 11.2144 | 10.9567 |
| 20 | 18.4256 | 18.2010 | 17.9819 | 17.7680 | 17.5591 | 17.1557 | |
| 30 | 20.6574 | 20.4057 | 20.1600 | 19.9202 | 19.6860 | 19.2337 | |
| 50 | 22.0620 | 21.7931 | 21.5307 | 21.2746 | 21.0244 | 20.5414 |
| L/h | µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | |
|---|---|---|---|---|---|---|---|
| UD-CNTRC | 10 | 153.2617 | 148.6762 | 144.3571 | 140.2818 | 136.4303 | 129.3288 |
| 20 | 575.5663 | 558.3455 | 542.1252 | 526.8208 | 512.3568 | 485.6873 | |
| 30 | 1247.1406 | 1209.8265 | 1174.6804 | 1141.5187 | 1110.1779 | 1052.3904 | |
| 50 | 3353.4099 | 3253.0768 | 3158.5732 | 3069.4054 | 2985.1338 | 2829.7502 | |
| FG-CNTRC | 10 | 150.8821 | 146.3677 | 142.1157 | 138.1037 | 134.3120 | 127.3207 |
| 20 | 564.4312 | 547.5436 | 531.6372 | 516.6288 | 502.4446 | 476.2911 | |
| 30 | 1228.5852 | 1191.8263 | 1157.2031 | 1124.5348 | 1093.6603 | 1036.7326 | |
| 50 | 3327.6844 | 3228.1210 | 3134.3424 | 3045.8586 | 2962.2334 | 2808.0419 |
| L/h | µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | |
|---|---|---|---|---|---|---|---|
| UD-CNTRC | 10 | 316.4206 | 301.5402 | 287.9965 | 275.6171 | 264.2581 | 244.1351 |
| 20 | 1230.3705 | 1172.5095 | 1119.8461 | 1071.7102 | 1027.5419 | 949.2954 | |
| 30 | 2714.6098 | 2586.9490 | 2470.7560 | 2364.5519 | 2267.1018 | 2094.4639 | |
| 50 | 7393.5474 | 7045.8487 | 6729.3838 | 6440.1251 | 6174.7087 | 5704.5098 | |
| FG-CNTRC | 10 | 314.4762 | 299.6872 | 286.2267 | 273.9234 | 262.6343 | 242.6349 |
| 20 | 1218.4960 | 1161.1934 | 1109.0383 | 1061.3669 | 1017.6249 | 940.1336 | |
| 30 | 2691.1353 | 2564.5784 | 2449.3901 | 2344.1045 | 2247.4971 | 2076.3521 | |
| 50 | 7355.7738 | 7009.8515 | 6695.0035 | 6407.2225 | 6143.1622 | 5675.3655 |
| α | µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | |
|---|---|---|---|---|---|---|---|
| UD-CNTRC | π/4 | 28.3891 | 28.0431 | 27.7055 | 27.3759 | 27.0540 | 26.4325 |
| π/3 | 14.3533 | 14.1784 | 14.0077 | 13.8411 | 13.6783 | 13.3641 | |
| π/2 | 4.5393 | 4.4840 | 4.4300 | 4.3773 | 4.3258 | 4.2264 | |
| 2π/3 | 1.4001 | 1.3830 | 1.3664 | 1.3501 | 1.3342 | 1.3036 | |
| FG-CNTRC | π/4 | 23.3784 | 23.0935 | 22.8155 | 22.5440 | 22.2790 | 21.7672 |
| π/3 | 11.7678 | 11.6244 | 11.4844 | 11.3478 | 11.2144 | 10.9567 | |
| π/2 | 3.6889 | 3.6440 | 3.6001 | 3.5573 | 3.5155 | 3.4347 | |
| 2π/3 | 1.1279 | 1.1141 | 1.1007 | 1.0876 | 1.0748 | 1.0501 |
| α | µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | |
|---|---|---|---|---|---|---|---|
| UD-CNTRC | π/4 | 172.4731 | 167.3128 | 162.4523 | 157.8662 | 153.5319 | 145.5402 |
| π/3 | 153.2617 | 148.6762 | 144.3571 | 140.2818 | 136.4303 | 129.3288 | |
| π/2 | 139.5855 | 135.4092 | 131.4754 | 127.7638 | 124.2560 | 117.7882 | |
| 2π/3 | 134.8634 | 130.8284 | 127.0277 | 123.4417 | 120.0526 | 113.8035 | |
| FG-CNTRC | π/4 | 168.1669 | 163.1354 | 158.3962 | 153.9246 | 149.6986 | 141.9064 |
| π/3 | 150.8821 | 146.3677 | 142.1157 | 138.1037 | 134.3120 | 127.3207 | |
| π/2 | 138.6057 | 134.4586 | 130.5525 | 126.8670 | 123.3838 | 116.9614 | |
| 2π/3 | 134.3841 | 130.3633 | 126.5762 | 123.0029 | 119.6258 | 113.3990 |
| α | µ = 0 | µ = 0.5 | µ = 1 | µ = 1.5 | µ = 2 | µ = 3 | |
|---|---|---|---|---|---|---|---|
| UD-CNTRC | π/4 | 337.8116 | 321.9253 | 307.4660 | 294.2497 | 282.1228 | 260.6394 |
| π/3 | 316.4206 | 301.5402 | 287.9965 | 275.6171 | 264.2581 | 244.1351 | |
| π/2 | 301.1614 | 286.9986 | 274.1080 | 262.3256 | 251.5144 | 232.3618 | |
| 2π/3 | 295.8488 | 281.9358 | 269.2726 | 257.6981 | 247.0776 | 228.2628 | |
| FG-CNTRC | π/4 | 334.3510 | 318.6274 | 304.3162 | 291.2353 | 279.2327 | 257.9693 |
| π/3 | 314.4762 | 299.6872 | 286.2267 | 273.9234 | 262.6343 | 242.6349 | |
| π/2 | 300.3202 | 286.1970 | 273.3424 | 261.5930 | 250.8119 | 231.7128 | |
| 2π/3 | 295.4045 | 281.5124 | 268.8683 | 257.3111 | 246.7066 | 227.9201 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karami, B.; Janghorban, M.; Shahsavari, D.; Dimitri, R.; Tornabene, F. Nonlocal Buckling Analysis of Composite Curved Beams Reinforced with Functionally Graded Carbon Nanotubes. Molecules 2019, 24, 2750. https://doi.org/10.3390/molecules24152750
Karami B, Janghorban M, Shahsavari D, Dimitri R, Tornabene F. Nonlocal Buckling Analysis of Composite Curved Beams Reinforced with Functionally Graded Carbon Nanotubes. Molecules. 2019; 24(15):2750. https://doi.org/10.3390/molecules24152750
Chicago/Turabian StyleKarami, Behrouz, Maziar Janghorban, Davood Shahsavari, Rossana Dimitri, and Francesco Tornabene. 2019. "Nonlocal Buckling Analysis of Composite Curved Beams Reinforced with Functionally Graded Carbon Nanotubes" Molecules 24, no. 15: 2750. https://doi.org/10.3390/molecules24152750
APA StyleKarami, B., Janghorban, M., Shahsavari, D., Dimitri, R., & Tornabene, F. (2019). Nonlocal Buckling Analysis of Composite Curved Beams Reinforced with Functionally Graded Carbon Nanotubes. Molecules, 24(15), 2750. https://doi.org/10.3390/molecules24152750







