Indexing Natural Products for Their Potential Anti-Diabetic Activity: Filtering and Mapping Discriminative Physicochemical Properties
Abstract
:1. Introduction
2. Results and Discussion
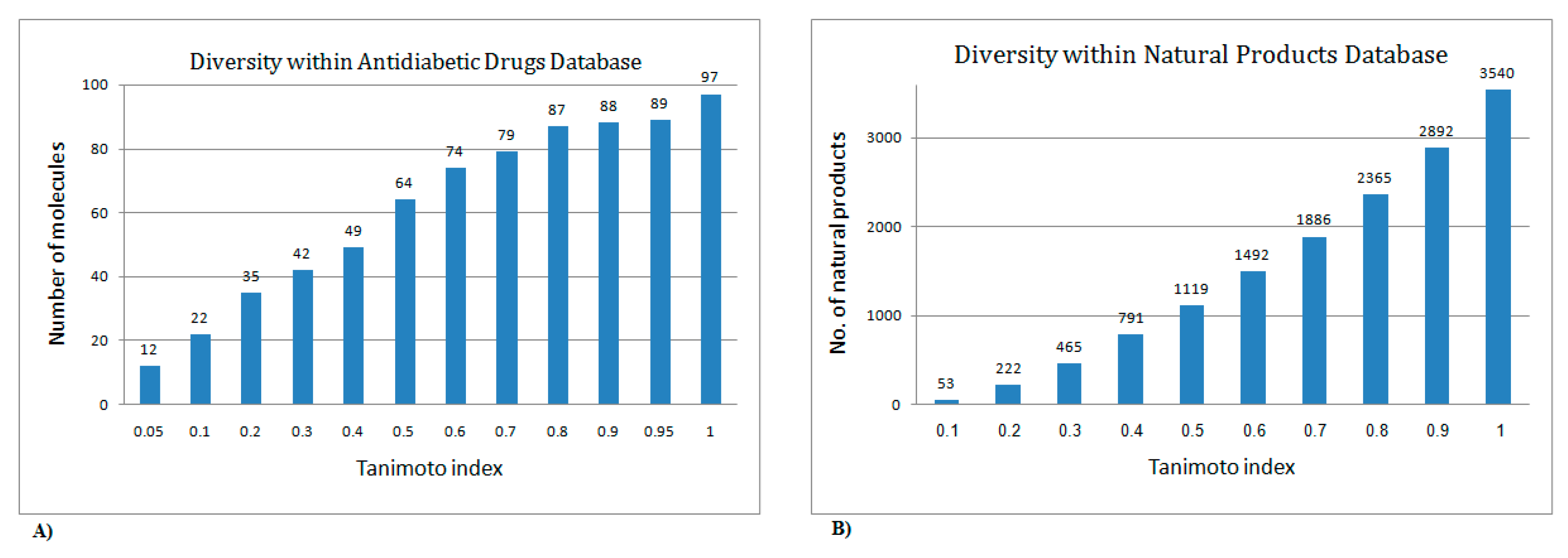
2.1. Utilization of the Iterative Stochastic Elimination Algorithm for Indexing Natural Compounds for Their Potential Anti-Diabetic Drug Likeness
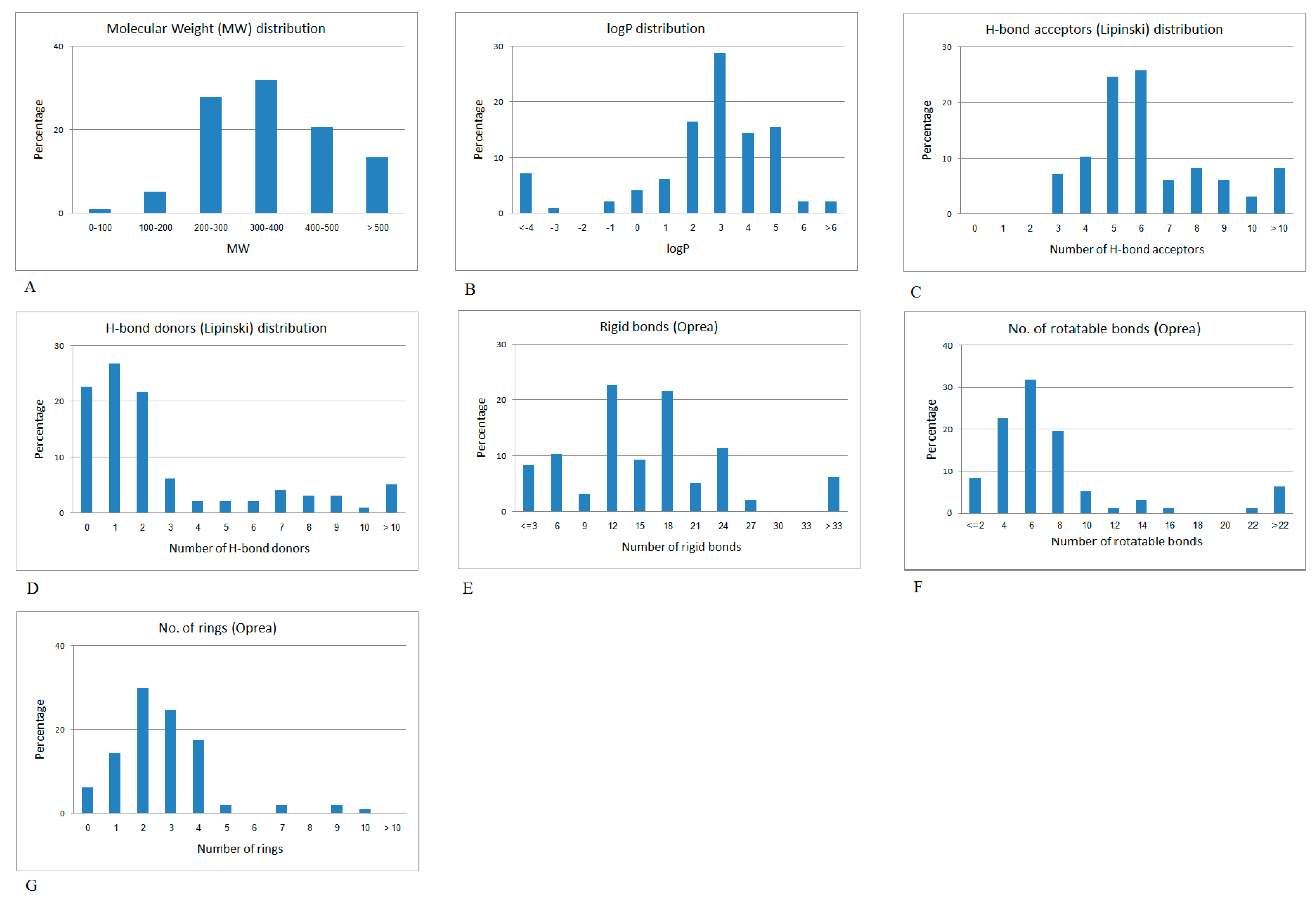
2.2. Mapping the Discriminative Physicochemical Properties Responsible for Anti-Diabetic Activity
2.3. Filters and Descriptors Produced for Constructing the Predictive Model for Indexing Chemicals
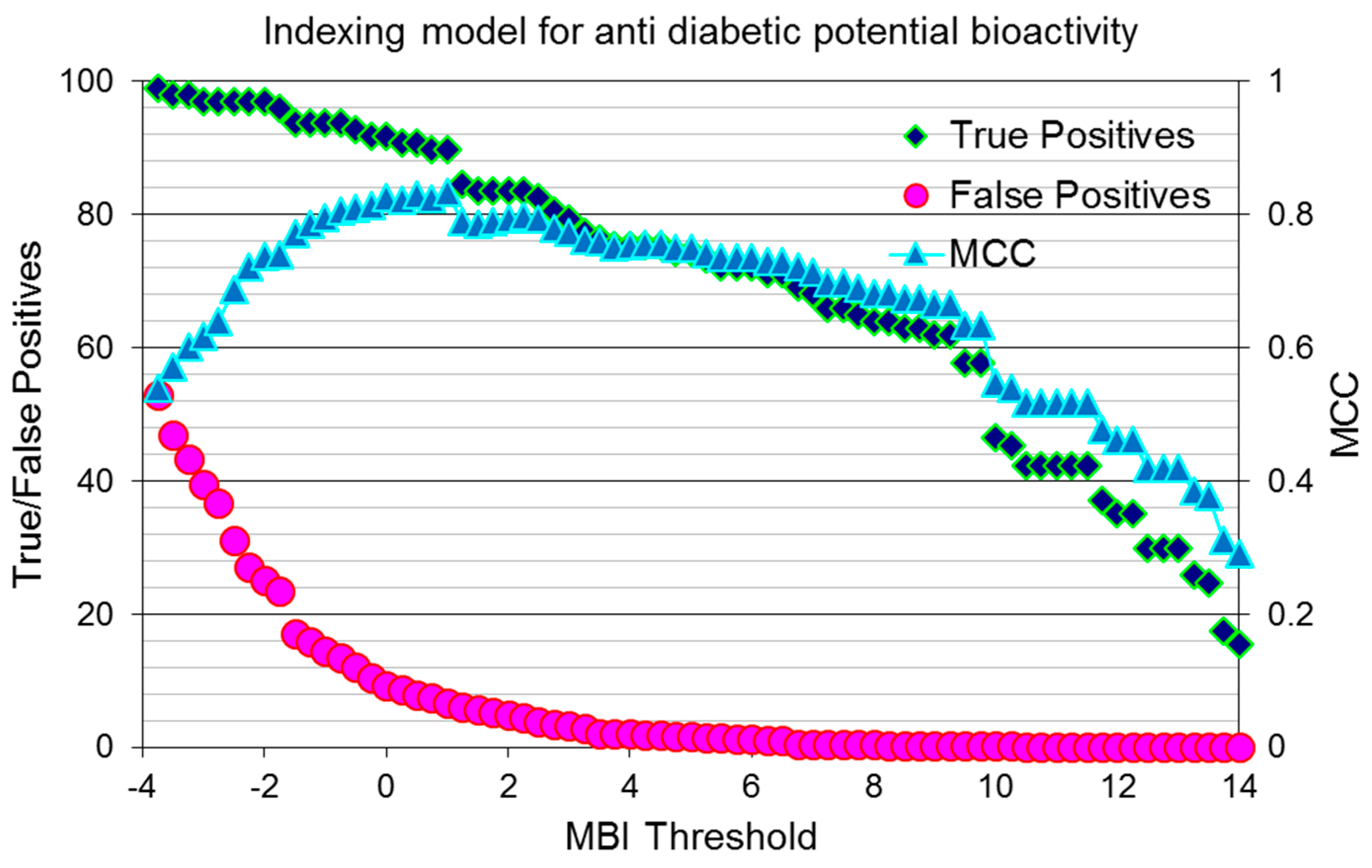
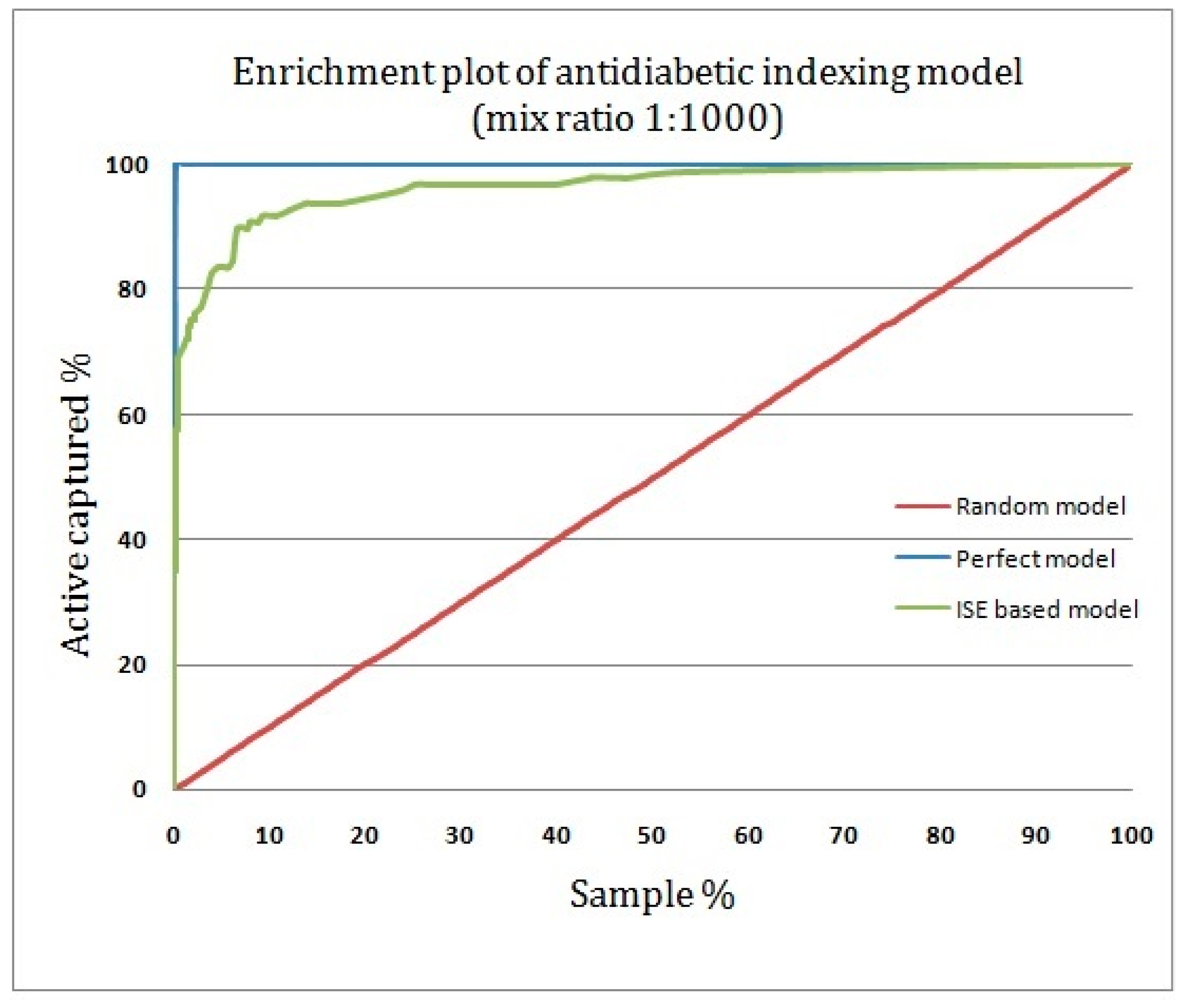
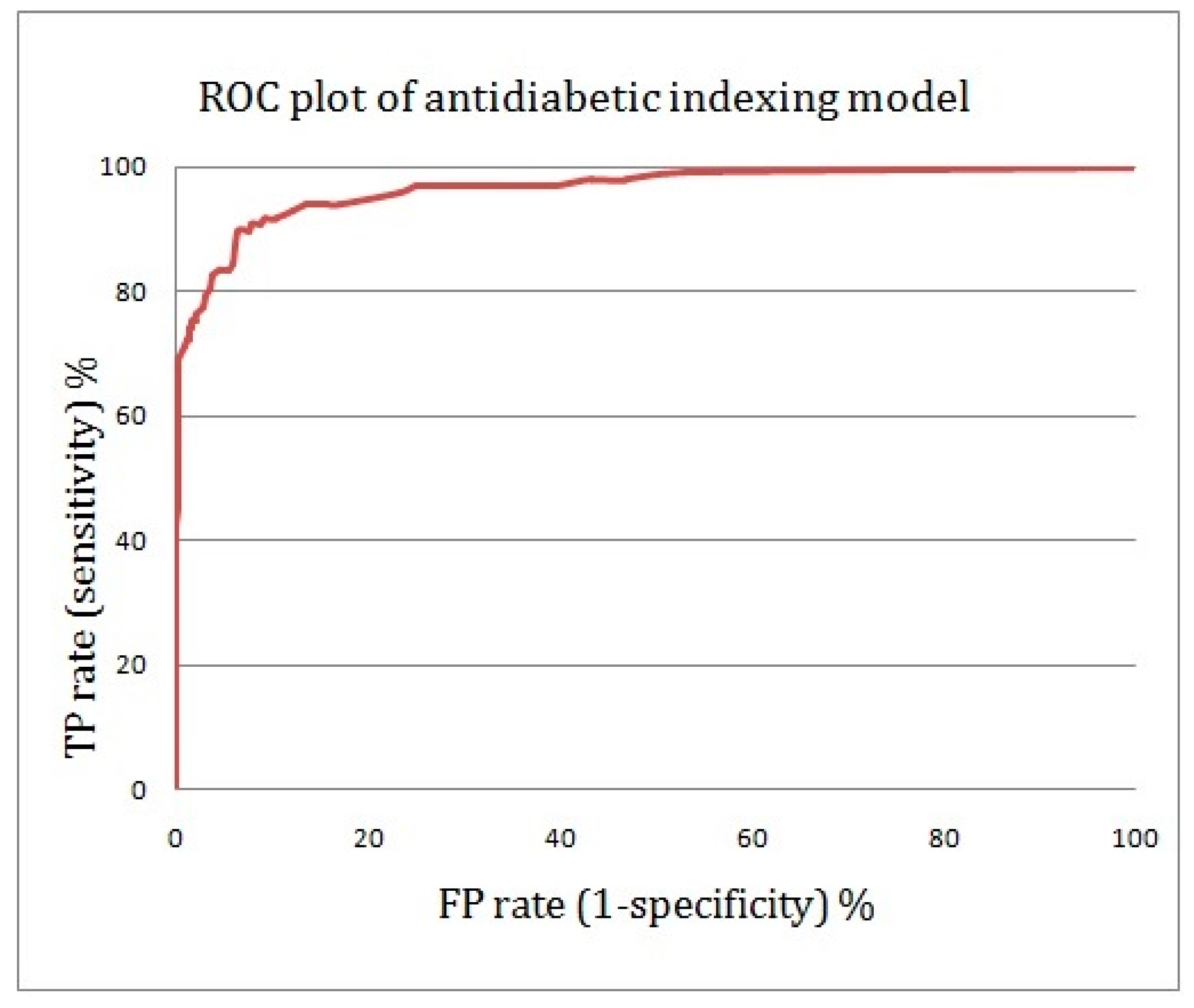
2.4. Assessing the Quality of Anti-Diabetic Activity-Indexing Model Potential
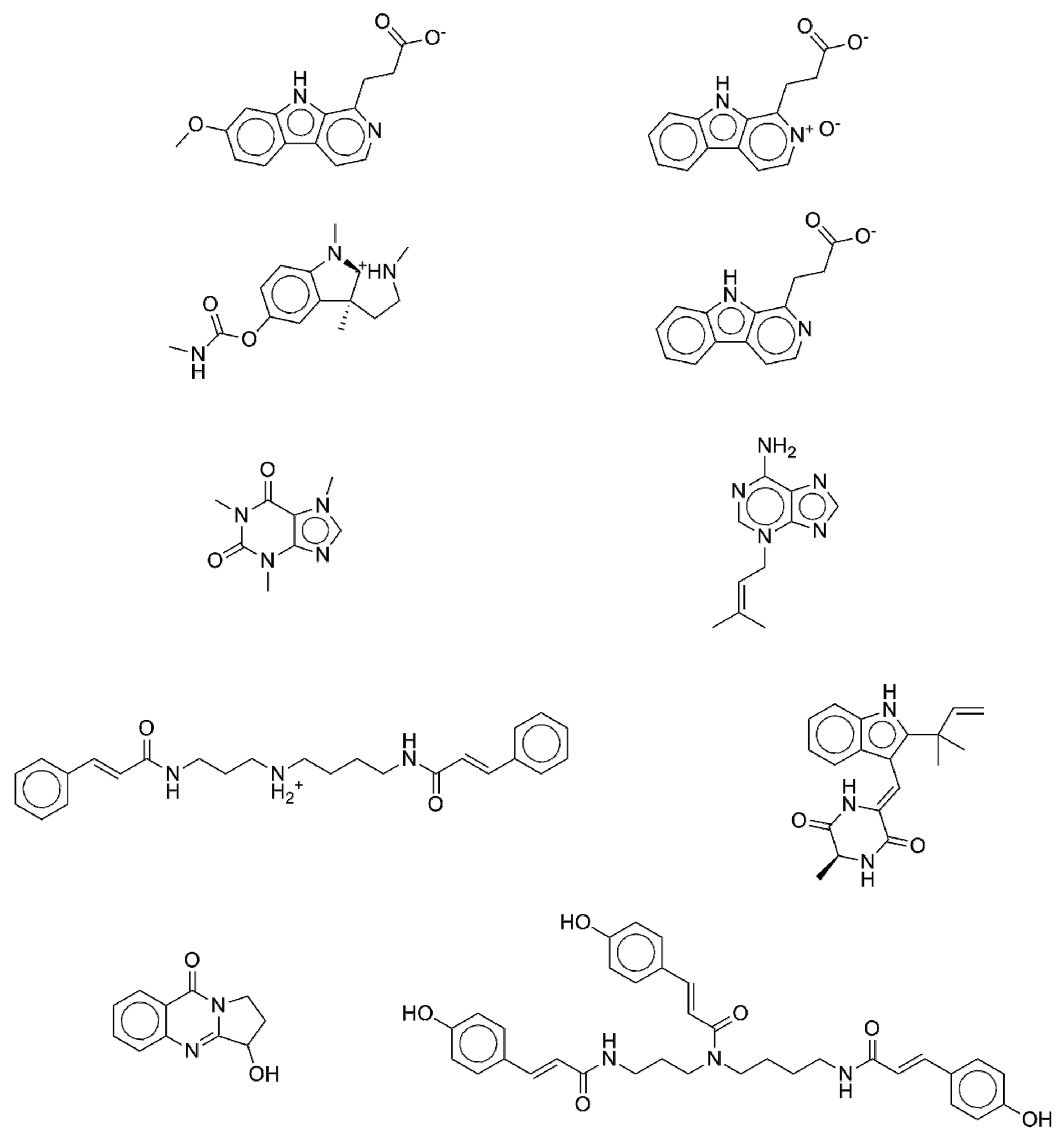
2.5. New Potential Anti-Diabetic Drug Candidates as Disclosed by the ISE-Indexing Model
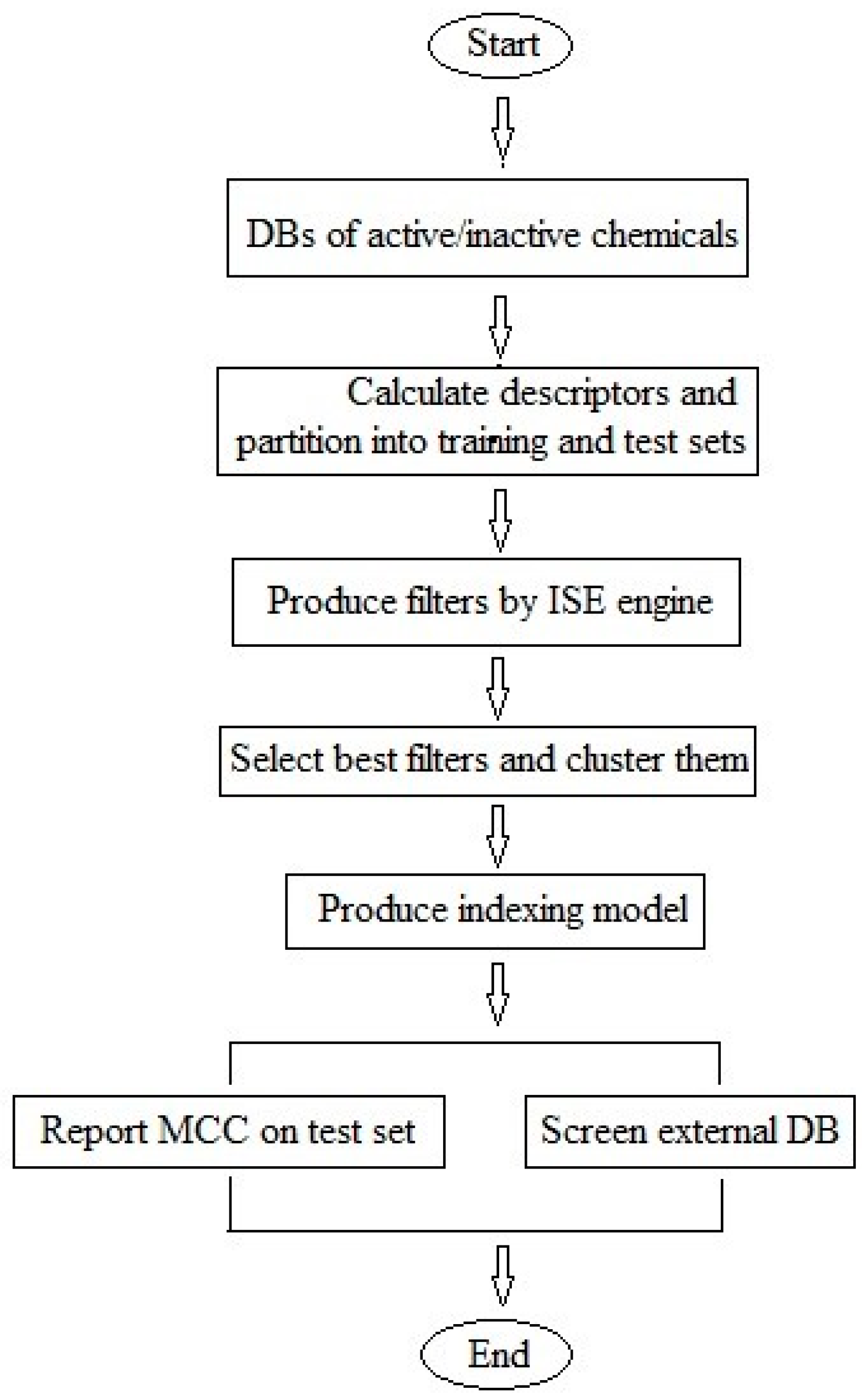
3. Materials and Methods
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alberti, K.G.; Zimmet, P.Z. Definition, diagnosis and classification of diabetes mellitus and its complications. Part 1: Diagnosis and classification of diabetes mellitus provisional report of a WHO consultation. Diabet. Med. 1998, 15, 539–553. [Google Scholar] [CrossRef]
- Whiting, D.R.; Guariguata, L.; Weil, C.; Shaw, J. IDF diabetes atlas: Global estimates of the prevalence of diabetes for 2011 and 2030. Diabetes Res. Clin. Pract. 2011, 94, 311–321. [Google Scholar] [CrossRef] [PubMed]
- International Diabetes Federation. IDF Diabetes Atlas, 7th ed.; International Diabetes Federation: Brussels, Belgium, 2015. [Google Scholar]
- Kahn, S.E.; Cooper, M.E.; Del Prato, S. Pathophysiology and treatment of type 2 diabetes: Perspectives on the past, present, and future. Lancet 2014, 383, 1068–1083. [Google Scholar] [CrossRef]
- World Health Organization. Global Health Estimates (GHE), 2000–2015 estimates. Available online: http://www.who.int/mediacentre/factsheets/fs312/en/ (accessed on 12 August 2017).
- Muoio, D.M.; Newgard, C.B. Mechanisms of disease:Molecular and metabolic mechanisms of insulin resistance and beta-cell failure in type 2 diabetes. Nat. Rev. Mol. Cell Biol. 2008, 9, 193–205. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, V.A. Defining and characterizing the progression of type 2 diabetes. Diabetes Care 2009, 32 (Suppl. 2), S151–S156. [Google Scholar] [CrossRef] [PubMed]
- Pessin, J.E.; Saltiel, A.R. Signaling pathways in insulin action: Molecular targets of insulin resistance. J. Clin. Investig. 2000, 106, 165–169. [Google Scholar] [CrossRef] [PubMed]
- DeFronzo, R.A. Lilly lecture 1987. The triumvirate: Beta-cell, muscle, liver. A collusion responsible for NIDDM. Diabetes 1988, 37, 667–687. [Google Scholar] [CrossRef] [PubMed]
- Defronzo, R.A. Banting Lecture. From the triumvirate to the ominous octet: A new paradigm for the treatment of type 2 diabetes mellitus. Diabetes 2009, 58, 773–795. [Google Scholar] [CrossRef] [PubMed]
- Bavenholm, P.N.; Kuhl, J.; Pigon, J.; Saha, A.K.; Ruderman, N.B.; Efendic, S. Insulin resistance in type 2 diabetes: Association with truncal obesity, impaired fitness, and atypical malonyl coenzyme A regulation. J. Clin. Endocrinol. Metab. 2003, 88, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Gustat, J.; Srinivasan, S.R.; Elkasabany, A.; Berenson, G.S. Relation of self-rated measures of physical activity to multiple risk factors of insulin resistance syndrome in young adults: The Bogalusa Heart Study. J. Clin. Epidemiol. 2002, 55, 997–1006. [Google Scholar] [CrossRef]
- Kahn, R.; Buse, J.; Ferrannini, E.; Stern, M.; American Diabetes Association; European Association for the Study of Diabetes. The metabolic syndrome: Time for a critical appraisal: Joint statement from the American Diabetes Association and the European Association for the Study of Diabetes. Diabetes Care 2005, 28, 2289–2304. [Google Scholar] [CrossRef] [PubMed]
- Wingard, D.L.; Barrett-Connor, E.; Criqui, M.H.; Suarez, L. Clustering of heart disease risk factors in diabetic compared to nondiabetic adults. Am. J. Epidemiol. 1983, 117, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Miranda, P.J.; DeFronzo, R.A.; Califf, R.M.; Guyton, J.R. Metabolic syndrome: Evaluation of pathological and therapeutic outcomes. Am. Heart J. 2005, 149, 20–32. [Google Scholar] [CrossRef] [PubMed]
- Miranda, P.J.; DeFronzo, R.A.; Califf, R.M.; Guyton, J.R. Metabolic syndrome: Definition, pathophysiology, and mechanisms. Am. Heart J. 2005, 149, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Adler, A.I.; Stratton, I.M.; Neil, H.A.; Yudkin, J.S.; Matthews, D.R.; Cull, C.A.; Wright, A.D.; Turner, R.C.; Holman, R.R. Association of systolic blood pressure with macrovascular and microvascular complications of type 2 diabetes (UKPDS 36): Prospective observational study. BMJ 2000, 321, 412–419. [Google Scholar] [CrossRef] [PubMed]
- Reaven, G.M. Role of insulin resistance in human disease (syndrome X): An expanded definition. Annu. Rev. Med. 1993, 44, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Inzucchi, S.E.; Bergenstal, R.M.; Buse, J.B.; Diamant, M.; Ferrannini, E.; Nauck, M.; Peters, A.L.; Tsapas, A.; Wender, R.; Matthews, D.R. Management of hyperglycemia in type 2 diabetes, 2015: A patient-centered approach: Update to a position statement of the American Diabetes Association and the European Association for the Study of Diabetes. Diabetes Care 2015, 38, 140–149. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.J.; Nathan, D.M.; Arslanian, S.A.; Groop, L.; Rizza, R.A.; Rotter, J.I. Individualizing therapies in type 2 diabetes mellitus based on patient characteristics: What we know and what we need to know. J. Clin. Endocrinol. Metab. 2010, 95, 1566–1574. [Google Scholar] [CrossRef] [PubMed]
- Stratton, I.M.; Adler, A.I.; Neil, H.A.; Matthews, D.R.; Manley, S.E.; Cull, C.A.; Hadden, D.; Turner, R.C.; Holman, R.R. Association of glycaemia with macrovascular and microvascular complications of type 2 diabetes (UKPDS 35): Prospective observational study. BMJ 2000, 321, 405–412. [Google Scholar] [CrossRef] [PubMed]
- UK Prospective Diabetes Study (UKPDS) Group. Intensive blood-glucose control with sulphonylureas or insulin compared with conventional treatment and risk of complications in patients with type 2 diabetes (UKPDS 33). Lancet 1998, 352, 837–853. [Google Scholar]
- Holman, R.R.; Paul, S.K.; Bethel, M.A.; Matthews, D.R.; Neil, H.A. 10-year follow-up of intensive glucose control in type 2 diabetes. New Engl. J. Med. 2008, 359, 1577–1589. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.B.; Manson, J.E.; Stampfer, M.J.; Colditz, G.; Liu, S.; Solomon, C.G.; Willett, W.C. Diet, lifestyle, and the risk of type 2 diabetes mellitus in women. New Engl. J. Med. 2001, 345, 790–797. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, A.K.; van den Donk, M.; Hilding, A.; Ostenson, C.G. Work stress, sense of coherence, and risk of type 2 diabetes in a prospective study of middle-aged Swedish men and women. Diabetes Care 2013, 36, 2683–2689. [Google Scholar] [CrossRef] [PubMed]
- Ostenson, C.G.; Hilding, A.; Grill, V.; Efendic, S. High consumption of smokeless tobacco ('snus') predicts increased risk of type 2 diabetes in a 10-year prospective study of middle-aged Swedish men. Scand. J. Public Health 2012, 40, 730–737. [Google Scholar] [CrossRef] [PubMed]
- Helmrich, S.P.; Ragland, D.R.; Leung, R.W.; Paffenbarger, R.S., Jr. Physical activity and reduced occurrence of non-insulin-dependent diabetes mellitus. New Engl. J. Med. 1991, 325, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Wikner, C.; Gigante, B.; Hellenius, M.L.; de Faire, U.; Leander, K. The risk of type 2 diabetes in men is synergistically affected by parental history of diabetes and overweight. PLoS ONE 2013, 8, e61763. [Google Scholar] [CrossRef] [PubMed]
- Hilding, A.; Eriksson, A.K.; Agardh, E.E.; Grill, V.; Ahlbom, A.; Efendic, S.; Ostenson, C.G. The impact of family history of diabetes and lifestyle factors on abnormal glucose regulation in middle-aged Swedish men and women. Diabetologia 2006, 49, 2589–2598. [Google Scholar] [CrossRef] [PubMed]
- Prasad, R.B.; Groop, L. Genetics of type 2 diabetes-pitfalls and possibilities. Genes 2015, 6, 87–123. [Google Scholar] [CrossRef] [PubMed]
- Bailey, C.J.; Day, C. Traditional plant medicines as treatments for diabetes. Diabetes Care 1989, 12, 553–564. [Google Scholar] [CrossRef] [PubMed]
- Clarence, O.K.; Donatus, B.C.; Samuel, E.C. Prophylaxis and treatment of types 1 and 2 diabetes mellitus. Int. J. Dis. Disord. 2014, 2, 65–73. [Google Scholar]
- Ivorra, M.D.; Paya, M.; Villar, A. A review of natural products and plants as potential antidiabetic drugs. J. Ethnopharmacol. 1989, 27, 243–275. [Google Scholar] [CrossRef]
- Rai, M.K. A review on some antidiabetic plants of India. Anc. Sci. Life 1995, 14, 168–180. [Google Scholar] [PubMed]
- Zatsepin, M.; Mattes, A.; Rupp, S.; Finkelmeier, D.; Basu, A.; Burger-Kentischer, A.; Goldblum, A. Computational Discovery and Experimental Confirmation of TLR9 Receptor Antagonist Leads. J. Chem. Inf. Model. 2016, 56, 1835–1846. [Google Scholar] [CrossRef] [PubMed]
- Basu, A.; Sohn, Y.S.; Alyan, M.; Nechushtai, R.; Domb, A.J.; Goldblum, A. Discovering Novel and Diverse Iron-Chelators in Silico. J. Chem. Inf. Model. 2016, 56, 2476–2485. [Google Scholar] [CrossRef] [PubMed]
- Pappalardo, M.; Shachaf, N.; Basile, L.; Milardi, D.; Zeidan, M.; Raiyn, J.; Guccione, S.; Rayan, A. Sequential application of ligand and structure based modeling approaches to index chemicals for their hH4R antagonism. PLoS ONE 2014, 9, e109340. [Google Scholar] [CrossRef] [PubMed]
- Zaid, H.; Raiyn, J.; Osman, M.; Falah, M.; Srouji, S.; Rayan, A. In silico modeling techniques for predicting the tertiary structure of human H4 receptor. Front Biosci. 2016, 21, 597–619. [Google Scholar]
- Schuller, A.; Schneider, G. Identification of hits and lead structure candidates with limited resources by adaptive optimization. J. Chem. Inf. Model. 2008, 48, 1473–1491. [Google Scholar] [CrossRef] [PubMed]
- Hao, M.; Zhang, S.; Qiu, J. Toward the Prediction of FBPase Inhibitory Activity Using Chemoinformatic Methods. Int. J. Mol. Sci. 2012, 13, 7015–7037. [Google Scholar] [CrossRef] [PubMed]
- Lusci, A.; Pollastri, G.; Baldi, P. Deep architectures and deep learning in chemoinformatics: The prediction of aqueous solubility for drug-like molecules. J. Chem. Inf. Model. 2013, 53, 1563–1575. [Google Scholar] [CrossRef] [PubMed]
- Heikamp, K.; Bajorath, J. Comparison of confirmed inactive and randomly selected compounds as negative training examples in support vector machine-based virtual screening. J. Chem. Inf. Model. 2013, 53, 1595–1601. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Beguin, C.; Golbraikh, A.; Stables, J.P.; Kohn, H.; Tropsha, A. Application of predictive QSAR models to database mining: Identification and experimental validation of novel anticonvulsant compounds. J. Med. Chem. 2004, 47, 2356–2364. [Google Scholar] [CrossRef] [PubMed]
- Rayan, A.; Falah, M.; Mawasi, H.; Raiyn, N. Assessing drugs for their cardio-toxicity. Lett. Drug Des. Discov. 2010, 7, 409–414. [Google Scholar] [CrossRef]
- Deeb, O.; Jawabreh, S.; Goodarzi, M. Exploring QSARs of vascular endothelial growth factor receptor-2 (VEGFR-2) tyrosine kinase inhibitors by MLR, PLS and PC-ANN. Curr. Pharm. Des. 2013, 19, 2237–2244. [Google Scholar] [CrossRef] [PubMed]
- Rayan, A.; Marcus, D.; Goldblum, A. Predicting oral druglikeness by iterative stochastic elimination. J. Chem. Inf. Model. 2010, 50, 437–445. [Google Scholar] [CrossRef] [PubMed]
- Mussa, H.Y.; Hawizy, L.; Nigsch, F.; Glen, R.C. Classifying large chemical data sets: Using a regularized potential function method. J. Chem. Inf. Model. 2011, 51, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Pappalardo, M.; Rayan, M.; Abu-Lafi, S.; Leonardi, M.E.; Milardi, D.; Guccione, S.; Rayan, A. Homology-based Modeling of Rhodopsin-like Family Members in the Inactive State: Structural Analysis and Deduction of Tips for Modeling and Optimization. Mol. Inform. 2017, 36. [Google Scholar] [CrossRef] [PubMed]
- Shahaf, N.; Pappalardo, M.; Basile, L.; Guccione, S.; Rayan, A. How to Choose the Suitable Template for Homology Modelling of GPCRs: 5-HT7 Receptor as a Test Case. Mol. Inform. 2016, 35, 414–423. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sosa, A.T.; Oja, M.; Hetenyi, C.; Maran, U. DrugLogit: Logistic discrimination between drugs and nondrugs including disease-specificity by assigning probabilities based on molecular properties. J. Chem. Inf. Model. 2012, 52, 2165–2180. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sosa, A.T.; Oja, M.; Hetenyi, C.; Maran, U. Disease-Specific Differentiation Between Drugs and Non-Drugs Using Principal Component Analysis of Their Molecular Descriptor Space. Mol. Inform. 2012, 31, 369–383. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sosa, A.T.; Maran, U.; Hetenyi, C. Molecular property filters describing pharmacokinetics and drug binding. Curr. Med. Chem. 2012, 19, 1646–1662. [Google Scholar] [CrossRef] [PubMed]
- Rayan, A.; Noy, E.; Chema, D.; Levitzki, A.; Goldblum, A. Stochastic algorithm for kinase homology model construction. Curr. Med. Chem. 2004, 11, 675–692. [Google Scholar] [CrossRef] [PubMed]
- Rayan, A. The utility of Intelligent Learning Engine in Drug Discovery Informatics. Proc. Br. Pharmacol. Soc. 2010, 7, 26. [Google Scholar]
- Rayan, A.; Falah, M.; Raiyn, J.; Da'adoosh, B.; Kadan, S.; Zaid, H.; Goldblum, A. Indexing molecules for their hERG liability. Eur. J. Med. Chem. 2013, 65, 304–314. [Google Scholar] [CrossRef] [PubMed]
- Glick, M.; Goldblum, A. A novel energy-based stochastic method for positioning polar protons in protein structures from X-rays. Proteins 2000, 38, 273–287. [Google Scholar] [CrossRef]
- Glick, M.; Rayan, A.; Goldblum, A. A stochastic algorithm for global optimization and for best populations: A test case of side chains in proteins. Proc. Natl. Acad. Sci. USA 2002, 99, 703–708. [Google Scholar] [CrossRef] [PubMed]
- Michaeli, A.; Rayan, A. Modeling Ensembles of Loop Conformations by Iterative Stochastic Elimination. Lett. Drug Des. Discov. 2016, 13, 1–6. [Google Scholar] [CrossRef]
- Rayan, A.; Senderowitz, H.; Goldblum, A. Exploring the conformational space of cyclic peptides by a stochastic search method. J. Mol. Graph. Model. 2004, 22, 319–333. [Google Scholar] [CrossRef] [PubMed]
- Zaid, H.; Raiyn, J.; Nasser, A.; Saad, B.; Rayan, A. Physicochemical properties of natural based products versus synthetic chemicals. Open Nutraceuticals J. 2010, 3, 194–202. [Google Scholar] [CrossRef]
- Frank, A.; Abu-Lafi, S.; Adawi, A.; Schwed, J.S.; Stark, H.; Rayan, A. From medicinal plant extracts to defined chemical compounds targeting the histamine H4 receptor: Curcuma longa in the treatment of inflammation. Inflamm. Res. 2017, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kacergius, T.; Abu-Lafi, S.; Kirkliauskiene, A.; Gabe, V.; Adawi, A.; Rayan, M.; Qutob, M.; Stukas, R.; Utkus, A.; Zeidan, M.; et al. Inhibitory capacity of Rhus coriaria L. extract and its major component methyl gallate on Streptococcus mutans biofilm formation by optical profilometry: Potential applications for oral health. Mol. Med. Rep. 2017, 16, 949–956. [Google Scholar] [CrossRef] [PubMed]
- Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 2001, 46, 3–26. [Google Scholar] [CrossRef]
- Hann, M.M.; Oprea, T.I. Pursuing the leadlikeness concept in pharmaceutical research. Curr. Opin. Chem. Biol. 2004, 8, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Chemical Computing Group. QuaSAR-Descriptor. Available online: http://www.chemcomp.com/journal/descr.htm (accessed on 12 August 2017).
- Fang, C.Y.; Wang, X.J.; Huang, Y.W.; Hao, S.M.; Sheng, J. Caffeine is responsible for the bloodglucose-lowering effects of green tea and Puer tea extractsin BALB/c mice. Chin. J. Nat. Med. 2015, 13, 595–601. [Google Scholar] [CrossRef]
- Matsuda, Y.; Kobayashi, M.; Yamauchi, R.; Ojika, M.; Hiramitsu, M.; Inoue, T.; Katagiri, T.; Murai, A.; Horio, F. Coffee and caffeine improve insulin sensitivity and glucose tolerance in C57BL/6J mice fed a high-fat diet. Biosci. Biotechnol. Biochem. 2011, 75, 2309–2315. [Google Scholar] [CrossRef] [PubMed]
- Ozmen, O.; Topsakal, S.; Haligur, M.; Aydogan, A.; Dincoglu, D. Effects of Caffeine and Lycopene in Experimentally Induced Diabetes Mellitus. Pancreas 2016, 45, 579–583. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: The natural products database is available from the corresponding author upon request. |


| Filter 1 | Filter 2 | Filter 3 |
|---|---|---|
| MCC = 0.642 | MCC = 0.640 | MCC = 0.638 |
| TP = 86.59% | TP = 62.88% | TP = 81.4% |
| TN = 77.42% | TN = 97.23% | TN = 82.3% |
| a_n O (0–6.99) | BCUT_PEOE_2 (0–0.67) | SMR_VSA3 (0–37.82) |
| PEOE_VSA + 4 (0–30.95) | GCUT_SLOGP_2 (0.11–0.27) | SMR_VSA1 (0–94.72) |
| Chiral (0–4.99) | Chiral_u (0–3) | GCUT_PEOE_3 (0–2.88) |
| SlogP_VSA2 (0–65.17) | GCUT_SLOGP_0 (−2.26–−0.91) | Reactive (0–0.00) |
| Descriptor Name | No. of Appearances | Redundant More Times than Random |
|---|---|---|
| GCUT_SLOGP_0 | 24 | 23.7 |
| a_ICM | 16 | 15.8 |
| PEOE_VSA + 4 | 12 | 11.9 |
| SMR_VSA1 | 10 | 9.9 |
| logS | 9 | 8.9 |
| Nmol | 9 | 8.9 |
| lip_druglike | 9 | 8.9 |
| Chi1_C | 8 | 7.9 |
| GCUT_PEOE_0 | 8 | 7.9 |
| opr_leadlike | 7 | 6.9 |
| Q_VSA_FPOS | 7 | 6.9 |
| SMR_VSA3 | 7 | 6.9 |
| a_don | 6 | 5.9 |
| a_hyd | 6 | 5.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeidan, M.; Rayan, M.; Zeidan, N.; Falah, M.; Rayan, A. Indexing Natural Products for Their Potential Anti-Diabetic Activity: Filtering and Mapping Discriminative Physicochemical Properties. Molecules 2017, 22, 1563. https://doi.org/10.3390/molecules22091563
Zeidan M, Rayan M, Zeidan N, Falah M, Rayan A. Indexing Natural Products for Their Potential Anti-Diabetic Activity: Filtering and Mapping Discriminative Physicochemical Properties. Molecules. 2017; 22(9):1563. https://doi.org/10.3390/molecules22091563
Chicago/Turabian StyleZeidan, Mouhammad, Mahmoud Rayan, Nuha Zeidan, Mizied Falah, and Anwar Rayan. 2017. "Indexing Natural Products for Their Potential Anti-Diabetic Activity: Filtering and Mapping Discriminative Physicochemical Properties" Molecules 22, no. 9: 1563. https://doi.org/10.3390/molecules22091563




