Molecular Dynamic Analysis of Hyaluronic Acid and Phospholipid Interaction in Tribological Surgical Adjuvant Design for Osteoarthritis
Abstract
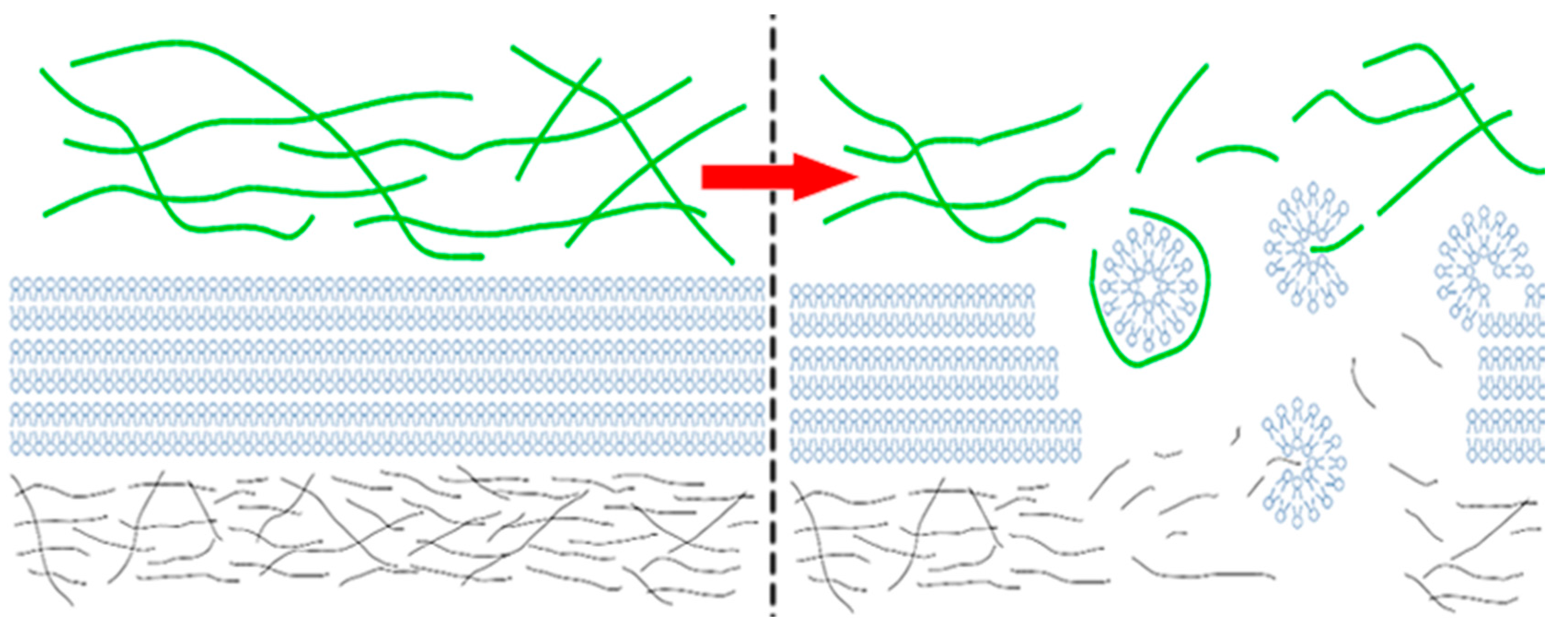
:1. Introduction
2. Results
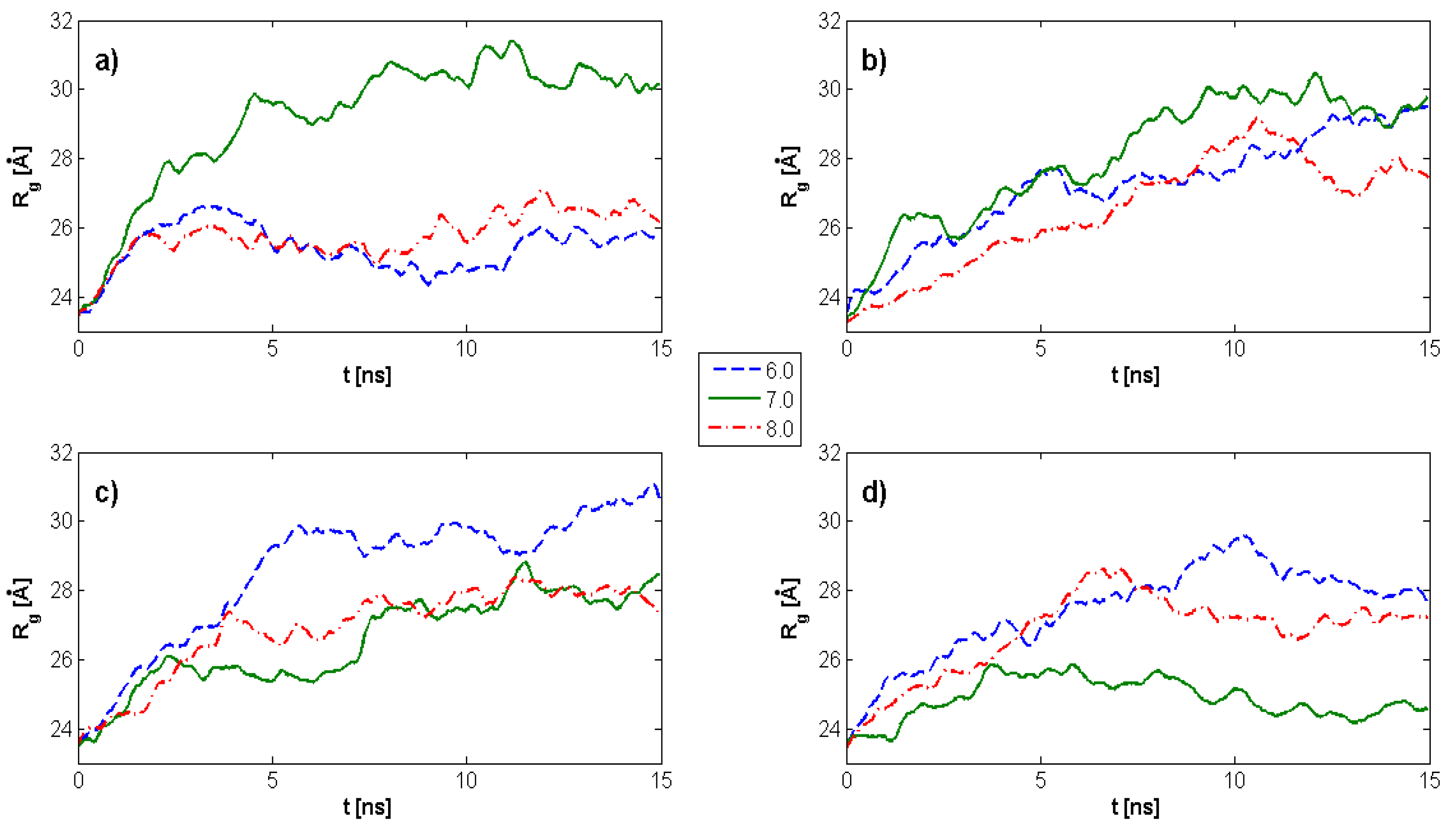
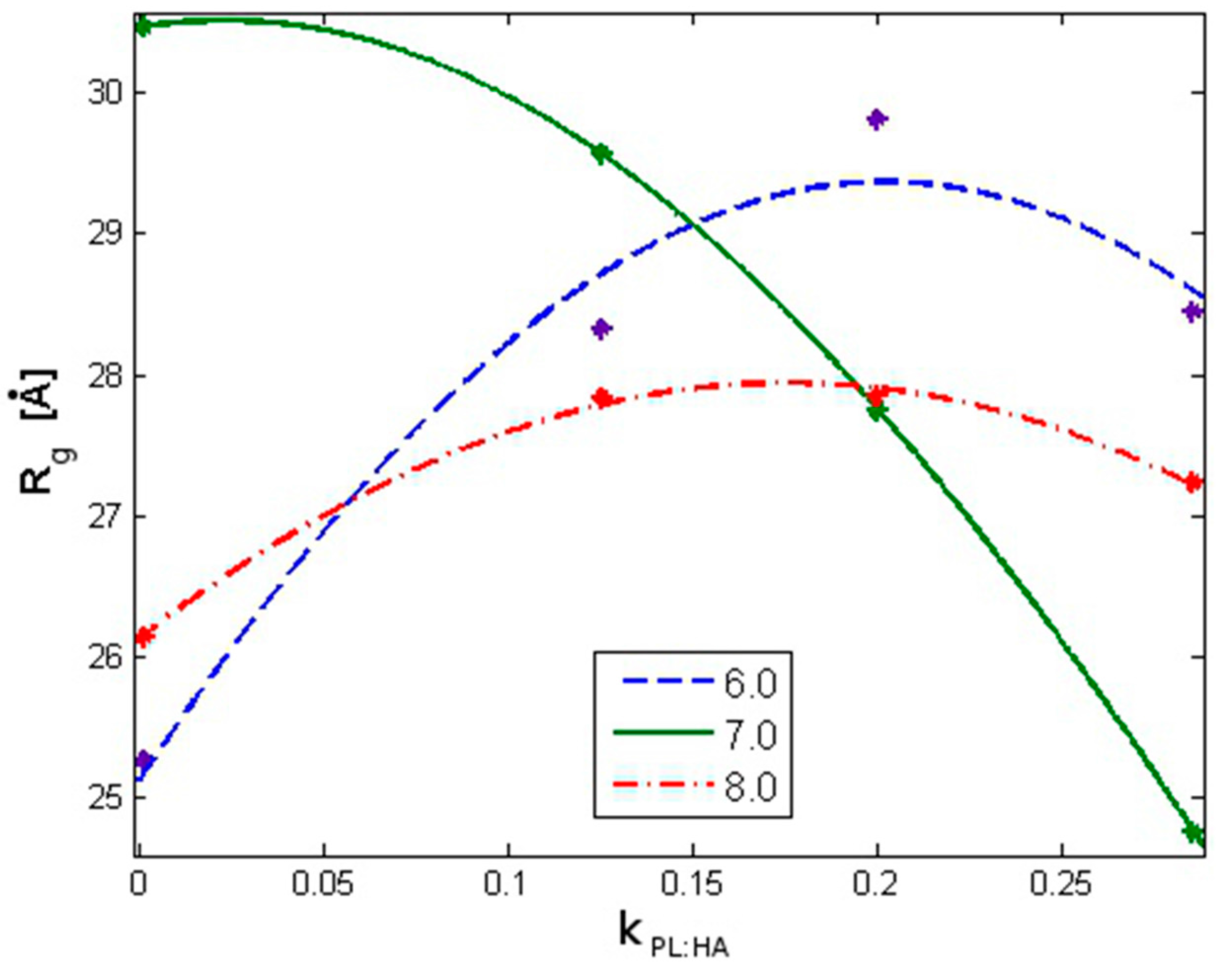
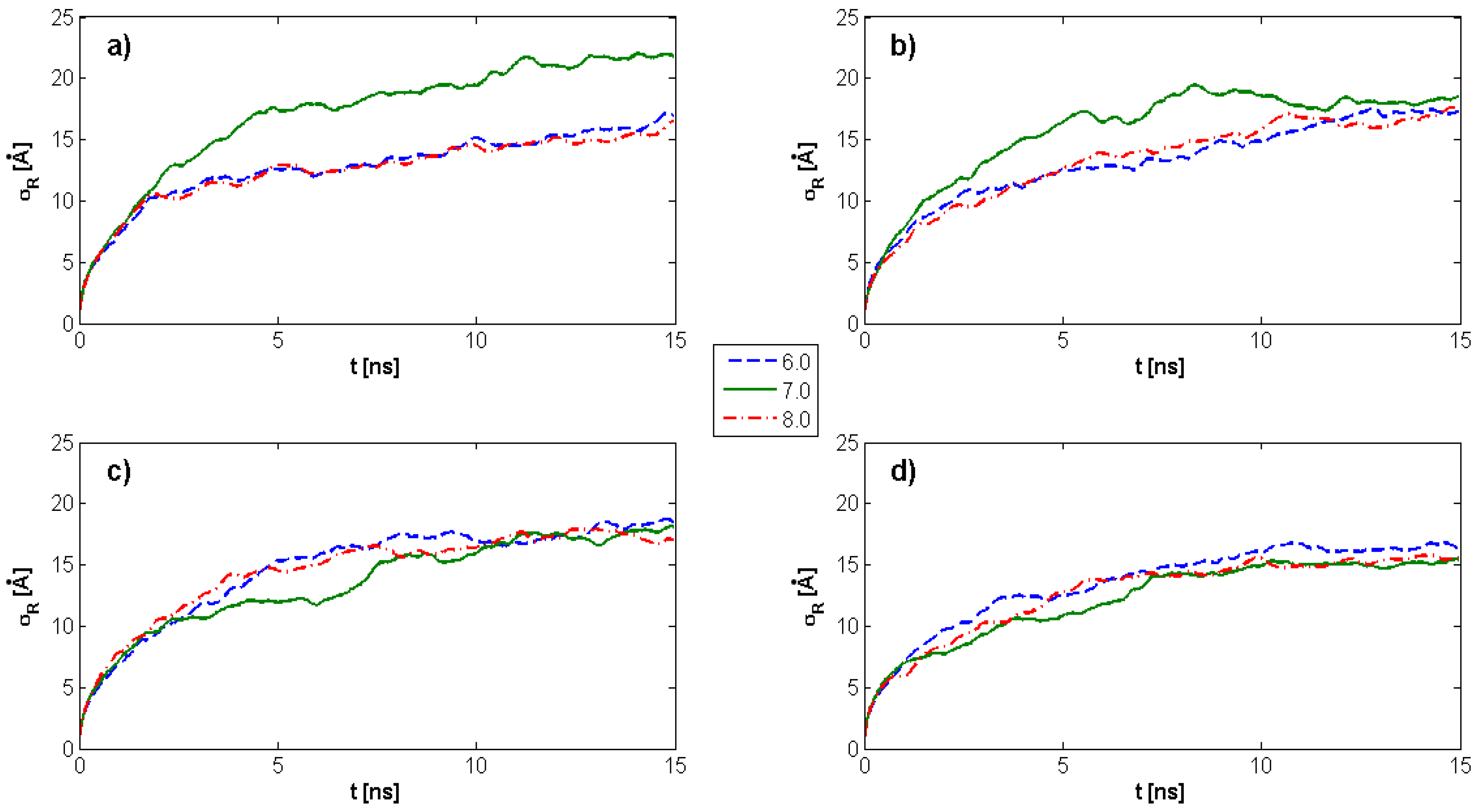
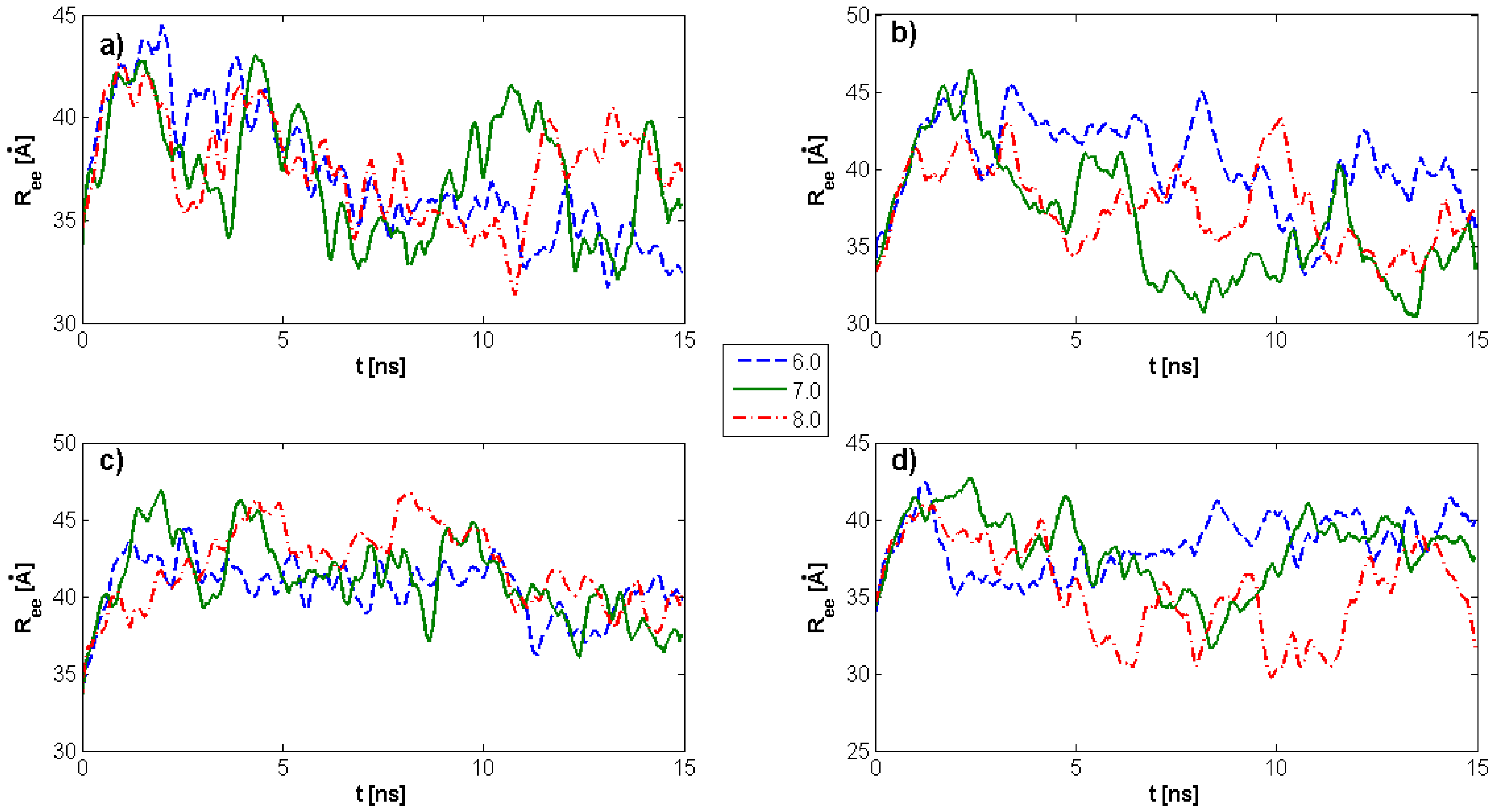
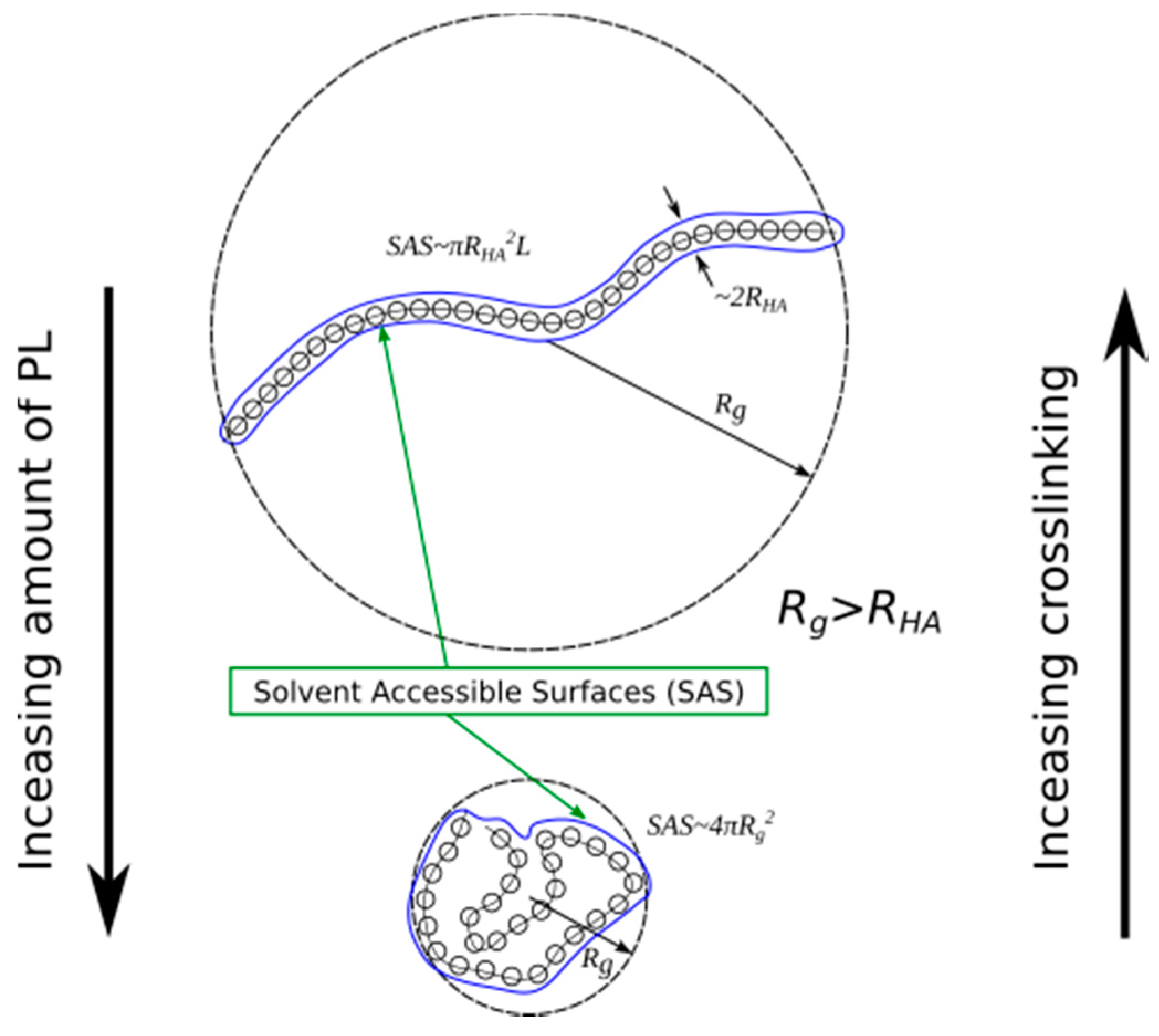
2.1. Radius of Gyration: Time Evolution; pH Value; and PL Concentration Dependence
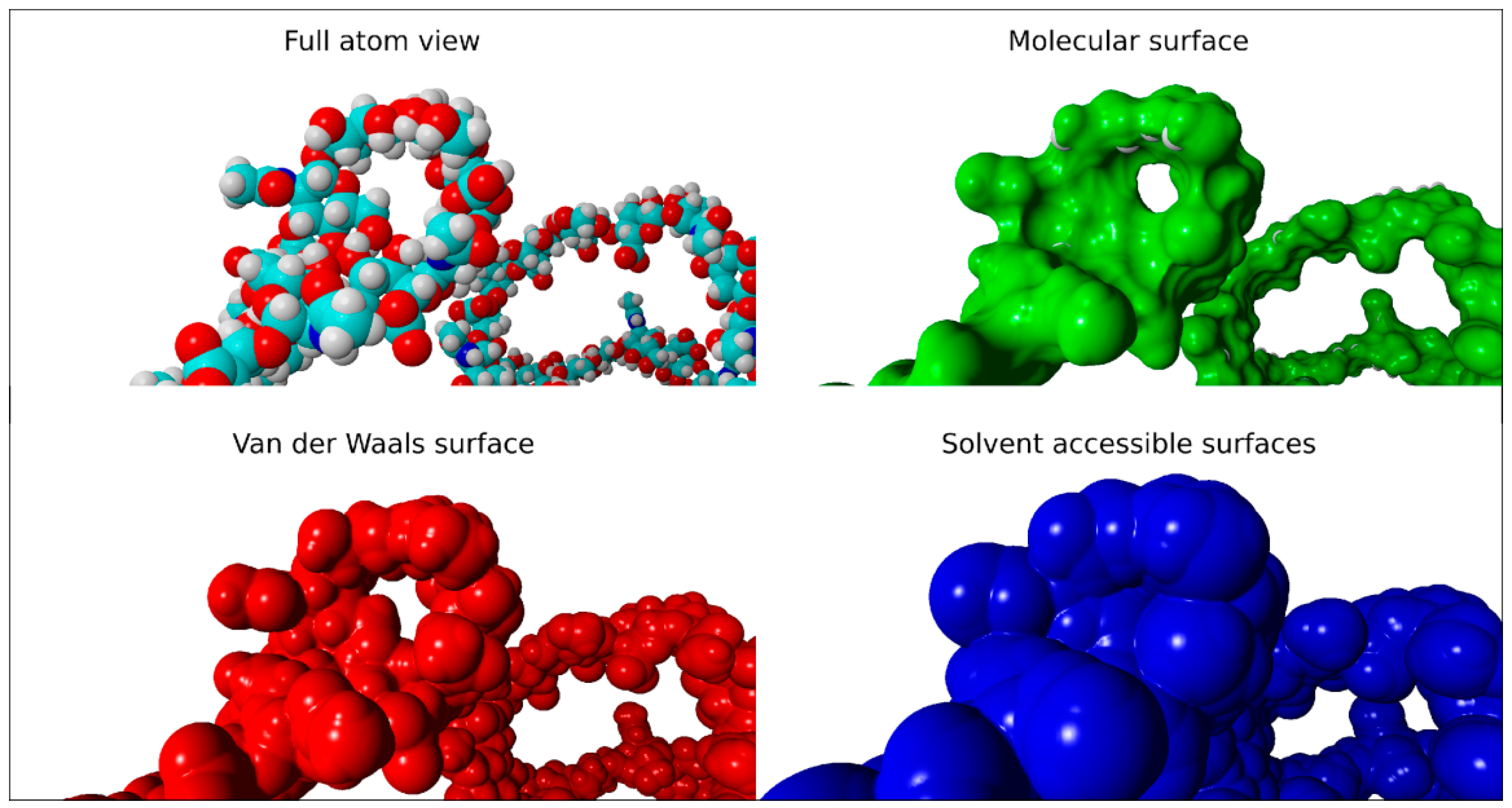
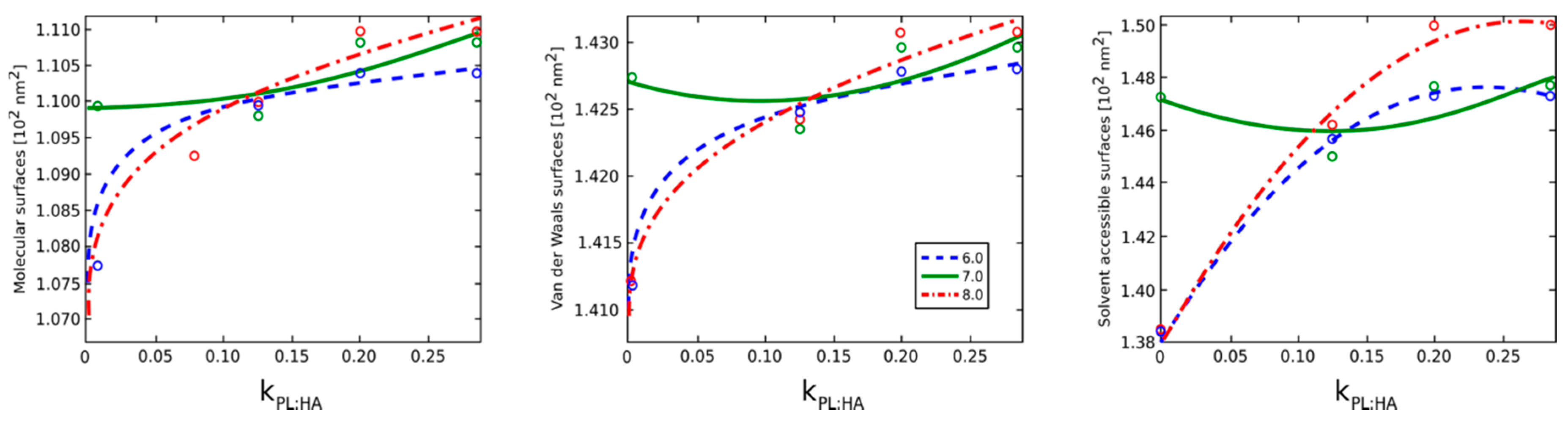
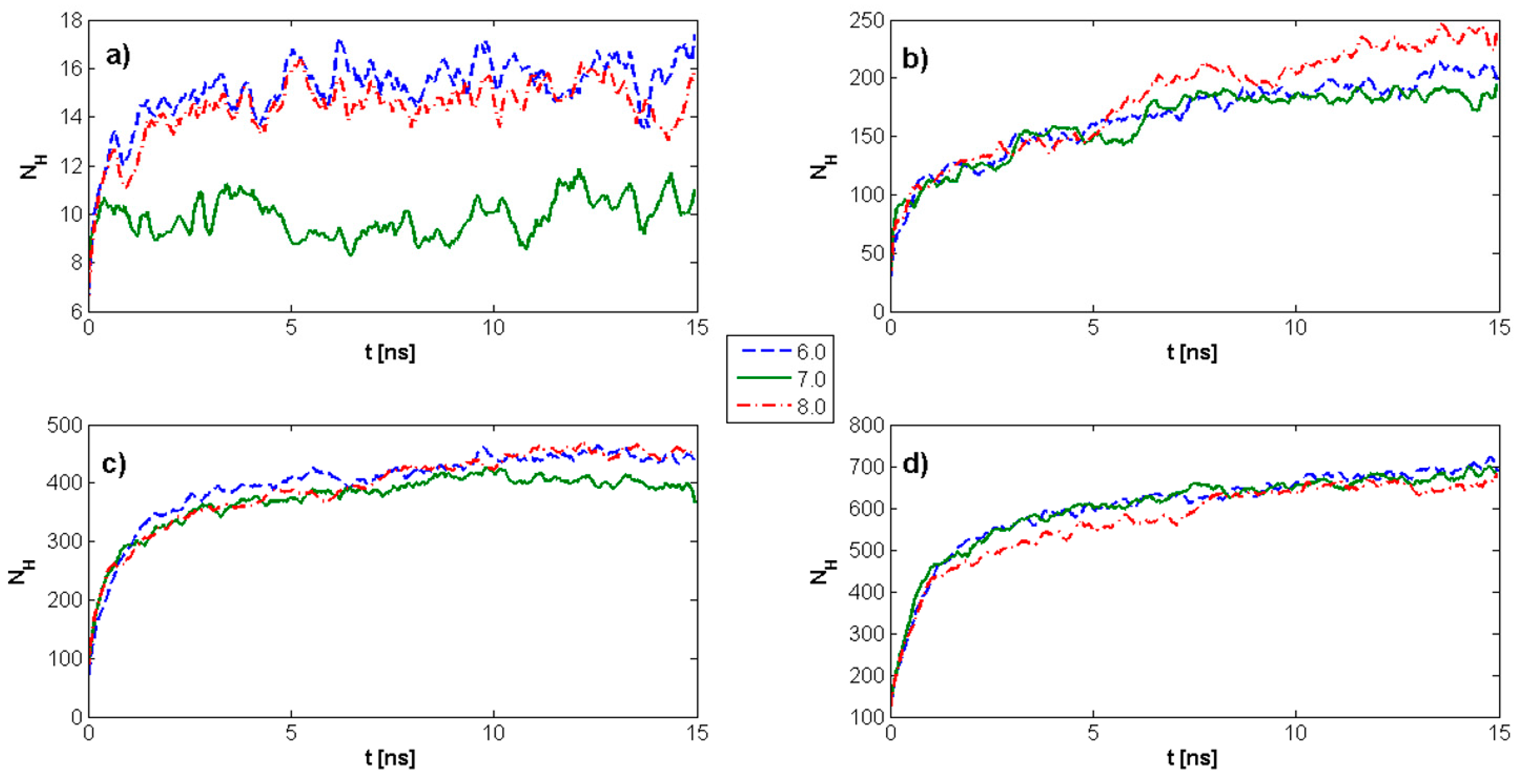
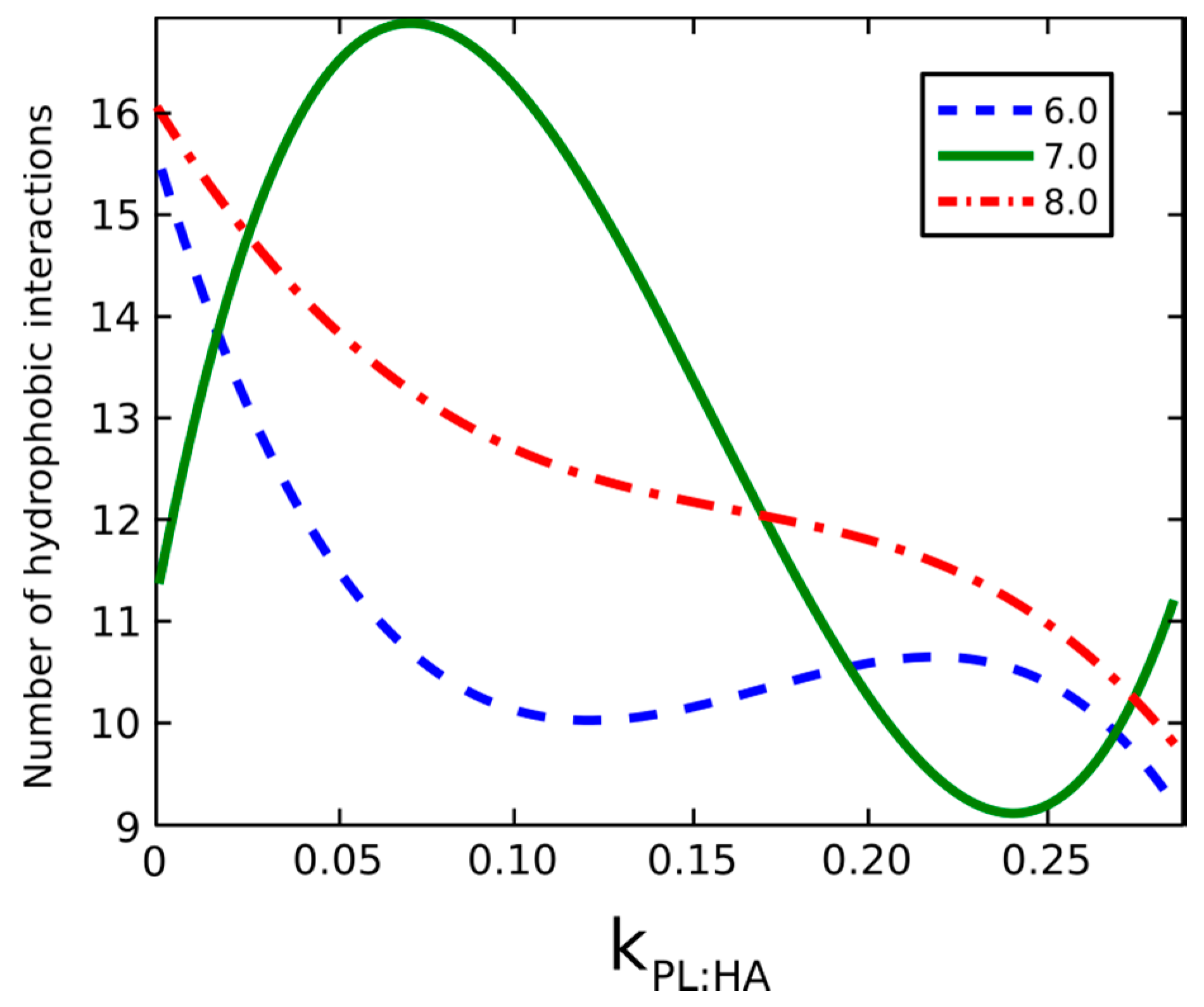
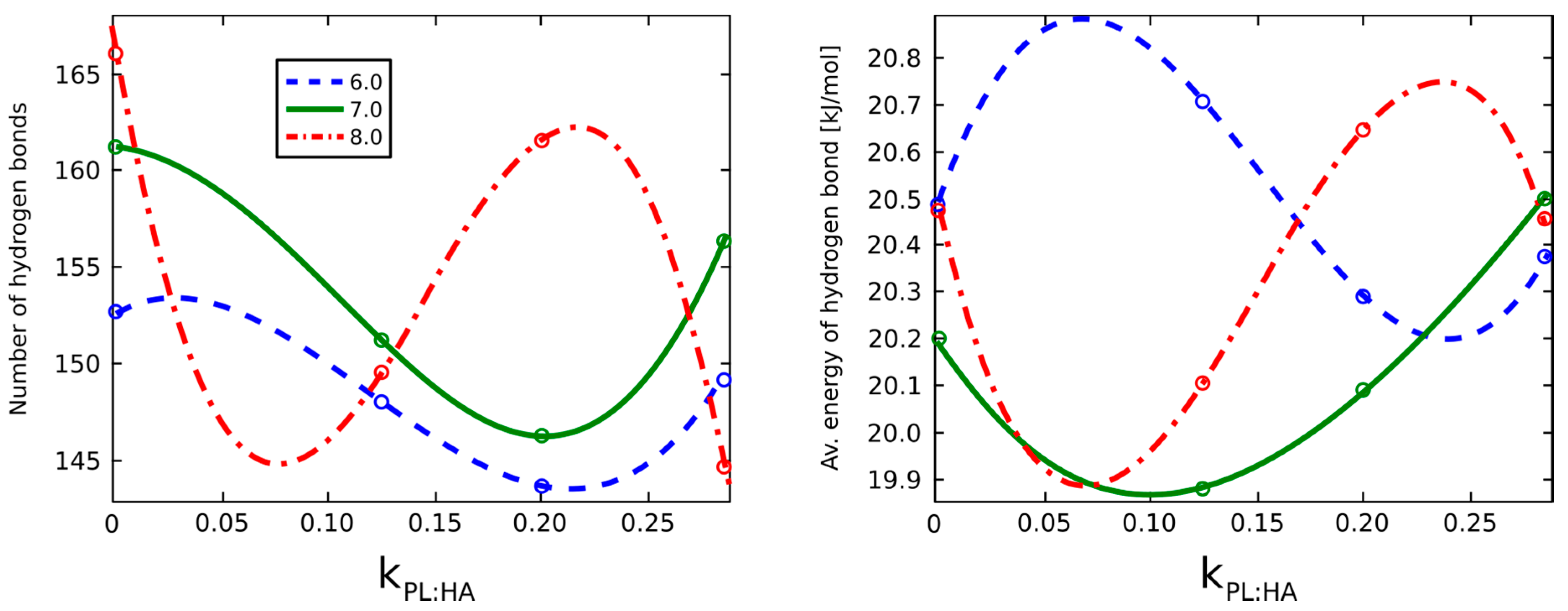
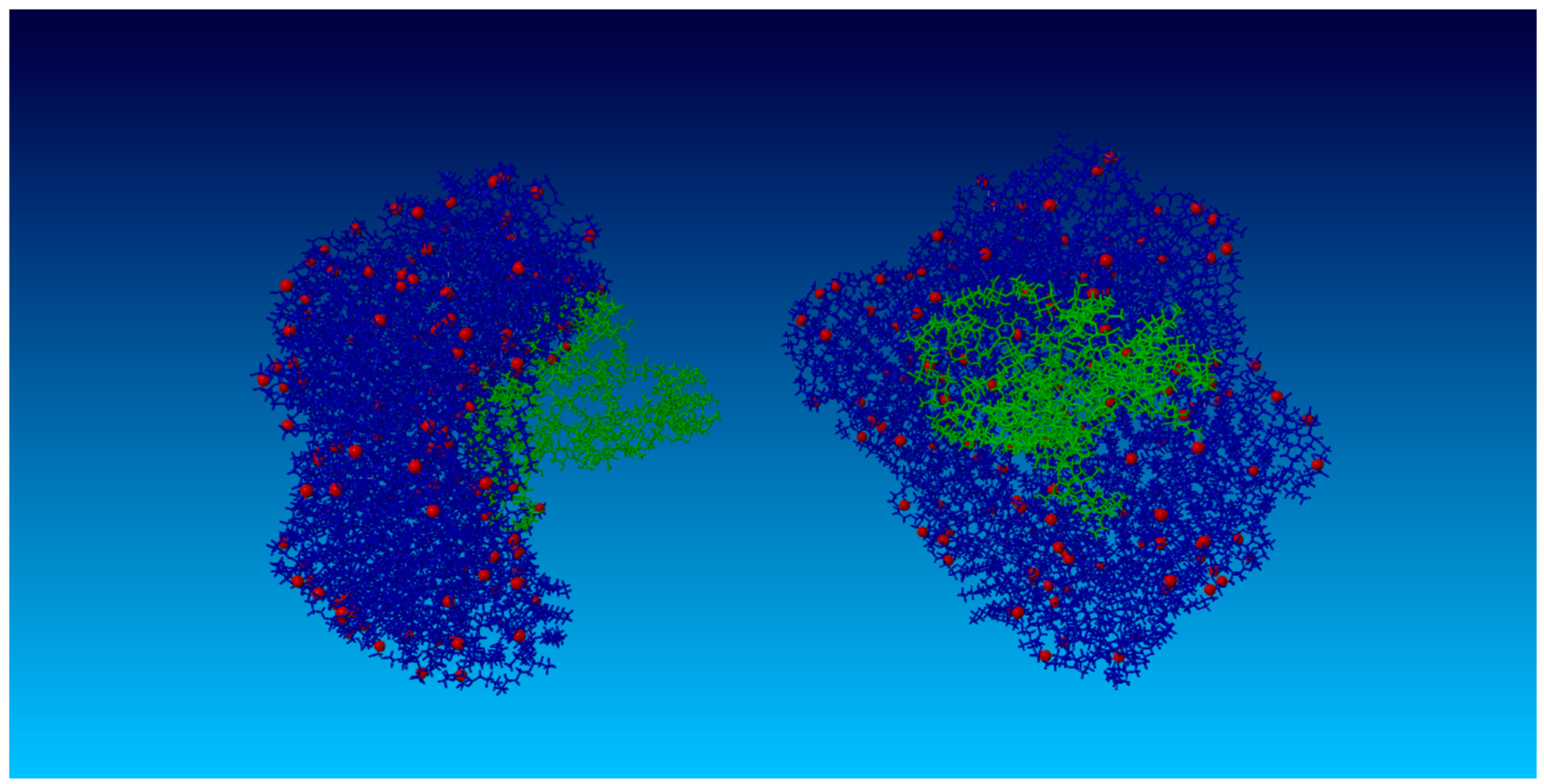
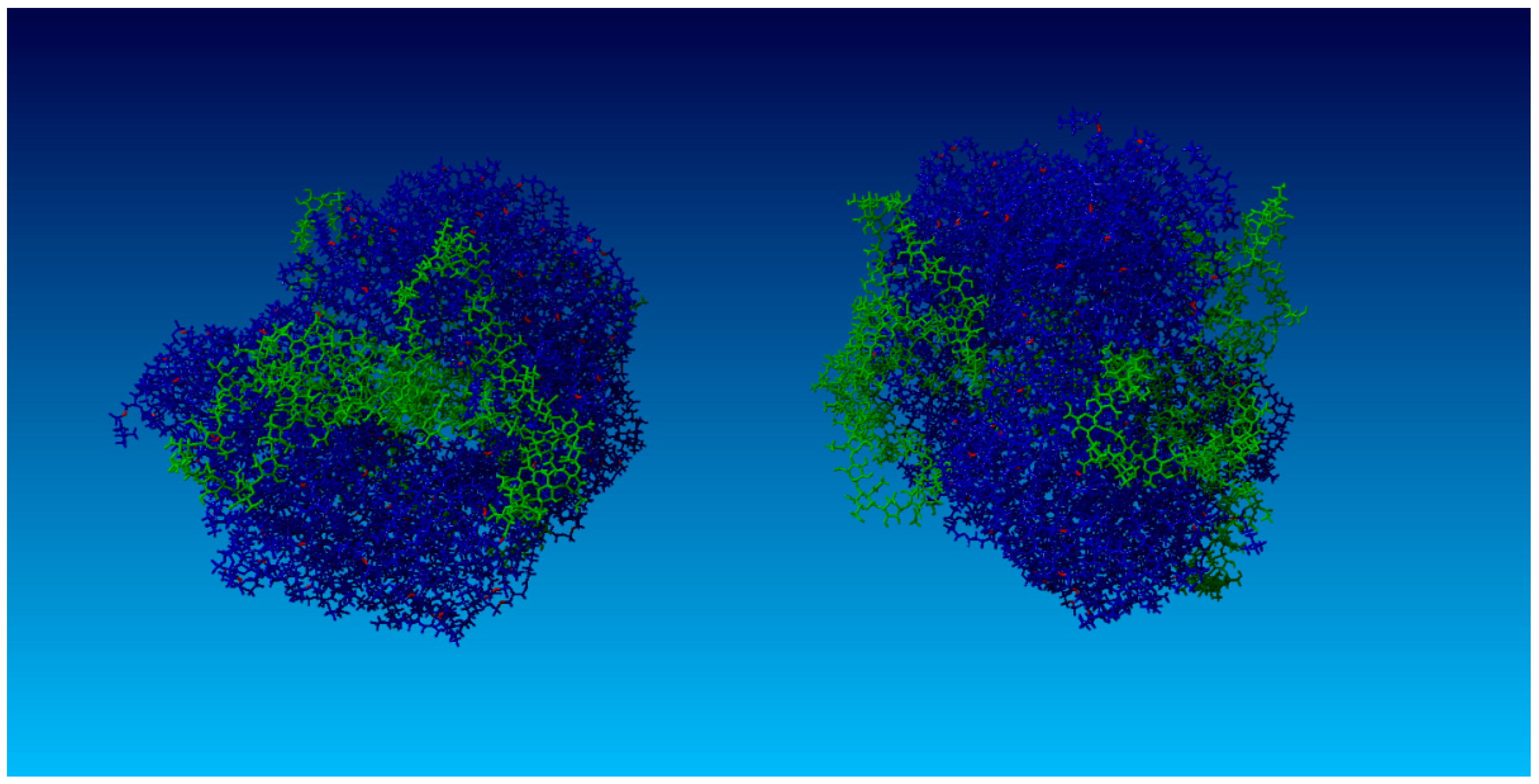
2.2. Surface Visualization: Surface Area Accessibility, Hydrophobicity, and Hydrogen Bonds
3. Discussion
4. Materials and Methods
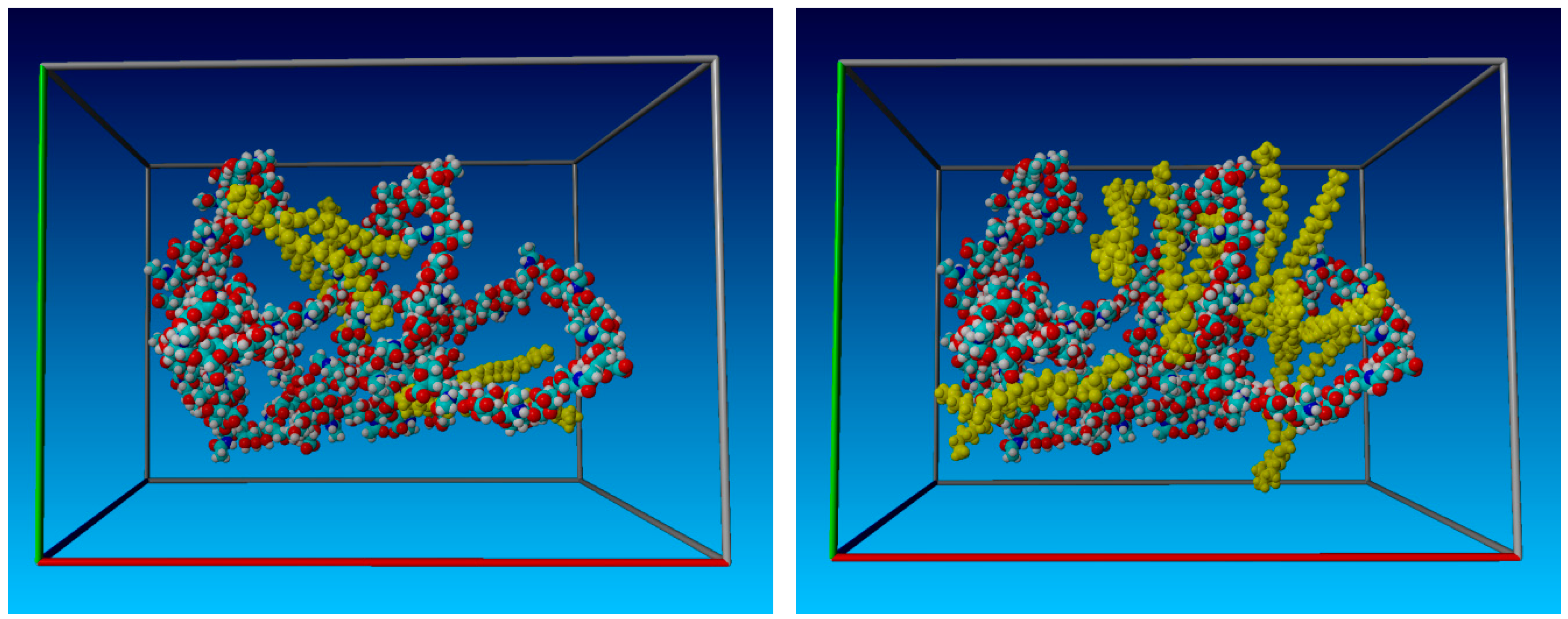
4.1. The Simulation Setup
4.2. Force Field
4.3. pH Setting and Control
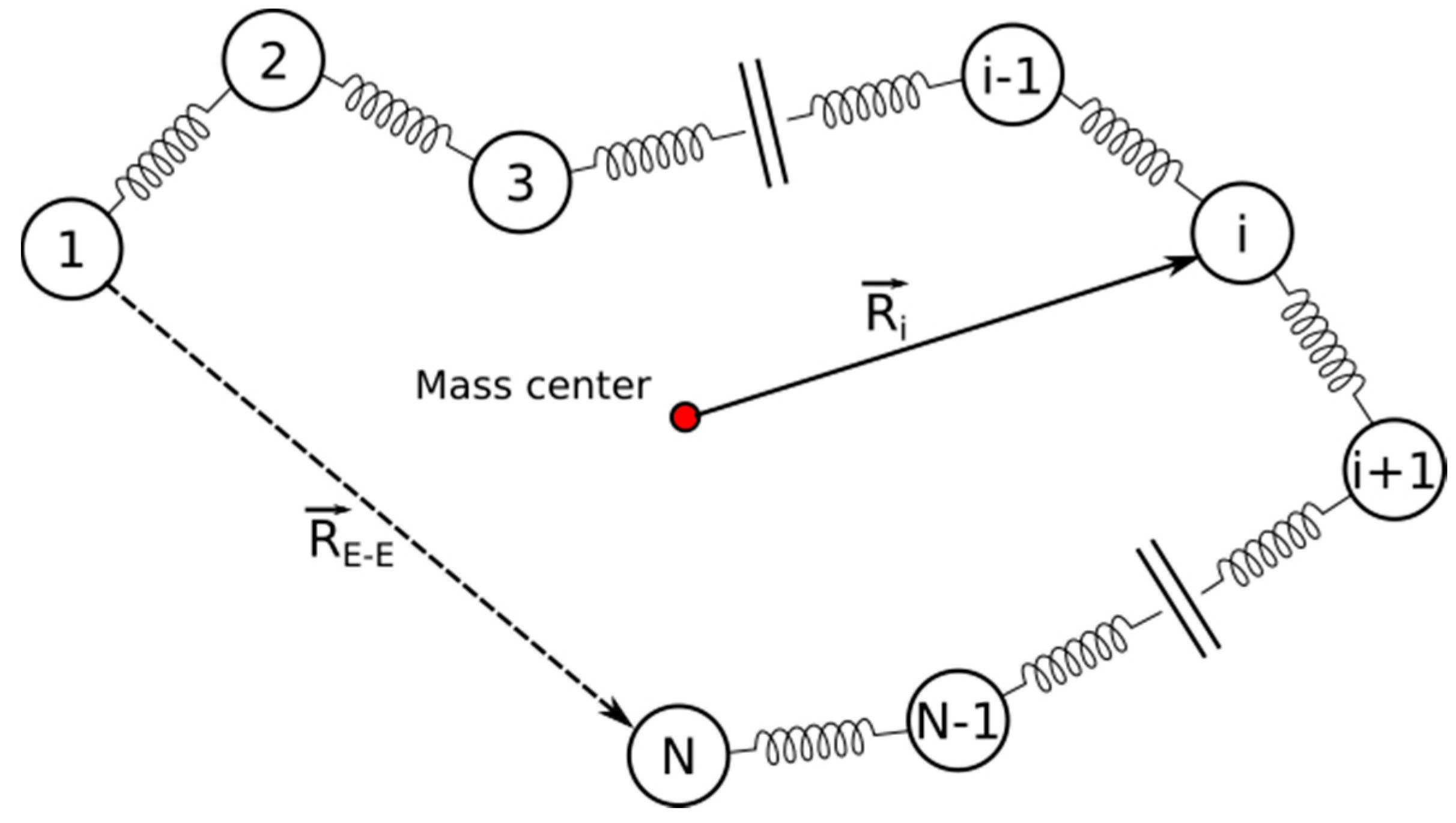
4.4. Radius of Gyration
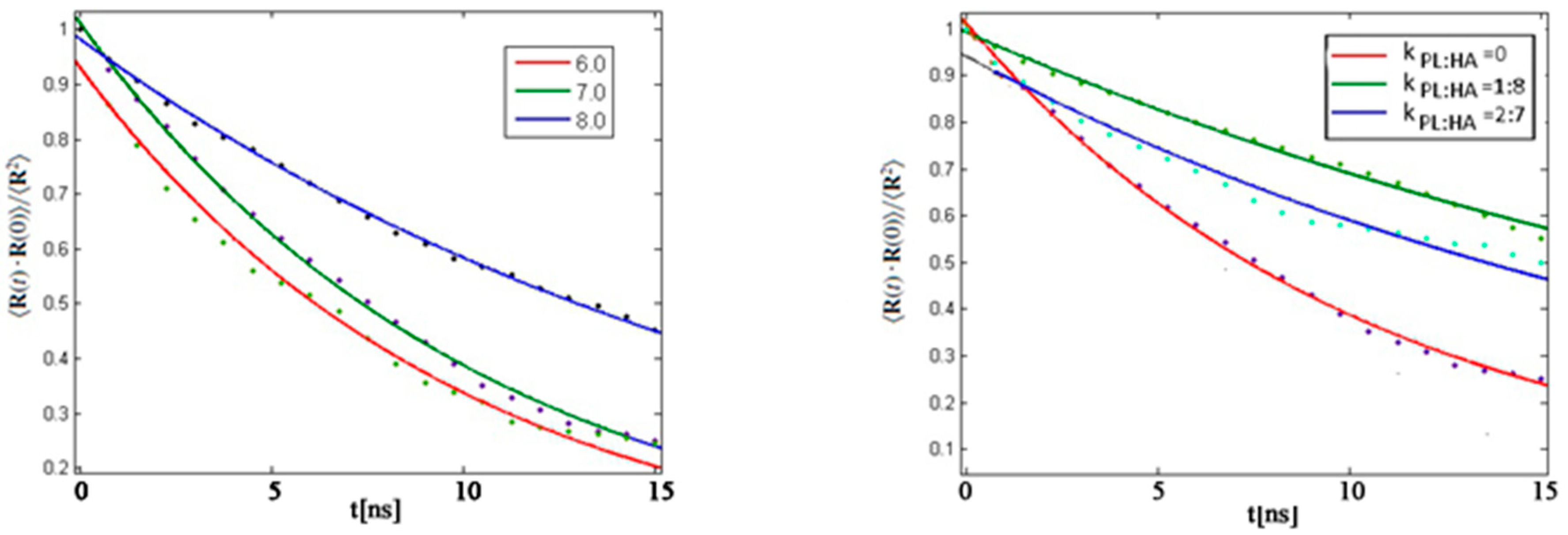
4.5. Rouse Model Application
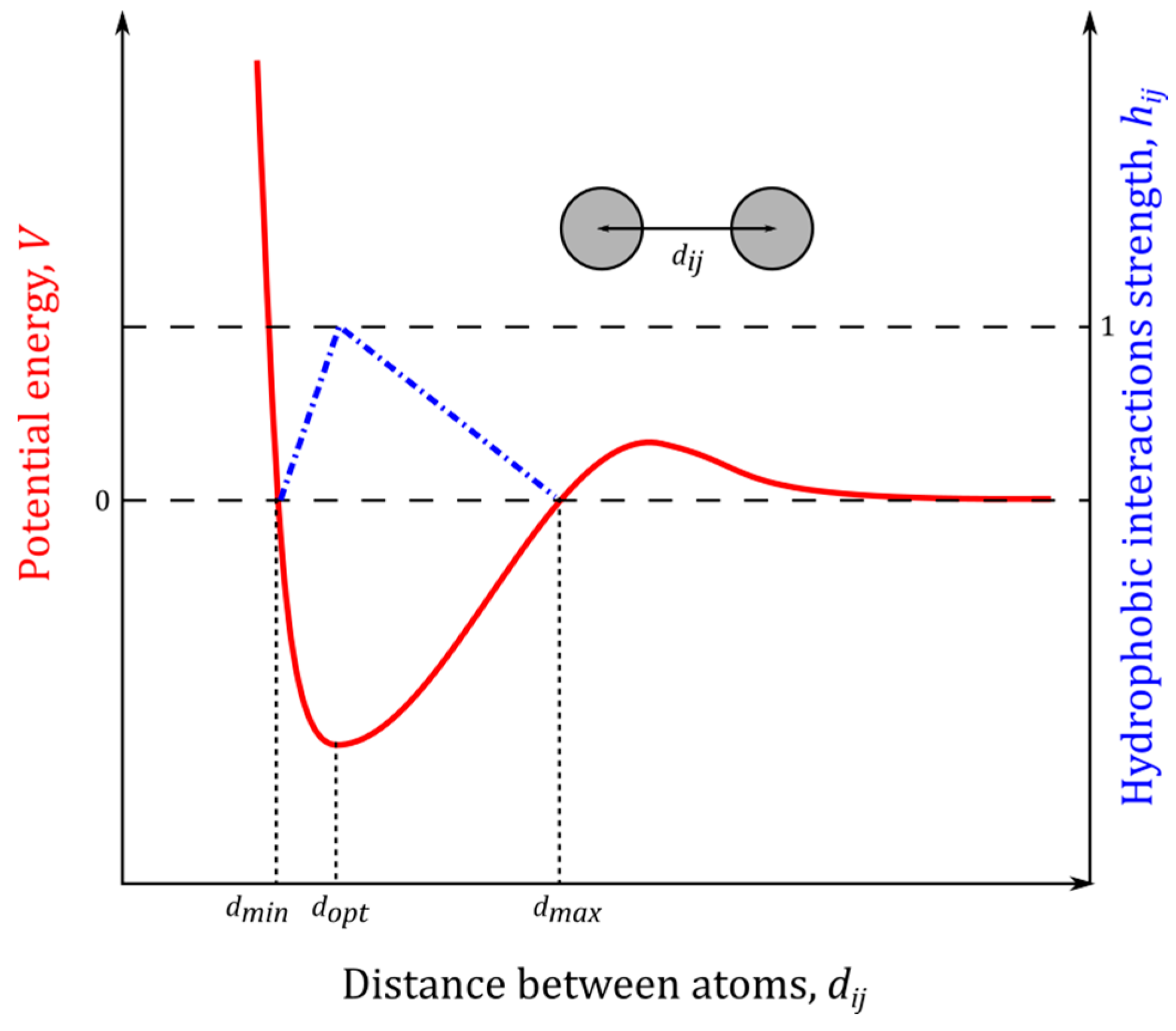
4.6. Hydrophobic Interactions
4.7. Hydrogen Bond Identification and Strength
4.8. Other Simulations
4.9. Limitations
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jung, S.; Petelska, A.; Beldowski, P.; Augé, W.K.; Casey, T.; Walczak, D.; Lemke, K.; Gadomski, A. Hyaluronic acid and phospholipid interactions useful for repaired articular cartilage surfaces—A mini review toward tribological surgical adjuvants. Colloid Polym. Sci. 2017, 295, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Augé, W.K. Addressing the large world-wide disease burden of osteoarthritis through targeted induction of biosynthetic gene expression: Early intervention engineered to reverse articular cartilage lesions. In Proceedings of the World DNA and Genome Day, Chair—Track 4-3 Human Genetics and Diseases and 4-2 Genetic Testing and Applications, Dalian, China, 25–29 April 2011. [Google Scholar]
- Snelling, S.; Rout, R.; Davidson, R.; Clark, I.; Carr, A.; Hulley, P.A.; Price, A.J. A gene expression study of normal and damaged cartilage in anteromedial gonarthrosis, a phenotype of osteoarthritis. Osteoarthr. Cartil. 2014, 22, 334–343. [Google Scholar] [CrossRef] [PubMed]
- Augé, W.K. Conceptualization of surface-confined nano-assemblies as a biophysical battery circuit during tissue rescue: A bridge to accessing genomic control mechanisms. Int. J. Nanosyst. 2012, 5, 1–18. [Google Scholar]
- Augé, W.K.; Ganguly, K.; Goodwin, P.M.; Gadomski, A.; Gehlert, R.J. Lipid distribution in human knee and hip articular cartilage correlated to tissue surface roughness and surface active phospholipid layer presence: Evidence of cooperative interfacial lipid delivery mechanisms. Osteoarthr. Cartil. 2014, 22, S312–S313. [Google Scholar] [CrossRef]
- Ganguly, K.; McRury, I.D.; Goodwin, P.M.; Morgan, R.E.; Augé, W.K. Targeted in situ biosynthetic transcriptional activation in native surface level human articular chondrocytes during lesion stabilization. Cartilage 2012, 3, 141–155. [Google Scholar] [CrossRef] [PubMed]
- Augé, W.K. Inverse mass ratio batteries: An in situ energy source generated from motive proton delivery gradients. Nano Energy 2012, 1, 309–315. [Google Scholar] [CrossRef]
- Jebens, E.H.; Monk-Jones, E. On the viscosity and pH of synovial fluid and the pH of blood. J. Bone Jt. Surg. 1952, 41, 388–400. [Google Scholar]
- Goldie, I.; Nachemson, A. Synovial pH in rheumatoid knee joints: II. The effect of local corticosteroid treatment. Acta Orthop. Scand. 1970, 41, 354–362. [Google Scholar] [CrossRef]
- Treuhaft, P.S.; McCarty, D.J. Synovial fluid pH, lactate, oxygen and carbon dioxide partial pressure in various joint diseases. Arthritis Rheumatol. 1971, 14, 475–484. [Google Scholar] [CrossRef]
- Milošev, I.; Levašič, V.; Vidmar, J.; Kovač, S.; Trebše, R. pH and metal concentration of synovial fluid of osteoarthritic joints and joints with metal replacements. J. Biomed. Mater. Res. Part B Appl. Biomater. 2016. [Google Scholar] [CrossRef] [PubMed]
- Kosinska, M.; Ludwig, T.E.; Liebisch, G.; Zhang, R.; Siebert, H.C.; Wilhelm, J.; Kaesser, U.; Dettmeyer, R.B.; Klein, H.; Ishaque, B.; et al. Articular joint lubricants during osteoarthritis and rheumatoid arthritis display altered levels and molecular species. PLoS ONE 2015, 10, e0125192. [Google Scholar] [CrossRef] [PubMed]
- Band, P.A.; Heeter, J.; Wisniewski, H.G.; Liublinska, V.; Pattanayak, C.W.; Karia, R.J.; Stabler, T.; Balazs, E.A.; Kraus, V.B. Hyaluronan molecular weight distribution is associated with the risk of knee osteoarthritis progression. Osteoarthr. Cartil. 2015, 23, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Kosinska, M.K.; Liebisch, G.; Lochnit, G.; Wilhelm, J.; Klein, H.; Kaesser, U.; Lasczkowski, G.; Rickert, M.; Schmitz, G.; Steinmeyer, J. A lipidomic study of phospholipid classes and species in human synovial fluid. Arthritis Rheum. 2013, 65, 2323–2333. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Crawford, R.W.; Oloyede, A. Unsaturated phosphatidylcholines lining on the surface of cartilage and its possible physiological roles. J. Orthop. Surg. Res. 2007, 2, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, S.; Banquy, X.; Zappone, B.; Israelachvili, J. Synergistic interactions between grafted hyaluronic acid and lubricin provide enhanced wear protection and lubrication. Biomacromolecules 2013, 14, 1669–1677. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.W.; Banquy, X.; Das, S.; Cadirov, N.; Jay, G.; Israelachvili, J. Effects of molecular weight of grafted hyaluronic acid on wear initiation. J. Acta Biomater. 2014, 10, 1817–1823. [Google Scholar] [CrossRef] [PubMed]
- Banquy, X.; Lee, D.W.; Das, S.; Israelachvili, J. Shear-induced aggregation of mammalian synovial fluid components under boundary lubrication conditions. Adv. Funct. Mater. 2014, 24, 3152–3161. [Google Scholar] [CrossRef]
- Kwiecinski, J.J.; Dorosz, S.G.; Ludwig, T.E.; Abubacker, S.; Cowman, M.K.; Schmidt, T.A. The effect of molecular weight on hyaluronan’s cartilage boundary lubricating ability—Alone and in combination with proteoglycan 4. Osteoarthr. Cartil. 2011, 19, 1356–1362. [Google Scholar] [CrossRef] [PubMed]
- Temple-Wong, M.M.; Ren, S.; Quach, P.; Hansen, B.C.; Chen, A.C.; Hasegawa, A.; D’Lima, D.D.; Koziol, J.; Masuda, K.; Lotz, M.K.; et al. Hyaluronan concentration and size distribution in human knee synovial fluid: Variations with age and cartilage degeneration. Arthritis Res. Ther. 2016, 18, 18. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, M.Y.; Bogatyreva, N.S.; Galzitskaya, O.V. Radius of gyration as an indicator of protein structure compactness. Mol. Biol. 2008, 42, 623–628. [Google Scholar] [CrossRef]
- Mendichi, R.; Šoltés, L.; Giacometti Schieroni, A. Evaluation of radius of gyration and intrinsic viscosity molar mass dependence and stiffness of hyaluronan. Biomacromolecules 2003, 4, 1805–1810. [Google Scholar] [CrossRef] [PubMed]
- Hong, L.; Lei, J. Scaling law for the radius of gyration of proteins and its dependence on hydrophobicity. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 207–214. [Google Scholar] [CrossRef]
- Gebeshuner, I.C.; Drack, M.; Scherge, M. Tribology in biology. Tribology 2008, 2, 200–212. [Google Scholar]
- Seror, J.; Zhu, L.; Goldberg, R.; Day, A.J.; Klien, J. Supramolecular synergy in the boundary lubrication of synovial joints. Nat. Commun. 2015, 6, 6497. [Google Scholar] [CrossRef] [PubMed]
- Wierzcholski, K. Joint cartilage lubrication with phospholipid bilayer. Tribologia 2016, 2, 145–157. [Google Scholar]
- Gadomski, A.; Beldowski, P.; Rubi, J.M.; Urbaniak, W.; Augé, W.K.; Santamaria-Holek, I.; Pawlak, Z. Some conceptual thoughts toward nanoscale oriented friction in a model of articular cartilage. Math. Biosci. 2013, 244, 188–200. [Google Scholar] [CrossRef] [PubMed]
- Gadomski, A.; Beldowski, P.; Augé, W.K.; Hladyszowski, J.; Pawlak, Z.; Urbaniak, W. Toward a governing mechanism of nanoscale articular cartilage (physiologic) lubrication: Smoluchowski-type dynamics in amphiphile proton channels. Acta Phys. Pol. 2013, 44, 1801–1820. [Google Scholar] [CrossRef]
- Augé, W.K. Translamellar dynamics of the surface active phospholipid layer: Proton wave propagation through sphingomyelin raft channels. Cartilage 2013, 4, 131S. [Google Scholar]
- Bełdowski, P.; Gadomski, A.; Wilczyńska, I.; Augé, W.K. Discussion of nanoscale friction—Lubrication effects on model articulating systems. Curr. Top. Biophys. 2013, 36 (Suppl. B), 5–18. [Google Scholar]
- Bełdowski, P.; Winkler, R.G.; Augé, W.K.; Hładyszowski, J.; Gadomski, A. Micelle confined in aqueous environment: Lubrication at the nanoscale and its nonlinear characteristics. In Dynamical Systems: Modelling; Springer Proceedings in Mathematics and Statistics; Springer: Cham, Switzerland, 2016; pp. 73–80. ISBN 978-3-319-42401-9. [Google Scholar]
- Bełdowski, P.; Augé, W.K.; Gadomski, A. Nanoscale friction requirements for the boundary lubrication behavior of model articular systems. In Current Topics in Quantum Biology; Michalak, K., Nawrocka-Bogusz, H., Eds.; Publishing House of Adam Mickiewicz University of Poznań: Poznań, Poland, 2014; pp. 79–93. ISBN 978-83-232-2775-5. [Google Scholar]
- Ermakov, S.; Beletskii, A.; Eismont, O.; Nikolaev, V. Liquid Crystals in Biotribology, Synovial Joint Treatment; Biological and Medicinal Physics, Biomedical Engineering; Springer: Cham, Switzerland, 2016; ISBN 978-3-319-20348-5. [Google Scholar]
- Bełdowski, P.; Gadomski, A.; Jung, S.; Augé, W.K. Hyaluronan crosslinking in synovial fluid as controlled by comprehensive biopolymer elastic diffusion. In Proceedings of the Biophysical Society on the Significance of Knotted Structures for Function of Proteins and Nucleic Acids, Warsaw, Poland, 17–21 September 2014. [Google Scholar]
- Maleki, A.; Kjøniksen, A.-L.; Nyström, B. Effect of pH on the behavior of hyaluronic acid in dilute and semidilute aqueous solutions. Macromol. Symp. 2008, 274, 131–140. [Google Scholar] [CrossRef]
- Dėdinaitė, A. Biomimetic lubrication. Soft Matter 2012, 8, 273–284. [Google Scholar] [CrossRef]
- Hills, B.A. Boundary lubrication in vivo. Proc. Inst. Mech. Eng. Part H 2000, 214, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Greene, G.W.; Banquy, X.; Lee, D.W.; Lowrey, D.D.; Yu, J.; Israelachvili, J. Adaptive mechanically controlled lubrication mechanism found in articular joints. Proc. Natl. Acad. Sci. USA 2011, 108, 5255–5259. [Google Scholar] [CrossRef] [PubMed]
- Matej, D. Boundary cartilage lubrication: Review of current concepts. Wien. Med. Wochenschr. 2014, 164, 88–94. [Google Scholar]
- Nitzan, D.W.; Nitzan, U.; Dan, P.; Yedgar, S. The role of hyaluronic acid in protecting surface-active phospholipids from lysis by exogenous phospholipase A2. Rheumatology 2001, 40, 335–340. [Google Scholar] [CrossRef]
- Wieland, D.C.F.; Degen, P.; Zander, T.; Gayer, S.; Raj, A.; An, J.; Dédinaité, A.; Claesson, P.; Willumeit-Römer, R. Structure of DPPC-hyaluronan interfacial layers—Effects of molecular weight and ion composition. Soft Matter 2016, 12, 729–740. [Google Scholar] [CrossRef] [PubMed]
- Hari, G.G.; Hales, C.A. Chemistry and Biology of Hyaluronan; Elsevier Science: Amsterdam, The Netherlands, 2008; ISBN 9780080472225. [Google Scholar]
- Pasquali-Ronchetti, I.; Quaglino, D.; Mori, G.; Bacchelli, B.; Ghosh, P. Hyaluronan–phospholipid interactions. J. Struct. Biol. 1997, 120, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Kullberg, A.; Ekholm, O.O.; Slotte, J.P. Miscibility of sphingomyelin and phosphatidylcholines in unsaturated phosphatidylcholine bilayers. Biophys. J. 2015, 109, 1907–1916. [Google Scholar] [CrossRef] [PubMed]
- Pathak, P.; London, F. The effect of membrane lipid composition on the formation of lipid ultrananodomains. Biophys. J. 2015, 109, 1630–1638. [Google Scholar] [CrossRef] [PubMed]
- Augé, W.K. Mimicking the respiratory burst myeloperoxidase system of polymorphonuclear neutrophil granulocytes to aid the wound healing behaviors of articular cartilage. Osteoarthr. Cartil. 2012, 20, S147–S148. [Google Scholar] [CrossRef]
- Moghadam, M.N.; Abel-Sayed, P.; Camine, V.M.; Pioletti, D.P. Impact of synovial fluid flow on temperature regulation in knee cartilage. J. Biomech. 2015, 48, 370–374. [Google Scholar] [CrossRef] [PubMed]
- Raj, A.; Wang, M.; Zander, T.; Wieland, D.C.F.; Liu, X.; An, J.; Garamus, V.M.; Willumeit-Römer, R.; Fielden, M.; Claesson, P.M.; et al. Lubrication synergy: Mixture of hyaluronan and dipalmitoylphosphatidylcholine (DPPC) vesicles. J. Colloid Inter. Sci. 2017, 488, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Sorkin, R.; Kampf, N.; Zhu, L.; Klein, J. Hydration lubrication and shear-induced self-healing of lipid bilayer boundary lubricants in phosphatidylcholine dispersions. Soft Matter 2016, 12, 2773–2784. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Liu, C.; Thormann, E.; Dédinaité, A. Hyaluronan and phospholipid association in biolubrication. Biomacromolecules 2013, 14, 4198–4206. [Google Scholar] [CrossRef] [PubMed]
- Rath, E.; Sharfman, Z.T.; Paret, M.; Amar, E.; Drexler, M.; Bonin, N. Hip arthroscopy protocol: Expert opinions on post-operative weight bearing and return to sports guidelines. J. Hip Preserv. Surg. 2017, 23, 60–66. [Google Scholar] [CrossRef] [PubMed]
- Bortel, E.; Charbonnier, B.; Heuberger, R. Development of a synthetic synovial fluid for tribological testing. Lubricants 2015, 3, 664–686. [Google Scholar] [CrossRef]
- Connoly, M.L. Analytical molecular surface calculation. J. Appl. Cryst. 1983, 16, 548–558. [Google Scholar] [CrossRef]
- Richmond, T.J. Solvent accessible surface area and excluded volume in proteins. Analytical equations for overlapping spheres and implications for the hydrophobic effect. J. Mol. Biol. 1984, 178, 63–89. [Google Scholar] [CrossRef]
- Rouse, P.E., Jr. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272. [Google Scholar] [CrossRef]
- Goudoulas, T.B.; Kastrinakis, E.G.; Nychas, S.G.; Papazoglou, L.G.; Kazakos, G.M.; Kosmas, P.V. Rheological study of synovial fluid obtained from dogs: Healthy, pathological, and post-surgery, after spontaneous rupture of cranial cruciate ligament. Ann. Biomed. Eng. 2010, 38, 57–65. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are available from the authors. |


| pH | R2 | μ | |
|---|---|---|---|
| 6.0 | 0.9661 | 0.2021 | 0.152 |
| 7.0 | 1.0000 | 0.0230 | 0.165 |
| 8.0 | 0.9964 | 0.1756 | 0.217 |
| pH | R2 | β |
|---|---|---|
| 6.0 | 0.9493 | 0.6167 |
| 7.0 | 0.9969 | 0.6744 |
| 8.0 | 0.9834 | 1.0932 |
| Atom Types | Type 1 (–CH3) | Type 2 (–CH2–; HCC3) | Type 3 (Aromatic) |
|---|---|---|---|
| Type 1 (–CH3) | |||
| Type 2 (–CH2–; HCC3) | |||
| Type 3 (aromatic) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siódmiak, J.; Bełdowski, P.; Augé, W.K., II; Ledziński, D.; Śmigiel, S.; Gadomski, A. Molecular Dynamic Analysis of Hyaluronic Acid and Phospholipid Interaction in Tribological Surgical Adjuvant Design for Osteoarthritis. Molecules 2017, 22, 1436. https://doi.org/10.3390/molecules22091436
Siódmiak J, Bełdowski P, Augé WK II, Ledziński D, Śmigiel S, Gadomski A. Molecular Dynamic Analysis of Hyaluronic Acid and Phospholipid Interaction in Tribological Surgical Adjuvant Design for Osteoarthritis. Molecules. 2017; 22(9):1436. https://doi.org/10.3390/molecules22091436
Chicago/Turabian StyleSiódmiak, Jacek, Piotr Bełdowski, Wayne K. Augé, II, Damian Ledziński, Sandra Śmigiel, and Adam Gadomski. 2017. "Molecular Dynamic Analysis of Hyaluronic Acid and Phospholipid Interaction in Tribological Surgical Adjuvant Design for Osteoarthritis" Molecules 22, no. 9: 1436. https://doi.org/10.3390/molecules22091436







