Determination of the Bridging Ligand in the Active Site of Tyrosinase
Abstract
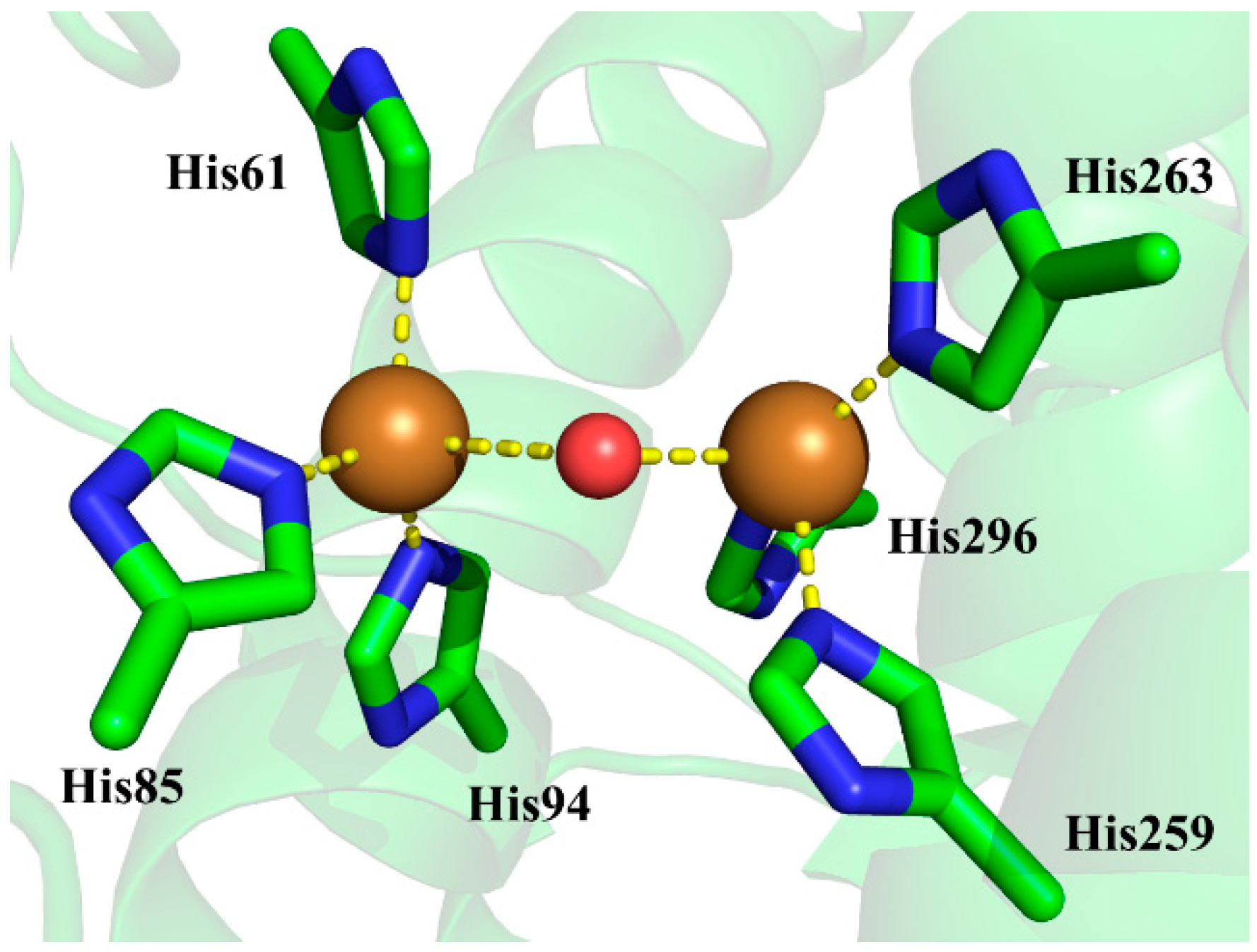
:1. Introduction
2. Methods
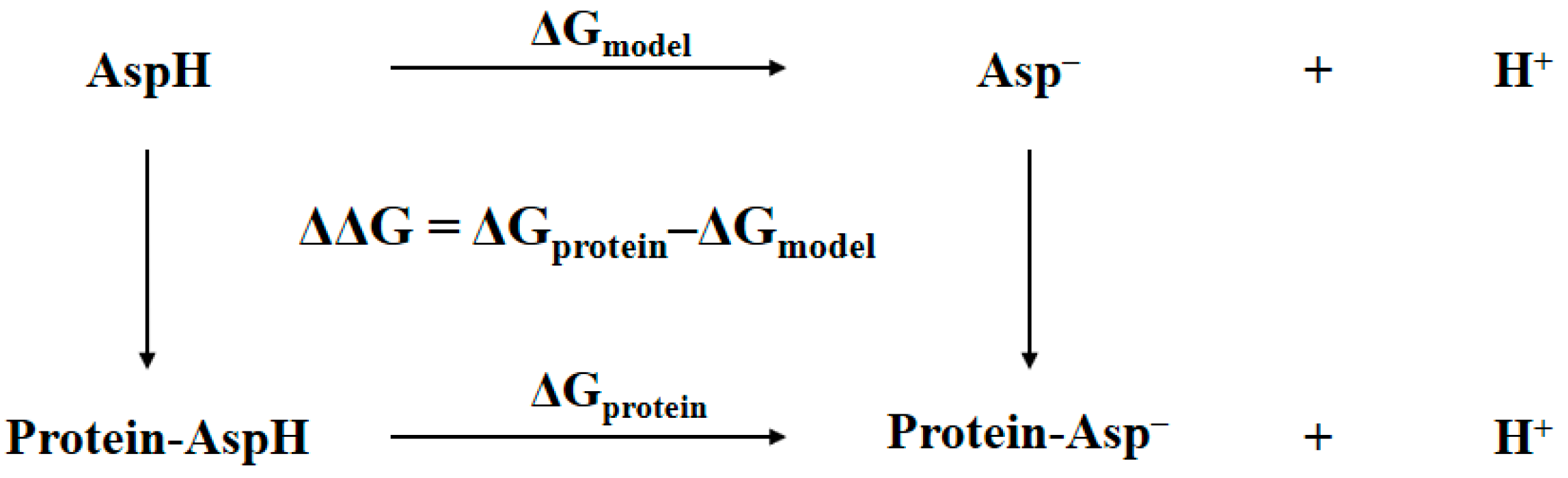
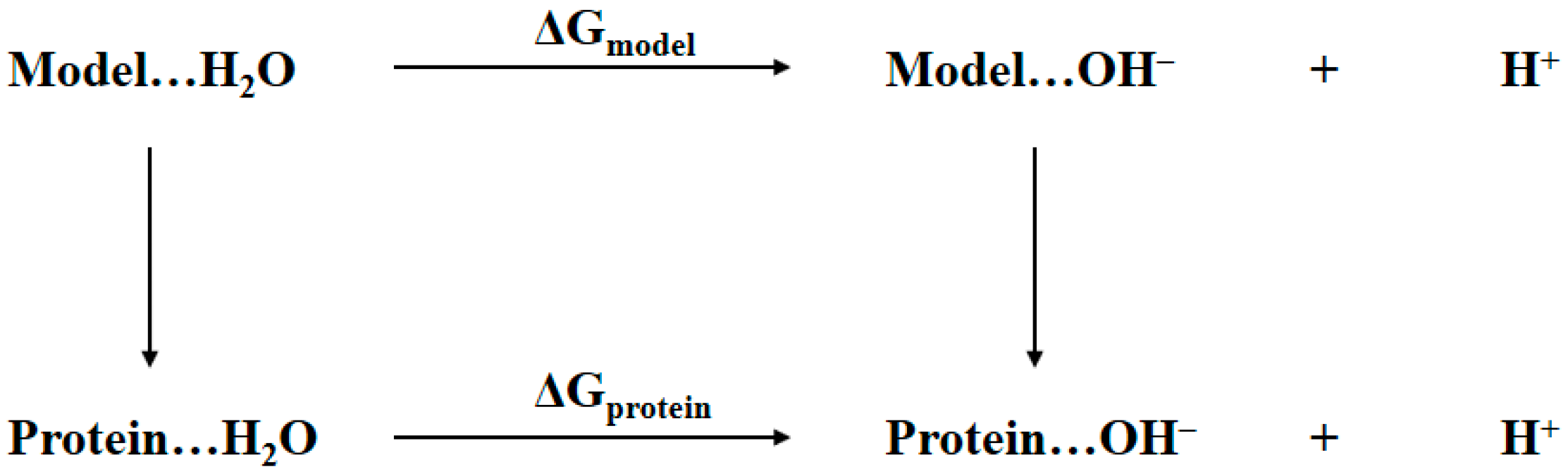
2.1. Thermodynamic Cycle
2.2. QM/MM-PBSA Calculation
2.3. QM Calculation for pKa Determination
3. Results and Discussion
3.1. Charge States of Copper Ions
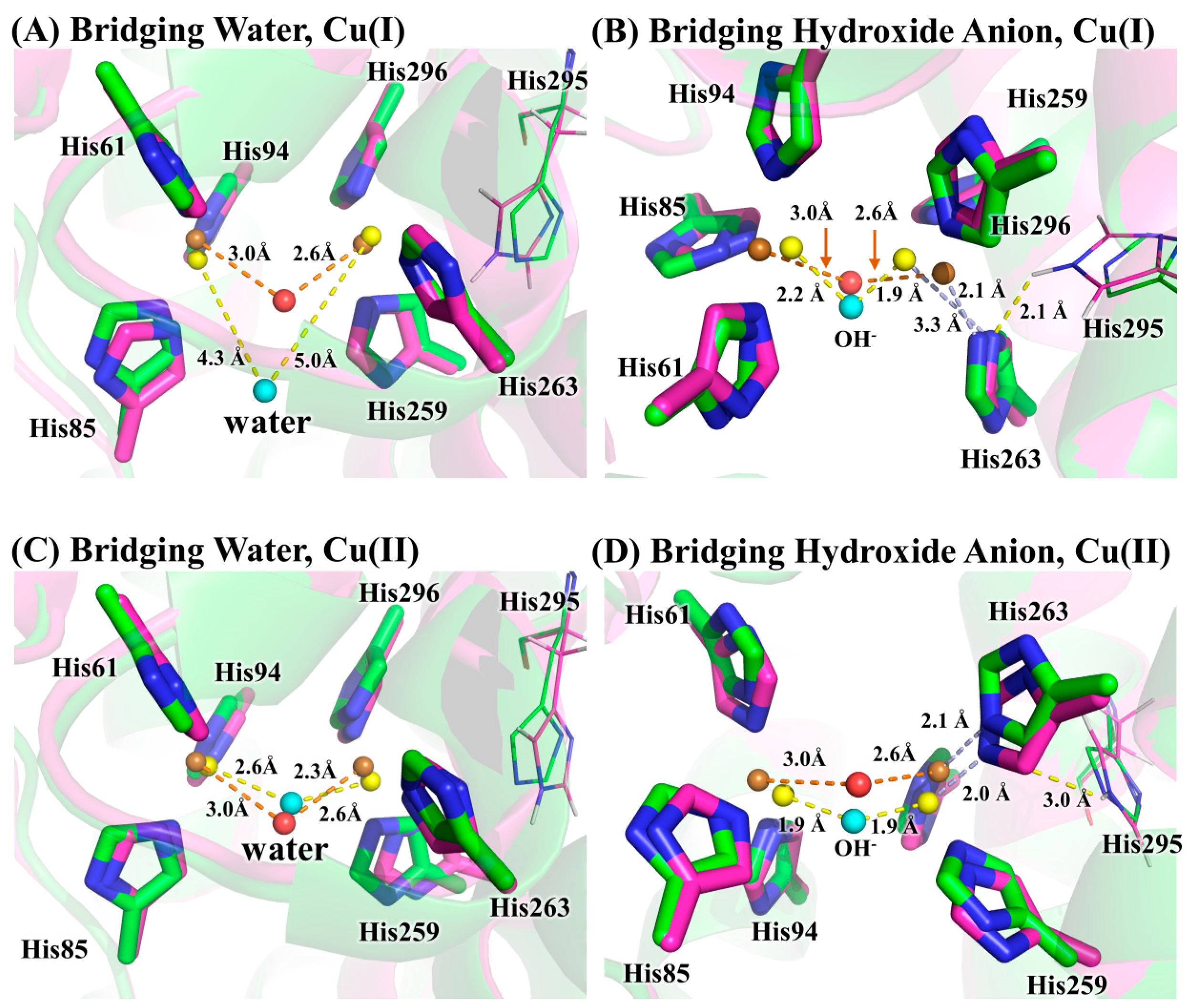
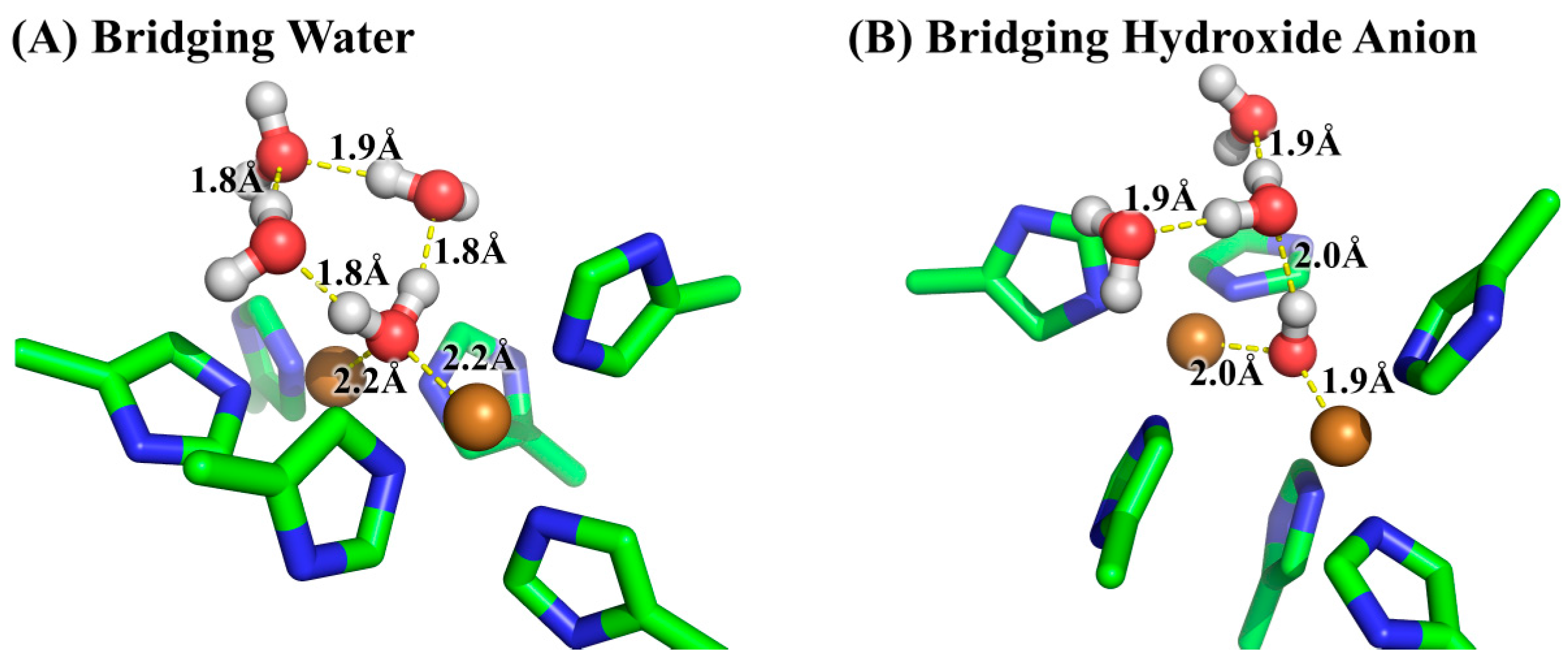
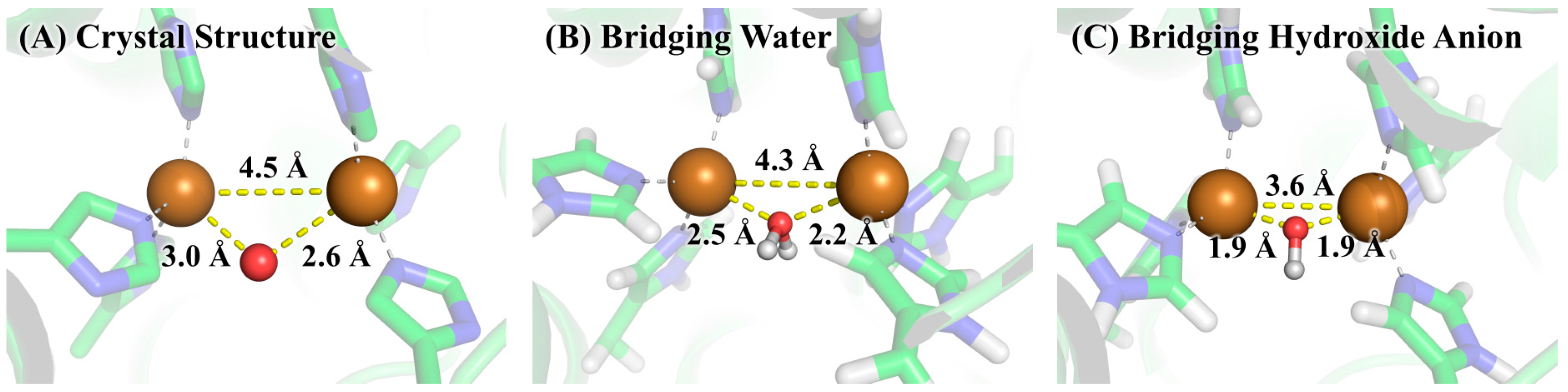
3.2. Determination of Bridging Ligand Identity
3.3. Implication for the Design of Tyrosinase Inhibitors
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Olivares, C.; Solano, F. New insights into the active site structure and catalytic mechanism of tyrosinase and its related proteins. Pigment Cell Melanoma Res. 2009, 22, 750–760. [Google Scholar] [CrossRef] [PubMed]
- Mayer, A.M. Polyphenol oxidases in plants and fungi: Going places? A review. Phytochemistry 2006, 67, 2318–2331. [Google Scholar] [CrossRef] [PubMed]
- Guerrero, A.; Rosell, G. Biorational Approaches for Insect Control by Enzymatic Inhibition. Curr. Med. Chem. 2005, 12, 461–469. [Google Scholar] [CrossRef] [PubMed]
- Gandia-Herrero, F.; Jimenez, M.; Cabanes, J.; Garcia-Carmona, F.; Escribano, J. Tyrosinase inhibitory activity of cucumber compounds: Enzymes responsible for browning in cucumber. J. Agric. Food. Chem. 2003, 51, 7764–7769. [Google Scholar] [CrossRef] [PubMed]
- Ray, K.; Chaki, M.; Sengupta, M. Tyrosinase and ocular diseases: Some novel thoughts on the molecular basis of oculocutaneous albinism type 1. Prog. Retin. Eye Res. 2007, 26, 323–358. [Google Scholar] [CrossRef] [PubMed]
- Asanuma, M.; Miyazaki, I.; Ogawa, N. Dopamine- or L-DOPA-induced neurotoxicity: The role of dopamine quinone formation and tyrosinase in a model of Parkinson’s disease. Neurotox. Res. 2003, 5, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Ni-hang, L.; Hong, L.; Huan-wen, Y. The Influence of Polyphenol Oxidase Inhibitors to the Fluecured Tobacco Polyphenol During Curing. J. Yunnan Agric. Univ. 2007, 1, 015. [Google Scholar]
- Chang, T.S. An updated review of tyrosinase inhibitors. Int. J. Mol. Sci. 2009, 10, 2440–2475. [Google Scholar] [CrossRef] [PubMed]
- Bernard, P.; Berthon, J.Y. Resveratrol: An original mechanism on tyrosinase inhibition. Int. J. Cosmet. Sci. 2000, 22, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Blesa, J.; Trigo-Damas, I.; Quiroga-Varela, A.; Jackson-Lewis, V.R. Oxidative stress and Parkinson’s disease. Front. Neuroanat. 2015, 9, 91. [Google Scholar] [CrossRef] [PubMed]
- Casanola-Martin, G.; Le-Thi-Thu, H.; Marrero-Ponce, Y.; Castillo-Garit, J.; Torrens, F.; Rescigno, A.; Abad, C.; Khan, M. Tyrosinase Enzyme: 1. An Overview on a Pharmacological Target. Curr. Top. Med. Chem. 2014, 14, 1494–1501. [Google Scholar] [CrossRef] [PubMed]
- Ismaya, W.T.; Rozeboom, H.J.; Weijn, A.; Mes, J.J.; Fusetti, F.; Wichers, H.J.; Dijkstra, B.W. Crystal structure of Agaricus bisporus mushroom tyrosinase: Identity of the tetramer subunits and interaction with tropolone. Biochemistry 2011, 50, 5477–5486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simonson, T.; Carlsson, J.; Case, D.A. Proton binding to proteins: pKa calculations with explicit and implicit solvent models. J. Am. Chem. Soc. 2004, 126, 4167–4180. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Sun, B.; Yao, Y.; Liu, J. Fast and Reliable Thermodynamic Approach for Determining the Protonation State of the Asp Dyad. J. Chem. Inf. Model. 2017, 57, 2273–2280. [Google Scholar] [CrossRef] [PubMed]
- Kaukonen, M.; Soderhjelm, P.; Heimdal, J.; Ryde, U. QM/MM-PBSA method to estimate free energies for reactions in proteins. J. Phys. Chem. B 2008, 112, 12537–12548. [Google Scholar] [CrossRef] [PubMed]
- Tsitsanou, K.E.; Hayes, J.M.; Keramioti, M.; Mamais, M.; Oikonomakos, N.G.; Kato, A.; Leonidas, D.D.; Zographos, S.E. Sourcing the affinity of flavonoids for the glycogen phosphorylase inhibitor site via crystallography, kinetics and QM/MM-PBSA binding studies: Comparison of chrysin and flavopiridol. Food Chem. Toxicol. 2013, 61, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Manta, S.; Xipnitou, A.; Kiritsis, C.; Kantsadi, A.L.; Hayes, J.M.; Skamnaki, V.T.; Lamprakis, C.; Kontou, M.; Zoumpoulakis, P.; Zographos, S.E. 3′-Axial CH2OH Substitution on Glucopyranose does not Increase Glycogen Phosphorylase Inhibitory Potency. QM/MM-PBSA Calculations Suggest Why. Chem. Biol. Drug. Des. 2012, 79, 663–673. [Google Scholar] [CrossRef] [PubMed]
- Ryde, U.; Soderhjelm, P. Ligand-Binding Affinity Estimates Supported by Quantum-Mechanical Methods. Chem. Rev. 2016, 116, 5520–5566. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Caldararu, O.; Ryde, U. Protonation States of Homocitrate and Nearby Residues in Nitrogenase Studied by Computational Methods and Quantum Refinement. J. Phys. Chem. B 2017, 121, 8242–8262. [Google Scholar] [CrossRef] [PubMed]
- Chipman, D.M.; Chen, F.W. Cation electric field is related to hydration energy. J. Chem. Phys. 2006, 124. [Google Scholar] [CrossRef] [PubMed]
- Chipman, D.M. Anion electric field is related to hydration energy. J. Chem. Phys. 2003, 118, 9937–9942. [Google Scholar] [CrossRef]
- Liu, J.; Kelly, C.P.; Goren, A.C.; Marenich, A.V.; Cramer, C.J.; Truhlar, D.G.; Zhan, C.-G. Free Energies of Solvation with Surface, Volume, and Local Electrostatic Effects and Atomic Surface Tensions to Represent the First Solvation Shell. J. Chem. Theory Comput. 2010, 6, 1109–1117. [Google Scholar] [CrossRef] [PubMed]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Aqueous solvation free energies of ions and ion-water clusters based on an accurate value for the absolute aqueous solvation free energy of the proton. J. Phys. Chem. B 2006, 110, 16066–16081. [Google Scholar] [CrossRef] [PubMed]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. SM6: A Density Functional Theory Continuum Solvation Model for Calculating Aqueous Solvation Free Energies of Neutrals, Ions, and Solute-Water Clusters. J. Chem. Theory Comput. 2005, 1, 1133–1152. [Google Scholar] [CrossRef] [PubMed]
- Zhan, C.G.; Dixon, D.A. Absolute hydration free energy of the proton from first-principles electronic structure calculations. J. Phys. Chem. A 2001, 105, 11534–11540. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Thapa, B.; Schlegel, H.B. Improved pKa Prediction of Substituted Alcohols, Phenols, and Hydroperoxides in Aqueous Medium Using Density Functional Theory and a Cluster-Continuum Solvation Model. J. Phys. Chem. A 2017, 121, 4698–4706. [Google Scholar] [CrossRef] [PubMed]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. Engl. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Betz, R.M.; Botello-Smith, W.; Cerutti, D.S.; Cheatham, I.; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; et al. AMBER 16; University of California: San Francisco, CA, USA, 2016. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Cieplak, P.; Cornell, W.D.; Bayly, C.; Kollman, P.A. Application of the multimolecule and multiconformational RESP methodology to biopolymers: Charge derivation for DNA, RNA, and proteins. J. Comput. Chem. 1995, 16, 1357–1377. [Google Scholar] [CrossRef]
- Bryantsev, V.S.; Diallo, M.S.; Goddard, W.A. Calculation of solvation free energies of charged solutes using mixed cluster/continuum models. J. Phys. Chem. B 2008, 112, 9709–9719. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Choi, K.-E.; Park, S.J.; Kim, S.Y.; Jee, J.-G. Ensemble-Based Virtual Screening Led to the Discovery of New Classes of Potent Tyrosinase Inhibitors. J. Chem. Inf. Model. 2016, 56, 354–367. [Google Scholar] [CrossRef] [PubMed]
- Hassani, S.; Haghbeen, K.; Fazli, M. Non-specific binding sites help to explain mixed inhibition in mushroom tyrosinase activities. Eur. J. Med. Chem. 2016, 122, 138–148. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Not available. |
| EQM b | dGQM c | GQM d | |
|---|---|---|---|
| water | −3,250,650.3 | 389.7 | −3,250,260.6 |
| hydroxide anion | −3,250,365.7 | 378.2 | −3,249,985.3 |
| proton | N/A | N/A | −270.3 e |
| EQM/MM b | dGQM/MM c | EPBSA d | GQM/MM-PBSA e | ΔG(QM/MM-PBSA) f | ||
|---|---|---|---|---|---|---|
| protein | water | −3,111,906.7 | 354.9 | −4967.8 | −3,116,519.6 | 295.3 |
| hydroxide anion | −3,111,396.4 | 357.4 | −5185.3 | −3,116,224.3 | ||
| model | water | −3,105,710.4 | 350.1 | −463.6 | −3,105,823.9 | 260.9 |
| hydroxide anion | −3,105,646.3 | 344.3 | −260.9 | −3,105,563.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, C.; Huang, W.; Zhao, G.; Wan, X.; Hu, X.; Jin, Y.; Li, J.; Liu, J. Determination of the Bridging Ligand in the Active Site of Tyrosinase. Molecules 2017, 22, 1836. https://doi.org/10.3390/molecules22111836
Zou C, Huang W, Zhao G, Wan X, Hu X, Jin Y, Li J, Liu J. Determination of the Bridging Ligand in the Active Site of Tyrosinase. Molecules. 2017; 22(11):1836. https://doi.org/10.3390/molecules22111836
Chicago/Turabian StyleZou, Congming, Wei Huang, Gaokun Zhao, Xiao Wan, Xiaodong Hu, Yan Jin, Junying Li, and Junjun Liu. 2017. "Determination of the Bridging Ligand in the Active Site of Tyrosinase" Molecules 22, no. 11: 1836. https://doi.org/10.3390/molecules22111836





