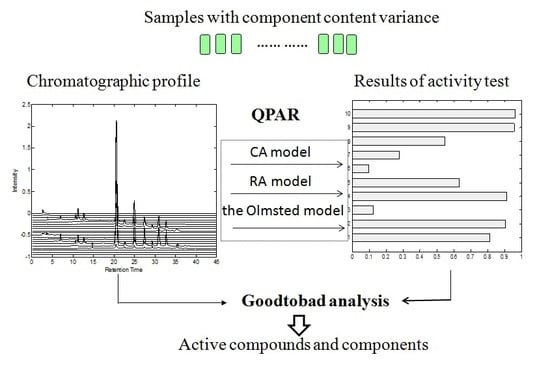
Rapid Screening of Active Components with an Osteoclastic Inhibitory Effect in Herba epimedii Using Quantitative Pattern–Activity Relationships Based on Joint-Action Models
Abstract
:1. Introduction
2. Results and Discussion
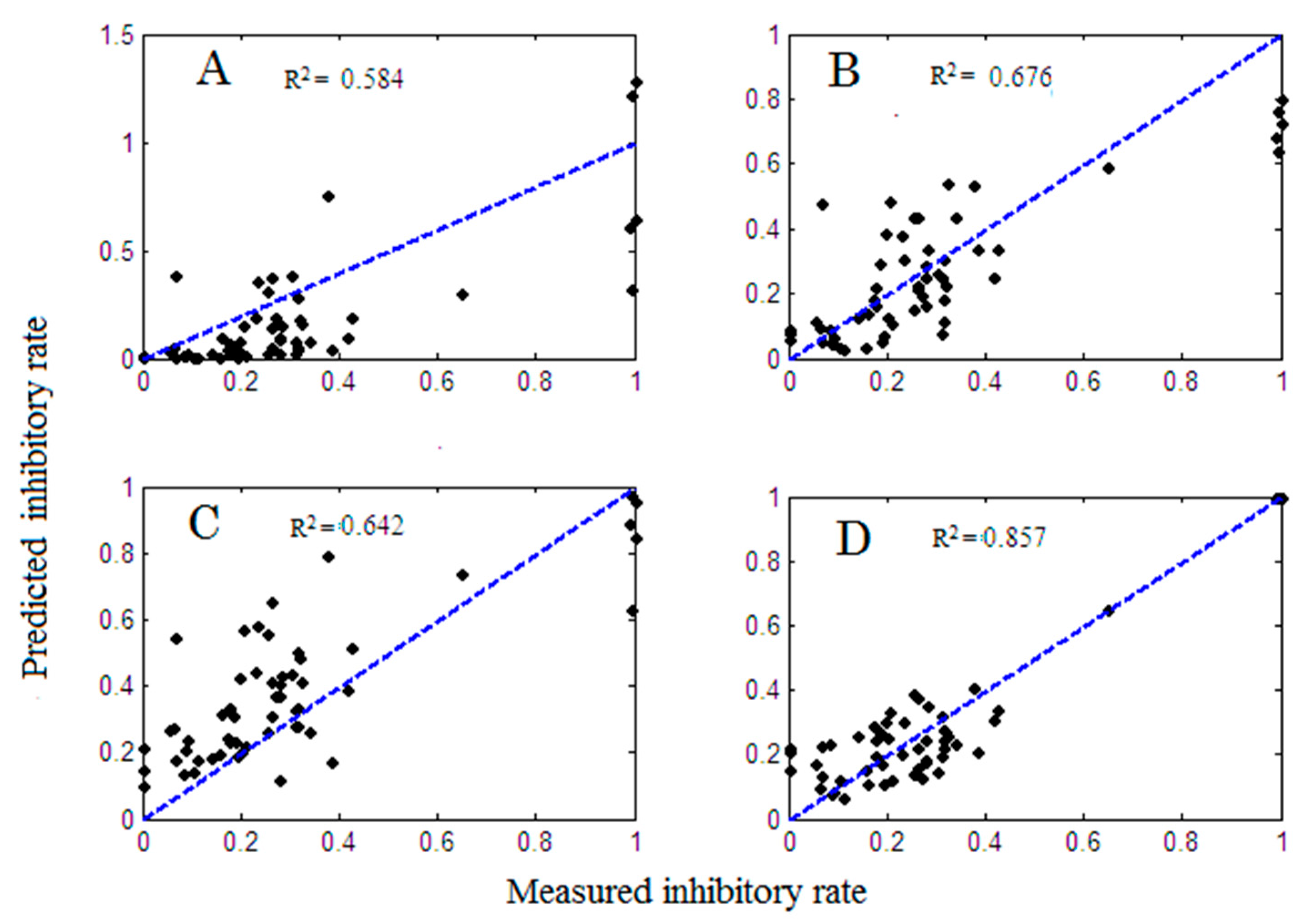
2.1. Model Comparison
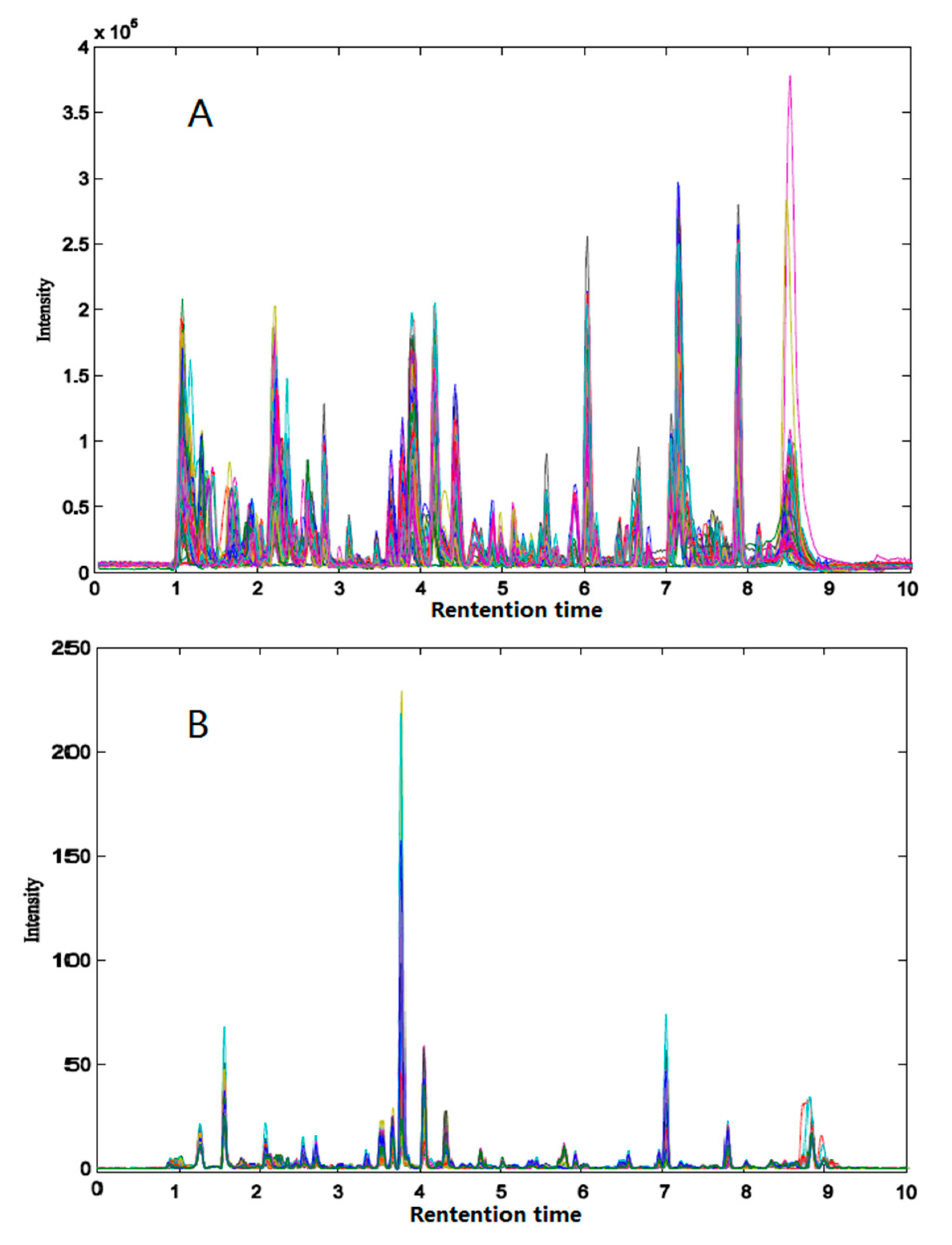
2.2. Chromatographic Profile of Herba epimedii and Feature Extraction
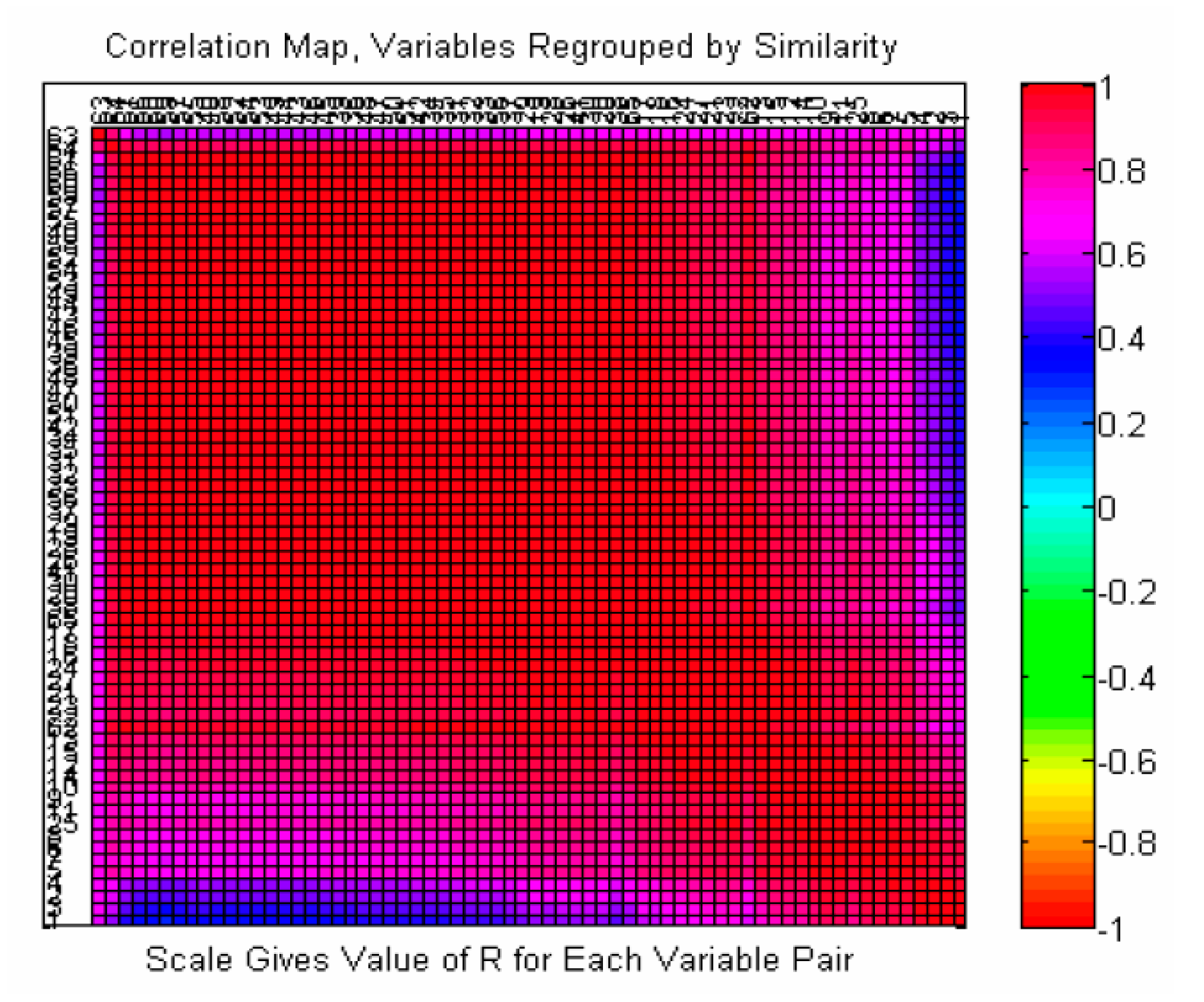
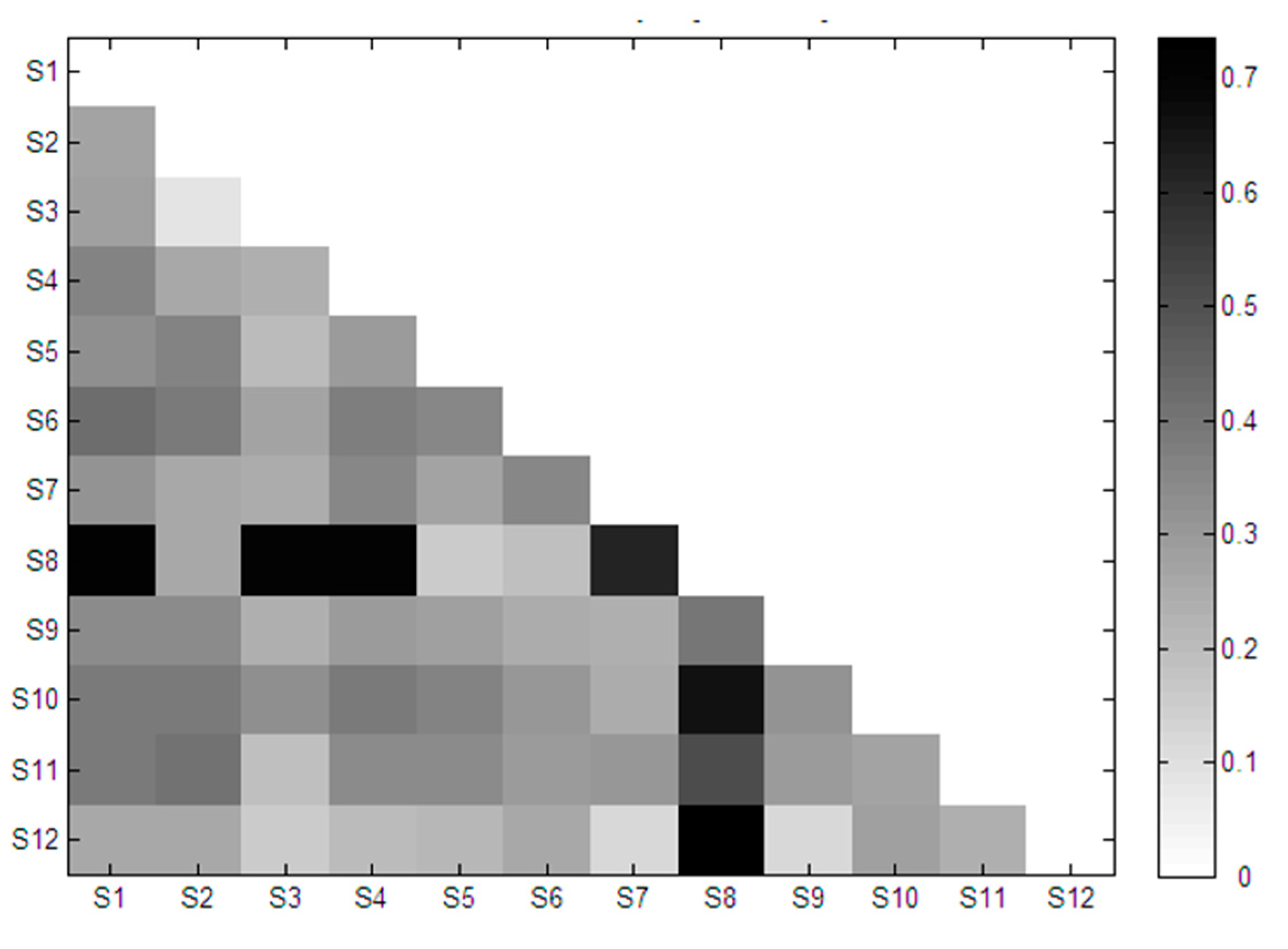
2.3. Similarity Analysis of Extracted Features
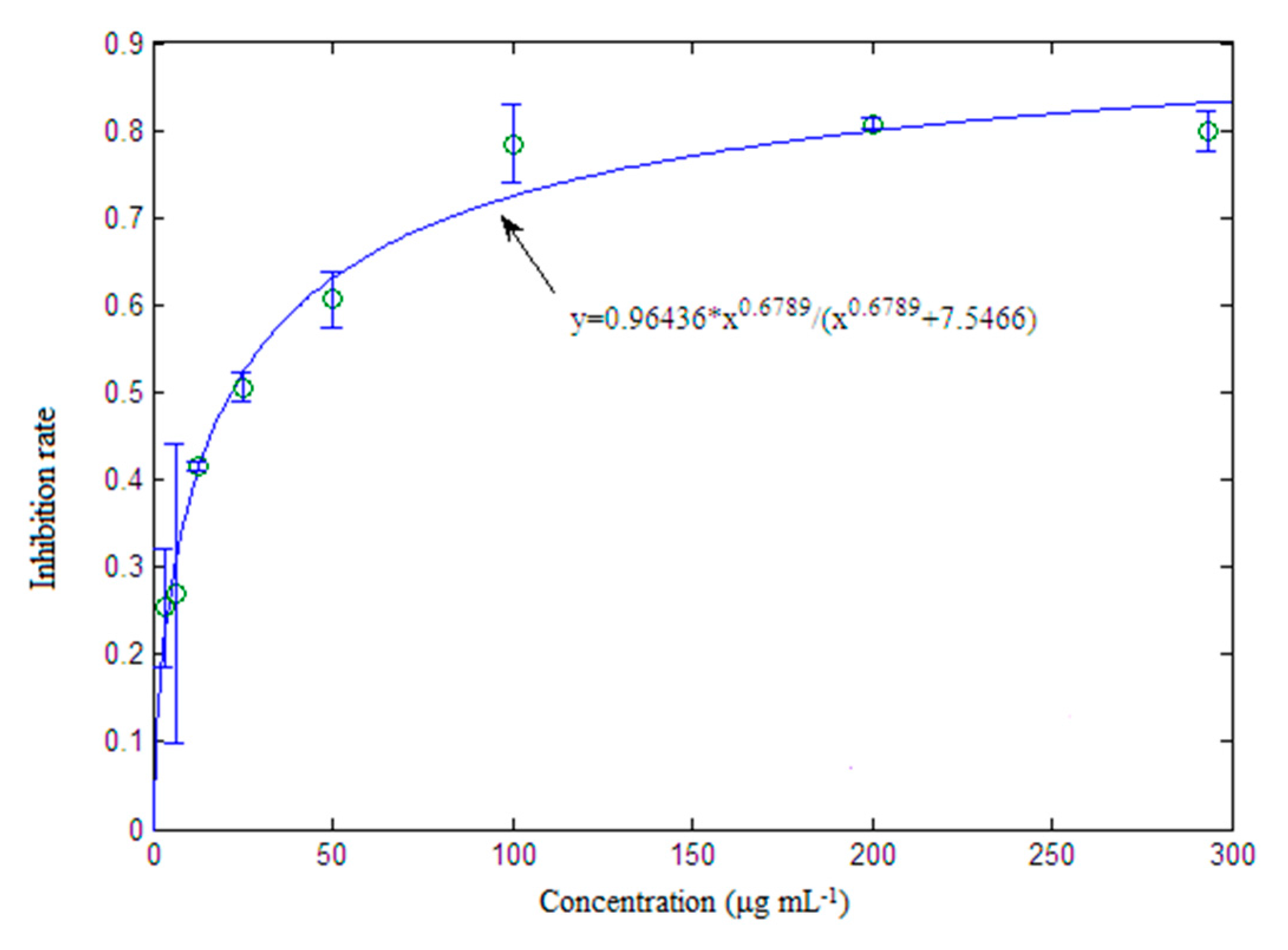
2.4. Inhibition Activity to RAW264.7
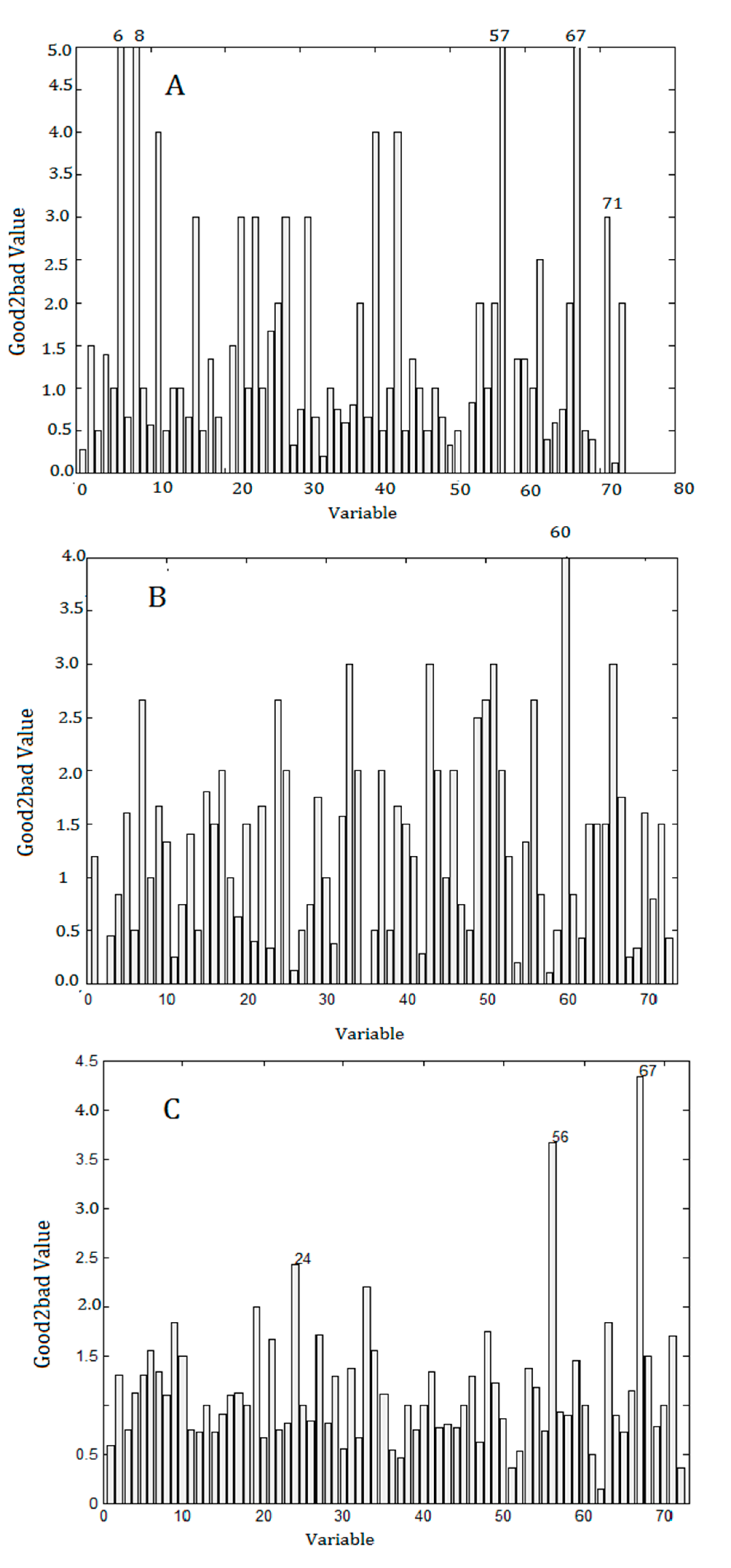
2.5. Results of Data Processing
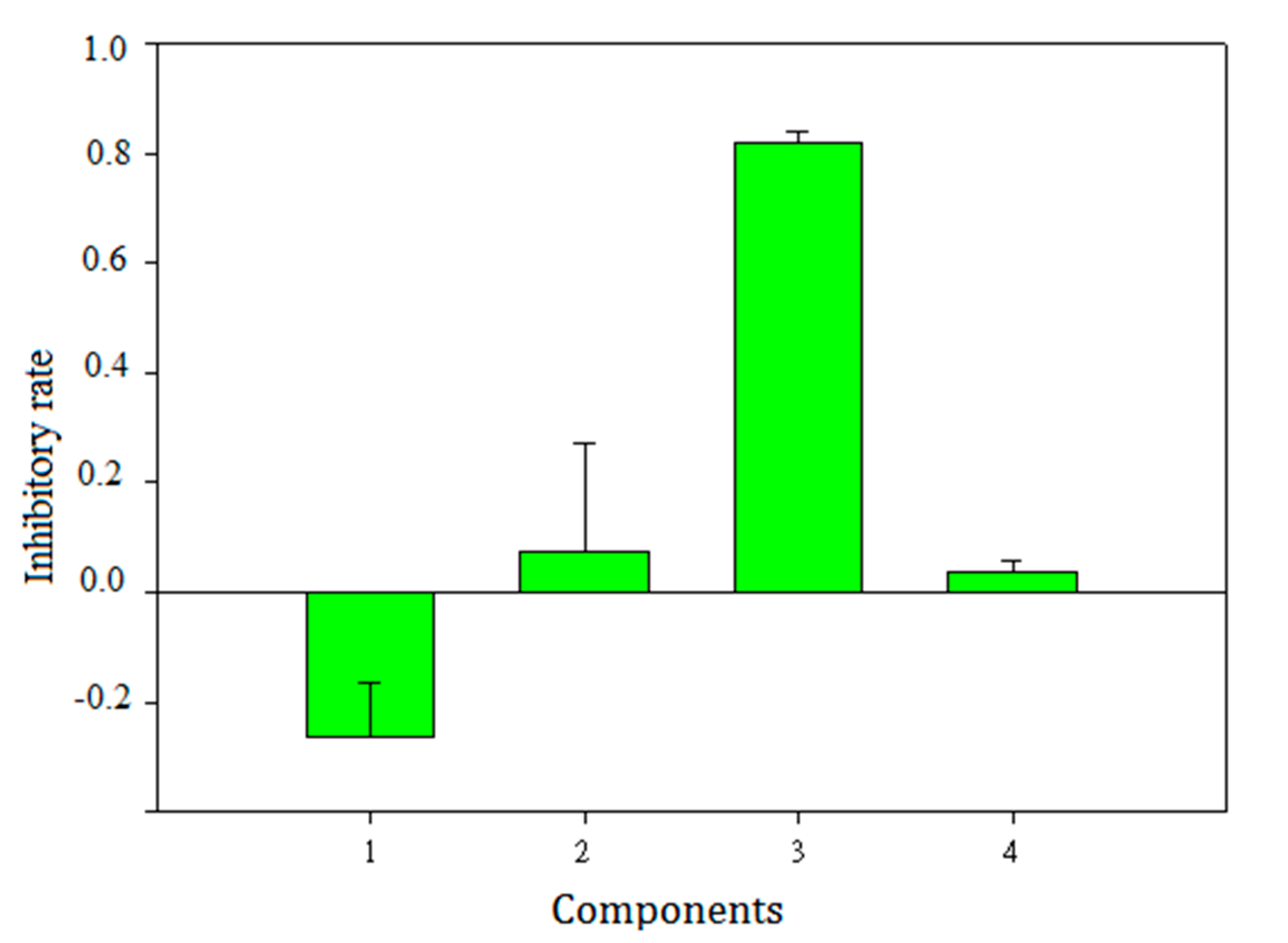
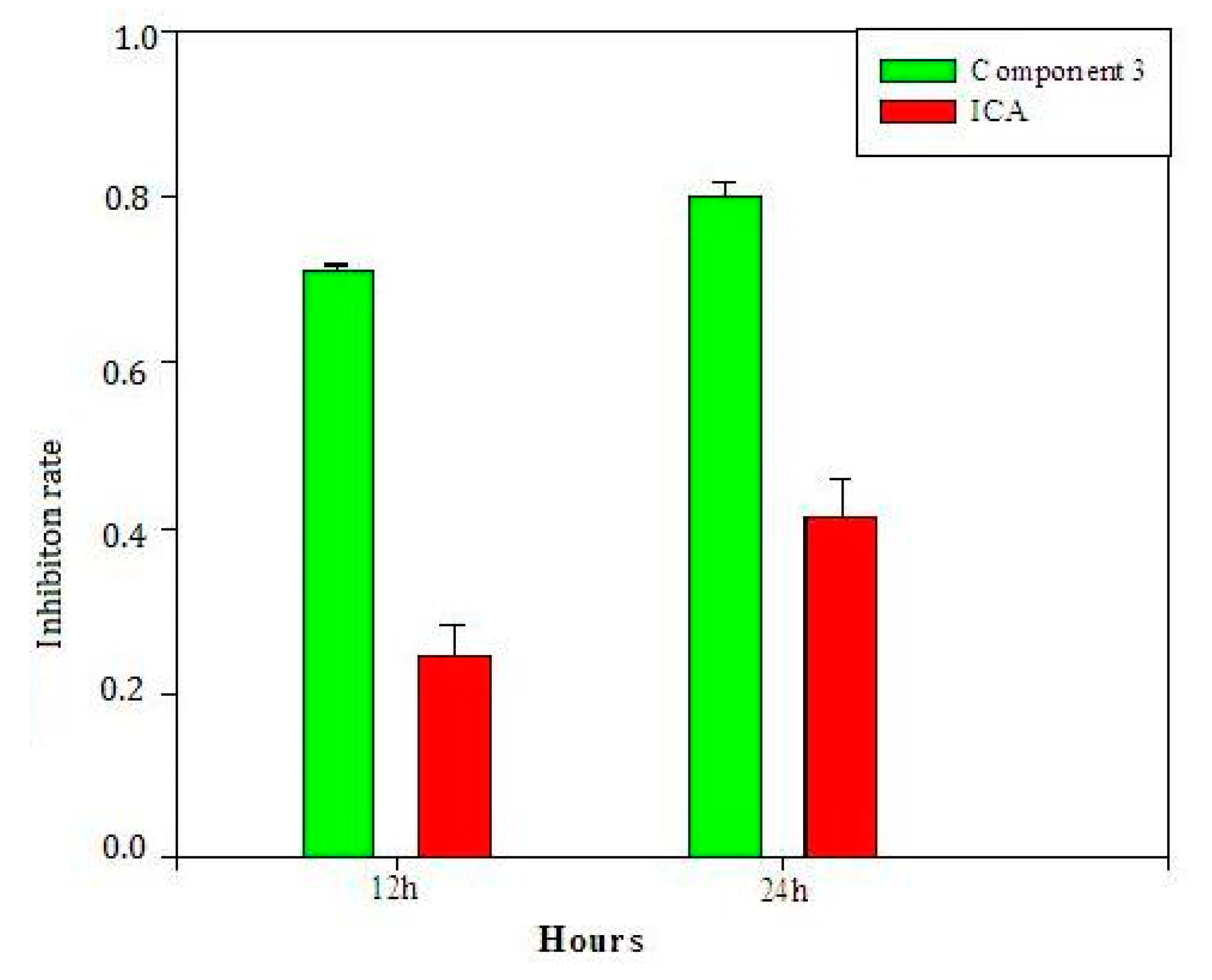
2.6. Validation of Selected Components and Compounds
3. Materials and Methods
3.1. Reagents and Materials
3.2. Sample Preparation
3.2.1. Preparation of Standard Mixtures for Model Comparisons
3.2.2. Preparation of Herba epimedii Pairwise Samples
3.3. Apparatus and Analytical Conditions
3.3.1. Chromatographic Analysis
3.3.2. Q-TOF/MS Analysis
3.4. Activity Test
3.5. Theoretical Basis of Data Analysis
3.5.1. Joint-Action Models
3.5.2. Cassette-Number Evaluation of the Olmstead Model
3.5.3. Good2bad Value Analysis Based on Monte Carlo Sampling
3.6. Bioactive-Component Screening Procedure and Parameter-Setting
3.6.1. Feature Extraction from Chromatographic Profile
3.6.2. Obtain UV Spectrum of Each Compound and Cluster Analysis
3.6.3. Construct Quantitative Pattern–Activity Model Based on Subsets
3.6.4. Good2bad Analysis
3.6.5. Verification
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jiang, M.; Zhang, C.; Cao, H.X.; Chan, K.; Lu, A.P. The role of Chinese medicine in the treatment of chronic diseases in China. Planta Med. 2011, 77, 873–881. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.X.; Gu, W.; Liang, L.; Yan, H.L.; Wang, Y.F.; Bi, Q.; Zhang, T.; Yu, J.; Rao, G.X. Screening for the bioactive constituents of traditional Chinese medicines—Progress and challenges. RSC Adv. 2017, 7, 3089–3100. [Google Scholar] [CrossRef]
- Ghosh, N.; Ali, A.; Ghosh, R.; Das, S.; Mandal, S.C.; Pal, M. Chronic inflammatory diseases: Progress and prospect with Herbal Medicine. Curr. Pharm. Des. 2016, 22, 247–264. [Google Scholar] [CrossRef] [PubMed]
- Li, J.W.H.; Vederas, J.C. Drug discovery and natural products: End of an era or an endless frontier? Science 2009, 325, 161–165. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.C. Kidney toxicity related to herbs and dietary supplements: Online table of case reports. Part 3 of 5 series. Food Chem. Toxicol. 2017, 107 Pt A, 502–519. [Google Scholar] [CrossRef]
- Tarantino, G.; Pezzullo, M.G.; di Minno, M.N.D.; Milone, F.; Pezzullo, L.S.; Milone, M.; Capone, D. Drug-induced liver injury due to “natural products” used for weight loss: A case report. World J. Gastroenterol. 2009, 15, 2414–2417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ng, M.C.H.; Lau, T.Y.; Fan, K.; Xu, Q.S.; Poon, J.; Poon, S.K.; Lam, M.K.; Chau, F.T.; Sze, D.M.Y. Prediction of Radix Astragali immunomodulatory effect of CD80 expression from chromatograms by quantitative pattern-activity relationship. Biomed. Res. Int. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Koehn, F.E.; Carter, G.T. The evolving role of natural products in drug discovery. Nat. Rev. Drug Discov. 2005, 4, 206–220. [Google Scholar] [CrossRef] [PubMed]
- Rauf, A.; Uddin, G.; Khan, H.; Arfan, M.; Siddiqui, B.S. Bioassay-guided isolation of antibacterial constituents from Diospyros lotus roots. Nat. Prod. Res. 2016, 30, 426–428. [Google Scholar] [CrossRef] [PubMed]
- Erenler, R.; Meral, B.; Sen, O.; Elmastas, M.; Aydin, A.; Eminagaoglu, O.; Topcu, G. Bioassay-guided isolation, identification of compounds from Origanum rotundifolium and investigation of their antiproliferative and antioxidant activities. Pharm. Biol. 2017, 55, 1646–1653. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Qian, F.; Tan, J.J.; Guo, F.J.; Kulka, M.; Xu, J.W.; Li, Y.M. Bioassay-guided isolation of bisepoxylignans from the flower buds of Magnolia biondii Pamp and their antiallergic effects. RSC Adv. 2017, 7, 34236–34243. [Google Scholar] [CrossRef]
- Zhao, C.X.; Yuan, D.L.; Chan, H.Y.; Chau, F.T.; Liu, L.Q.; Tan, X.Y.; Wang, X.M.; Liang, Y.Z. Rapid screening of antioxidant active constituents from Puerariae Lobatae Radix based on the investigation of quantitative patteren-activity relationship. Curr. Anal. Chem. 2015, 11, 265–272. [Google Scholar] [CrossRef]
- Hu, X.Q.; Sun, Y.; Lau, E.; Zhao, M.; Su, S.B. Advances in synergistic combinations of Chinese herbal medicine for the treatment of cancer. Curr. Cancer Drug Targets 2016, 16, 346–356. [Google Scholar] [CrossRef] [PubMed]
- Yuliana, N.D.; Khatib, A.; Verpoorte, R.; Choi, Y.H. Comprehensive extraction method integrated with NMR metabolomics: A new bioactivity screening method for plants, adenosine A1 receptor binding compounds in orthosiphon stamineus benth. Anal. Chem. 2011, 83, 6902–6906. [Google Scholar] [CrossRef] [PubMed]
- Chau, F.T.; Chan, H.Y.; Cheung, C.Y.; Xu, C.J.; Liang, Y.; Kvalheim, O.M. Recipe for uncovering the bioactive components in herbal medicine. Anal. Chem. 2009, 81, 7217–7225. [Google Scholar] [CrossRef] [PubMed]
- Cabrera, A.C.; Prieto, J.M. Application of artificial neural networks to the prediction of the antioxidant activity of essential oils in two experimental in vitro models. Food Chem. 2010, 118, 141–146. [Google Scholar] [CrossRef]
- Cai, W.S.; Li, Y.K.; Shao, X.G. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra. Chemom. Intell. Lab. Syst. 2008, 90, 188–194. [Google Scholar] [CrossRef]
- Tistaert, C.; Dejaegher, B.; Heyden, Y.V. Chromatographic separation techniques and data handling methods for herbal fingerprints: A review. Anal. Chim. Acta 2011, 690, 148–161. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.D.; Dong, X.L. Improved partial least squares regression for rapid determination of reducing sugar of potato flours by near infrared spectroscopy and variable selection method. J. Food Meas. Charact. 2014, 9, 95–103. [Google Scholar] [CrossRef]
- Chou, T.C.; Talalay, P. Quantitative analysis of dose-effect relationships: The combined effects of multiple drugs or enzyme inhibitors. Adv. Enzym. Regul. 1984, 22, 27–55. [Google Scholar] [CrossRef]
- Chou, T.C. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in drug combination studies. Pharmacol. Rev. 2006, 58, 621–681. [Google Scholar] [CrossRef] [PubMed]
- Kovačević, S.Z.; Tepić, A.N.; Jevrić, L.R.; Podunavac-Kuzmanović, S.O.; Vidović, S.S.; Šumić, Z.M.; Ilin, Ž.M. Chemometric guidelines for selection of cultivation conditions influencing the antioxidant potential of beetroot extracts. Comput. Electron. Agric. 2015, 118, 332–339. [Google Scholar] [CrossRef]
- Gadagkar, S.R.; Call, G.B. Computational tools for fitting the Hill equation to dose—Response curves. J. Pharmacol. Toxicol. Methods 2015, 71, 68–76. [Google Scholar] [CrossRef] [PubMed]
- Drescher, K.; Boedeker, W. Assessment of the combined effects of substances: The relationship between concentration addition and independent action. Biometrics 1995, 51, 716–730. [Google Scholar] [CrossRef]
- Feron, V.; Groten, J. Toxicological evaluation of chemical mixtures. Food Chem. Toxicol. 2002, 40, 825–839. [Google Scholar] [CrossRef]
- Backhaus, T.; Arrhenius, Å.; Blanck, H. Toxicity of a mixture of dissimilarly acting substances to natural algal communities: Predictive power and limitations of independent action and concentration addition. Environ. Sci. Technol. 2004, 38, 6363–6370. [Google Scholar] [CrossRef] [PubMed]
- Diaz, F.J.; Mcdonald, P.R.; Pinter, A.; Chaguturu, R. Measuring and statistically testing the size of the effect of a chemical compound on a continuous in vitro pharmacological response through a new statistical model of response detection limit. J. Biopharm. Stat. 2015, 25, 757–780. [Google Scholar] [CrossRef] [PubMed]
- Olmstead, A.W.; Leblanc, G.A. Toxicity assessment of environmentally relevant pollutant mixtures using a heuristic model. Integr. Environ. Assess. Manag. 2005, 1, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.S.; He, M.C.; Chen, M.H.; Chen, Z.Q.; Yang, F.; Wang, H.B.; Zhang, J.; He, W. Icariin stimulates osteogenic differentiation of rat bone marrow stromal stem cells by increasing TAZ expression. Biomed. Pharmacother. 2017, 91, 581–589. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.H.; Mao, Z.; He, S.C.; Zhan, Y.R.; Ning, R.; Liu, W.; Yan, B.F.; Yang, J. Icariin protects against glucocorticoid induced osteoporosis, increases the expression of the bone enhancer DEC1 and modulates the PI3K/Akt/GSK3b/b-catenin integrated signaling pathway. Biochem. Pharmacol. 2017, 136, 109–121. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Guo, Z.M.; Jin, Y.; Zhang, X.L.; Wang, L.; Xue, X.Y.; Liang, X.M. Identification of prenyl flavonoid glycosides and phenolic acids in Epimedium koreanum Nakai by Q-TOF-MS combined with selective enrichment on “click oligo (ethylene glycol)” column. J. Pharm. Biomed. Anal. 2010, 51, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Zhang, C.J.; Wang, X. Cytotoxic Effects of Flavonol Glycosides and Nonflavonoid Constituents of Epimedium koreanum on Primary Osteoblasts. Pharm. Biol. 2008, 46, 185–190. [Google Scholar] [CrossRef]
- Hsieh, T.P.; Sheu, S.Y.; Sun, J.S.; Chen, M.H. Icariin inhibits osteoclast differentiation and bone resorption by suppression of MAPKs/NF-κB regulated HIF-1α and PGE(2) synthesis. Phytomedicine 2011, 18, 176–185. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.X.; Liu, Y.Q.; Wang, L.; Xiao, H.B. Screening of bioactive components in epimedium for osteoporosis treatment by model population analysis. Acta Pharm. Sin. 2012, 47, 1205–1209. [Google Scholar]
- Zhai, Y.K.; Chen, K.M.; Ge, B.F.; Ma, H.P.; Ming, L.G.; Cheng, G.Z. The changes of iNOS and NO in the osteogenic differentiation process of rat bone marrow stromal cells promoted by icariside II. Acta Pharm. Sin. 2011, 46, 383–389. [Google Scholar]
- Liu, Y.Q.; Yang, Q.X.; Cheng, M.C.; Xiao, H.B. Synergistic inhibitory effect of Icariside II with Icaritin from Herba epimedii on pre-osteoclastic. Phytomedicine 2014, 21, 1633–1637. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Fang, K. A note on uniform distribution and experimental design. Kexue Tongbao 1981, 26, 485–489. [Google Scholar]
- Qin, L.T.; Liu, S.S.; Zhang, J.; Xiao, Q.F. A novel model integrated concentration addition with independent action for the prediction of toxicity of multi-component mixture. Toxicology 2011, 280, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Varmuza, K.; Karlovits, M.; Demuth, W. Spectral similarity versus structural similarity: Infrared spectroscopy. Anal. Chim. Acta 2003, 490, 313–324. [Google Scholar] [CrossRef]
- Johnson, S.C. Hierarchical clustering schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Li, H.D.; Liang, Y.Z.; Xu, Q.S.; Cao, D.S. Model population analysis for variable selection. J. Chemom. 2010, 24, 418–423. [Google Scholar] [CrossRef]
- Yang, L.; Yang, Q.X.; Yang, S.H.; Wang, J.J.; Hou, Y.; Wang, B.X.; Tang, Q.; Pan, X.J. Application of near infrared spectroscopy to detect mould contamination in tobacco. J. Near Infrared Spectrosc. 2015, 23, 391–400. [Google Scholar] [CrossRef]
- Smith, C.A.; Elizabeth, J.; O’Maille, G.; Abagyan, R.; Siuzdak, G. XCMS: Processing mass spectrometry data for metabolite profiling using nonlinear peak alignment, matching, and identification. Anal. Chem. 2006, 78, 779–787. [Google Scholar] [CrossRef] [PubMed]
- Sales, C.; Cervera, M.I.; Gil, R.; Portolés, T.; Pitarch, E.; Beltran, J. Quality classification of Spanish olive oils by untargeted gas chromatography coupled to hybrid quadrupole-time of flight mass spectrometry with atmospheric pressure chemical ionization and metabolomics-based statistical approach. Food Chem. 2017, 216, 365–373. [Google Scholar] [CrossRef] [PubMed]
- Ugray, Z.; Leon, L.; John, P.; Fred, G.; James, K.; Rafael, M. Scatter search and local NLP solvers: A multistart framework for global optimization. Inf. J. Comput. 2007, 19, 328–340. [Google Scholar] [CrossRef]
- Yang, Q.X.; Wang, L.; Zhang, L.X.; Xiao, H.B. Baohuoside I production through enzyme hydrolysis and parameter optimization by using response surface and subset selection. J. Mol. Catal. B Enzym. 2013, 90, 132–138. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
| Standards | Name | EC5 | EC10 | EC20 | EC30 | EC40 | EC50 |
|---|---|---|---|---|---|---|---|
| 1 | epimedin A | 8.11 | 41.00 | 238.09 | 766.50 | 1998.72 | 4816.47 |
| 2 | epimedin B | 7.14 | 19.86 | 60.32 | 126.22 | 231.21 | 402.92 |
| 3 | epimedin C | 0.02 | 0.52 | 18.53 | 199.07 | 1394.17 | 8318.58 |
| 4 | icariin | 0.91 | 3.24 | 12.80 | 31.91 | 67.48 | 134.17 |
| 5 | baohuoside I | 13.77 | 21.32 | 34.26 | 46.95 | 60.79 | 77.06 |
| 6 | icartin | 1.90 | 4.73 | 12.73 | 24.56 | 42.09 | 69.02 |
| No. a | M− | RT (min) | Data Source | Model | Compounds |
|---|---|---|---|---|---|
| 6 | 448.1861 | 1.68 | DAD | CA | NA b |
| 8 | 609.0456 | 1.80 | DAD | CA | NA |
| 11 | 564.4197, 627.4082 | 2.39 | TIC | RA/CA | NA |
| 33 | 661.2183, 724.2124 | 5.12 | TIC | RA | Icarisoside B |
| 50 | 659.2383, 722.2349 | 7.16 | TIC | RA | 2″-O-Rhamnosyl icariside II |
| 56 | 675.2338, 738.2297 | 6.94 | DAD | Olmstead | Sagittatoside A |
| 57 | 659.2383, 722.2349 | 7.04 | DAD | CA | 2″-O-Rhamnosyl icariside II |
| 60 | 717.2413, 780.2374 | 7.50 | DAD | RA | NA |
| 67 | 513.1794, 576.1794 | 7.90 | DAD | Olmsted/CA/PLS | Baohuoside-I |
| Mixtures b | Standards (μg/mL) a | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | EC5 | EC10 | EC20 | EC30 | EC40 | EC50 |
| 2 | EC10 | EC30 | EC50 | EC5 | EC20 | EC40 |
| 3 | EC20 | EC50 | EC10 | EC40 | EC5 | EC30 |
| 4 | EC30 | EC5 | EC40 | EC10 | EC50 | EC20 |
| 5 | EC40 | EC20 | EC5 | EC50 | EC30 | EC10 |
| 6 | EC50 | EC40 | EC30 | EC20 | EC10 | EC5 |
| 7 | EC50 | EC50 | EC50 | EC50 | EC50 | EC50 |
| 8 | EC5 | EC5 | EC5 | EC5 | EC5 | EC5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, X.-Y.; Wang, M.; Lei, S.; Yang, Q.-X.; Liu, Y.-Q. Rapid Screening of Active Components with an Osteoclastic Inhibitory Effect in Herba epimedii Using Quantitative Pattern–Activity Relationships Based on Joint-Action Models. Molecules 2017, 22, 1767. https://doi.org/10.3390/molecules22101767
Yuan X-Y, Wang M, Lei S, Yang Q-X, Liu Y-Q. Rapid Screening of Active Components with an Osteoclastic Inhibitory Effect in Herba epimedii Using Quantitative Pattern–Activity Relationships Based on Joint-Action Models. Molecules. 2017; 22(10):1767. https://doi.org/10.3390/molecules22101767
Chicago/Turabian StyleYuan, Xiao-Yan, Meng Wang, Sheng Lei, Qian-Xu Yang, and Yan-Qiu Liu. 2017. "Rapid Screening of Active Components with an Osteoclastic Inhibitory Effect in Herba epimedii Using Quantitative Pattern–Activity Relationships Based on Joint-Action Models" Molecules 22, no. 10: 1767. https://doi.org/10.3390/molecules22101767