1. Introduction
Quantum chemical calculations provide a powerful tool to investigate molecular properties and therefore support the interpretation of experimental findings. This applies especially to NMR chemical shieldings, as these contain a wealth of structural information that is, however, only indirectly related to the molecular structure itself. Nevertheless, in the interplay of theory and experiment, detailed structural information can be obtained by computing and comparing the molecular structure and the associated NMR parameters. In recent years, several studies have demonstrated that NMR chemical shifts can be calculated quantitatively using highly accurate methods [
1–
3]. For
19F chemical shieldings, for example, which range from about −200 to +500 ppm, Harding
et al. presented a detailed benchmark study [
4]: For the level of electron correlation they find, that compared to CCSD(T), HF leads to 10–20 ppm deviation and MP2 leads to about 5 ppm deviation. With respect to the shieldings obtained at the CCSD(T)/13s9p4d3f level of theory, basis set errors of about 10 ppm occur when the tzp basis is used, about 3 ppm when qz2p is used, and less than 1 ppm when the pz3d2f basis set is used. Furthermore, vibrational corrections range between −5 and −21 ppm while temperature corrections are typically one order of magnitude smaller (−0.2 to −2.9 ppm) and are treated in similar quality on HF and MP2 level of theory. In related studies, similar observations were made for
13C,
17O and
15N chemical shieldings [
1,
2,
5].
The possibility to calculate zero-point vibrational effects and temperature corrections on NMR chemical shieldings also allows to predict secondary isotope shifts on chemical shieldings Δ
σ via Δ
σ =
σl −
σh. These shifts occur when a lighter nucleus
l different from the resonant one is substituted by a heavier isotope
h [
6]. If this effect is calculated using quantum chemical methods, it has to be noted that the electronic Schrödinger equation in the framework of the Born–Oppenheimer approximation is independent of the nuclear masses. Thus, one has to consider the nuclear Schrödinger equation, where isotope effects occur as vibrational and rotational effects [
2,
7]. Since the average positions of the nuclei do not change under change of masses of the nuclei in the harmonic-oscillator model, at least a cubic force field model has to be considered [
8–
10] when isotope effects on chemical shieldings are computed.
In order to calculate isotope shifts, several theoretical approaches have been propsed in the past [
11–
13]. In this work, we apply vibrational perturbation theory of second order (VPT2 [
14]), which allows to include vibrational, temperature, and rotational corrections. In the framework of VPT2 the vibrationally averaged isotropic shieldings are obtained as:
On the right hand side appears the isotropic shielding
σ(
re) at the equilibrium geometry
re, the sum of all derivatives of the shielding with respect to the normal coordinates
times the mean displacements of the nuclei 〈
Qr〉 and the sum of all second derivatives
times the mean-square displacements of the nuclei 〈
QrQs〉 with respect to the normal coordinates. The mean and the mean-square displacements are given by the following equations:
Here ωr denotes the vibrational frequencies, krss the cubic force constant, T the temperature, Iαα the momentum of inertia with respect to the α'th principal axis and
the first coefficient in the expansion of Iαα with respect to the normal coordinates.
While calculations of secondary isotope shifts are far from routine applications of quantum chemical methods, previous work has shown that for small molecular systems these calculations can yield quantitative results, provided the correct treatment of vibrational effects on nuclear shieldings is used [
3]. The focus of this study was on the secondary isotope effects on methanol for which it was not only demonstrated that highly accurate ab-initio methods yield quantitative results, but that the secondary isotope shifts could even be reproduced in acceptable agreement with experimental values at a very cost effective level of theory (namely Hartree–Fock) owing to systematic cancellation of errors. In this work, we investigate whether and how the calculation of secondary isotope shifts on NMR chemical shieldings can be applied to identify different stereoisomers using electronic structure methods. After discussing computational details, we present a benchmark study for fluroethane, a compound that is small enough to carry out high level CCSD(T) calculations. Note that here, we focus on quantifying the different sources of error from method, basis set and treatment of virbrational- and temperature effects by comparison to the highest available level, rather than by comparison to experimental values.
As an example, for which quantum chemical calculations can actually resolve ambiguities in the literature, we would like to revisit in the second part of this work one of the first studies in which various effects on secondary isotope shifts on NMR chemical shieldings were systematically investigated. Lambert
et al. [
15] experimentally investigated secondary isotope effects on NMR chemical shieldings on
endo-2-fluoronorbornanes and fluorocyclohexanes in order to identify major influences on secondary isotope shifts. Especially the results for the
endo-2-fluoronorbornanes are interesting as our results [
16] suggest that in contrast to what has been assumed by Lambert
et al., the synthesis chosen does not lead to the desired
endo-2-fluoronorbornanes. Instead, mixtures of
exo-2-fluoronorbornanes are obtained with deuterium nuclei bound to the 3- and 7-carbon atom.
2. Computational Details
All calculations were carried out using the CFOUR program package [
17] where vibrational averaged nuclear shieldings are calculated as follows:
Given the molecular geometry as obtained from a well converged geometry optimization, the nuclear shieldings and the harmonic force field are calculated. In order to compute the first and second derivative of the nuclear shieldings with respect to the normal coordinates as well as the cubic force field numerically, the nuclei of the molecule have to be displaced along the normal coordinates and at each geometry the nuclear shieldings and the quadratic force field are determined. Subsequently, the vibrational averaged isotropic shieldings are obtained using
Equations (1)–
(3) [
14].
For systems with many degrees of freedom, this procedure leads to a large number of calculations owing to the number of vibrational modes, especially in case of unsymmetrical molecules like 2-fluoronorbornanes, where 204 single calculations per compound are required.
As the calculation of the cubic force field and the nuclear shielding are done in two separate calculations, they can be carried out at two different levels of theory. This is advisable as for reliable results for the force field, a different level of theory is required than for NMR chemical shieldings [
2,
4]. In the following, this was done for benchmark calculations on fluoroethane, where the cubic force field was calculated using the HF method with tz2p and qz2p basis sets [
18] and at the MP2/cc-pVTZ level of theory [
19], while the nuclear shieldings were calculated using the HF [
20,
21], MP2 [
22,
23], and CCSD(T) [
24] methods with tz2p and qz2p basis sets. The calculations on the much larger fluoronorbornanes presented in the subsequent section, where carried out at the HF/tz2p level of theory. All calculations of nuclear shieldings were carried out using gauge including atomic orbitals (GIAOs) [
20,
25,
26].
It should be noted that the choice of the stepsize of displacement of the nuclei along the normal coordinates in the numerical third derivative procedure introduces an error of about 10
−3 ppm for the
13C isotope shifts, while for the
19F isotope shifts this error is one order of magnitude larger. In the case of small frequencies (
ω ≤ 100 cm
−1) the contributions to the vibrational correction are overestimated, and contributions with (
ω ≤ 200 cm
−1) are excluded [
5,
27]. When introducing the nuclear mass of
13C
5 in
endo-2-fluoro(
exo-3-
2H)norbornane, the value of the
13C secondary isotope shift on C
5 is the same as if the nuclear mass of
12C is used. Therefore, all calculations were done using the mass of
12C for all carbon nuclei, which has been shown to have very little effect on the calculated values as in contrast to the substitution of
1H by
2H (100% mass increase), the mass difference between
12C and
13C is only 8%.
Benchmark Calculations of Secondary Isotope Shifts on Fluoroethane
If species are to be identified by their secondary isotope shifts, the relative differences between the values of different compounds are important as well as the absolute values for each species. At the appropriate level of theory, to allow a reasonable assignment, the corresponding error due to method and basis set needs to be lower than the relative isotope shifts.
To estimate the errors of different computational methods, benchmark calculations were carried out for fluoroethane, which constitutes a small model system for which high-level calculations are feasible. The calculated
13C secondary isotope shifts on chemical shieldings of carbon nuclei on the 1 and 2 position and the secondary isotope shifts on chemical shieldings of the
19F nucleus are given in
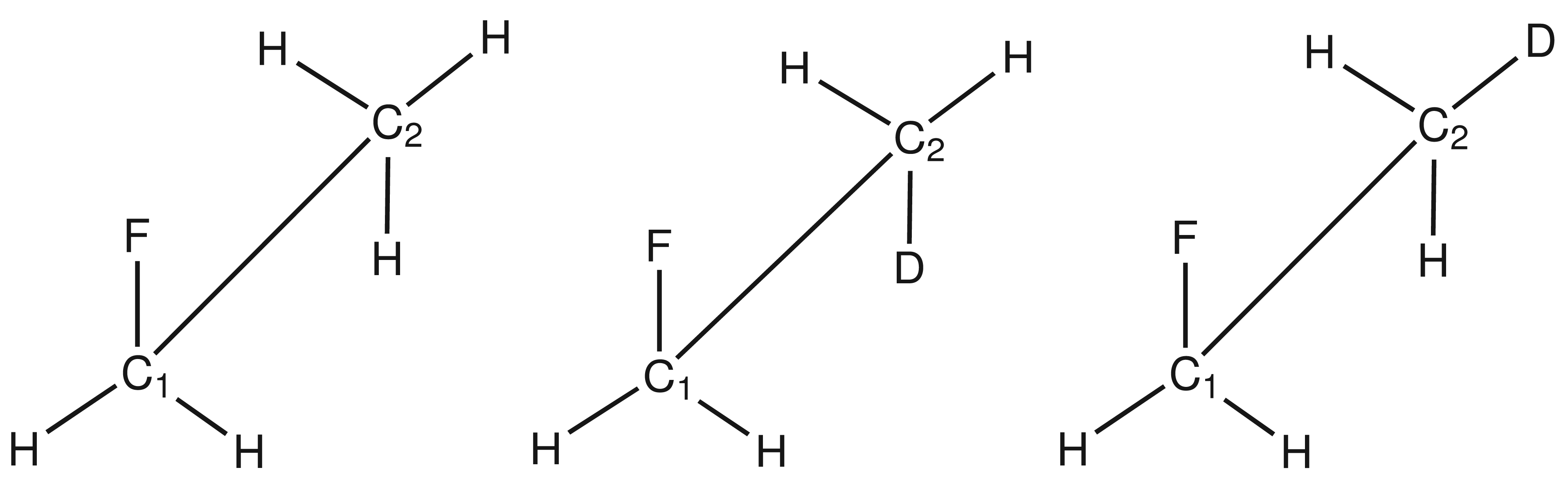
Table 1. In fluoroethane, deuterium is located in the gauche and antiperiplanar conformations relative to the fluorine atom (
Figure 1).
All isotope shifts are given for T = 0 K and T = 300 K to assess the influence of the temperature correction on the isotope shifts. Temperature effects on secondary isotope shifts can be sizeable, as the inclusion of temperature corrections lowers isotope shifts on fluorine by about 20% at all levels of theory. For carbon atoms, on the other hand, the inclusion of temperature corrections leads to larger isotope effects, especially in the case of C1 with deuterium in the antiperiplanar conformation.
Comparison of the isotope shifts obtained at HF/tz2p with those obtained at HF/qz2p level of theory shows that deviations of about 10% arise for the fluorine atom while they amount to about 7% for C1 and amount to less than 1% for C2.
While at CCSD(T)/qz2p + MP2/cc-pVTZ level of theory correlation effects are incorporated, at HF/tz2p level of theory this is not the case. This leads to an underestimation of the 19F secondary isotope shifts of at most 0.057 ppm and 0.050 ppm on average at the HF/tz2p level of theory. The isotope effects at C1 are underestimated by at most 0.007 ppm and 0.006 ppm on average and at C2 they are at most 0.013 ppm larger and on average they are about 0.010 ppm larger than at the CCSD(T)/qz2p + MP2/cc-pVTZ level of theory. The values at the CCSD(T)/qz2p + MP2/cc-pVTZ level show only little deviations from the values given at the MP2/qz2p + MP2/cc-pVTZ level of theory, which leads to the conclusion that, already at the MP2/qz2p level, correlation effects are sufficiently taken into account.
In order to assess the main sources of error at the most cost-effcient level of theory, namely HF/tz2p,
Table 1 also contains results from calculations, for which either the chemical shifts or the force field has been calculated at the MP2 level of theory. While generally both influences are of equal importance, there is a slight trend visible, that the calculation of the chemical shifts at the MP2 level of theory improves the results more than if only the force field is calcuated at the MP2 level of theory, which in some cases leads to an overestimation of the secondary isotop effects with respect to the full MP2 result.
Next, we turn to the errors in the difference between isotope effects on the shieldings of the gauche and antiperiplanar conformations, which is the decisive quantity if the different conformers are to be distinguished by the computed values. As the errors due to basis set effects and level of theory are very systematic, a favourable error compensation can be observed, such that the errors for the relative values are of the same order or less than for the secondary isotope shifts themselves. While the error in the chemical shifts is in the order of 10 ppm [
29], the error in the vibrational corrections is in the order of less than 0.1 ppm while the error in the secondary isotope effects is in the order of 0.01 ppm. Thus, similar differences on all levels of theory (
Table 1) are obtained. While the inclusion of the temperature correction leads to almost the same difference in the carbon isotope shifts of both conformations, the difference in the fluorine isotope shift decreases by about 0.04 ppm at all levels of theory. As a consequence, relative values of secondary isotope shifts can be calculated qualitatively even at the HF/tz2p level of theory, although the error on the absolute value of the isotope shifts might be fairly large. This is in agreement with previous results and also enables us to carry out calculations for much larger molecular systems, for which the computational effort for calculations at the CCSD(T) level of theory, for example, would be prohibitive.
3. Configurational Analysis of endo-2-Fluoronorbornanes—Challenging Literature
An early example for exploring dependencies of various parameters on secondary isotope effects on
19F chemical shieldings was conducted by Lambert
et al. [
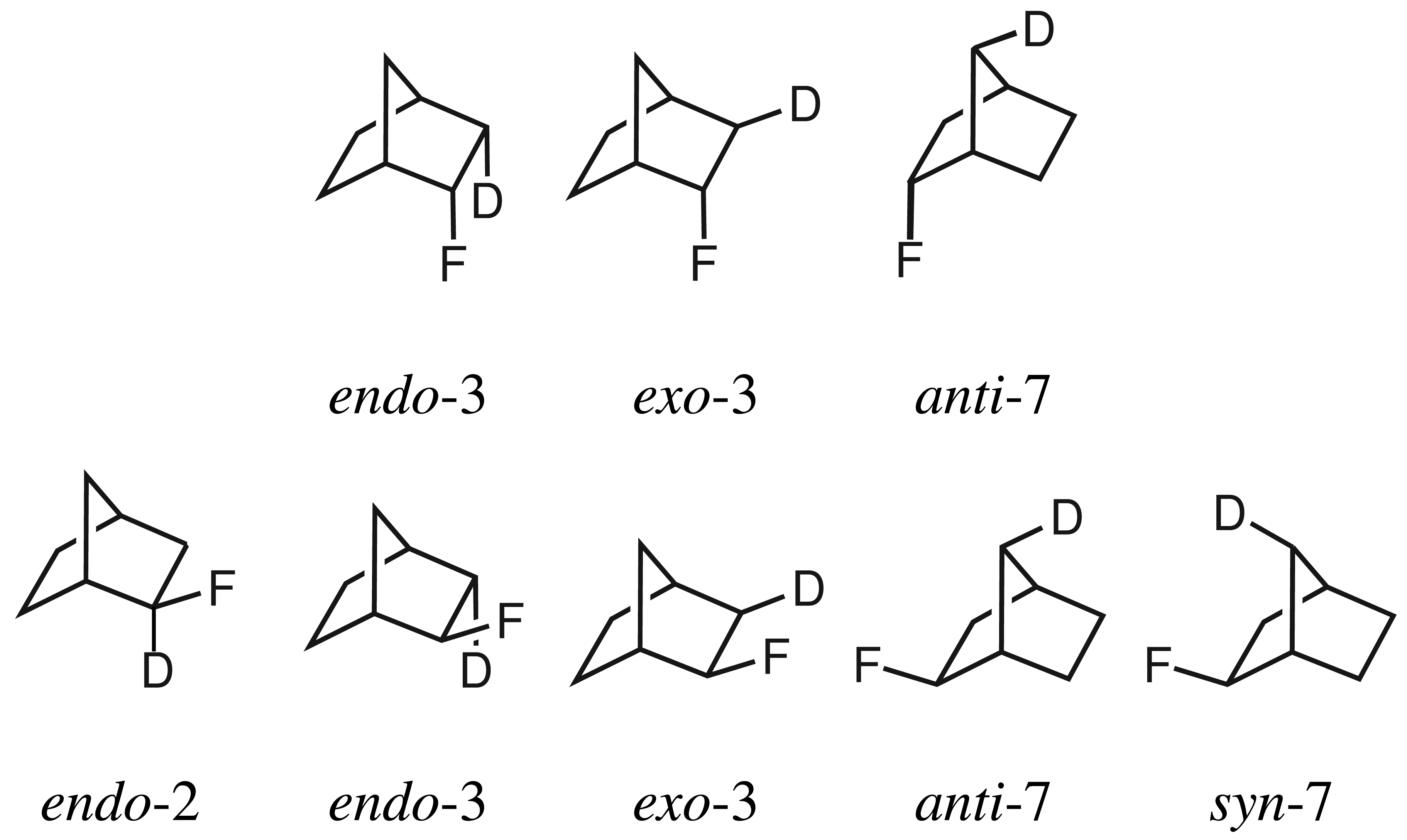
15]. Aiming to understand the dependence on the distance and the dihedral angle between substituted and resonating nuclei as well as on the number of substituted nuclei on secondary isotope shifts, several compounds were studied including 2-fluoronorbornanes, where
1H in the
endo-3 and
exo-3 positions were substituted by deuterium (
Figure 2). It was claimed that the correspondingly deuterated
exo-2-norbornanoles react via a S
N2 mechanism under inversion to
endo-2-fluoronorbornanes. However, the postulated S
N2 mechanism is questionable and the reaction may proceed via a S
N1 mechanism [
16,
27].
It is well known that inverting S
N2 displacements at 2-norbornyl substrates proceed very slowly because of substancial steric hindrance. This is quite different to analogous reactions of monocyclic starting compounds such as cyclopentyl or cyclohexyl derivatives [
30]. In the case of
exo-2-norbornyl substrates, the comprehensively investigated S
N1 reactions are reported to be unusually fast if compared to similar transformations of other compounds. Such competing unimolecular ionization reactions lead to equilibration of a single deuterium label and to exclusive formation
exo-2-norbornyl substitution products via an intermediate ambident nonclassical carbenium ion or, alternatively, via very rapid Wagner–Meerwein rearrangement of classical carbocations [
31].
The secondary isotope shifts of the molecules which were claimed by Lambert et al. and of the products of a SN1 substitution, can be calculated using quantum chemical methods to assess whether the the values of the configurations are correctly assigned in the work of Lambert et al.
In
Table 2, the calculated secondary isotope shifts of the
endo-2-fluoronorbornanes with deuterium in the
endo-3,
exo-3 and
anti-7 position are given. While deuteration at the
endo-3 position leads to an isotope shift of −0.291 ppm, deuteration at the
exo-3 position leads to an isotope shift of −0.108 ppm. Therefore, the compounds should be distinguishable with the help of the computational results, due to the significant differences in the isotope shifts. Note that from the previous section, uncertainties of less than 0.020 ppm can be anticipated for the calculated relative differences in the isotope shifts. In contrast to the calculated values, the secondary isotope shifts obtained by Lambert
et al. [
15] amount to −0.15 ± 0.06 ppm for the
endo-3-deutero compound and −0.40 ± 0.06 ppm for the
exo-3-deutero compound. Within the given computational and experimental uncertainties these results do not coincide.
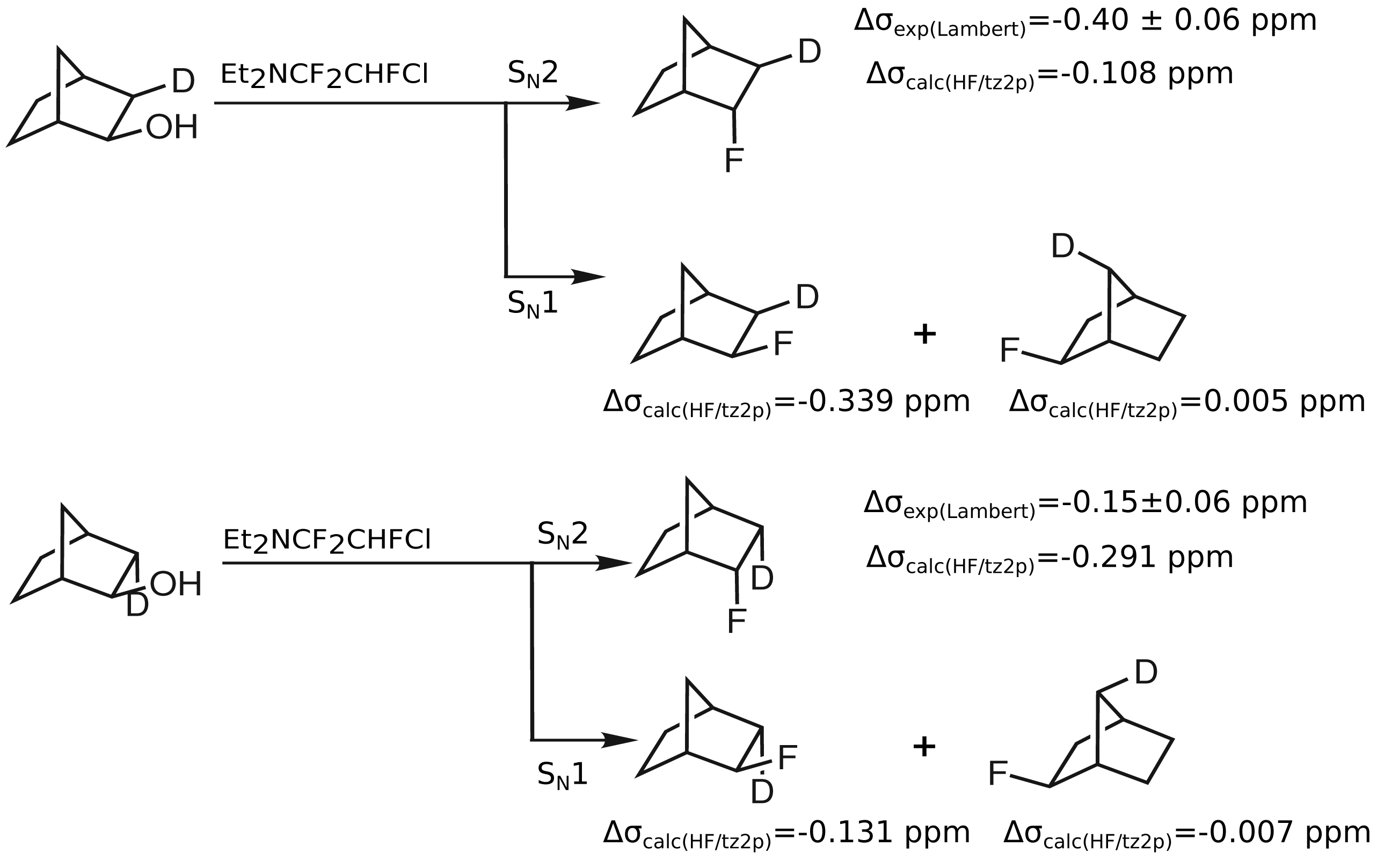
As the synthesis pathway proposed by Lambert
et al. may also proceed via a S
N1 mechanism and lead to
exo-2-fluoronorbornanes, the corresponding computed isotope effects are given in
Table 3. Secondary isotope shifts on
19F shieldings of −0.339 ppm for
exo-2-fluoro(
exo-3-
2H)norbornane and of 0.005 ppm for
exo-2-fluoro(
syn-7-
2H)norbornane are computed. In the case of the
exo-2-fluoro(
endo-3-
2H)norbornane, a secondary isotope shift on
19F of −0.131 ppm is obtained and in the case of
exo-2-fluoro(
anti-7-
2H)norbornane, this shift amounts to −0.007 ppm. These computed secondary isotope shifts on
19F shieldings are in much better agreement with those observed by Lambert
et al. In contrast to this, the computed values of the proposed
endo-2-fluoronorbornanes differ significantly from the secondary isotope shifts of products of S
N1 reactions. This discrepancy suggests that rather
exo-2-fluoronorbornanes than
endo-2-fluoronorbornanes result from the substitution of
endo-2-norbornanols with Et
2NCF
2CHFCl (
Figure 3).
We carried out the synthesis of
endo-2-fluoronorbornanes using the pathway proposed by Lambert
et al., starting from
exo-2-norbornanoles [
16]. While details on the experimental work will be given elsewhere, preliminary results on the
19F and
13C secondary isotope shifts of the corresponding products are given in
Table 3. These experimental values show good agreement with the calculated ones of the corresponding
exo-2-fluoronorbornanes and agree less well with the values of the
endo-2-fluoronorbornanes proposed by Lambert
et al. Our further investigations led to an alternative synthesis pathway, where the 2-fluoronorbornanes were prepared from 2-norbornyl tosylates or the corresponding deuterated compounds by nucleophilic substitution via S
N1 and S
N2 reactions; details will be reported elsewhere [
16]. For
endo-2-fluoro(
anti-7-
2H)norbornane and
endo-2-fluoro(
endo-3-
2H)norbornane,
19F and
13C secondary isotope shifts were measured and show good agreement with the calculated ones (
Table 2), while the secondary isotope shift on the
19F chemical shielding of
endo-2-fluoro(
endo-3-
2H)norbornane observed by Lambert
et al. could not be confirmed.
Since a mixture of compounds with
2H in 7- and 3-positions exists after the synthesis, an assignment of the secondary isotope shifts to the corresponding compounds is difficult. As mentioned in Section 2, the uncertainties in the
13C secondary isotope shifts are smaller than those for
19F, and this allows a better assignment of experimental values to the resonating nuclei. Using the calculated isotope shifts leads to assignments given in
Table 2 and
Tables 3, although for some nuclei the assignment is not unique, as for example in the case of
exo-2-fluoro(
endo-3-
2H)norbornane and
exo-2-fluoro(
anti-7-
2H)norbornane for carbons 4 and 5.
4. Conclusions
In the present study, we demonstrate how calculations of secondary isotope shifts can be used in order to distinguish different stereoisomers. Benchmark calculations for fluoroethane show, that compared to CCSD(T) calculations, secondary isotope shifts obtained at the MP2 level of theory exhibit an error in the order of 5%. While at the HF level of theory using triple-zeta basis sets, errors can amount 25%, this accuracy is usually still sufficient to even identify different conformers, as the relative secondary isotope effects often differ by more than 50% and sometimes even by an order of magnitude. Therefore, quantum chemical calculations of the differences in secondary isotope shifts can be applied in order to reliably distinguish between various compounds.
An example, where such calculations can be used to resolve ambiguous results in the literature are measurements by Lambert
et al., who presented secondary isotope shifts of
endo-2-fluoronorbornanes with deuterium in
exo-3- and
endo-3-positions, which are now convincingly explained by the corresponding effects in
exo-2-fluoronorbornanes with deuterium labels at the 3- and 7-positions (
Figure 3). Our recent experimental results contradict the assignments of Lambert
et al. and suggest that the deviations are due to different products as a consequence of a different mechanism than the one assumed in the original work. Calculations of the secondary isotope shifts of all possible products exhibit deviations from the results of Lambert
et al. that are far outside the error bars of the computations but in very good agreement with the preliminary experimental results [
16].