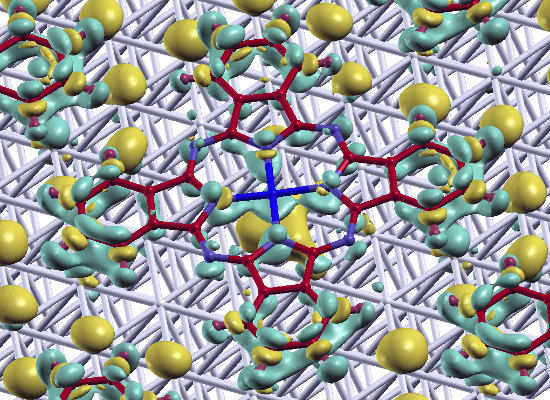
Understanding the Adsorption of CuPc and ZnPc on Noble Metal Surfaces by Combining Quantum-Mechanical Modelling and Photoelectron Spectroscopy
Abstract
:1. Introduction
2. Results and Discussion
2.1. Adsorption Geometries and Binding Energy
 epitaxy matrix, which fulfills the commensurability requirement imposed by our computational approach and, thus, has been chosen for the calculations. This is also consistent with the above-mentioned STM investigations, where lattice vectors in the highest symmetric axes of the substrate with length between 14 Å and 15 Å have been observed. To start the calculations, the Pc molecules were initially chosen to be planar with a vertical distance of 3.4 Å to the top metal layer. The lobes of the MePcs were initially aligned 30° off the unit cell axes, which correspond to the [1 2 1] and [−1 0 1] directions in accordance with Ref. [50,51,52,53]; the deviation of the optimized molecular orientation from the starting geometry was small (<5°), resulting in (essentially equivalent) minimum H-H distances of 2.8 Å (2.9 Å) between nearest neighbor molecules on Ag(111) (and Au(111)), respectively.
epitaxy matrix, which fulfills the commensurability requirement imposed by our computational approach and, thus, has been chosen for the calculations. This is also consistent with the above-mentioned STM investigations, where lattice vectors in the highest symmetric axes of the substrate with length between 14 Å and 15 Å have been observed. To start the calculations, the Pc molecules were initially chosen to be planar with a vertical distance of 3.4 Å to the top metal layer. The lobes of the MePcs were initially aligned 30° off the unit cell axes, which correspond to the [1 2 1] and [−1 0 1] directions in accordance with Ref. [50,51,52,53]; the deviation of the optimized molecular orientation from the starting geometry was small (<5°), resulting in (essentially equivalent) minimum H-H distances of 2.8 Å (2.9 Å) between nearest neighbor molecules on Ag(111) (and Au(111)), respectively. 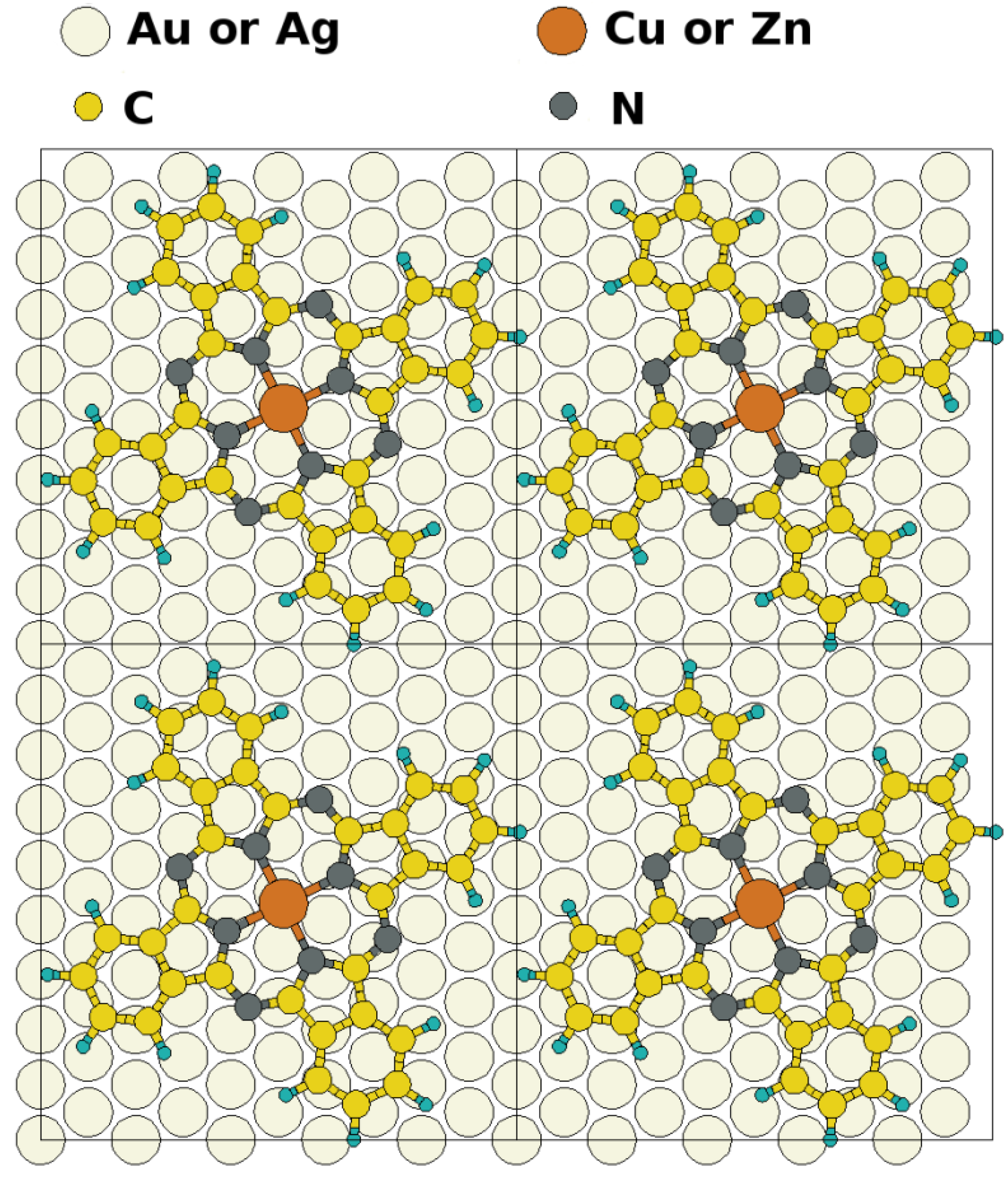
| CuPc | ZnPC | |||||
|---|---|---|---|---|---|---|
| (i) Au(111) | (ii) Ag(111) | (iii) Au(111) | (v) Ag(111) | |||
| atoms | dDFT+vdw-surf | dNIXSW-1ML-300K | dDFT+vdw-surf | dNIXSW-1ML-300K/Å | dDFT+vdw-surf | dDFT+vdw-surf |
| Cu/Zn | 3.15 | 3.25(7) | 2.84 | 2.89 | 2.73 | |
| 3.13 | 3.32(7) | 2.81 | 2.97(4) | 2.88 | 2.70 | |
| C | 3.18 | 3.31(7) | 2.95 | 3.17 | 2.93 | |
| 3.16 | 3.38(7) | 2.91 | 3.08(3) | 3.15 | 2.90 | |
| N | 3.22 | 3.26(7) | 2.94 | 3.17 | 2.94 | |
| 3.20 | 3.33(7) | 2.90 | 3.04(4) | 3.16 | 2.90 | |
| H | 3.11 | 2.95 | 3.13 | 2.92 | ||
| 3.10 | 2.91 | 2.12 | 2.89 | |||

2.2. Electronic Structures of the Monolayer-Metal Systems
| CuPc | ZnPc | |||||
|---|---|---|---|---|---|---|
| ∆ΦUPS/eV | ∆ΦPBE/eV | ∆ΦHSE/eV | ∆ΦUPS/eV | ∆ΦPBE/eV | ∆ΦHSE/eV | |
| Au(111) | −0.69 (−0.71 *) | −0.69 | −0.65 | −0.66 | −0.61 | −0.58 |
| Ag(111) | −0.44 | −0.44 | −0.38 | −0.43 | −0.41 | −0.38 |

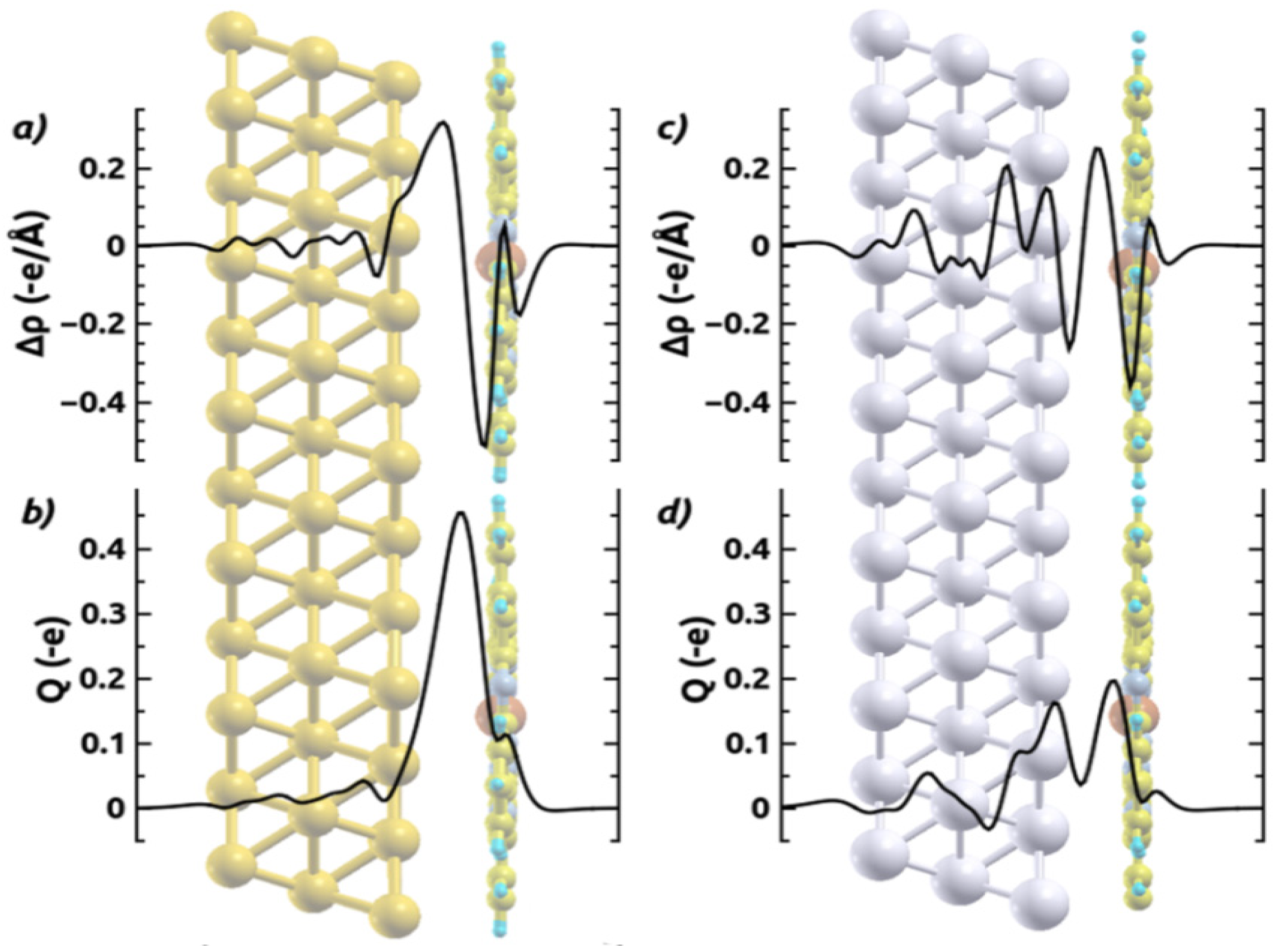
 [32,64,67]; the latter describes how much charge has been redistributed from the right to the left of a plane at position z.
[32,64,67]; the latter describes how much charge has been redistributed from the right to the left of a plane at position z. 

| CuPc | ZnPc | |||||
|---|---|---|---|---|---|---|
| ΕΗΟΜΟ,UPS/eV | ΕΗΟΜΟ,PBE/eV | ΕΗΟΜΟ,HSE/eV | ΕΗΟΜΟ,UPS/eV | ΕΗΟΜΟ,PBE/eV | ΕΗΟΜΟ,HSE/eV | |
| Au(111) | −0.81 | −0.78 | −0.91 | −0.78 | −0.74 | −0.91 |
| Ag(111) | −1.23 | −1.28 | −1.41/ −1.67 | −1.20 | −1.26 | −1.54 |

3. Experimental and Computational Section
3.1. DFT Calculations and System Setup
3.2. UPS Measurements
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflictts of Interest
References and Notes
- De Boer, R.W.I.; Stassen, A.F.; Craciun, M.F.; Mulder, C.L.; Molinari, A.; Rogge, S.; Morpurgo, A.F. Ambipolar Cu- and Fe-phthalocyanine single-crystal field-effect transistors. Appl. Phys. Lett. 2005, 86, 262109. [Google Scholar] [CrossRef]
- Bao, Z.; Lovinger, A.J.; Dodabalapur, A. Organic field-effect transistors with high mobility based on copper phthalocyanine. Appl. Phys. Lett. 1996, 69, 3066. [Google Scholar] [CrossRef]
- Pfeiffer, M.; Leo, K.; Zhou, X.; Huang, J.S.; Hofmann, M.; Werner, A.; Blochwitz-Nimoth, J. Doped organic semiconductors: Physics and application in light emitting diodes. Org. Electron. 2003, 4, 89–103. [Google Scholar] [CrossRef]
- Hung, L.S.; Tang, C.W. Interface engineering in preparation of organic surface-emitting diodes. Appl. Phys. Lett. 1999, 74, 3209. [Google Scholar] [CrossRef]
- Parthasarathy, G.; Burrows, P.E.; Khalfin, V.; Kozlov, V.G.; Forrest, S.R. A metal-free cathode for organic semiconductor devices. Appl. Phys. Lett. 1998, 72, 2138. [Google Scholar] [CrossRef]
- Mabeck, J.T.; Malliaras, G.G. Chemical and biological sensors based on organic thin-film transistors. Anal. Bioanal. Chem. 2006, 384, 343–353. [Google Scholar] [CrossRef]
- Bouvet, M. Phthalocyanine-based field-effect transistors as gas sensors. Anal. Bioanal. Chem. 2006, 384, 366–373. [Google Scholar] [CrossRef]
- Martinez-Diaz, M.V.; de la Torre, G.; Torres, T. Lighting porphyrins and phthalocyanines for molecular photovoltaics. Chem. Commun. 2010, 46, 7090–7108. [Google Scholar] [CrossRef]
- Singh, V.P.; Singh, R.S.; Parthasarathy, B.; Aguilera, A.; Anthony, J.; Payne, M. Copper-phthalocyanine-based organic solar cells with high open-circuit voltage. Appl. Phys. Lett. 2005, 86, 082106. [Google Scholar] [CrossRef]
- Annese, E.; Fujii, J.; Vobornik, I.; Panaccione, G.; Rossi, G. Control of the magnetism of cobalt phthalocyanine by a ferromagnetic substrate. Phys. Rev. B 2011, 84, 174443. [Google Scholar] [CrossRef]
- Cinchetti, M.; Heimer, K.; Wüstenberg, J.-P.; Andreyev, O.; Bauer, M.; Lach, S.; Ziegler, C.; Gao, Y.; Aeschlimann, M. Determination of spin injection and transport in a ferromagnet/organic semiconductor heterojunction by two-photon photoemission. Nat. Mater. 2009, 8, 115–119. [Google Scholar] [CrossRef]
- Liu, Y.; Lee, T.; Katz, H.E.; Reich, D.H. Effects of carrier mobility and morphology in organic semiconductor spin valves. J. Appl. Phys. 2009, 105, 07C708. [Google Scholar]
- Van den Brink, J.; Morpurgo, A.F. Magnetic blue. Nature 2007, 450, 177–178. [Google Scholar] [CrossRef]
- Lach, S.; Altenhof, A.; Tarafder, K.; Schmitt, F.; Ali, M.E.; Vogel, M.; Sauther, J.; Oppeneer, P.M.; Ziegler, C. Metal-Organic Hybrid interface states of a ferromagnet/organic semiconductor hybrid junction as basis for engineering spin injection in organic spintronics. Adv. Funct. Mater. 2012, 22, 989–997. [Google Scholar] [CrossRef]
- Atodiresei, N.; Brede, J.; Lazić, P.; Caciuc, V.; Hoffmann, G.; Wiesendanger, R.; Blügel, S. Design of the local spin polarization at the organic-ferromagnetic interface. Phys. Rev. Lett. 2010, 105, 066601. [Google Scholar] [CrossRef]
- Heutz, S.; Mitra, C.; Wu, W.; Fisher, A.J.; Kerridge, A.; Stoneham, M.; Harker, A.H.; Gardener, J.; Tseng, H.H.; Jones, T.S.; et al. Molecular thin films: A new type of magnetic switch. Adv. Mater. 2007, 19, 3618–3622. [Google Scholar] [CrossRef]
- Salomon, E.; Amsalem, P.; Marom, N.; Vondracek, M.; Kronik, L.; Koch, N.; Angot, T. Electronic structure of CoPc adsorbed on Ag(100): Evidence for molecule-substrate interaction mediated by Co 3d orbitals. Phys. Rev. B 2013, 87, 075407. [Google Scholar] [CrossRef]
- Mugarza, A.; Robles, R.; Krull, C.; Korytár, R.; Lorente, N.; Gambardella, P. Electronic and magnetic properties of molecule-metal interfaces: Transition-metal phthalocyanines adsorbed on Ag(100). Phys. Rev. B 2012, 85, 155437. [Google Scholar] [CrossRef]
- Petraki, F.; Peisert, H.; Aygül, U.; Latteyer, F.; Uihlein, J.; Vollmer, A.; Chassé, T. Electronic structure of fepc and interface properties on Ag(111) and Au(100). J. Phys. Chem. C 2012, 116, 11110–11116. [Google Scholar] [CrossRef]
- Petraki, F.; Peisert, H.; Latteyer, F.; Aygül, U.; Vollmer, A.; Chassé, T. Impact of the 3d electronic states of cobalt and manganese phthalocyanines on the electronic structure at the interface to Ag(111). J. Phys. Chem. C 2011, 115, 21334–21340. [Google Scholar] [CrossRef]
- Witte, G.; Lukas, S.; Bagus, P.S.; Wöll, C. Vacuum level alignment at organic/metal junctions: “Cushion” effect and the interface dipole. Appl. Phys. Lett. 2005, 87, 263502. [Google Scholar] [CrossRef]
- Bagus, P.; Staemmler, V.; Wöll, C. Exchangelike Effects for Closed-Shell Adsorbates: Interface Dipole and Work Function. Phys. Rev. Lett. 2002, 89, 096104. [Google Scholar] [CrossRef]
- Lang, N. Interaction between Closed-Shell Systems and Metal Surfaces. Phys. Rev. Lett. 1981, 46, 842–845. [Google Scholar] [CrossRef]
- Marom, N.; Ren, X.; Moussa, J.E.; Chelikowsky, J.R.; Kronik, L. Electronic structure of copper phthalocyanine from G0W0 calculations. Phys. Rev. B 2011, 84, 195143. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Du, S.X.; Gao, H.J. Binding configuration, electronic structure, and magnetic properties of metal phthalocyanines on a Au(111) surface studied with ab initio calculations. Phys. Rev. B 2011, 84, 125446. [Google Scholar] [CrossRef]
- Stradi, D.; Díaz, C.; Martín, F.; Alcamí, M. A density functional theory study of the manganese-phthalocyanine. Theor. Chem. Acc. 2010, 128, 497–503. [Google Scholar]
- Calvete, M.J.; Dini, D.; Hanack, M.; Sancho-Garcia, J.C.; Chen, W.; Ji, W. Synthesis, DFT calculations, linear and nonlinear optical properties of binuclear phthalocyanine gallium chloride. J. Mol. Model. 2006, 12, 543–550. [Google Scholar] [CrossRef]
- Casarin, M.; Marino, M.D.; Forrer, D.; Sambi, M.; Sedona, F.; Tondello, E.; Vittadini, A.; Barone, V.; Pavone, M. Coverage-Dependent Architectures of Iron Phthalocyanine on Ag(110): a comprehensive STM/DFT Study. J. Phys. Chem. C 2010, 114, 2144–2153. [Google Scholar] [CrossRef]
- Brede, J.; Atodiresei, N.; Kuck, S.; Lazić, P.; Caciuc, V.; Morikawa, Y.; Hoffmann, G.; Blügel, S.; Wiesendanger, R. Spin- and Energy-dependent tunneling through a single molecule with intramolecular spatial resolution. Phys. Rev. Lett. 2010, 105, 047204. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Romaner, L.; Hofmann, O.T.; Zojer, E.; Ambrosch-Draxl, C.; Scheffler, M. van der Waals interactions in organic adsorbates and organic/inorganic interfaces. MRS Bull. 2010, 35, 435–442. [Google Scholar] [CrossRef]
- Klimes, J.; Michaelides, A. Perspective: Advances and challenges in treating van der Waals dispersion forces in density functional theory. J. Chem. Phys. 2012, 137, 120901. [Google Scholar] [CrossRef]
- Romaner, L.; Nabok, D.; Puschnig, P.; Zojer, E.; Ambrosch-Draxl, C. Theoretical study of PTCDA adsorbed on the coinage metal surfaces, Ag(111), Au(111) and Cu(111). New J. Phys. 2009, 11, 053010. [Google Scholar] [CrossRef]
- Tautz, F.S. Structure and bonding of large aromatic molecules on noble metal surfaces: The example of PTCDA. Prog. Surf. Sci. 2007, 82, 479–520. [Google Scholar] [CrossRef]
- Rohlfing, M.; Temirov, R.; Tautz, F. Adsorption structure and scanning tunneling data of a prototype organic-inorganic interface: PTCDA on Ag(111). Phys. Rev. B 2007, 76, 115421. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef]
- Wu, X.; Vargas, M.C.; Nayak, S.; Lotrich, V.; Scoles, G. Towards extending the applicability of density functional theory to weakly bound systems. J. Chem. Phys. 2001, 115, 8748. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate molecular Van Der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Lee, K.; Murray, É.D.; Kong, L.; Lundqvist, B.I.; Langreth, D.C. Higher-accuracy van der Waals density functional. Phys. Rev. B 2010, 081101. [Google Scholar]
- Risthaus, T.; Grimme, S. Benchmarking of london dispersion-accounting density functional theory methods on very large molecular complexes. J. Chem. Theory Comput. 2013, 9, 1580–1591. [Google Scholar] [CrossRef]
- Vydrov, O.A.; van Voorhis, T. Benchmark Assessment of the accuracy of several van der waals density functionals. J. Chem. Theory Comput. 2012, 8, 1929–1934. [Google Scholar] [CrossRef]
- Ruiz, V.G.; Liu, W.; Zojer, E.; Scheffler, M.; Tkatchenko, A. Density-functional theory with Screened van der Waals interactions for the modeling of hybrid inorganic-organic systems. Phys. Rev. Lett. 2012, 108, 146103. [Google Scholar] [CrossRef]
- Egger, D.A.; Ruiz, V.G.; Saidi, W.A.; Bucko, T.; Tkatchenko, A.; Zojer, E. Understanding structure and bonding of multilayered metal-organic nanostructures. J. Phys. Chem. C 2013, 117, 3055–3061. [Google Scholar] [CrossRef]
- Marom, N.; Hod, O.; Scuseria, G.E.; Kronik, L. Electronic structure of copper phthalocyanine: A comparative density functional theory study. J. Chem. Phys. 2008, 128, 164107. [Google Scholar] [CrossRef]
- Marom, N.; Kronik, L. Density functional theory of transition metal phthalocyanines, I: Electronic structure of NiPc and CoPc—self-interaction effects. Appl. Phys. A 2008, 95, 159–163. [Google Scholar] [CrossRef]
- Kümmel, S.; Kronik, L. Orbital-dependent density functionals: Theory and applications. Rev. Mod. Phys. 2008, 80, 3–60. [Google Scholar] [CrossRef]
- Garcia-Lastra, J.M.; Rostgaard, C.; Rubio, A.; Thygesen, K.S. Polarization-induced renormalization of molecular levels at metallic and semiconducting surfaces. Phys. Rev. B 2009, 80, 245427. [Google Scholar] [CrossRef] [Green Version]
- Neaton, J.; Hybertsen, M.; Louie, S. Renormalization of molecular electronic levels at metal-molecule interfaces. Phys. Rev. Lett. 2006, 97, 216405. [Google Scholar] [CrossRef]
- Koudia, M.; Abel, M.; Maurel, C.; Bliek, A.; Catalin, D.; Mossoyan, M.; Mossoyan, J.-C.; Louis, P. Influence of chlorine substitution on the self-assembly of zinc phthalocyanine. J. Phys. Chem. B 2006, 110, 10058–10062. [Google Scholar] [CrossRef]
- Kröger, I.; Stadtmüller, B.; Stadler, C.; Ziroff, J.; Kochler, M.; Stahl, A.; Pollinger, F.; Lee, T.-L.; Zegenhagen, J.; Reinert, F.; et al. Submonolayer growth of copper-phthalocyanine on Ag(111). New J. Phys. 2010, 12, 083038. [Google Scholar] [CrossRef]
- Chizhov, I.; Scoles, G.; Kahn, A. The influence of steps on the orientation of copper phthalocyanine monolayers on Au(111). Langmuir 2000, 16, 4358–4361. [Google Scholar] [CrossRef]
- Kröger, I.; Stadtmüller, B.; Kleimann, C.; Rajput, P.; Kumpf, C. Normal-incidence X-ray standing-wave study of copper phthalocyanine submonolayers on Cu(111) and Au(111). Phys. Rev. B 2011, 83, 195414. [Google Scholar] [CrossRef]
- Henze, S.K.M.; Bauer, O.; Lee, T.L.; Sokolowski, M.; Tautz, F.S. Vertical bonding distances of PTCDA on Au(111) and Ag(111): Relation to the bonding type. Surf. Sci. 2007, 601, 1566–1573. [Google Scholar] [CrossRef]
- Sandy, A.; Mochrie, S.; Zehner, D.; Huang, K.; Gibbs, D. Structure and phases of the Au(111) surface: X-ray-scattering measurements. Phys. Rev. B 1991, 43, 4667–4687. [Google Scholar] [CrossRef]
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Note that the spacings of the crystalline (111) planes are essentially identical: 2.35 (2.41) Å for Au vs. 2.36 (2.40) Å for Ag in the experiments [Swanson, H.E.; Tatge, E. Standard X-ray Diffraction Powder Pattern, Standard X-ray Diffraction Powder Pattern, National Bureau of Standards (U.S.), 1953, Circular 539, 1, 1–95] (in our simulations).
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207, 2006, 124, 219906. [Google Scholar] [CrossRef]
- Hofmann, O.T.; Atalla, V.; Moll, N.; Rinke, P.; Scheffler, M. Interface dipoles of organic molecules on Ag(111) in hybrid density-functional theory. New J. Phys. 2013, 15, 123028. [Google Scholar] [CrossRef]
- Ishii, H.; Sugiyama, K.; Ito, E.; Seki, K. Energy level alignment and interfacial electronic structures at organic/metal and organic/organic interfaces. Adv. Mater. 1999, 11, 605–625. [Google Scholar] [CrossRef]
- Tautz, F.; Eremtchenko, M.; Schaefer, J.; Sokolowski, M.; Shklover, V.; Umbach, E. Strong electron-phonon coupling at a metal/organic interface: PTCDA/Ag(111). Phys. Rev. B 2002, 65, 125405. [Google Scholar] [CrossRef]
- Koch, N. Organic electronic devices and their functional interfaces. ChemPhysChem 2007, 8, 1438–1455. [Google Scholar] [CrossRef]
- Romaner, L.; Heimel, G.; Brédas, J.-L.; Gerlach, A.; Schreiber, F.; Johnson, R.; Zegenhagen, J.; Duhm, S.; Koch, N.; Zojer, E. Impact of bidirectional charge transfer and molecular distortions on the electronic structure of a metal-organic interface. Phys. Rev. Lett. 2007, 99, 256801. [Google Scholar] [CrossRef]
- Hill, I.G.; Rajagopal, A.; Kahn, A.; Hu, Y. Molecular level alignment at organic semiconductor-metal interfaces. Appl. Phys. Lett. 1998, 73, 662. [Google Scholar] [CrossRef]
- Hofmann, O.T.; Rangger, G.M.; Zojer, E. Reducing the metal work function beyond pauli pushback: A computational investigation of tetrathiafulvalene and viologen on coinage metal surfaces. J. Phys. Chem. C 2008, 112, 20357–20365. [Google Scholar] [CrossRef]
- Stadler, R.; Jacobsen, K. Fermi level alignment in molecular nanojunctions and its relation to charge transfer. Phys. Rev. B 2006, 74, 161405. [Google Scholar] [CrossRef]
- Rangger, G.; Hofmann, O.; Romaner, L.; Heimel, G.; Bröker, B.; Blum, R.-P.; Johnson, R.; Koch, N.; Zojer, E. F4TCNQ on Cu, Ag, and Au as prototypical example for a strong organic acceptor on coinage metals. Phys. Rev. B 2009, 79, 165306. [Google Scholar] [CrossRef]
- Bröker, B.; Hofmann, O.T.; Rangger, G.M.; Frank, P.; Blum, R.P.; Rieger, R.; Venema, L.; Vollmer, A.; Müllen, K.; Rabe, J.P.; et al. Density-dependent reorientation and rehybridization of chemisorbed conjugated molecules for controlling interface electronic structure. Phys. Rev. Lett. 2010, 104, 246805. [Google Scholar] [CrossRef]
- The metal work-functions determined from the energetic difference between the Fermi-level and the vacuum potential below the metal slab amount to 5.20 eV for Au(111) and 4.41 eV for Ag(111).
- Perdew, J.P. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Biller, A.; Tamblyn, I.; Neaton, J.B.; Kronik, L. Electronic level alignment at a metal-molecule interface from a short-range hybrid functional. J. Chem. Phys. 2011, 135, 164706. [Google Scholar] [CrossRef]
- Track, A.M.; Rissner, F.; Heimel, G.; Romaner, L.; Kafer, D.; Bashir, A.; Rangger, G.M.; Hofmann, O.T.; Bucko, T.; Witte, G.; et al. Simultaneously understanding the geometric and electronic structure of anthraceneselenolate on Au(111): A combined theoretical and experimental study. J. Phys. Chem. C 2010, 114, 2677–2684, J. Phys. Chem. C, 2010, 114, 12838. [Google Scholar] [CrossRef]
- Körzdörfer, T.; Kümmel, S.; Marom, N.; Kronik, L. When to trust photoelectron spectra from Kohn-Sham eigenvalues: The case of organic semiconductors. Phys. Rev. B 2009, 79, 201205, Phys. Rev. B, 2010, 82, 129903. [Google Scholar] [CrossRef]
- Rissner, F.; Egger, D.A.; Natan, A.; Korzdorfer, T.; Kummel, S.; Kronik, L.; Zojer, E. Collectively induced quantum-confined Stark effect in monolayers of molecules consisting of polar repeating units. J. Am. Chem. Soc. 2011, 133, 18634–18645. [Google Scholar] [CrossRef]
- Evangelista, F.; Carravetta, V.; Stefani, G.; Jansik, B.; Alagia, M.; Stranges, S.; Ruocco, A. Electronic structure of copper phthalocyanine: An experimental and theoretical study of occupied and unoccupied levels. J. Chem. Phys. 2007, 126, 124709. [Google Scholar] [CrossRef]
- Ziroff, J.; Hame, S.; Kochler, M.; Bendounan, A.; Schöll, A.; Reinert, F. Low-energy scale excitations in the spectral function of organic monolayer systems. Phys. Rev. B 2012, 85, 161404. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Natan, A.; Kronik, L.; Haick, H.; Tung, R.T. Electrostatic properties of ideal and non-ideal polar organic monolayers: Implications for electronic devices. Adv. Mater. 2007, 19, 4103–4117. [Google Scholar] [CrossRef]
- Heimel, G.; Rissner, F.; Zojer, E. Modeling the electronic properties of pi-conjugated self-assembled monolayers. Adv. Mater. 2010, 22, 2494–513. [Google Scholar] [CrossRef]
- Monti, O.L.A. Understanding interfacial electronic structure and charge transfer: An electrostatic perspective. J. Phys. Chem. Lett. 2012, 3, 2342–2351. [Google Scholar] [CrossRef]
- Monti, O.L.; Steele, M.P. Influence of electrostatic fields on molecular electronic structure: Insights for interfacial charge transfer. Phys. Chem. Chem. Phys. 2010, 12, 12390–12400. [Google Scholar] [CrossRef]
- Neugebauer, J.; Scheffler, M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111). Phys. Rev. B 1992, 46, 16067–16080. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Lifshits, E.M. The Theory of Molecular Attractive Forces between Solids. Sov. Phys. 1956, 2, 73–83. [Google Scholar]
- Zaremba, E.; Kohn, W. Van der Waals interaction between an atom and a solid surface. Phys. Rev. B 1976, 13, 2270–2285. [Google Scholar] [CrossRef]
- Bučko, T.; Lebègue, S.; Hafner, J.; Ángyán, J.G. Tkatchenko-Scheffler van der Waals correction method with and without self-consistent screening applied to solids. Phys. Rev. B 2013, 87, 064110. [Google Scholar] [CrossRef]
- Bucko, T.; Hafner, J.; Angyan, J.G. Geometry optimization of periodic systems using internal coordinates. J. Chem. Phys. 2005, 122, 124508. [Google Scholar] [CrossRef]
- Farkas, O.; Schlegel, H.B. Methods for optimizing large molecules. Part III. An improved algorithm for geometry optimization using direct inversion in the iterative subspace (GDIIS). Phys. Chem. Chem. Phys. 2002, 4, 11–15. [Google Scholar] [CrossRef]
- Csaszar, P.; Pulay, P. Geometry optimization by direct inversion in the iterative subspace. J. Mol. Stuct. 1984, 114, 31–34. [Google Scholar] [CrossRef]
- Marom, N.; Tkatchenko, A.; Scheffler, M.; Kronik, L. Describing both dispersion interactions and electronic structure using density functional theory: The case of Metal−Phthalocyanine dimers. J. Chem. Theory Comput. 2010, 6, 81–90. [Google Scholar] [CrossRef]
- The single-point calculation of CuPc on Au using the HSE functional took about 75 times longer than the PBE calculation and it would, therefore, be computationally unfeasible to perform the whole geometry optimization with the HSE functional.
- Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comp. Mater. Sci. 2003, 28, 155–168. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Kakuta, H.; Ono, M.; Sakamoto, K.; Kera, S.; Ueno, N. Band gap states of copper phthalocyanine thin films induced by nitrogen exposure. Appl. Phys. Lett. 2010, 96, 093303. [Google Scholar] [CrossRef]
- Bussolotti, F.; Kera, S.; Kudo, K.; Kahn, A.; Ueno, N. Gap states in Pentacene Thin Film Induced by Inert Gas Exposure. Phys. Rev. Lett. 2013, 110, 267602. [Google Scholar] [CrossRef]
- Huang, Y.L.; Chen, W.; Bussolotti, F.; Niu, T.C.; Wee, A.T.S.; Ueno, N.; Kera, S. Impact of molecule-dipole orientation on energy level alignment at the submolecular scale. Phys. Rev. B 2013, 87, 085205. [Google Scholar]
- Noteworthy, a similar observation has recently been made by Hofmann et al. for interfaces between inorganic and organic semiconductors (c.f., Hofmann, O.T.; Deinert, J.C.; Xu, Y.; Rinke, P.; Stähler, J.; Wolf, M.; Scheffler, M. Large work function reduction by adsorption of a molecule with a negative electron affinity: Pyridine on ZnO(10-10). J. Chem. Phys. 2013, 139, 174701. [Google Scholar] [CrossRef]
- Sample Availability: Not available.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huang, Y.L.; Wruss, E.; Egger, D.A.; Kera, S.; Ueno, N.; Saidi, W.A.; Bucko, T.; Wee, A.T.S.; Zojer, E. Understanding the Adsorption of CuPc and ZnPc on Noble Metal Surfaces by Combining Quantum-Mechanical Modelling and Photoelectron Spectroscopy. Molecules 2014, 19, 2969-2992. https://doi.org/10.3390/molecules19032969
Huang YL, Wruss E, Egger DA, Kera S, Ueno N, Saidi WA, Bucko T, Wee ATS, Zojer E. Understanding the Adsorption of CuPc and ZnPc on Noble Metal Surfaces by Combining Quantum-Mechanical Modelling and Photoelectron Spectroscopy. Molecules. 2014; 19(3):2969-2992. https://doi.org/10.3390/molecules19032969
Chicago/Turabian StyleHuang, Yu Li, Elisabeth Wruss, David A. Egger, Satoshi Kera, Nobuo Ueno, Wissam A. Saidi, Tomas Bucko, Andrew T.S. Wee, and Egbert Zojer. 2014. "Understanding the Adsorption of CuPc and ZnPc on Noble Metal Surfaces by Combining Quantum-Mechanical Modelling and Photoelectron Spectroscopy" Molecules 19, no. 3: 2969-2992. https://doi.org/10.3390/molecules19032969