A Variable Temperature X-ray Diffraction Investigation of [PPN+][S4N5−]: Supramolecular Interactions Governing an Order/Disorder Transformation and the First High Resolution X-ray Structure of the Anion
Abstract
:1. Introduction
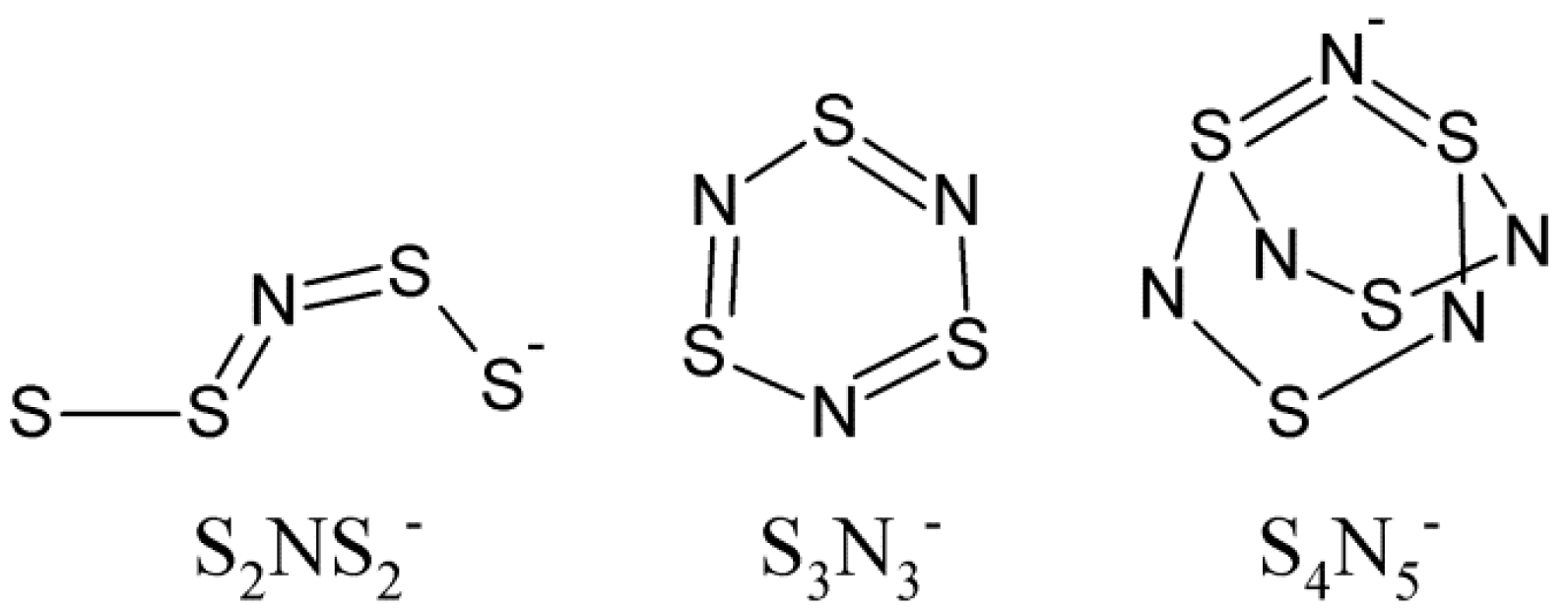
2. Results and Discussion
2.1. Sample Preparation and X-ray Diffraction Experiments
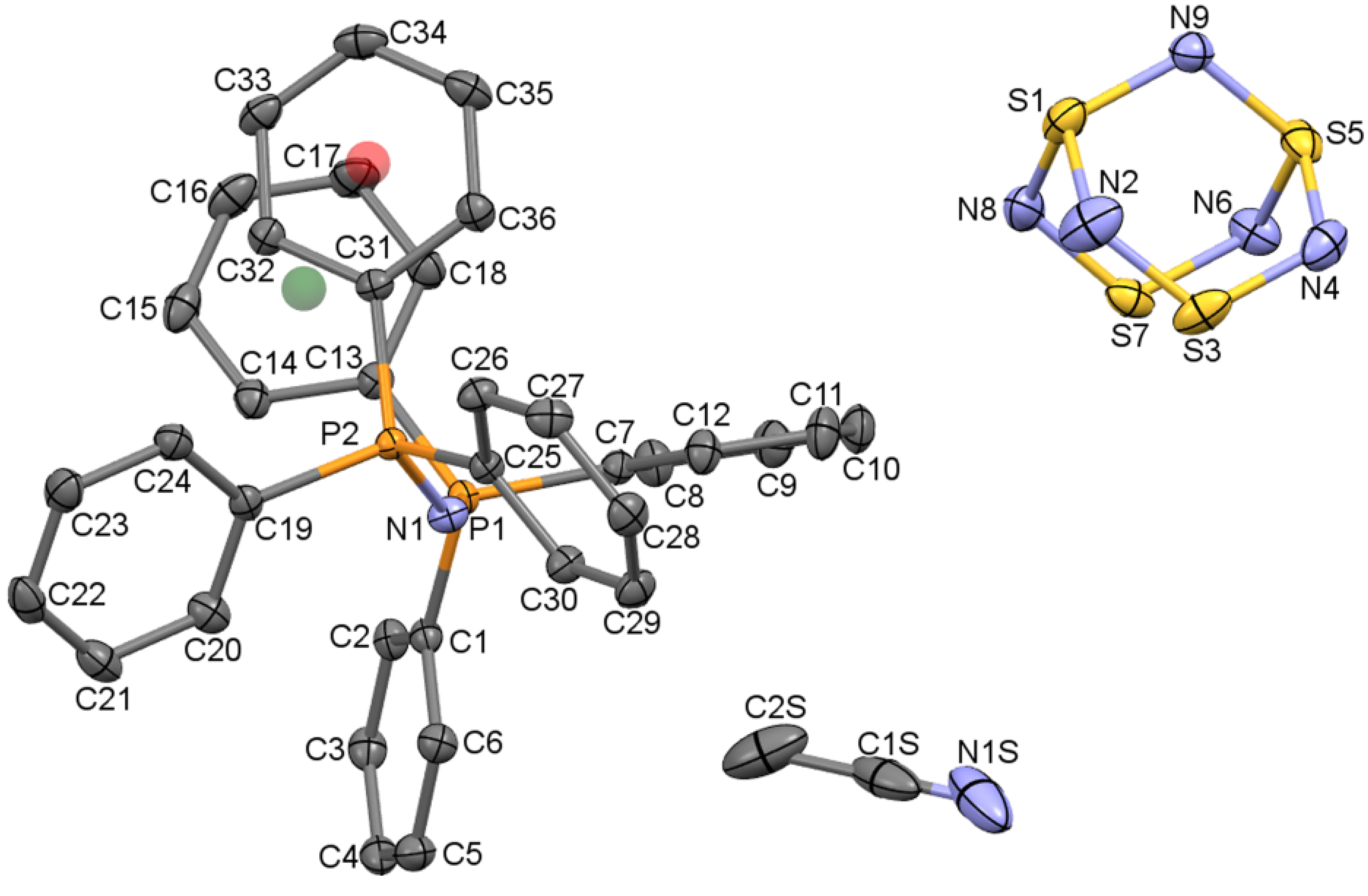
2.1.1. The structure of [PPN+][S4N5−]∙CH3CN
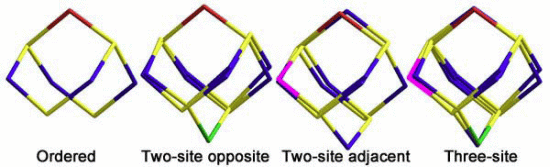
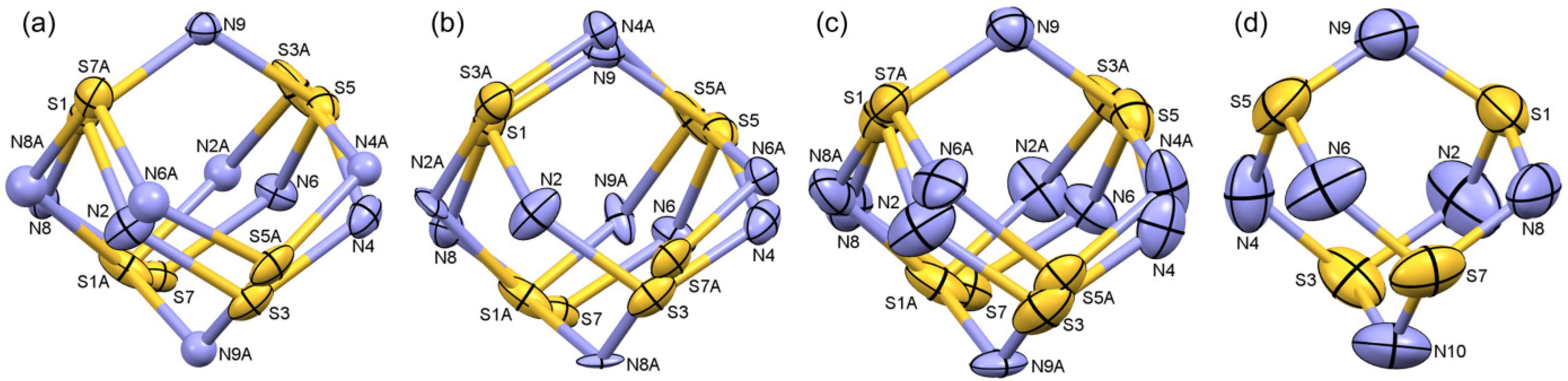
2.1.2. S4N5− Disorder as a Function of Temperature

| Parameter, Å or ° | 100 K a | 120 K a | 172 K a | Flues et al. b | Martan et al. c | DFT d |
|---|---|---|---|---|---|---|
| S3∙∙∙S7 | 2.695(1) | 2.697(2) | 2.724(6) | 2.71(1) | 2.657(10) | 2.8417 |
| S1∙∙∙S5 | 2.769(1) | 2.763(3) | 2.760(6) | 2.75(1) | 2.795 | 2.7913 |
| S1–N2 | 1.657(2) | 1.657(3) | 1.690(8) | 1.62(2) | 1.67(1) | 1.6667 |
| S1–N8 | 1.666(2) | 1.668(3) | 1.655(6) | 1.65(2) | 1.67(1) g | 1.6688 |
| S5–N4 | 1.677(2) | 1.676(4) | 1.703(8) | 1.63(2) | 1.67(2) | 1.6687 |
| S5–N6 | 1.6710(17) | 1.670(3) | 1.683(8) | 1.66(2) | 1.67(2) g | 1.6667 |
| S3–N2 | 1.614(2) | 1.619(3) | 1.605(9) | 1.61(2) | 1.61(1) | 1.6171 |
| S3–N4 | 1.604(2) | 1.599(4) | 1.574(8) | 1.63(2) | 1.61(1) | 1.6164 |
| S7–N6 | 1.6080(17) | 1.608(3) | 1.581(6) | 1.60(2) | 1.61(1) g | 1.6172 |
| S7–N8 | 1.6170(18) | 1.615(3) | 1.610(6) | 1.57(2) | 1.61(1) g | 1.6164 |
| S1–N9 | 1.6450(17 | 1.640(4) | 1.664(5) | 1.68(2) | 1.64(2) | 1.6484 |
| S5–N9 | 1.6446(19) | 1.621(5) | 1.665(5) | 1.64(2) | 1.64(2) | 1.6485 |
| P1–N1 | 1.5855(11) | 1.5838(14) | 1.5803(12) | — | — | — |
| P2–N1 | 1.5824(11) | 1.5794(14) | 1.5788(13) | — | — | — |
| S1–N2–S3 | 114.15(12) | 114.06(15) | 115.1(5) | 113(1) | 113.2(8) | 114.80 |
| N2–S3–N4 | 115.20(12) | 114.32(17) | 112.9(4) | 114(1) | 113.5(8) | 114.21 |
| S3–N4–S5 | 113.03(11) | 113.3(2) | 113.8(6) | 114(1) | 113.7(9) | 114.82 |
| N4–S5–N6 | 99.33(10) | 99.14(18) | 100.0(4) | 100(1) | 101(1) | 101.69 |
| S5–N6–S7 | 113.57(10) | 113.51(19) | 114.5(4) | 115(1) | 113.7(9) g | 114.80 |
| N6–S7–N8 | 113.82(9) | 113.83(16) | 113.6(4) | 114(1) | 113.5(8) g | 114.21 |
| S7–N8–S1 | 113.13(10) | 112.76(18) | 112.7(4) | 114(1) | 113.2(8) g | 114.81 |
| N8–S1–N2 | 99.65(11) | 100.91(17) | 101.3(4) | 101(1) | 100(1) g | 101.68 |
| N2–S1–N9 | 109.47(11) | 108.7(3) | 107.6(4 | 110(1) | 117(1) | 108.49 |
| N8–S1–N9 | 109.34(9) | 108.6(2) | 111.1(3) | 111(1) | 108.3(6) g | 108.41 |
| N4–S5–N9 | 109.62(11) | 110.0(3) | 108.2(4) | 110(1) | 107.7(6) | 108.41 |
| N6–S5–N9 | 109.52(11) | 108.8(2) | 110.3(3) | 109(1) | 107.7(6) g | 108.49 |
| S1–N9–S5 | 114.68(10) | 115.8(3) | 112.1(2) | 112(1) | 117(1) | 115.70 |
| ∠S1N8N6S5:S1N9S5 e | 49.51(9) | 50.7(4) | 47.6(2) | — | 50.2 | 50.86 |
| ∠S1N2N4S5:S1N9S5 e | 50.01(9) | 49.3(3) | 53.1(3) | — | 50.2 g | 50.86 |
| P1–N1–P2 | 137.81(7) | 138.16(10) | 138.98(9) | — | — | — |
| Ct1–P1–P2–Ct2 f | −32.99 | −33.05 | −33.33 | — | — | — |
| Parameter, b Å or ° | 100 K | 120 K | 172 K | Flues et al. c | Martan et al. d | DFT e |
|---|---|---|---|---|---|---|
| S3∙∙∙S7 | 2.695(1) | 2.697(2) | 2.724(6) | 2.71(1) | 2.667(10) | 2.8427 |
| S3–N2 | 1.611(6) | 1.610(9) | 1.593(18) | 1.60(3) | 1.61(1) | 1.6166 |
| S1–N2 | 1.668(8) | 1.668(8) | 1.68(2) | 1.640(18) | 1.67(1) | 1.6675 |
| S1–N9 | 1.6448(3) | 1.631(13) | 1.665(1) | 1.66(3) | 1.64(1) | 1.6486 |
| S1∙∙∙S5 | 2.769(1) | 2.763(3) | 2.760(6) | 2.75(1) | 2.795 | 2.7914 |
| S1–N2–S3 | 113.5(5) | 113.4(5) | 114.0(10) | 113.5(10) | 113(2) | 114.81 |
| N2–S3–N4 | 114.5(10) | 114.4(3) | 113.3(5) | 113.5(10) | 113.5(10) | 114.21 |
| N2–S1–N8 | 99. 5(2) | 100.0(13) | 100.7(9) | 100.5(10) | 100(1) | 101.69 |
| N2–S1–N9 | 109.49(12) | 109.0(7) | 109.3(17) | 110.1(10) | 110(3) | 108.45 |
| S1–N9–S5 | 114.68(10) | 115.8(3) | 112.1(2) | 112(1) | 117 | 115.70 |
2.1.3. On the Structure of PPN+
2.1.4. Supramolecular Interactions in the [PPN+][S4N5−] Lattice
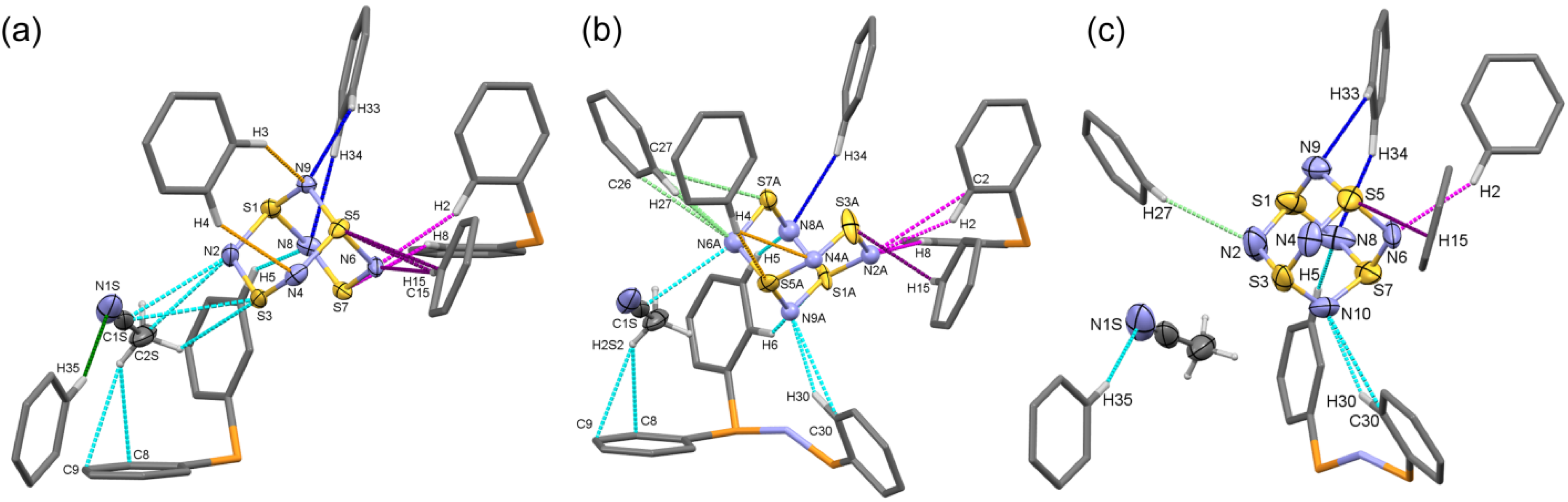
| Component | Atom1 | Atom2 | Symm. op. 1 | Symm. op. 2 | Length | d−∑rvdW | d−Wk | Type |
|---|---|---|---|---|---|---|---|---|
| 100K Main | N6 | H2 | x,y,z | 1−x,1−y,−z | 2.479 | −0.271 | −0.051 | n.c. H-bond |
| 100K Main | N6 | H15 | x,y,z | x,1+y,z | 2.481 | −0.269 | −0.049 | n.c. H-bond |
| 100K Main | N1S | H35 | 1−x,1/2+y,1/2−z | x,1.5−y,1/2+z | 2.531 | −0.219 | 0.001 | n.c. H-bond |
| 100K Main | S5 | H15 | x,y,z | x,1+y,z | 2.796 | −0.204 | −0.104 | n.c. H-bond |
| 100K Main | S7 | H8 | x,y,z | 1−x,1−y,−z | 2.865 | −0.135 | −0.035 | n.c. H-bond |
| 100K Main | S5 | C15 | x,y,z | x,1+y,z | 3.376 | −0.124 | n/a | n.c. H-bond |
| 100K Main | N2 | C2S | x,y,z | 1−x,1/2+y,1/2−z | 3.143 | −0.107 | n/a | N≡C carbon π |
| 100K Minor | N6A | H27 | x,y,z | −x,1/2+y,1/2−z | 2.35 | −0.400 | −0.180 | n.c. H-bond |
| 100K Minor | N9A | H30 | x,y,z | 1−x,1/2+y,1/2−z | 2.365 | −0.385 | −0.165 | n.c. H-bond |
| 100K Minor | N2A | H2 | x,y,z | 1−x,1−y,−z | 2.432 | −0.318 | −0.098 | n.c. H-bond |
| 100K Minor | N6A | C27 | x,y,z | −x,1/2+y,1/2−z | 3.022 | −0.228 | n/a | n.c. H-bond |
| 100K Minor | N8A | H5 | x,y,z | 1−x,1/2+y,1/2−z | 2.524 | −0.226 | −0.006 | n.c. H-bond |
| 100K Minor | S5A | H4 | x,y,z | −1+x,1+y,z | 2.801 | −0.199 | −0.099 | n.c. H-bond |
| 100K Minor | S1A | H6 | x,y,z | 1−x,1/2+y,1/2−z | 2.807 | −0.193 | −0.093 | n.c. H-bond |
| 100K Minor | N4A | H4 | x,y,z | −1+x,1+y,z | 2.62 | −0.130 | 0.090 | n.c. H-bond |
| 100K Minor | N6A | C1S | x,y,z | 1−x,1/2+y,1/2−z | 3.126 | −0.124 | n/a | N≡C carbon π |
| 100K Minor | S3A | H15 | x,y,z | x,1+y,z | 2.893 | −0.107 | −0.007 | n.c. H-bond |
| 100K Minor | N9A | C30 | x,y,z | 1−x,1/2+y,1/2−z | 3.15 | −0.100 | n/a | n.c. H-bond |
| 280K Single | N10 | H30 | x,y,z | 1−x,1/2+y,1/2−z | 2.511 | −0.239 | −0.019 | n.c. H-bond |
| 280K Single | N6 | H2 | x,y,z | 1−x,1/2+y,1/2−z | 2.531 | −0.219 | 0.001 | n.c. H-bond |
| 280K Single | N8 | H5 | x,y,z | 1−x,1/2+y,1/2−z | 2.617 | −0.133 | 0.087 | n.c. H-bond |
| 280K Single | N1S | H35 | 1−x,1/2+y,1/2−z | x,1.5−y,1/2+z | 2.625 | −0.125 | 0.095 | n.c. H-bond |
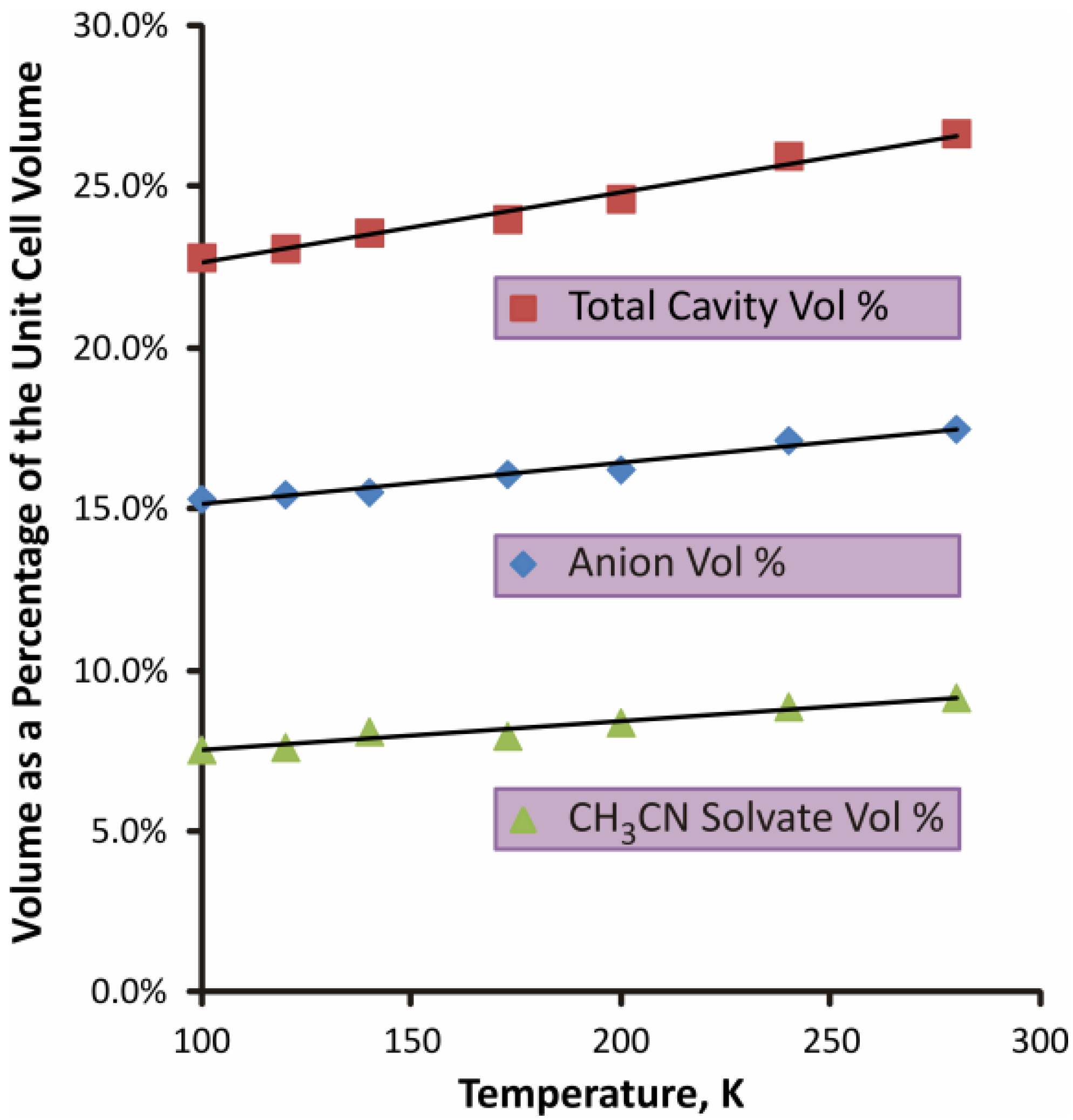
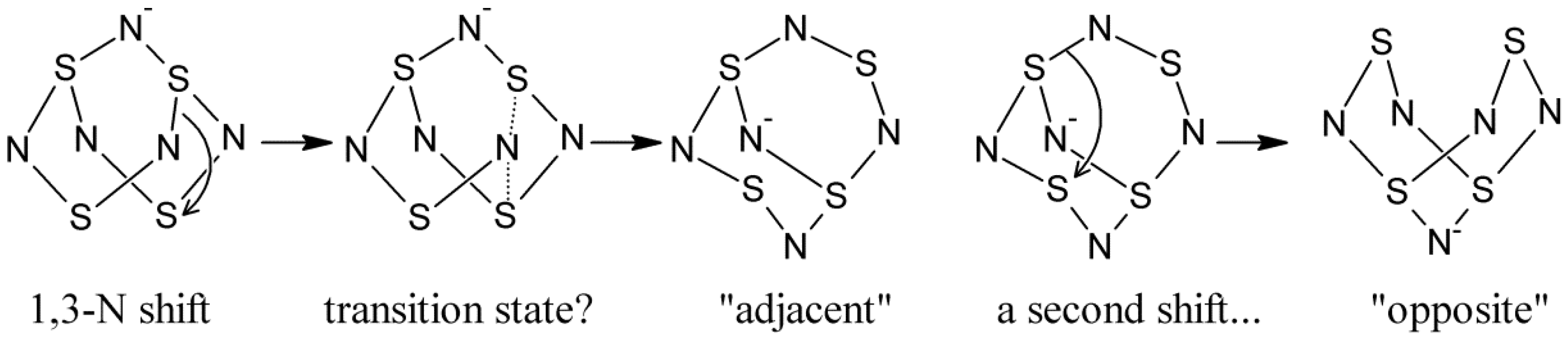
2.2. Density Functional Theory Study of the Geometry of S4N5− in the Gas Phase
2.3. Confirmation and Assignment of the Bands in Infra-red Spectra of S4N5−
| Mode | DFT calc. cm−1 a | Calc. rel. intensity a | Ave. exptl. cm−1 b | PPN+ c nujol/CsI | Li+ d nujol/CsI | NH4+ d nujol/CsI | PipNH2+ e nujol/CsI | Na+ f KBr |
|---|---|---|---|---|---|---|---|---|
| 1b2 | 940 | 1.00 | 946, vs | 955, s | 940, vs | 940, vs | 945, vs | 950, vs |
| 1a1 | 897 | 0.50 | 906, vs | 916, s | 910, vs | 910, vs | 910, vs | 885, sh |
| 1a2 | 798 | 0.00 | not obs. | — | — | — | — | — |
| 2a1 | 706 | 0.01 | 744, m | 757, m | 750, m | 735, s | 735, s | 745, s |
| 2b2 | 688 | 0.01 | 731, m g | 747, m | — | 725, s | 725, s | 725, w |
| 1b1 | 688 | 0.27 | 693, s g | — | 700,s s | 685, s | 685, s | 700, s |
| 3a1 | 659 | 0.18 | 667, m | 666, w | 670, s | 663, s | 670, s | 665, vs |
| 3b2 | 631 | 0.11 | 645, w | 647, w | — | — | 652, m | 635, w |
| 2b1 | 620 | 0.07 | 623, w | — | 625, w | 620, w | 625, m | — |
| 4a1 | 597 | 0.02 | not obs. | — | — | — | — | — |
| 3b1 | 573 | 0.23 | 600, s | 598, m | 600, s | 600, s | 600, s | 600, vs |
| 2a2 | 562 | 0.00 | not obs. | — | — | — | — | — |
| 5a1 | 516 | 0.10 | 531, s | — | 530, s | 530, s | 532, s | 530, vs |
| 4b2 | 489 | 0.04 | 505, s | — | 510, m | 500, s | 503, s | 505, s |
| 4b1 | 423 | 0.10 | 436, s | 428, m | 440, s | 435, m | 435, s | 440, vs |
| 6a1 | 387 | 0.01 | 406, m | — | 410, m | 405, m | 400, m | 410, s |
| 3a2 | 322 | 0.00 | 338, w | — | 345, w | 335, w | 335, w | 335, w |
| 5b2 | 314 | 0.00 | not obs. | — | — | — | — | — |
| 5b1 | 286 | 0.06 | 304, w | 300, vw | 310, m | 300, w | 305, m | 305, m |
| 4a2 | 252 | 0.00 | not obs. | — | — | — | — | |
| 7a1 | 155 | 0.00 | not obs. | Beyond range of experiments. | ||||
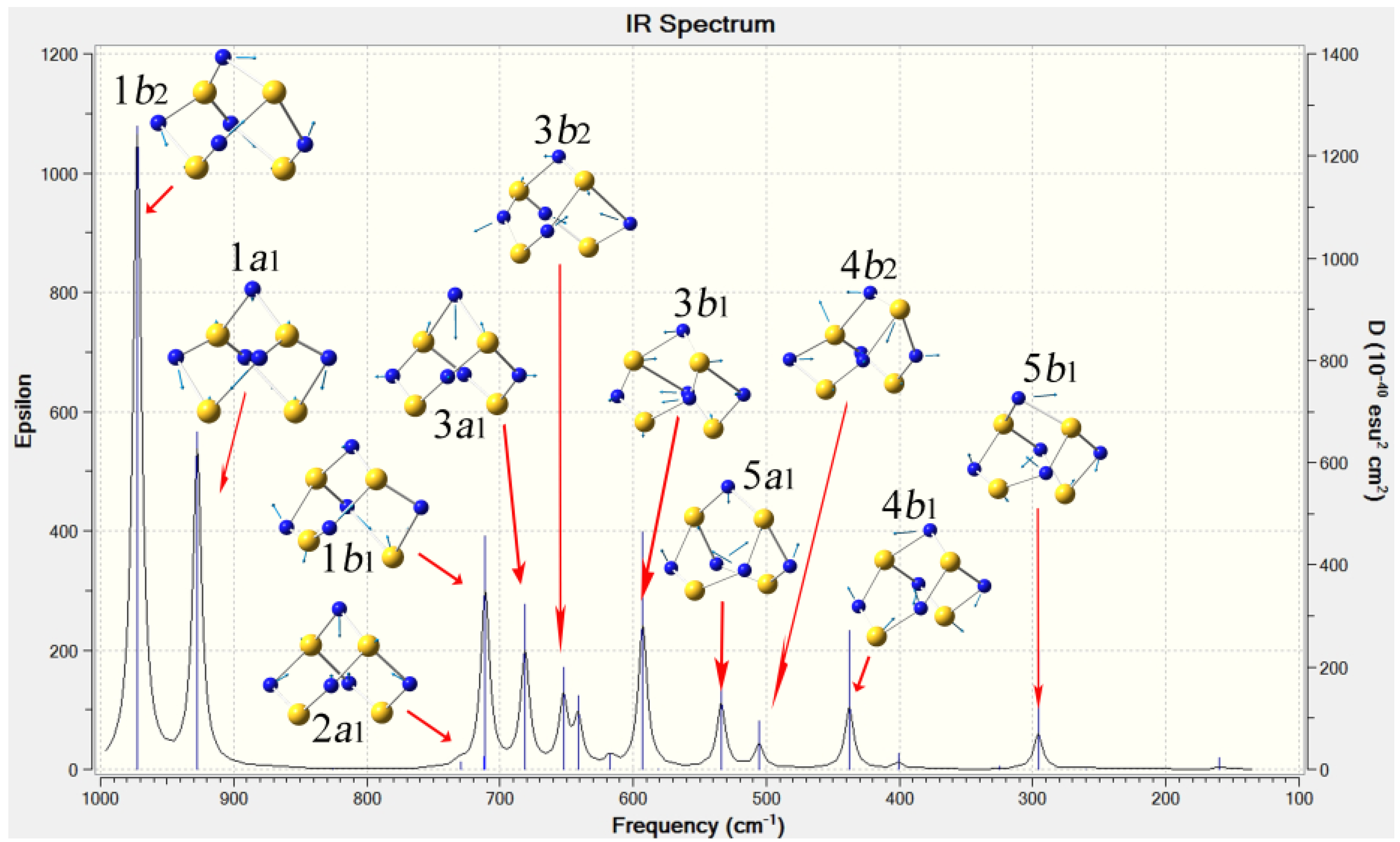
3. Experimental
CAUTION: salts of S4N5− and other binary sulfur-nitrides are notorious contact explosives. Any attempts to prepare or handle them must only be undertaken by appropriately qualified personnel, properly supervised, and taking all necessary precautionary measures.
| Parameter | 100 K | 120 K | 140 K | 172 K | 200 K | 240 K | 280 K |
|---|---|---|---|---|---|---|---|
| a, Å | 10.8717(5) | 10.8904(6) | 10.9331(5) | 10.9878(6) | 11.0218(5) | 11.0664(7) | 11.131(18) |
| b, Å | 17.7722(8) | 17.7756(10) | 17.8025(8) | 17.8189(10) | 17.8463(8) | 17.8745(11) | 17.92(3) |
| c, Å | 18.8902(8) | 18.8948(11) | 18.9084(9) | 18.9099(11) | 18.9487(9) | 18.9951(11) | 19.14(3) |
| β, ° | 95.0291(5)° | 95.0132(7) | 94.9623(5) | 94.8670(10) | 94.8131(5) | 94.7601(7) | 94.601(19) |
| Volume, Å3 | 3635.8(3) | 3643.7(4) | 3666.5(3) | 3689.0(4) | 3714.0(3) | 3744.4(4) | 3805(11) |
| Dcalc, g cm−1 | 1.421 | 1.418 | 1.409 | 1.401 | 1.391 | 1.380 | 1.358 |
| μ, mm−1 | 0.390 | 0.389 | 0.387 | 0.384 | 0.382 | 0.378 | 0.372 |
| Tmin | 0.7456 | 0.4305 | 0.7456 | 0.4309 | 0.7456 | 0.7456 | 0.7456 |
| Tmax | 0.6942 | 0.3780 | 0.6971 | 0.3928 | 0.7059 | 0.6858 | 0.5867 |
| Cr. max, mm | 0.41 | 0.21 | 0.41 | 0.35 | 0.41 | 0.41 | 0.41 |
| mid, mm | 0.20 | 0.11 | 0.20 | 0.22 | 0.20 | 0.20 | 0.20 |
| min, mm | 0.17 | 0.10 | 0.17 | 0.15 | 0.17 | 0.17 | 0.17 |
| Rfl. Measured | 51759 | 41490 | 41636 | 38803 | 52563 | 42717 | 41322 |
| Index ranges: h | −14, 14 | −14, 14 | −14, 14 | −13, 13 | −14, 14 | −14, 14 | −14, 14 |
| k | −23, 23 | −23, 23 | −23, 23 | −22, 22 | −23, 23 | −23, 23 | −23, 23 |
| l | −24, 24 | −24, 24 | −24, 24 | −23, 23 | −24, 24 | −24, 24 | −24, 24 |
| θ limit, ° | 27.480 | 27.437 | 27.427 | 26.373 | 27.388 | 27.440 | 27.448 |
| Unique data | 8283 | 8298 | 8302 | 7522 | 8381 | 8517 | 8594 |
| Restraints | 34 | 64 | 46 | 170 | 62 | 0 | 0 |
| Parameters | 516 | 536 | 542 | 542 | 542 | 470 | 470 |
| G.O.F. on F2 | 1.038 | 1.051 | 1.041 | 1.027 | 1.026 | 1.055 | 1.051 |
| R1 | 0.0298 | 0.0361 | 0.0357 | 0.0326 | 0.0339 | 0.0467 | 0.0492 |
| wR2 [I ≥ 2σ(I)] | 0.0765 | 0.0800 | 0.0935 | 0.0853 | 0.0903 | 0.1216 | 0.1287 |
| Largest pk, eÅ−3 | 0.422 | 0.391 | 0.584 | 0.378 | 0.359 | 0.529 | 0.548 |
| Largest hl, eÅ−3 | −0.297 | −0.333 | −0.281 | −0.287 | −0.289 | −0.565 | −0.497 |
4. Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- Chivers, T. A Guide to Chalcogen-Nitrogen Chemistry; World Scientific: Singapore, 2005. [Google Scholar]
- Oakley, R.T. Cyclic and heterocyclic thiazenes. Prog. Inorg. Chem. 1988, 36, 299–391. [Google Scholar] [CrossRef]
- Chivers, T. Synthetic methods and structure-reactivity relationships in electron-rich sulfur-nitrogen rings and cages. Chem. Rev. 1985, 85, 341–365. [Google Scholar] [CrossRef]
- Chivers, T.; Oakley, R.T. Sulfur-nitrogen anions and related compounds. Top. Curr. Chem. 1982, 102, 117–147. [Google Scholar] [CrossRef]
- Chivers, T.; Oakley, R.T. Thermal decomposition of binary sulphur-nitrogen anions; preparation and X-ray crystal structure of (Ph3P)2N+ S4N−. J. Chem. Soc. Chem. Commun. 1979, 17, 752–753. [Google Scholar] [CrossRef]
- Chivers, T.; Laidlaw, W.G.; Oakley, R.T.; Trsic, M. Synthesis and Crystal and Molecular Structure of [(Ph3P)2N+][S4N−] and the electronic structure of the planar acyclic anion, S4N−. J. Am. Chem. Soc. 1980, 102, 5773–5781. [Google Scholar]
- Burford, N.; Chivers, T.; Cordes, A.W.; Oakley, R.T.; Pennington, W.T.; Swepston, P.N. Molecular structure of Ph4As+S4N− and a re-refinement of the structure of PPN+S4N−. Inorg. Chem. 1981, 20, 4430–4432. [Google Scholar] [CrossRef]
- Chivers, T.; Cordes, A.W.; Oakley, R.T.; Pennington, W.T. The oxidation of the trisulphur trinitride anion S3N3− by molecular oxygen; preparation and the crystal and molecular structure of [(Ph3P)2N]+ [S3N3O] −. J. Chem. Soc. Chem. Commun. 1981, 23, 1214–1215. [Google Scholar]
- Bojes, J.; Chivers, T.; Codding, P.W. Preparation and X-ray crystal structures of copper(I) complexes of the S3N− ion. J. Chem. Soc. Chem. Commun. 1981, 22, 1171–1173. [Google Scholar] [CrossRef]
- Chivers, T.; Cordes, A.W.; Oakley, R.T.; Pennington, W.T. I5N NMR study of the oxidation of the trisulfur trinitride anion by molecular oxygen: A comparison of the molecular and electronic structures of the S3N3−, S3N3O−, and S3N3O2– ions. Inorg. Chem. 1983, 22, 2429–2435. [Google Scholar] [CrossRef]
- Seel, F.; Kuhn, R.; Simon, G. Bis(triphenylphosphane)iminium-monothionitrate. Z. Naturforsch. Sect. B 1984, 39, 1622–1623. [Google Scholar]
- Seel, F.; Kuhn, R.; Simon, G. PNP-perthionitrite and PNP-monothionitrite. Z. Naturforsch. Sect. B 1985, 40, 1607–1617. [Google Scholar]
- Weiss, J. Metal sulfur-nitrogen compounds. 19. Novel complex of Cu-I with the S3N− chelate ligand. Preparation and structure of [Ph4As][Cu(S3N)(CN)], [(Ph3P)2N][Cu(S3N)(S7N)], and [Ph4As]2[(S3N)Cu(S2O3)Cu(S3N)]. Z. Anorg. Allg. Chem. 1986, 532, 184–192. [Google Scholar] [CrossRef]
- Weiss, J. Metal sulfur-nitrogen compounds. 20. Reaction products of PdCl2 and Pd(CN)2 with the S7NH. Preparation and structure of the complexes [(Ph6P2N][Pd(S3N)(S5)] and X[Pd(S3N)(CN)2] X = [Me4N]+, [Ph4P]+. Z. Anorg. Allg. Chem. 1986, 542, 137–143. [Google Scholar] [CrossRef]
- El-Kholi, A.; Christophersen, R.; Muller, U.; Dehnicke, K. Synthesis and crystal-structures of [N (Ph3P)2][VCl3(N3S2)]∙C7H8. Z. Naturforsch. Sect. B 1987, 42, 410–414. [Google Scholar]
- Weiss, J. Metal sulfur-nitrogen compounds. 22. S4N3Cl as a starting material for the preparation of complexes containing the S3N− ligand. Complexes [(Ph6P2N][Cu3(S3N)2(CN)2] and [(Ph4As][(CuS3N)2(CN)]. Z. Anorg. Allg. Chem. 1988, 559, 106–110. [Google Scholar] [CrossRef]
- Kabanos, T.A.; Slawin, A.M.Z.; Williams, D.J.; Woollins, J.D. Non-oxo molybdenum compounds: The preparation and X-ray structure of [(Ph3P)2N][Mo(N3S3)(dtbc)]∙CH2Cl2. Polyhedron 1992, 11, 995–997. [Google Scholar]
- Chivers, T.; Oakley, R.T.; Scherer, O.J.; Wolmershäuser, G. Synthesis and nuclear magnetic resonance spectra of 15N-enriched sulfur-nitrogen compounds. Inorg. Chem. 1981, 20, 914–917. [Google Scholar]
- Chivers, T.; Schmidt, K.J.; McIntyre, D.D.; Vogel, H.J. Spectroscopic studies of N-S-O anions: The reactions of NSO− with elemental sulphur and with S4N4. Can. J. Chem. 1989, 67, 1788–1794. [Google Scholar] [CrossRef]
- Chivers, T.; Schmidt, K.J. Sulphur-nitrogen anions: 14N and 15N NMR investigations of the deprotonation of cyclic sulphur imides and sulphur-ammonia solutions. Can. J. Chem. 1992, 70, 710–718. [Google Scholar] [CrossRef]
- Chivers, T.; Hojo, M. Electrochemical studies of sulfur-nitrogen compounds. 1. The trisulfur trinitride and tetrasulfur pentanitride anions and further investigations of tetrasulfur tetranitride. Inorg. Chem. 1984, 23, 1526–1530. [Google Scholar] [CrossRef]
- Fritz, H.P.; Bruchhaus, R.; Mews, R.; Höfs, H.-U. Electrochemical syntheses. XXIII. Electrochemical and EPR-spectroscopic investigation of the redox behaviour of (SN)+ and [S3N3]−. Z. Anorg. Allg. Chem. 1985, 525, 214–220. [Google Scholar] [CrossRef]
- Fritz, H.P.; Bruchhaus, R. Electrochemical syntheses. 21. Cyclovoltammetric and EPR-spectroscopic study of redox behaviour of [S4N5]− ions. Electrochim. Acta 1984, 29, 947–950. [Google Scholar]
- Boeré, R.T.; Chivers, T.; Roemmele, T.L.; Tuononen, H.M. Electrochemical and electronic structure investigations of the [S3N3]∙ radical and kinetic modeling of the [S4N4]n/[S3N3]n (n = 0, −1) interconversion. Inorg. Chem. 2009, 48, 7294–7306. [Google Scholar]
- Waluk, J.W.; Michl, J. Magnetic crcular dichroism of cyclic π-electron systems. 21. The trisulfur trinitride anion. Inorg. Chem. 1981, 20, 963–965. [Google Scholar] [CrossRef]
- Klein, H.-P.; Oakley, R.T.; Michl, J. Magnetic crcular dichroism of cyclic π-electron systems. 28. Sulfur-nitrogen heterocycles. Inorg. Chem. 1986, 25, 3194–3201. [Google Scholar] [CrossRef]
- Bojes, T.; Chivers, T.; Laidlaw, W.G.; Trsic, M. The thio analogue of peroxynitrite, [SSNS−]: Preparation, electronic structure, resonance raman spectrum, and formation of complexes with nickel and cobalt. J. Am. Chem. Soc. 1982, 104, 4837–4841. [Google Scholar]
- Chivers, T.; Rao, M.N.S. Reactions of the trisulfur trinitride anion, S3N3−, with halogens and other electrophilic substrates. Can. J. Chem. 1983, 61, 1957–1962. [Google Scholar] [CrossRef]
- Boeré, R.T.; Tuononen, H.M.; Chivers, T.; Roemmele, T.L. Structures and EPR spectra of binary sulfur–nitrogen radicals from DFT calculations. J. Organomet. Chem. 2007, 692, 2683–2696. [Google Scholar] [CrossRef]
- Boeré, R.T.; Roemmele, T.L. Chalcogen–Nitrogen Radicals. In Comprehensive Inorganic Chemistry: From Elements to Applications, 2nd ed.; Reedijk, J., Poeppelmeier, K., Eds.; Elsevier: Oxford, UK, 2013; Volume 1, pp. 375–411. [Google Scholar]
- Roemmele, T.L.; Konu, J.; Boeré, R.T.; Chivers, T. Electrochemical and chemical reduction of Disulfur dinitride: Formation of [S4N4]−, EPR spectroscopic characterization of the [S2N2H]∙ radical, and X-ray structure of [Na(15-crown-5)][S3N3]. Inorg. Chem. 2009, 48, 9454–9462. [Google Scholar] [CrossRef]
- Flues, W.; Scherer, O.J.; Weiss, J.; Wolmershäuser, G. Crystal and molecular structure of the tetrasulfur pentanitride anion. Angew. Chem. Int. Ed. 1976, 15, 379–380. [Google Scholar] [CrossRef]
- Martan, H.; Weiss, J. Dithaliumtrischweveltrinitrid-tetraschwefelpentanitrid, Tl2S7N8. Acta Cryst. 1983, B39, 959–960. [Google Scholar]
- Braga, D.; Maini, L.; Polito, M.; Grepioni, F. Hydrogen bonding interactions between ions: A powerful tool in molecular crystal engineering. Struct. Bond. 2004, 111, 1–32. [Google Scholar]
- Scherer, O.J.; Wolmershäuser, G. Synthesis of the tetrasulfur pentanitride anion. Angew. Chem. Int. Ed. 1975, 14, 485–486. [Google Scholar] [CrossRef]
- Chivers, T.; Drummond, I. Studies of sulfur imides in basic organic solvents. Synthesis and characterization of tetra-n-butylammonium perthionitrate, (n-C4H9)N(NS4). Inorg. Chem. 1974, 13, 1222–1225. [Google Scholar]
- Scherer, O.J.; Wolmershäuser, G. Ubiquitous ammonium tetrasulfur pentanitride, NH4[S4N5]. Chem. Ber. 1977, 111, 3241–3466. [Google Scholar]
- Bojes, J.; Chivers, T. Preparation of the binary sulfur-nitrogen anions S3N3− and S4N5− from tetrasulfur tetranitride and azides and the vibrational spectra of S3N3− and S4N5−. Inorg. Chem. 1978, 17, 318–321. [Google Scholar] [CrossRef]
- Bojes, J.; Chivers, T.; Drummond, I.; MacLean, G. Central role of the S3N3− and S4N5− ions in the deprotonation of tetrasulfur tetraimide and in the reductive or nucleophilic degradation of tetrasulfur tetranitride. Inorg. Chem. 1978, 17, 3668–3672. [Google Scholar] [CrossRef]
- Bojes, J.; Chivers, T.; Oakley, R.T. Binary cyclic nitrogen-sulfur anions. Inorg. Synth. 1989, 25, 30–35. [Google Scholar] [CrossRef]
- Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent radii revisited. Dalton Trans. 2008, 2832–2838. [Google Scholar] [CrossRef]
- Moock, K.H.; Wong, K.M.; Boeré, R.T. 1,5,2,4,6,8-Dithiatetrazocine. Synthesis, computation, crystallography and voltammetry of the parent heterocycle. Dalton Trans. 2011, 40, 11599–11604. [Google Scholar] [CrossRef]
- Bondi, A. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar]
- Mantina, M.; Chamberlin, A.C.; Valero, R.; Cramer, C.J.; Truhlar, D.G. Consistent van der Waals radii for the whole main group. J. Phys. Chem. A 2009, 113, 5806–5812. [Google Scholar] [CrossRef]
- Allen, F.H. The Cambridge Structural Database: A quarter of a million crystal structures and rising. Acta Cryst. 2002, B58, 380–388. [Google Scholar]
- Lewis, G.R.; Dance, I. Crystal supramolecularity. Multiple phenyl embraces by [PPN] cations. Dalton Trans. 2000, 299–306. [Google Scholar] [CrossRef]
- Blake, A.J.; Freeman, G.; Johnson, B.F.G.; McDougall, G.S. Bis(triphenylphosphine)iminium hexafluorophosphate dichloromethane solvate (1/1). Acta Cryst. 1994, C50, 1301–1303. [Google Scholar]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Defining the hydrogen bond: An account (IUPAC Technical Report). Pure Appl. Chem. 2011, 83, 1619–1636. [Google Scholar] [CrossRef]
- Lakshmi, B.; Samuelson, A.G.; Jovan Jose, K.V.; Gadreb, S.R.; Arunan, E. Is there a hydrogen bond radius? Evidence from microwave spectroscopy, neutron scattering and X-ray diffraction results. New J. Chem. 2005, 29, 371–377. [Google Scholar] [CrossRef]
- Raghavendra, B.; Mandal, P.K.; Arunan, E. Ab initio and AIM theoretical analysis of hydrogen-bond radius of HD (D = F, Cl, Br, CN, HO, HS and CCH) donors and some acceptors. Phys. Chem. Chem. Phys. 2006, 8, 5276–5286. [Google Scholar]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond in Structural Chemistry and Biology, 2nd ed.; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Macrae, C.F.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Shields, G.P.; Taylor, R.; Towler, M.; van de Streek, J. Mercury: Visualization and analysis of crystal structures. J. Appl. Cryst. 2006, 39, 453–457. [Google Scholar]
- Boeré, R.T.; Oakley, R.T.; Shevalier, M. Thermal stability and fluxional behaviour of bicyclic sulphur-nitrogen structures of formula EN5S3 (E = CR, PR2, or SO2−). J. Chem. Soc. Chem. Commun. 1987, 2, 110–112. [Google Scholar]
- Bestari, K.T.; Boeré, R.T.; Oakley, R.T. Degenerate and pseudodegenerate 1,3-nitrogen shifts in sulfur-nitrogen chemistry: 15N NMR analysis of skeletal scrambling in PhCN5S3. J. Am. Chem. Soc. 1989, 111, 1579–1584. [Google Scholar] [CrossRef]
- Boeré, R.T.; Cordes, A.W.; Oakley, R.T. 1,3-Nitrogen shift reaction in sulfur-nitrogen chemistry. Preparation and interconversion of exo- and endo-trithiatetrazocines. J. Am. Chem. Soc. 1987, 109, 7781–7785. [Google Scholar]
- Bartetzko, R.; Gleiter, R. The structures of S4N5−, S4N5+, and S5N6. A rationalization based upon molecular orbital theory. Chem. Ber. 1980, 113, 1138–1144. [Google Scholar]
- Gleiter, R. Structure and bonding in cyclic sulfur-nitrogen compounds-molecular orbital considerations. Angew. Chem. Int. Ed. 1981, 20, 444–452. [Google Scholar]
- Rzepa, H.S.; Woollins, J.D. A PM3 SCF-MO study of the structure and bonding in the cage systems S4N4 and S4N4X (X = N+, S, N2S, P+, C, Si, B− and Al−). Polyhedron 1990, 9, 107–111. [Google Scholar] [CrossRef]
- Chivers, T.; Fielding, L.; Laidlaw, W.G.; Trsic, M. Synthesis and structure of salts of the bicyclic sulfur-nitrogen cation S4N5+ and a comparison of the electronic structures of the tetrasulfur pentanitride (1+) and (l−) ions. Inorg. Chem. 1979, 12, 3379–3388. [Google Scholar]
- Johnson, R.D., III (Ed.) NIST Computational chemistry comparison and benchmark database. NIST standard reference database number 101, release 16a. August 2013. Available online: http://cccbdb.nist.gov/ (accessed on 2 January 2014).
- Sheldrick, G.M. A short history of SHELX. Acta Cryst. 2008, A64, 112–122. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03W; Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Zhang, G.-H.; Zhao, Y.-F.; Wu, J.I.; Schleyer, P.R. Why Are SnN4 (n = 1−4) species “missing”? Answers in a broader theoretical context of binary S−N compounds. Inorg. Chem. 2012, 51, 13321–13327. [Google Scholar] [CrossRef]
- Sample Availability: Not available.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Boeré, R.T.; Roemmele, T.L.; Krall, M.K. A Variable Temperature X-ray Diffraction Investigation of [PPN+][S4N5−]: Supramolecular Interactions Governing an Order/Disorder Transformation and the First High Resolution X-ray Structure of the Anion. Molecules 2014, 19, 1956-1975. https://doi.org/10.3390/molecules19021956
Boeré RT, Roemmele TL, Krall MK. A Variable Temperature X-ray Diffraction Investigation of [PPN+][S4N5−]: Supramolecular Interactions Governing an Order/Disorder Transformation and the First High Resolution X-ray Structure of the Anion. Molecules. 2014; 19(2):1956-1975. https://doi.org/10.3390/molecules19021956
Chicago/Turabian StyleBoeré, René T., Tracey L. Roemmele, and Maria K. Krall. 2014. "A Variable Temperature X-ray Diffraction Investigation of [PPN+][S4N5−]: Supramolecular Interactions Governing an Order/Disorder Transformation and the First High Resolution X-ray Structure of the Anion" Molecules 19, no. 2: 1956-1975. https://doi.org/10.3390/molecules19021956
APA StyleBoeré, R. T., Roemmele, T. L., & Krall, M. K. (2014). A Variable Temperature X-ray Diffraction Investigation of [PPN+][S4N5−]: Supramolecular Interactions Governing an Order/Disorder Transformation and the First High Resolution X-ray Structure of the Anion. Molecules, 19(2), 1956-1975. https://doi.org/10.3390/molecules19021956