Langevin approach to the Porto system
Abstract
:1 Introduction
- Second, the present model and its present treatment, though they are perhaps more realistic than often in similar situations, are still just theoretical and their relation to Nature may be not as obvious as it might seem at the first sight.
2 Formulation of the problem
- the Θ(t) variable has its time-dependence determined also from a dynamic equation, and
- this approach respects existing connections between dissipation (friction) incorporated and by its effect decisive in the Porto model, and properties of the stochastic forces on the right hand side of the Langevin equations that were completely ignored in [6].


 and
and  fulfil the equipartition theorem with temperature TK. Here
fulfil the equipartition theorem with temperature TK. Here  designates the en-semble average. The stochastic forces are here represented as
designates the en-semble average. The stochastic forces are here represented as

 and
and  are statistically independent times of impact events. Times between two such succeeding impacts are exponentially distributed
are statistically independent times of impact events. Times between two such succeeding impacts are exponentially distributed

 and
and  being the mean waiting times) while distributions
being the mean waiting times) while distributions  and
and  of (also stochastic and statistically independent) impact ‘forces’
of (also stochastic and statistically independent) impact ‘forces’  and
and  are, on grounds of physical arguments, assumed Gaussian. For (2) to be satisfied, these distributions should read
are, on grounds of physical arguments, assumed Gaussian. For (2) to be satisfied, these distributions should read

 . It is connected with the definition of the system as given by Porto [6]. The track consists of charges q > 0 at
. It is connected with the definition of the system as given by Porto [6]. The track consists of charges q > 0 at  and
and  with n being arbitrary integer. So, the track is neutral, periodic but without inversion symmetry. The rotor has the total mass m and apart from potentially other neutral atoms, it consists of four point charges
with n being arbitrary integer. So, the track is neutral, periodic but without inversion symmetry. The rotor has the total mass m and apart from potentially other neutral atoms, it consists of four point charges  or 2. Designating as above position of the rotor center of mass as x, their positions are
or 2. Designating as above position of the rotor center of mass as x, their positions are  , 0,
, 0,  . The two radii are
. The two radii are  and
and  . The parameter γ,
. The parameter γ,  , determines the ‘gear’ of the Porto molecular motor model. With that, the potential energy
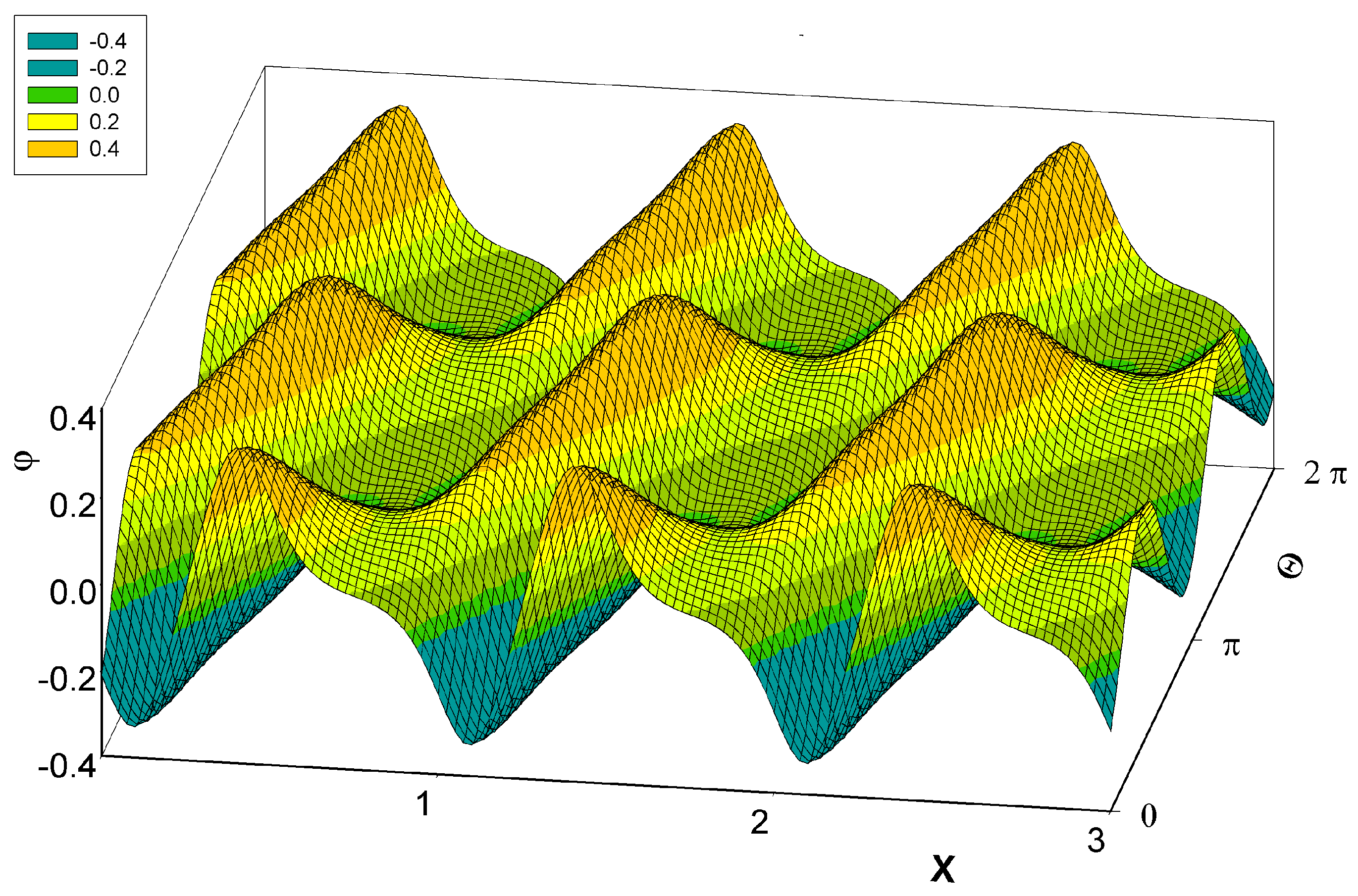
, determines the ‘gear’ of the Porto molecular motor model. With that, the potential energy  of the configuration of the charges reads
of the configuration of the charges reads

 requires some care because the individual sums
requires some care because the individual sums  are divergent.
are divergent.3 Numerical treatment




 and
and 

 and
and  , we have
, we have



 sec,
sec,  sec, temperature TK = 300 K and J = 10mb2.
sec, temperature TK = 300 K and J = 10mb2.4 Numerical solution
 . The Gaussian distributed impact forces
. The Gaussian distributed impact forces  and
and  were generated using procedure gasdev from [20].
were generated using procedure gasdev from [20]. and
and  are then .0101 and 127.5, respectively. The ratio
are then .0101 and 127.5, respectively. The ratio  . Initial values of X and Θ were always chosen at minimum points of the potential energy ϕ (see above); initial values of
. Initial values of X and Θ were always chosen at minimum points of the potential energy ϕ (see above); initial values of  and
and  were always chosen as zero.
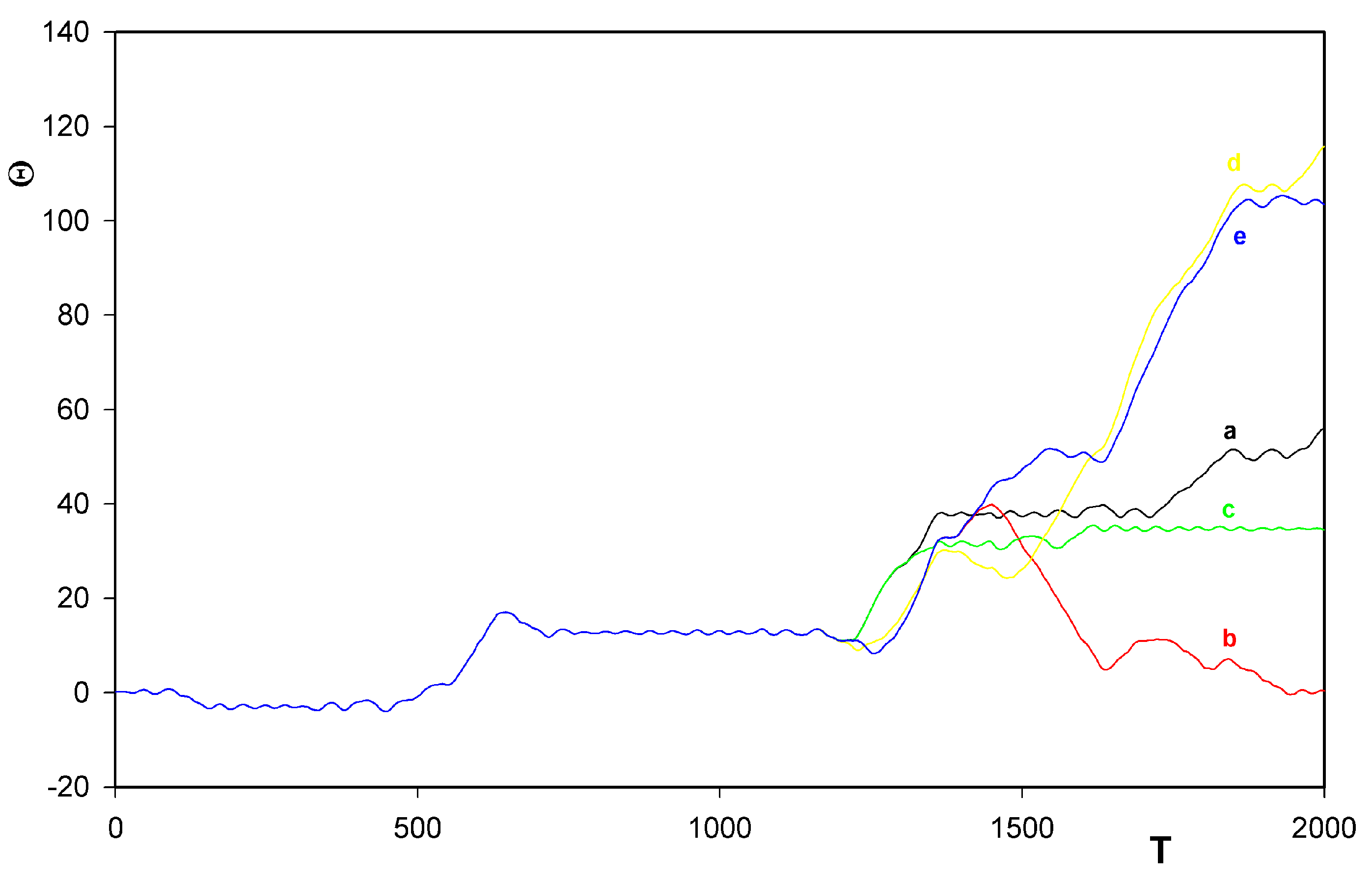
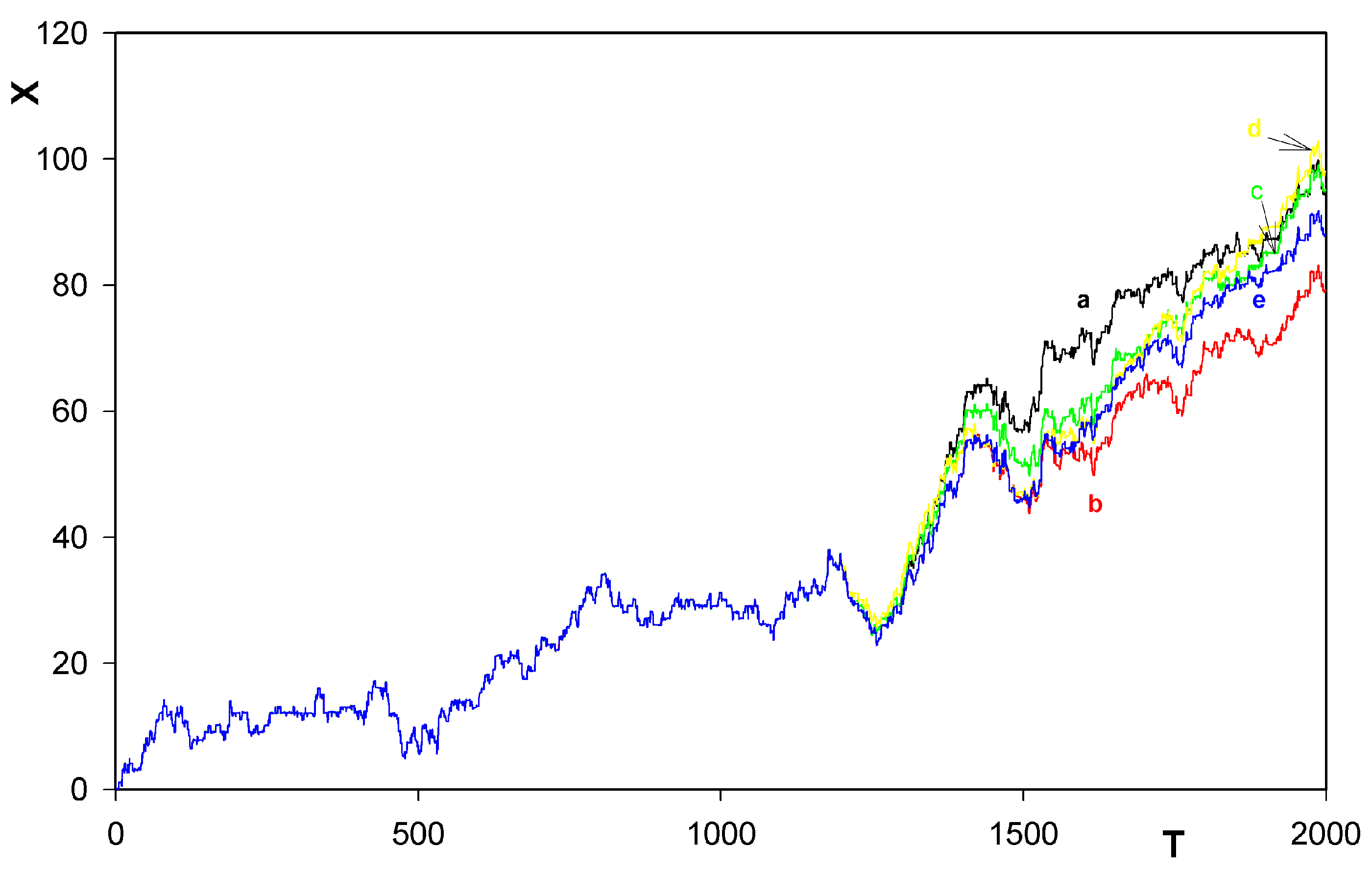
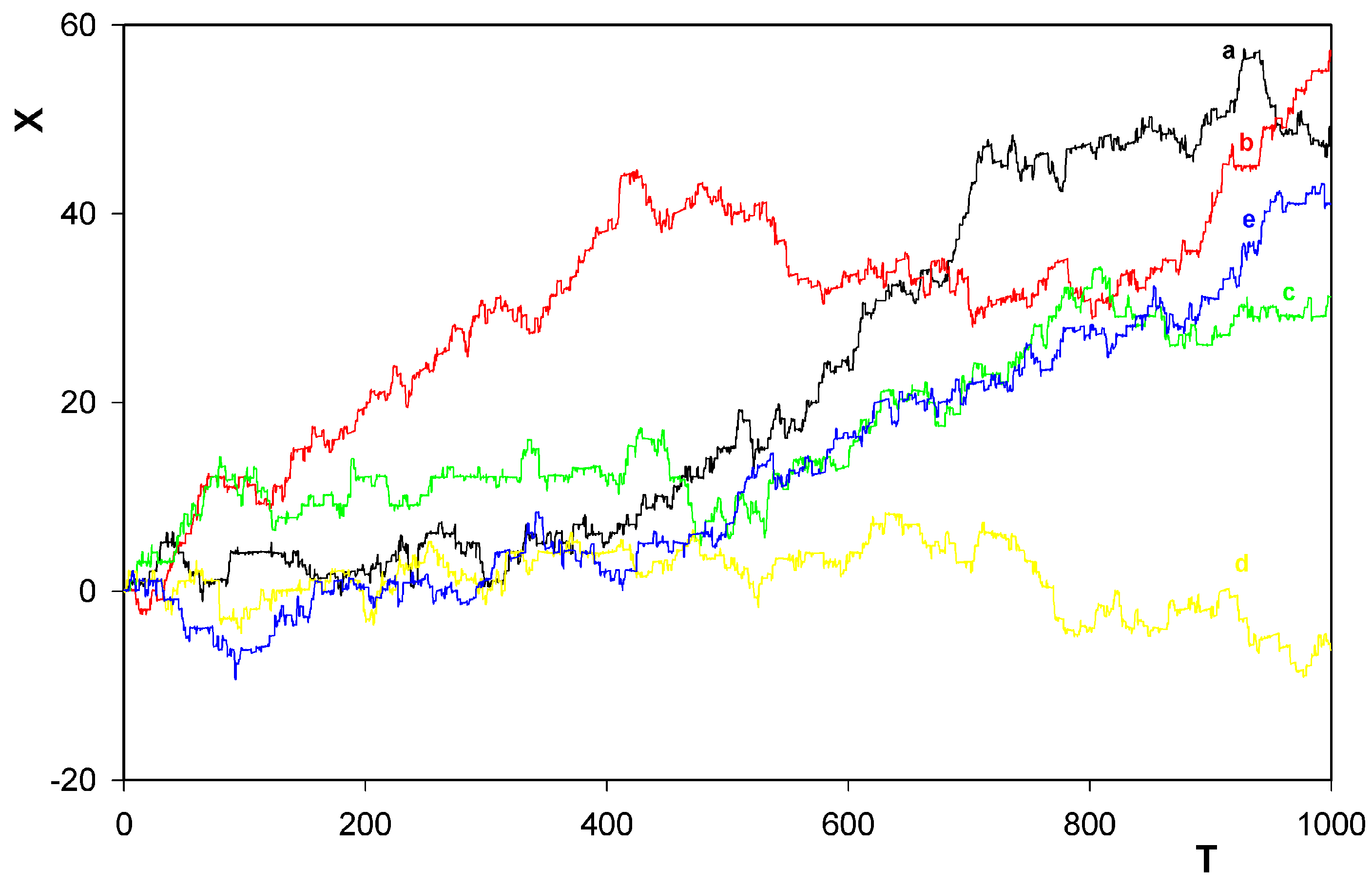
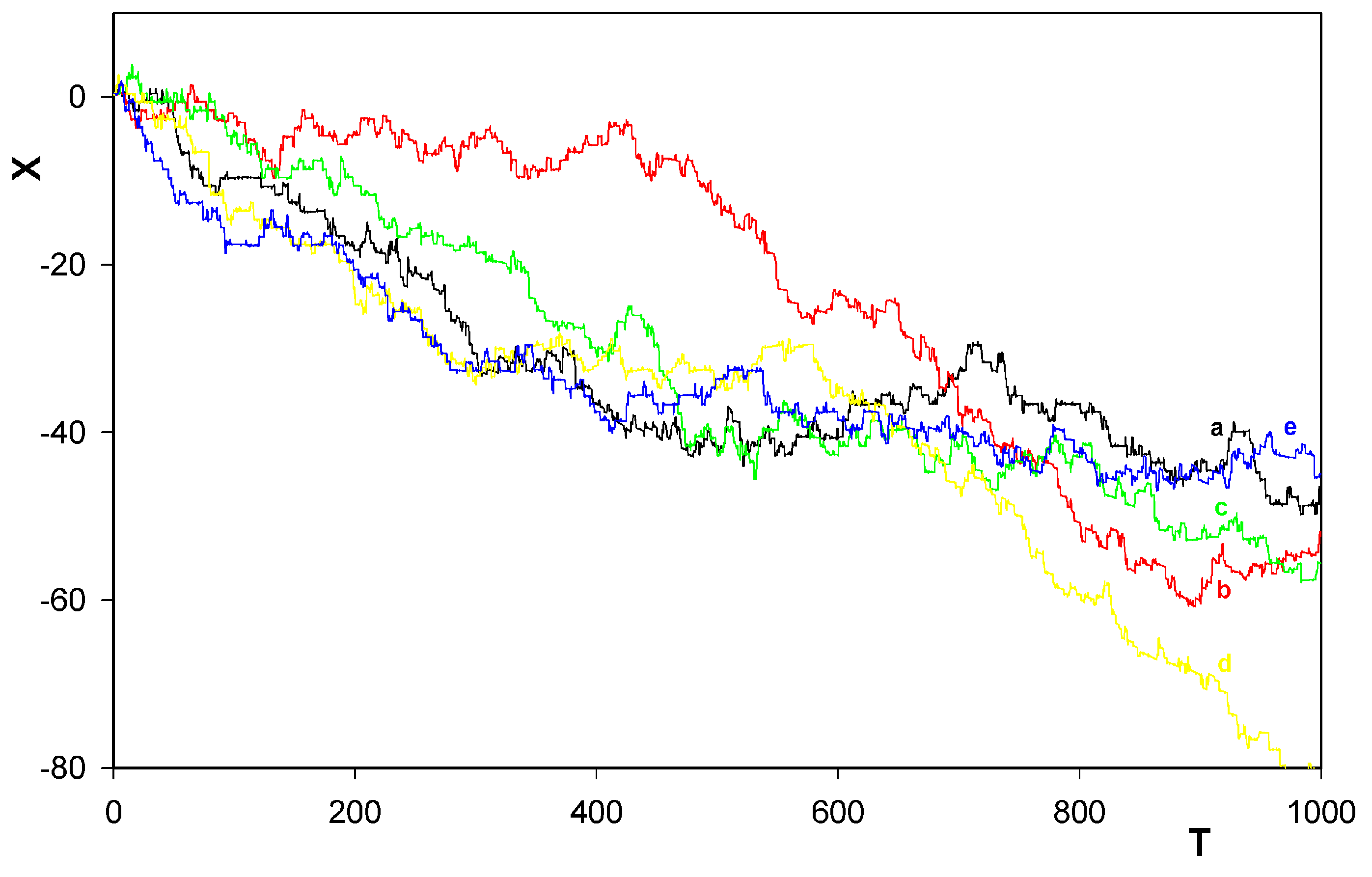
were always chosen as zero.5 Results

6 Conclusions
- Confirmation, at finite temperatures, that the rotor has a tendency to move along the track in prevailingly one direction only. This tendency was already found, in his simplified treatment corresponding inter alia to zero temperature, by Porto [6].
- Identification of another mechanism (in addition to that one found by Porto himself) also leading the unidirectional motion of the rotor along the train.
- Survival of the behavior even when the motion goes against a weak potential field.
7 Acknowledgement
References
- Feynman, R. P.; Leighton, R. B.; Sands, M. The Feynman Lectures in Physics (Addison-Wesley, Reading, 1963). Vol. 1. Chapter 46.
- Musser, G. Scientific American 280. No 2. 1999; 13. [Google Scholar]
- Porto, M.; Urbakh, M.; Klafter, J. Phys. Rev. Letters 84. 2000, 6058.
- Porto, M.; Urbakh, M.; Klafter, J. Phys. Rev. Letters 85. 2000, 491.
- Porto, M.; Urbakh, M.; Klafter, J. Acta Physica Polonica B 2001, 32, 295.
- Porto, M. Phys. Rev. E 2001, 63, 030102.
- Mori, H. Progr. Theor. Phys. 1995, 33, 423.
- Tokuyama, M.; Mori, H. Progr. Theor. Phys. 1976, 55, 411.
- Fick, E.; Sauermann, G. The Quantum Statistics of Dynamic Processes. Springer Series in Solid-State Sciences 86, (Springer-Verlag, Berlin - Heidelberg - New York - London - Paris - Tokyo - Hong Kong - Barcelona, 1990.).
- Čápek, V.; Czech. J. Phys. 1997, 47, 845.
- Čápek, V. Phys. Rev. E 1998, 57, 3846.
- Čápek, V.; Bok, J. Physica A 2001, 290, 379.
- Nikulov, A. V. Phys. Rev. B 2001, 64, 012505.
- Čápek, V. Europ. J. Phys. B 2002, 25, 101. [Google Scholar]
- Čápek, V.; Mančal, T. J. Phys. A 2002, 35, 2111.
- Sheehan, D. P. Phys. Plasmas 1995, 2, 1993.
- Nikulov, A. V.; Zhilyaev, I. N. J. Low Temp. Phys. 1998, 112, 227.
- Dubonos, S. V.; Kuznetsov, V. I.; Nikulov, V. http://arxiv.org/abs/physics/0105059.
- Čápek, V.; Sheehan, D. P. Physica A 2002, 304, 461.
- Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. Numerical Recipes in Fortran; Cambridge University Press: Cambridge (UK), 1992. [Google Scholar]
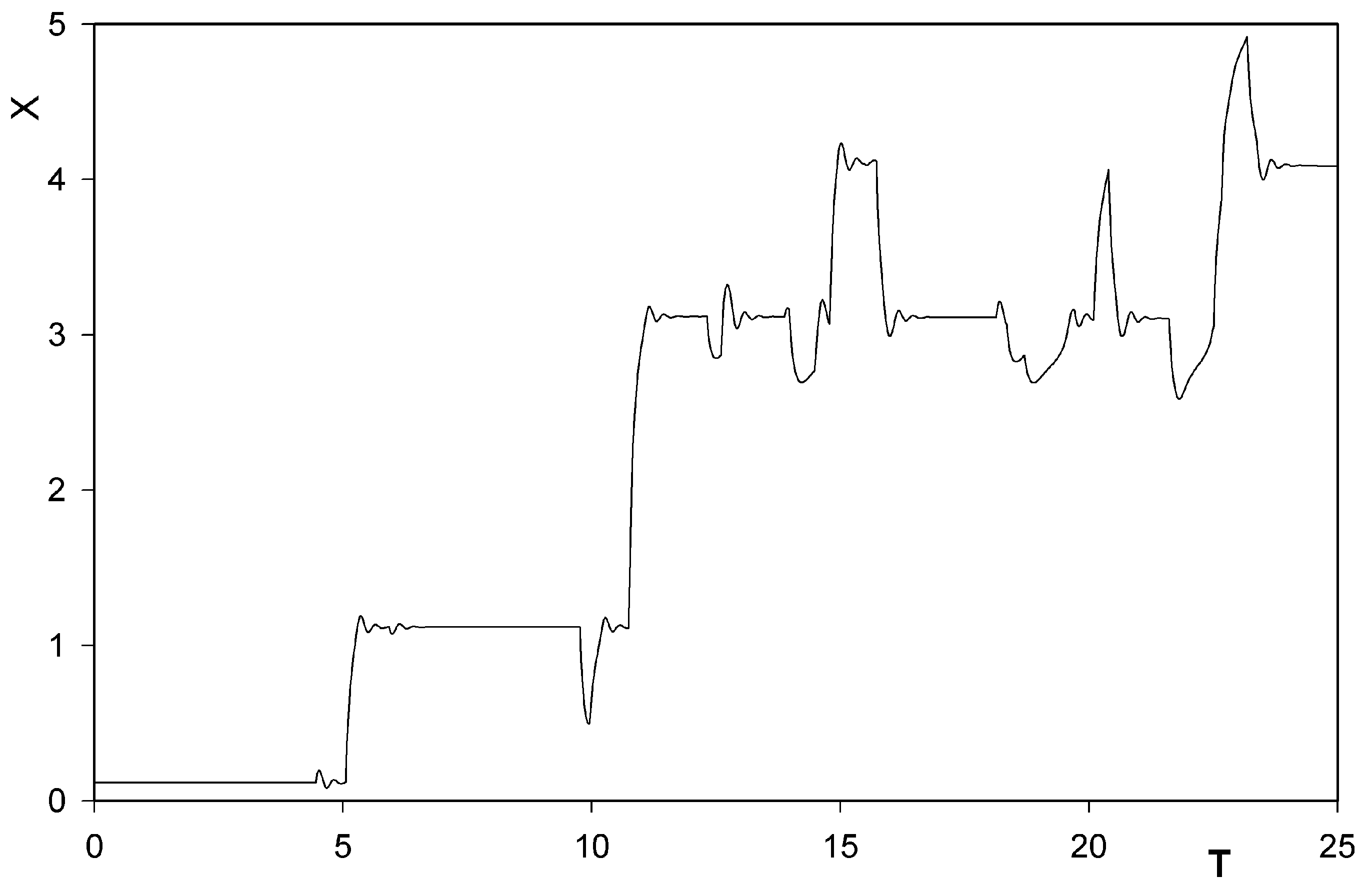

© 2004 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Bok, J.; Cápek, V. Langevin approach to the Porto system. Entropy 2004, 6, 57-67. https://doi.org/10.3390/e6010057
Bok J, Cápek V. Langevin approach to the Porto system. Entropy. 2004; 6(1):57-67. https://doi.org/10.3390/e6010057
Chicago/Turabian StyleBok, Jirí, and Vladislav Cápek. 2004. "Langevin approach to the Porto system" Entropy 6, no. 1: 57-67. https://doi.org/10.3390/e6010057



