Admissible Consensus for Descriptor Multi-Agent Systems with Exogenous Disturbances
Abstract
:1. Introduction
2. Preliminaries and Problem Formulation
2.1. Preliminaries
2.2. Problem Formulation
3. Main Results
- (i)
- The matrix is Hurwitz;
- (ii)
- , where matrix P is the unique admissible solution of (5) and , i = .
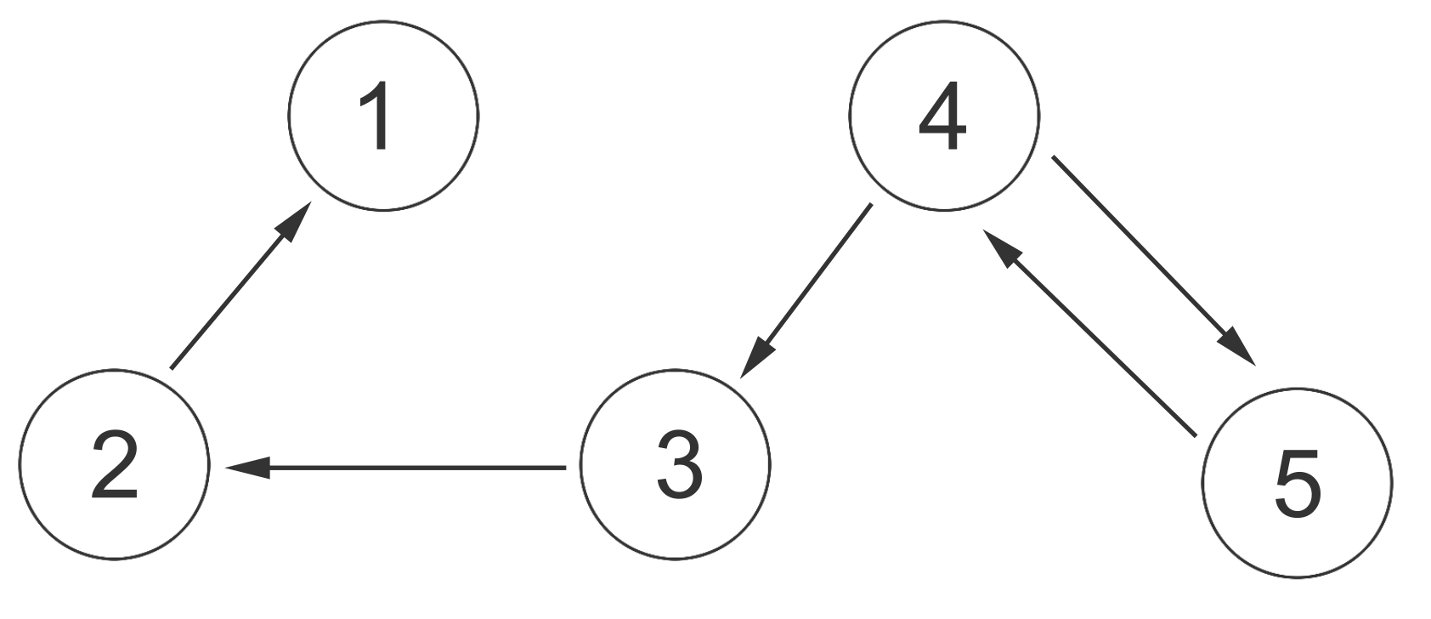
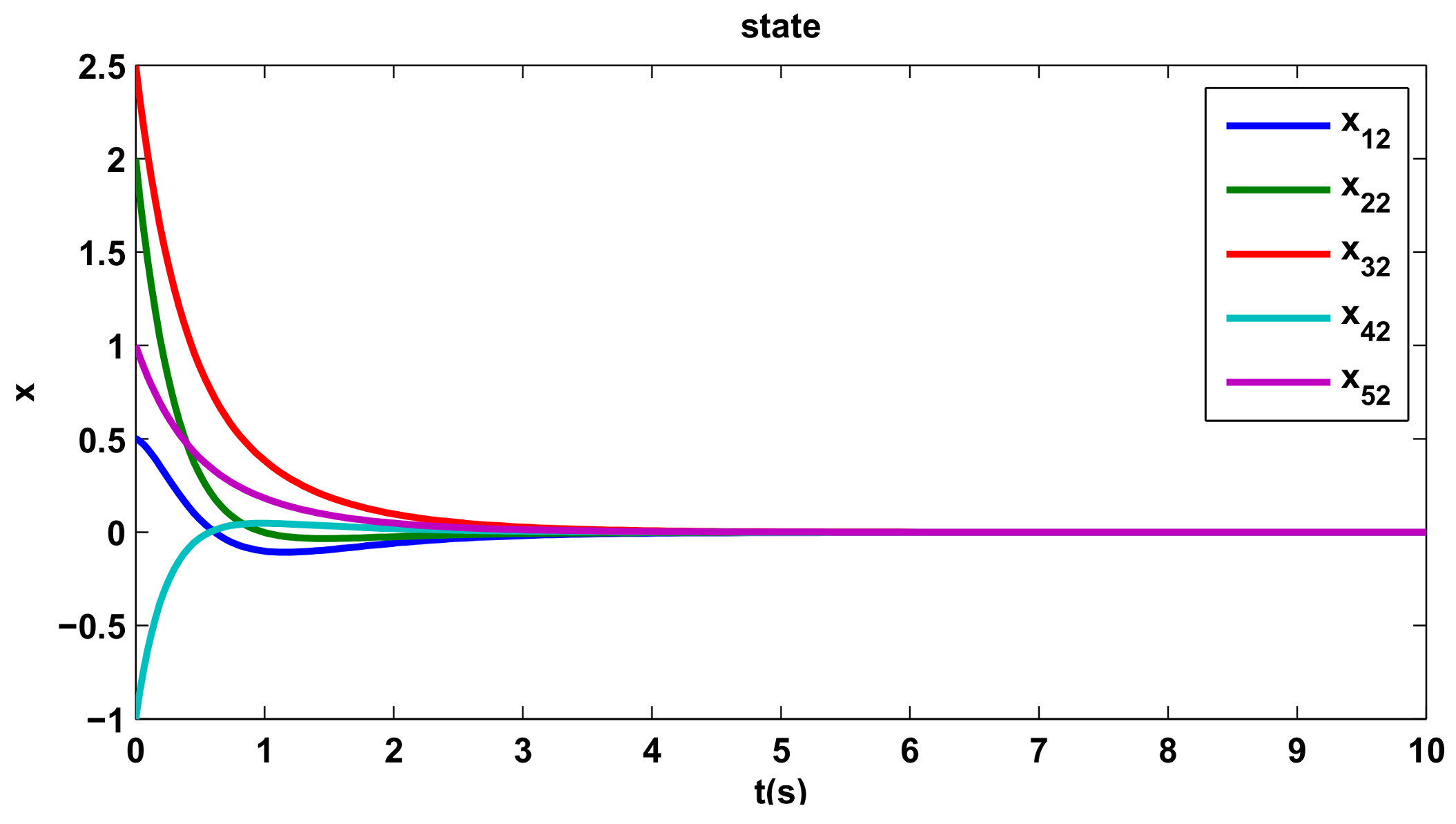
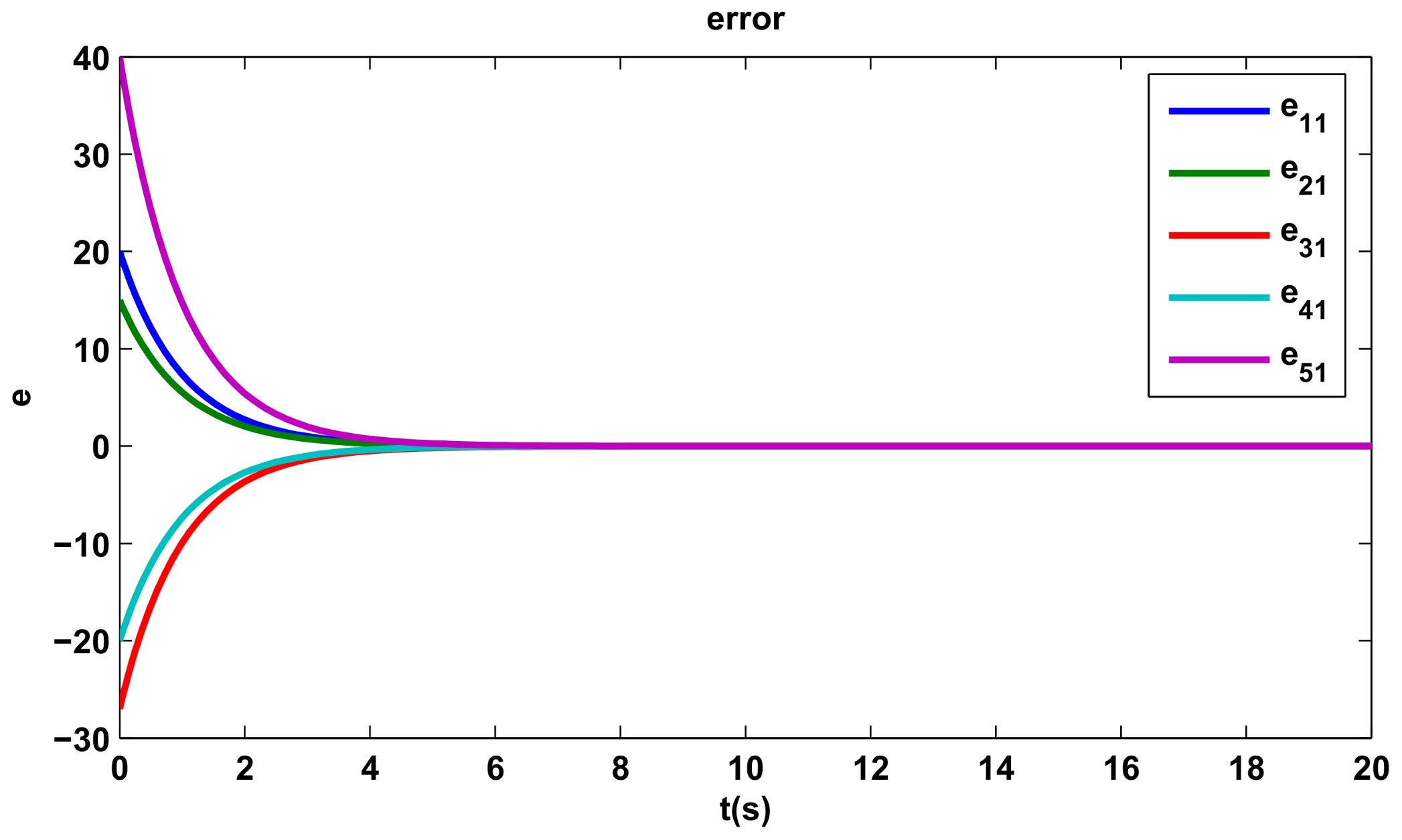
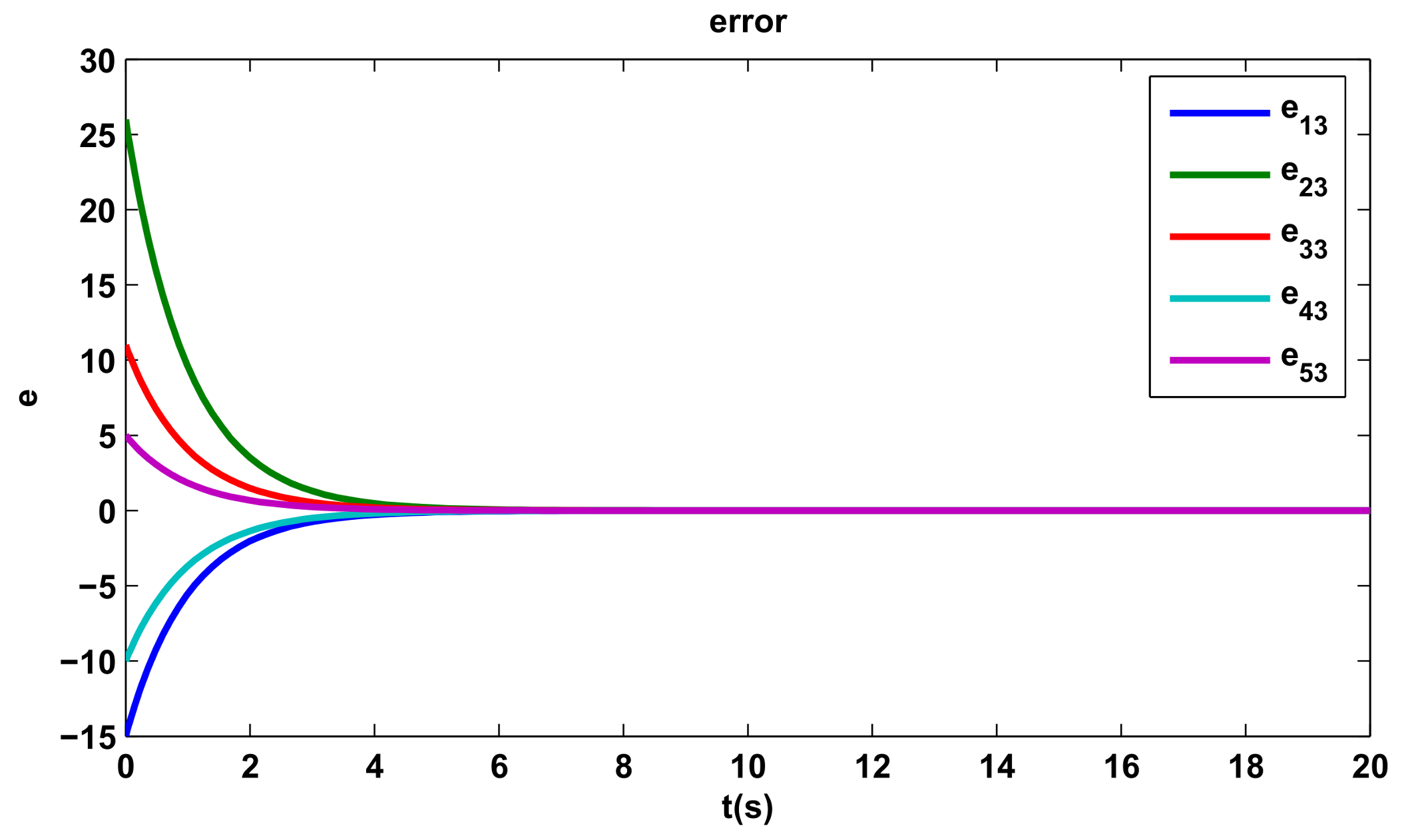
4. Simulations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rosenbrock, H.H. Structural properties of linear dynamical systems. Int. J. Control 1974, 20, 191–202. [Google Scholar] [CrossRef]
- Stevens, B.L.; Lewis, F.L. Aircraft Control and Simulation; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Hill, D.J.; Mareels, I.M.Y. Stability theory for differential/algebraic systems with application to power systems. IEEE Trans. Circuits Syst. 1990, 37, 1416–1423. [Google Scholar] [CrossRef]
- Durfee, E.H.; Lesser, V.R.; Corkill, D.D. Trends in cooperative distributed problem solving. IEEE Trans. Knowl. Data Eng. 1989, 1, 63–83. [Google Scholar] [CrossRef]
- Sastry, S.S.; Desoer, C.A. Jump behavior of circuits and systems. IEEE Conf. Decis. Control Incl. Symp. Adapt. Process. 1981, 28, 109–1124. [Google Scholar]
- Lin, Z.; Franeis, B.; Maggiore, M. Necessary and suffcient graphical condition for formation control of unicycles. IEEE Trans. Autom. Control 2005, 50, 121–127. [Google Scholar]
- Chamoso, P.; Prieta, F.D.L.; Perez, J.B.; Rodriguez, J.M.C. Conflict resolution with agents in smart cities. Interdiscip. Perspect. Contemp. Confl. Resolut. 2016, 14, 244–262. [Google Scholar]
- Heras, S.; Prieta, F.D.L.; Julian, V.; Rodriguez, S.; Botti, V.; Bajo, J.; Rodriguez, J.M.C. Agreement technologies and their use in cloud computing environments. Prog. Artif. Intell. 2012, 1, 277–290. [Google Scholar] [CrossRef]
- Yang, X.; Liu, G. Necessary and sufficient consensus conditions of linear descriptor multi-agent system. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2669–2676. [Google Scholar] [CrossRef]
- Wang, B.; Sun, Y. Consensus analysis of heterogeneous multi-agent systems with time-varying delay. Entropy 2015, 17, 3631–3644. [Google Scholar] [CrossRef]
- Sedziwy, A.; Kotulski, L. Multi-agent system supporting automated large-scale photometric computations. Entropy 2016, 18, 76. [Google Scholar] [CrossRef]
- Mustafa, A.; Islam, M.N.U.; Ahmed, S.; Tufail, M.A. A novel approach for fast average consensus under unreliable communication in distributed multi-agent networks. Wirel. Pers. Commun. 2018, 99, 1423–1441. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, H.; Luo, Y.; Xiao, G. Data-driven optimal consensus control for discrete-time multi-agent systems with unknown dynamics using reinforcement learning method. IEEE Trans. Ind. Electron. 2017, 64, 4091–4100. [Google Scholar] [CrossRef]
- Feng, Y.; Duan, Z.; Ren, W.; Chen, G. Consensus of multi-agent systems with fixed inner connections. Int. J. Robust Nonlinear Control 2018, 28, 154–173. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, L. Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays. Syst. Control Lett. 2008, 57, 175–183. [Google Scholar] [CrossRef]
- Shang, Y. Average consensus in multi-agent systems with uncertain topologies and multiple time-varying delays. Linear Algebra Appl. 2014, 459, 411–429. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Q.; Liu, X. Consensus of second order multi-agent systems with exogenous disturbance generated by unknown exosystems. Entropy 2016, 18, 423. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Chen, G.; Huang, L. Consensus of multi-agent systems and synchronization of complex networks: A unified viewpoint. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 213–224. [Google Scholar]
- Zhang, H.; Lewis, F.L.; Das, A. Optimal design for synchronization of cooperative systems: State feedback, observer and output feedback. IEEE Trans. Autom. Control 2011, 56, 1948–1952. [Google Scholar] [CrossRef]
- Chen, K.; Wang, J.; Zhang, Y. Distributed consensus of nonlinear multi-agent systems on state-controlled switching topologies. Entropy 2016, 18, 29. [Google Scholar] [CrossRef]
- Yang, X.; Liu, G. Consensus of descriptor multi-agent systems via dynamic compensators. IET Control Theory Appl. 2014, 8, 389–398. [Google Scholar] [CrossRef]
- Chen, W.; Gao, L.; Xu, X.; Cui, J. Distributed observer-based consensus protocol for descriptor multi-agent systems. Proc. Instiyution Mech. Eng. Part I J. Syst. Control Eng. 2015, 229, 927–938. [Google Scholar] [CrossRef]
- Gao, L.; Cui, Y.; Chen, W. Admissible consensus for descriptor multi-agent systems via distributed observer-based protocols. J. Frankl. Inst. 2017, 354, 257–276. [Google Scholar] [CrossRef]
- Liu, Y.; Jia, Y. Adaptive leader-following consensus control of multi-agent systems using model reference adaptive control approach. IET Control Theory Appl. 2012, 6, 2002–2008. [Google Scholar] [CrossRef]
- Liu, Y.; Jia, Y. Consensus problem of high-order multi-agent systems with external disturbances: An H∞ analysis approach. Int. J. Robust Nonlinear Control 2010, 20, 1579–1593. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Z.; Zhang, S. Consensus of second-order multi-agent systems with exogenous disturbances. Int. J. Robust Nonlinear Control 2011, 21, 945–956. [Google Scholar] [CrossRef]
- Xu, C.; Zheng, Y.; Su, H.; Zeng, H. Containment for linear multi-agent systems with exogenous disturbances. Neurocomputing 2015, 160, 206–212. [Google Scholar] [CrossRef]
- Shang, Y. L1 group consensus of multi-agent systems with switching topologies and stochastic inputs. Phys. Lett. A 2013, 377, 1582–1586. [Google Scholar] [CrossRef]
- Shang, Y. Group consensus of multi-agent systems in directed networks with noises and time delays. Int. J. Syst. Sci. 2015, 46, 2481–2492. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X. Consensus of linear multi-agent systems with exogenous disturbance generated from heterogeneous exosystems. Int. J. Syst. Sci. 2017, 48, 3147–3159. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, S.; Lewis, F.L. Cooperative output regulation of singular heterogeneous multi-agent systems. IEEE Trans. Cybern. 2017, 46, 1471–1475. [Google Scholar] [CrossRef] [PubMed]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, S. Admissible Consensus for Descriptor Multi-Agent Systems with Exogenous Disturbances. Entropy 2018, 20, 276. https://doi.org/10.3390/e20040276
Zhang X, Wang S. Admissible Consensus for Descriptor Multi-Agent Systems with Exogenous Disturbances. Entropy. 2018; 20(4):276. https://doi.org/10.3390/e20040276
Chicago/Turabian StyleZhang, Xuxi, and Siqi Wang. 2018. "Admissible Consensus for Descriptor Multi-Agent Systems with Exogenous Disturbances" Entropy 20, no. 4: 276. https://doi.org/10.3390/e20040276
APA StyleZhang, X., & Wang, S. (2018). Admissible Consensus for Descriptor Multi-Agent Systems with Exogenous Disturbances. Entropy, 20(4), 276. https://doi.org/10.3390/e20040276




