1. Introduction
A system is complex when it entails a number of components intricately entwined altogether (e.g., the subway network of the New York City) [
1]. Following Costa’s framework [
2,
3], the complexity in univariate signals denotes “meaningful structural richness”, which may be in contrast with regularity measures defined from entropy metrics such as sample entropy (SampEn), permutation entropy, (PerEn), and dispersion entropy (DispEn) [
3,
4,
5,
6]. In fact, these entropy techniques assess repetitive patterns and return maximum values for completely random processes [
3,
5,
7]. However, a completely ordered signal with a small entropy value or a completely disordered signal with maximum entropy value is the least complex [
3,
5,
8]. For instance, white noise is more irregular than
noise (pink noise), although the latter is more complex because
noise contains long-range correlations and its
decay produces a fractal structure in time [
3,
5,
8].
From the perspective of physiology, some diseased individuals’ recordings, when compared with those for healthy subjects, are associated with the emergence of more regular behavior, thus leading to lower entropy values [
3,
9]. In contrast, certain pathologies, such as cardiac arrhythmias, are associated with highly erratic fluctuations with statistical characteristics resembling uncorrelated noise. The entropy values of these noisy signals are higher than those of healthy individuals, even though the healthy individuals’ time series show more physiologically complex adaptive behavior [
3,
10].
In brief, the concept of complexity for univariate physiological signals builds on the following three hypotheses [
3,
5]:
The complexity of a biological or physiological time series indicates its ability to adapt and function in an ever-changing environment.
A biological time series requires operating across multiple temporal and spatial scales and so its complexity is similarly multiscaled and hierarchical.
A wide class of disease states, in addition to ageing, which decrease the adaptive capacity of the individual, appear to degrade the information carried by output variables.
Therefore, the multiscale-based methods focus on quantifying the information expressed by the physiological dynamics over multiple temporal scales.
To provide a unified framework for the evaluation of impact of diseases in physiological signals, multiscale SampEn (MSE) [
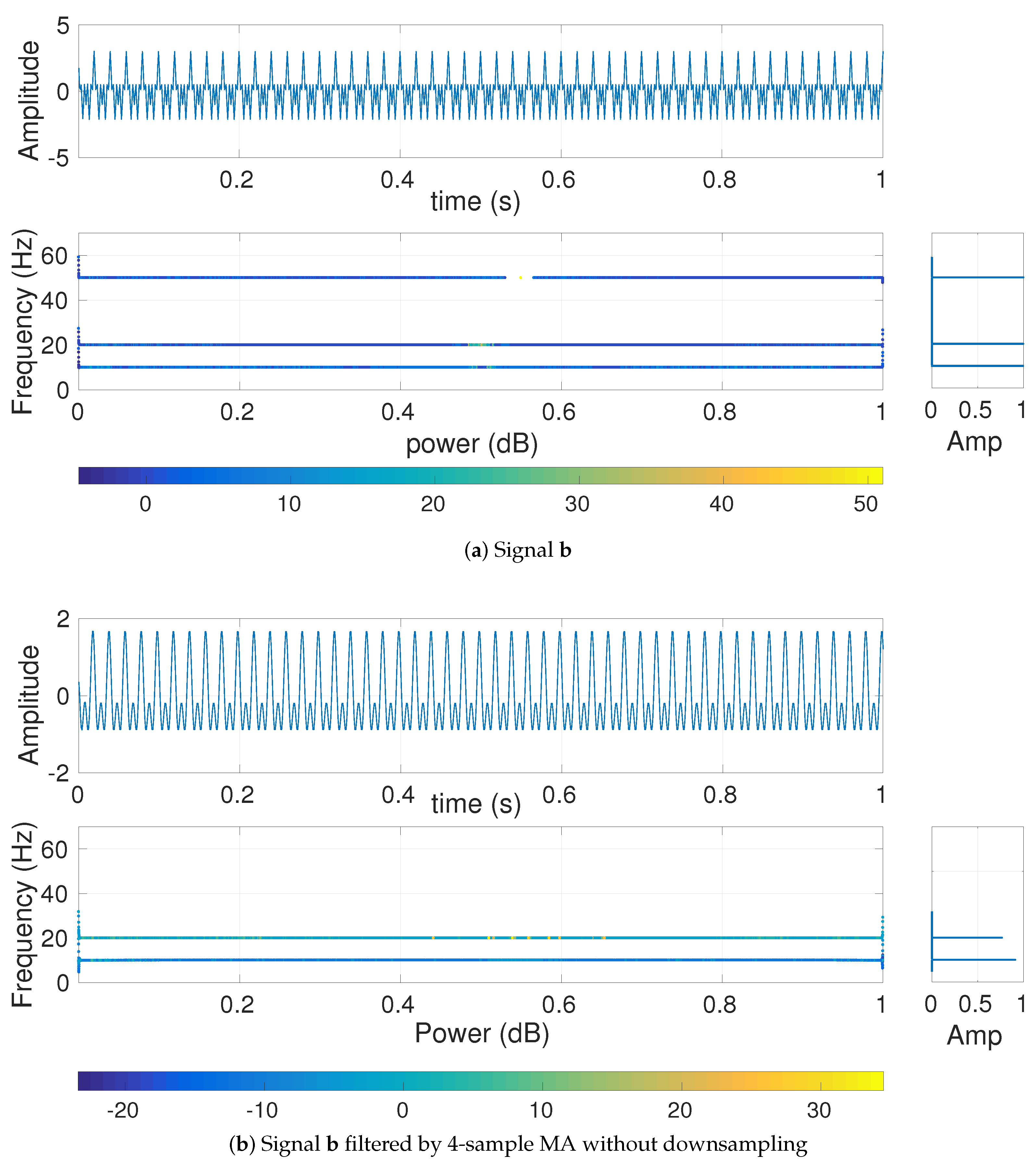
3] was proposed to quantify the complexity of signals over multiple temporal scales. The MSE algorithm includes two main steps: (1) coarse-graining technique—i.e., combination of moving average (MA) filter and downsampling (DS) process—; and (2) calculation of SampEn of the coarse-grained signals at each scale factor
[
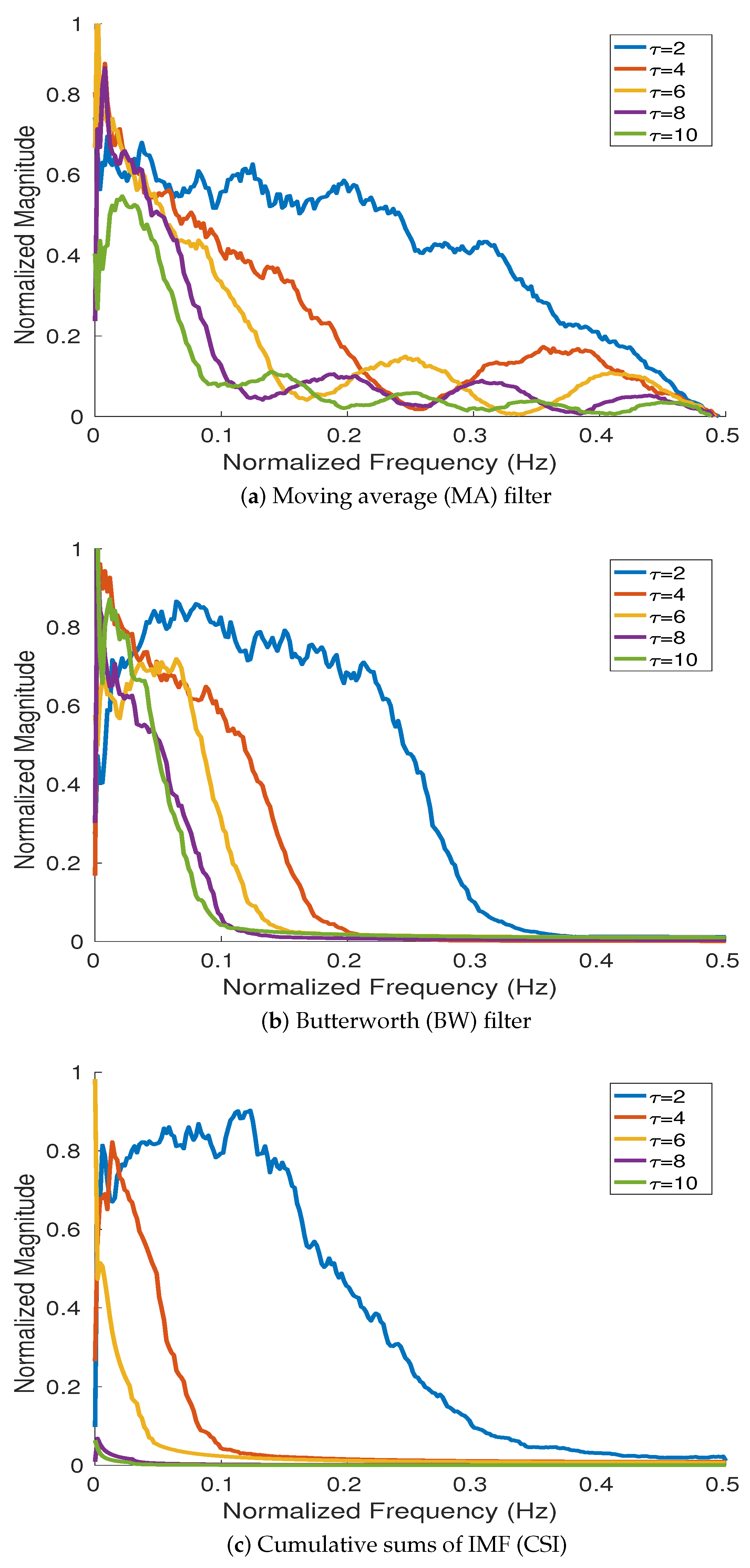
3]. A low-pass Butterworth (BW) filter was used as an alternative to MA to limit aliasing and avoid ripples [
11]. To differentiate it from the original MSE, we call this method MSE
BW herein.
Since their introduction, MSE and MSE
BW have been widely used to characterize physiological and non-physiological signals [
12]. However, they have several main shortcomings [
12,
13,
14]. First, the coarse-graining process causes the length of a signal to be shortened by the scale factor
as a consequence of the downsampling in the process. Therefore, when the scale factor increases, the number of samples in the coarse-grained sequence decreases considerably [
14]. This may yield an unstable estimation of entropy. Second, SampEn is either undefined or unreliable for short coarse-grained time series [
13,
14].
To alleviate the first problem of MSE, intrinsic mode SampEn (InMSE) [
15] and refined composite MSE (RCMSE) [
14] were developed [
15]. The coarse-graining technique is substituted by an approach based on empirical mode decomposition (EMD) in InMSE. The length of coarse-grained series obtained by InMSE is equal to that of the original signal, leading to more stable entropy values. Nevertheless, EMD-based approaches have certain limitations such as sensitivity to noise and sampling [
16]. At the scale factor
, RCMSE considers
different coarse-grained signals, corresponding to different starting points of the coarse-graining process [
14]. Therefore, RCMSE yields more stable results in comparison with MSE. Nevertheless, both InMSE and RCMSE may lead to undefined values for short signals as a consequence of using SampEn in the second step of their algorithms [
13]. Additionally, the SampEn-based approaches may not be fast enough for some real-time applications.
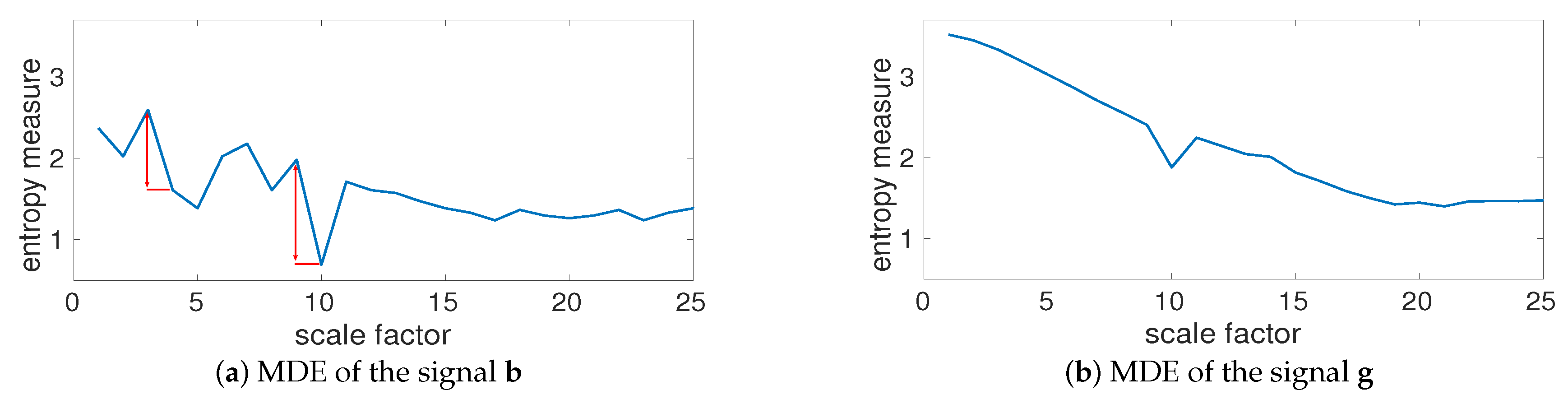
To deal with these deficiencies, multiscale DispEn (MDE) based on our introduced DispEn was developed [
13]. Refined composite MDE (RCMDE) was then proposed to improve the stability of the MDE-based values [
13]. It was found that MDE and RCMDE have the following advantages over MSE and RCMSE: (1) they are noticeably faster as a consequence of using DispEn with computational cost of O(
N)—where
N is the signal length—, compared with the O
for SampEn; (2) they result in more stable profiles for synthetic and real signals; (3) MDE and RCMDE discriminate different kinds of physiological time series better than MSE and RCMSE; and (4) they do not yield undefined values [
13].
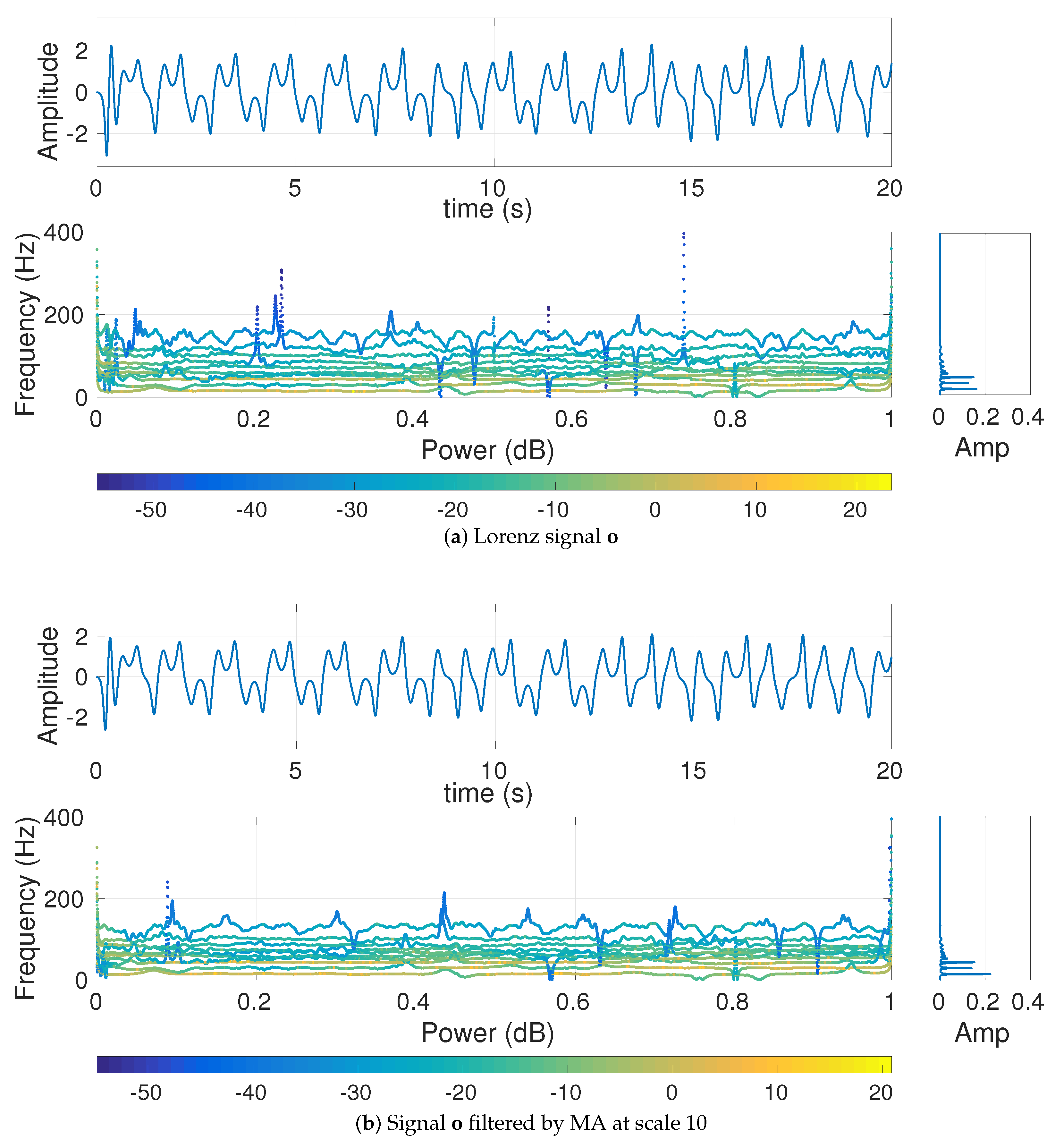
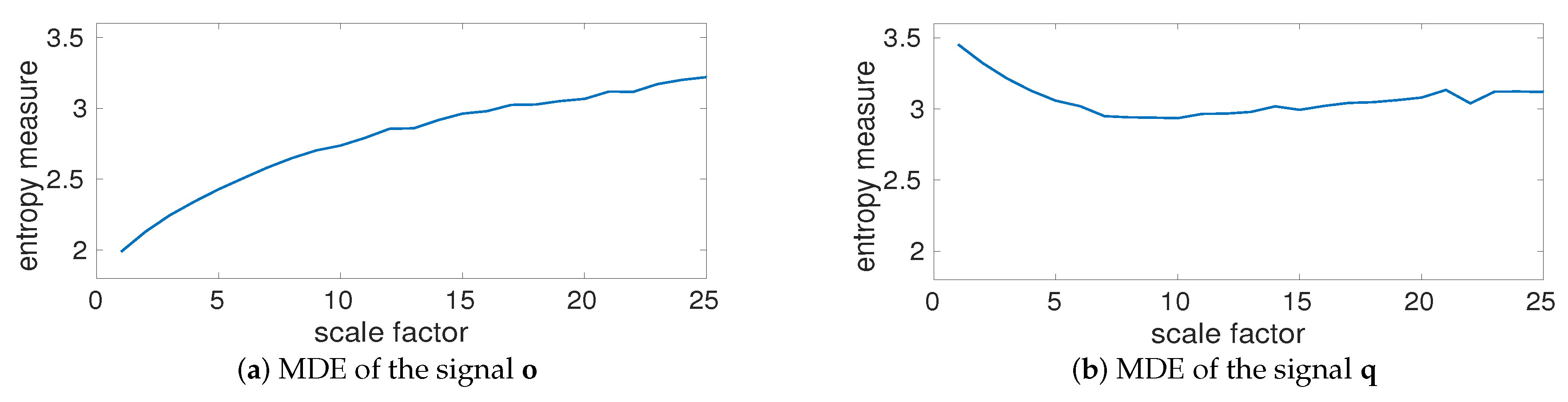
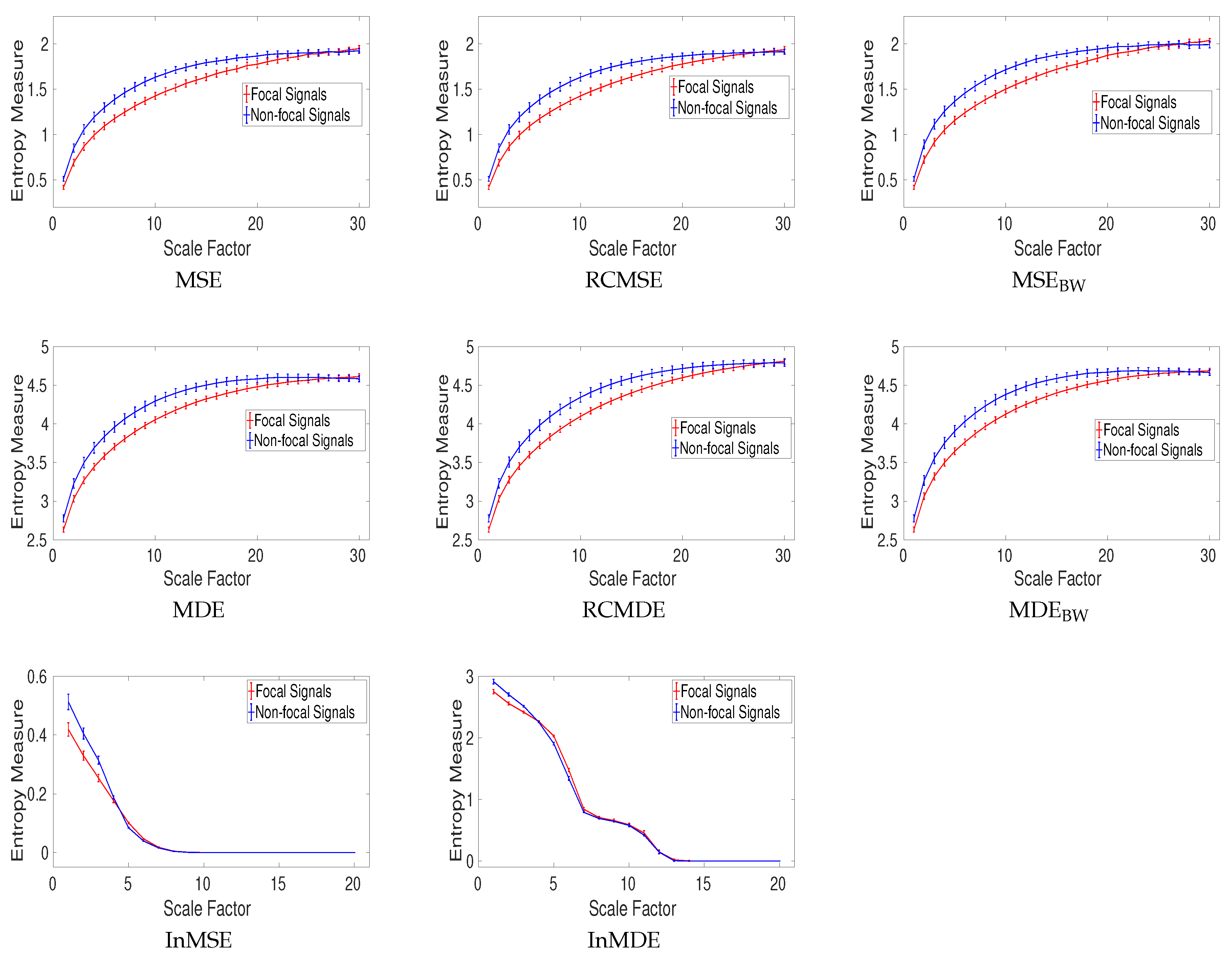
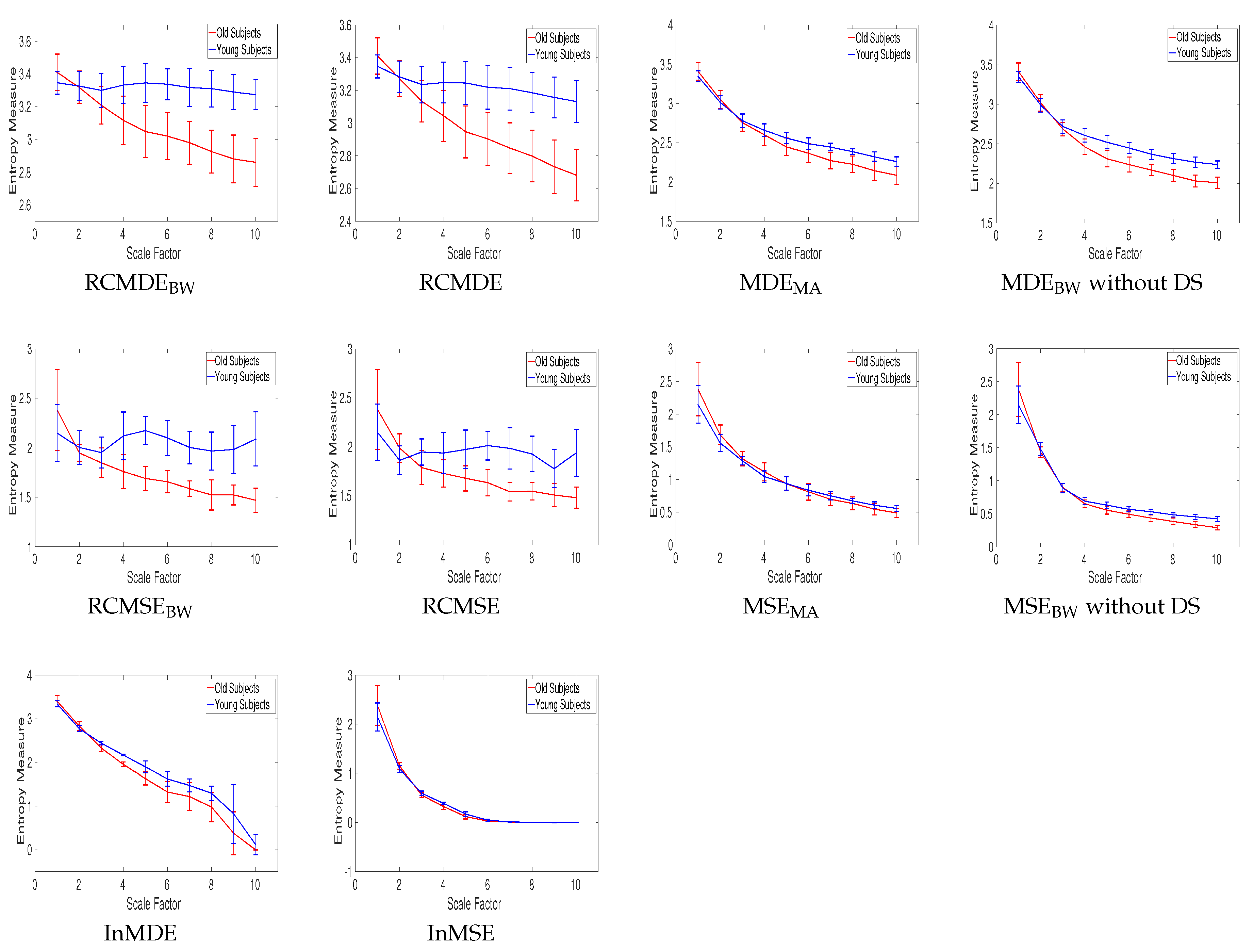
The aim of this research is to contribute to the understanding of different alternatives to coarse-graining in complexity approaches. To this end, we first revise the frequency responses for the three main filtering processes (i.e., MA, BW, and EMD) used in such methods. The role of downsampling in the classical coarse-graining process, which has not been systematically explored yet, is then investigated in the article. We assess the impact of coarse-graining in multiscale entropy estimations based on both SampEn and DispEn. To compare these methods, several synthetic data and two real physiological datasets are employed. For the sake of clarity, a flowchart of the alternatives to the coarse-graining method in addition to the datasets used in this article is shown in
Figure 1.
7. Conclusions
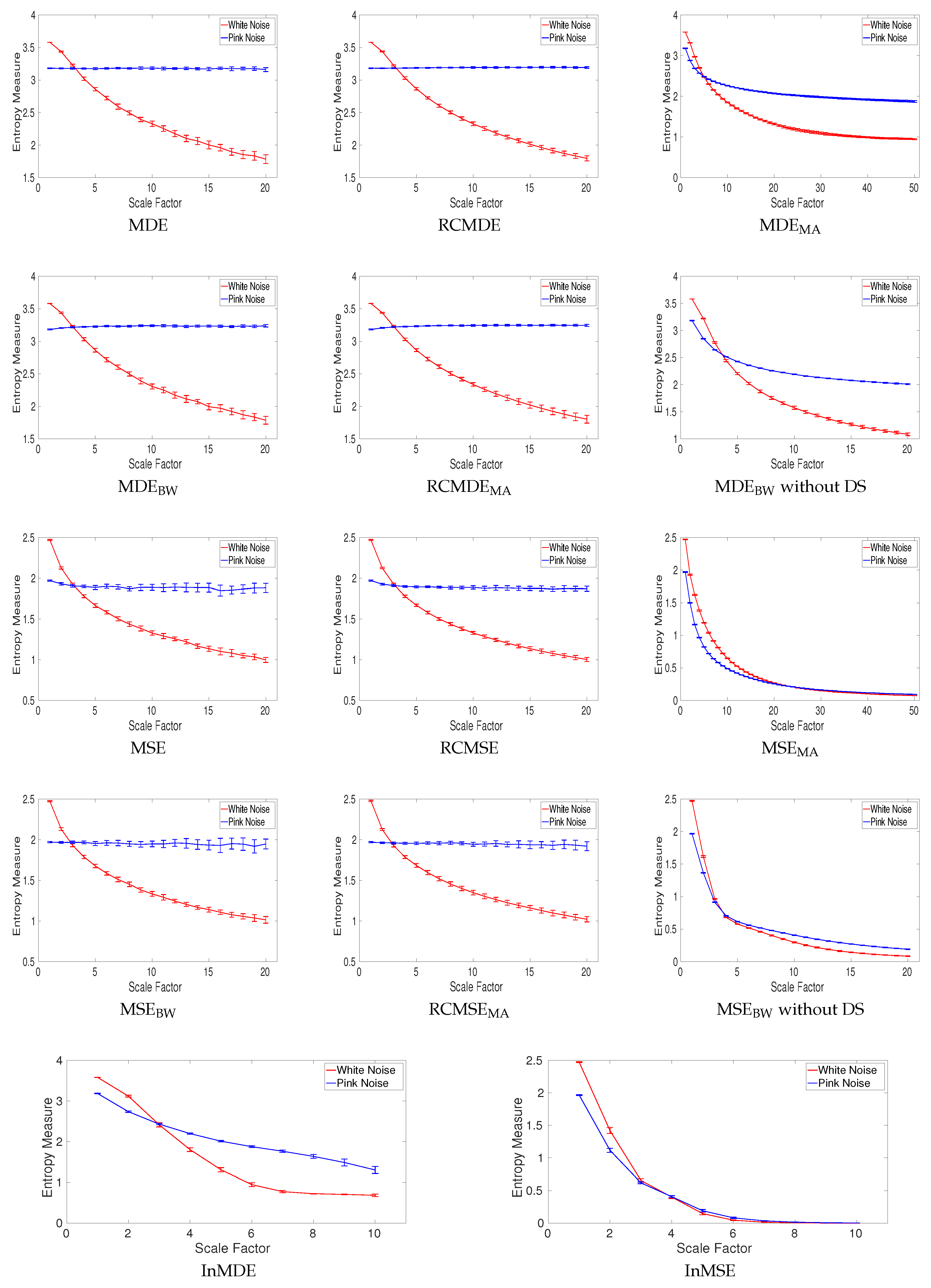
In summary, we have compared existing and newly proposed coarse-graining approaches for univariate multiscale entropy estimation. Our results indicate that, as expected due to the filter bank properties of the EMD [
33] in comparison with moving average and Butterworth filtering, the cut-off frequencies at each temporal scale
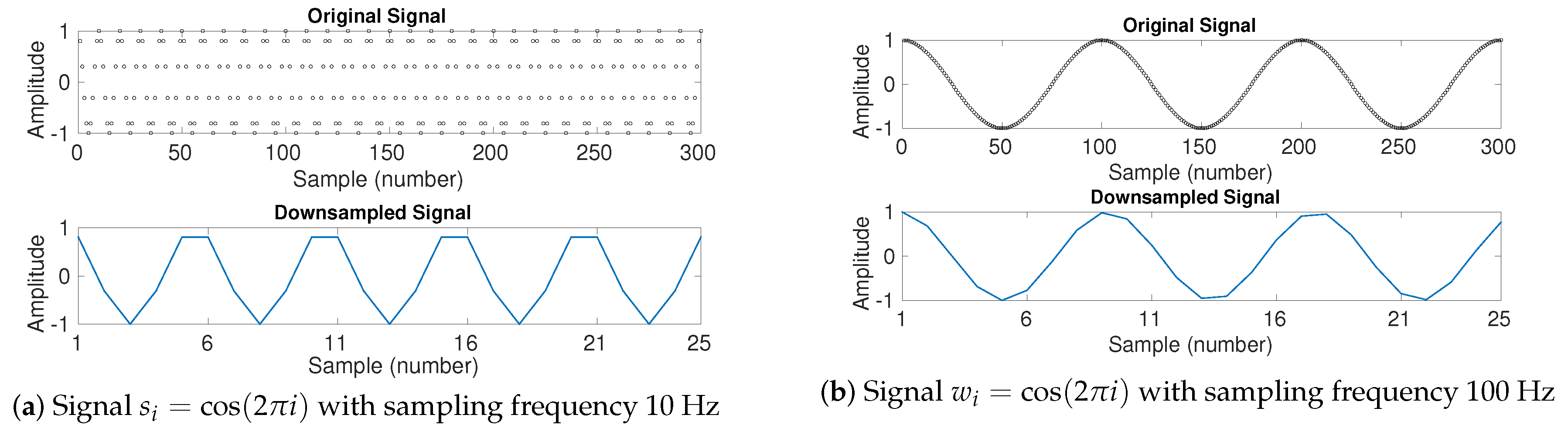
of the former are considerably smaller than those for the latter. Therefore, InMSE and our developed InMDE have entropy values very close to 0 for relatively low values of temporal scales due to the exponential, rather than linear, dependency of the bandwidth at each scale. We also inspected the effect of the downsampling in the coarse-graining process in the entropy values, showing that it may lead to increased or decreased values of entropy depending on the sampling frequency of the time series.
Our results confirmed previous reports indicating that, when dealing with short or noisy signals, the refined composite approach [
14,
25] may improve the stability of entropy results. On the other hand, for long signals with relatively low levels of noise, the refined composite method makes little difference in the quality of the entropy estimation at the expense of a considerable additional computational cost. In any case, the use of dispersion entropy over sample entropy in the estimations led to more stable results based on CV values and ensured that the entropy values were defined at all temporal scales.
Finally, the profiles obtained by the multiscale techniques with and without downsampling led to similar findings (e.g., pink noise is more complex than white noise based on all the complexity methods) although the specific values of entropy may differ depending on the coarse-graining used. This suggests that downsampling within the coarse-graining procedure may not be needed to quantify the complexity of signals, especially for short ones. In fact, these kinds of techniques still eliminate the fast temporal scales to deal with progressively slower time scales as increases and take into account multiple time scales inherent in time series.
On the whole, it is expected that these findings contribute to the ongoing discussion regarding the development of stable, fast, and less sensitive-to-noise complexity approaches appropriate for either short or long time series. We recommend that future studies explicitly justify their choices for coarse-graining procedure in the light of the characteristics of the signals under analysis and the hypothesis of the study, and that they discuss their findings on the light of the behaviour of the selected entropy metric and coarse-graining procedure.