Triphase Separation of a Ternary Symmetric Highly Viscous Mixture
Abstract
:1. Introduction
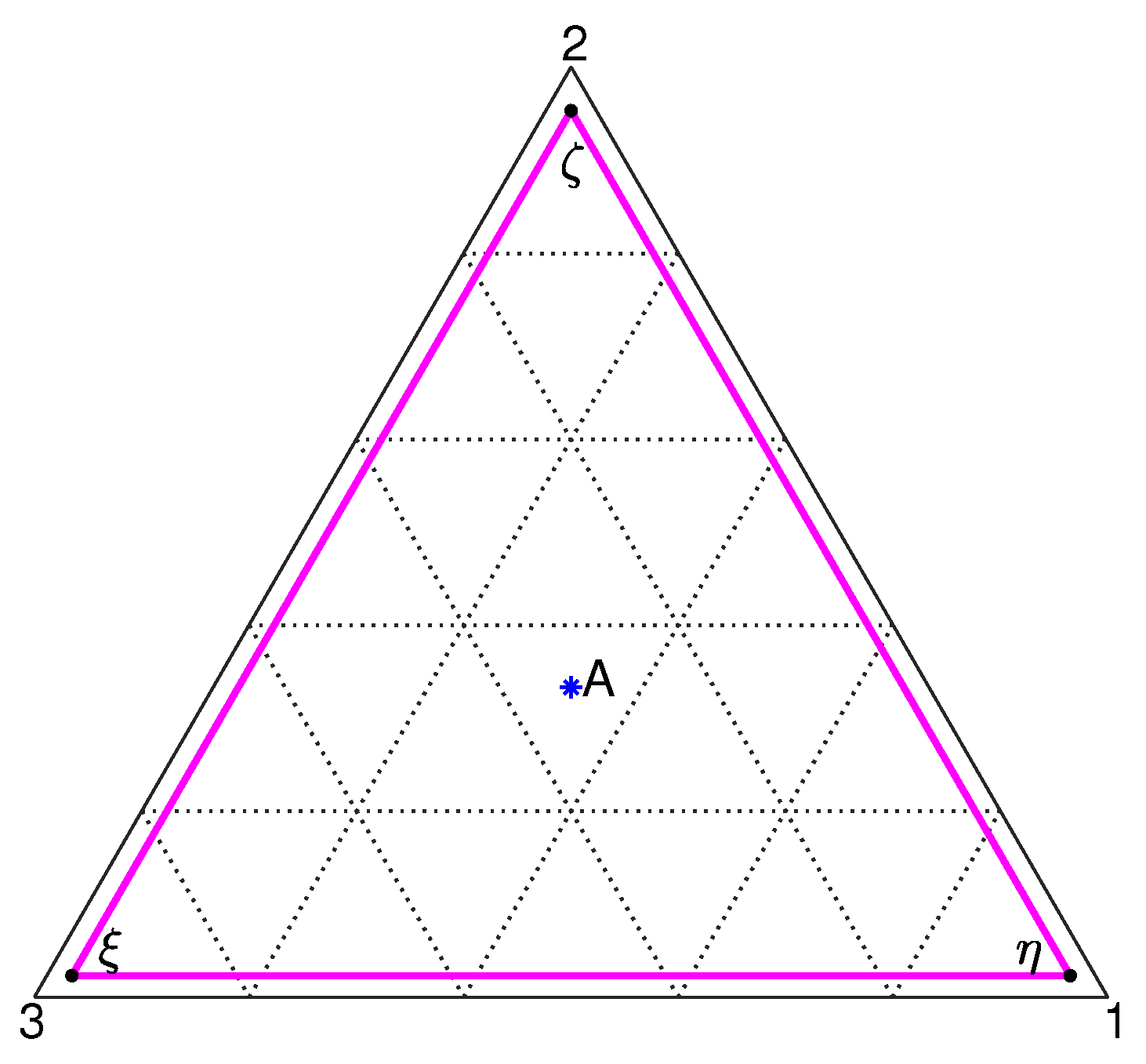
2. Model Description
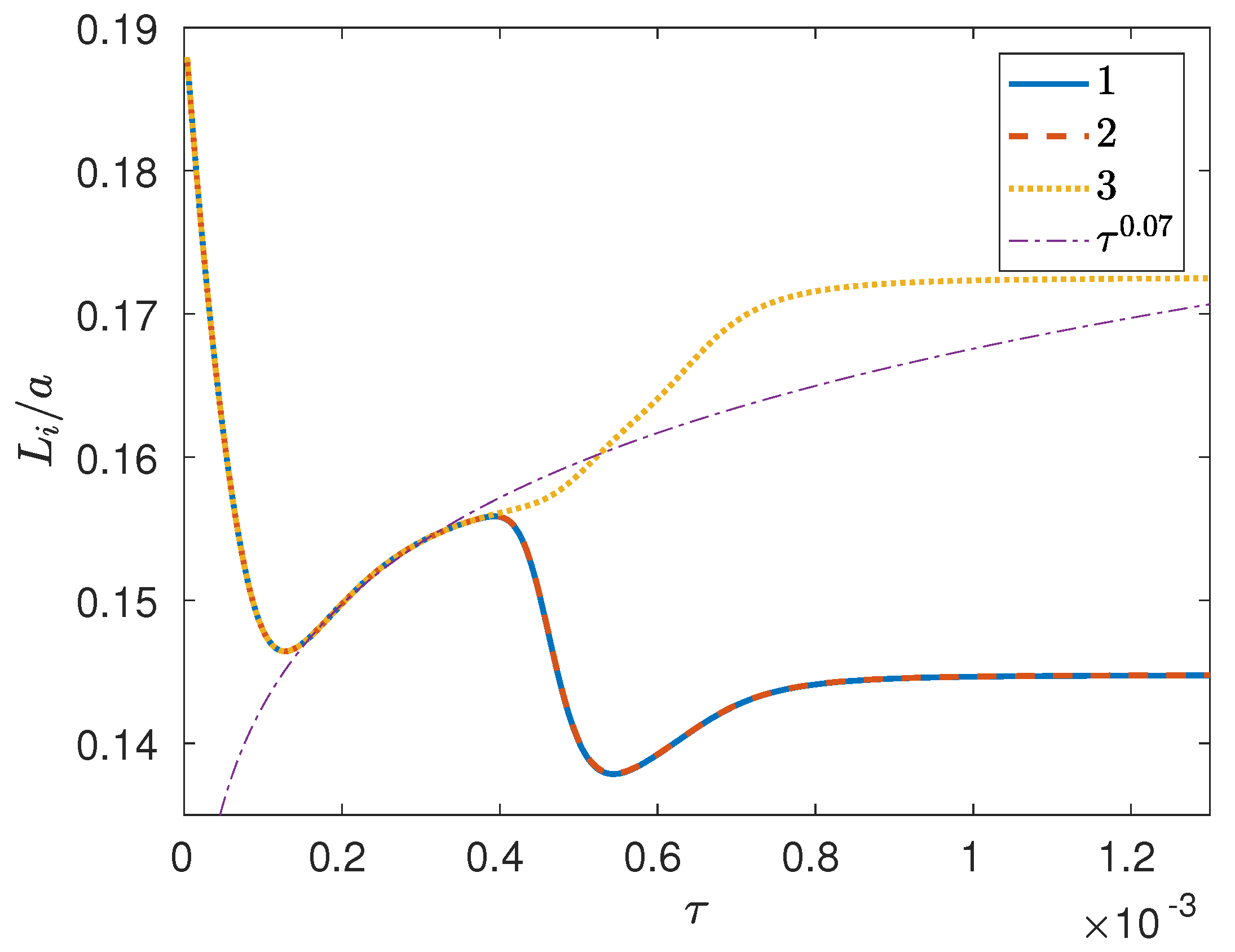
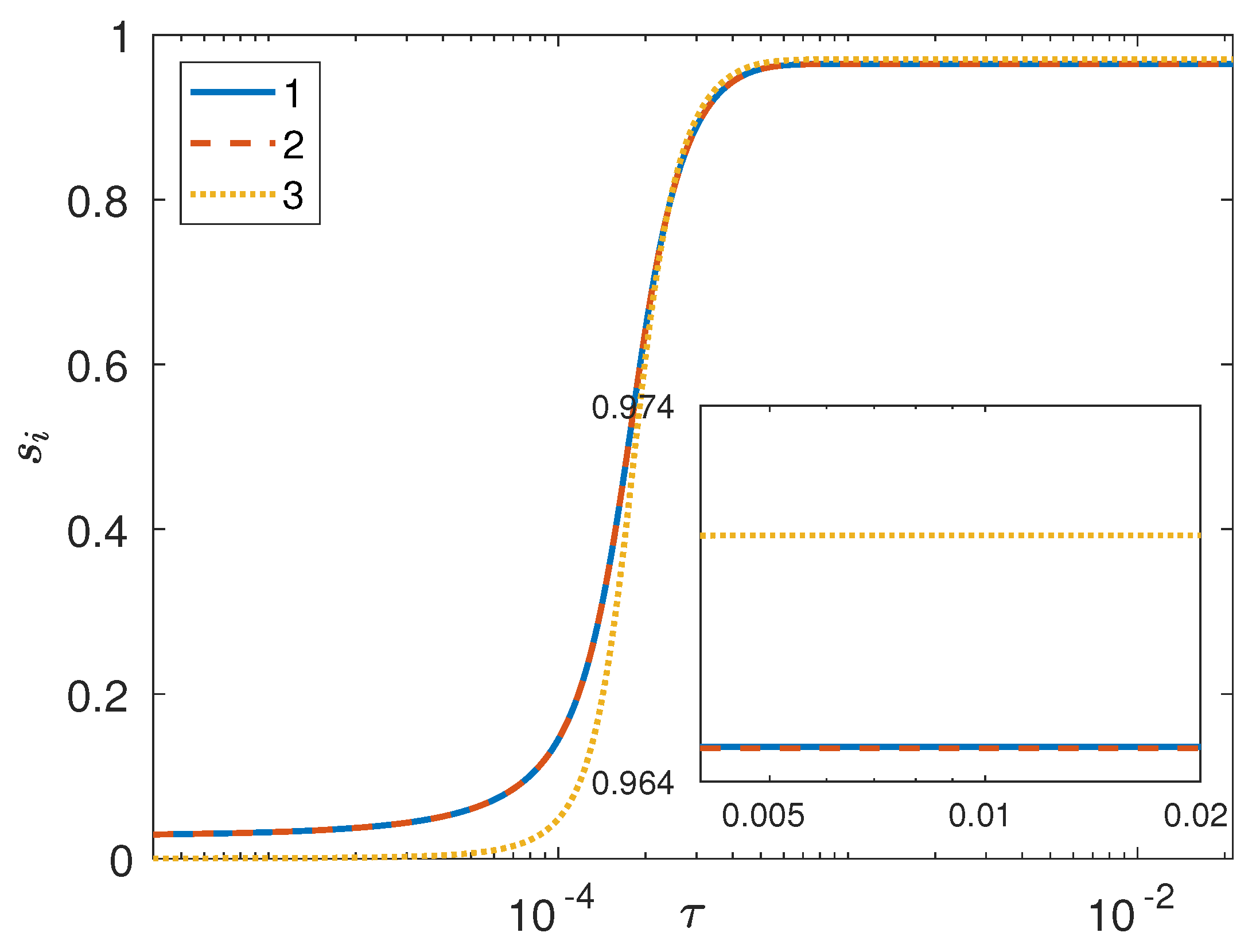
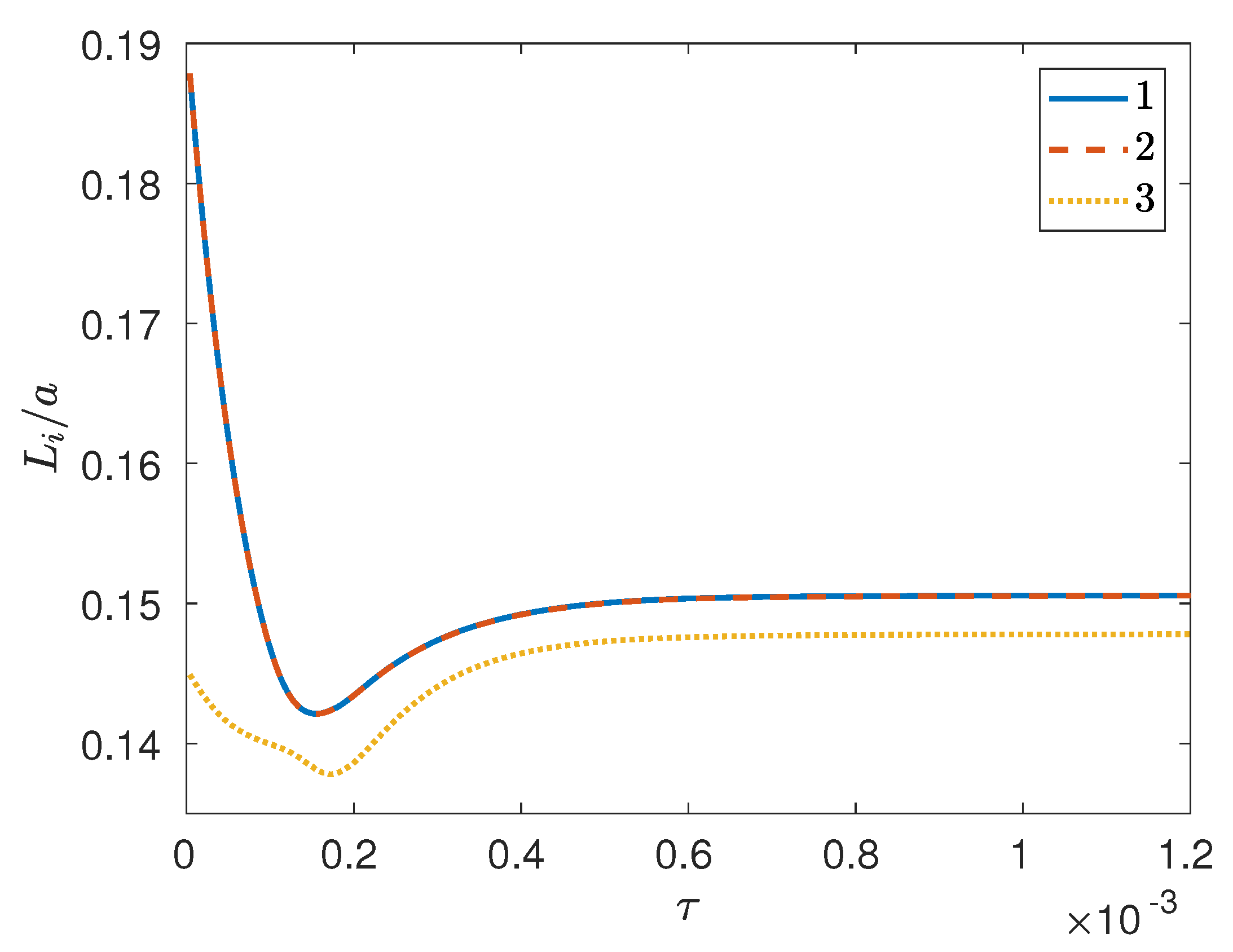
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| NRTL | Non-Random, Two-Liquid |
References
- Huang, C.; Olvera de la Cruz, M.; Swift, B.W. Phase separation of ternary mixtures: Symmetric polymer blends. Macromolecules 1995, 28, 7996–8005. [Google Scholar] [CrossRef]
- Park, J.M.; Mauri, R.; Anderson, P.D. Phase separation of viscous ternary liquid mixtures. Chem. Eng. Sci. 2012, 80, 270–278. [Google Scholar] [CrossRef]
- Liu, B.; Tong, C.; Yang, Y. The kinetics and phase patterns in a ternary mixture coupled with chemical reaction of A + B ⇌ C. J. Phys. Chem. B 2001, 105, 10091–10100. [Google Scholar] [CrossRef]
- Tong, C.; Zhang, H.; Yang, Y. Phase separation dynamics and reaction kinetics of ternary mixture coupled with interfacial chemical reaction. J. Phys. Chem. B 2002, 106, 7869–7877. [Google Scholar] [CrossRef]
- Tong, C.; Yang, Y. Phase-separation dynamics of a ternary mixture coupled with reversible chemical reaction. J. Chem. Phys. 2002, 116, 1519–1529. [Google Scholar] [CrossRef]
- Good, K.; Kuksenok, O.; Buxton, G.A.; Ginzburg, V.V.; Balazs, A.C. Effect of hydrodynamic interactions on the evolution of chemically reactive ternary mixtures. J. Chem. Phys. 2004, 121, 6052–6063. [Google Scholar] [CrossRef] [PubMed]
- Travasso, R.D.M.; Buxton, G.A.; Kuksenok, O.; Good, K.; Balazs, A.C. Modeling the morphology and mechanical properties of sheared ternary mixtures. J. Chem. Phys. 2005, 122, 194906. [Google Scholar] [CrossRef] [PubMed]
- Kuksenok, O.; Travasso, R.D.M.; Balazs, A.C. Dynamics of ternary mixtures with photosensitive chemical reactions: Creating three-dimensionally ordered blends. Phys. Rev. E 2006, 74, 011502. [Google Scholar] [CrossRef]
- Shukutani, T.; Myojo, T.; Nakanishi, H.; Norisuye, T.; Tran-Cong-Miyata, Q. Tricontinuous morphology of ternary polymer blends driven by photopolymerization: Reaction and phase separation kinetics. Macromolecules 2014, 47, 4380–4386. [Google Scholar] [CrossRef]
- Tran-Cong-Miyata, Q.; Nakanishi, H. Phase separation of polymer mixtures driven by photochemical reactions: Current status and perspectives. Polym. Int. 2017, 66, 213–222. [Google Scholar] [CrossRef]
- Zucchi, I.A.; Galante, M.J.; Borrajo, J.; Williams, R.J. A model system for the thermodynamic analysis of reaction-induced phase separation: Solutions of polystyrene in bifunctionalepoxy/amine monomers. Macromol. Chem. Phys. 2004, 205, 676–683. [Google Scholar] [CrossRef]
- Chan, P.K.; Rey, A.D. Polymerization-induced phase separation. 1. Droplet size selection mechanism. Macromolecules 1996, 29, 8934–8941. [Google Scholar] [CrossRef]
- Chan, P.K.; Rey, A.D. Polymerization-induced phase separation. 2. Morphological analysis. Macromolecules 1997, 30, 2135–2143. [Google Scholar] [CrossRef]
- Lee, K.W.D.; Chan, P.K.; Feng, X. A computational study of the polymerization-induced phase separation phenomenon in polymer solutions under a temperature gradient. Macromol. Theory Simul. 2003, 12, 413–424. [Google Scholar] [CrossRef]
- Oh, J.; Rey, A. Computational simulation of polymerization-induced phase separation under a temperature gradient. Comput. Theor. Polymer Sci. 2001, 11, 205–217. [Google Scholar] [CrossRef]
- Stubbs, J.M.; Durant, Y.G.; Sundberg, D.C. Polymer phase separation in composite latex particles. 1. Considerations for the nucleation and growth mechanism. C.R. Chimie 2003, 6, 1217–1232. [Google Scholar] [CrossRef]
- Sutton, D.; Stanford, J.; Ryan, A. Reaction-induced phase-separation in polyoxyethylene/polystyrene blends. II. Structure development. J. Macromol. Sci. B 2004, 43, 233–251. [Google Scholar] [CrossRef]
- Girard-Reydet, E.; Sautereau, H.; Pascault, J.P.; Keates, P.; Navard, P.; Thollet, G.; Vigier, G. Reaction-induced phase separation mechanisms in modified thermosets. Polymer 1998, 39, 2269–2279. [Google Scholar] [CrossRef]
- Nauman, E.B.; He, D.Q. Morphology predictions for ternary polymer blends undergoing spinodal decomposition. Polymer 1994, 35, 2243–2255. [Google Scholar] [CrossRef]
- Huang, C.; Olvera de la Cruz, M. Adsorption of a minority component in polymer blend interfaces. Phys. Rev. E 1996, 53, 812–819. [Google Scholar] [CrossRef]
- Tafa, K.; Puri, S.; Kumar, D. Kinetics of phase separation in ternary mixtures. Phys. Rev. E 2001, 64, 056139. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.Q. Domain patterns in ternary mixtures with different interfacial properties. J. Chem. Phys. 2001, 114, 3734–3738. [Google Scholar] [CrossRef]
- Lakshmi, K.C.; Kumar, P.B.S. Scale invariance in coarsening of binary and ternary fluids. Phys. Rev. E 2003, 67, 011507. [Google Scholar] [CrossRef] [PubMed]
- Puri, S.; Kumar, D. Autocorrelation functions for phase separation in ternary mixtures. Phys. Rev. E 2004, 70, 051501. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Puri, S. Phase separation in ternary fluid mixtures: a molecular dynamics study. Soft Matter 2015, 11, 2213–2219. [Google Scholar] [CrossRef] [PubMed]
- Lamorgese, A.; Mauri, R. Dissolution or growth of a liquid drop via phase-field ternary mixture model based on the non-random, two-liquid equation. Entropy 2018, 20, 125. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE. J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.N.; Gomes de Azevedo, E. Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999; Chapter 6. [Google Scholar]
- O’Connell, J.P.; Haile, J.M. Thermodynamics: Fundamentals for Applications; Cambridge University Press: New York, NY, USA, 2005; Chapter 11. [Google Scholar]
- Lamorgese, A.; Mauri, R. Diffusion-driven dissolution or growth of a liquid drop embedded in a continuous phase of another liquid via phase-field ternary mixture model. Langmuir 2017, 33, 13125–13132. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. III. Nucleation in a two-component incompressible fluid. J. Chem. Phys. 1959, 31, 688–699. [Google Scholar] [CrossRef]
- Lamorgese, A.; Molin, D.; Mauri, R. Phase-field approach to multiphase flow modeling. Milan J. Math. 2011, 79, 597–642. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R.; Sagis, L.M.C. Modeling soft interface dominated systems: A comparison of phase field and Gibbs dividing surface models. Phys. Rep. 2017, 675, 1–54. [Google Scholar] [CrossRef]
- Sandler, S.I. Chemical, Biochemical, and Engineering Thermodynamics, 4th ed.; Wiley: New York, NY, USA, 2006; Chapter 9. [Google Scholar]
- Serrin, J. Mathematical principles of classical fluid mechanics. In Encyclopedia of Physics, Vol. VIII/1; Springer: Berlin, Germany, 1959; pp. 125–263. [Google Scholar]
- Vladimirova, N.; Malagoli, A.; Mauri, R. Two-dimensional model of phase segregation in liquid binary mixtures with an initial concentration gradient. Chem. Eng. Sci. 2000, 55, 6109–6128. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R. Phase separation of liquid mixtures. In Nonlinear Dynamics and Control in Process Engineering; Continillo, G., Crescitelli, S., Giona, M., Eds.; Springer: Rome, Italy, 2002; pp. 139–152. [Google Scholar]
- Lamorgese, A.; Mauri, R. Nucleation and spinodal decomposition of liquid mixtures. Phys. Fluids 2005, 17, 034107. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R. Mixing of macroscopically quiescent liquid mixtures. Phys. Fluids 2006, 18, 044107. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R. Diffuse-Interface modeling of phase segregation in liquid mixtures. Int. J. Multiphase Flow 2008, 34, 987–995. [Google Scholar] [CrossRef]
- Tanaka, H.; Araki, T. Spontaneous double phase separation induced by rapid hydrodynamic coarsening in two-dimensional fluid mixtures. Phys. Rev. Lett. 1998, 81, 389–392. [Google Scholar] [CrossRef]
- Vladimirova, N.; Malagoli, A.; Mauri, R. Diffusiophoresis of two-dimensional liquid droplets in a phase-separating system. Phys. Rev. E 1999, 60, 2037–2044. [Google Scholar] [CrossRef]
- Gupta, R.; Mauri, R.; Shinnar, R. Liquid-liquid extraction using the composition-induced phase separation process. Ind. Eng. Chem. Res. 1996, 35, 2360–2368. [Google Scholar] [CrossRef]
- Gupta, R.; Mauri, R.; Shinnar, R. Phase separation of liquid mixtures in the presence of surfactants. Ind. Eng. Chem. Res. 1999, 38, 2418–2424. [Google Scholar] [CrossRef]
- Mauri, R.; Califano, F.; Calvi, E.; Gupta, R.; Shinnar, R. Convection-driven phase segregation of deeply quenched liquid mixtures. J. Chem. Phys. 2003, 118, 8841–8846. [Google Scholar] [CrossRef]
- Santonicola, G.; Mauri, R.; Shinnar, R. Phase separation of initially inhomogeneous liquid mixtures. Ind. Eng. Chem. Res. 2001, 40, 2004–2010. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R. Phase-field modeling of interfacial dynamics in emulsion flows: Nonequilibrium surface tension. Int. J. Multiphase Flow 2016, 85, 164–172. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R. Phase-field modeling of mixing/demixing of regular binary mixtures with a composition-dependent viscosity. J. Appl. Phys. 2017, 121, 134302. [Google Scholar] [CrossRef]
- Prigogine, I.; Defay, R. Chemical Thermodynamics, 4th ed.; Longmans: London, UK, 1967. [Google Scholar]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479. [Google Scholar] [CrossRef]
- Vladimirova, N.; Malagoli, A.; Mauri, R. Two-dimensional model of phase segregation in liquid binary mixtures. Phys. Rev. E 1999, 60, 6968–6977. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R. Liquid mixture convection during phase separation in a temperature gradient. Phys. Fluids 2011, 23, 034102. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R. Spinodal decomposition of chemically reactive binary mixtures. Phys. Rev. E 2016, 94, 022605. [Google Scholar] [CrossRef]
- Vladimirova, N.; Malagoli, A.; Mauri, R. Diffusion-driven phase separation of deeply quenched mixtures. Phys. Rev. E 1998, 58, 7691–7699. [Google Scholar] [CrossRef]
- Lamorgese, A.G.; Mauri, R. Diffuse-interface modeling of liquid-vapor phase separation in a van der Waals fluid. Phys. Fluids 2009, 21, 044107. [Google Scholar] [CrossRef] [Green Version]
- Cavanaugh, T.J.; Buttle, K.; Turner, J.N.; Nauman, E.B. Confirmation of predicted polymer blend morphologies from bulk specimens. Polymer 1998, 39, 3611–3621. [Google Scholar] [CrossRef]
- Alfarraj, A.A.; Nauman, E.B. Spinodal decomposition in ternary systems with significantly different component diffusivities. Macromol. Theory Simul. 2007, 16, 627–631. [Google Scholar] [CrossRef]
- Nauman, E.B.; He, D.Q. Nonlinear diffusion and phase separation. Chem. Eng. Sci. 2001, 56, 1999–2018. [Google Scholar] [CrossRef]
- Alfarraj, A.A. Muticomponent Diffusion and Phase Separation in Asymmetric Ternary Polymer Systems. Ph.D. Thesis, Rensselaer Polytechnic Institute, New York, NY, USA, 2007. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamorgese, A.; Mauri, R. Triphase Separation of a Ternary Symmetric Highly Viscous Mixture. Entropy 2018, 20, 936. https://doi.org/10.3390/e20120936
Lamorgese A, Mauri R. Triphase Separation of a Ternary Symmetric Highly Viscous Mixture. Entropy. 2018; 20(12):936. https://doi.org/10.3390/e20120936
Chicago/Turabian StyleLamorgese, Andrea, and Roberto Mauri. 2018. "Triphase Separation of a Ternary Symmetric Highly Viscous Mixture" Entropy 20, no. 12: 936. https://doi.org/10.3390/e20120936




