Analytical Approximate Solutions of (n + 1)-Dimensional Fractal Heat-Like and Wave-Like Equations
Abstract
:1. Introduction
2. Preliminaries
- (i)
- for ,
- (ii)
- ,
- (iii)
- .
3. Main Results
3.1. Two-Dimensional LFRDTM
3.2. (n + 1)-Dimensional LFRDTM
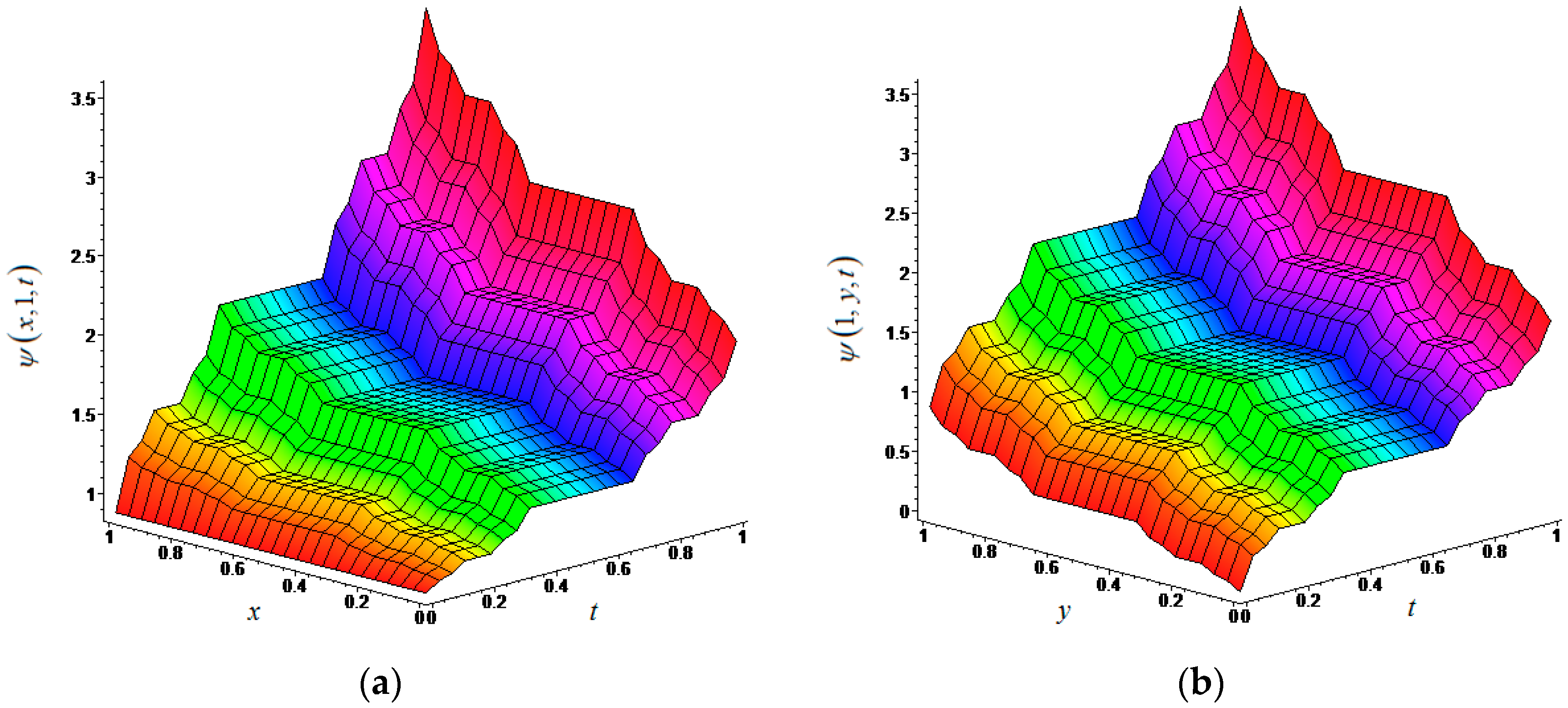
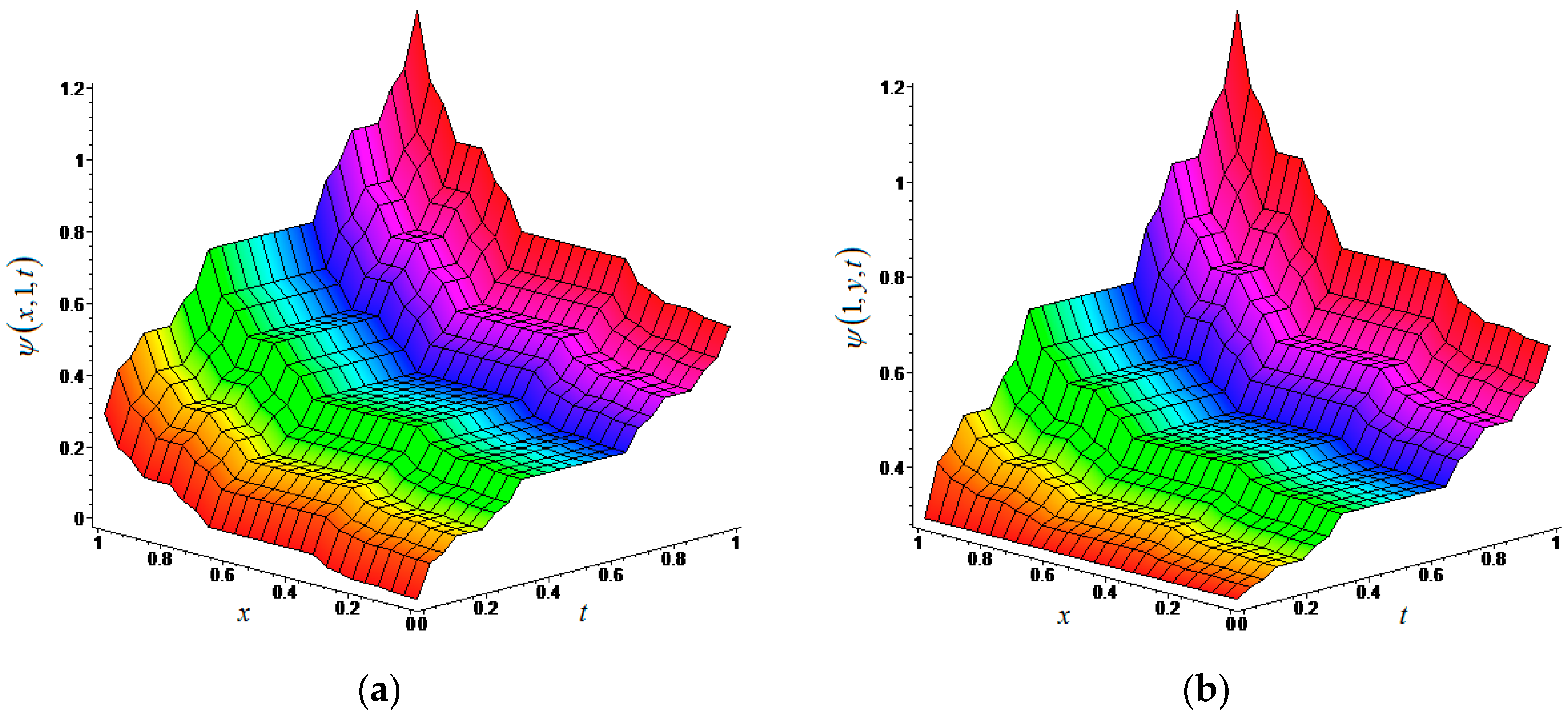
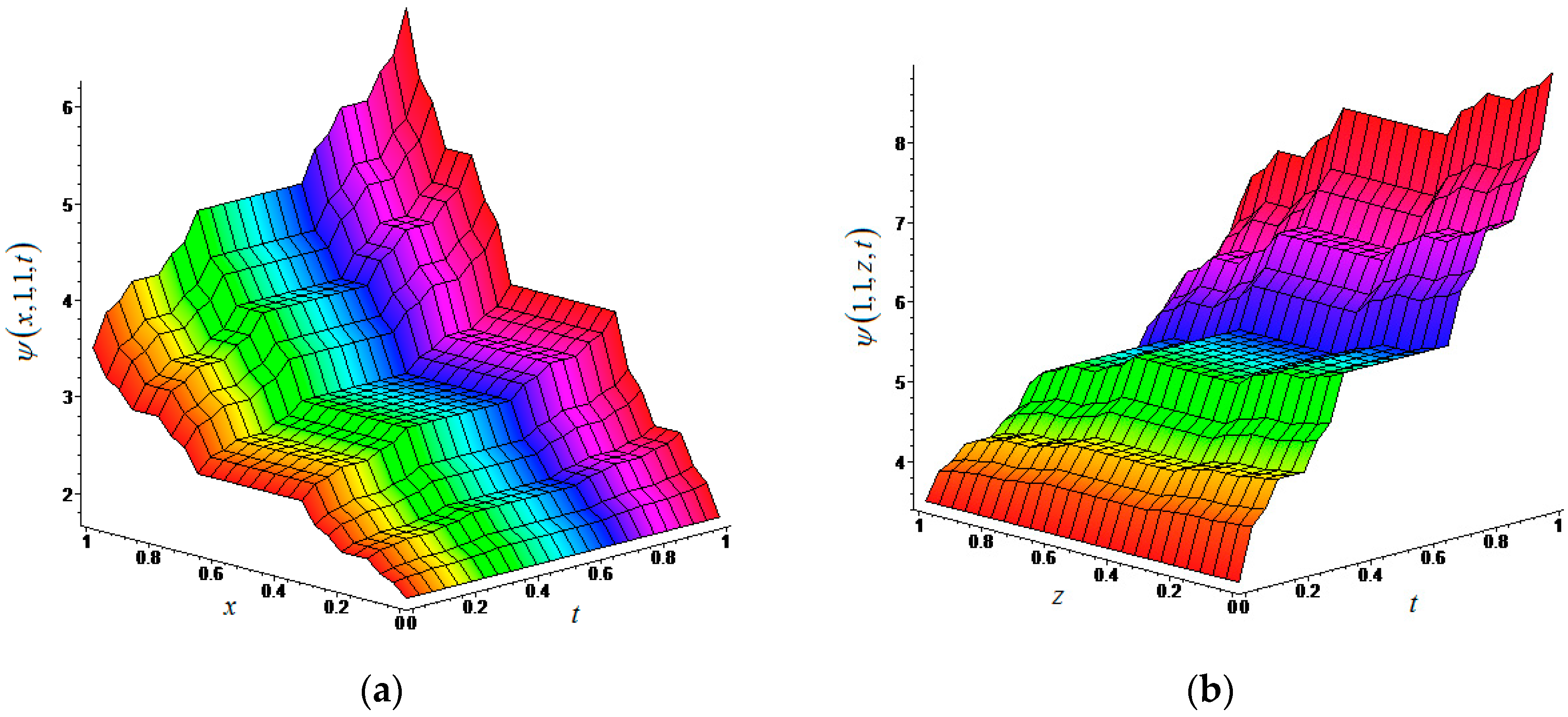
4. Applications of (n + 1)-Dimensional LFRDTM
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Hoffmann, K.H.; Essex, C.; Schulzky, C. Fractional Diffusion and Entropy Production. J. Non-Equilib. Thermodyn. 1998, 23, 166–175. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Essex, C.; Schulzky, C.; Franz, A. Tsallis and Renyi entropies in fractional diffusion and entropy production. Phys. A Stat. Mech. Appl. 2000, 284, 299–308. [Google Scholar] [CrossRef]
- Li, X.; Essex, C.; Davison, M.; Hoffmann, K.H.; Schulzky, C. Fractional Diffusion, Irreversibility and Entropy. J. Non-Equilib. Thermodyn. 2003, 28, 279–291. [Google Scholar] [CrossRef]
- Magin, R.L.; Ingo, C. Entropy and Information in a Fractional Order Model of Anomalous Diffusion. IFAC Proc. Vol. 2012, 45, 428–433. [Google Scholar] [CrossRef]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science: New York, NY, USA, 2012. [Google Scholar]
- He, J.H. A Tutorial Review on Fractal Spacetime and Fractional Calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]
- Zhang, Y.; Baleanu, D.; Yang, X. On a Local Fractional Wave Equation under Fixed Entropy Arising in Fractal Hydrodynamics. Entropy 2014, 16, 6254–6262. [Google Scholar] [CrossRef]
- Baleanu, D.; Khan, H.; Jafari, H.; Khan, R.A. On the exact solution of wave equations on cantor sets. Entropy 2015, 17, 6229–6237. [Google Scholar] [CrossRef]
- Rogosin, S. The Role of the Mittag-Leffler Function in Fractional Modeling. Mathematics 2015, 3, 368–381. [Google Scholar]
- Salahshour, S.; Ahmadian, A.; Senu, N.; Baleanu, D.; Agarwal, P. On analytical solutions of the fractional differential equation with uncertainty: Application to the basset problem. Entropy 2015, 17, 885–902. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett. 2015, 47, 54–60. [Google Scholar] [CrossRef]
- Ahmad, J.; Mohyud-din, S.T. Solving Wave and Diffusion Equations on Cantor Sets. Proc. Pak. Acad. Sci. 2015, 52, 81–87. [Google Scholar]
- Yang, X.J.; Machado, J.A.T.; Hristov, J. Nonlinear dynamics for local fractional Burgers’ equation arising in fractal flow. Nonlinear Dyn. 2016, 84, 3–7. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.; Al Qurashi, M.; Baleanu, D. On the Existence and Uniqueness of Solutions for Local Fractional Differential Equations. Entropy 2016, 18, 420. [Google Scholar] [CrossRef]
- Yang, Y.J.; Baleanu, D.; Yang, X.J. A local fractional variational iteration method for laplace equation within local fractional operators. Abstr. Appl. Anal. 2013, 2013, 202650. [Google Scholar] [CrossRef]
- Baleanu, D.; Machado, J.A.T.; Cattani, C.; Baleanu, M.C.; Yang, X.J. Local fractional variational iteration and decomposition methods for wave equation on cantor sets within local fractional operators. Abstr. Appl. Anal. 2014, 2014, 535048. [Google Scholar] [CrossRef]
- Yang, Y.J.; Hua, L.Q. Variational Iteration Transform Method for Fractional Differential Equations with Local Fractional Derivative. Abstr. Appl. Anal. 2014, 2014, 760957. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Yang, A.M.; Long, Y. Initial boundary value problem for fractal heat equation in the semi-infinite region by Yang-Laplace transform. Therm. Sci. 2014, 18, 677–681. [Google Scholar] [CrossRef]
- Yang, X.J.; Srivastava, H.M.; Cattani, C. Local fractional homotopy perturbation method for solving fractal partial differential equations arising in mathematical physics. Rom. Rep. Phys. 2015, 67, 752–761. [Google Scholar]
- Zhang, Y.; Cattani, C.; Yang, X.J. Local Fractional Homotopy Perturbation Method for Solving Non-Homogeneous Heat Conduction Equations in Fractal Domains. Entropy 2015, 17, 6753–6764. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.A.T.; Srivastava, H.M. A new numerical technique for solving the local fractional diffusion equation: Two-dimensional extended differential transform approach. Appl. Math. Comput. 2016, 274, 143–151. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Moshokoa, S.P.; Ariyan, V.M.; Tchier, F. Reduced differential transform method for partial differential equations within local fractional derivative operators. Adv. Mech. Eng. 2016, 8, 1–6. [Google Scholar] [CrossRef]
- Guo, Z.H.; Acan, O.; Kumar, S. Sumudu transform series expansion method for solving the local fractional Laplace equation in fractal thermal problems. Therm. Sci. 2016, 20, 739–742. [Google Scholar] [CrossRef]
- Liemert, A.; Kienle, A. Fractional Schrödinger Equation in the Presence of the Linear Potential. Mathematics 2016, 4, 31. [Google Scholar] [CrossRef]
- Yang, X.J.; Gao, F.; Srivastava, H.M. Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations. Comput. Math. Appl. 2017, 73, 203–210. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.A.T.; Cattani, C.; Gao, F. On a fractal LC-electric circuit modeled by local fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 200–206. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Lopes, A.M. Complex and fractional dynamics. Entropy 2017, 19, 62. [Google Scholar] [CrossRef]
- Su, N. Exact and Approximate Solutions of Fractional Partial Differential Equations for Water Movement in Soils. Hydrology 2017, 4, 8. [Google Scholar] [CrossRef]
- Jassim, H.K. The analytical solutions for volterra integro-differential equations within local fractional operators by yang-laplace transform. Commun. Math. Anal. 2017, 6, 69–76. [Google Scholar]
- Yang, X.J.; Machado, J.A.T.; Nieto, J.J. A new family of the local fractional PDEs. Fundam. Inform. 2017, 151, 63–75. [Google Scholar] [CrossRef]
- Baleanu, D.; Machado, J.A.T.; Luo, A.C.J. Fractional Dynamics and Control; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Pinto, C.M.A.; Machado, J.A.T. Fractional model for malaria transmission under control strategies. Comput. Math. Appl. 2013, 66, 908–916. [Google Scholar] [CrossRef]
- Bayour, B.; Torres, D.F.M. Existence of solution to a local fractional nonlinear differential equation. J. Comput. Appl. Math. 2017, 312, 127–133. [Google Scholar] [CrossRef]
- Zhou, J.K. Differential Transformation and its Application for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986. [Google Scholar]
- Chen, C.; Ho, S. Solving partial differential equations by two-dimensional differential transform method. Appl. Math. Comput. 1999, 106, 171–179. [Google Scholar]
- Ayaz, F. On the two-dimensional differential transform method. Appl. Math. Comput. 2003, 143, 361–374. [Google Scholar] [CrossRef]
- Ayaz, F. Solutions of the system of differential equations by differential transform method. Appl. Math. Comput. 2004, 147, 547–567. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z.; Erturk, V.S. Generalized differential transform method for solving a space- and time-fractional diffusion-wave equation. Phys. Lett. A 2007, 370, 379–387. [Google Scholar] [CrossRef]
- Ertürk, V.S.; Momani, S. Solving systems of fractional differential equations using differential transform method. J. Comput. Appl. Math. 2008, 215, 142–151. [Google Scholar] [CrossRef]
- Zedan, H.A.; Alghamdi, M.A. Solution of (3 + 1)-Dimensional Nonlinear Cubic Schrodinger Equation by Differential Transform Method. Math. Probl. Eng. 2012, 2012, 1–14. [Google Scholar] [CrossRef]
- Abuteen, E.; Momani, S.; Alawneh, A. Solving the fractional nonlinear Bloch system using the multi-step generalized differential transform method. Comput. Math. Appl. 2014, 68, 2124–2132. [Google Scholar] [CrossRef]
- Di Matteo, A.; Pirrotta, A. Generalized differential transform method for nonlinear boundary value problem of fractional order. Commun. Nonlinear Sci. Numer. Simul. 2015, 29, 88–101. [Google Scholar] [CrossRef]
- Kurnaz, A.; Oturanc, G.; Kiris, M.E. n-Dimensional differential transformation method for solving PDEs. Int. J. Comput. Math. 2005, 82, 369–380. [Google Scholar] [CrossRef]
- Keskin, Y.; Oturanc, G. Reduced differential transform method for partial differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 741–749. [Google Scholar] [CrossRef]
- Keskin, Y.; Oturanc, G. The reduced differential transform method: A new approach to factional partial differential equations. Nonlinear Sci. Lett. A 2010, 1, 207–217. [Google Scholar]
- Keskin, Y.; Oturanc, G. Reduced Differential Transform Method for Generalized KdV Equations. Math. Comput. Appl. 2010, 15, 382–393. [Google Scholar] [CrossRef]
- Saha Ray, S. Numerical solutions and solitary wave solutions of fractional KDV equations using modified fractional reduced differential transform method. Comput. Math. Math. Phys. 2013, 53, 1870–1881. [Google Scholar] [CrossRef]
- Acan, O.; Keskin, Y. Reduced differential transform method for (2 + 1) dimensional type of the Zakharov–Kuznetsov ZK(n,n) equations. In Proceedings of the 12th International Conference of Numerical Analysis and Applied Mathematics (ICNAAM-2014), Rhodes, Greece, 22–28 September 2014. [Google Scholar]
- Acan, O.; Keskin, Y. Approximate solution of Kuramoto–Sivashinsky equation using reduced differential transform method. In Proceedings of the 12th International Conference of Numerical Analysis and Applied Mathematics (ICNAAM-2014), Rhodes, Greece, 22–28 September 2014. [Google Scholar]
- Acan, O.; Keskin, Y. A new technique of Laplace Pade reduced differential transform method for (1 + 3) dimensional wave equations. New Trends Math. Sci. 2017, 5, 164–171. [Google Scholar] [CrossRef]
- Acan, O.; Keskin, Y. A Comparative Study of Numerical Methods for Solving (n + 1) Dimensional and Third-Order Partial Differential Equations. J. Comput. Theor. Nanosci. 2016, 13, 8800–8807. [Google Scholar] [CrossRef]
- Acan, O.; Firat, O.; Keskin, Y.; Oturanc, G. Solution of Conformable Fractional Partial Differential Equations by Reduced Differential Transform Method. Selcuk J. Appl. Math. 2016, in press. [Google Scholar]
- Acan, O.; Firat, O.; Keskin, Y. The Use of Conformable Variational Iteration Method, Conformable Reduced Differential Transform Method and Conformable Homotopy Analaysis Method for Solving Different Types of Nonlinear Partial Differential Equations. In Proceedings of the 3rd International Conference on Recent Advances in Pure and Applied Mathematics, Bodrum, Turkey, 19–23 May 2016. [Google Scholar]
- Wazwaz, A.M.; Gorguis, A. Exact solutions for heat-like and wave-like equations with variable coefficients. Appl. Math. Comput. 2004, 149, 15–29. [Google Scholar] [CrossRef]
- Momani, S. Analytical approximate solution for fractional heat-like and wave-like equations with variable coefficients using the decomposition method. Appl. Math. Comput. 2005, 165, 459–472. [Google Scholar] [CrossRef]
- Molliq, R.Y.; Noorani, M.S.M.; Hashim, I. Variational iteration method for fractional heat- and wave-like equations. Nonlinear Anal. Real World Appl. 2009, 10, 1854–1869. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, R.; Zhang, L. Exact solutions of fractional heat-like and wave-like equations with variable coefficients. Therm. Sci. 2016, 20, 689–693. [Google Scholar] [CrossRef]
- Avcı, D.; İskender Eroğlu, B.B.; Özdemir, N. Conformable Fractional Wave-Like Equation on a Radial Symmetric Plate; Springer International Publishing: New York, NY, USA, 2017; pp. 137–146. [Google Scholar]

| Special Functions | ||
|---|---|---|
| Original Function | Transformed Function |
|---|---|
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acan, O.; Baleanu, D.; Qurashi, M.M.A.; Sakar, M.G. Analytical Approximate Solutions of (n + 1)-Dimensional Fractal Heat-Like and Wave-Like Equations. Entropy 2017, 19, 296. https://doi.org/10.3390/e19070296
Acan O, Baleanu D, Qurashi MMA, Sakar MG. Analytical Approximate Solutions of (n + 1)-Dimensional Fractal Heat-Like and Wave-Like Equations. Entropy. 2017; 19(7):296. https://doi.org/10.3390/e19070296
Chicago/Turabian StyleAcan, Omer, Dumitru Baleanu, Maysaa Mohamed Al Qurashi, and Mehmet Giyas Sakar. 2017. "Analytical Approximate Solutions of (n + 1)-Dimensional Fractal Heat-Like and Wave-Like Equations" Entropy 19, no. 7: 296. https://doi.org/10.3390/e19070296






