An Entropy-Based Generalized Gamma Distribution for Flood Frequency Analysis
Abstract
:1. Introduction
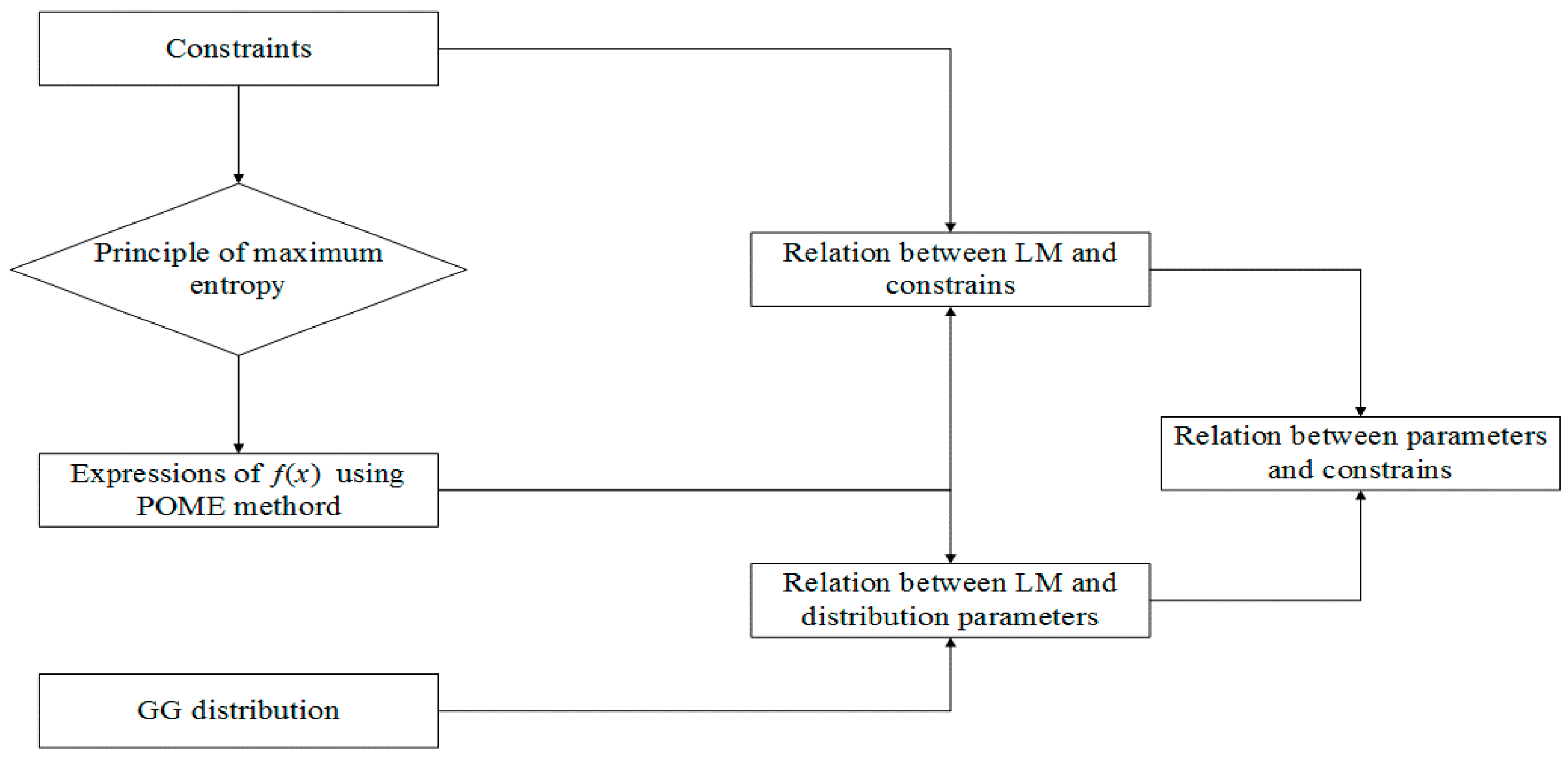
2. Methodology
2.1. Generalized Gamma Distribution
2.2. Estimation of Parameters of GB2 Distribution by POME
2.2.1. Specification of Constraints
2.2.2. Maximization of Entropy Using the Method of Lagrange Multipliers
2.2.3. Relation between Lagrange multipliers and parameters
2.2.4. Relation between Lagrange Multipliers and Constraints
2.2.5. Relation between Parameters and Constraints
3. The Descriptive Ability of GG Distribution
4. Monte Carlo Simulation
5. T-Year Design Flood Calculation
6. Conclusions
- (1)
- The GG distribution is appealing for FFA. The cumulative distributions and histograms show that the GG distribution can fit both low and high skewed data well.
- (2)
- The parameters estimated by POME are found reasonable. Both the marginal distributions and histograms indicates that the GG distribution with so estimated parameters can successfully be fitted to empirical values.
- (3)
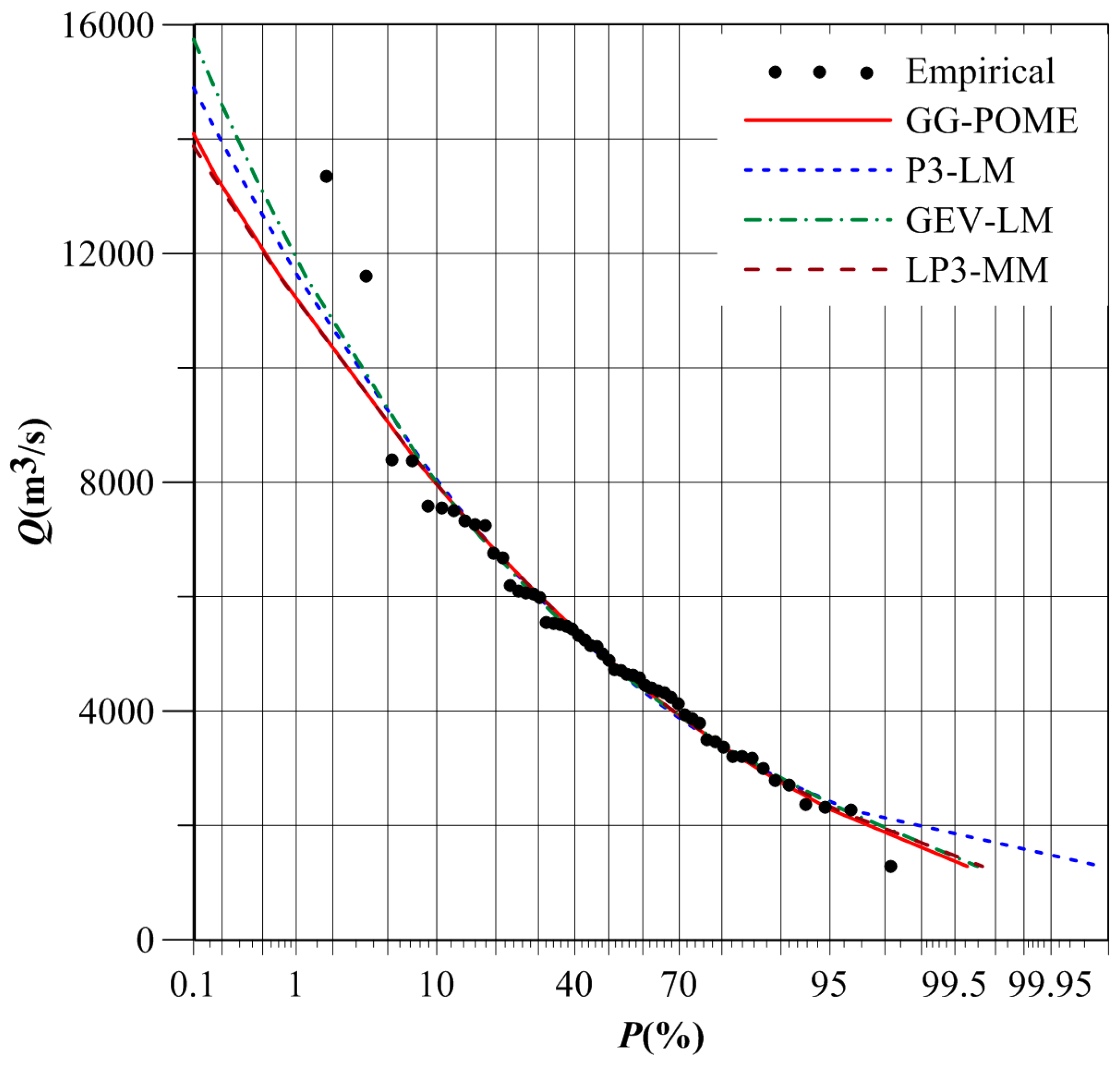
- The performance of the GG distribution is comparable or superior to that of the other distributions. Results illustrate that for sites 1, 2, 4, 5, 8, 9 and 10, the GG distribution has the smallest RMSE values. In addition, the GG distribution has the smallest AIC values for sites 2, 5, 8, and 10. Thus, the GG distribution is preferred to other distributions for those sites. Furthermore, the GG, P3, GEV, and LP3 distributions give similar performance for most of the selected sites. However, the GG distribution fits better than them for a few sites.
- (4)
- The predictive ability of the GG distribution is found to be comparable or superior to widely accepted distributions. The GG distribution performs significantly better than the other three distributions when sample sizes are small. Thus it is less effected by sample size and is more robust.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- American Society of Civil Engineers. Hydrology Handbook, 2nd ed.; ACSE: New York, NY, USA, 1996. [Google Scholar]
- Chen, L.; Guo, S.; Yan, B.; Liu, P.; Fang, B. A new seasonal design flood method based on bivariate joint distribution of flood magnitude and date of occurrence. Hydrol. Sci. J. 2010, 55, 1264–1280. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Hao, Z.; Li, T. Flood coincidence risk analysis using multivariate copula functions. J. Hydrol. Eng. 2012, 17, 742–755. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; He, J.X.; Tay, J.H. Flood frequency analysis using multi-objective optimization based interval estimation approach. J. Hydrol. 2017, 545, 251–262. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Zhou, J.; Zhang, J. Copula-based method for multisite monthly and daily streamflow simulation. J. Hydrol. 2015, 528, 369–384. [Google Scholar] [CrossRef]
- Benameur, S.; Benkhaled, A.; Meraghni, D.; Chebana, F.; Necir, A. Complete flood frequency analysis in Abiod watershed, Biskra (Algeria). Nat. Hazards 2017, 86, 519–534. [Google Scholar] [CrossRef]
- Natural Environment Research Council. Flood Studies Report; Institute of Hydrology: London, UK, 1975. [Google Scholar]
- Natural Environment Research Council. Flood Studies Report; Institute of Hydrology: Wallingford, UK, 1999. [Google Scholar]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2012, 45, 51–57. [Google Scholar] [CrossRef]
- Chebana, F.; Adlouni, S.; Bobée, B. Mixed estimation methods for Halphen distributions with applications in extreme hydrologic events. Stoch. Environ. Res. Risk. Assess. 2010, 24, 359–376. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-moments: analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. 1990, 52, 105–124. [Google Scholar]
- Singh, V.P. Entropy-Based Parameter Estimation in Hydrology; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy Theory and Its Application in Environmental and Water Engineering; John Wiley & Sons: Chichester, UK, 2013. [Google Scholar]
- Singh, V.P. Entropy Theory in Hydrologic Science and Engineering; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Deuflhard, P. Newton Methods for Nonlinear Problems: Affine Invariance and Adaptive Algorithms; Springer: Berlin, Germany, 2011. [Google Scholar]
- Liang, Z.; Hu, Y.; Li, B.; Yu, Z. A modified weighted function method for parameter estimation of Pearson type three distribution. Water Resour. Res. 2014, 50, 3216–3228. [Google Scholar] [CrossRef]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press: New York, NY, USA, 2000. [Google Scholar]
- Griffis, V.W.; Stedinger, J.R. Log-Pearson type 3 distribution and its application in flood frequency analysis. II: Parameter estimation methods. J. Hydrol. Eng. 2007, 12, 482–491. [Google Scholar] [CrossRef]
- Cunnane, C. Statistical distribution for flood frequency analysis. Oper. Hydrol. Rep. 1989, 44, 369. [Google Scholar]
- Houghton, J.C. Birth of a parent: The Wakeby distribution for modeling flood flows. Water Resour. Res. 1978, 14, 1105–1109. [Google Scholar] [CrossRef]
- Li, S.; Xu, Z.; Cheng, X.; Zhang, Q. Dissolved trace elements and heavy metals in the Danjiangkou Reservoir, China. Environ. Geol. 2008, 55, 977–983. [Google Scholar] [CrossRef]
- Qi, S.; Yan, F.; Wang, S.; Xu, R. Characteristics, mechanism and development tendency of deformation of Maoping landslide after commission of Geheyan reservoir on the Qingjiang River, Hubei Province, China. Eng. Geol. 2006, 86, 37–51. [Google Scholar] [CrossRef]
- Ji, X.; Ding, J.; Shen, H.; Salas, J.D. Plotting positions for Pearson type-III distribution. J. Hydrol. 1984, 74, 1–29. [Google Scholar]
- Shao, Q.; Wong, H.; Xia, J.; Ip, W. Models for extremes using the extended three-parameter Burr XII system with application to flood frequency analysis. Hydrol. Sci. J. 2004, 49, 685–702. [Google Scholar] [CrossRef]


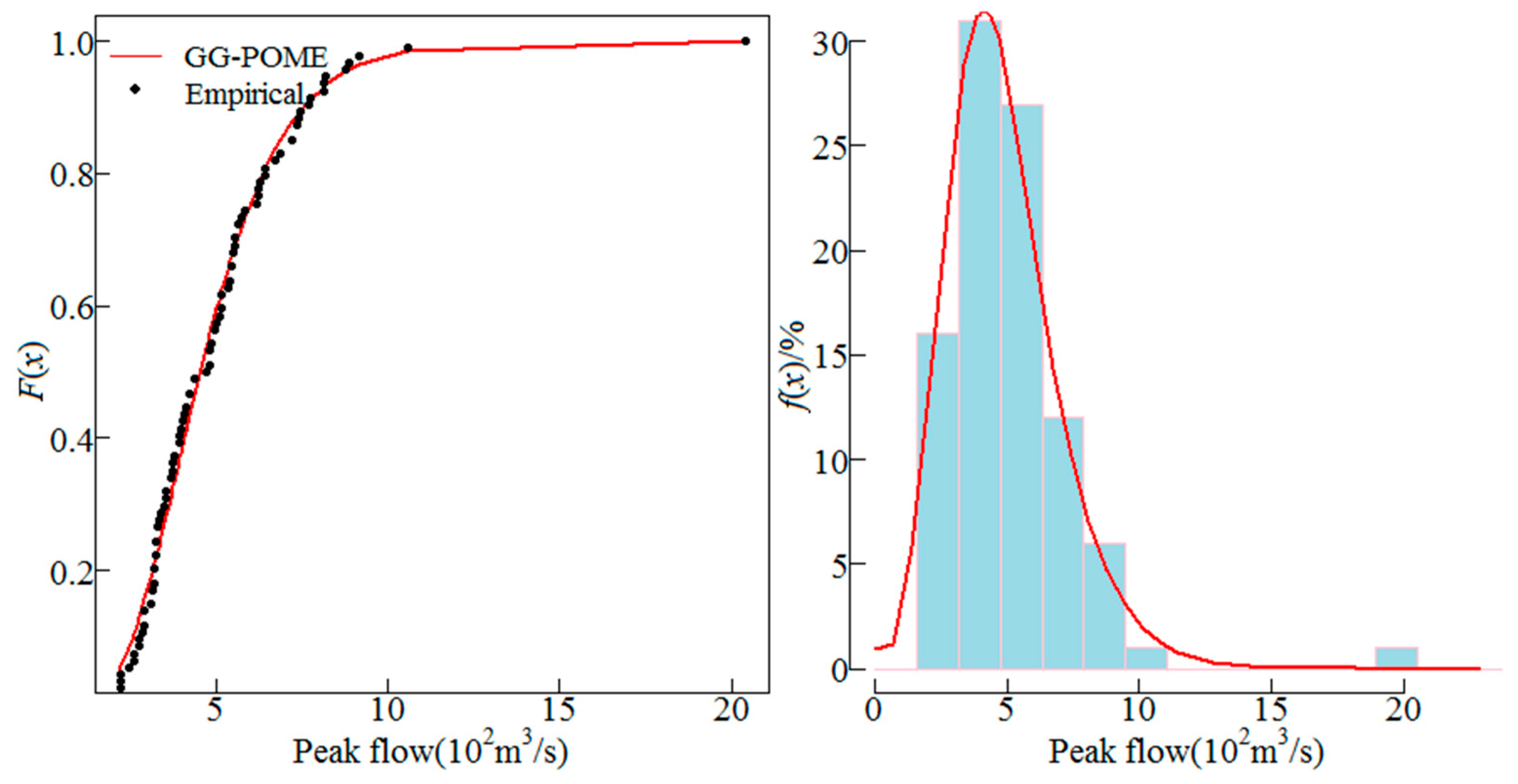
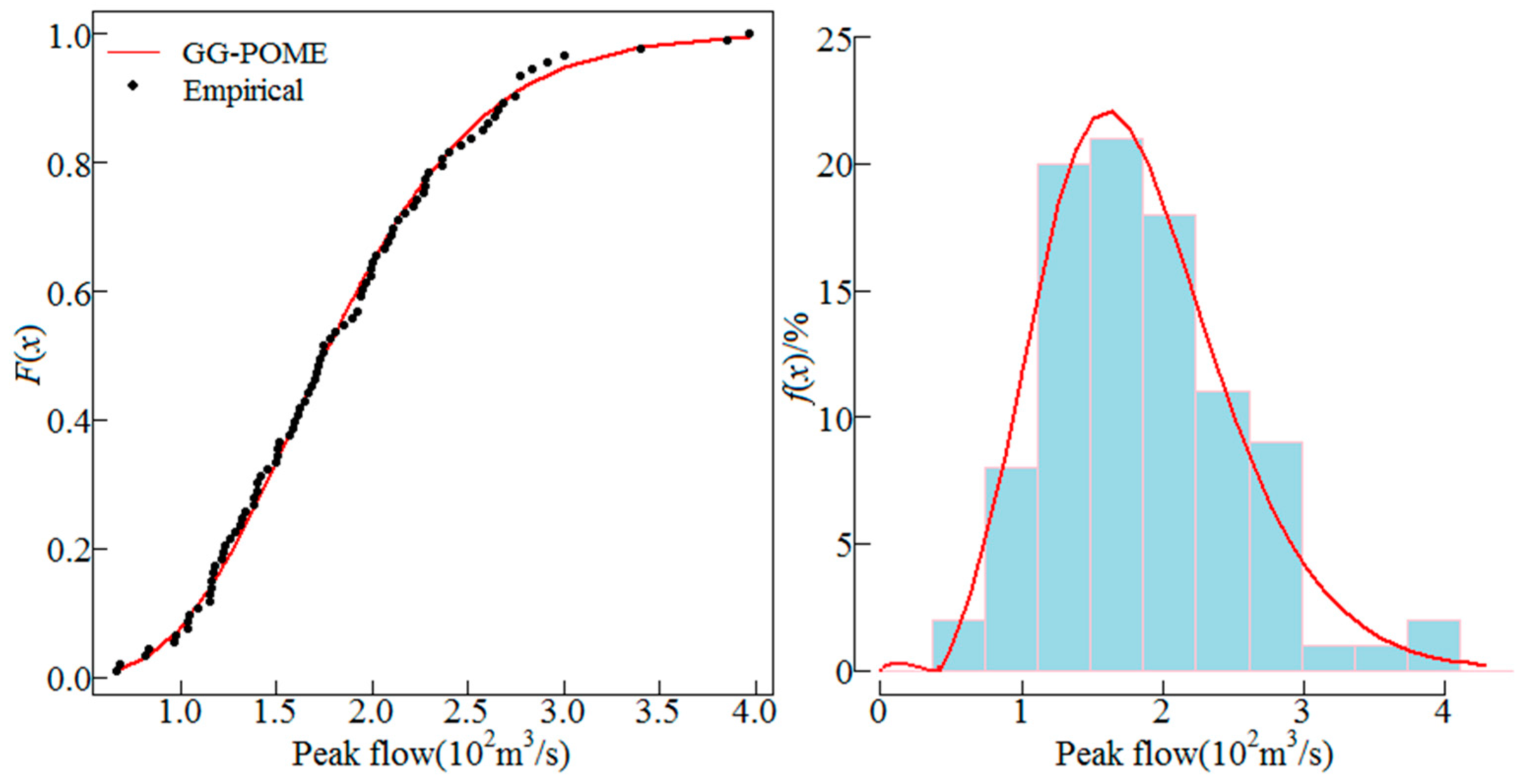

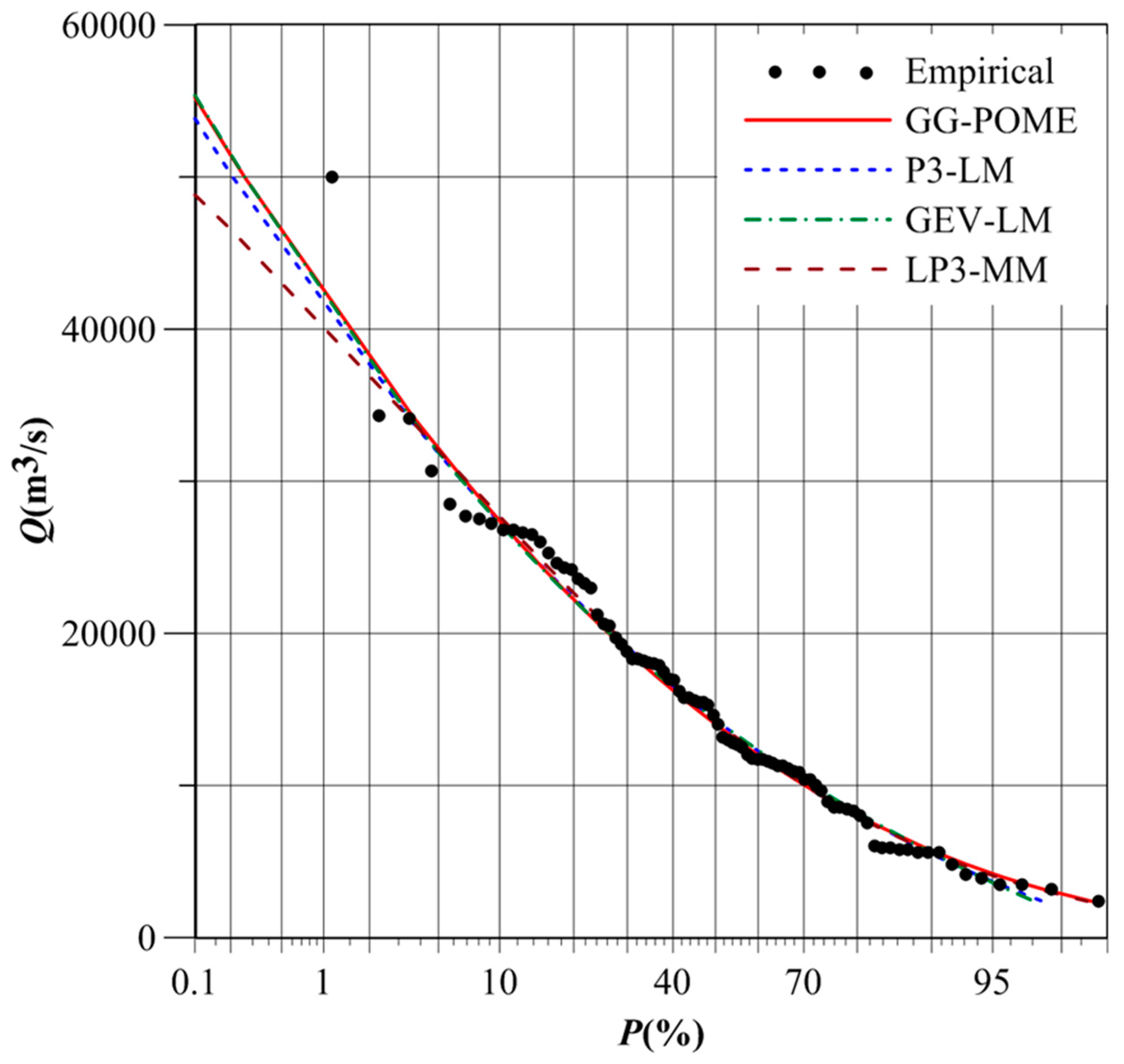
| Site No. | Gauging Station | Period | Cv | Cs | Ck |
|---|---|---|---|---|---|
| 1 | Rogue River at Raygold near Central Point, US | 1906–2001 | 0.67 | 1.94 | 5.66 |
| 2 | Quinault River at Quinault Lake, US | 1912–2001 | 0.40 | 0.52 | −0.6 |
| 3 | Eel R A Scotla, US | 1911–2001 | 0.51 | 0.61 | −0.44 |
| 4 | White River Near Meeker, US | 1910–2001 | 0.34 | 0.65 | 0.77 |
| 5 | Yellowstone River at Corwin Springs, US | 1890–2001 | 0.30 | 0.66 | 0.59 |
| 6 | Genesee River at Portageville, US | 1909–2001 | 0.48 | 2.93 | 15.67 |
| 7 | White River Near Meeker, US | 1910–2001 | 0.34 | 0.65 | 0.77 |
| 8 | Brokenstraw Creek at Younsville, US | 1910–2001 | 0.33 | 0.75 | 0.65 |
| 9 | Danjiangkou reservior at Danjiangkou, China | 1929–2014 | 0.56 | 0.95 | 1.57 |
| 10 | Geheyan reservior at Changyang, China | 1951–2005 | 0.42 | 1.34 | 3.34 |
| Model | Site 1 | Site 2 | Site 3 | Site 4 | Site 5 | Mean Value | |||||
| RMSE | AIC | RMSE | AIC | RMSE | AIC | RMSE | AIC | RMSE | AIC | RMSE | |
| GG-POME | 0.016 | −508.12 | 0.028 | −417.67 | 0.023 | −430.63 | 0.021 | −462.6 | 0.013 | −578.63 | 0.020 |
| NM-MM | 0.078 | −258.88 | 0.047 | −306.32 | 0.048 | −316.43 | 0.037 | −394.91 | 0.038 | −407.87 | 0.053 |
| EXP-LM | 0.021 | −468.96 | 0.056 | −273.3 | 0.054 | −218.65 | 0.069 | −244.39 | 0.058 | −286.44 | 0.054 |
| GLO-LM | 0.025 | −446.68 | 0.046 | −303.81 | 0.035 | −362.47 | 0.021 | −474.16 | 0.015 | −560.19 | 0.027 |
| GM-LM | 0.029 | −447.1 | 0.032 | −362.45 | 0.021 | −447.48 | 0.021 | −467.06 | 0.017 | −550.61 | 0.027 |
| GPA-LM | 0.019 | −504.1 | 0.029 | −413.67 | 0.021 | −444.15 | 0.042 | −346.33 | 0.036 | −389.21 | 0.030 |
| GB-LM | 0.039 | −386.64 | 0.036 | −343.98 | 0.025 | −421.83 | 0.024 | −430.95 | 0.015 | −530.05 | 0.031 |
| WB-LM | 0.017 | −522.29 | 0.029 | −372.34 | 0.019 | −459.48 | 0.025 | −441.45 | 0.019 | −515.48 | 0.024 |
| P3-LM | 0.016 | −533.04 | 0.033 | −351.64 | 0.023 | −434.97 | 0.021 | −468.95 | 0.015 | −561.44 | 0.024 |
| GEV-LM | 0.019 | −495.44 | 0.034 | −347.79 | 0.025 | −419.06 | 0.021 | −472.43 | 0.014 | −572.29 | 0.022 |
| LP3-MM | 0.016 | −528.15 | 0.028 | −376.18 | 0.021 | −450.45 | 0.024 | −451.6 | 0.016 | −559.41 | 0.021 |
| Site 6 | Site 7 | Site 8 | Site 9 | Site 10 | Mean Value | ||||||
| RMSE | AIC | RMSE | AIC | RMSE | AIC | RMSE | AIC | RMSE | AIC | AIC | |
| GG-POME | 0.024 | −427.53 | 0.021 | −447.25 | 0.013 | −562.19 | 0.021 | −421.51 | 0.023 | −269.84 | −452.60 |
| NM-MM | 0.038 | −407.87 | 0.113 | −198.3 | 0.035 | −400.26 | 0.046 | −313.47 | 0.051 | −210.33 | −321.46 |
| EXP-LM | 0.058 | −286.44 | 0.04 | −373.78 | 0.059 | −271.25 | 0.064 | −233.3 | 0.061 | −150.65 | −280.72 |
| GLO-LM | 0.033 | −377.21 | 0.014 | −520.86 | 0.023 | −449.16 | 0.031 | −368.25 | 0.023 | −267.35 | −413.01 |
| GM-LM | 0.038 | −393.42 | 0.046 | −374.75 | 0.014 | −541.17 | 0.023 | −404.7 | 0.027 | −264.86 | −425.36 |
| GPA-LM | 0.024 | −444.17 | 0.032 | −359.81 | 0.025 | −464.21 | 0.027 | −384.59 | 0.044 | −194.88 | −394.51 |
| GB-LM | 0.033 | −404.93 | 0.072 | −282.68 | 0.019 | −475.75 | 0.024 | −406.35 | 0.024 | −262.96 | −394.61 |
| WB-LM | 0.022 | −454.57 | 0.042 | −312.87 | 0.013 | −559.08 | 0.021 | −429.65 | 0.030 | −237.83 | −430.50 |
| P3-LM | 0.022 | −452.78 | 0.051 | −275.86 | 0.014 | −538.15 | 0.023 | −419.04 | 0.027 | −249.79 | −428.57 |
| GEV-LM | 0.027 | −411.21 | 0.021 | −438.69 | 0.015 | −525.05 | 0.024 | −409.68 | 0.024 | −260.26 | −435.19 |
| LP3-MM | 0.026 | −418.17 | 0.022 | −450.08 | 0.014 | −536.12 | 0.021 | −426.08 | 0.026 | −262.16 | −445.84 |
| ξ | α | β | γ | δ | Cv | Cs | |
|---|---|---|---|---|---|---|---|
| Case 1 | 30.4 | 114.2 | 11.3 | 19.2 | −0.5 | 0.2 | 0.16 |
| Case 2 | 15.4 | 308.8 | 10.25 | 38.5 | −0.3 | 0.36 | 0.48 |
| Case 3 | 23.5 | 198.6 | 3.7 | 109.2 | −0.2 | 0.55 | 0.95 |
| GG-POME | P3-LM | GEV-LM | LP3-MM | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RB | RRMSE | RB | RRMSE | RB | RRMSE | RB | RRMSE | |||
| T = 10 | −1.71 | 4.54 | −1.21 | 3.64 | −0.87 | 3.78 | −0.89 | 4.07 | ||
| n = 20 | T = 100 | 6.11 | 7.95 | 4.6 | 9.26 | 4.89 | 9.31 | 2.56 | 8.84 | |
| T = 1000 | 2.02 | 6.46 | 2.29 | 9.08 | 5.11 | 10.84 | 4.15 | 10.03 | ||
| T = 10 | −1.32 | 2.73 | −0.87 | 2.45 | −0.75 | 2.43 | −0.81 | 2.48 | ||
| Case 1 | n = 50 | T = 100 | 5.53 | 6.5 | 4.38 | 6.28 | 6.12 | 8.02 | 4.25 | 6.77 |
| T = 1000 | 1.85 | 4.9 | 0.02 | 6.73 | 2.87 | 8.1 | 0.65 | 7.31 | ||
| T = 10 | −1.06 | 1.82 | −1.05 | 1.86 | −0.72 | 1.84 | −0.71 | 1.82 | ||
| n = 100 | T = 100 | 6.02 | 6.55 | 4.97 | 5.72 | 5.47 | 6.34 | 4.74 | 5.82 | |
| T = 1000 | 1.46 | 3.42 | 0.21 | 4.29 | 2.93 | 6.03 | 0.55 | 5.46 | ||
| T = 10 | −2.65 | 9.78 | −0.82 | 9.78 | −0.58 | 9.34 | −0.35 | 14.78 | ||
| n = 20 | T = 100 | 1.93 | 10.23 | 2.25 | 16.85 | 3.64 | 19.23 | 5.97 | 39.86 | |
| T = 1000 | 3.59 | 14.18 | 8.69 | 24.29 | 16.48 | 34.45 | 11.62 | 44.85 | ||
| T = 10 | −1.93 | 8.44 | −1.57 | 6.76 | −1.76 | 6.21 | −1.26 | 6.63 | ||
| Case 2 | n = 50 | T = 100 | 1.66 | 7.55 | 1.76 | 10.27 | 1.37 | 10.74 | −1.67 | 12.54 |
| T = 1000 | 3.27 | 10.33 | 8.64 | 16.46 | 6.67 | 18.96 | 4.32 | 21.43 | ||
| T = 10 | −1.21 | 5.86 | −1.18 | 4.73 | −0.58 | 4.34 | −0.86 | 4.52 | ||
| n = 100 | T = 100 | 1.94 | 5.87 | 1.37 | 6.24 | 0.87 | 7.52 | −1.24 | 7.88 | |
| T = 1000 | 4.22 | 8.4 | 9.49 | 12.78 | 8.72 | 16.35 | 0.29 | 13.51 | ||
| T = 10 | −0.42 | 11.46 | −0.58 | 13.43 | −2.34 | 12.57 | 2.64 | 14.79 | ||
| n = 20 | T = 100 | 5.1 | 14 | 7.86 | 21.95 | 8.54 | 23.35 | 4.96 | 31.38 | |
| T = 1000 | 17.67 | 28.16 | 13.57 | 29.87 | 21.82 | 42.72 | 26.58 | 57.28 | ||
| T = 10 | -0.41 | 8.78 | 0.86 | 7.96 | −1.25 | 7.38 | 1.78 | 8.67 | ||
| Case 3 | n = 50 | T = 100 | 6.34 | 12.38 | 4.62 | 13.94 | 6.44 | 15.86 | 4.41 | 16.34 |
| T = 1000 | 16.86 | 22.85 | 14.53 | 24.63 | 21.02 | 33.68 | 8.29 | 27.32 | ||
| T = 10 | −0.42 | 5.72 | −0.87 | 5.87 | −1.15 | 5.46 | 0.26 | 5.74 | ||
| n = 100 | T = 100 | 6.37 | 8.54 | 4.75 | 8.98 | 6.65 | 11.87 | 3.54 | 12.64 | |
| T = 1000 | 17.52 | 19.32 | 15.67 | 19.78 | 17.98 | 23.92 | 7.66 | 20.67 | ||
| Site | Model | Return Period (Year) | ||||
|---|---|---|---|---|---|---|
| 1000 | 500 | 100 | 50 | 10 | ||
| GG-POME | 55,234 | 51,432 | 42,204 | 38,803 | 27,398 | |
| Danjiangkou | P3-LM | 53,838 | 50,202 | 41,407 | 37,411 | 27,311 |
| (m3/s) | GEV-LM | 55,369 | 51,490 | 42,054 | 37,785 | 27,217 |
| LP3-MM | 48,822 | 46,561 | 40,261 | 36,999 | 27,692 | |
| GG-POME | 13,992 | 13,745 | 11,186 | 10,277 | 7957 | |
| Geheyan | P3-LM | 14,896 | 13,941 | 11,648 | 10,616 | 8039 |
| (m3/s) | GEV-LM | 15,746 | 14,594 | 11,910 | 10,746 | 7991 |
| LP3-MM | 13,877 | 13,099 | 11,171 | 10,276 | 7963 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Singh, V.P.; Xiong, F. An Entropy-Based Generalized Gamma Distribution for Flood Frequency Analysis. Entropy 2017, 19, 239. https://doi.org/10.3390/e19060239
Chen L, Singh VP, Xiong F. An Entropy-Based Generalized Gamma Distribution for Flood Frequency Analysis. Entropy. 2017; 19(6):239. https://doi.org/10.3390/e19060239
Chicago/Turabian StyleChen, Lu, Vijay P. Singh, and Feng Xiong. 2017. "An Entropy-Based Generalized Gamma Distribution for Flood Frequency Analysis" Entropy 19, no. 6: 239. https://doi.org/10.3390/e19060239





