Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis
Abstract
:1. Introduction
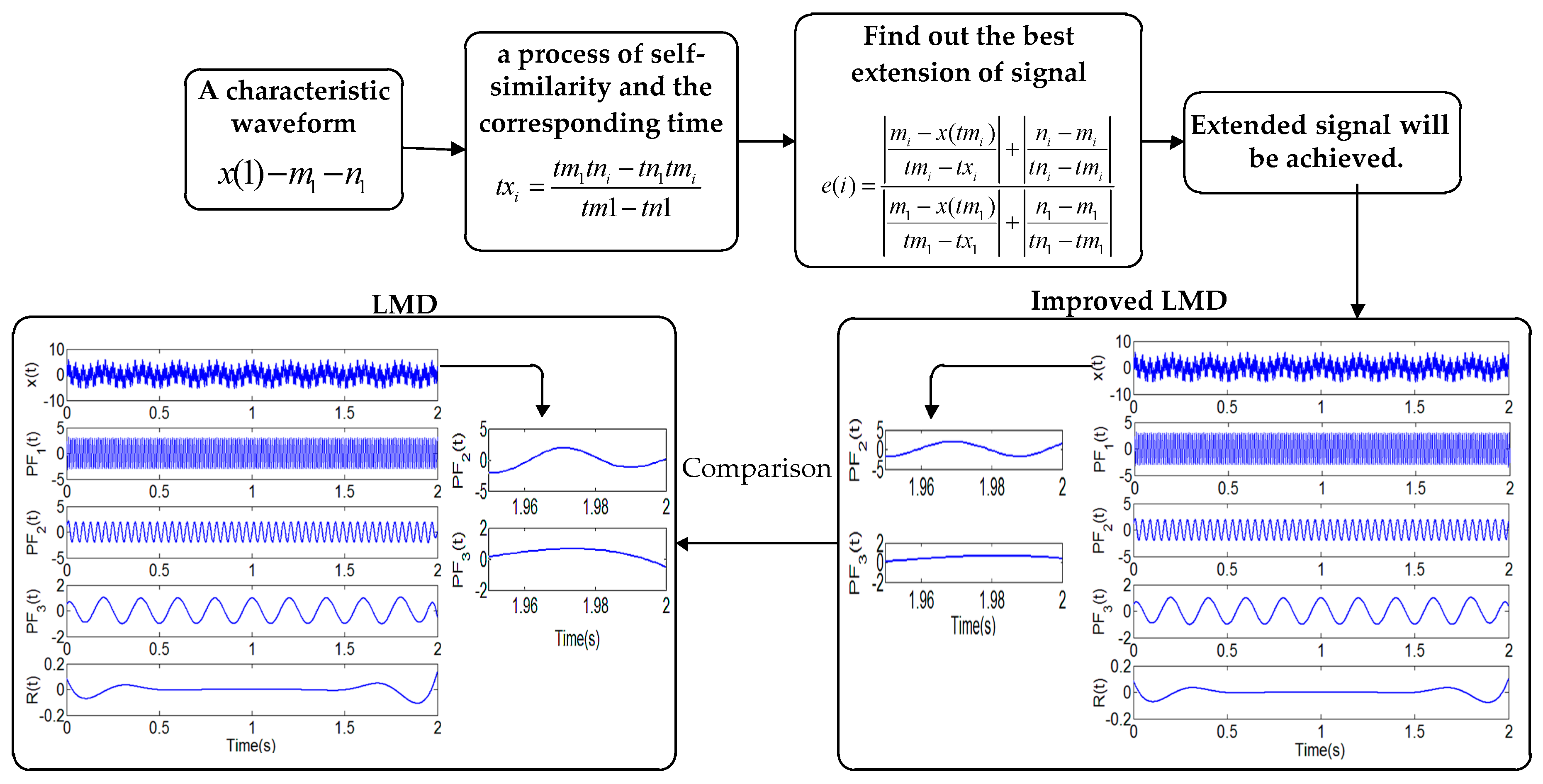
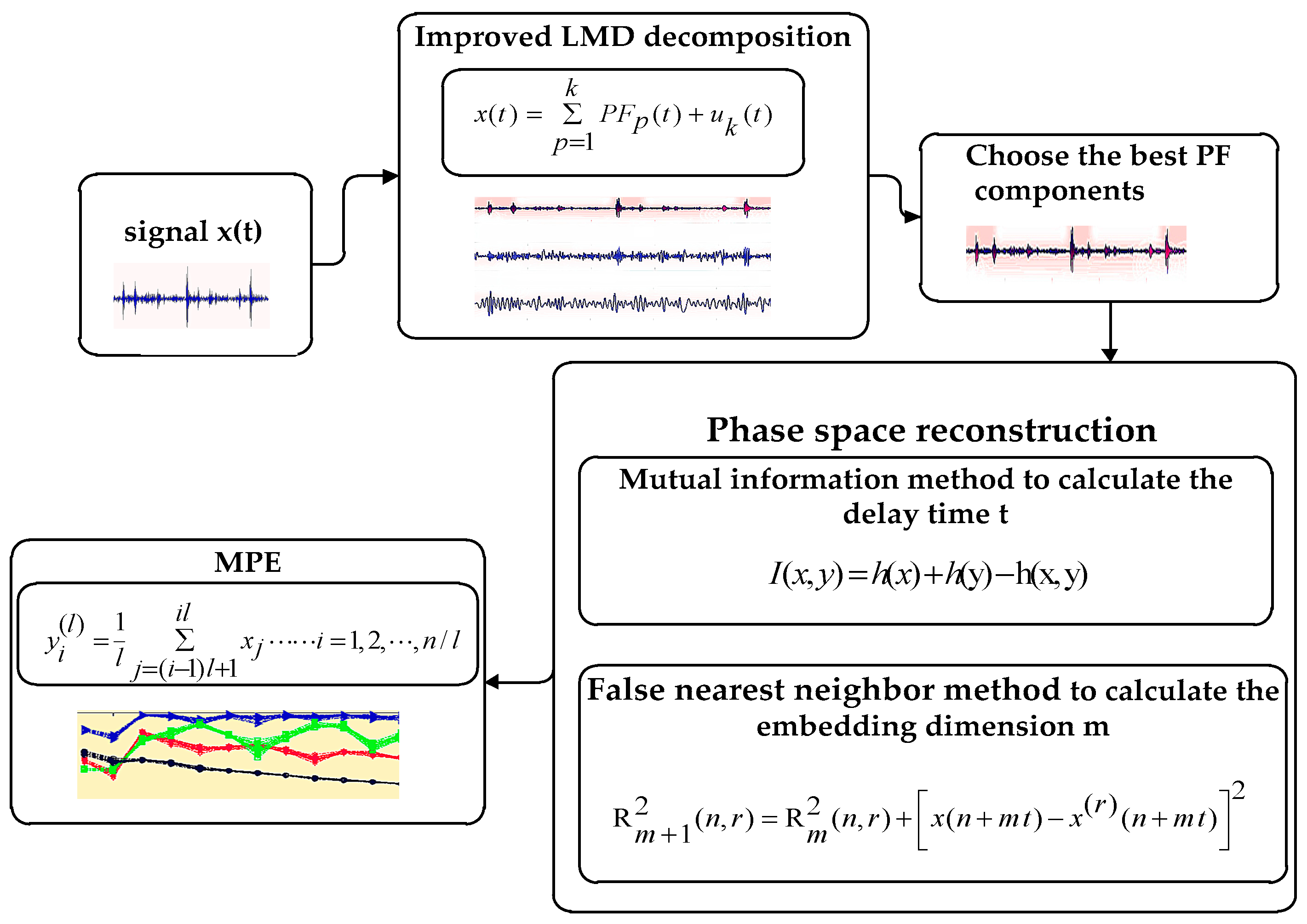
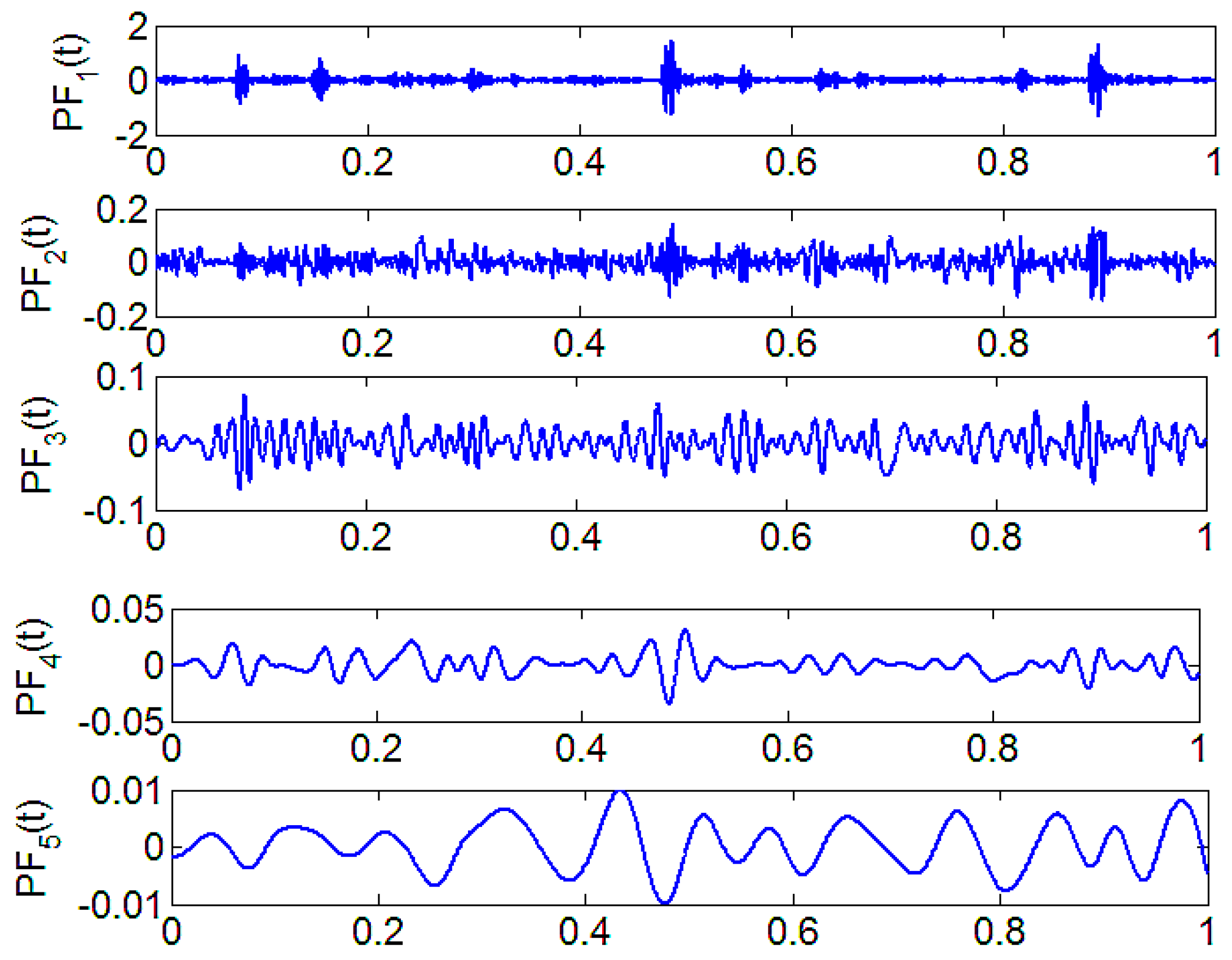
2. Improved LMD Method and Phase Space Reconstruction of MPE
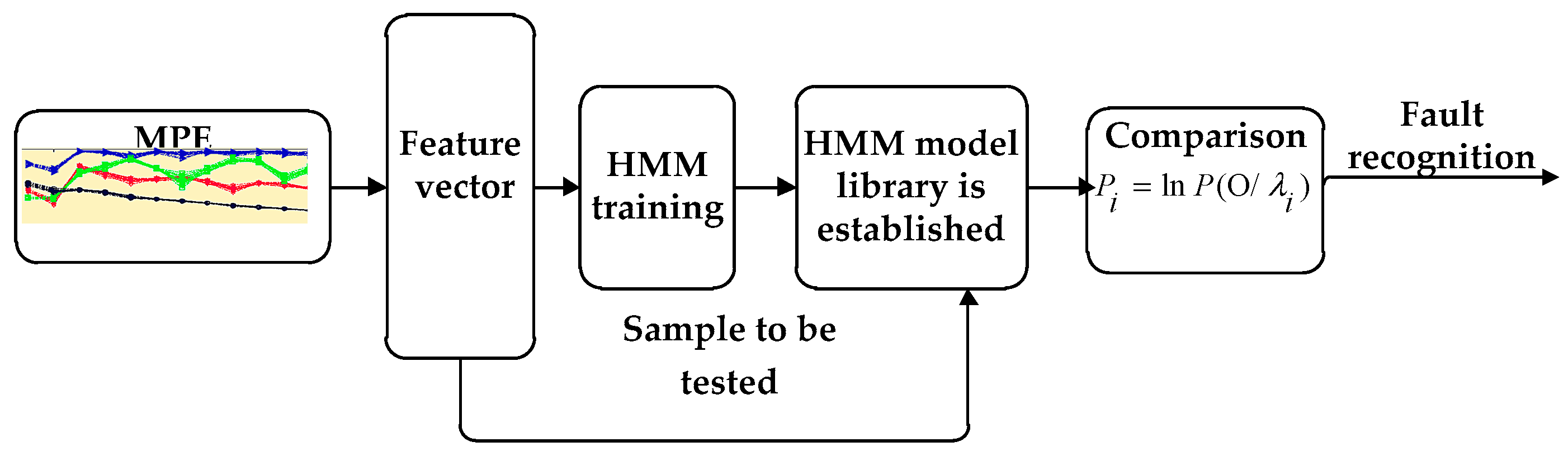
3. Diagnosis Flow Based on HMM
- (1)
- The characteristic index of bearing failure degree is extracted from the fault signal of the needle roller bearing with different degrees of damage, and the feature index is normalized and quantized [24]. When the HMM is established, the sequence of observations should be a finite discrete value, and the discretized value can be used as the model training eigenvalue after quantization.
- (2)
- Diagnosis Flow Based on HMM [25] in Figure 5. The Baum–Welch algorithm [26,27] is used to train, adjust and optimize the parameters of the observation sequence, so that the observed sequence of probability values in the observed sequence is similar to the observed value sequence. We calculate the maximum, HMM state identification, different fault levels of the state to establish the corresponding HMM, the unknown fault state data and in turn enter the various models, calculate and compare the likelihood. The output probability of the largest model is the unknown signal fault type. It is estimated that the most probable path through the sequence is observed by the Baum–Welch algorithm.
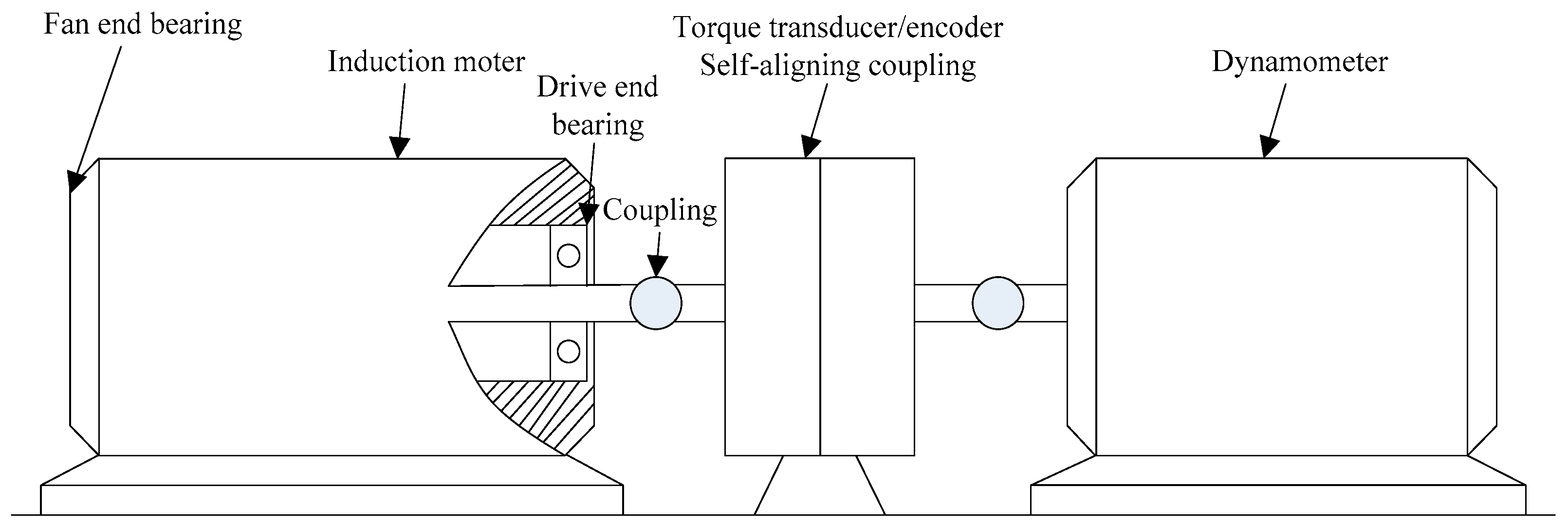
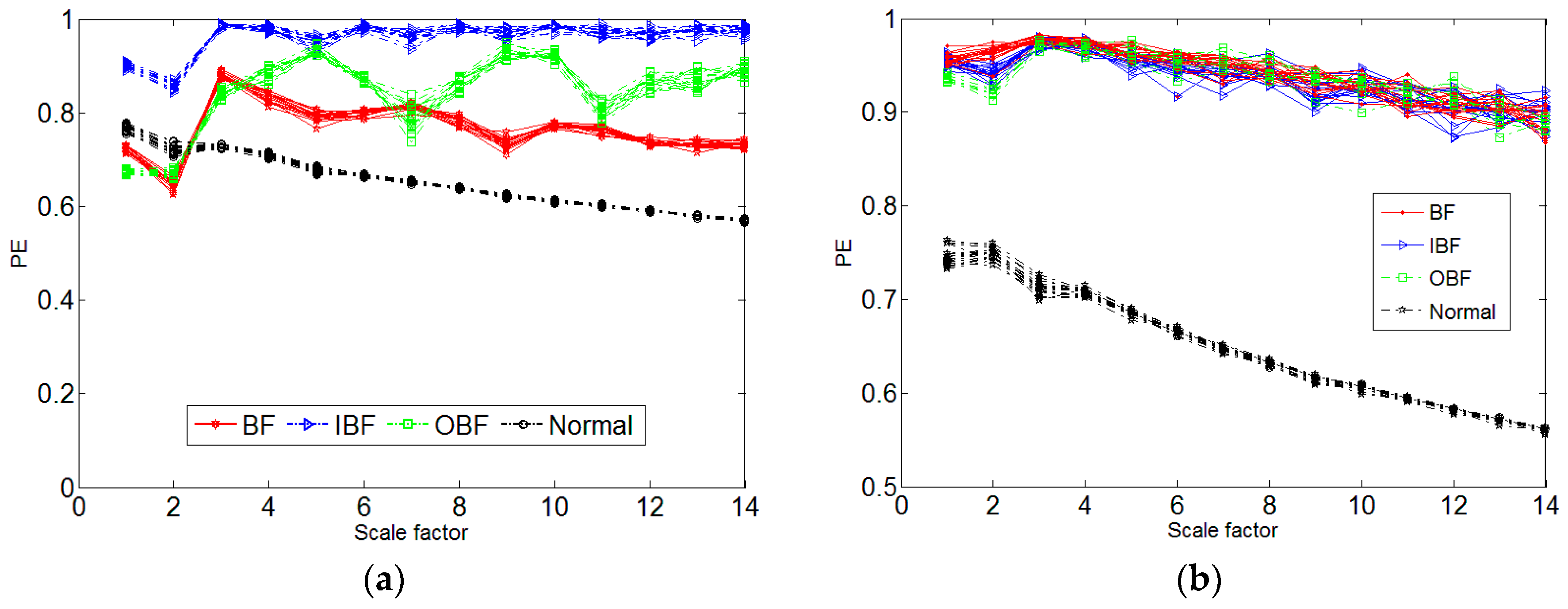
4. Experimental Data Analysis
5. Conclusions
- (1)
- Improved LMD for bearing non-stationary signal processing has a strong signal frequency domain recognition capability. The experiment shows that the improved LMD has greatly improved the reduction of the border. The improved LMD can effectively remove the excess noise and extract important information.
- (2)
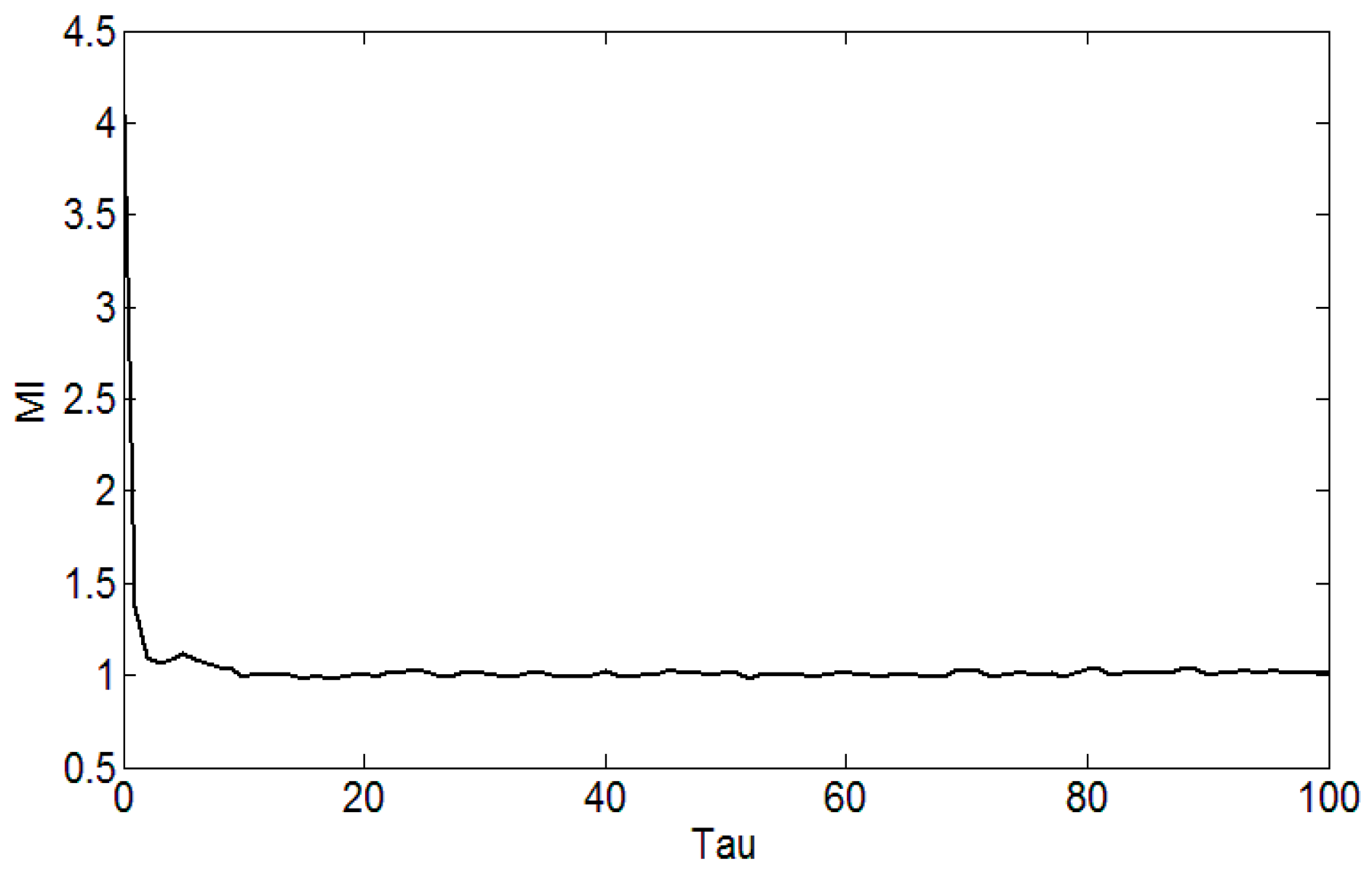
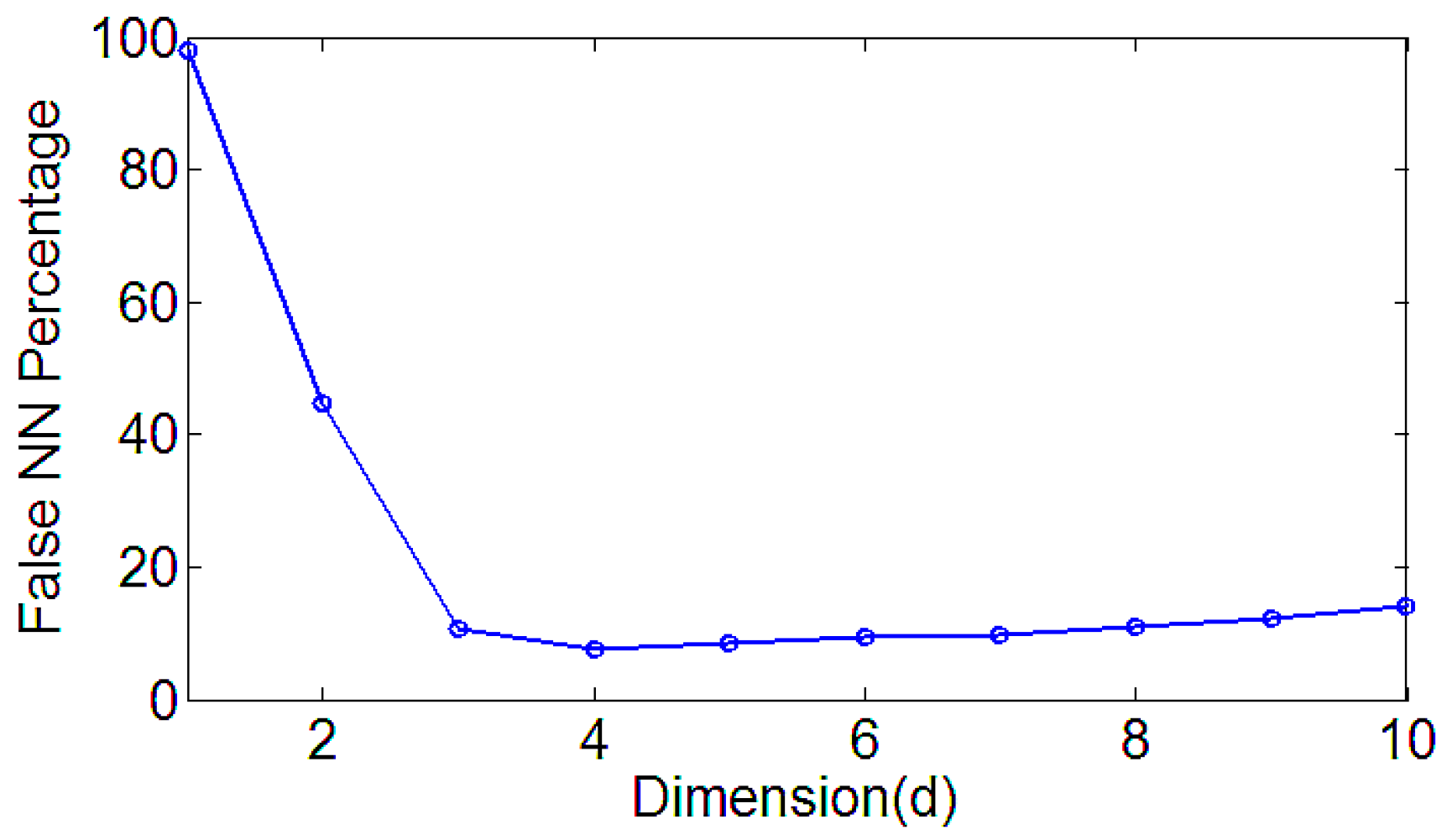
- The MI and the FNN can effectively reconstruct the space, reflecting the multi-scale permutation entropy and the mutation performance under different scales.
- (3)
- HMM model of the various states of the bearings can be trained, and successfully diagnoses the bearing fault features. Improved LMD and HMM has a high recognition rate and it is very suitable for a large amount of information, and non-stationarity of the characteristic repeatability fault signal.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, T.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Li, T.; Xu, M.; Wei, Y.; Huang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- Henao, H.; Capolino, G.A.; Fernandez-Cabanas, M.; Filippetti, F. Trends in fault diagnosis for electrical machines: A review of diagnostic techniques. IEEE Ind. Electron. Mag. 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Frosini, L.; HarlişCa, C.; Szabó, L. Induction machine bearing fault detection by means of statistical processing of the stray flux measurement. IEEE Trans. Ind. Electron. 2015, 62, 1846–1854. [Google Scholar] [CrossRef]
- Immovilli, F.; Bellini, A.; Rubini, R.; Tassoni, C. Diagnosis of bearing faults in induction machines by vibration or current signals: A critical comparison. IEEE Trans. Ind. Appl. 2010, 46, 1350–1359. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, X.; Wang, J. Online machining chatter forecast based on improved local mean decomposition. Int. J. Adv. Manuf. Technol. 2016, 84, 1–12. [Google Scholar] [CrossRef]
- Liu, W.T.; Gao, Q.W.; Ye, G.; Ma, R.; Lu, X.N.; Han, J.G. A novel wind turbine bearing fault diagnosis method based on Integral Extension LMD. Measurement 2015, 74, 70–77. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, M.; Zhao, H.; Yu, W.; Huang, W. A new rotating machinery fault diagnosis method based on improved local mean decomposition. Digit. Signal Process. 2015, 46, 201–214. [Google Scholar] [CrossRef]
- Lei, X.; Xun, L.; Chen, J.; Alexander, H.; Su, H. Time-varying oscillation detector base Don improved robust l EMP El-Z IV complexity. Control Eng. Pract. 2016, 51, 48–57. [Google Scholar]
- Liu, W.Y.; Zhou, L.Q.; Hu, N.N.; He, Z.Z.; Yang, C.Z.; Jiang, J.L. A novel integral extension LMD method based on integral local waveform matching. Neural Comput. Appl. 2016, 27, 761–768. [Google Scholar] [CrossRef]
- Wei, G.; Huang, L.; Chen, C.; Zou, H.; Liu, Z. Elimination of end effects in local mean decomposition using spectral coherence and applications for rotating machinery. Digit. Signal Process. 2016, 55, 52–63. [Google Scholar]
- Shi, Z.; Song, W.; Taheri, S. Improved LMD, permutation entropy and optimized k-means to fault diagnosis for roller bearings. Entropy 2016, 18, 70. [Google Scholar] [CrossRef]
- Yang, Z.-X.; Zhong, J.H. A hybrid eemd-based sampen and svd for acoustic signal processing and fault diagnosis. Entropy 2016, 18, 112. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Zhou, J.; Zang, Y. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Rohit, T.; Gupta, K.V.; Kankar, P.K. Bearing fault diagnosis based on multi-scale permutation entropy and adaptive neuro fuzzy classifier. J. Vib. Control 2015, 21, 461–467. [Google Scholar]
- Fan, C.-L.; Jin, N.-D.; Chen, X.-T.; Gao, Z.-K. Multi-scale permutation entropy: A complexity measure for discriminating two-phase flow dynamics. Chin. Phys. Lett. 2013, 30, 90501–90505. [Google Scholar] [CrossRef]
- Zhao, L.-Y.; Wang, L.; Yan, R.-Q. Rolling bearing fault diagnosis based on wavelet packet decomposition and multi-scale permutation entropy. Entropy 2015, 17, 6447–6461. [Google Scholar] [CrossRef]
- Mohammad, A.S.; Ralf, R.M.; Rachinger, C. Phase modulation on the hypersphere. IEEE Trans. Wirel. Commun. 2016, 15, 5763–5774. [Google Scholar]
- Ghasemzadeha, H.; Khassb, M.T.; Arjmandic, M.K.; Pooyanda, M. Detection of vocal disorders based on phase space parameters and Lyapunov spectrum. Biomed. Signal Process. Control 2015, 22, 135–145. [Google Scholar] [CrossRef]
- Rakshith, R.; Hanzo, L. Hybrid beamforming in mm-wave MIMO systems having a finite input alphabet. IEEE Trans. Commun. 2016, 64, 3337–3349. [Google Scholar]
- Vignesh, R.; Jothiprakash, V.; Sivakumar, B. Streamflow variability and classification using false nearest neighbor method. J. Hydrol. 2015, 531, 706–715. [Google Scholar] [CrossRef]
- Hyun, G.; Kim, J. A simple and efficient finite difference method for the phase-field crystal equation on curved surfaces. Comput. Methods Appl. Mech. Eng. 2016, 307, 32–43. [Google Scholar]
- Wu, C.L.; Chau, K.W. Data-driven models for monthly stream flow time series prediction. Eng. Appl. Artif. Intell. 2010, 23, 1350–1367. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, J.; Dong, G.M.; Wang, R. Detection and diagnosis of bearing faults using shift-invariant dictionary learning and hidden Markov model. Mech. Syst. Signal Process. 2015, 72–73, 65–79. [Google Scholar] [CrossRef]
- Yuwono, M.; Qin, Y.; Zhou, J.; Guo, Y.; Celler, B.G.; Su, S.W. Automatic bearing fault diagnosis using particles warm clustering and hidden Markov model. Eng. Appl. Artif. Intell. 2016, 47, 88–100. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, J.; Dong, G. Hidden Markov model and nuisance attribute projection base bearing performance degradation assessment. Mech. Syst. Signal Process. 2016, 72–73, 184–205. [Google Scholar] [CrossRef]
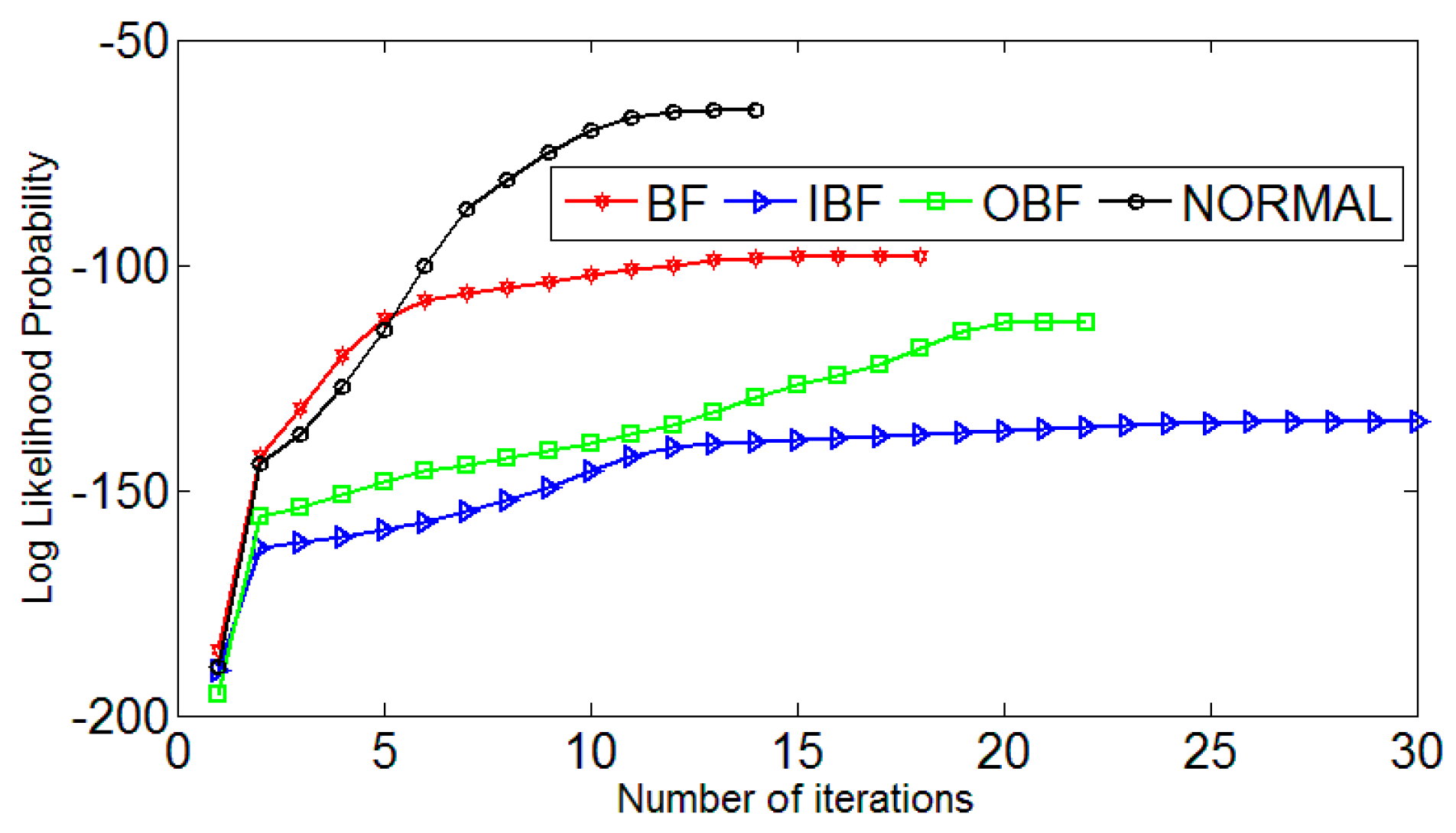
| Section | BF | OBF | IBF | Normal |
|---|---|---|---|---|
| t | 1 | 1 | 1 | 2 |
| m | 6 | 4 | 5 | 7 |
| Fault Condition | Logarithm Likelihood Probabilities of the Input Sample Model | ||||
|---|---|---|---|---|---|
| λ1 | λ2 | λ3 | λ4 | Recognition Result | |
| BF | −9.75854 | −24.5979 | λ1 | ||
| OBF | −157.594 | −15.1449 | λ2 | ||
| IBF | −55.9402 | −9.33311 | −792.054 | λ3 | |
| Normal | −24.0932 | −59.6398 | −5.63077 | λ4 | |
| Recognition Model | BF | OBF | IBF | Normal | Recognition Rate | |
|---|---|---|---|---|---|---|
| Improved LMD | HMM | 5 | 5 | 4 | 5 | 95.0% |
| BP | 5 | 4 | 5 | 4 | 90.0% | |
| LMD | HMM | 5 | 4 | 4 | 5 | 90.0% |
| BP | 5 | 4 | 4 | 4 | 85.0% | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. https://doi.org/10.3390/e19040176
Gao Y, Villecco F, Li M, Song W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy. 2017; 19(4):176. https://doi.org/10.3390/e19040176
Chicago/Turabian StyleGao, Yangde, Francesco Villecco, Ming Li, and Wanqing Song. 2017. "Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis" Entropy 19, no. 4: 176. https://doi.org/10.3390/e19040176
APA StyleGao, Y., Villecco, F., Li, M., & Song, W. (2017). Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy, 19(4), 176. https://doi.org/10.3390/e19040176








