1. Introduction
In the beginning of the last century, important results concerning Brownian motion were obtained by Einstein [
1], Langevin [
2], Fokker [
3], and Planck [
4], among others. Those investigations were mainly based on the random walk of a particle moving in a fluid in thermodynamical equilibrium. In this context, the particle’s position could be essentially viewed as a composition of successive aleatory steps due to the action of a random force, related to the interaction with other particles of the medium. Thus, the particle’s position can be found by solving the corresponding Langevin equation [
2,
5]. Another approach to describing the diffusive aspect of the particle motion focuses on the probabilities of finding a particle in their possible positions (states), whose dynamics is governed by a linear Fokker–Planck equation [
3,
4,
6]. An important particular solution of this equation is the Gaussian distribution.
The limiting behavior of the probability of the composition of successive aleatory steps in a random walk when the number of steps is very large is directly related to the central limit theorem [
5,
6,
7]. Basically, this theorem says that the limiting distribution of the sum of independent random variables is a Gaussian distribution [
7,
8]. Probably the most famous situation where this fact occurs is in a simple random walk where the steps are independent and of the same length. In this case, the probability of finding the walker in a certain position after taking a determined number of steps corresponds to a binomial distribution, which—in agreement with the central limit theorem—approximates a Gaussian distribution when the number of steps is sufficiently large [
7,
9].
Starting from a random walk (discrete case) with steps that are independent and of equal length, we can obtain a normal diffusion process (continuous case) when we let the number of steps increase without bound. This diffusion process is governed by a linear Fokker–Planck equation, whose solution is the Gaussian distribution. Thus, obtaining a diffusion process as the continuous limit of a random walk can be visualized as a verification of the central limit theorem. On the other hand, starting from a normal diffusion process governed by a Fokker–Planck equation whose solution is a Gaussian distribution, we can employ a discretization process in order to obtain a random walk. This random walk will be such that the distribution of the position of the walker after taking a determined number of steps converges to the solution of the Fokker–Planck equation—namely the Gaussian distribution—when the number of steps tends to infinity. Thus, we generate a random walk that verifies the central limit theorem.
Generalizations of the central limit theorem that consider weak relaxation of the basic hypothesis of independence (weak dependence) are available in the literature [
7,
10,
11]. More recently, some results concerning the central limit theorem have been obtained for strongly correlated situations [
12,
13,
14] (see also [
15,
16,
17]) in scenarios related to nonextensive statistical mechanics [
18,
19]. For instance, when the usual statistical mechanics does not give a good description of the thermodynamical equilibrium state, it was verified by using numerical simulations that a system with long-range interactions leads to a strong violation of the central limit theorem [
20,
21,
22,
23]. In addition, there are many situations where the diffusive-like process of particles in a medium is not the usual one, and is usually described in terms of phenomenological anomalous diffusion equations. In particular, these equations have solutions which are different from the Gaussian distribution.
The idea of the present article is to study a generalized random walk by starting from a nonlinear diffusion equation (or nonlinear Fokker–Planck equation). This random walk will show strong correlations since—as we will show—the distribution of the position of the walker after taking a large number of steps will approximate the solution of the nonlinear Fokker–Planck equation, which is not the Gaussian distribution. In this direction, we will verify a kind of generalization of the central limit theorem. The organization of this article is as follows:
Section 2 contains a brief discussion of relevant aspects of random walks and master equations in order to motivate the corresponding generalizations based on a nonlinear Fokker–Planck equation, which will be shown in
Section 3; a more general scenario is indicated in
Section 4; and finally, we conclude in
Section 5.
2. Usual Random Walk
Consider the basic problem of a particle performing one-dimensional successive steps, each of length
a and time interval
, with equal waits. The equation for the probabilities is
where
is the probability of finding the particle in position
at time
with
m and
being integers. As it is known, when the initial condition is localized in a given position
m (i.e.,
; here,
if
, and otherwise
) , the above equation leads to the binomial distribution
where
m is odd (even) if
n is odd (even) and
;
for other values of
m. This solution, when multiplied by
, may be written as the following table
where the nonzero numbers form the Pascal triangle. If the variables
and
are employed, the distribution given in Equation (
2) reduces to the usual form of the binomial distribution,
.
Formally, using the approximations
for large
n and
with
and
, the random walk Equation (
1) can be approximated by the linear Fokker–Planck equation (usual diffusion one)
with
,
,
and
. In fact, subtracting
from both sides of Equation (
1) and taking a macroscopic limit, we can obtain Equation (
5) directly.
The solutions of Equation (
5) that have probabilistic interpretation, with
or
, are given by
Both expressions are related to the Gaussian distribution, defined by
where
and
are, respectively, the mean and the variance of the distribution. For instance, from the last expression in Equation (
6), we have
.
We have shown that—starting from the random walk Equation (
1) and using the approximations given in Equation (
4)—it is possible to obtain the linear Fokker–Planck Equation (
5). So, we went from a discrete case to a continuous one. Consistently, the distribution given in Equation (
2) should converge to the Gaussian distribution given in Equation (
6) when the number of steps
n in the random walk increases without bound. This actually happens by virtue of the central limit theorem (indeed, this can be verified directly from Equation (
2) by using Stirling’s formula). Thus, the mentioned procedure can be seen as a verification of the central limit theorem. Conversely, starting from Equation (
5) and using the discretizations given in Equation (
4), we can obtain an equation of a random walk (in particular, we can obtain Equation (
1)). This random walk will be such that the distribution of the position of the walker after taking a determined number of steps converges to the solution of the Fokker–Planck Equation (
6) when the number of steps tends to infinity. Thus, we generate a random walk that verifies the central limit theorem.
As we pointed out, there are anomalous diffusive processes where Equation (
5) does not give the correct description. In this direction, generalizations of Equation (
5) that preserve linearity have been made by the introduction of a diffusion coefficient which depends on time and space [
24], spatial fractional derivatives (Lévy diffusion) [
25,
26,
27], and a combination of them [
28,
29]. These anomalous cases and many others may be viewed as a continuous limit of
where the sum covers all possible states and
is the probability of moving from the position
to the position
m at the
th step. When the process is continuous in time, the master equation must be used instead of Equation (
8). Moreover, Equation (
8) can be written in the usual form
where
. Note that recursive application of Equation (
8) naturally leads to a generalization of the binomial distribution given in Equation (
2), since by using
and the initial condition
, one recovers Equations (
1) and (
2). Notice also that this choice for the transition probabilities
is the simplest one related to Equation (
5) for large
n. Other choices basically may arise as convenient discretizations of the derivatives in Equation (
5).
3. Nonlinear Random Walk
In addition to linear diffusions, there are anomalous diffusive situations that involve nonlinearities. Theoretically, we could ask ourselves if it is possible to generalize what has been shown in the previous section to a nonlinear context. As a guide for a possible generalization, we will start with the porous media equation [
30], considering it in the frame of probability distributions (i.e., as a kind of a Fokker–Planck equation). We choose to begin our study from the porous media equation because it is one of the best-known nonlinear diffusion equations. We believe that this type of investigation provides new insights into recent studies of nonlinear diffusive processes like the ones related to non-extensive statistical mechanics [
31,
32,
33,
34,
35,
36]. In general (as we shall see), the approach presented here aims to indicate a possible route to investigating a broad class of central limit theorems, which can be useful in physical contexts.
The porous media equation [
30] reads
where
is a real parameter. This equation appears, for instance, in the discussion of the percolation of gases through porous media (
[
37]), thin saturated regions in porous media (
[
38]), thin liquid films spreading under gravity (
[
39]), radiative heat transfer by Marshak waves (
[
40]), solid-on-solid model for surface growth (
[
30]), among others (see also [
41]). Moreover, this nonlinear equation was firstly investigated as a Fokker–Planck one in connection with Tsallis statistics by Plastino and Plastino [
42]. After that, several other studies were performed [
31,
32,
33,
34,
35,
36,
43,
44]. In particular, a nonlinear master equation that may be used to reobtain the nonlinear Fokker–Planck equation was proposed [
45]. Related to the last equation, generalized Block [
46] (with its path integral solution) and von Neumann [
47] equations were also investigated.
The
q-Gaussian distribution of parameters
and
is characterized by the density [
12]
where
is the
q-exponential function, defined for every real
y such that
, and
is a normalization constant (if
, the normalization integral diverges). We note immediately that for
, a
q-Gaussian distribution has compact support—namely, the interval
; if
, the support of this distribution is the whole real line.
The solution of Equation (
10), which generalizes the usual Gaussian solution given in Equation (
6), is written in terms of a
q-Gaussian distribution as
where
and
is given in Equation (
13). We note immediately that Equation (
6) is recovered from Equation (
14) when
(
). We also mention that the nonlinear logarithmic equation corresponds to
and that using
finite instead of
D is more convenient [
48].
Following the line of reasoning of the previous section, it is possible to obtain a simple nonlinear random walk from the nonlinear Fokker–Planck Equation (
10) by considering a discrete version of the spatial derivatives. Indeed, using the substitutions
,
and
, Equation (
10) yields
where, for simplicity, we have also considered that
. Using the discretizations given in Equation (
4) in Equation (
15), we obtain
In fact, as in the linear case given in Equation (
5), this equation is formally approximated by Equation (
15) for large
n and
. Note that Equation (
16) generalizes the simplest random walk (Equation (
1)) and goes in the direction of Equation (
10) for long time. In contrast to Equation (
1), we will see later that Equation (
16) for
allows the walker to remain in the same position after taking one step. If instead of considering
we put
, the procedure of discretization of Equation (
10) described above yields
which says that the walker can stay in the same position after taking one step, even in the case
.
For
, the solution of Equation (
16) with the initial condition
will approximate the solution of the nonlinear Fokker–Planck Equation (
10), given in Equation (
14). This can be seen as a verification of a generalized central limit theorem that involves a
q-Gaussian distribution [
12]. Before we continue with our line of reasoning, we mention that another point of view based on Equation (
5) and its associated stochastic differential equation has been employed to discuss a random walk [
49].
A more general framework than that of Equation (
16) is to consider the random walk described by
where in this case
is a quantity related to the probability of moving from the position
to the position
m at the
th step. By choosing
conveniently, a large class of equations that mix nonlinearities, spatial- and time-dependent diffusion coefficients, and spatial fractional derivatives may be obtained as a limiting case.
We note that the dynamics generated by Equation (
18) may preserve the normalization of the probabilities. Indeed, we have
If
for any
m and
,
for any
, and
and
are finite, then we can change the order of the summation in the first term of the right-hand side of Equation (
19) and obtain
. We see from Equation (
18) that
is certainly non-negative if each initial probability
is also non-negative and
, which leads to
. In contrast, if
and every initial probability
is non-negative,
remains unchanged for any
n, but some of the
’s became imaginary for a sufficiently large
n. However, if we consider Equation (
17) rather than Equation (
16), we can choose
small enough to avoid imaginary probabilities for a large number of steps. In the following, our discussion will focus on the case
, which is compatible with the examples of anomalous diffusion cited in the first paragraph of this section.
Let us consider that the quantities
do not depend on the position
m; i.e.,
for any
m. Defining the expected values
and
, which contains the usual one,
, as the particular case
, it follows from Equation (
18) that
Adding these equations yields
Using the binomial theorem, we obtain
and, therefore,
If one considers Equation (
16), then
and
,
,
,
, and so on. Moreover,
, since
. Thus, using these facts, we obtain
and
For
, we have
, and consequently,
. Thus, the case
is consistent with a subdiffusive regime. In this case we also have that
which implies that
. Finally, we see from Equation (
25) that for
, we obtain
, recovering the variance of the simple random walk.
The solution of Equation (
16) multiplied by
gives a generalized version of the Pascal triangle shown in Equation (
3). However, for
, when
m is odd (even) and
n even (odd), the values in this generalized triangle are usually different from zero, as we show in the following:
Simple relations for generic elements of this triangle are generally cumbersome when compared with the usual case (). For instance, the element corresponding to is , which reduces just to 1 when .
As we pointed out, the solution of the simplest random walk given in Equation (
2) becomes equal to zero for
m odd (even) when
n even (odd). This fact does not occur for
when
, but its signature can be identified for
close to 1 and
n not so large. Thus, these facts justify using the term “formally” when obtaining Equations (
5) and (
15) from Equations (
1) and (
16), respectively. In order to get rid of the null probabilities in the solution of the simple random walk (
) given in Equation (
2), we will consider the distribution
. We could have considered, for instance, the arithmetic mean of
n values; however, our choice is the simplest one.
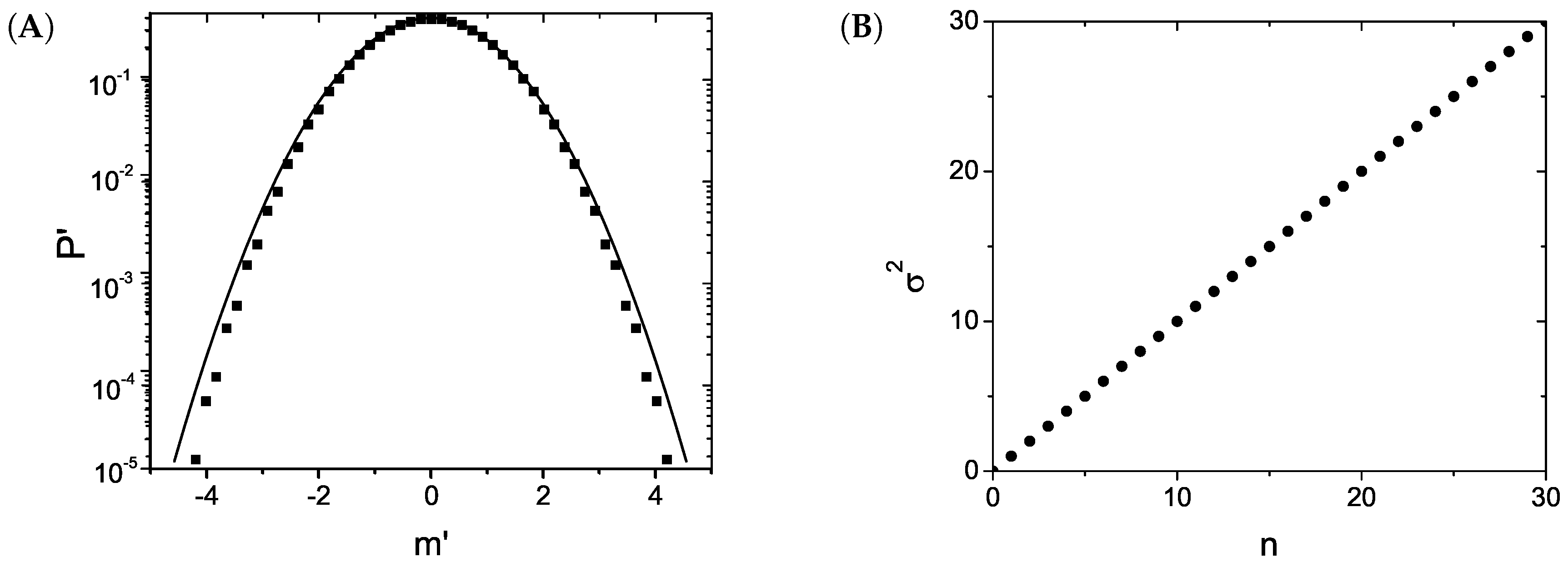
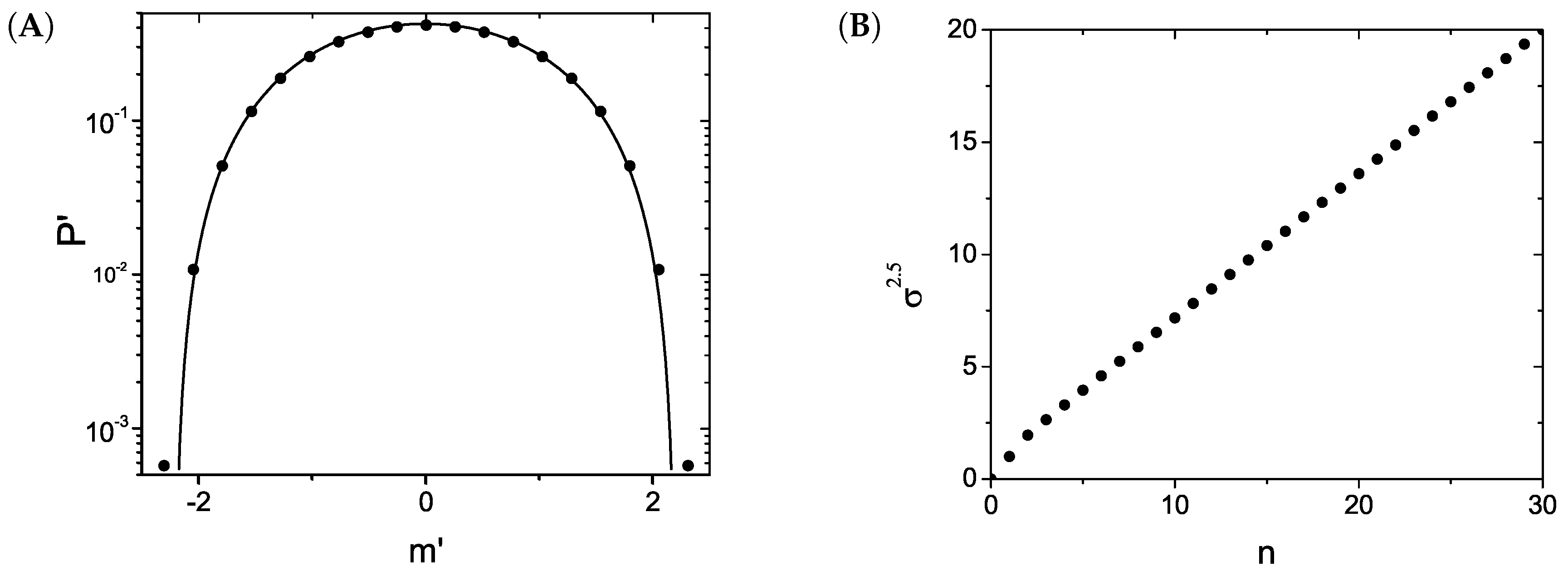
Figure 1 shows
for
compared with the Gaussian distribution given in Equation (
6), and also exhibits the corresponding standard deviation. Analogous illustrations are shown in
Figure 2 for the case
. We have chosen to represent
versus
n in panel (B) of
Figure 1 and
Figure 2, since from Equation (
14), we verify that
. In the case
, we remarked after Equation (
19) that it is possible to obtain the random walk given in Equation (
17) by choosing
to be small enough. More precisely, for each
, there will be a maximum step number
such that
is not imaginary for all
. In addition, for
, we can obtain an analogous version of
Figure 2A that shows an agreement with a
q-Gaussian distribution with unbounded support (
), and consequently, with
.
Recent efforts have obtained a generalization of the central limit theorem for sequences of random variables that show a special type of strong correlation, usually referred to as
q-independence [
12,
14] (see also [
15,
16,
17]). The attractor in this generalized theorem is a
q-Gaussian distribution with
, which has unbounded support. In contrast, in this work we have exhibited a nonlinear random walk such that when the number of steps increases without bound, the distribution of the position of the walker converges to a
q-Gaussian distribution with compact support (
).
4. A More General Perspective
Before we conclude this work, we would like to remark that the introduction of the nonlinear Markov framework (see Equation (
18))—proposed in connection with the nonlinear Fokker–Planck equation—may be extended to other kinds of generalized random walks. In this direction, we briefly indicate two scenarios. First, a very general nonlinear Markov process may be described by
where
is related to a transition probability from
-state to
m-state, and may depend on the probabilities
’s. If the transition matrices
do not depend on the
’s, the usual case given in Equation (
9) is recovered. In addition, if
for
and
, one obtains Equation (
18). If in this context
has the status of probability, one has for all
n,
m, and
that
This equality is a consequence of the normalization condition
. Furthermore, when there is a stationary distribution
, it must satisfy the equation
Rather than discussing further general properties of a nonlinear Markov chain, we conclude with an extension related to the porous media Equation (
10). According to the central limit theorem, the distribution of the random variable
—where
and
are independent and identically distributed random variables with null expectation and finite variance—converges to the Gaussian distribution
as
. On the other hand, when one looks for generalizations of the central limit theorem, several possibilities may be considered going from
to non-Gaussian probability distributions. In fact, in addition to the previous discussion about the nonlinear Fokker–Planck Equation (
10), several other situations could be considered. A very general illustrative possibility is to consider a diffusion coefficient that depends on space and time, spatial fractional derivatives, and nonlinearities; for instance,
with
(
and
). Instead of considering the discrete version of Equation (
31) and analyzing the random walk as in the previous section, we conclude our discussion with the following observation on the exponent
. Noting that the normalization condition for
P implies
(via dimensional analysis), Equation (
31) leads to the scaling law
, with
In addition to the usual diffusion (
,
, and
), where
, this expression contains several relevant particular cases. For example, the Richardson diffusion [
24] (
,
, and
) has
, Lévy diffusion [
25,
26,
27] (
,
, and
) leads to
, and porous media diffusion [
37] (
,
, and
) exhibits
.