1. Introduction
Synchronization is the coordination of events which allow a system to operate in unison [
1]. This effect appears in Nature at any size, from the smallest systems, as in the quantum world [
2], to the rotation of binary stars [
3,
4], going through something as mundane as the passage of people on public transportation during rush hour. In the specific case of mesoscales, from nanometers to microns, the use of colloidal particles is widely accepted to study synchronization. Different mechanisms have been proposed to induce interactions between particles. For example, hydrodynamics [
5,
6], magnetic [
7] or electric [
8], even Janus colloidal particles have been used to test what the synchronization may be like at the origin of structure formations [
9]. In this article we present a new form of synchronization between two colloidal particles inside a binary mixture close to its mixing critical point. We show that this synchronization is induced by the critical Casimir force and it is temperature-controlled. We also study the energy transfer properties of this two particles system using the stochastic thermodynamics framework [
10,
11,
12]. A binary mixture at the critical concentration is a specific case of a system presenting a second order phase transition. When the mixture approaches the critical temperature,
, the correlation length
ξ of its thermal fluctuations diverges, i.e.,
, where
is the reduced temperature and
is the characteristic correlation length of the mixture. The exponent
ν = 0.63 is the universal exponent associated with the transition. If the fluctuating field
is confined on length scales comparable to
ξ the critical Casimir force between the confining walls appears [
13]. This force presents a great interest in the nanotechnology area due to its long-range nature and to the possibility of being switched on-off in a simple way, because small changes in the temperature of the system will power those forces. In the last decade, the number of experimental studies of such a kind of systems has increased exponentially, because the possibility of exploring those fluctuating fields locally, of managing nanometric systems and of detecting femtoNewton forces has allowed the direct observation of these forces a few years ago by Hertlein et al. [
14]. Indeed the application of critical Casimir force to nanotechnologies has been proposed since its theoretical development in the seventies. For example, very recently, aggregation of particles was induced by critical Casimir interactions [
15]. The perspectives of implementing these forces in more complex mechanisms are giant. For example, an important application could be the miniaturization of thermodynamic engines to single-molecule devices, which require the development of switches with the ability of being turn on/off in a controllable way.
In our experiment, a dual optical trap holds two colloidal particles inside a binary mixture. The equilibrium positions of the two optical traps are independent, one is kept fixed while the other is periodically moved in order to change the distance between the two particles. The moving trap injects energy into the system and we study the transfer of energy from the moving particle to the fixed one. The novelty of our experiment is that the particles are able to interact by means of the Critical Casimir force which can be easily activated by tuning the temperature of the mixture close to .
2. Results
The experiment is carried out in the following way: first, the two microsized beads 1 (fixed) and 2 (moving) are optically trapped in the low critical temperature micelles-solvent solution at a stabilized temperature ( mK) and at a constant trap stiffness, . Then, the protocol in the positions of the traps Γ is imposed by fixing the position of the first trap at m while the position of the second trap is periodically moved according to the following procedure which lasts s. The trap 2 is kept for at m. It is then driven at a constant speed ( 1.7 m/s) from this static position to a new position at m in the time τ. Again, this position is kept constant during the time τ. The cycle is closed with a symmetric backward process, giving a total cycle time of s. Notice that τ is much larger than the bead relaxation time ( ), so we consider as equilibrium the last 0.4 s of each time interval in which the trap position is kept constant. This periodic protocol is repeated 400 times at each fixed temperature to obtain enough statistics on the measure of the bead positions. The temperature is increased at different steps depending on the distance from the critical temperature. After each temperature step, we wait 1 min to let the system thermalize before acquiring data. This scheme is repeated up to the achievement of the critical temperature.
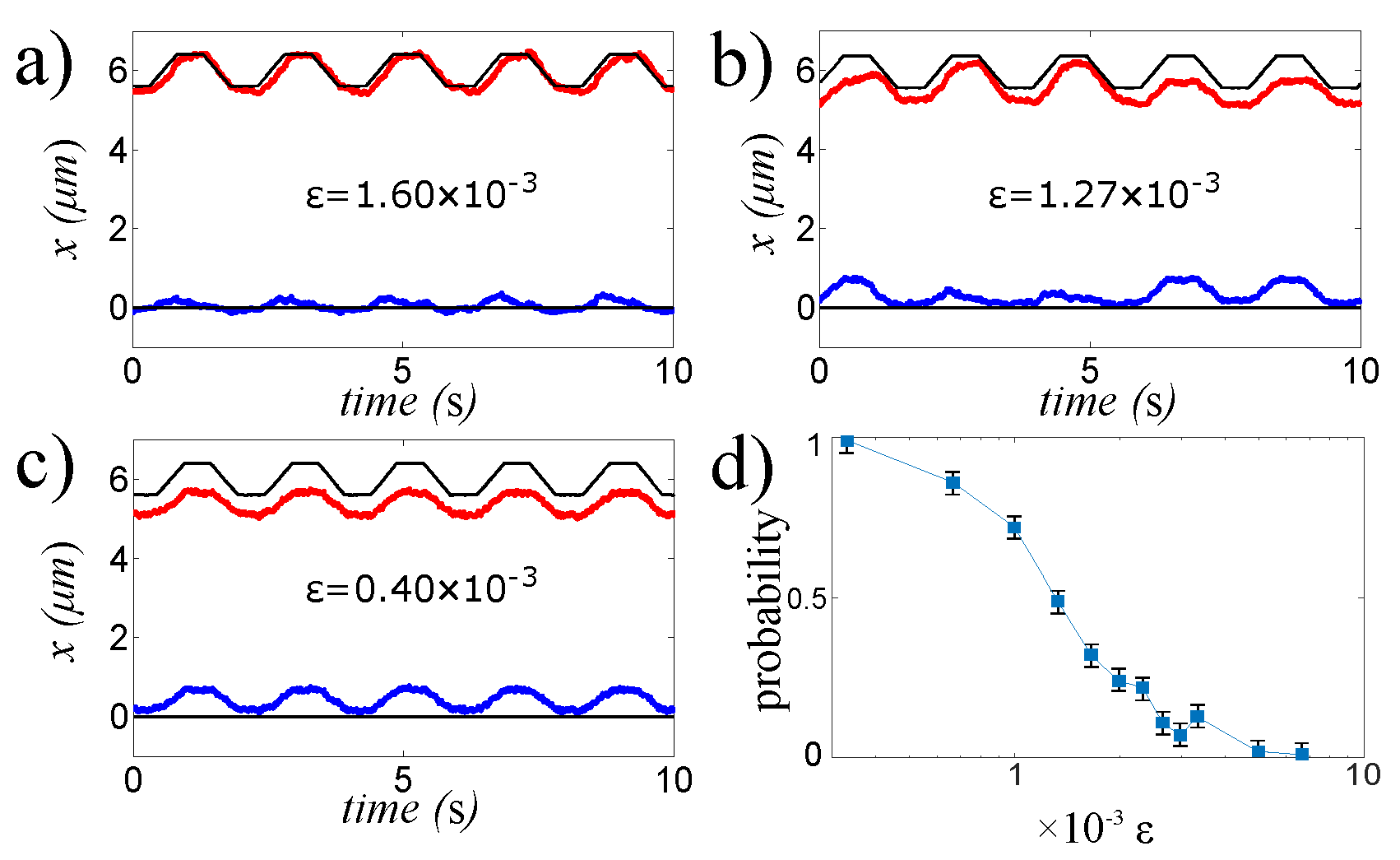
In
Figure 1, we plot the time evolution of the two beads positions
and
measured at different
ϵ when the above mentioned protocol is applied. Looking at
Figure 1, we see that particle motion depends on
ϵ. Specifically when
ϵ (
Figure 1c) is decreased, the motion tends to synchronize and the mean
and
are shifted with respect to the mean positions of the optical traps. Therefore, we use the mean position of the particles during the two equilibrium periods of the protocols to define if the particles are synchronized (S) or not-synchronized(NS). More precisely, at each
ϵ, we count the number
of periods where the fixed particle is displaced from its normal optical equilibrium position to a new one. We define the probability
of being synchronized as the ratio between
and 400, that is the total number of times in which the protocol is applied. The probability
(see
Figure 1d) clearly depends on the fluid temperature. When this gets close to
,
increases monotonically in this range of temperature, because the critical Casimir force becomes dominant.
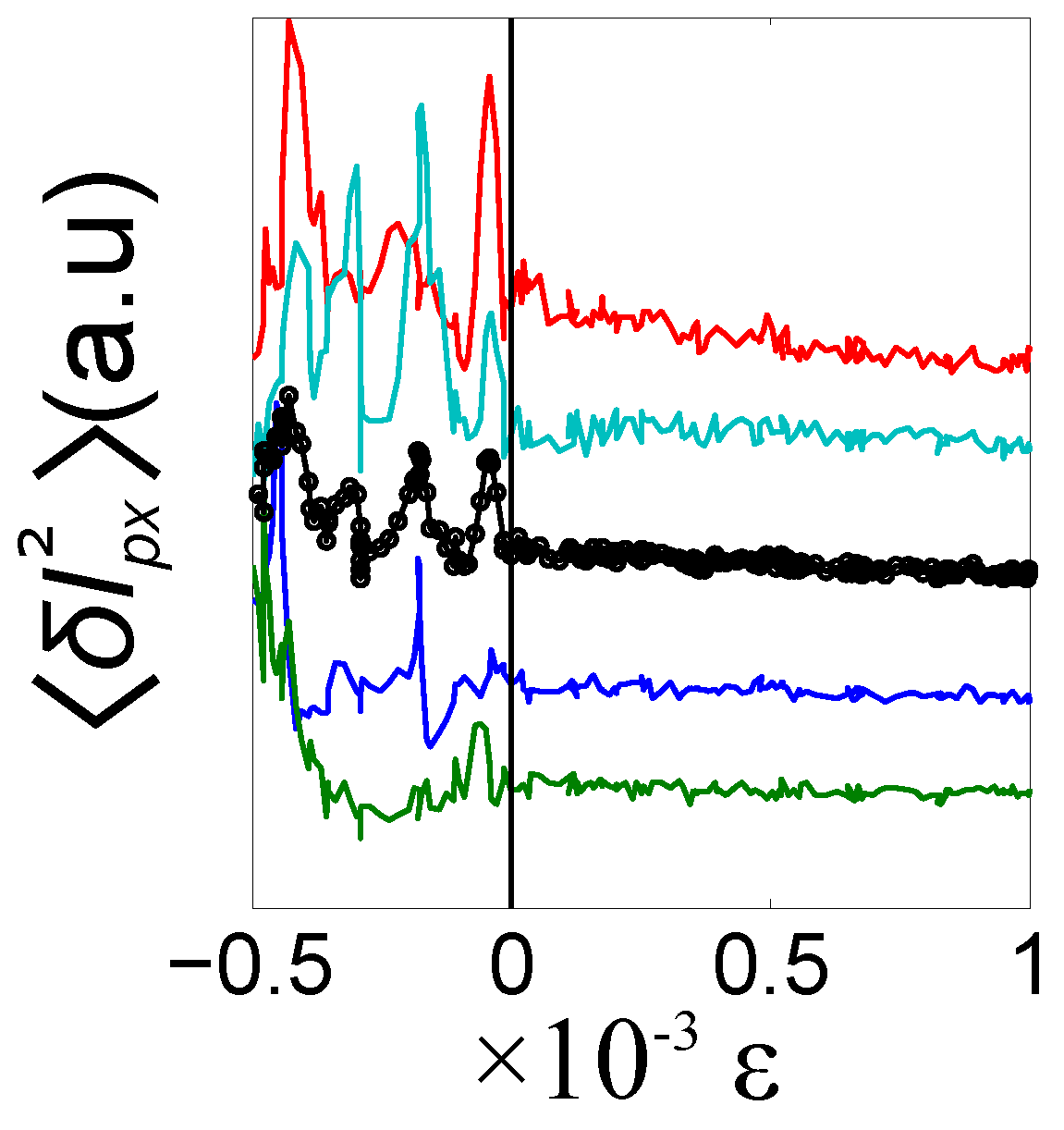
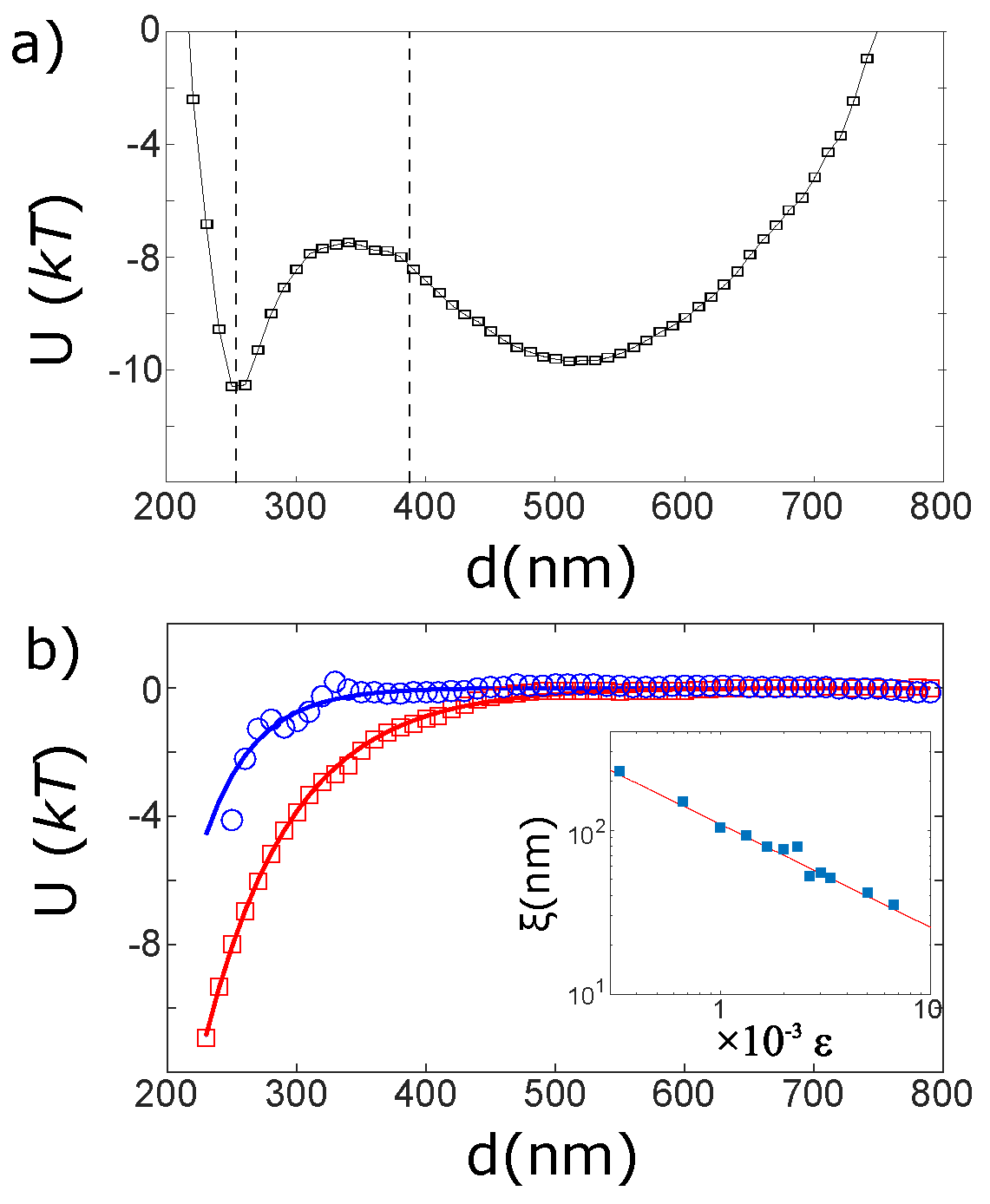
Up to this point we have defined a phenomenological feature: the dynamics of our system depends on the temperature of the surrounding critical mixture. The next step is to analyze the origin of this behavior by measuring the probability density function
, where
is the distance between the beads surfaces when the trap 2 is in one of the two equilibrium positions. From the logarithm of
we obtain the total potential
(Notice that in equilibrium this is valid even when the dissipation is a function of
d as in this case (see Equation (
4)).
The total potential can be split in three main parts: at shortest distances, the electrostatic repulsion between the beads dominates
where
σ is the Debye screening length and
depends on the surface charges of the particles. At large distances the harmonic potentials of the optical traps dominate and create a local energy minimum. The optical trapping potential can be assumed as parabolic at these distances,
[
16]. Between them, the Casimir potential defines a local minimum, see
Figure 2a. Indeed in our experiment the Casimir force is attractive because both beads are made of the same material. Thus their surfaces have the same affinity for the mixture components and this produces an attractive critical Casimir force [
17].
3. Discussion
Under this assumption, we subtract the Casimir interaction from our experimental results, see
Figure 2b. The Casimir potential is evaluated under the Derjaguin approximation for two spheres geometry and symmetric boundary conditions:
where
is the distance between the surfaces and
is a numerical constant from the numerical approximation under Derjaguin approach [
17]. The only free parameter in this equation is
ξ, which is obtained by fitting the experimental data of
Figure 2b. The measured evolution of
ξ as a function of temperature is plotted in the inset of
Figure 2b. The behavior is in agreement with the values measured from light scattering [
18,
19], from which one estimates
. These results show in a convincing way the contribution of the critical Casimir effect in the observed synchronization. It is important to notice that the temperature range where we observe the critical effects is almost one order of magnitude larger than in previous experiments [
14]. This increase is due to the fact that the characteristic correlation length of our mixture (
) is much larger than that of water-lutidine, i.e.,
.
Let us analyze the energetics of the applied protocols. The system has the following forces acting on it: optical,
; electrostatic,
; viscous,
where
and
η is the dynamic viscosity of the mixture; stochastic,
; Casimir,
, where
and
. It is important to notice that there is a non negligible cross correlation between the particles because the distance between their surfaces, during the experimental protocol, is smaller than the radius of the beads [
20]. This cross correlation can be interpreted as a viscosity gradient, which implies the presence of a multiplicative noise compensated by an entropic force
, where
and
is an
r dependent damping (see
Appendix A and References [
21,
22,
23,
24]). The dynamical evolution of the two positions is expressed by the coupled Langevin equations:
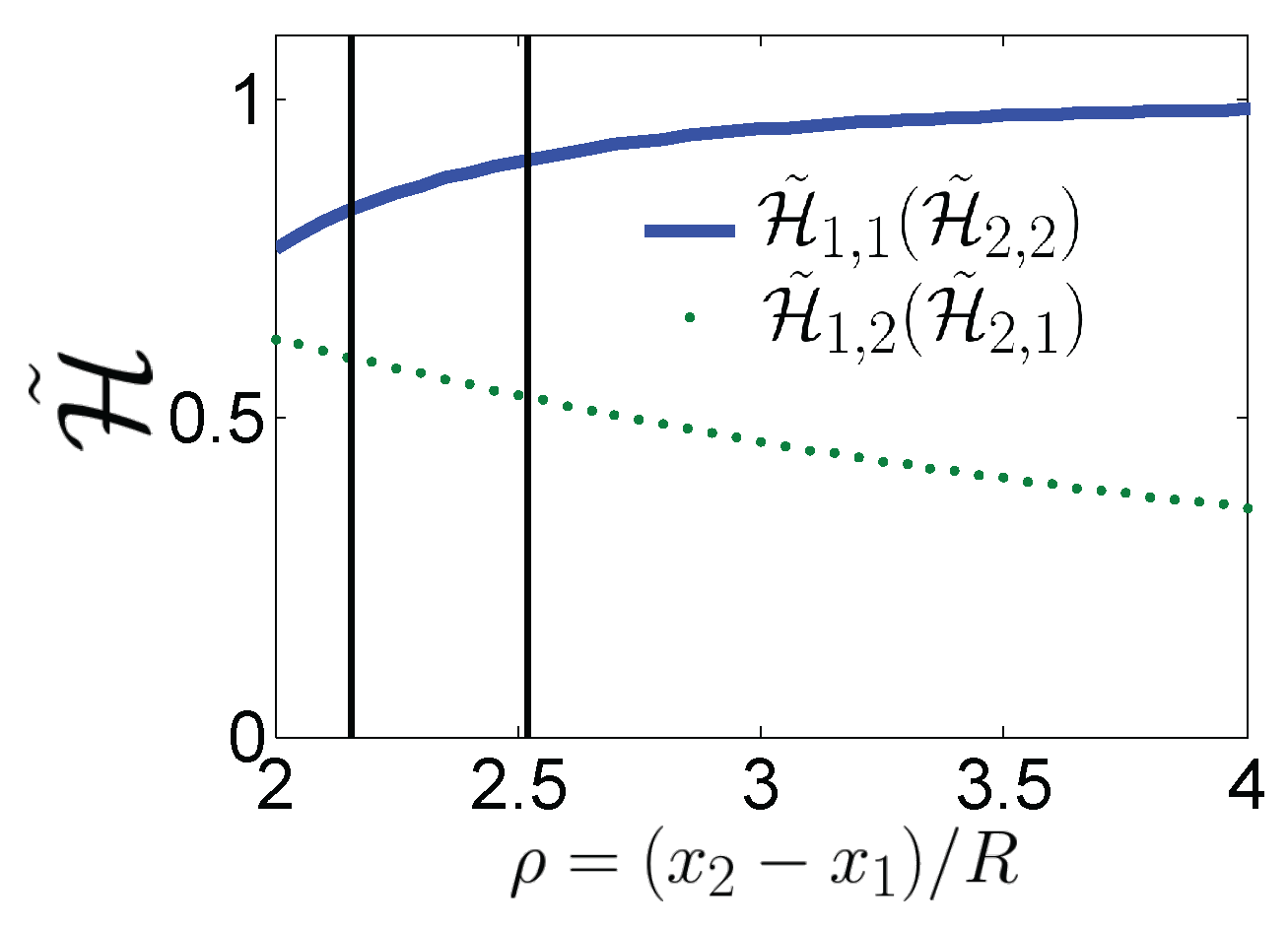
where
is the hydrodynamic coupling tensor [
6] with dependence on
, see
Appendix A:
The stochastic force has zero mean and correlation given by .
The strong dependence of the dynamics on the hydrodynamical coupling can be simplified using the eigenvectors of the system: the relative motion
and the collective motion
of the particles. The evolution of the new coordinates can be expressed by two Langevin equations as:
where
and
, with correlations
,
=
and
. The drag terms are defined including the hydrodynamic coupling as
and
. Notice that both viscosities depend on the relative position
r, but not on the position of the center of mass because of the isotropy of the surrounding fluid.
Once the change of coordinates is done, we must point out two important features in the new Langevin equations. First, the Casimir and electrostatic forces only appears explicitly in the relative coordinate, even if the global dynamics is linked with them. Second, the only variable with an explicit dependence on time is the position of the moving trap
. Within the stochastic energetics framework [
11], we can define the work exerted on (by) the system as the change of energy produced by the external parameters. The differential of the work in each coordinate during the given process is defined as:
where the subindex
δ corresponds to each coordinate
and ∘ denotes the Stratonovich integration [
11]. The external force
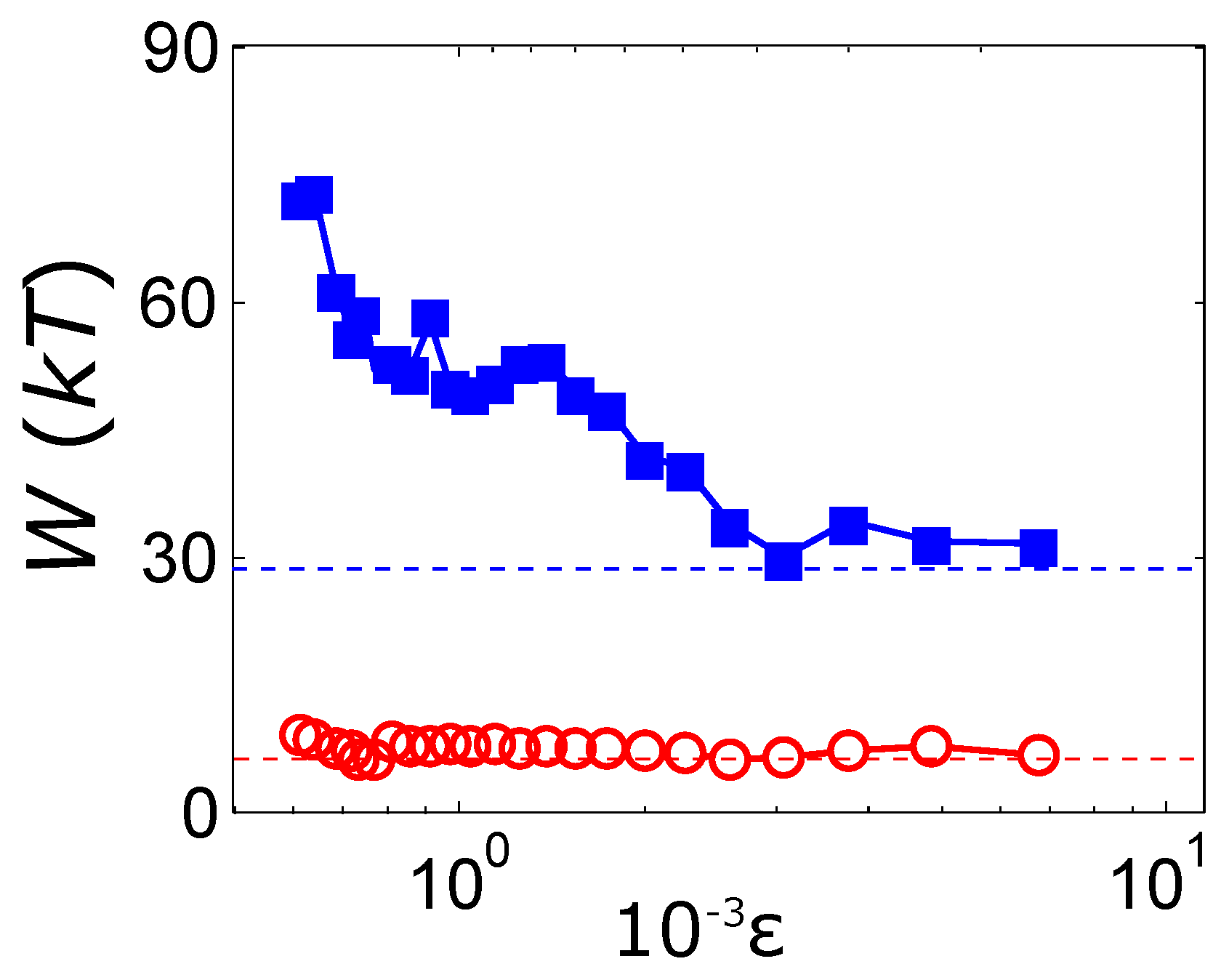
is directly measured from the displacement of each particle from the equilibrium point. The values of work are averaged on the 400 trajectories to obtain the average value
in the both coordinates, see
Figure 3.
Then, we can combine the definition of work, Equation (
5), with the Langevin equations, Equation (
4), to obtain a global view of the evolution of the system energetics. We can split the total work in a dissipative part and in a part associated to the external force:
where Γ defines the imposed protocol, that, in our particular case, moves the particles from a close to a further position at a velocity
m/s.
As
has only a dissipative nature, there is no change in the free energy associated to this coordinate during the protocol. Then, we can obtain a value of this energy as:
kT, which is in agreement with the observed value
kT. The case of
is different, because the free energy increases when the traps are taken away and it decreases when they are approached. This fact is shown in
Figure 3, where the mean values of the work when the beads are taken away is plotted as function of the reduced temperature. We see how the energetics of the collective motion is not significantly affected by the Casimir force, while the relative work increases when the critical interaction arises. The change in the exerted work agrees with the increase of the depth of the Casimir potential, once we take into account the dissipated work along the protocol in the relative position coordinate.
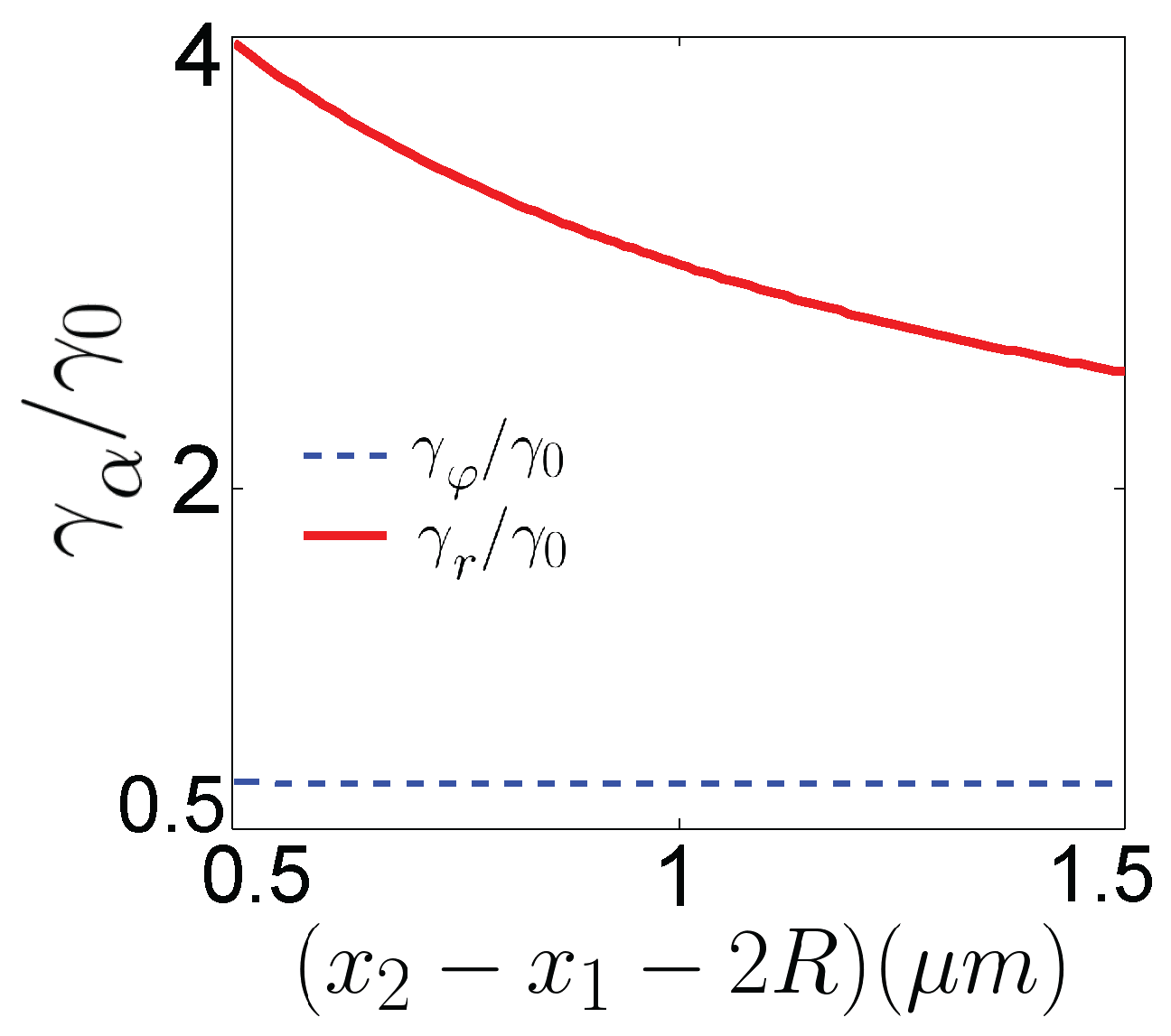
The fact that the collective motion is not significantly affected by the Casimir force is in agreement with the implicit assumption that the global dynamics of the system is not changing when approaching the criticality. Indeed, the critical exponent for the viscosity is known to be very small, about 0.036 [
25]. We tried to measure the critical change of the viscosity with the beads motion, but the effect is very small and remains within the experimental error. Thus we can safely conclude that the critical heterogeneities affect the interaction through the Casimir force but not the hydrodynamic coupling. Finally one may wonder whether the electrostatic interaction and the stiffness of the trap are affected by the critical point. We carefully checked that these two quantities remain constant within error bars in the temeperature range of our experiment.
4. Materials and Methods
Our experiments are done in a low critical temperature micelle-solvent solution,
in milliQ water at 1.2% mass concentration. The sample is always prepared under nitrogen atmosphere to prevent external contamination. This mixture has a correlation length of
nm and a critical temperature
C [
18,
19]. Few microspheres (Fluka silica,
m) per milliliter are added to the final mixture in a low concentration to allow long time measurement without interference. The mixture is injected into a custom made cell
m thick and mechanically sealed to avoid contamination. Within the fluid cell, the two optical traps are created by a near infrared laser beams (LaserQuantum
1064 nm) which is focused thanks to a high NA immersion oil objective (Leica × 63, NA = 1.4). The laser beam position is controlled by an acousto optical deflector (AA optoelectronics) which allows us to create two different traps using the time sharing regime at 5 kHz as well as to change their relative positions. One of the two position is kept fixed (1) and the other is periodically moved (2). The two optical trap are kept 15
m from the cell bottom slide. The beads images are acquired by a high speed camera (Mikrotron MC1310) and their positions are tracked in real time by a suitable software. The tracking resolution is ±5 nm. The acquisition frequency is fixed at 500 frames per second for all experiments. The images of the camera are also used to precisely determined the critical temperature close to the two particles as explained in
Appendix B.
The temperature is controlled by a double feedback system one on the objective and one inside the cell. As the system uses a high NA objective, the cell is in contact with the objective via the immersion oil. Without the second feedback, the objective would act as a thermal bath at lower temperature, creating a temperature gradient within the cell. Temperature is registered with two independent sensors (Pt 1000 Ω) and sent to a programmable temperature controller (Stanford research instruments). The objective and the cell are heated with heater mats (Minco 40 Ω and 80 Ω respectively). The whole system is isolated from environment by a box to reduce the effect of environmental perturbations both on the position of the particles and on the temperature.