On the Binary Input Gaussian Wiretap Channel with/without Output Quantization

Abstract

In this paper, we investigate the effect of output quantization on the secrecy capacity of the binary-input Gaussian wiretap channel. As a result, a closed-form expression with infinite summation terms of the secrecy capacity of the binary-input Gaussian wiretap channel is derived for the case when both the legitimate receiver and the eavesdropper have unquantized outputs. In particular, computable tight upper and lower bounds on the secrecy capacity are obtained. Theoretically, we prove that when the legitimate receiver has unquantized outputs while the eavesdropper has binary quantized outputs, the secrecy capacity is larger than that when both the legitimate receiver and the eavesdropper have unquantized outputs or both have binary quantized outputs. Further, numerical results show that in the low signal-to-noise ratio (SNR) (of the main channel) region, the secrecy capacity of the binary input Gaussian wiretap channel when both the legitimate receiver and the eavesdropper have unquantized outputs is larger than the capacity when both the legitimate receiver and the eavesdropper have binary quantized outputs; as the SNR increases, the secrecy capacity when both the legitimate receiver and the eavesdropper have binary quantized outputs tends to overtake.

1. Introduction

The capacity of the Gaussian channel with binary inputs is a particularly important metric on the performance of practical communication systems. If there exists an eavesdropper besides the legitimate users, the capacity of the Gaussian wiretap channel is usually studied from the perspective of information-theoretic secrecy. The concept of information-theoretic secrecy was first introduced by Shannon in [1], where he proposed a cipher system with perfect secrecy to ensure the confidentiality of communication. Later, Wyner introduced a wiretap channel in [2] to achieve the information-theoretic secrecy under a weak secrecy constraint (i.e., the rate of information leaked to the eavesdropper is made vanishing). In [3], Csiszár and Körner extended Wyner’s work to a general broadcast channel model with one common message and one confidential message.

In the Gaussian wiretap channel, a wiretapper eavesdrops the communication through another Gaussian channel. Recently, the Gaussian wiretap channel with constrained/finite inputs has attracted increasing research attention [4,5,6,7,8]. The closed-form expression of the secrecy capacity of the Gaussian wiretap channel with continuous input signal was given in [9]. The work in [4] considered the Gaussian wiretap channel with M-ary pulse amplitude modulation (M-PAM) inputs and established the necessary conditions for the input power allocation and the input distribution in order to maximize the achievable secrecy rate. The effects of finite-alphabet inputs on the achievable secrecy rate of the multi-antenna wiretap systems were investigated in [5,6].

In this paper, two constraints are imposed on the Gaussian wiretap channel: the input signal is binary; the output is restricted to the binary quantized output and the unquantized output. Roughly speaking, the unquantized output is the original continuous channel output signal, while the binary quantized output is obtained from the binary quantization of the original continuous channel output. In the binary-input Gaussian wiretap channel (BI-GWC), since the legitimate receiver and the wiretapper can have either binary quantized outputs or unquantized outputs, there are four cases under consideration:

• Both the legitimate receiver and the wiretapper have unquantized outputs;
• Both the legitimate receiver and the wiretapper have binary quantized outputs;
• The legitimate receiver has binary quantized outputs, while the wiretapper has unquantized outputs;
• The legitimate receiver has unquantized outputs, while the wiretapper has binary quantized outputs.

So far, all the known works about BI-GWC [4,5,6] focus on Case 1, where the classical results in [2,3,9] were used to optimize the input power and the input distribution. However, no closed-form expression was derived. For the other three cases, their secrecy capacities have not yet been studied. In this paper, for Case 1, we give a close-form expression of the secrecy capacity. To reduce the computational complexity, tight upper and lower bounds on the secrecy capacity are also obtained. For Case 2, we transform the channel to a binary symmetric wiretap channel, and hence obtain its secrecy capacity. For Cases 3 and 4, we derive lower bounds on the secrecy capacity, respectively.

Moreover, it is known that the quantized output leads to a lower channel capacity than the unquantized output does for the binary input Gaussian channel [10]. However, in the binary-input Gaussian wiretap channel, the problem is whether quantized output would still lead to a lower secrecy capacity. In this paper, we investigate this problem by comparing the secrecy capacities of these four cases. We theoretically prove that secrecy capacity for Case 4 is larger than those of Cases 1 and 2. Further, we observe from the numerical results that the secrecy capacity for Case 1 is larger than that for Case 2 in the low signal-to-noise ratio (SNR) (main channel) region; however, the later tends to overtake when SNR increases. In other words, unlike the binary-input Gaussian Channel, the impact of quantization of the output signal becomes insignificant in the high SNR region for Cases 1 and 2 of binary-input Gaussian wiretap channel.

The rest of the paper is organized as follows. Firstly, the system model of the binary-input Gaussian wiretap channel is introduced in Section 2. Next, the secrecy capacities of the four cases are studied in Section 3, and the numerical results are demonstrated in Section 4 respectively. Finally, the conclusion is given in Section 5.

2. System Model

2.1. Gaussian Channel with Binary Inputs

The model of Gaussian channel with binary input is shown in Figure 1. Let $X\in \{+\sqrt{p},-\sqrt{p}\}$ be the binary input of the channel, where p is the signal power constraint. The channel output is described by

$$\begin{array}{c}\hfill Y=X+N,\end{array}$$

where N is a Gaussian noise with variance ${\sigma }^2$, and N is independent of the channel input X. Without loss of generality, we assume that N is zero-mean; i.e., $N\sim \mathcal{N}(0,{\sigma }^2)$. Denote the signal-to-noise ratio (SNR) between the input signal and noise as $\gamma \triangleq p/{\sigma }^2$.

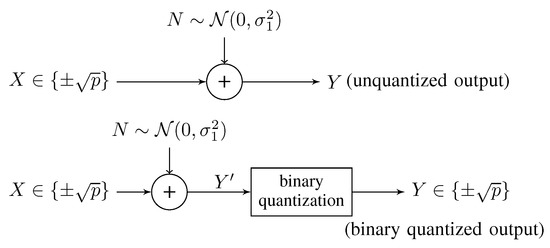
Figure 1. The Gaussian channel with binary inputs and quantized/unquantized outputs.

In particular, we restrict to two output schemes:

• Unquantized outputs:
  If the channel output signal is directly processed by the receiver without binary quantization as shown in Figure 1, we call it the unquantized output. The channel output Y is a continuous signal, having the conditional probability density function

  $$\begin{array}{cc}\hfill P(Y=y|X=+\sqrt{p})=& \frac{1}{\sqrt{2\pi {\sigma }^2}}exp[-\frac{{(y-\sqrt{p})}^2}{2{\sigma }^2}]\hfill \\ \hfill P(Y=y|X=-\sqrt{p})=& \frac{1}{\sqrt{2\pi {\sigma }^2}}exp[-\frac{{(y+\sqrt{p})}^2}{2{\sigma }^2}].\hfill \end{array}$$

  With the unquantized output, a closed-form expression of the channel capacity for the BI-GWC was given in [11] as

  $$\begin{array}{cc}\hfill C_B\left(\gamma \right)& =\left[-\sqrt{\frac{2\gamma }{\pi }}{e}^{-\frac{\gamma }{2}}+(2\gamma -1)Q\left(\sqrt{\gamma }\right)+{\displaystyle \sum _{k=1}^{\infty }}{\displaystyle \frac{{(-1)}^k}{k(k+1)}}Q\left(\sqrt{\gamma }(2k+1)\right)e^{2\gamma k(k+1)}\right]{log}_{2}e+1,\hfill \end{array}$$

  (1)

  where $Q\left(a\right)\triangleq \frac{1}{\sqrt{2\pi }}{\int }_a^{\infty }{e}^{-\frac{x^2}{2}}dx$. This channel capacity $C_B\left(\gamma \right)$ is achieved if and only if the input signal is uniformly distributed [11].
  For the sake of simplifying computation in what follows, the channel capacity can be approximated by keeping the first m terms of the summation as [11]

  $$\begin{array}{cc}\hfill C_B^{\left(m\right)}\left(\gamma \right)& =\left[-\sqrt{\frac{2\gamma }{\pi }}{e}^{-\frac{\gamma }{2}}+(2\gamma -1)Q\left(\sqrt{\gamma }\right)+{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{{(-1)}^k}{k(k+1)}}Q\left(\sqrt{\gamma }(2k+1)\right)e^{2\gamma k(k+1)}\right]{log}_{2}e+1.\hfill \end{array}$$

  (2)
• Binary quantized outputs:
  Through a binary quantization, the binary quantized output is

  $$Y=\left\{\begin{array}{cc}-\sqrt{p},\hfill & \hfill \mathrm{if}{Y}^{\prime }\in (-\infty ,0]\\ +\sqrt{p},\hfill & \hfill \mathrm{if}{Y}^{\prime }\in (0,\infty )\end{array}\right.$$

  (3)

  where $Y^{\prime }$ is the original continuous channel output signal.
  In fact, this case can be modeled as the a binary symmetric channel with transition probability $Q\left(\sqrt{\gamma }\right)=p(y=-\sqrt{p}|x=+\sqrt{p})=p(y=+\sqrt{p}|x=-\sqrt{p})$ [10]. By means of the results for binary symmetric channel [12], we can obtain the channel capacity for the BI-GWC with binary quantized outputs as

  $$C_H\left(\gamma \right)=1-h\left(Q\left(\sqrt{\gamma }\right)\right),$$

  (4)

  where $h(·)$ is the binary entropy function. Note that $C_H\left(\gamma \right)$ is achieved iff the binary input distribution is uniform [12].

2.2. Gaussian Wiretap Channel with Binary Inputs

The binary-input Gaussian wiretap channel is shown in Figure 2, where an external wiretapper eavesdrops the communication through another Gaussian channel. The channel output Y at the legitimate receiver and the channel output Z at the eavesdropper are described by

$$\begin{array}{cc}\hfill Y=& X+N_1,\hfill \\ \hfill Z=& X+N_2,\hfill \end{array}$$

where X is the antipodal transmission signal; $N_1$ and $N_2$ are the additive Gaussian noises of the main channel and the wiretap channel, respectively. Without loss of generality, we assume that $N_1$ and $N_2$ are zero-mean, and $N_1\sim \mathcal{N}(0,{\sigma }_1^2),N_2\sim \mathcal{N}(0,{\sigma }_2^2)$. Then, the SNR of the legitimate channel and the wiretap channel are ${\gamma }_1$ and ${\gamma }_2$, respectively. Particularly, we only consider ${\gamma }_2<{\gamma }_1$, since a reliable and secure communication is possible only in this case [9].

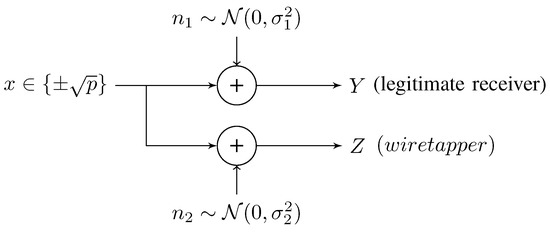
Figure 2. The binary-input Gaussian wiretap channel.

3. BI-GWC with/without Output Quantization

In this section, we study the secrecy capacities of the four cases mentioned in Section 1, which are denoted by $C_{SS},C_{HH},C_{HS}$, and $C_{SH}$, respectively. Since only if both the legitimate receiver and the eavesdropper have unquantized outputs or both have binary quantized outputs, the original channel is a stochastically degraded Gaussian wiretap channel (detailed explanation to follow). Then, we investigate the secrecy capacity of the four cases in two groups.

3.1. Both the Legitimate Receiver and the Eavesdropper Have Unquantized Outputs or Both Have Binary Quantized Outputs

If both the legitimate receiver and the eavesdropper have unquantized outputs, the difference between the channel output Y and Z is caused by the the additive Gaussian noise $N_1$ and $N_2$. According to the assumption ${\gamma }_2<{\gamma }_1$, the wiretap channel output Z is stochastically degraded of the main channel output Y, which means that there exists a $Z^{\prime }$ such that $X\to Y\to Z^{\prime }$, where $Z^{\prime }$ has the same conditional marginal distribution as Z; i.e., $p_{Z^{\prime }|X}=p_{Z|X}$. Hence, in this case, the binary-input Gaussian wiretap channel is a stochastically degraded binary-input Gaussian wiretap channel.

If the legitimate receiver and the eavesdropper have binary quantized outputs (as mentioned in Section 2.2), the main channel and the wiretap channel are equal to the corresponding binary symmetric channels with transition probability $Q\left(\sqrt{{\gamma }_1}\right)$ and $Q\left(\sqrt{{\gamma }_2}\right)$, respectively. Similarly, under this assumption ${\gamma }_2<{\gamma }_1$, this case can be modeled as a stochastically degraded binary symmetric wiretap channel.

By means of the results of a stochastically degraded wiretap channel [2,3], we can obtain the secrecy capacities for these two cases, whose proof will given in Appendix A.

Theorem 1.

If both the eavesdropper and the legitimate receiver have unquantized outputs or both have binary quantized outputs, the secrecy capacity of the binary-input Gaussian wiretap channel is

$$\begin{array}{c}\hfill C_S=\underset{p_X^{}}{max}[I(X;Y)-I(X;Z)]=I_{p_X^{\ast }}(X;Y)-I_{p_X^{\ast }}(X;Z)\end{array}$$

where $p_X^{}$ is the probability distribution of the input signals; $p_X^{\ast }$ is the uniform input distribution.

Based on Theorem 1, we can derive their closed-form expressions in Section 3.1.1 and Section 3.1.2, respectively.

3.1.1. BI-GWC: Secrecy Capacity When the Legitimate Receiver and the Eavesdropper Have Unquantized Outputs

For this case, we first derive a closed-form expression for the secrecy capacity in the following theorem.

Theorem 2.

When both the legitimate receiver and the eavesdropper have unquantized outputs, the secrecy capacity for the binary-input Gaussian wiretap channel is

$$C_{SS}=C_B\left({\gamma }_1\right)-C_B\left({\gamma }_2\right),$$

(5)

where $C_B\left(\gamma \right)$ is as defined in Equation (1).

Proof. 

Recall that the channel capacity of the binary-input Gaussian channel with unquantized outputs is achieved by uniform input distribution [11]. This means $I_{p_X^{\ast }}(X;Y)=C_B\left({\gamma }_1\right)$ and $I_{p_X^{\ast }}(X;Z)=C_B\left({\gamma }_2\right)$. Following Theorem 1, we then have

$$\begin{array}{cc}\hfill C_{SS}=& I_{p_X^{\ast }}(X;Y)-I_{p_X^{\ast }}(X;Z)\hfill \\ \hfill =& C_B\left({\gamma }_1\right)-C_B\left({\gamma }_2\right)\hfill \end{array}$$

☐

According to Theorem 2, we deduce the closed-form expression of the secrecy capacity $C_{SS}$. However, $C_B\left(\gamma \right)$ contains a summation of infinite series, and so $C_{SS}$ does. In order to give a computable expression of the channel capacity, we make use of an approximation of $C_{SS}$ by Equation (2); i.e.,

$$C_{SS}^{\left(m\right)}=C_B^{\left(m\right)}\left({\gamma }_1\right)-C_B^{\left(m\right)}\left({\gamma }_2\right).$$

(6)

Specifically, we study the behaviour of $C_{SS}^{\left(m\right)}\left(\gamma \right)$ and thus derive upper and lower bounds on $C_{SS}$ as follows.

Property 1.

Let $C_B^{\left(m\right)}\left(\gamma \right)$ and $C_{SS}^{\left(m\right)},$$\gamma >0$, $m=1,2,\dots$, be defined as in Equations (2) and (6), respectively.

1. 

Let $C_B^{\left(m\right)}{\left(\gamma \right)}^{\prime }$ be the first derivative of $C_B^{\left(m\right)}\left(\gamma \right)$. Then

$$\begin{array}{c}\hfill C_B^{\left(1\right)}{\left(\gamma \right)}^{\prime }>C_B^{\left(3\right)}{\left(\gamma \right)}^{\prime }>C_B^{\left(5\right)}{\left(\gamma \right)}^{\prime }>\cdots >C_B^{(2m+1)}{\left(\gamma \right)}^{\prime }>C_B^{\left(2m\right)}{\left(\gamma \right)}^{\prime }>\\ \hfill \cdots >C_B^{\left(6\right)}{\left(\gamma \right)}^{\prime }>C_B^{\left(4\right)}{\left(\gamma \right)}^{\prime }>C_B^{\left(2\right)}{\left(\gamma \right)}^{\prime }.\end{array}$$

2. 

The sequence $C_{SS}^{(2m-1)},$ $m=1,2,...,$ is monotonically decreasing as m increasing;

3. 

The sequence $C_{SS}^{\left(2m\right)},$ $m=1,2,...,$ is monotonically increasing as m increasing; and

4. 

Both sequences $C_{SS}^{(2m-1)}$ and $C_{SS}^{\left(2m\right)},$$m=1,2,...,$ converge to $C_{SS}$ as $m\to \infty :$

$${\displaystyle \underset{m\to \infty }{lim}}{C}_{SS}^{(2m-1)}={\displaystyle \underset{m\to \infty }{lim}}{C}_{SS}^{\left(2m\right)}={\displaystyle \underset{m\to \infty }{lim}}{C}_{SS}^{\left(m\right)}=C_{SS}.$$

The following corollary is a direct consequence of Property 1.

Corollary 1.

$C_{SS}$ can be upper and lower bounded by $C_{SS}^{(2m-1)}$ and $C_{SS}^{\left(2m\right)},$ $m=1,2,...,$ respectively, as follows:

$$C_{SS}^{\left(1\right)}>C_{SS}^{\left(3\right)}>C_{SS}^{\left(5\right)}>\cdots >C_{SS}>\cdots >C_{SS}^{\left(6\right)}>C_{SS}^{\left(4\right)}>C_{SS}^{\left(2\right)}.$$

In fact, Corollary 1 provides computable lower bounds and upper bounds on $C_{SS}$ with low computational complexity. Note from the Corollary 1, the series $C_{SS}^m$ at an even/odd number m of summation terms results in a lower/upper bound on the channel capacity $C_{SS}$, which can be arbitrarily tight provided that m is sufficiently large. As an illustration, in Section 4, we show the upper and the lower bound are very tight, even for $m=6,7$.

3.1.2. BI-GWC: Secrecy Capacity When the Legitimate Receiver and the Eavesdropper Have Binary Quantized Outputs

Note that there exists a method in [10] which can be used to transform a binary-input and binary quantized-output Gaussian channel into a binary symmetric channel. That is, under the assumption ${\gamma }_2<{\gamma }_1$, this case can be modeled as a stochastically degraded binary symmetric channel. Based on the results of a degraded binary symmetric wiretap channel [8], we get its secrecy capacity in the following theorem.

Theorem 3.

The secrecy capacity of the Gaussian channel with binary inputs and binary quantized outputs is

$$C_{HH}=C_H\left({\gamma }_1\right)-C_H\left({\gamma }_2\right)=h\left(Q\left(\sqrt{{\gamma }_2}\right)\right)-h\left(Q\left(\sqrt{{\gamma }_1}\right)\right),$$

(7)

where $Q\left(a\right)\triangleq \frac{1}{\sqrt{2\pi }}{\int }_a^{\infty }{e}^{-\frac{x^2}{2}}dx$, and $Q\left(\sqrt{{\gamma }_1}\right)$ and $Q\left(\sqrt{{\gamma }_2}\right)$ are the transition probabilities of the equivalent binary symmetric channels of the main channel and the wiretap channel, respectively.

3.2. One of the Legitimate Receiver and the Eavesdropper Has Binary Quantized Outputs and the Other Has Unquantized Outputs

3.2.1. BI-GWC: Secrecy Capacity When the Legitimate Receiver Has Binary Quantized Outputs and the Eavesdropper Has Unquantized Outputs

In this case, the channel for the legitimate receiver is equal to a binary symmetric channel, whilst the channel for the eavesdropper remains a binary-input Gaussian channel. Since the channel cannot be seen as a degraded one, Theorem 1 is not suitable for this case. Then, we give a lower bound on the secrecy capacity base on the result of normal broadcast channel [3] as follows.

$$\begin{array}{cc}\hfill C_{HS}\ge & {\displaystyle \underset{p_X}{max}}{|I(X;Y)-I(X;Z)|}^{+}\hfill \\ \hfill \ge & |I_{p_X^{\ast }}(X;Y)-I_{p_X^{\ast }}{(X;Z)|}^{+}\hfill \\ \hfill \stackrel{\left(a\right)}{=}& |C_H\left({\gamma }_1\right)-C_B\left({\gamma }_2\right){|}^{+}\hfill \\ \hfill \triangleq & {\left(C_{HS}\right)}_{lower},\hfill \end{array}$$

(8)

where ${\left|a\right|}^{+}=max\{0,a\}$; ${\left(C_{HS}\right)}_{lower}$ denotes the lower bound on the secrecy capacity $C_{HS}$; and (a) follows from the fact that the uniform input distribution achieves the channel capacity of $C_H\left({\gamma }_1\right)$ and $C_B\left({\gamma }_2\right)$ [11,12].

3.2.2. BI-GWC: Secrecy Capacity When the Legitimate Receiver Has Unquantized Outputs and the Eavesdropper Has Binary Quantized Outputs

In this subsection, the case is considered when the legitimate receiver has unquantized outputs, whilst the eavesdropper has binary quantized outputs. As same as the above case, a lower bound on the secrecy capacity $C_{SH}$ can be given by

$$\begin{array}{cc}\hfill C_{SH}\ge & {\displaystyle \underset{p_X}{max}}{|I(X;Y)-I(X;Z)|}^{+}\hfill \\ \hfill \ge & |I_{p_X^{\ast }}(X;Y)-I_{p_X^{\ast }}{(X;Z)|}^{+}\hfill \\ \hfill \stackrel{\left(a\right)}{=}& |C_B\left({\gamma }_1\right)-C_H\left({\gamma }_2\right){|}^{+}\hfill \\ \hfill \triangleq & {\left(C_{SH}\right)}_{lower}.\hfill \end{array}$$

(9)

where ${\left(C_{SH}\right)}_{lower}$ denotes the lower bound on the secrecy capacity $C_{SH}$, and (a) follows from the fact that the uniform input distribution achieves the channel capacity of $C_B\left({\gamma }_1\right)$ and $C_H\left({\gamma }_2\right)$ [11,12].

Based on the secrecy capacities and the lower bounds on the secrecy capacity derived for the four cases above, we are able to have the following comparison.

Corollary 2.

${\left(C_{HS}\right)}_{lower}<C_{HH},C_{SS}<{\left(C_{SH}\right)}_{lower}$.

Proof. 

Recall that unquantized output leads to a higher channel capacity than quantized output does for the binary-input Gaussian channel [10]; i.e., $C_B\left(\gamma \right)>C_H\left(\gamma \right)$ (γ is the SNR of the channel). Then, applying it to Equations (5), (7), (8), and (9), we have

$$\begin{array}{c}\hfill |C_H\left({\gamma }_1\right)-C_B\left({\gamma }_2\right){|}^{+}<C_H\left({\gamma }_1\right)-C_H\left({\gamma }_2\right),C_B\left({\gamma }_1\right)-C_B\left({\gamma }_2\right)<{|C_B\left({\gamma }_1\right)-C_H\left({\gamma }_2\right)|}^{+}\end{array}$$

That is,

$$\begin{array}{c}\hfill {\left(C_{HS}\right)}_{lower}<C_{HH},C_{SS}<{\left(C_{SH}\right)}_{lower}.\end{array}$$

☐

From this corollary, we see that when the legitimate receiver has unquantized outputs and the eavesdropper has binary quantized outputs, the secrecy capacity is larger than those when both the legitimate receiver and the eavesdropper have unquantized outputs or both have binary quantized outputs. This is because the unquantized output provides a higher channel capacity for the legitimate receiver while the binary quantized output leads to a lower wiretap channel capacity for the eavesdropper.

Note that when the legitimate receiver has binary quantized outputs and the eavesdropper has unquantized outputs, we give a lower bound ${\left(C_{HS}\right)}_{lower}$ on the secrecy capacity, and thus it is not sufficient to compare with the capacities of the other cases. In addition, it is also hard to compare $C_{HH}$ and $C_{SS}$ through the closed-form expression. The comparison of $C_{HH}$ and $C_{SS}$ will be given through numerical results in the next section.

4. Numerical Results

4.1. Comparison of $C_{SS}$, $C_{HH}$, ${\left(C_{HS}\right)}_{lower}$ and ${\left(C_{SH}\right)}_{lower}$

In this subsection, we give the numerical comparison of the secrecy capacity $C_{SS}$, $C_{HH}$, ${\left(C_{HS}\right)}_{lower}$, and ${\left(C_{SH}\right)}_{lower}$. Recall that ${\gamma }_1,{\gamma }_2$ are the SNRs of the legitimate channel and the wiretap channel, respectively. Denote the SNR gap to be $\Delta \gamma ={\gamma }_1-{\gamma }_2$.

First, in Figure 3, we evaluate the tightness of the upper and the lower bounds on $C_{SS}$ by plotting the approximation $C_{SS}^{\left(m\right)}$. The curves of $C_{SS}^{\left(m\right)}$ for $m=1,2,6,7$ are plotted versus ${\gamma }_1$. It can be seen that the gap between the upper and the lower bounds becomes indistinguishable as m increases. Especially, when $m=6,7$, the gap between $C_{SS}^{\left(6\right)}$ and $C_{SS}^{\left(7\right)}$ is already quite small. This indicates that an accurate evaluation of $C_{SS}$ can be done with less computational complexity by only involving $m\ge 6$ summation terms in $C_{SS}^{\left(m\right)}$.

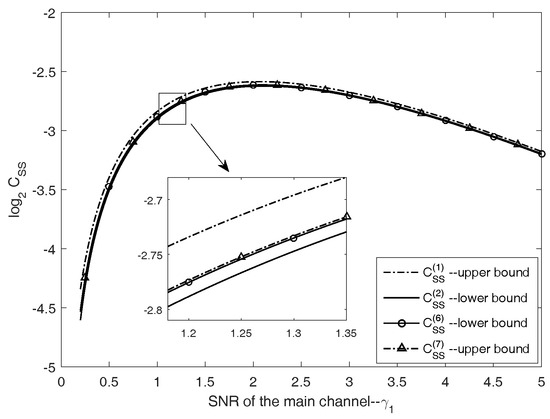
Figure 3. Lower and upper bounds on $C_{SS}$ as $\Delta \gamma ={\gamma }_1/2$.

In Figure 4, we compare the $C_{SS}^{\left(m\right)}$, $C_{HH}$, ${\left(C_{HS}\right)}_{lower}$ and ${\left(C_{SH}\right)}_{lower}$. $C_{SS}^{\left(7\right)}$ and $C_{SS}^{\left(6\right)}$ are plotted as an upper and a lower bound on $C_{SS}$, respectively. Moreover, Figure 4 also depicts the approximations on ${\left(C_{HS}\right)}_{lower}$ and ${\left(C_{SH}\right)}_{lower}$ by $m=6,7$. All the curves are plotted with respect to ${\gamma }_1$ with ${\gamma }_2$ = $\Delta \gamma$ = ${\gamma }_1/2$. From Figure 4, it is clear that ${\left(C_{SH}\right)}_{lower}$—as a lower bound on $C_{SH}$—is strictly larger than both $C_{SS}$ and $C_{HH}$. ${\left(C_{HS}\right)}_{lower}$—as a lower bound on $C_{HS}$—is strictly smaller than both $C_{SS}$ and $C_{HH}$. This confirms the result in Corollary 2. Further, we notice that there is a crossing point where $C_{SS}=C_{HH}$, and the secrecy capacity $C_{SS}$ is larger than $C_{HH}$ at low SNR; whilst as SNR increases, $C_{HH}$ overtakes $C_{SS}$. This gives a rough numerical comparison of $C_{SS}$ and $C_{HH}$. In the following subsection, we will give more details about the comparison of $C_{SS}$ and $C_{HH}$.

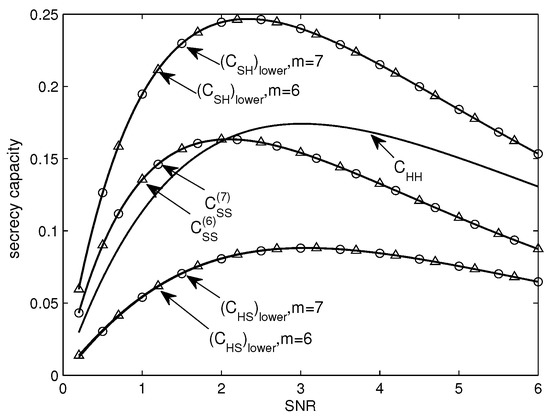
Figure 4. Bounds on secrecy capacities of binary-input Gaussian wiretap channel (BI-GWC) as $\Delta \gamma ={\gamma }_1/2$. SNR: signal-to-noise ratio.

4.2. Comparison from the Perspectives of SNR and SNR/bit

In this subsection, we look into the comparison of $C_{SS}$ and $C_{HH}$ from the perspectives of the SNR and the SNR per bit of the channel to the legitimate receiver. Following the numerical evaluations in the previous subsection, we use $C_B^{\left(6\right)}\left(\gamma \right)$ and $C_{SS}^{\left(6\right)}$ to approximate $C_B\left(\gamma \right)$ and $C_{SS},$ respectively.

Figure 5 consists of two sub-figures to illustrate how the crossing point occurs as $\Delta \gamma ={\gamma }_1/2$. In Figure 5a, we plot the curves $C_B^{\left(6\right)}\left({\gamma }_1\right)$ and $C_H\left({\gamma }_1\right)$, which are the capacity of the legitimate channel with unquantized outputs and with binary quantized outputs, respectively. Correspondingly, the capacity of the wiretap channel $C_B^{\left(6\right)}\left({\gamma }_2\right)$ and $C_H\left({\gamma }_2\right)$ are also plotted. In Figure 5b, the comparison of the secrecy capacities $C_{SS}$ and $C_{HH}$ are shown versus a series of ${\gamma }_1$.

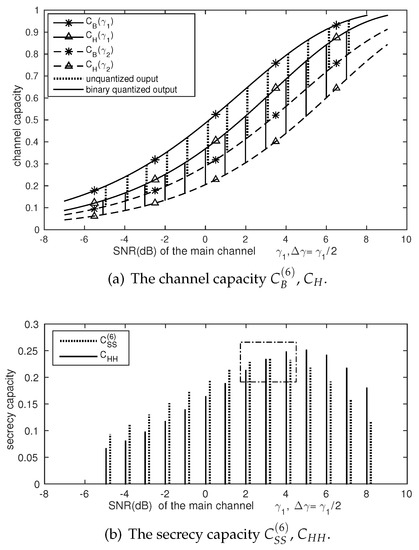
Figure 5. $C_B^{\left(6\right)}\left({\gamma }_1\right)$, $C_H\left({\gamma }_1\right)$, $C_{SS}^{\left(6\right)}$,$C_{HH}$, $\Delta \gamma ={\gamma }_1/2$.

In Figure 5a, $C_B^{\left(6\right)}\left({\gamma }_1\right),C_B^{\left(6\right)}\left({\gamma }_2\right),C_H\left({\gamma }_1\right)$, and $C_H\left({\gamma }_2\right)$ increase with an increasing SNR ${\gamma }_1$. However, this phenomenon does not apply to the secrecy capacities $C_{SS}$ and $C_{HH}$ in Figure 5b. In fact, as shown in Figure 5b, both $C_{SS}$ and $C_{HH}$ first increase and then decrease with an increasing ${\gamma }_1$. In other words, unlike in the traditional communication scenario, increasing SNR does not always help to achieve a higher transmission rate when secrecy is also under consideration. The underlying cause is that $C_{SS}$ is the increase from $C_B\left({\gamma }_2\right)$ to $C_B\left({\gamma }_1\right)$, while $C_{HH}$ is the increase from $C_H\left({\gamma }_2\right)$ to $C_H\left({\gamma }_1\right)$. However, these two increases do not always result in the increase of $C_B\left({\gamma }_1\right)-C_B\left({\gamma }_2\right)$ and $C_H\left({\gamma }_1\right)-C_H\left({\gamma }_2\right)$. The crossing point occurs when these two increases $C_B\left({\gamma }_1\right)-C_B\left({\gamma }_2\right)$ and $C_H\left({\gamma }_1\right)-C_H\left({\gamma }_2\right)$ are the same.

Figure 6 shows the relation between energy and the secrecy capacity. The channel capacities $C_B\left({\gamma }_1\right)$ and $C_H\left({\gamma }_1\right)$, the secrecy capacities $C_{SS}$ and $C_{HH}$ are plotted against the SNR per bit for $\Delta \gamma =\gamma /2,3\gamma /4$.

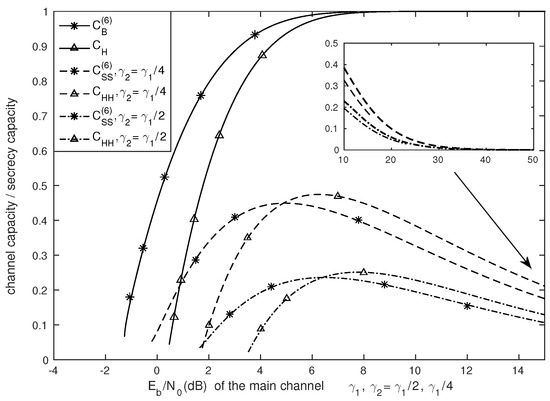
Figure 6. $C_B^{\left(6\right)}$, $C_H$, $C_{SS}^{\left(6\right)}$, $C_{HH}$ by SNR/bit, $\Delta \gamma ={\gamma }_1/2,3{\gamma }_1/4$.

Note that SNR per bit is the energy per bit to noise power spectral density ratio (i.e., $E_B/N_0$), where $E_B$ is the average energy per information bit and $N_0/2={\sigma }^2$ is the variance of Gaussian noise of the main channel. Since $E_B=P/R$ and the SNR $=E_S/{\sigma }^2=P/{\sigma }^2$, SNR per bit $=E_B/N_0$ is related to the SNR definition as follows:

$$\begin{array}{c}\hfill \frac{E_B}{N_0}=\frac{P}{R{N}_0}=\frac{P}{2R{\sigma }^2}.\end{array}$$

Comparing $C_{SS}$ with $C_B$ and comparing $C_{HH}$ with $C_H$ under the same value, it can be seen how much extra SNR per bit is needed when considering secrecy. For instance, as shown in Figure 6, to approach the channel capacity $C_B=0.3\mathrm{bps}$, the SNR per bit $E_B/N_0=-0.6141\mathrm{dB}$ is needed. While to approach the same secrecy capacity with the unquantized output (i.e., $C_{SS}=0.3\mathrm{bps}$), the SNR per bit $E_B/N_0=1.6095\mathrm{dB}$ is needed. Therefore, the secure communication comes with an additional cost of more than $2\mathrm{dB}$. A similar behavior applies to the case when both the legitimate receiver and the eavesdropper have binary quantized outputs.

Besides, as shown in Figure 6, with respect to SNR per bit, $C_{SS}$ and $C_{HH}$ do not increase monotonically, and this phenomenon is the same as that in Figure 4. Interestingly, as $\mathrm{SNR}\to \infty$ (also $E_B/N_0\to \infty$), we observe that $C_{SS}$ and $C_{HH}$ approach to zero as shown in Figure 6. The underlying reason is that both $C_B\left(\gamma \right)$ and $C_H\left(\gamma \right)$ approach to $1\mathrm{bps}$ for the high SNR region, irrespectively of unquantized or quantized outputs.

Furthermore, we denote $R^{\ast }$ to be the secrecy capacity and ${(E_B/N_0)}^{\ast }$ to be the corresponding SNR per bit at the crossing point ($C_{SS}=C_{HH}$). In Figure 6, we observe that $R^{\ast }$ increases with respect to $\Delta \gamma$, while ${(E_B/N_0)}^{\ast }$ decreases with respect to $\Delta \gamma$. This indicates a reduction in energy cost per bit and an increase of the secrecy capacity in case of a weaker eavesdropper (which results in a larger $\Delta \gamma$).

In addition, since $C_{SS},C_{HH}$ approach to 0 as $E_B/N_0\to \infty$, for an admissible secrecy rate, there are two possible SNR per bit $E_B/N_0$ to achieve it. For the sake of energy saving, a smaller $E_B/N_0$ is of great interest. For instance, if the targeted secrecy rate is less than $R^{\ast }$, then it is possible to achieve the secure communication with an SNR per bit smaller than ${(E_B/N_0)}^{\ast }$.

5. Conclusions

In this paper, we studied the secrecy capacity of the Gaussian wiretap channel under two practical constraints: (1) binary inputs; and (2) binary output quantization. Consequently, a closed-form expression for the secrecy capacity was derived when both the legitimate receiver and eavesdropper have unquantized outputs, and a tight upper and a lower bound on the secrecy capacity were obtained with less computational complexity. Besides, lower bounds were provided for other cases. Numerical results show the comparison of the secrecy capacities of the four cases, and provide insights into the energy cost for the secrecy.