Spin Interaction under the Collision of Two Kerr-(Anti-)de Sitter Black Holes
Abstract
:1. Introduction
2. Kerr-(A)dS Black Hole
3. Spin Interaction and Gravitational Radiation
3.1. Gravitational Radiation Released by a Collision between Two Kerr-(A)dS Black Holes
3.2. Spin Interaction Potential from the MPD Equation
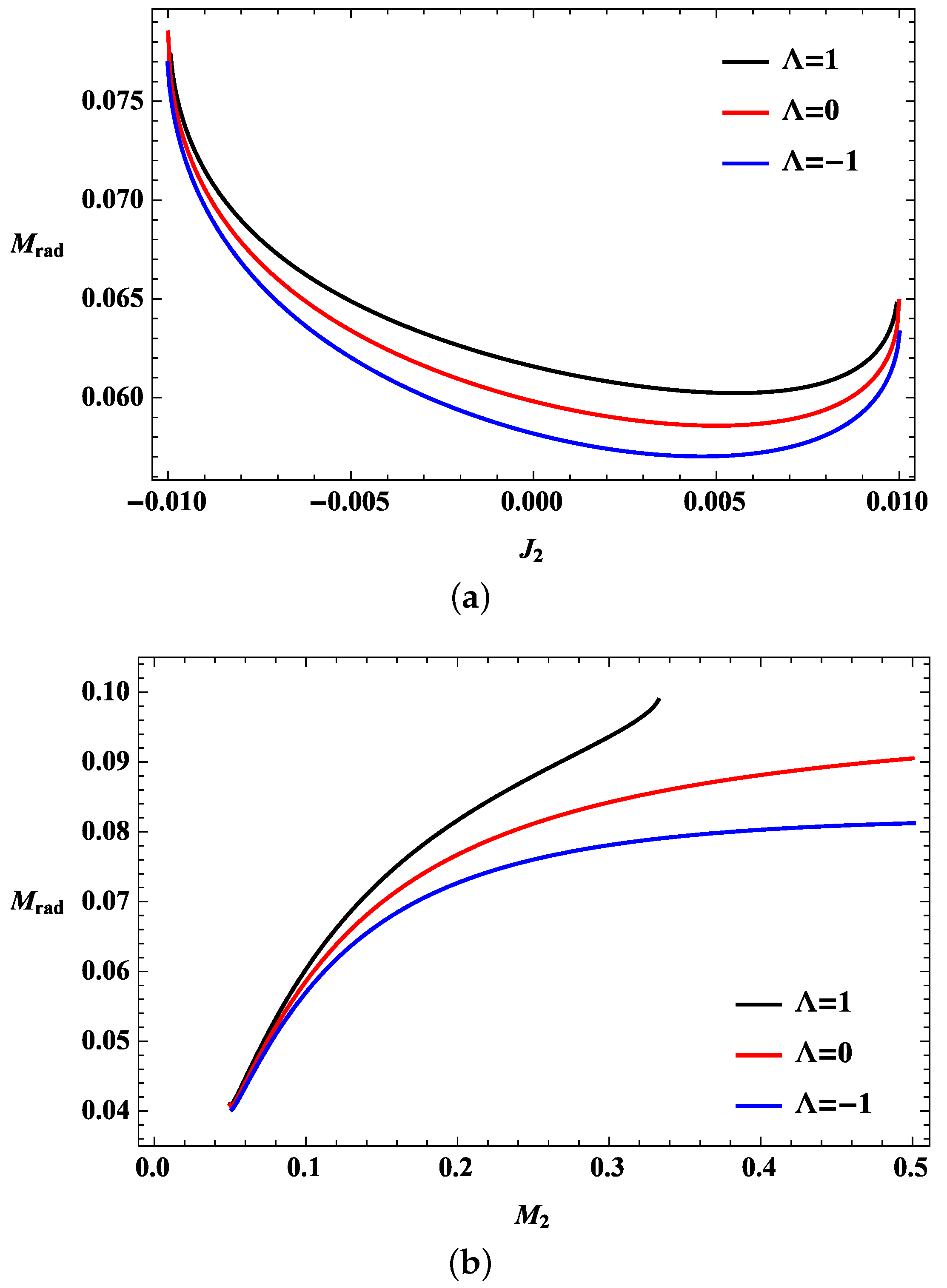
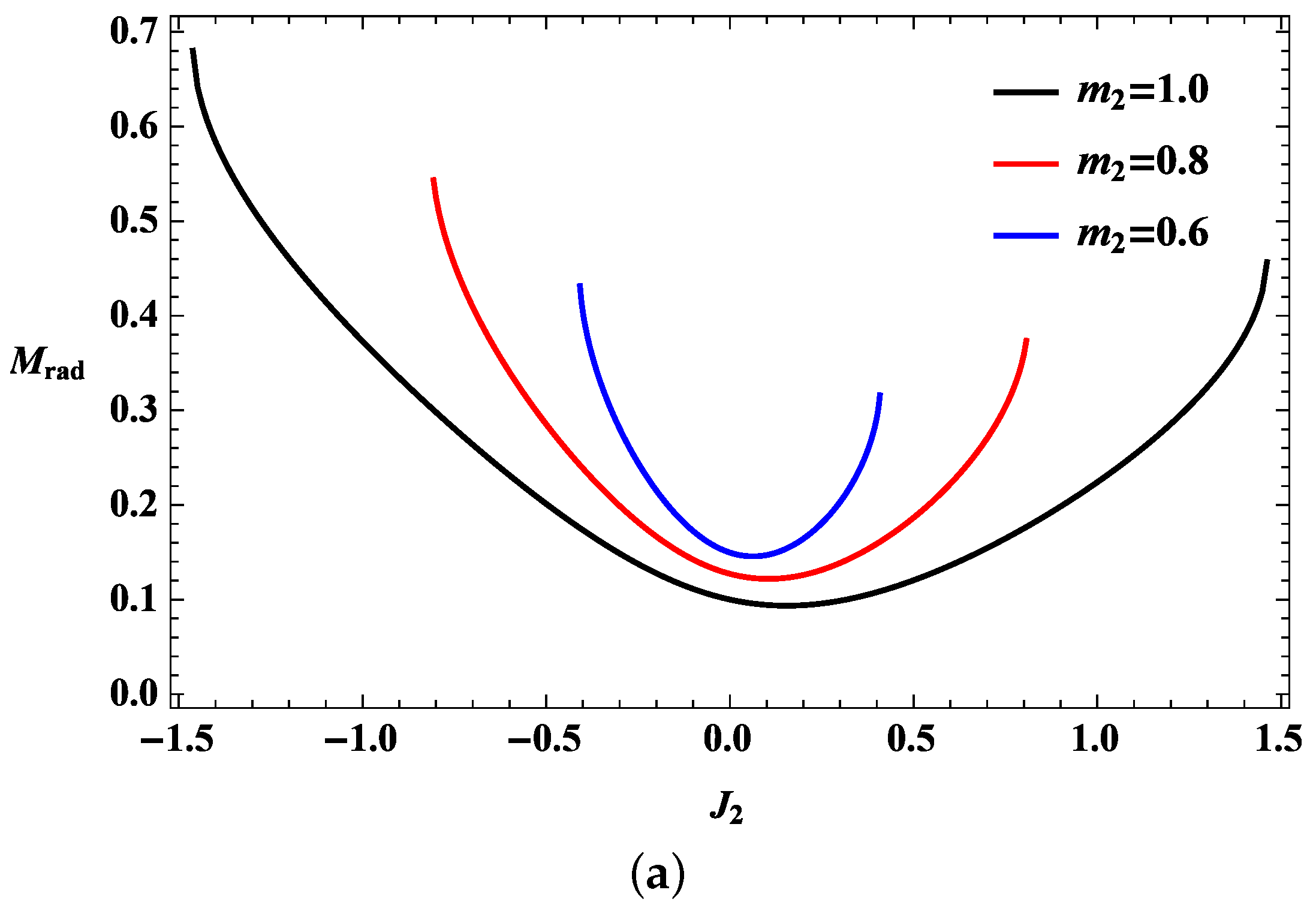
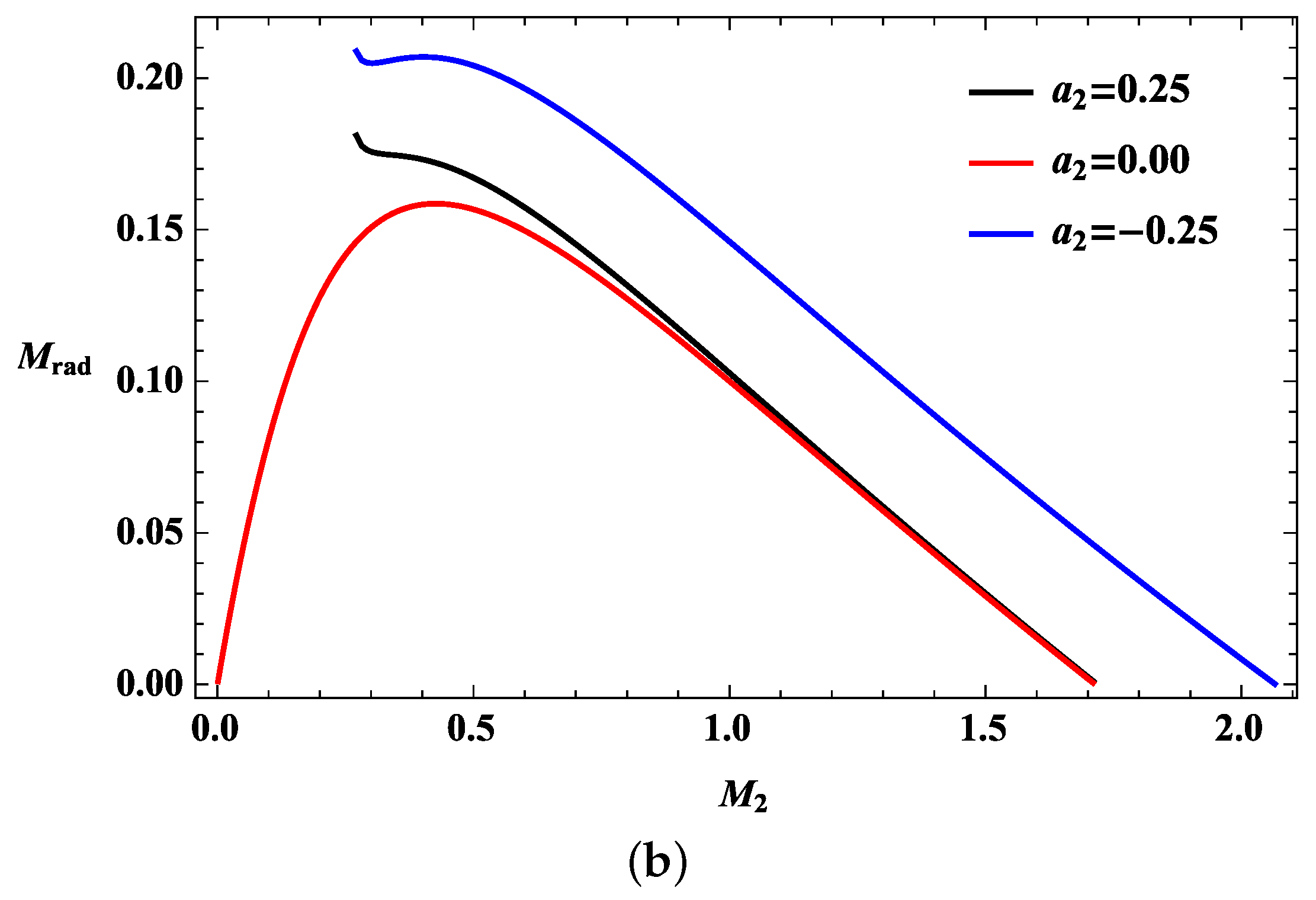
4. Upper Bound on the Radiation under the Collision
5. Summary
Acknowledgments
Conflicts of Interest
References
- LIGO Scientific Collaboration; Virgo Collaboration; Abbott, B. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LIGO Scientific Collaboration; Virgo Collaboration; Abbott, B. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration; Virgo Collaboration; Abbott, B. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [PubMed]
- Supernova Cosmology Project Collaboration; Perlmutter, S.; Gabi, S.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pennypacker, C.R.; et al. Measurements of the cosmological parameters Omega and Lambda from the first 7 supernovae at z>=0.35. Astrophys. J. 1997, 483, 565. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equation of state. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Supernova Search Team Collaboration; Garnavich, P.M.; Jha, S.; Challis, P.; Clocchiatti, A.; Diercks, A.; Filippenko, A.V.; Gilliland, R.L.; Hogan, C.J.; Kirshner, R.P.; et al. Supernova limits on the cosmic equation of state. Astrophys. J. 1998, 509, 74–79. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys. 1998, 2, 505–532. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef] [Green Version]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. 1998, B428, 105–114. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Aharony, O.; Gubser, S.S.; Maldacena, J.M.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Phys. Rep. 2000, 323, 183–386. [Google Scholar] [CrossRef]
- Chaturvedi, P.; Sengupta, G. Rotating BTZ Black Holes and One Dimensional Holographic Superconductors. Phys. Rev. 2014, D90, 046002. [Google Scholar] [CrossRef]
- Haehl, F.M.; Loganayagam, R.; Rangamani, M. Effective actions for anomalous hydrodynamics. JHEP 2014, 3, 34. [Google Scholar] [CrossRef]
- Chang, H.-C.; Fujita, M.; Kaminski, M. From Maxwell-Chern-Simons theory in AdS3 towards hydrodynamics in 1 + 1 dimensions. JHEP 2014, 10, 118. [Google Scholar] [CrossRef] [Green Version]
- Bardeen, J.M. Kerr Metric Black Holes. Nature 1970, 226, 64–65. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R.; Floyd, R.M. Extraction of rotational energy from a black hole. Nature 1971, 229, 177–179. [Google Scholar] [CrossRef]
- Christodoulou, D. Reversible and irreversible transforations in black hole physics. Phys. Rev. Lett. 1970, 25, 1596–1597. [Google Scholar] [CrossRef]
- Christodoulou, D.; Ruffini, R. Reversible transformations of a charged black hole. Phys. Rev. 1971, D4, 3552–3555. [Google Scholar] [CrossRef]
- Smarr, L. Mass formula for Kerr black holes. Phys. Rev. Lett. 1973, 30, 71–73. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. 1973, D7, 2333–2346. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Generalized second law of thermodynamics in black hole physics. Phys. Rev. 1974, D9, 3292–3300. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Hawking, S.W. Black Holes and Thermodynamics. Phys. Rev. 1976, D13, 191–197. [Google Scholar] [CrossRef]
- Hawking, S.W. Gravitational radiation from colliding black holes. Phys. Rev. Lett. 1971, 26, 1344–1346. [Google Scholar] [CrossRef]
- Eardley, D.M.; Giddings, S.B. Classical black hole production in high-energy collisions. Phys. Rev. 2002, D66, 044011. [Google Scholar] [CrossRef]
- Sperhake, U.; Cardoso, V.; Pretorius, F.; Berti, E.; Gonzalez, J.A. The High-energy collision of two black holes. Phys. Rev. Lett. 2008, 101, 161101. [Google Scholar] [CrossRef] [PubMed]
- Coelho, F.S.; Herdeiro, C.; Sampaio, M.O.P. Radiation from a D-dimensional collision of shock waves: A remarkably simple fit formula. Phys. Rev. Lett. 2012, 108, 181102. [Google Scholar] [CrossRef] [PubMed]
- Smarr, L.; Cadez, A.; DeWitt, B.S.; Eppley, K. Collision of Two Black Holes: Theoretical Framework. Phys. Rev. 1976, D14, 2443–2452. [Google Scholar] [CrossRef]
- Smarr, L. Gravitational Radiation from Distant Encounters and from Headon Collisions of Black Holes: The Zero Frequency Limit. Phys. Rev. 1977, D15, 2069–2077. [Google Scholar]
- Smarr, L.; York, J.W., Jr. Kinematical conditions in the construction of space-time. Phys. Rev. 1978, D17, 2529–2551. [Google Scholar]
- Witek, H.; Zilhao, M.; Gualtieri, L.; Cardoso, V.; Herdeiro, C.; Nerozzi, A.; Sperhake, U. Numerical relativity for D dimensional space-times: head-on collisions of black holes and gravitational wave extraction. Phys. Rev. 2010, D82, 104014. [Google Scholar] [CrossRef]
- Bantilan, H.; Romatschke, P. Simulation of Black Hole Collisions in Asymptotically Anti-de Sitter Spacetimes. Phys. Rev. Lett. 2015, 114, 081601. [Google Scholar] [CrossRef] [PubMed]
- Bednarek, W.; Banasinski, P. Non-thermal radiation from collisions of compact objects with intermediate scale jets in active galaxies. Astrophys. J. 2015, 807, 168. [Google Scholar] [CrossRef]
- Hirotani, K.; Pu, H.-Y. Energetic Gamma Radiation from Rapidly Rotating Black Holes. Astrophys. J. 2016, 818, 50. [Google Scholar] [CrossRef]
- Sperhake, U.; Berti, E.; Cardoso, V.; Pretorius, F. Gravity-dominated unequal-mass black hole collisions. Phys. Rev. 2016, D93, 044012. [Google Scholar] [CrossRef]
- Barkett, K.; Scheel, M.A.; Haas, R.; Ott, C.D.; Bernuzzi, S.; Brown, D.A.; Szilágyi, B.; Kaplan, J.D.; Lippuner, J.; Muhlberger, C.D.; et al. Gravitational waveforms for neutron star binaries from binary black hole simulations. Phys. Rev. 2016, D93, 044064. [Google Scholar] [CrossRef]
- Hinderer, T.; Taracchini, A.; Foucart, F.; Buonanno, A.; Steinhoff, J.; Duez, M.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A.; Szilagyi, B.; et al. Effects of neutron-star dynamic tides on gravitational waveforms within the effective-one-body approach. Phys. Rev. Lett. 2016, 116, 181101. [Google Scholar] [CrossRef] [PubMed]
- Schiff, L.I. Motion of a Gyroscope According to Einstein’s Theory of Gravitation. Proc. Nat. Acad. Sci. USA 1960, 46, 871. [Google Scholar] [CrossRef] [PubMed]
- Wilkins, D. General equation for the precession of a gyroscope. Ann. Phys. 1970, 61, 277–293. [Google Scholar] [CrossRef]
- Mashhoon, B. Particles with spin in a gravitational field. J. Math. Phys. 1971, 12, 1075–1077. [Google Scholar] [CrossRef]
- Wald, R.M. Gravitational spin interaction. Phys. Rev. 1972, D6, 406–413. [Google Scholar] [CrossRef]
- Plyatsko, R.; Fenyk, M. Highly relativistic spin-gravity coupling for fermions. Phys. Rev. 2015, D91, 064033. [Google Scholar] [CrossRef]
- d’Ambrosi, G.; Kumar, S.S.; van de Vis, J.; van Holten, J.W. Spinning bodies in curved spacetime. Phys. Rev. 2016, D93, 044051. [Google Scholar] [CrossRef]
- Majar, J.; Mikoczi, B. Second order spin effects in the spin precession of compact binaries. Phys. Rev. 2012, D86, 064028. [Google Scholar] [CrossRef]
- Zilhão, M.; Cardoso, V.; Herdeiro, C.; Lehner, L.; Sperhake, U. Collisions of oppositely charged black holes. Phys. Rev. 2014, D89, 044008. [Google Scholar] [CrossRef]
- Teukolsky, S.A. Rotating black holes—Separable wave equations for gravitational and electromagnetic perturbations. Phys. Rev. Lett. 1972, 29, 1114–1118. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. Perturbations of a Rotating Black Hole. II. Dynamical Stability of the Kerr Metric. Astrophys. J. 1973, 185, 649–674. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N.; Ruffini, R. On Quantum Resonances in Stationary Geometries. Lett. Nuovo Cimento 1976, 15, 257–262. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Eardley, D.M. Instabilities of Massive Scalar Perturbations of a Rotating Black Hole. Ann. Phys. 1979, 118, 139–155. [Google Scholar] [CrossRef]
- Detweiler, S.L. Klein-Gordon Equation and Rotating Black Holes. Phys. Rev. 1980, D22, 2323–2326. [Google Scholar] [CrossRef]
- Dolan, S.R. Instability of the massive Klein-Gordon field on the Kerr spacetime. Phys. Rev. 2007, D76, 084001. [Google Scholar] [CrossRef]
- Hod, S. Quasi-Bound States of Massive Scalar Fields in the Kerr Black-Hole Spacetime: Beyond the Hydrogenic Approximation. Phys. Lett. 2015, B749, 167–171. [Google Scholar] [CrossRef] [Green Version]
- Press, W.H.; Teukolsky, S.A. Floating Orbits, Superradiant Scattering and the Black-hole Bomb. Nature 1972, 238, 211–212. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C. Small Kerr-anti-de Sitter black holes are unstable. Phys. Rev. 2004, D70, 084011. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C.; Yoshida, S. Classical instability of Kerr-AdS black holes and the issue of final state. Phys. Rev. 2006, D74, 044008. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C.; Lemos, J.P.S.; Yoshida, S. The Black hole bomb and superradiant instabilities. Phys. Rev. 2004, D70, 044039. [Google Scholar] [CrossRef]
- Kunduri, H.K.; Lucietti, J.; Reall, H.S. Gravitational perturbations of higher dimensional rotating black holes: Tensor perturbations. Phys. Rev. 2006, D74, 084021. [Google Scholar] [CrossRef]
- Zhang, C.-Y.; Zhang, S.-J.; Wang, B. Superradiant instability of Kerr-de Sitter black holes in scalar-tensor theory. JHEP 2014, 8, 11. [Google Scholar] [CrossRef]
- Emparan, R.; Myers, R.C. Instability of ultra-spinning black holes. JHEP 2003, 9, 025. [Google Scholar] [CrossRef]
- Shibata, M.; Yoshino, H. Nonaxisymmetric instability of rapidly rotating black hole in five dimensions. Phys. Rev. 2010, D81, 021501. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Figueras, P.; Monteiro, R.; Santos, J.E.; Emparan, R. Instability and new phases of higher-dimensional rotating black holes. Phys. Rev. 2009, D80, 111701. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Figueras, P.; Monteiro, R.; Reall, H.S.; Santos, J.E. An instability of higher-dimensional rotating black holes. JHEP 2010, 5, 76. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Figueras, P.; Monteiro, R.; Santos, J.E. Ultraspinning instability of rotating black holes. Phys. Rev. 2010, D82, 104025. [Google Scholar] [CrossRef]
- Durkee, M.; Reall, H.S. Perturbations of higher-dimensional spacetimes. Class. Quantum Gravity 2011, 28, 035011. [Google Scholar] [CrossRef]
- Murata, K. Instability of higher dimensional extreme black holes. Class. Quantum Gravity 2013, 30, 075002. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Hartnett, G.S.; Santos, J.E. Quasinormal modes of asymptotically flat rotating black holes. Class. Quantum Gravity 2014, 31, 245011. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.-H. Instability of rotating anti-de Sitter black holes. Phys. Rev. 2015, D91, 064020. [Google Scholar] [CrossRef]
- Ahn, W.-K.; Gwak, B.; Lee, B.-H.; Lee, W. Instability of Black Holes with a Gauss-Bonnet Term. Eur. Phys. J. 2015, C75, 372. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.-H.; Ro, D. Instability of Charged Anti-de Sitter Black Holes. Phys. Lett. 2016, B761, 437–443. [Google Scholar] [CrossRef]
- Chrusciel, P.T.; Maerten, D.; Tod, P. Rigid upper bounds for the angular momentum and centre of mass of non-singular asymptotically anti-de Sitter space-times. JHEP 2006, 11, 084. [Google Scholar] [CrossRef]
- Dolan, B.P.; Kastor, D.; Kubiznak, D.; Mann, R.B.; Traschen, J. Thermodynamic Volumes and Isoperimetric Inequalities for de Sitter Black Holes. Phys. Rev. 2013, D87, 104017. [Google Scholar] [CrossRef]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quantum Gravity 2000, 17, 399–420. [Google Scholar] [CrossRef]
- Akcay, S.; Matzner, R.A. Kerr-de Sitter Universe. Class. Quantum Gravity 2011, 28, 085012. [Google Scholar] [CrossRef]
- Mathisson, M. Neue mechanik materieller systemes. Acta Phys. Pol. 1937, 6, 163–2900. [Google Scholar]
- Papapetrou, A. Spinning test particles in general relativity. 1. Proc. R. Soc. Lond. 1951, A209, 248–258. [Google Scholar] [CrossRef]
- Dixon, W.G. Dynamics of extended bodies in general relativity. I. Momentum and angular momentum. Proc. R. Soc. Lond. 1970, A314, 499–527. [Google Scholar] [CrossRef]
- Beiglböck, W. The center-of-mass in Einsteins theory of gravitation. Commun. Math. Phys. 1967, 5, 106–130. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.-H. Cosmic Censorship of Rotating Anti-de Sitter Black Hole. JCAP 2016, 1602, 15. [Google Scholar] [CrossRef]
- Gwak, B.; Ro, D. Dilaton field released under collision of dilatonic black holes with Gauss-Bonnet term. Eur. Phys. J. 2017, C77, 554. [Google Scholar] [CrossRef]
- Gwak, B. Collision of Two Rotating Hayward Black Holes. Eur. Phys. J. 2017, C77, 482. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.-H. The Upper Bound of Radiation Energy in the Myers-Perry Black Hole Collision. JHEP 2016, 7, 79. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gwak, B.; Ro, D. Spin Interaction under the Collision of Two Kerr-(Anti-)de Sitter Black Holes. Entropy 2017, 19, 691. https://doi.org/10.3390/e19120691
Gwak B, Ro D. Spin Interaction under the Collision of Two Kerr-(Anti-)de Sitter Black Holes. Entropy. 2017; 19(12):691. https://doi.org/10.3390/e19120691
Chicago/Turabian StyleGwak, Bogeun, and Daeho Ro. 2017. "Spin Interaction under the Collision of Two Kerr-(Anti-)de Sitter Black Holes" Entropy 19, no. 12: 691. https://doi.org/10.3390/e19120691



