Fast EEMD Based AM-Correntropy Matrix and Its Application on Roller Bearing Fault Diagnosis
Abstract
:1. Introduction
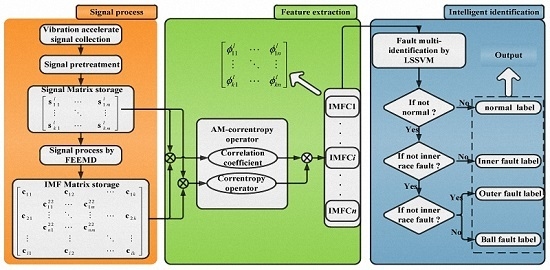
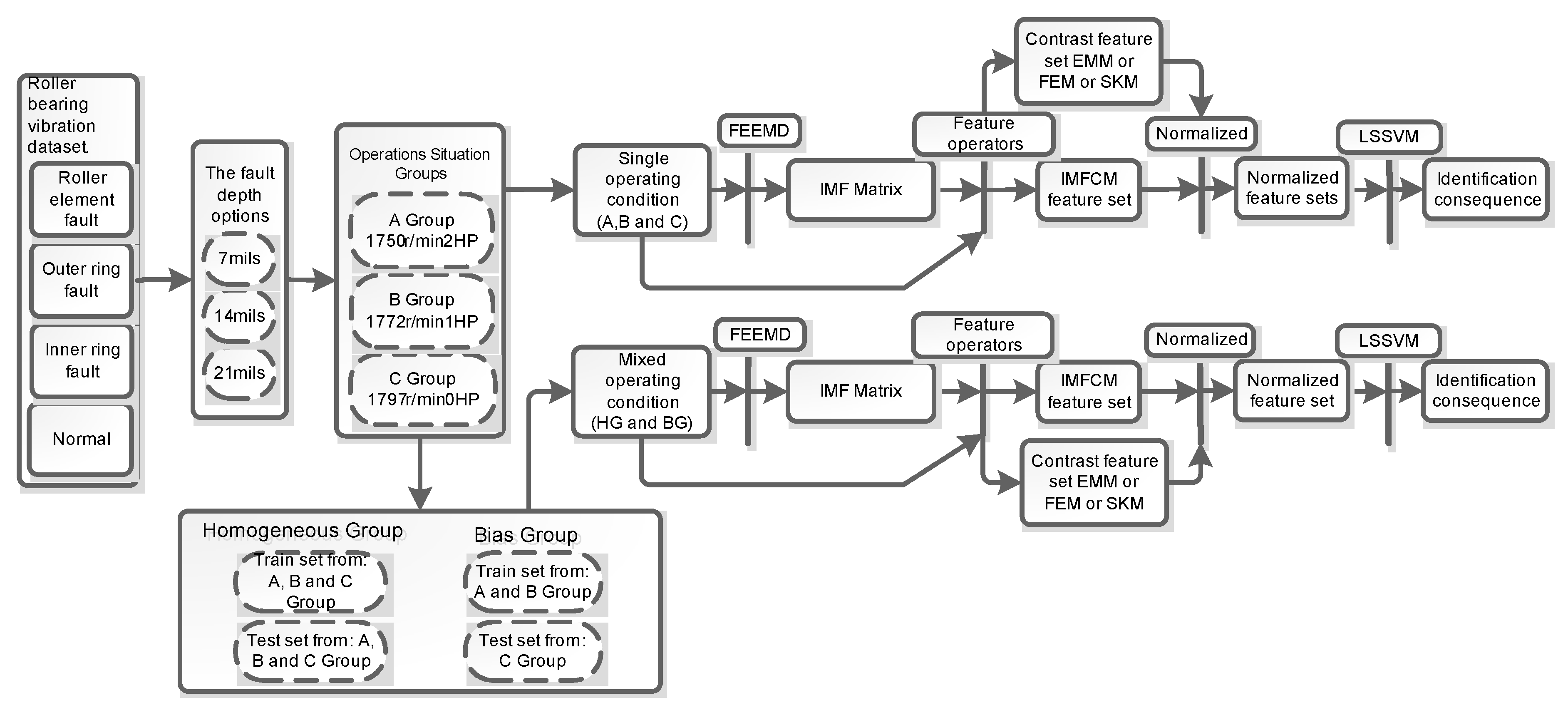
2. The Method Framework
3. Instruction of Algorithms to Extract Fault Feature
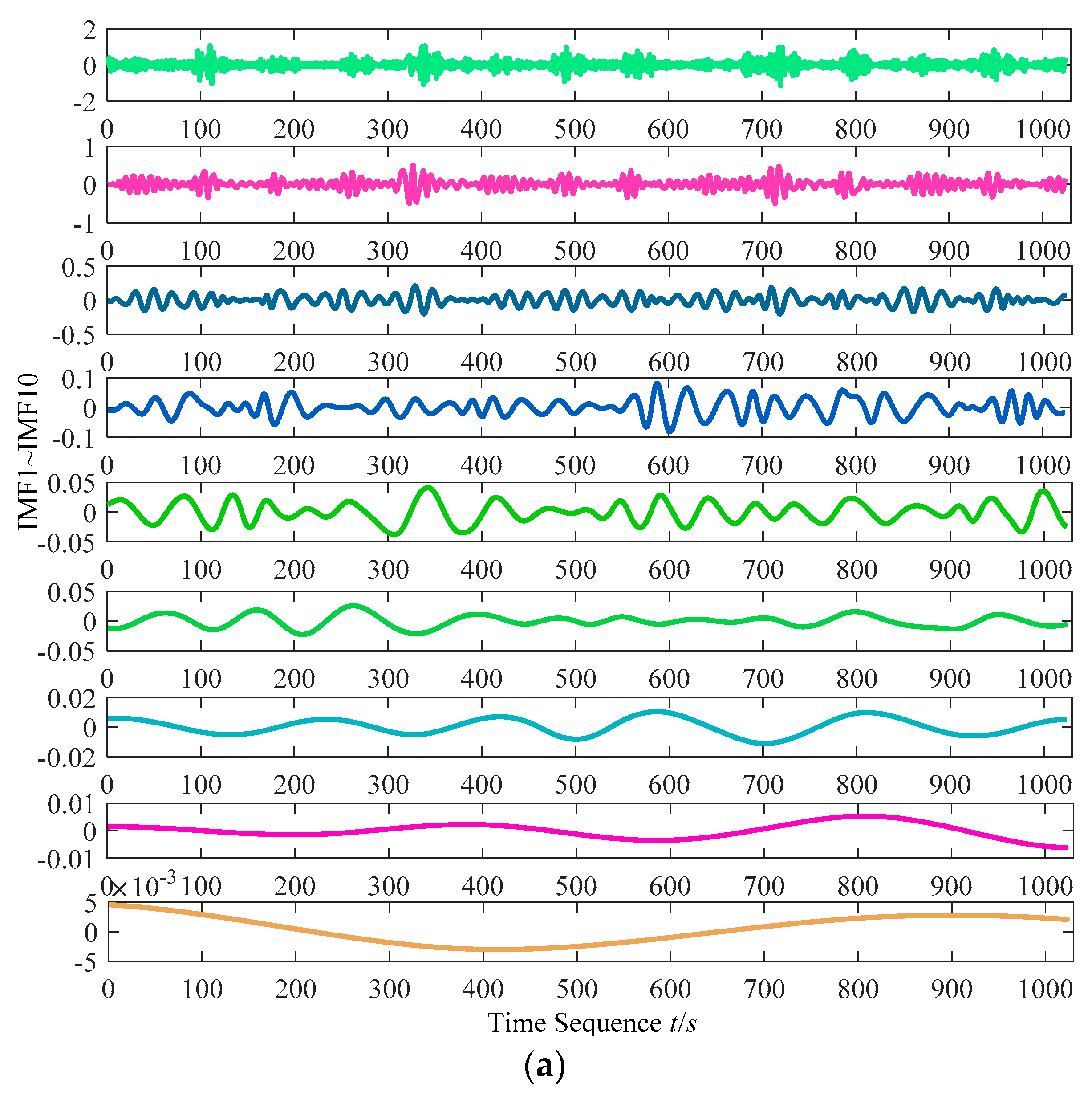
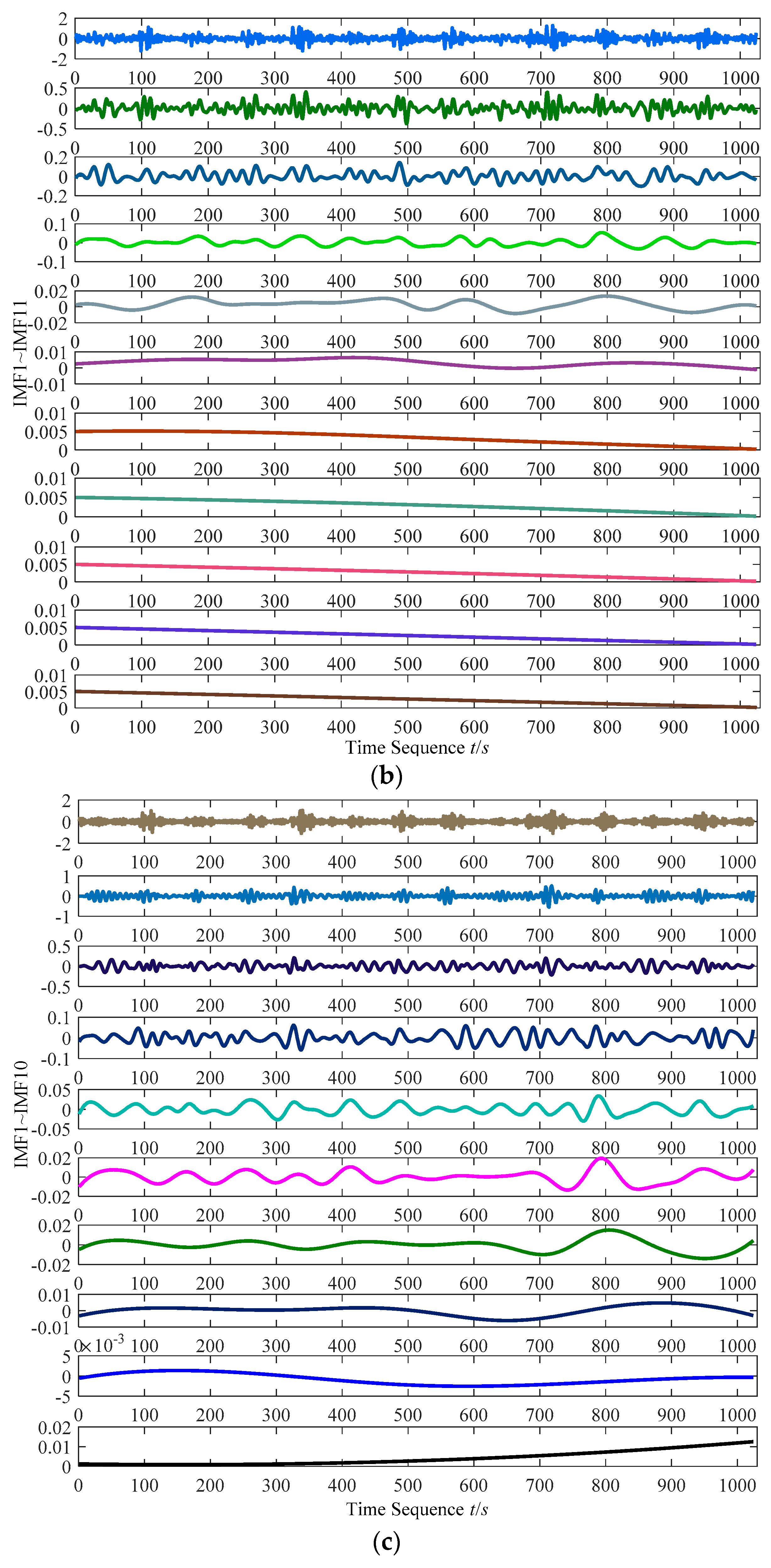
3.1. Fast Empirical Mode Decomposition Algorithm
3.1.1. Brief Overview of EMD and EEMD Algorithms
- The number of extreme value points and the number of zero-crossings must either be equal or differ at most by one in the whole primary signal.
- At any point, the mean value of the envelope defined by local maxima and the envelope defined by the local minima is zero. The upper and lower envelopes are of local symmetry about the timeline.
3.1.2. Brief Overview of Fast EEMD
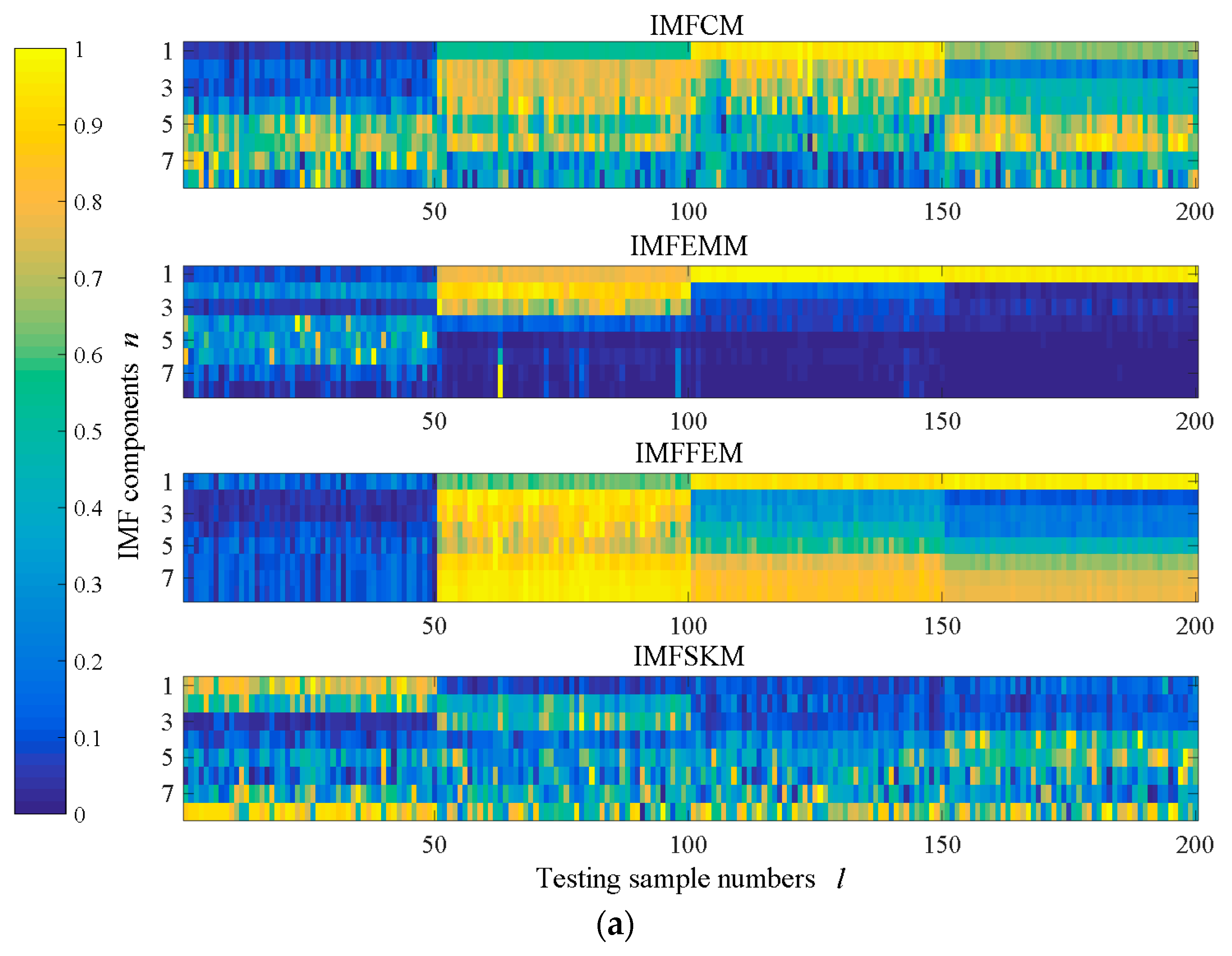
3.2. Definition and Computation Scheme of IMF Correntropy Matrix
3.2.1. Brief Overview of Correntropy
3.2.2. Derivation of IMF Correntropy Matrix
4. Application of IMFCM in Fault Identification
4.1. Brief Overview on Least Square Support Vector Machine
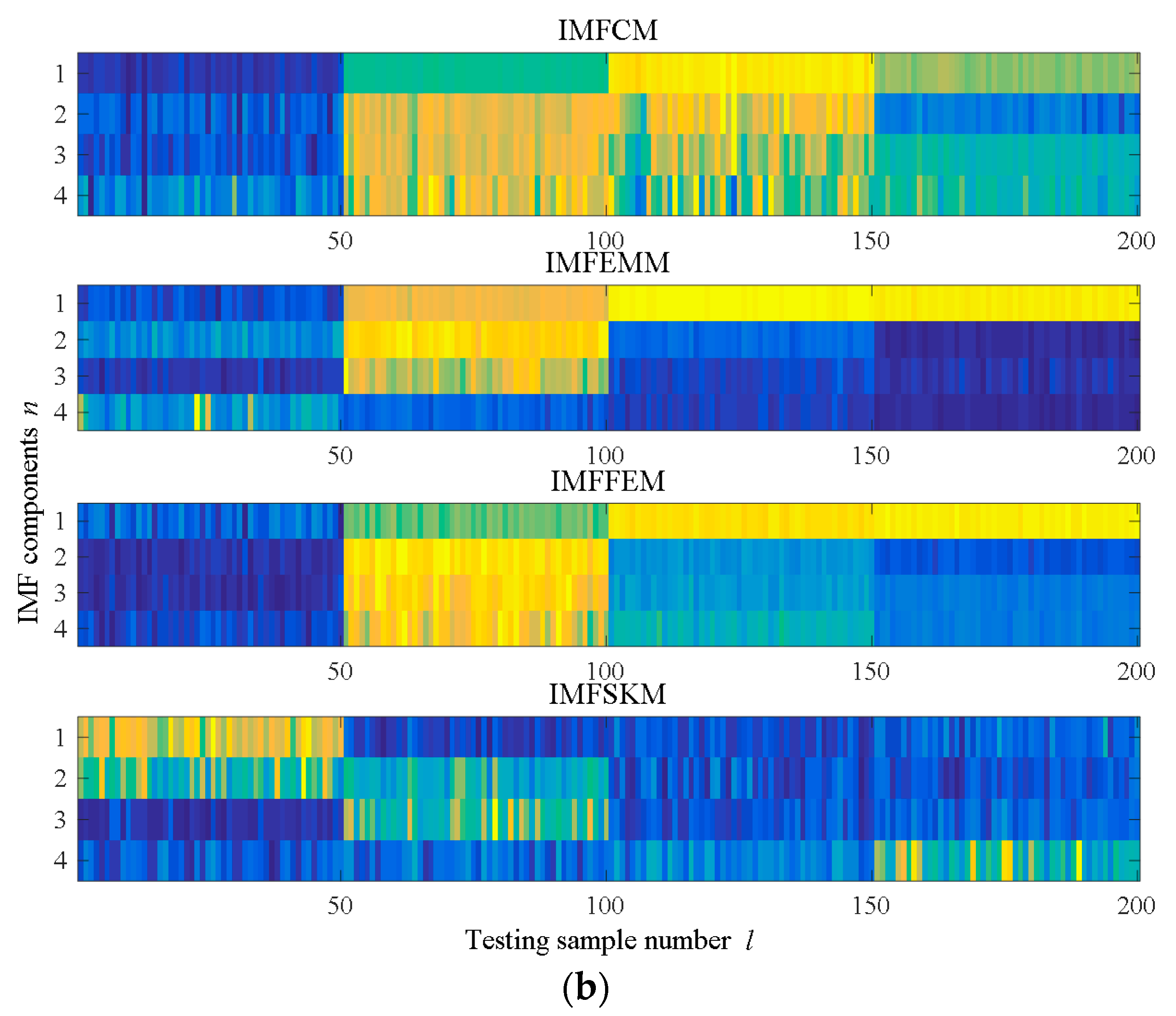
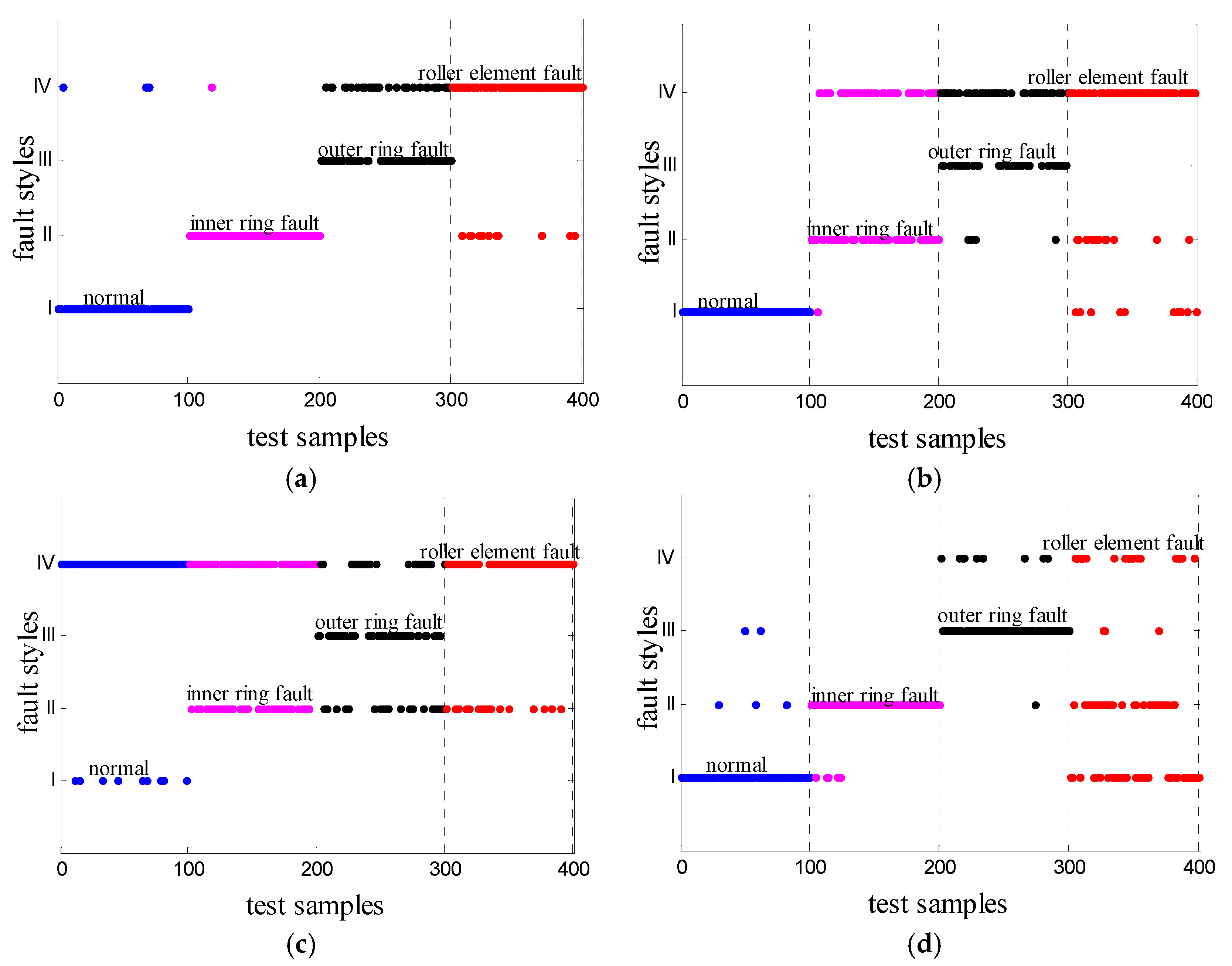
4.2. Evaluation of Identification Consequence
5. Case Study and Applicability Experiment
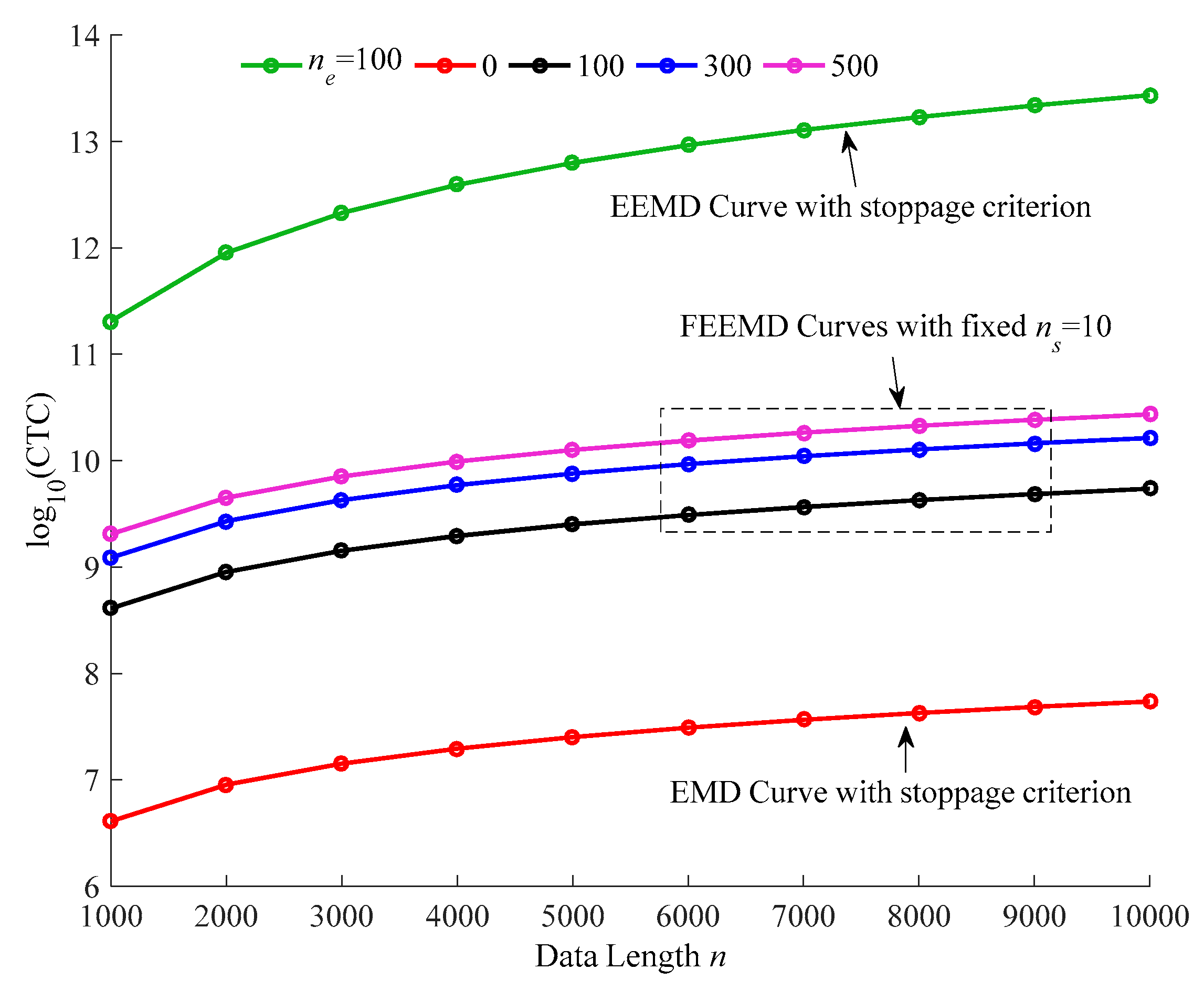
5.1. The Test of FEEMD Computational Time Complexity
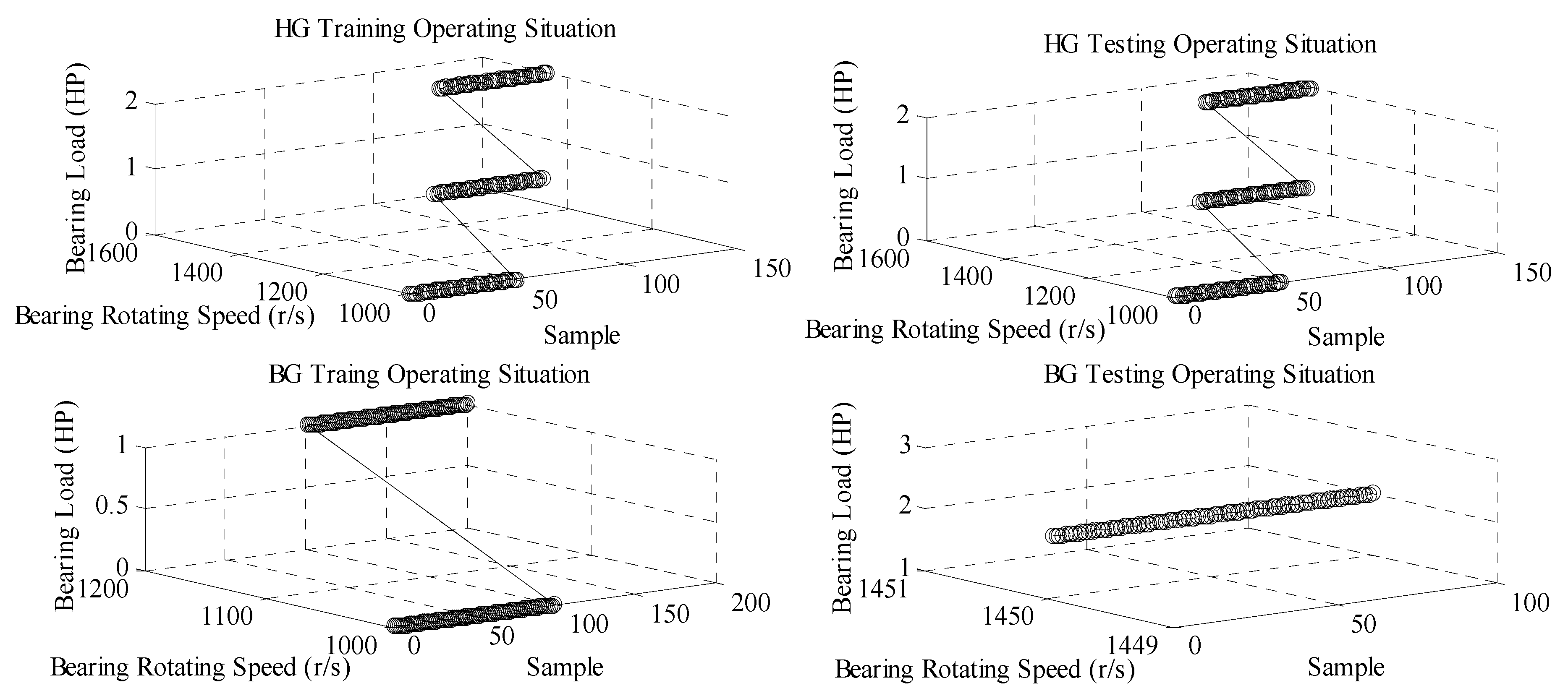
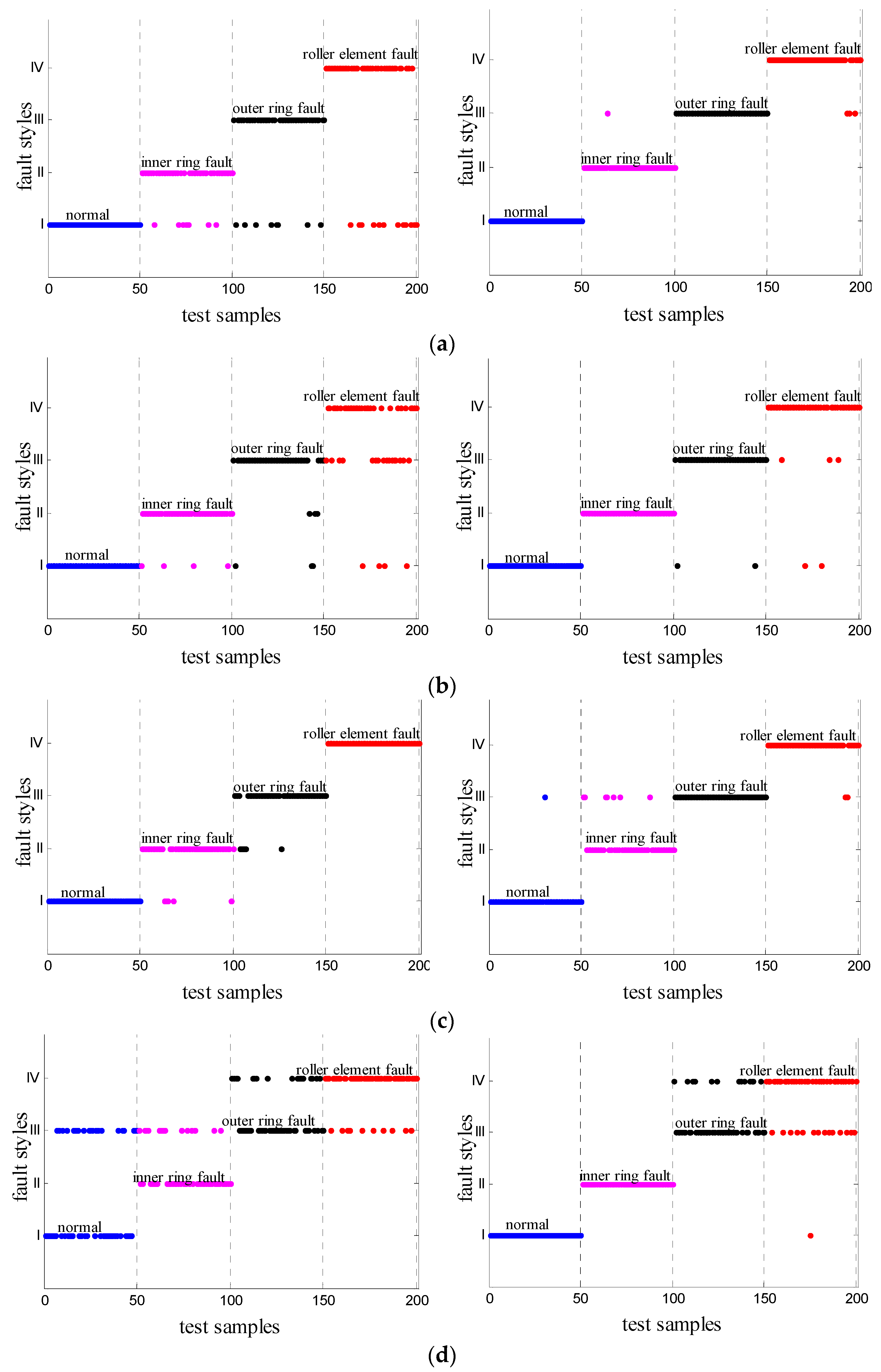
5.2. Stationary Operating Situations
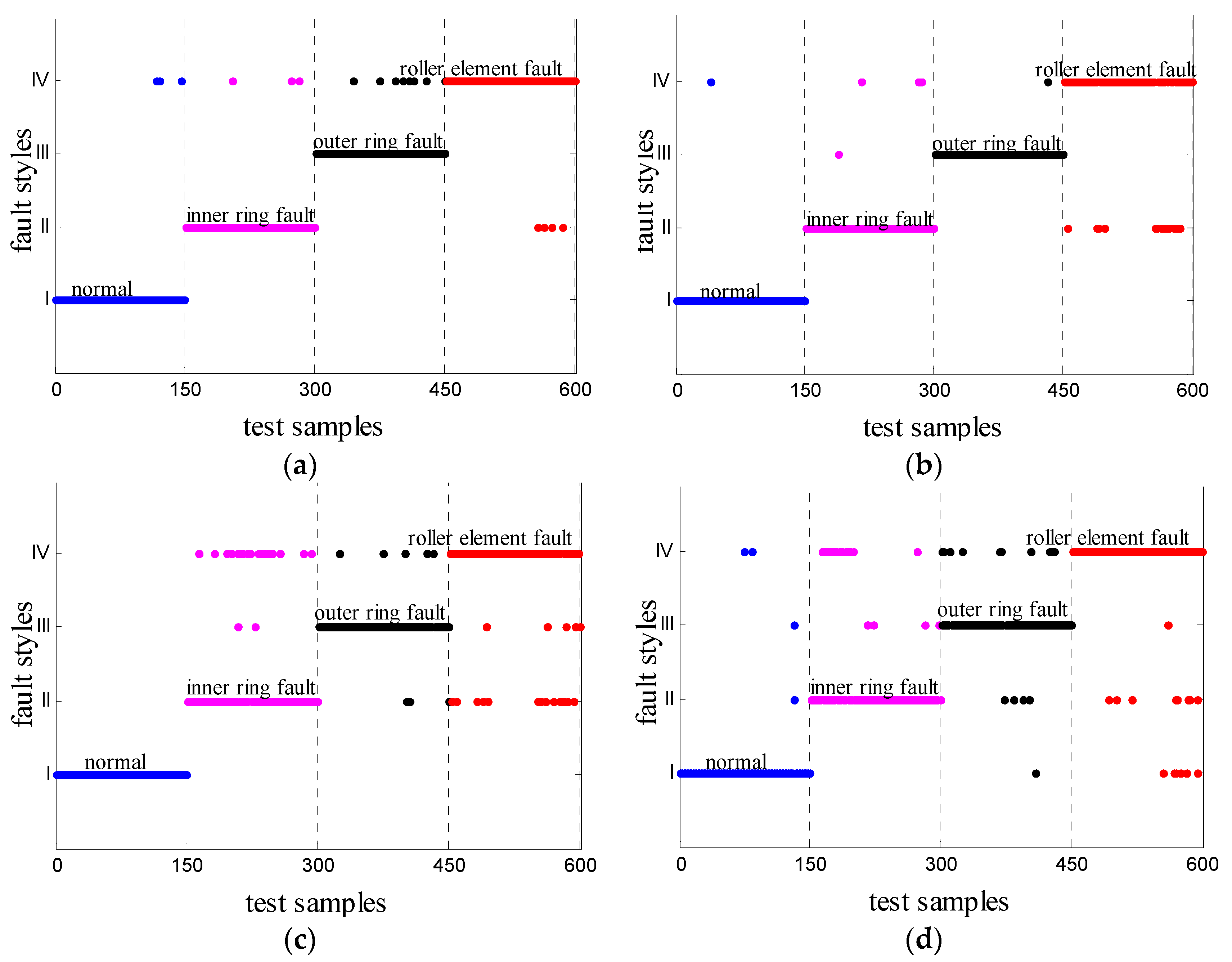
5.3. Cross-Mixed Operating Situations
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tabrizi, A.; Garibaldi, L.; Fasana, A. Early damage detection of roller bearings using wavelet packet decomposition, ensemble empirical mode decomposition and support vector machine. Meccanica 2015, 50, 865–874. [Google Scholar] [CrossRef]
- Frosini, L.; Harlisca, C.; Szabó, L. Induction machine bearing faults detection by means of statistical processing of the stray flux measurement. IEEE Trans. Ind. Electron. 2015, 62, 1846–1854. [Google Scholar] [CrossRef]
- Dalvand, F.; Keshavarzi, M.; Kalantar, A.; Cheraghar, A. Detection of generalized-roughness bearing fault using statistical-time indices of instantaneous frequency of motor voltage space vector. In Proceedings of the 23rd Iranian Conference on Electrical Engineering (ICEE’ 2015), Tehran, Iran, 10–14 May 2015; pp. 1516–1521.
- Renaudin, L.; Bonnardot, F.; Musy, O.; Doray, J.B.; Rémond, D. Natural roller bearing fault detection by angular measurement of true instantaneous angular speed. Mech. Syst. Signal Process. 2010, 24, 1998–2011. [Google Scholar] [CrossRef]
- Zhong, B.L.; Huang, R. Introduction to Machine Fault Diagnosis, 3rd ed.; China Machine Press: Beijing, China, 2007; pp. 1–16. [Google Scholar]
- Lim, G.M.; Bae, D.M.; Kim, J.K. Fault diagnosis of rotating machine by thermography method on support vector machine. J. Mech. Sci. Technol. 2014, 28, 2947–2952. [Google Scholar] [CrossRef]
- Rai, V.K.; Mohanty, A.R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert–Huang transform. Mech. Syst. Signal Process. 2007, 21, 2607–2615. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, D.J.; Cheng, J.S. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. J. Sound Vib. 2006, 204, 269–277. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. The Empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Han, M.H.; Pan, J.L. A fault diagnosis method combined with FEEMD, sample entropy and energy ratio for roller bearings. Measurement 2015, 75, 7–19. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A New View of Nonlinear Water Waves the Hilbert Spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–467. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble Empirical Mode Decomposition a Noise-assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wei, G.; Tse, P.W. A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals. J. Sound Vib. 2013, 332, 423–441. [Google Scholar]
- Xue, X.M.; Zhou, J.Z.; Xu, Y.H.; Zhu, W.L.; Li, C.C. An adaptively fast ensemble empirical mode decomposition method and its applications to rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2015, 62–63, 444–459. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yeha, C.H.; Young, H.V.; Hu, K.; Lo, M.T. On the computational complexity of the empirical mode decomposition algorithm. Physica A 2014, 390, 159–167. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Liang, X.F.; Li, Y.F. New wind speed forecasting approaches using fast ensemble empirical model decomposition, genetic algorithm, Mind Evolutionary Algorithm and Artificial Neural Networks. Renew. Energy 2015, 83, 1066–1075. [Google Scholar] [CrossRef]
- Shi, Z.L.; Song, W.Q.; Taheri, S. Improved LMD, Permutation Entropy and Optimized K-Means to Fault Diagnosis for Roller Bearings. Entropy 2016, 18, 70. [Google Scholar] [CrossRef]
- Hsieh, N.K.; Lin, W.Y.; Young, H.T. High-Speed Spindle Fault Diagnosis with the Empirical Mode Decomposition and Multiscale Entropy Method. Entropy 2015, 17, 2170–2183. [Google Scholar] [CrossRef]
- Bishara, A.J.; Hittner, J.B. Reducing Bias and Error in the Correlation Coefficient Due to Non-normality. Educ. Psychol. Meas. 2015, 75, 785–804. [Google Scholar] [CrossRef]
- Xu, W.C.; Chang, C.Q.; Hung, Y.S.; Fung, P.C.W. Asymptotic Properties of Order Statistics Correlation Coefficient in the Normal Cases. IEEE Trans. Signal Process. 2008, 56, 2239–2248. [Google Scholar] [Green Version]
- Puth, M.T.; Neuhäuser, M.; Ruxton, G.D. Effective use of Spearman’s and Kendall’s correlation coefficients for association between two measured traits. Anim. Behav. 2015, 102, 77–84. [Google Scholar] [CrossRef]
- Li, J.W.; Qian, H.D. Correntropy method for spectrum estimation in impulsive noise environment. Signal Process. 2014, 30, 944–948. [Google Scholar]
- Santamaria, I.; Pokharel, P.P.; Principe, J.C. Generalized correlation function: Definition, properties, and application to blind equalization. IEEE Trans. Signal Process. 2006, 54, 2187–2197. [Google Scholar] [CrossRef]
- Gunduz, A.; Principe, J.C. Correntropy as a novel measure for nonlinearity tests. Signal Process. 2009, 89, 14–23. [Google Scholar] [CrossRef]
- Xing, H.J.; Ren, H.R. Regularized correntropy criterion based feature extraction for novelty detection. Neurocomputing 2014, 133, 483–490. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, C.H.; Xiang, S.M.; Zhu, F.Y. Robust hyper spectral unmixing with correntropy-based metric. IEEE Trans. Image Process. 2015, 24, 3927–3939. [Google Scholar]
- Zhang, Z.J.; Chen, J.H. Correntropy based data reconciliation and gross error detection and identification for nonlinear dynamic processes. Comput. Chem. Eng. 2015, 75, 120–134. [Google Scholar] [CrossRef]
- Hassan, M.; Terrien, J.; Marque, C.; Karlsson, B. Comparison between approximate entropy, correntropy and time reversibility: Application to uterine electromyogram signals. Med. Eng. Phys. 2011, 33, 980–986. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Y.; Zhou, J.Z. Multi-fault diagnosis for rolling element bearings based on ensemble empirical mode decomposition and optimized support vector machines. Mech. Syst. Signal Process. 2013, 41, 127–139. [Google Scholar] [CrossRef]
- Wan, Y.; Wu, C.W. LSSVM Algorithm and Its Application Research in Non-Linear Reliability Identification. Adv. Sci. Lett. 2012, 6, 464–467. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Z.C.; Li, W.; Zhou, G.B.; Chen, G. Fault identification of rotor-bearing system based on ensemble empirical mode decomposition and self-zero space projection analysis. J. Sound Vib. 2014, 333, 3321–3331. [Google Scholar] [CrossRef]
- Penga, Z.K.; Tseb, P.W.; Chu, F.L. An improved Hilbert–Huang transform and its application in vibration signal analysis. J. Sound Vib. 2005, 286, 187–205. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Gonçalvés, P. On Empirical Mode Decomposition and Its Algorithms. In Proceedings of the 3rd IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, Grado, Italy, 8–11 June 2003.
- Cheng, J.S.; Yu, D.J.; Yang, Y. Research on the Intrinsic Mode Function (IMF) Criterion in EMD Method. Mech. Syst. Signal Process. 2005, 20, 817–824. [Google Scholar]
- Sun, W.; Liu, M.H.; Liang, Y. Wind Speed Forecasting Based on FEEMD and LSSVM Optimized by the Bat Algorithm. Energies 2015, 8, 6585–6607. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. On the filtering properties of the empirical mode decomposition. Adv. Adapt. Data Anal. 2010, 2, 397–414. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, Y.J.; Jing, B.Y.; Gao, X. Regularized maximum correntropy machine. Neurocomputing 2015, 16, 85–92. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, D.J.; Cheng, J.S. A Fault Diagnosis approach for roller bearing based on IMF envelope spectrum and SVM. Measurement 2007, 39, 943–950. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, Y.; Xing, Z.Y.; Jia, L.M.; Cheng, X.Q. Roller bearing safety region estimation and state identification based on LMD–PCA–LSSVM. Measurement 2013, 46, 1315–1324. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 23 June 2016).
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets—Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Li, Y.B.; Xu, M.Q.; Zhao, H.Y.; Huang, W. Hierarchical fuzzy entropy and improved support vector machine based binary tree approach for rolling bearing fault diagnosis. Mech. Mach. Theory 2016, 98, 114–132. [Google Scholar] [CrossRef]
- Tian, J.; Morillo, C.; Azarian, M.H.; Pecht, M. Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled With K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2016, 63, 1793–1803. [Google Scholar] [CrossRef]

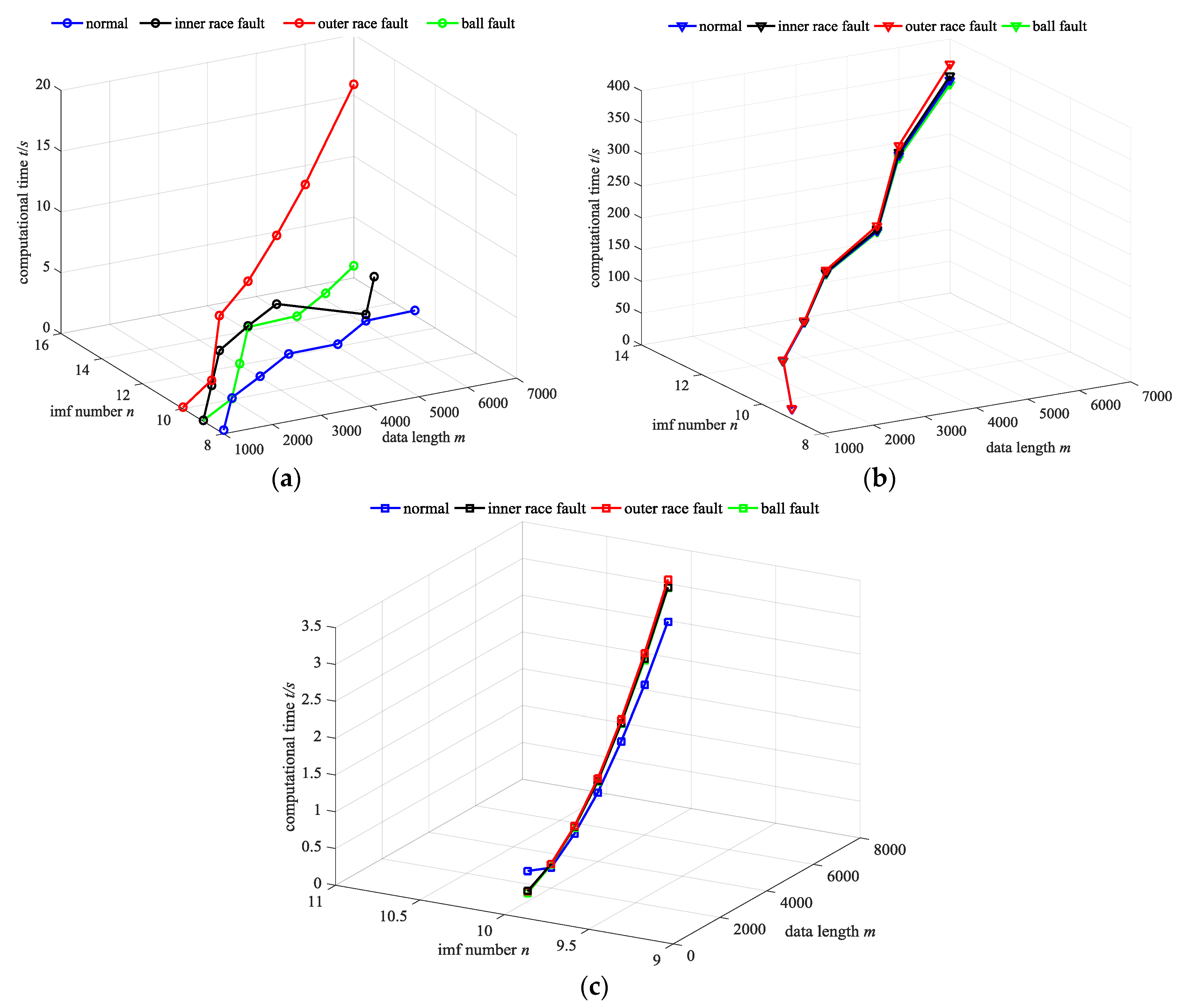
| Fault Style | Algorithm | Length of Data | ||||||
|---|---|---|---|---|---|---|---|---|
| 1000 | 2000 | 3000 | 3900 | 5000 | 6000 | 7000 | ||
| Normal | EMD | 0.344 | 0.062 | 0.086 | 0.141 | 0.164 | 0.250 | 0.297 |
| EEMD | 5.909 | 10.919 | 21.107 | 35.923 | 54.903 | 84.121 | 122.927 | |
| FEEMD | 0.282 | 0.219 | 0.438 | 0.719 | 1.108 | 1.546 | 2.103 | |
| Inner Race Fault | EMD | 0.062 | 0.063 | 0.141 | 0.281 | 0.312 | 0.641 | 0.859 |
| EEMD | 5.711 | 11.156 | 21.363 | 36.379 | 56.065 | 86.945 | 126.945 | |
| FEEMD | 0.125 | 0.25 | 0.5 | 0.828 | 1.282 | 1.797 | 2.466 | |
| Outer Race Fault | EMD | 0.078 | 0.422 | 2.315 | 3.104 | 4.55 | 6.395 | 12.31 |
| EEMD | 5.713 | 11.416 | 21.94 | 37.659 | 58.495 | 91.396 | 134.166 | |
| FEEMD | 0.094 | 0.266 | 0.5 | 0.844 | 1.313 | 1.859 | 2.5360 | |
| Ball Fault | EMD | 0.094 | 0.25 | 0.484 | 0.828 | 1.265 | 1.813 | 2.44 |
| EEMD | 5.539 | 10.952 | 20.96 | 35.441 | 54.699 | 85.544 | 122.701 | |
| FEEMD | 0.031 | 0.046 | 0.109 | 0.188 | 0.344 | 0.397 | 0.797 | |
| Operating Parameters | A Group | B Group | C Group |
|---|---|---|---|
| Speed | 1750 r/min | 1772 r/min | 1797 r/min |
| Load | 2HP | 1HP | 0 |
| Evaluation | Feature | A Group: 1750 r/min & 2HP | B Group: 1772 r/min & 1HP | C Group: 1797 r/min & 0HP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | I | II | III | IV | I | II | III | IV | ||
| θ (%) | CM | 100 | 98 | 100 | 94 | 100 | 96 | 100 | 94 | 98 | 90 | 100 | 100 |
| EMM | 100 | 100 | 96 | 90 | 100 | 100 | 96 | 98 | 100 | 98 | 100 | 96 | |
| FEM | 98 | 86 | 100 | 96 | 100 | 100 | 100 | 98 | 100 | 100 | 100 | 94 | |
| SKM | 100 | 100 | 74 | 70 | 100 | 100 | 76 | 94 | 94 | 92 | 94 | 92 | |
| η (%) | CM | 0 | 0 | 0.27 | 0 | 0 | 0 | 3.33 | 0 | 0 | 0 | 4 | 0 |
| EMM | 2.67 | 0 | 2 | 0 | 0 | 1.33 | 0.67 | 0.91 | 0.67 | 0 | 1.33 | 0 | |
| FEM | 0 | 0 | 6.67 | 0 | 0 | 0 | 0.67 | 0 | 0 | 0 | 2 | 0 | |
| SKM | 0.67 | 0 | 9.33 | 8.67 | 1.33 | 0.67 | 2 | 6 | 0.67 | 4.67 | 0 | 4 | |
| μ (%) | CM | 98 | 97.5 | 97 | |||||||||
| EMM | 96.5 | 98.5 | 98.5 | ||||||||||
| FEM | 95 | 99.5 | 98.5 | ||||||||||
| SKM | 86 | 92.5 | 93 | ||||||||||
| Evaluation | Feature | A Group: 1750 r/min & 2HP | B Group: 1772 r/min & 1HP | C Group: 1797 r/min & 0HP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | I | II | III | IV | I | II | IIII | IV | ||
| θ(%) | CM | 98 | 98 | 92 | 100 | 100 | 96 | 96 | 100 | 96 | 92 | 94 | 98 |
| EMM | 100 | 100 | 98 | 88 | 100 | 98 | 90 | 92 | 100 | 86 | 98 | 88 | |
| FEM | 100 | 84 | 98 | 98 | 100 | 92 | 98 | 98 | 100 | 96 | 94 | 92 | |
| SKM | 94 | 78 | 96 | 98 | 100 | 82 | 90 | 98 | 92 | 80 | 82 | 90 | |
| η (%) | CM | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 2.67 | 0 | 1.33 | 0 | 5.33 |
| EMM | 4 | 0.67 | 0 | 0 | 0.68 | 2.67 | 3.33 | 0 | 3.33 | 0.67 | 0 | 5.33 | |
| FEM | 0 | 0.67 | 0 | 6 | 0 | 1.33 | 2.67 | 0 | 0 | 1.33 | 2 | 2.67 | |
| SKM | 0 | 0.67 | 0 | 10.67 | 0 | 1.33 | 2.67 | 6 | 2 | 0 | 6.67 | 10 | |
| μ (%) | CM | 97 | 98 | 95 | |||||||||
| EMM | 96.5 | 95 | 93 | ||||||||||
| FEM | 95 | 97 | 95.5 | ||||||||||
| SKM | 91.5 | 92.5 | 86 | ||||||||||
| Evaluation | Feature | A Group: 1750 r/min & 2HP | B Group: 1772 r/min & 1HP | C Group: 1797 r/min & 0HP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | I | II | III | IV | I | I | III | IV | ||
| θ (%) | CM | 100 | 90 | 100 | 98 | 100 | 94 | 98 | 86 | 98 | 96 | 100 | 88 |
| EMM | 98 | 100 | 100 | 100 | 100 | 100 | 100 | 92 | 92 | 98 | 100 | 96 | |
| FEM | 100 | 96 | 100 | 100 | 100 | 96 | 100 | 84 | 100 | 100 | 100 | 96 | |
| SKM | 98 | 76 | 100 | 98 | 98 | 92 | 100 | 98 | 86 | 78 | 96 | 82 | |
| η (%) | CM | 0 | 0 | 4 | 0 | 0 | 1.33 | 6 | 0 | 0 | 0 | 6 | 0 |
| EMM | 0 | 0 | 0.67 | 0 | 0 | 0 | 2.67 | 0 | 0 | 0 | 4.67 | 0 | |
| FEM | 0 | 0 | 1.33 | 0 | 0 | 0 | 6.67 | 0 | 0 | 0 | 1.33 | 0 | |
| SKM | 0 | 0.67 | 1.33 | 7.33 | 0 | 10 | 2.67 | 1.33 | 4.67 | 1.33 | 3.33 | 10 | |
| μ (%) | CM | 97 | 94.5 | 95.5 | |||||||||
| EMM | 99.5 | 98 | 96.5 | ||||||||||
| FEM | 93 | 95 | 99 | ||||||||||
| SKM | 91.5 | 89.5 | 85.5 | ||||||||||
| Feature Index | Homogeneous Group | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | μ (%) | |||||
| θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | ||
| CM | 99.33 | 0 | 97.33 | 0 | 100 | 2.67 | 95.33 | 0 | 98 |
| EMM | 100 | 0.89 | 99.33 | 0 | 98 | 0.44 | 96.67 | 0.67 | 98.5 |
| FEM | 100 | 0 | 100 | 0 | 99.33 | 0.44 | 98.67 | 0.22 | 99.5 |
| SKM | 97.33 | 1.11 | 96 | 1.78 | 85 | 4 | 82 | 6.22 | 90.17 |
| Feature Index | Homogeneous Group | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | μ (%) | |||||
| θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | ||
| CM | 98 | 0 | 98 | 0.89 | 94.67 | 0 | 97.33 | 3.11 | 97 |
| EMM | 99.33 | 0 | 96 | 4 | 99.33 | 0.22 | 88 | 0.156 | 95.67 |
| FEM | 100 | 0 | 84 | 4.89 | 94.67 | 1.56 | 84 | 6 | 90.67 |
| SKM | 97.33 | 1.56 | 84 | 3.11 | 89.33 | 1.56 | 89.33 | 7.11 | 90 |
| Feature Index | Homogeneous Group | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | μ (%) | |||||
| θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | ||
| CM | 98.67 | 0 | 91.33 | 3.11 | 90 | 3.11 | 99.33 | 0.67 | 94.83 |
| EMM | 99.33 | 0 | 99.33 | 0 | 100 | 1.33 | 97.33 | 0 | 99 |
| FEM | 100 | 0 | 99.33 | 0 | 100 | 0.44 | 99.33 | 0 | 99.67 |
| SKM | 88.67 | 1.11 | 83.33 | 4 | 86.67 | 4 | 92.67 | 7.11 | 87.83 |
| Feature Index | Biased Group | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | μ (%) | |||||
| θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | ||
| CM | 96 | 0 | 93 | 0 | 100 | 7.33 | 89 | 0 | 94.5 |
| EMM | 100 | 1.67 | 99 | 0.67 | 96 | 22.33 | 28 | 10 | 80.75 |
| FEM | 42 | 0 | 100 | 19.33 | 99 | 8.33 | 75 | 0.33 | 79 |
| SKM | 95 | 15 | 95 | 13.33 | 88 | 1.67 | 21 | 3.67 | 74.75 |
| Feature Index | Biased Group | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | μ (%) | |||||
| θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | ||
| CM | 97 | 0 | 99 | 3.67 | 65 | 0 | 89 | 1.3 | 87.5 |
| EMM | 100 | 4.67 | 52 | 6 | 42 | 0 | 73 | 33.67 | 66.75 |
| FEM | 9 | 0 | 39 | 14.67 | 47 | 0 | 79 | 60.33 | 43.75 |
| SKM | 3 | 0 | 72 | 12.33 | 35 | 73.33 | 67 | 54.67 | 44.25 |
| Feature Index | Biased Group | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | μ (%) | |||||
| θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | θ (%) | η (%) | ||
| CM | 100 | 0 | 76 | 0.67 | 100 | 20.33 | 61 | 0 | 84.25 |
| EMM | 99 | 0 | 0 | 0 | 100 | 35.33 | 95 | 0 | 73.5 |
| FEM | 10 | 0 | 0 | 0 | 100 | 63.67 | 99 | 0 | 52.25 |
| SKM | 0 | 0 | 89 | 3.67 | 97 | 7 | 81 | 33.67 | 66.75 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Jia, L.; Qin, Y.; Yang, J.; Fu, D. Fast EEMD Based AM-Correntropy Matrix and Its Application on Roller Bearing Fault Diagnosis. Entropy 2016, 18, 242. https://doi.org/10.3390/e18070242
Fu Y, Jia L, Qin Y, Yang J, Fu D. Fast EEMD Based AM-Correntropy Matrix and Its Application on Roller Bearing Fault Diagnosis. Entropy. 2016; 18(7):242. https://doi.org/10.3390/e18070242
Chicago/Turabian StyleFu, Yunxiao, Limin Jia, Yong Qin, Jie Yang, and Ding Fu. 2016. "Fast EEMD Based AM-Correntropy Matrix and Its Application on Roller Bearing Fault Diagnosis" Entropy 18, no. 7: 242. https://doi.org/10.3390/e18070242