1. Introduction
The concept of entropy can be used to quantify uncertainty, complexity, randomness, and regularity [
1,
2,
3,
4]. Particularly, entropy is also a measure of variability (or dispersion) of the associated distribution [
5]. The most popular entropy functional is the Shannon entropy which is a central concept in information theory [
1]. In addition to Shannon entropy, there are many other entropy definitions, such as Renyi and Tsallis entropies [
2,
3]. Renyi entropy is a generalized entropy which depends on a parameter
and includes Shannon entropy as a limiting case (
). In this work, to simplify the discussion, we focus mainly on the Shannon and Renyi entropies.
Entropy has found applications in many fields such as statistics, physics, communication, ecology,
etc. In the past decades, especially in recent years, entropy and related information theoretic measures (e.g., mutual information) have also been successfully applied in machine learning and signal processing [
4,
6,
7,
8,
9,
10]. Information theoretic quantities can capture higher-order statistics and offer potentially significant performance improvement in machine learning applications. In
information theoretic learning (ITL) [
4], the measures from information theory (entropy, mutual information, divergences,
etc.) are often used as an optimization cost instead of the conventional second-order statistical measures such as variance and covariance. In particular, in many machine learning (supervised or unsupervised) problems, the goal is to optimize (maximize or minimize) the variability of the data, and in these cases one can optimize the entropy of the data so as to capture the underlying structure in the data. For example, in supervised learning, such as regression, the problem can be formulated as that of minimizing the entropy of the error between model output and desired response [
11,
12,
13,
14,
15,
16,
17]. This optimization criterion is called in ITL the
minimum error entropy (MEE) criterion [
4,
6].
In most practical applications, the data are multidimensional and multivariate. The
total dispersion (
i.e., the trace of the covariance matrix) and
generalized variance (
i.e., the determinant of the covariance matrix) are two widely used measures of multivariate variability, although both have some limitations [
18,
19,
20]. However, these measures of multivariate variability involve only second-order statistics and cannot describe well non-Gaussian distributions. Entropy can be used as a descriptive and comprehensive measure of multivariate variability especially when data are non-Gaussian, since it can capture higher-order statistics and information content of the data rather than simply their energy [
4]. There are strong relationships between entropy and traditional measures of multivariate variability (e.g., total dispersion and generalized variance). In the present work, we study this problem in detail and provide some new insights into the behavior of entropy as a measure of multivariate variability. We focus mainly on two types of multivariate entropy (or entropy power) measures, namely joint entropy and total marginal entropy. We show that for the jointly Gaussian case, the joint entropy and joint entropy power are equivalent to the generalized variance, while total marginal entropy is equivalent to the geometric mean of the marginal variances and total marginal entropy power is equivalent to the total dispersion. Further, we study the smoothed multivariate entropy measures and show that the smoothed joint entropy and smoothed total marginal entropy will be equivalent to a weighted version of total dispersion when the smoothing vector has independent entries and the smoothing factor approaches infinity. In particular, if the smoothing vector has independent and identically distributed entries, the two smoothed entropy measures will be equivalent to the total dispersion as the smoothing factor approaches infinity. Finally, we also show that with finite number of samples, the kernel density estimation (KDE) based entropy (joint or total marginal) estimator will be approximately equivalent to a total dispersion estimator if the kernel function is Gaussian with covariance matrix being an identity matrix and the smoothing factor is large enough.
The rest of the paper is organized as follows. In
Section 2, we present some entropy measures of multivariate variability and discuss the relationships between entropy and traditional measures of multivariate variability. In
Section 3, we study the smoothed multivariate entropy measures and gain insights into the links between the smoothed entropy and total dispersion. In
Section 4, we investigate the KDE based entropy estimator (with finite samples), and prove that under certain conditions the entropy estimator is approximately equivalent to a total dispersion estimator. Finally in
Section 5, we give the conclusion.
3. Smoothed Multivariate Entropy Measures
In most practical situations, the analytical evaluation of the entropy is not possible, and one has to estimate its value from the samples. So far there are many entropy estimators, among which the
k-nearest neighbors based estimators are important ones in a wide range of practical applications [
28]. In ITL, however, the
kernel density estimation (KDE) based estimators are perhaps the most popular ones due to their smoothness [
4]. By KDE approach [
29], with a fixed kernel function, the estimated entropy will converge asymptotically to the entropy of the underlying random variable plus an independent random variable whose PDF corresponds to the kernel function [
4]. This asymptotic value of entropy is called the
smoothed entropy [
16]. In this section, we will investigate some interesting properties of the smoothed multivariate entropy (joint or total marginal) as a measure of variability. Unless mentioned otherwise, the smoothed entropy studied in the following is based on the Shannon entropy, but the obtained results can be extended to many other entropies.
Given a
-dimensional random vector
, with PDF
, and a
smoothing vector that is independent of
and has PDF
, the
smoothed joint entropy of
, with smoothing factor
(
), is defined by [
16]:
where
denotes the PDF of
, which is:
where “
” denotes the convolution operator, and
is the PDF of
.
Let
be
independent, identically distributed (i.i.d.) samples drawn from
. By KDE approach, with a fixed kernel function
, the estimated PDF of
will be [
29]:
where
is the smoothing factor (or kernel width). As sample number
, the estimated PDF will uniformly converge (with probability 1) to the true PDF convolved with the kernel function. So we have:
Plugging the above estimated PDF into the entropy definition, one may obtain an estimated entropy of , which converges, almost surely (a.s.), to the smoothed entropy .
Remark 7. Theoretically, using a suitable annealing rate for the smoothing factor
, the KDE based entropy estimator can be asymptotically unbiased and consistent [
29]. In many machine learning applications, however, the smoothing factor is often kept fixed. The main reasons for this are basically two: (1) in practical situations, the training data are always finite; (2) in general the learning seeks extrema (either minimum or maximum) of the cost function, independently to its actual value, and the dependence on the estimation bias is decreased. Therefore, the study of the smoothing entropy will help us to gain insights into the asymptotic behaviors of the entropy based learning.
Similarly, one can define the
Smoothed Total Marginal Entropy of
:
where
denotes the smoothed marginal density,
.
The smoothing factor is a very important parameter in the smoothed entropy measures (joint or total marginal). As , the smoothed entropy measures will reduce to the original entropy measures, , . In the following, we study the case in which is very large. Before presenting Theorem 4, we introduce an important lemma.
Lemma 1. (De Bruijn's Identity [
30]
): For any two independent random d-dimensional vectors, and , with PDFs and , such that exists and has finite covariance, where denotes the Fisher Information Matrix (FIM):in which is the zero-mean Score of , then:where denotes the covariance matrix of .
Theorem 4. As is large enough, we have:where , and denotes the variance of .
Proof. The smoothed joint entropy
can be rewritten as:
Let
, we have:
Then, by
De Bruijn’s Identity:
where
denotes the higher-order infinitesimal term of the Taylor expansion. Similarly, one can easily derive:
Thus, as is large enough, will be very small, such that Equations (31) and (32) hold. □
Remark 8. In Equation (31), the term
is not related to
. So, when the smoothing factor
is large enough, the smoothed joint entropy
will be, approximately, equivalent to
, denoted by:
In the following, we consider three special cases of the smoothing vector .
Case 1. If
is a jointly Gaussian random vector, then
, and
, where
denotes the variance of
. In this case, we have:
Case 2. If
has independent entries, then
is a diagonal matrix, with
along the diagonal. It follows easily that:
Case 3. If
has independent and identically distributed (i.i.d.) entries, then
, where
is a
identity matrix. Thus:
Remark 9. It is interesting to observe that, if the smoothing vector
has independent entries, then the smoothed joint entropy and smoothed total marginal entropy will be equivalent to each other as
. In this case, they are both equivalent to a weighted version of total dispersion, with weights
. In particular, when
has i.i.d. entries, the two entropy measures will be equivalent (as
) to the ordinary total dispersion. Note that the above results hold even if
is non-Gaussian distributed. The equivalent measures of the smoothed joint and total marginal entropies as
are summarized in
Table 2.
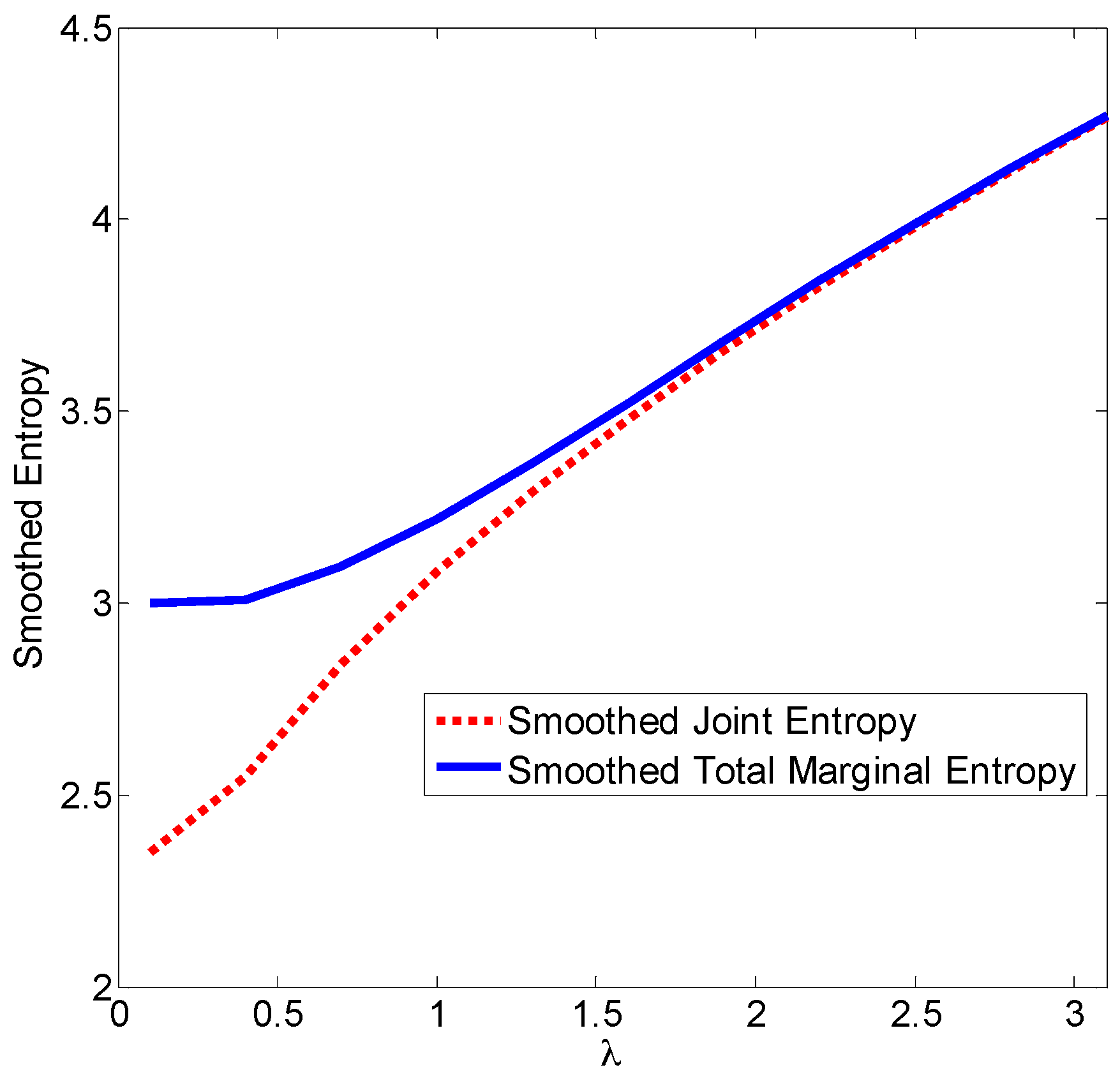
Example 1. According to Theorem 4, if has independent entries, the smoothed joint entropy and the smoothed total marginal entropy will approach a same value with increasing. Below we present a simple example to confirm this fact.
Consider a two-dimensional case in which
is mixed-Gaussian with PDF:
where
,
, and
is uniformly distributed over
.
Figure 1 illustrates the smoothed entropies (joint and total marginal) with different
values. As one can see clearly, when
is small (close to zero), the smoothed total marginal entropy is larger than the smoothed joint entropy, and the difference is significant; while when
gets larger (say, larger than 2.0), the discrepancy between the two entropy measures will disappear.
4. Multivariate Entropy Estimators with Finite Samples
The smoothed entropy is of only theoretical interest since in practical applications, the number of samples is always limited, and the asymptotic value of the entropy estimator can never be reached. In the following, we show, however, that similar results hold for finite samples case. Consider again the kernel density estimator Equation (26). For simplicity we assume that the kernel function is Gaussian with covariance matrix
, where
is a
identity matrix. In this case, the estimated PDF of
becomes:
where
denotes the
i-th element of vector
. With the above estimated PDF, a sample-mean estimator of the joint entropy
is [
4]:
Similarly, an estimator for the total marginal entropy can be obtained as follows:
The following theorem holds.
Theorem 5. As is large enough, we have:where is the estimated variance of .
Proof. When
, we have
. It follows that:
where (a) comes from
as
, (b) comes from
as
, and (c) comes from:
In a similar way, we prove:
Combining Equations (47) and (49) we obtain Equation (46). □
Remark 10. When the kernel function is Gaussian with covariance matrix being an identity matrix, the KDE based entropy estimators (joint or total marginal) will be, approximately, equivalent to the total dispersion estimator () as the smoothing factor is very large. This result coincides with Theorem 4. For the case in which the Gaussian covariance matrix is diagonal, one can also prove that the KDE based entropy (joint or total marginal) estimators will be approximately equivalent to a weighted total dispersion estimator as . Similar results hold for other entropies such as Renyi entropy.
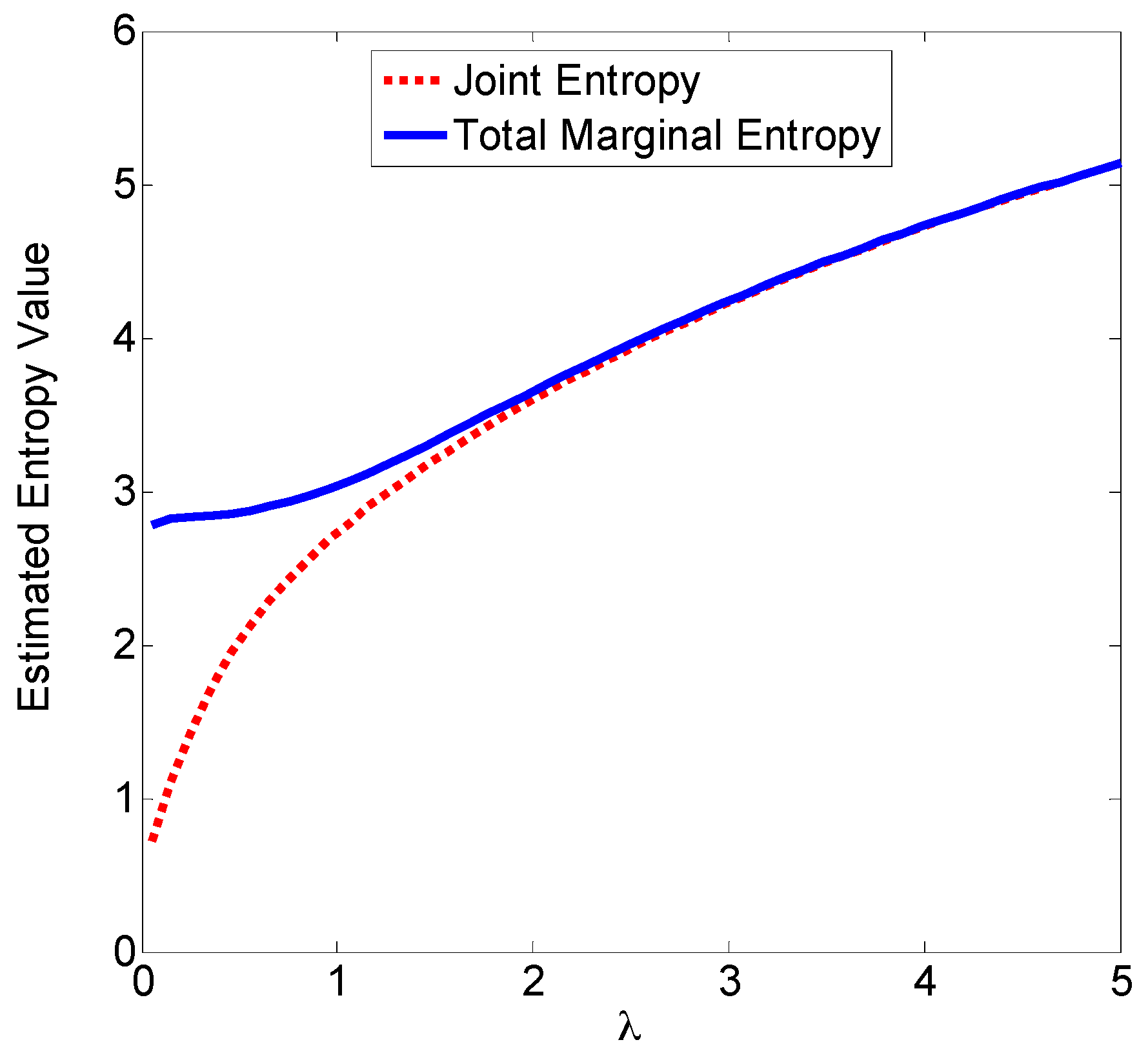
Example 2. Consider 1000 samples drawn from a two-dimensional Gaussian distribution with zero-mean and covariance matrix
.
Figure 2 shows the scatter plot of the samples. Based on these samples, we evaluate the joint entropy and total marginal entropy using Equations (44) and (45), respectively. The estimated entropy values with different
are illustrated in
Figure 3, from which we observe that when
becomes larger, the difference between the two estimated entropies will disappear. The results support the Theorem 5.
5. Conclusions
Measures of the variability of data play significant roles in many machine learning and signal processing applications. Recent studies suggest that machine learning (supervised or unsupervised) can benefit greatly from the use of entropy as a measure of variability, especially when data possess non-Gaussian distributions. In this paper, we have studied the behaviors of entropy as a measure of multivariate variability. The relationships between multivariate entropy (joint or total marginal) and traditional second-order statistics based multivariate variability measures, such as total dispersion and generalized variance, have been investigated. For the jointly Gaussian case, the joint entropy (or entropy power) is shown to be equivalent to the generalized variance, while total marginal entropy is equivalent to the geometric mean of the marginal variances, and total marginal entropy power is equivalent to the total dispersion. We have also gained insights into the relationships between the smoothed multivariate entropy (joint or total marginal) and the total dispersion. Under certain conditions, the smoothed multivariate entropy will be, approximately, equivalent to the total dispersion. Similar results hold for the multivariate entropy estimators (with finite number of samples) based on the kernel density estimation (KDE). The results of this work can help us to understand the behaviors of multidimensional information theoretic learning.