Nonlinear Phenomena of Ultracold Atomic Gases in Optical Lattices: Emergence of Novel Features in Extended States
Abstract
:1. Introduction
2. Theoretical Framework
2.1. Setup of the System
2.2. Bosons
2.3. Fermions
2.4. Discrete and Continuum Models
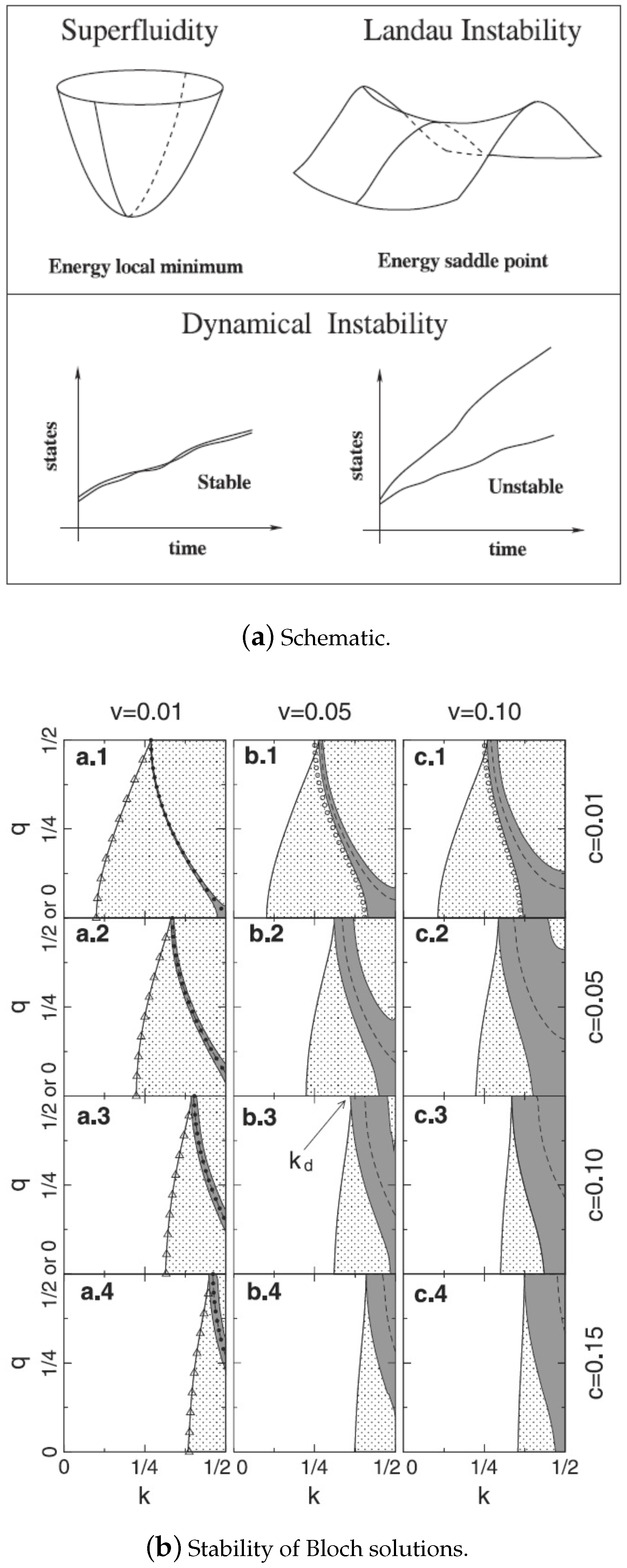
2.5. Energetic and Dynamical Stability
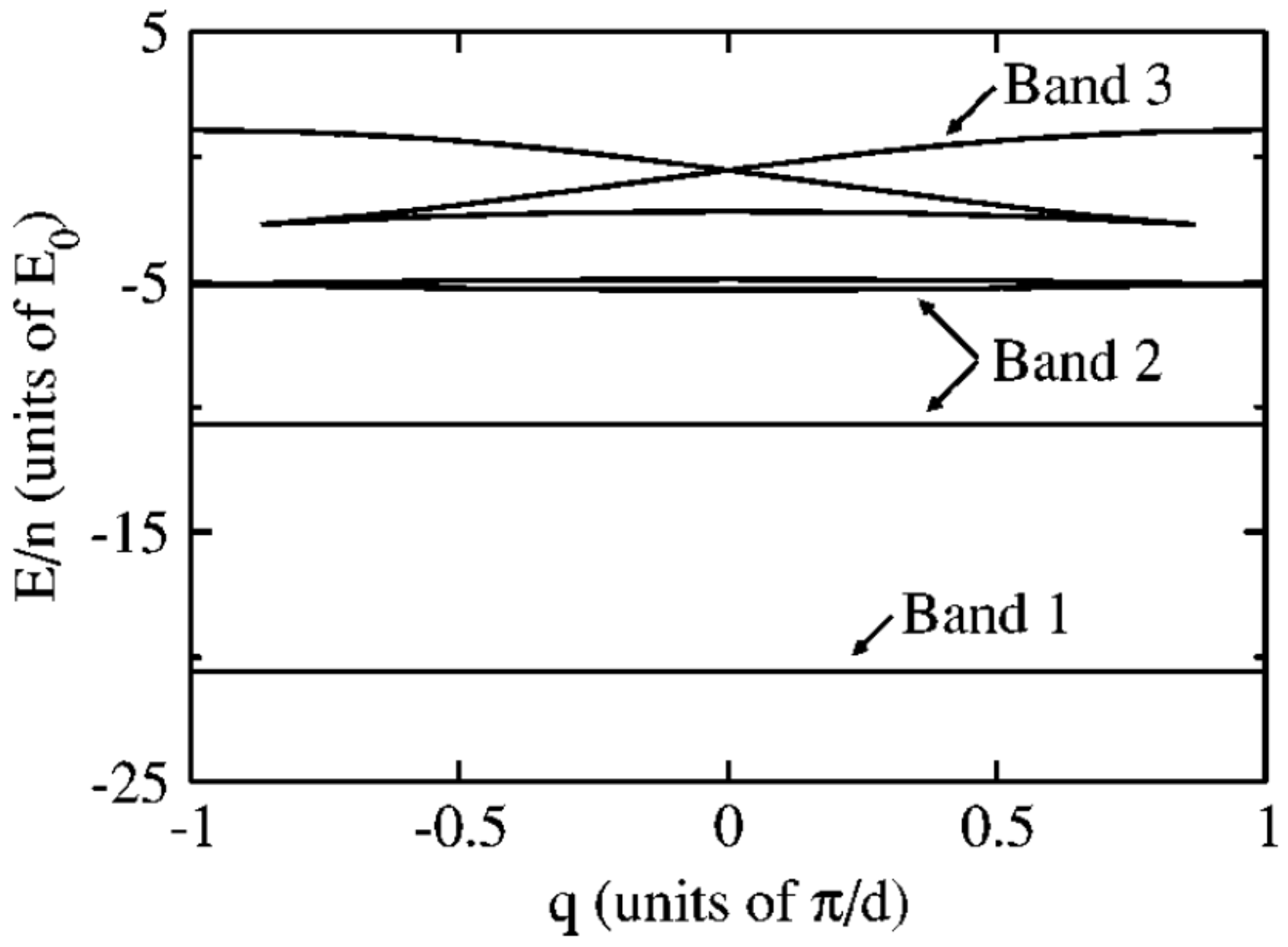
3. Swallowtail Loops in Band Structure
3.1. Basic Physical Idea: The Nonlinear Landau–Zener Model and Variational Ansatz for Condensate Wavefunction in Optical Lattices
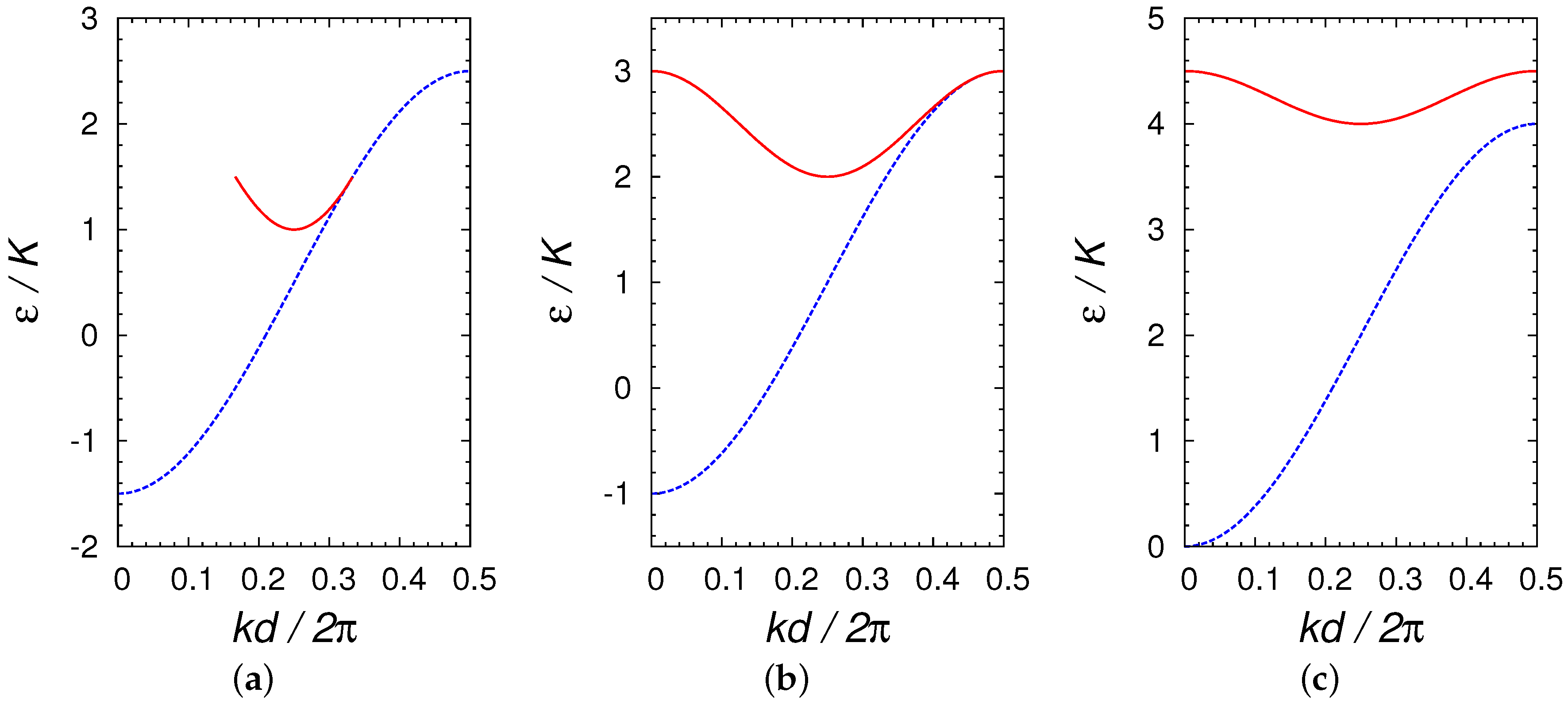
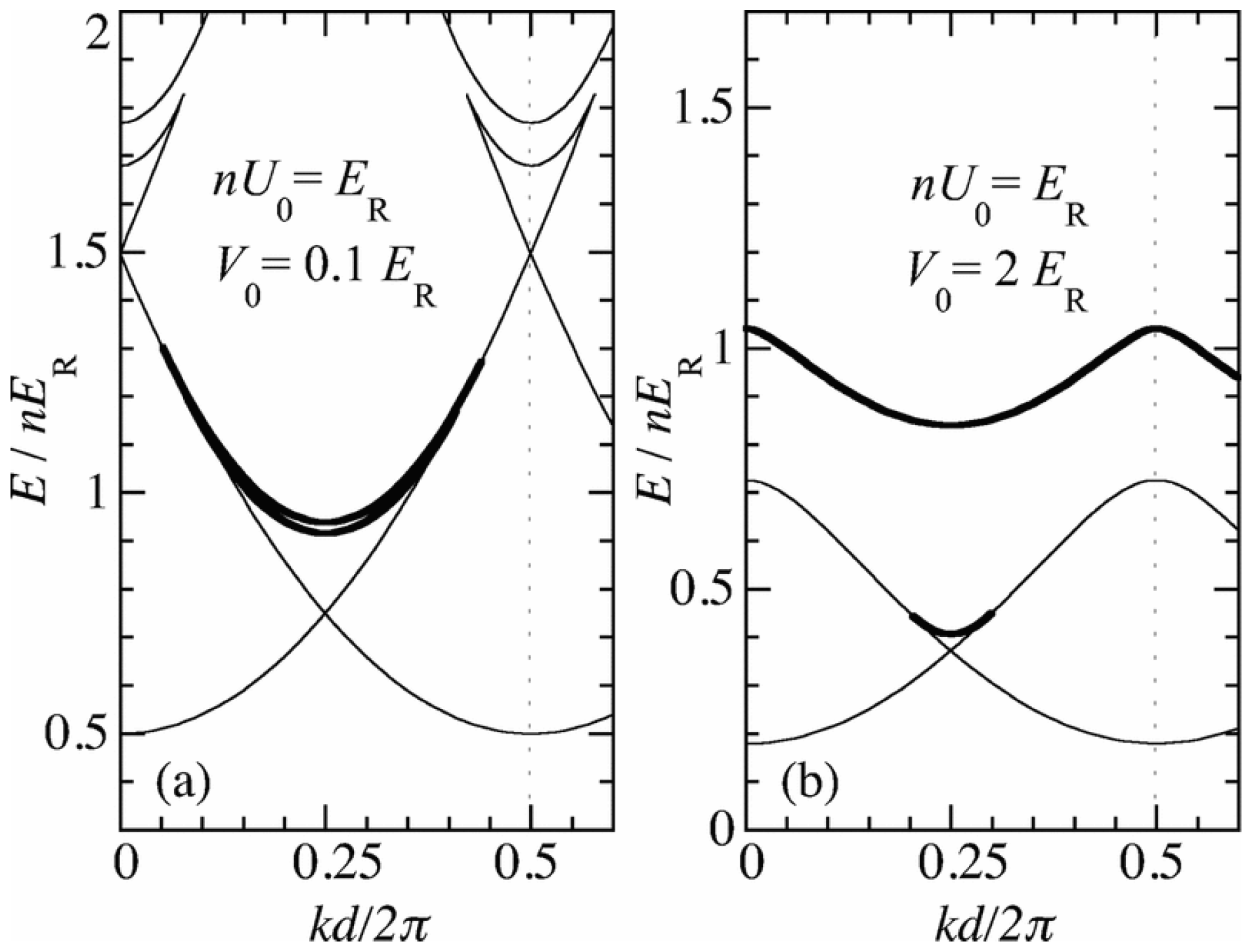
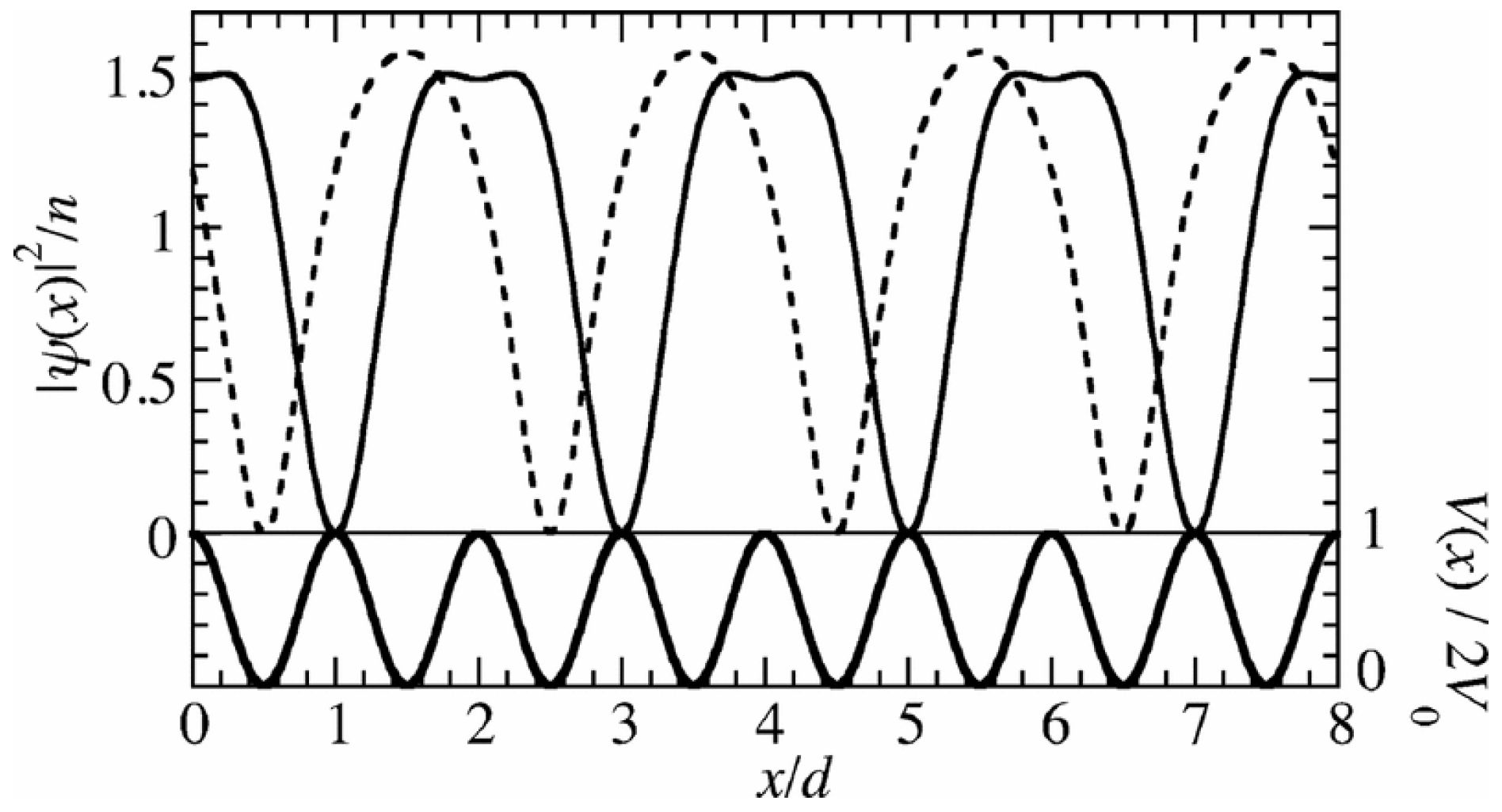
3.2. Swallowtail Loops Structures for Bosons in Optical Lattices
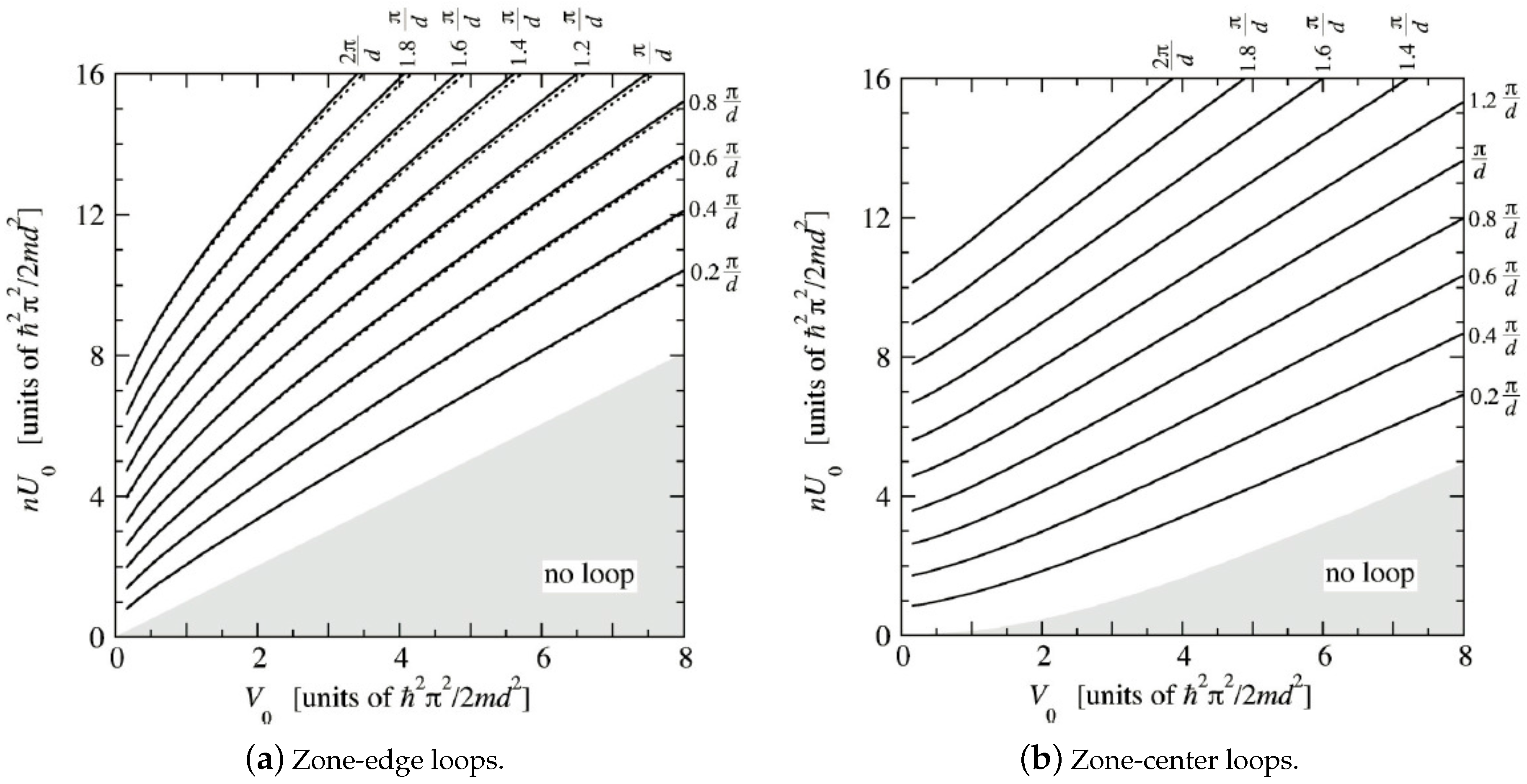
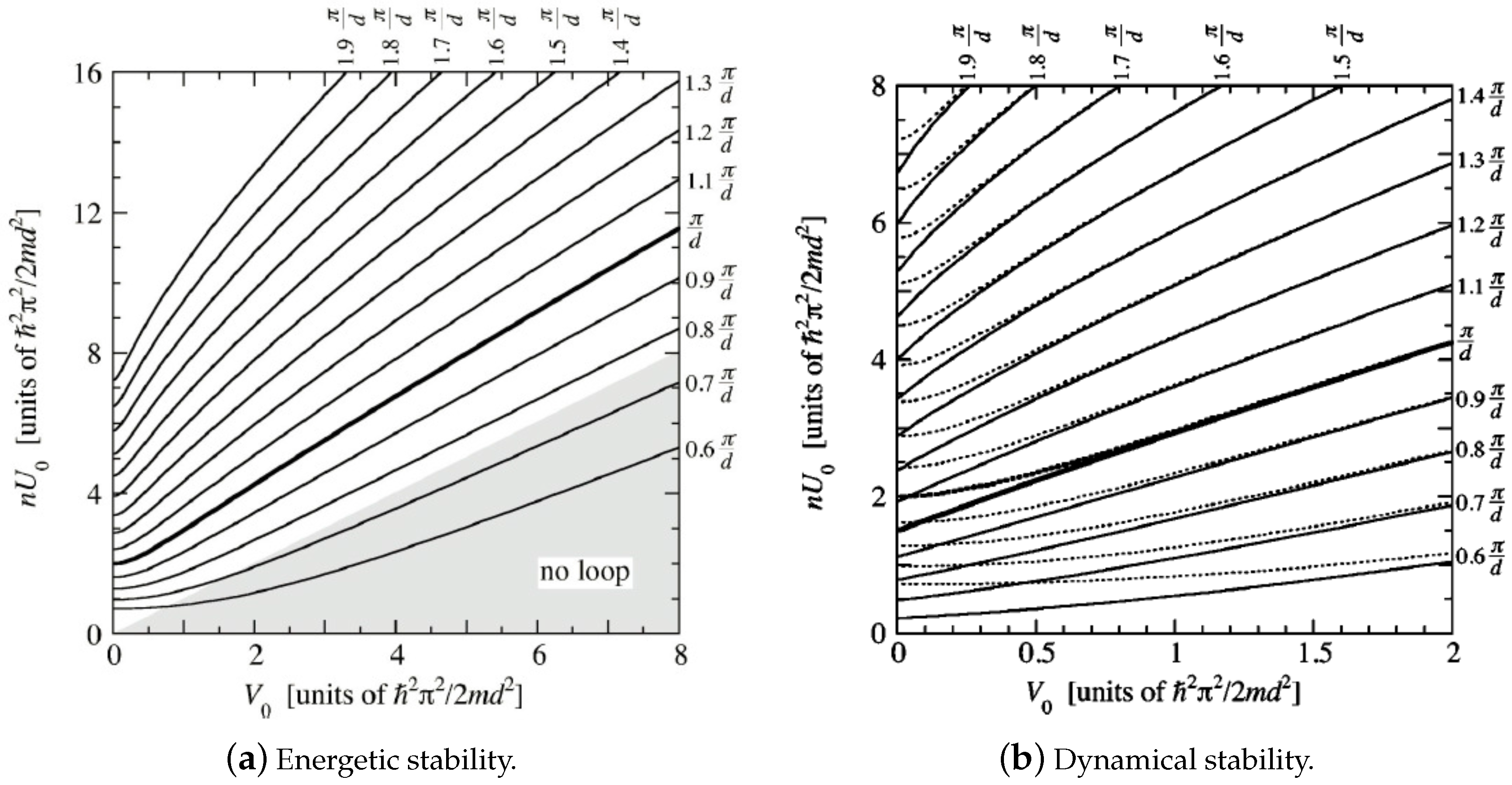
3.2.1. Occurrence of Loop Solutions
3.2.2. Stability of Loop Solutions
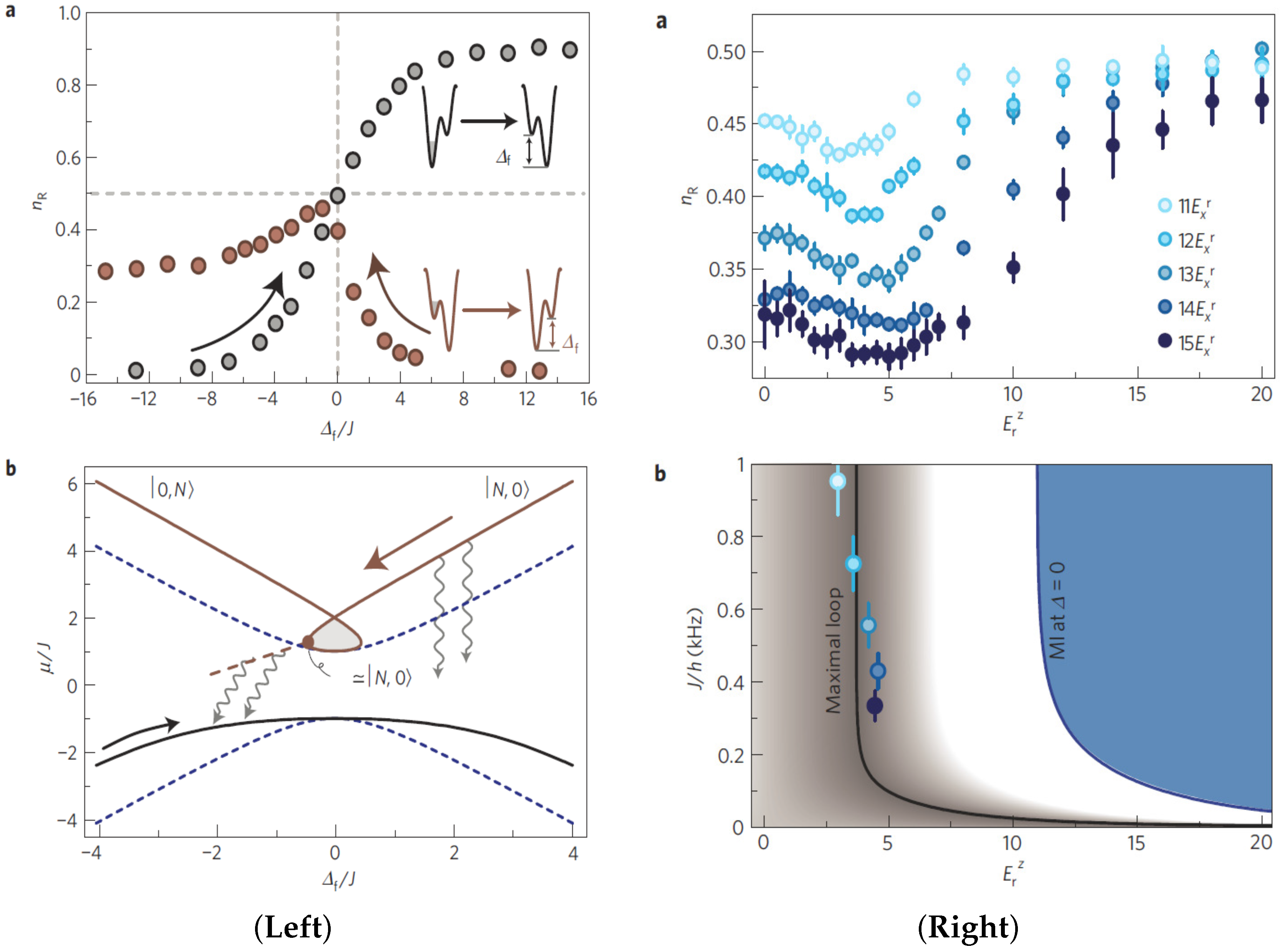
3.3. Experimental Realization
3.4. Other Extensions
3.5. Future Prospects
4. Multiple Period States in Cold Atomic Gases in Optical Lattices
4.1. Basic Physical Idea: A Simple Explanation of the Emergence of Multiple Period States by a Discrete Model
4.2. Multiple Period States in BECs
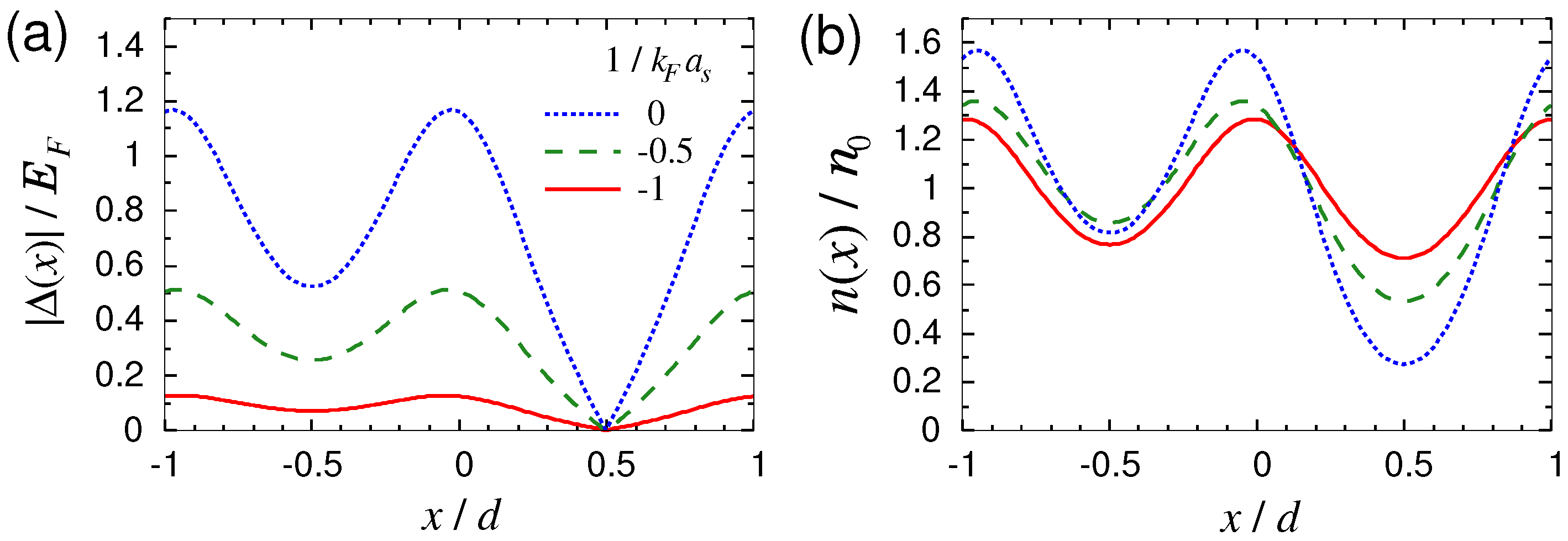
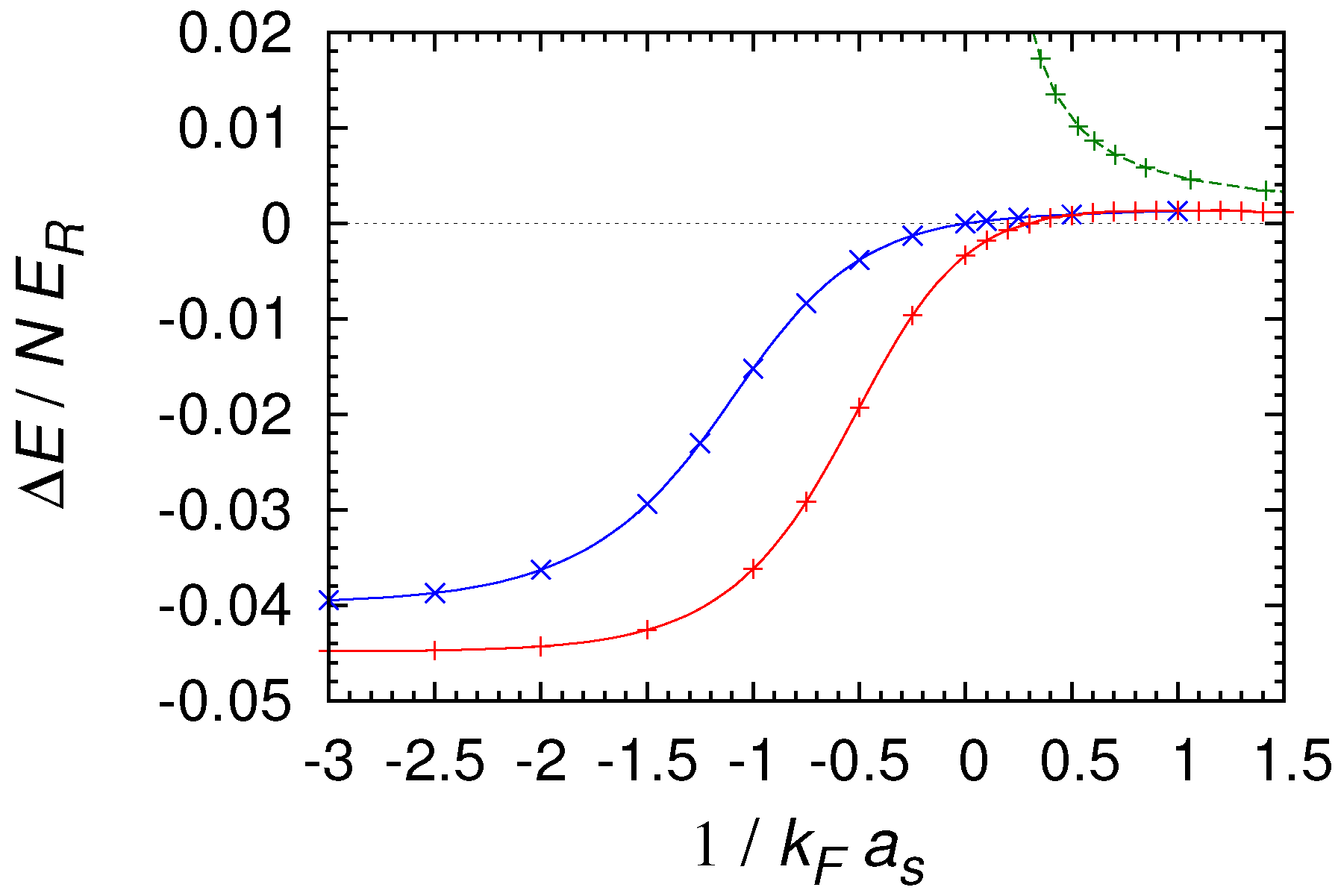
4.3. Multiple Period States in Superfluid Fermi Gases
5. Nonlinear Lattices
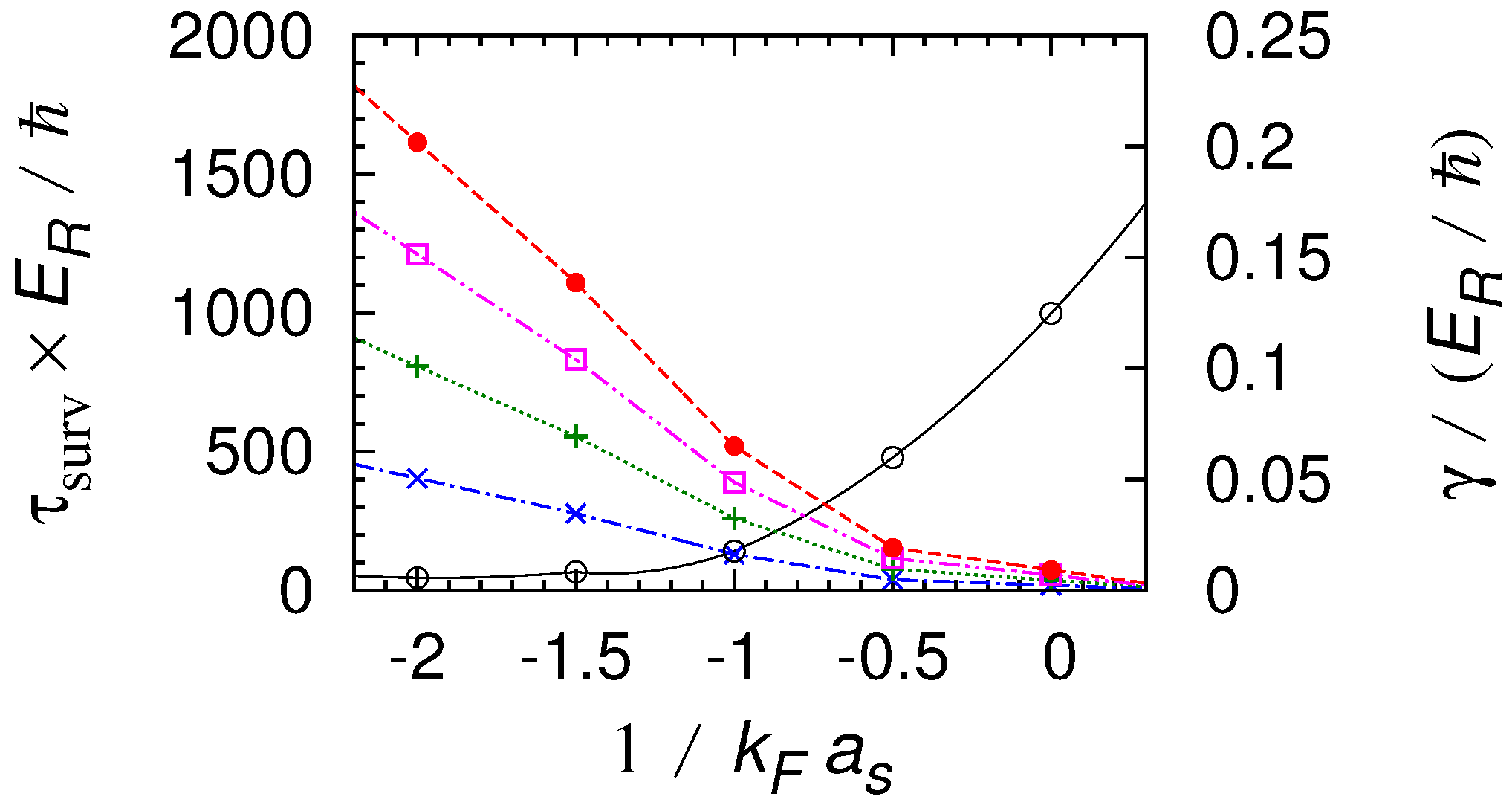
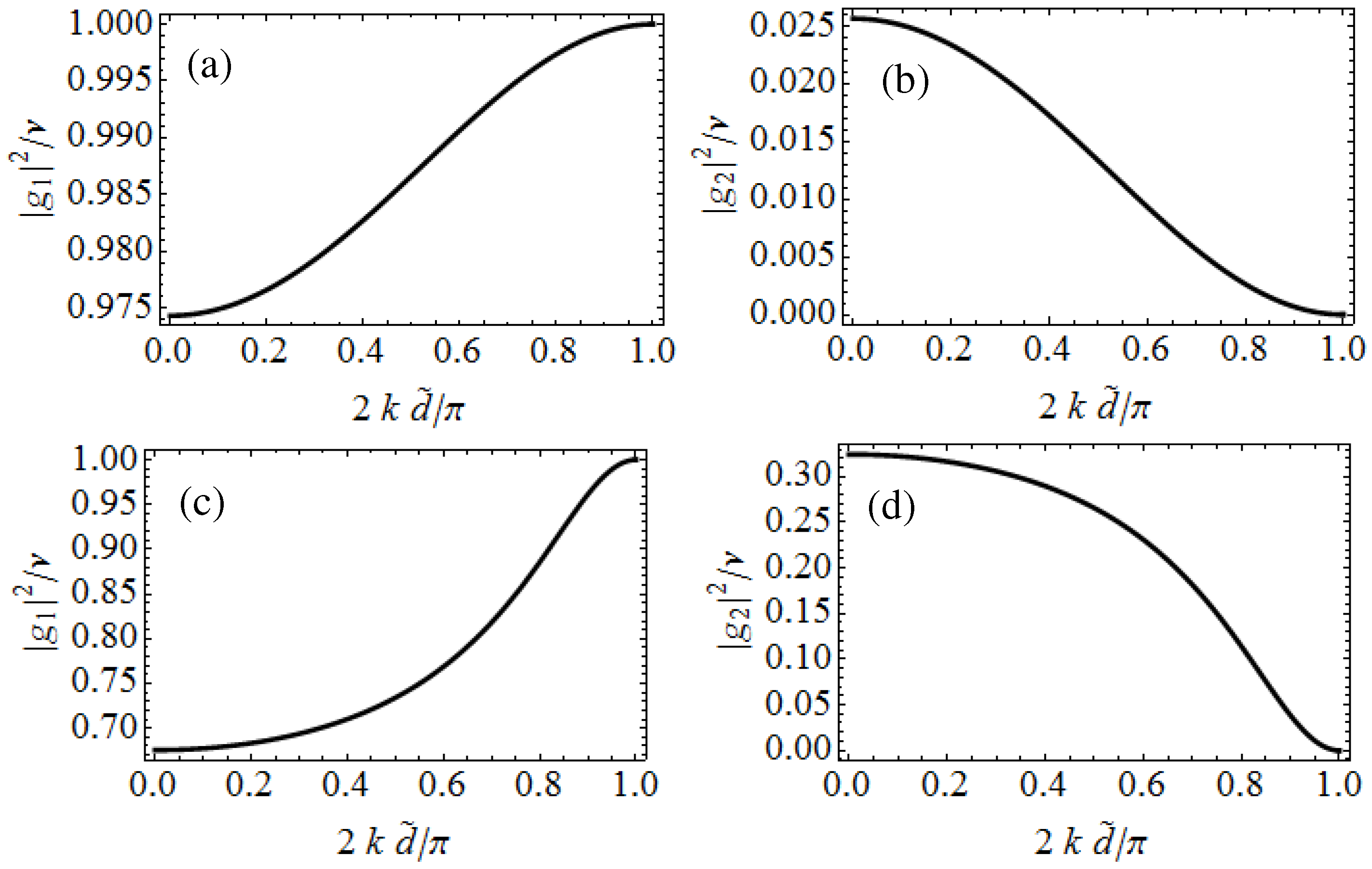
5.1. Dynamical Stability of the Superfluid: Special Properties of Nonlinear Lattices
5.2. Basic Physical Idea: The Dynamical Stability of Nonlinear Lattices
5.3. Superfluid Cold Atomic Gases in Nonlinear Lattices
5.4. Experimental Setup
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Pethick, C.J.; Smith, H. Bose–Einstein Condensation in Dilute Gases, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Pitaevskii, L.P.; Stringari, S. Bose–Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Leggett, A.J. Bose–Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307–356. [Google Scholar]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark solitons in Bose–Einstein condensates. Phys. Rev. Lett. 1999, 83, 5198–5201. [Google Scholar] [CrossRef]
- Denschlag, J.; Simsarian, J.E.; Feder, D.L.; Clark, C.W.; Collins, L.A.; Cubizolles, J.; Deng, L.; Hagley, E.W.; Helmerson, K.; Reinhardt, W.P.; et al. Generating solitons by phase engineering of a Bose–Einstein condensate. Science 2000, 287, 97–101. [Google Scholar] [CrossRef] [PubMed]
- Strecker, K.E.; Partridge, G.B.; Truscott, A.G.; Hulet, R.G. Formation and propagation of matter-wave soliton trains. Nature 2002, 417, 150–153. [Google Scholar] [CrossRef] [PubMed]
- Khaykovich, L.; Schreck, F.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Carr, L.D.; Castin, Y.; Salomon, C. Formation of a matter-wave bright soliton. Science 2002, 296, 1290–1293. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Hagley, E.W.; Wen, J.; Trippenbach, M.; Band, Y.; Julienne, P.S.; Simsarian, J.E.; Helmerson, K.; Rolston, S.L.; Phillips, W.D. Four-wave mixing with matter waves. Nature 1999, 398, 218–220. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-González, R. (Eds.) Emergent Nonlinear Phenomena in Bose–Einstein Condensates: Theory and Experiment; Springer: Berlin/Heidelberg, Germany, 2008.
- Zwierlein, M.W.; Abo-Shaeer, J.R.; Schirotzek, A.; Schunck, C.H.; Ketterle, W. Vortices and superfluidity in a strongly interacting Fermi gas. Nature 2005, 435, 1047–1051. [Google Scholar] [CrossRef] [PubMed]
- Eagles, D.M. Possible pairing without superconductivity at low carrier concentrations in bulk and thin-film superconducting semiconductors. Phys. Rev. 1969, 186, 456–463. [Google Scholar] [CrossRef]
- Leggett, A.J. Diatomic Molecules and Cooper Pairs. In Modern Trends in the Theory of Condensed Matter; Pekalski, A., Przystawa, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1980; Volume 115, pp. 13–27. [Google Scholar]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215–1274. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef]
- Morsch, O.; Oberthaler, M. Dynamics of Bose–Einstein condensates in optical lattices. Rev. Mod. Phys. 2006, 78, 179–215. [Google Scholar] [CrossRef]
- Yukalov, V.I. Cold bosons in optical lattices. Laser Phys. 2009, 19, 1–110. [Google Scholar] [CrossRef]
- Watanabe, G.; Yoon, S. Aspects of superfluid cold atomic gases in optical lattices. J. Korean Phys. Soc. 2013, 63, 839–857. [Google Scholar] [CrossRef]
- Wu, B.; Diener, R.B.; Niu, Q. Bloch waves and bloch bands of Bose–Einstein condensates in optical lattices. Phys. Rev. A 2002, 65, 025601. [Google Scholar] [CrossRef]
- Diakonov, D.; Jensen, L.M.; Pethick, C.J.; Smith, H. Loop structure of the lowest Bloch band for a Bose–Einstein condensate. Phys. Rev. A 2002, 66, 013604. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Torner, L. Solitons in nonlinear lattices. Rev. Mod. Phys. 2011, 83, 247–305. [Google Scholar] [CrossRef]
- Watanabe, G.; Maruyama, T. Nuclear pasta in supernovae and neutron stars. 2012; arXiv:1109.3511. [Google Scholar]
- Maruyama, T.; Watanabe, G.; Chiba, S. Molecular dynamics for dense matter. Prog. Theor. Exp. Phys. 2012, 2012, 01A201. [Google Scholar] [CrossRef]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose–Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463–512. [Google Scholar] [CrossRef]
- Pitaevskii, L.P. Vortex lines in an imperfect Bose gas. Sov. Phys. JETP 1961, 13, 451–454. [Google Scholar]
- Gross, E.P. Structure of a quantized vortex in boson systems. Nuovo Cimento 1961, 20, 454–477. [Google Scholar] [CrossRef]
- Gross, E.P. Hydrodynamics of a superfluid condensate. J. Math. Phys. 1963, 4, 195–207. [Google Scholar] [CrossRef]
- De Gennes, P.G. Superconductivity of Metals and Alloys; Benjamin: New York, NY, USA, 1966. [Google Scholar]
- Randeria, M. Crossover from BCS Theory to Bose–Einstein Condensation. In Bose Einstein Condensation; Griffin, A., Snoke, D., Stringari, S., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 355–392. [Google Scholar]
- Trombettoni, A.; Smerzi, A. Discrete solitons and breathers with dilute Bose–Einstein condensates. Phys. Rev. Lett. 2001, 86. [Google Scholar] [CrossRef] [PubMed]
- Kevrekidis, P.G. The Discrete Nonlinear Schrödinger Equation; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Wu, B.; Niu, Q. Landau and dynamical instabilities of the superflow of Bose–Einstein condensates in optical lattices. Phys. Rev. A 2001, 64, 061603(R). [Google Scholar] [CrossRef]
- Machholm, M.; Pethick, C.J.; Smith, H. Band structure, elementary excitations, and stability of a Bose–Einstein condensate in a periodic potential. Phys. Rev. A 2003, 67, 053613. [Google Scholar] [CrossRef]
- Machholm, M.; Nicolin, A.; Pethick, C.J.; Smith, H. Spatial period doubling in Bose–Einstein condensates in an optical lattice. Phys. Rev. A 2004, 69, 043604. [Google Scholar] [CrossRef]
- Wu, B.; Niu, Q. Nonlinear Landau–Zener tunneling. Phys. Rev. A 2000, 61, 023402. [Google Scholar] [CrossRef]
- Mueller, E.J. Superfluidity and mean-field energy loops: Hysteretic behavior in Bose–Einstein condensates. Phys. Rev. A 2002, 66, 063603. [Google Scholar] [CrossRef]
- Landau, L.D. Zur Theorie der Energieubertragung. II. Physikalische Zeitschrift der Sowjetunion 1932, 2, 46–51. (In German) [Google Scholar]
- Zener, C. Non-Adiabatic Crossing of Energy Levels. Proc. R. Soc. Lond. A 1932, 137, 696–702. [Google Scholar] [CrossRef]
- Bronski, J.C.; Carr, L.D.; Deconinck, B.; Kutz, J.N. Bose–Einstein condensates in standing wave: The cubic nonlinear Schrödinger equation with a periodic potential. Phys. Rev. Lett. 2001, 86, 1402–1405. [Google Scholar] [CrossRef] [PubMed]
- Eckel, S.; Lee, J.G.; Jendrzejewski, F.; Murray, N.; Clark, C.W.; Lobb, C.J.; Phillips, W.D.; Edwards, M.; Campbell, G.K. Hysteresis in a quantized superfluid ‘atomtronic’ circuit. Nature 2014, 506, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Thom, R. Structural Stability and Morphogenesis: An Outline of a General Theory of Models; W.A. Benjamin: Reading, MA, USA, 1975. [Google Scholar]
- Seaman, B.T.; Carr, L.D.; Holland, M.J. Nonlinear band structure in Bose–Einstein condensates: Nonlinear Schrödinger equation with a Kronig–Penney potential. Phys. Rev. A 2005, 71, 033622. [Google Scholar] [CrossRef]
- Dong, X.; Wu, B. Instabilities and sound speed of a Bose–Einstein condensate in the Kronig–Penney potential. Laser Phys. 2007, 17, 190–197. [Google Scholar] [CrossRef]
- Wu, B.; Niu, Q. Superfluidity of Bose–Einstein condensate in an optical lattice: Landau–Zener tunnelling and dynamical instability. New J. Phys. 2003, 5, 104. [Google Scholar] [CrossRef]
- Burger, S.; Cataliotti, F.S.; Fort, C.; Minardi, F.; Inguscio, M.; Chiofalo, M.L.; Tosi, M.P. Superfluid and dissipative dynamics of a Bose-Einstein condensate in a periodic optical potential. Phys. Rev. Lett. 2001, 86, 4447–4450. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Niu, Q. Dynamical or Landau instability? Phys. Rev. Lett. 2002, 89, 088901. [Google Scholar] [CrossRef] [PubMed]
- Burger, S.; Cataliotti, F.S.; Fort, C.; Minardi, F.; Inguscio, M.; Chiofalo, M.L.; Tosi, M.P. Burger et al. Reply. Phys. Rev. Lett. 2002, 89, 088902. [Google Scholar]
- Mamaladze, Y.G.; Cheĭshvili, O.D. Flow of a superfluid liquid in porous media. Sov. Phys. JETP 1966, 23, 112–117. [Google Scholar]
- Hakim, V. Nonlinear Schrödinger flow past an obstacle in one dimension. Phys. Rev. E 1997, 55, 2835–2845. [Google Scholar] [CrossRef]
- Watanabe, G.; Dalfovo, F.; Piazza, F.; Pitaevskii, L.P.; Stringari, S. Critical velocity of superfluid flow through single-barrier and periodic potentials. Phys. Rev. A 2009, 80, 053602. [Google Scholar] [CrossRef]
- Danshita, I.; Tsuchiya, S. Comment on “Nonlinear band structure in Bose–Einstein condensates: Nonlinear Schrödinger equation with a Kronig–Penney potential”. Phys. Rev. A 2007, 75, 033612. [Google Scholar] [CrossRef]
- Seaman, B.T.; Carr, L.D.; Holland, M.J. Reply to “Comment on ‘Nonlinear band structure in Bose–Einstein condensates: Nonlinear Schrödinger equation with a Kronig–Penney potential’”. Phys. Rev. A 2007, 76, 017602. [Google Scholar] [CrossRef]
- Barontini, G.; Modugno, M. Dynamical instability and dispersion management of an attractive condensate in an optical lattice. Phys. Rev. A 2007, 76, 041601(R). [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, B. Superfluidity of BEC in ultracold atomic gases. Chin. Phys. B 2015, 24, 050507. [Google Scholar] [CrossRef]
- Modugno, M.; Tozzo, C.; Dalfovo, F. Role of transverse excitations in the instability of Bose–Einstein condensates moving in optical lattices. Phys. Rev. A 2004, 70, 043625. [Google Scholar] [CrossRef]
- Fallani, L.; de Sarlo, L.; Lye, J.E.; Modugno, M.; Saers, R.; Fort, C.; Inguscio, M. Observation of Dynamical Instability for a Bose–Einstein Condensate in a Moving 1D Optical Lattice. Phys. Rev. Lett. 2004, 93, 140406. [Google Scholar] [CrossRef] [PubMed]
- De Sarlo, L.; Fallani, L.; Lye, J.E.; Modugno, M.; Saers, R.; Fort, C.; Inguscio, M. Unstable regimes for a Bose–Einstein condensate in an optical lattice. Phys. Rev. A 2005, 72, 013603. [Google Scholar] [CrossRef]
- Cataliotti, F.S.; Fallani, L.; Ferlaino, F.; Fort, C.; Maddaloni, P. Superfluid current disruption in a chain of weakly coupled Bose–Einstein condensates. New J. Phys. 2003, 5, 71. [Google Scholar] [CrossRef]
- Smerzi, A.; Trombettoni, A.; Kevrekidis, P.G.; and Bishop, A.R. Dynamical Superfluid-Insulator Transition in a Chain of Weakly Coupled Bose–Einstein Condensates. Phys. Rev. Lett. 2002, 89, 170402. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.K. Expansion of a Bose–Einstein condensate formed on a joint harmonic and one-dimensional optical-lattice potential. J. Phys. B 2003, 36, 3951–3959. [Google Scholar] [CrossRef]
- Nesi, F.; Modugno, M. Loss and revival of phase coherence in a Bose–Einstein condensate moving through an optical lattice. J. Phys. B 2004, 37, S101–S113. [Google Scholar] [CrossRef]
- Mun, J.; Medley, P.; Campbell, G.K.; Marcassa, L.G.; Pritchard, D.E.; Ketterle, W. Phase Diagram for a Bose–Einstein Condensate Moving in an Optical Lattice. Phys. Rev. Lett. 2007, 99, 150604. [Google Scholar] [CrossRef] [PubMed]
- Ferris, A.J.; Davis, M.J.; Geursen, R.W.; Blakie, P.B.; Wilson, A.C. Dynamical instabilities of Bose–Einstein condensates at the band edge in one-dimensional optical lattices. Phys. Rev. A 2008, 77, 012712. [Google Scholar] [CrossRef]
- Hamner, C.; Zhang, Y.; Khamehchi, M.A.; Davis, M.J.; Engels, P. Spin-Orbit-Coupled Bose–Einstein Condensates in a One-Dimensional Optical Lattice. Phys. Rev. Lett 2015, 114, 070401. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-A.; Huber, S.D.; Trotzky, S.; Bloch, I.; Altman, E. Many-body Landau–Zener dynamics in coupled one-dimensional Bose liquids. Nat. Phys. 2011, 7, 61–67. [Google Scholar]
- Baharian, S.; Baym, G. Bose–Einstein condensates in toroidal traps: Instabilities, swallowtail loops, and self-trapping. Phys. Rev. A 2013, 87, 013619. [Google Scholar] [CrossRef]
- Wright, K.C.; Blakestead, R.B.; Lobb, C.J.; Phillips, W.D.; Campbell, G.K. Driving phase slips in a superfluid atom circuit with a rotating weak link. Phys. Rev. Lett. 2013, 110, 025302. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.Y.; Lee, R.-K.; Kao, Y.-M.; Jiang, T.-F. Band structures of a dipolar Bose–Einstein condensate in one-dimensional lattices. Phys. Rev. A 2008, 78, 023629. [Google Scholar] [CrossRef]
- Venkatesh, B.P.; Larson, J.; O’Dell, D.H.J. Band-structure loops and multistability in cavity QED. Phys. Rev. A 2011, 83, 063606. [Google Scholar] [CrossRef]
- Watanabe, G.; Yoon, S.; Dalfovo, F. Swallowtail Band Structure of the Superfluid Fermi Gas in an Optical Lattice. Phys. Rev. Lett. 2011, 107, 270404. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wu, B. Bose–Einstein Condensate in a Honeycomb Optical Lattice: Fingerprint of Superfluidity at the Dirac Point. Phys. Rev. Lett. 2011, 107, 065301. [Google Scholar] [CrossRef] [PubMed]
- Hui, H.-Y.; Barnett, R.; Porto, J.V.; Sarma, S.D. Loop-structure stability of a double-well-lattice Bose–Einstein condensate. Phys. Rev. A 2012, 86, 063636. [Google Scholar] [CrossRef]
- Mumford, J.; Larson, J.; O’Dell, D.H.J. Impurity in a bosonic Josephson junction: Swallowtail loops, chaos, self-trapping, and Dicke model. Phys. Rev. A 2014, 89, 023620. [Google Scholar] [CrossRef]
- Haller, E.; Hart, R.; Mark, M.J.; Danzl, J.G.; Reichsöllner, L.; Nägerl, H.-C. Inducing Transport in a Dissipation-Free Lattice with Super Bloch Oscillations. Phys. Rev. Lett. 2010, 104, 200403. [Google Scholar] [CrossRef] [PubMed]
- Meinert, F.; Mark, M.J.; Kirilov, E.; Lauber, K.; Weinmann, P.; Gröbner, M.; Nägerl, H.-C. Interaction-induced quantum phase revivals and evidence for the transition to the quantum chaotic regime in 1D atomic Bloch oscillations. Phys. Rev. Lett. 2014, 112, 193003. [Google Scholar] [CrossRef] [PubMed]
- Karkuszewski, Z.P.; Sacha, K.; Smerzi, A. Mean field loops versus quantum anti-crossing nets in trapped Bose–Einstein condensates. Eur. Phys. J. D 2002, 21, 251–254. [Google Scholar] [CrossRef]
- Torrontegui, E.; Ibáñez, S.; Martínez-Garaot, S.; Modugno, M.; del Campo, A.; Guéry-Odelin, D.; Ruschhaupt, A.; Chen, X.; Muga, J.G. Shortcuts to adiabaticity. Adv. At. Mol. Opt. Phys. 2013, 62, 117–169. [Google Scholar]
- Li, W.; Smerzi, A. Nonlinear Kronig–Penney model. Phys. Rev. E 2004, 70, 016605. [Google Scholar] [CrossRef] [PubMed]
- Seaman, B.T.; Carr, L.D.; Holland, M.J. Period doubling, two-color lattices, and the growth of swallowtails in Bose–Einstein condensates. Phys. Rev. A 2005, 72, 033602. [Google Scholar] [CrossRef]
- Gemelke, N.; Sarajlic, E.; Bidel, Y.; Hong, S.; Chu, S. Parametric Amplification of Matter Waves in Periodically Translated Optical Lattices. Phys. Rev. Lett. 2005, 95, 170404. [Google Scholar] [CrossRef] [PubMed]
- Maluckov, A.; Gligorić, G.; Hadžievski, L. Long-lived double periodic patterns in dipolar cigar-shaped Bose–Einstein condensates in an optical lattice. Physica Scripta 2012, T149, 014004. [Google Scholar] [CrossRef]
- Maluckov, A.; Gligorić, G.; Hadžievski, L.; Malomed, B.A.; Pfau, T. Stable Periodic Density Waves in Dipolar Bose–Einstein Condensates Trapped in Optical Lattices. Phys. Rev. Lett. 2012, 108, 140402. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.; Dalfovo, F.; Nakatsukasa, T.; Watanabe, G. Multiple period states of the superfluid Fermi gas in an optical lattice. New J. Phys. 2015, 18, 023011. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Miller, D.E.; Chin, J.K.; Stan, C.A.; Liu, Y.; Setiawan, W.; Sanner, C.; Ketterle, W. Critical Velocity for Superfluid Flow across the BEC-BCS Crossover. Phys. Rev. Lett. 2007, 99, 070402. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.L.; Zhou, Z.W.; Wu, B. Superfluidity and stability of a Bose–Einstein condensate with periodically modulated interatomic interaction. Phys. Rev. A 2013, 87, 013633. [Google Scholar] [CrossRef]
- Dasgupta, R.; Venkatesh, B.P.; Watanabe, G. Attraction-induced dynamical stability of a Bose–Einstein condensate in a nonlinear lattice. 2016; arXiv:1603.07486. [Google Scholar]
- Sakaguchi, H.; Malomed, B.A. Matter-wave solitons in nonlinear optical lattices. Phys. Rev. A 2005, 72, 046610. [Google Scholar] [CrossRef] [PubMed]
- Abdullaev, F.; Abdumalikov, A.; Galimzyanov, R. Gap solitons in Bose–Einstein condensates in linear and nonlinear optical lattices. Phys. Lett. A 2007, 367, 149–155. [Google Scholar] [CrossRef]
- Yu, D.; Yi, W.; Zhang, W. Swallowtail Structure in Fermi Superfluids with Periodically Modulated Interactions. Phys. Rev. A 2015, 92, 033623. [Google Scholar] [CrossRef]
- Fatemi, F.K.; Jones, K.M.; Lett, P.D. Observation of optically induced Feshbach resonances in collisions of cold atoms. Phys. Rev. Lett. 2000, 85, 4462–4465. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225–1286. [Google Scholar] [CrossRef]
- Fedichev, P.O.; Kagan, Y.; Shlyapnikov, G.V.; Walraven, J.T.M. Influence of nearly resonant light on the scattering length in low-temperature atomic gases. Phys. Rev. Lett. 1996, 77, 2913–2916. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, R.; Taie, S.; Sugawa, S.; Takahashi, Y. Submicron spatial modulation of an interatomic interaction in a Bose–Einstein condensate. Phys. Rev. Lett. 2010, 105, 050405. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Sanpera, A.; Ahufinger, V. Ultracold Atoms in Optical Lattices: Simulating Quantum Many-Body Systems; Oxford University Press: Oxford, UK, 2012. [Google Scholar]






© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, G.; Venkatesh, B.P.; Dasgupta, R. Nonlinear Phenomena of Ultracold Atomic Gases in Optical Lattices: Emergence of Novel Features in Extended States. Entropy 2016, 18, 118. https://doi.org/10.3390/e18040118
Watanabe G, Venkatesh BP, Dasgupta R. Nonlinear Phenomena of Ultracold Atomic Gases in Optical Lattices: Emergence of Novel Features in Extended States. Entropy. 2016; 18(4):118. https://doi.org/10.3390/e18040118
Chicago/Turabian StyleWatanabe, Gentaro, B. Prasanna Venkatesh, and Raka Dasgupta. 2016. "Nonlinear Phenomena of Ultracold Atomic Gases in Optical Lattices: Emergence of Novel Features in Extended States" Entropy 18, no. 4: 118. https://doi.org/10.3390/e18040118