Self-Replicating Spots in the Brusselator Model and Extreme Events in the One-Dimensional Case with Delay
Abstract
:1. Introduction
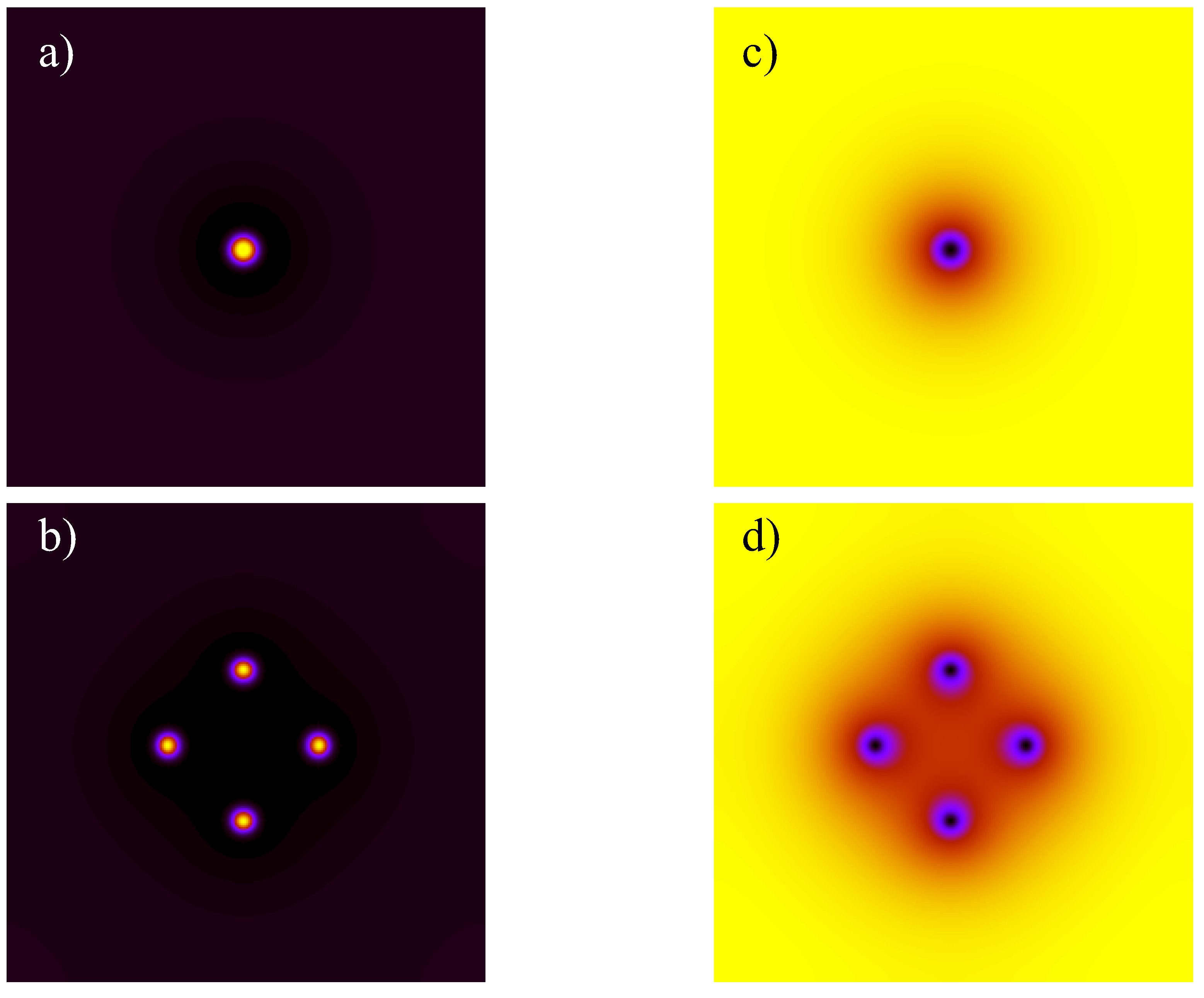
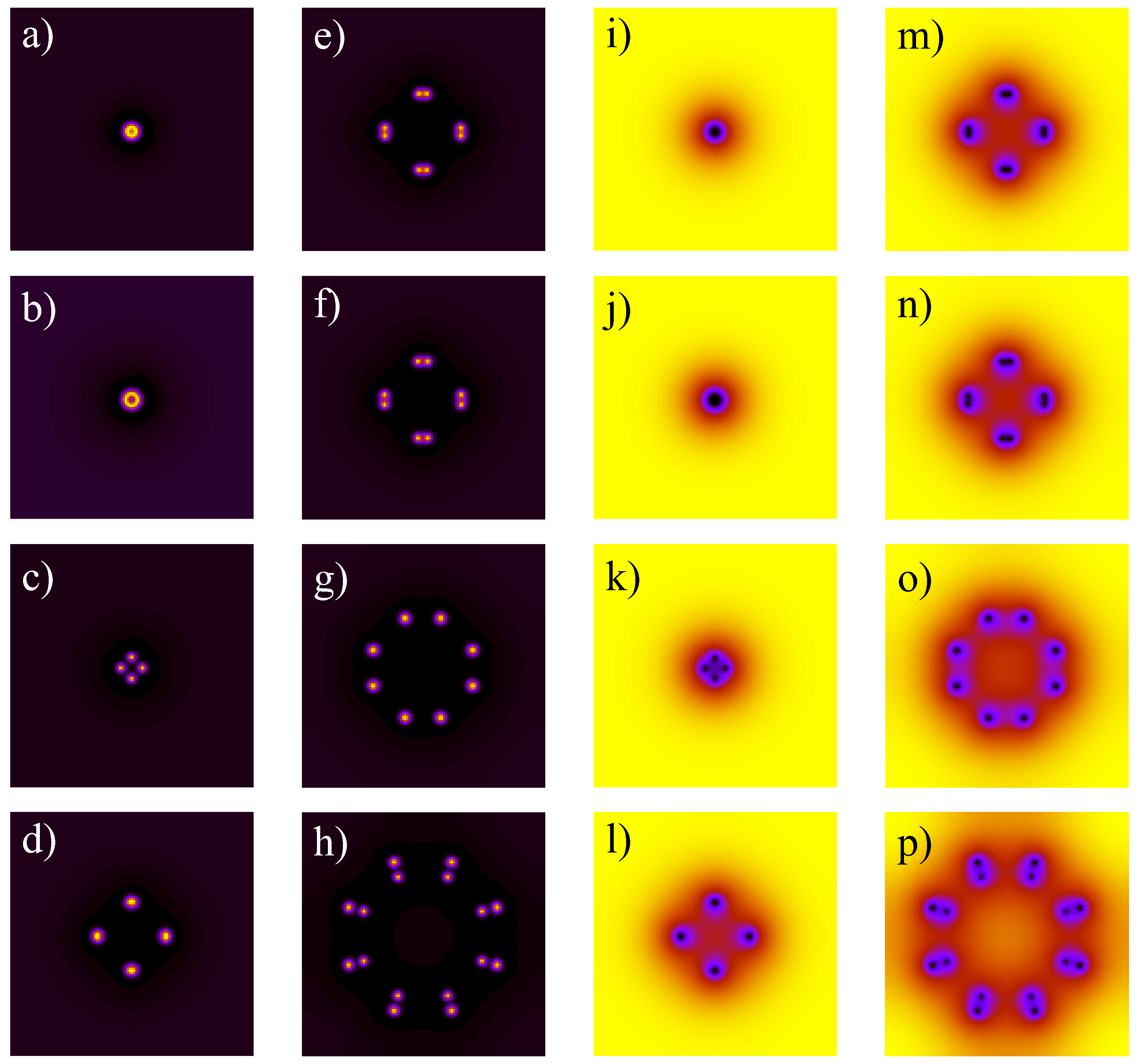
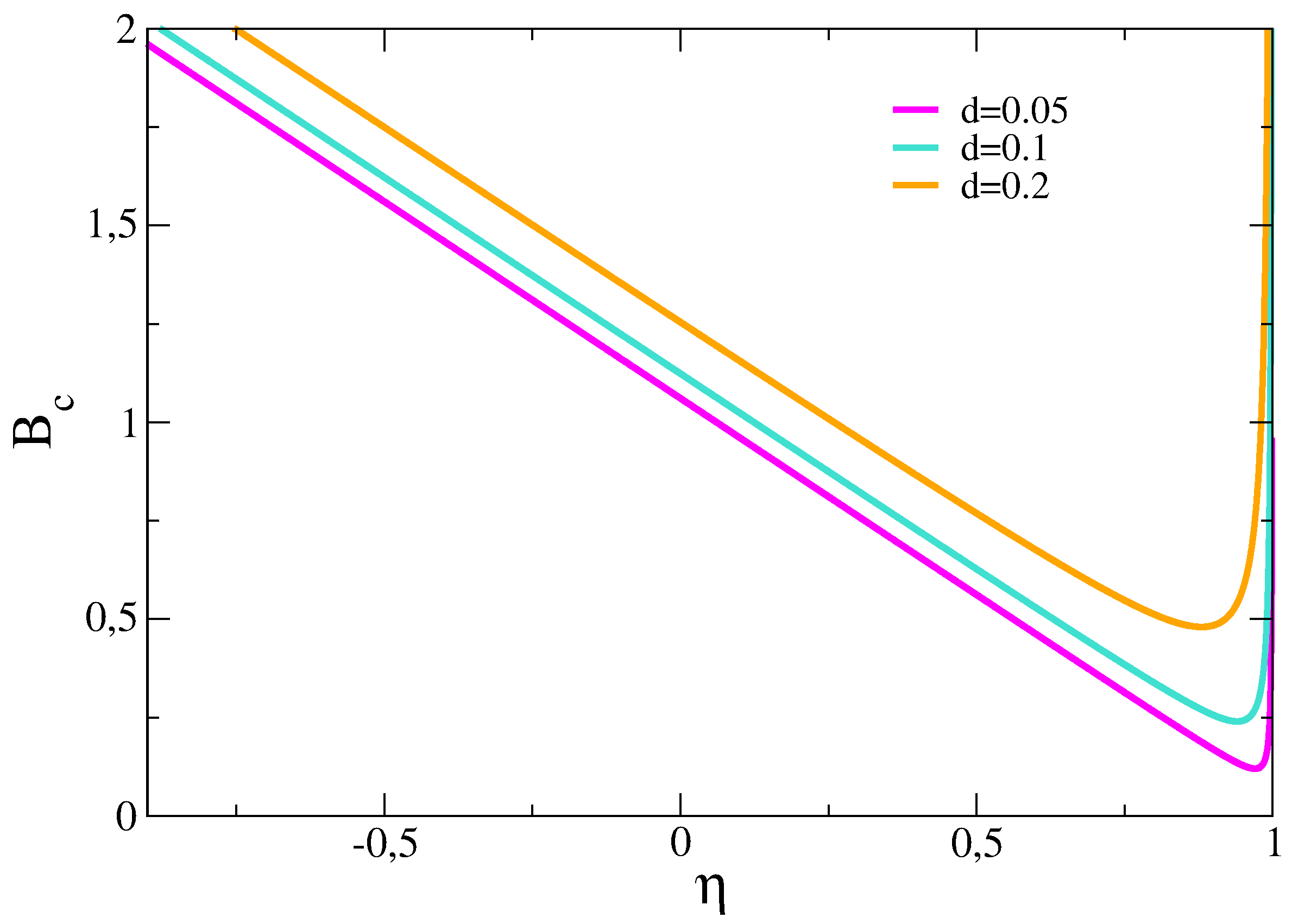
2. Reaction-Diffusion Model and Spot Replication
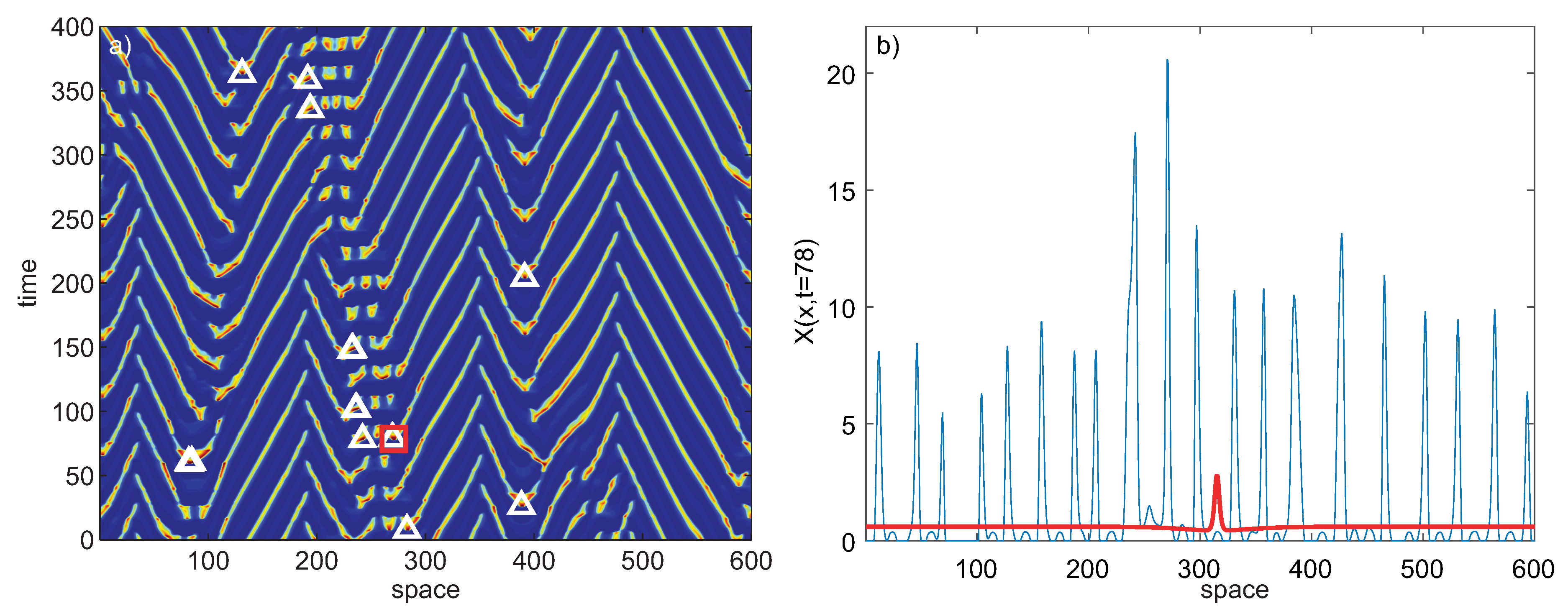
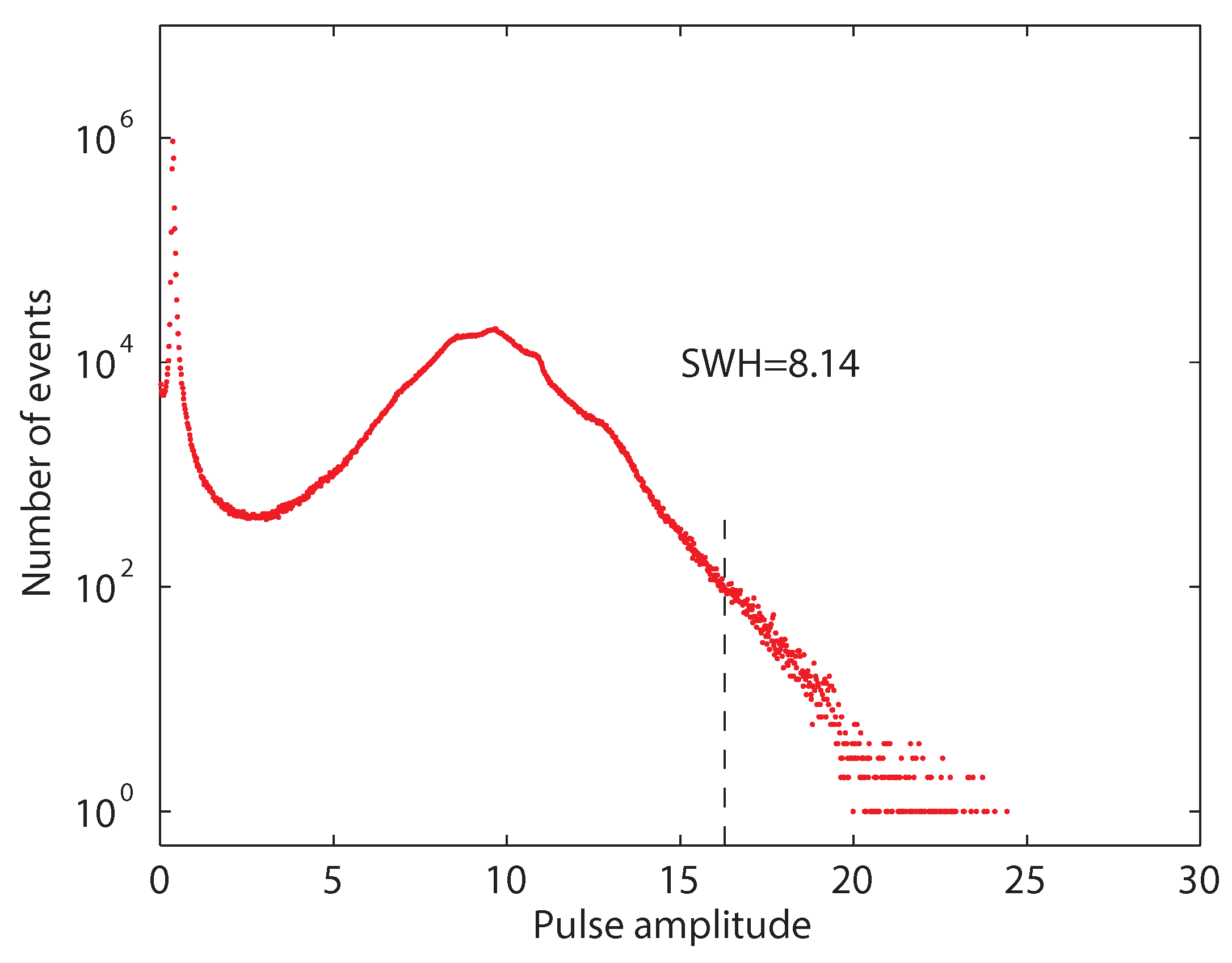
3. Extreme Events Induced by Delayed Feedback
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Prigogine, I.; Lefever, R. Symmetry breaking instabilities in dissipative systems. II. J. Chem. Phys. 1968, 48, 1695–1700. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley: Hoboken, NJ, USA, 1971. [Google Scholar]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Castets, V.; Dulos, E.; Boissonade, J.; de Kepper, P. Experimental evidence of a sustained standing Turing-type nonequilibrium chemical pattern. Phys. Rev. Lett. 1990, 64, 2953–2956. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, Q.; Swinney, H.L. Transition from a uniform state to hexagonal and striped Turing patterns. Nature 1991, 352, 610–612. [Google Scholar] [CrossRef]
- Belousov, B.P. A periodic reaction and its mechanism. Compil. Abstr. Radiat. Med. 1959, 147, 1. [Google Scholar]
- Zaikin, A.N.; Zhabotinsky, A.M. Concentration wave propagation in two-dimensional liquid-phase self-oscillating system. Nature 1970, 225, 535–537. [Google Scholar] [CrossRef] [PubMed]
- Koga, S.; Kuramoto, Y. Localized patterns in reaction-diffusion systems. Prog. Theor. Phys. 1980, 63, 106–121. [Google Scholar] [CrossRef]
- Pomeau, Y. Front motion, metastability and subcritical bifurcations in hydrodynamics. Physica D 1986, 23, 3–11. [Google Scholar] [CrossRef]
- Rosanov, N.N.; Khodova, G.V. Autosolitons in bistable interferometers. Opt. Spectrosc. 1988, 65, 449–450. [Google Scholar]
- Thual, O.; Fauve, S. Localized structures generated by subcritical instabilities. J. Phys. Fr. 1988, 49, 1829–1833. [Google Scholar] [CrossRef]
- Malomed, B.A.; Nepomnyashchy, A.A. Kinks and solitons in the generalized Ginzburg–Landau equation. Phys. Rev. A 1990, 42, 6009–6014. [Google Scholar] [CrossRef] [PubMed]
- Tlidi, M.; Mandel, P.; Lefever, R. Localized structures and localized patterns in optical bistability. Phys. Rev. Lett. 1994, 73, 640–643. [Google Scholar] [CrossRef] [PubMed]
- Scroggie, A.J.; Firth, W.J.; McDonald, G.S.; Tlidi, M.; Lefever, R.; Lugiato, L.A. Pattern formation in a passive Kerr cavity. Chaos Solitons Fractals 1994, 4, 1323–1354. [Google Scholar] [CrossRef]
- Tlidi, M.; Lefever, R.; Vladimirov, A. On Vegetation Clustering, Localized Bare Soil Spots and Fairy Circles. In Dissipative Solitons: From Optics to Biology and Medicine; Springer: Berlin/Heidelberg, Germany, 2008; p. 751. [Google Scholar]
- Vladimirov, A.G.; Lefever, R.; Tlidi, M. Relative stability of multipeak localized patterns of cavity solitons. Phys. Rev. A 2011, 84, 043848. [Google Scholar] [CrossRef]
- Dissipative Solitons: from Optics to Biology and Medicine; Akhmediev, N.; Ankiewicz, A. (Eds.) Springer: Berlin/Heidelberg, Germany, 2008; Volume 751.
- Leblond, H.; Mihalache, D. Models of few optical cycle solitons beyond the slowly varying envelope approximation. Phys. Rep. 2013, 523, 61–126. [Google Scholar] [CrossRef] [Green Version]
- Tlidi, M.; Staliunas, K.; Panajotov, K.; Vladimirov, A.G.; Clerc, M.G. Localized structures in dissipative media: from optics to plant ecology. Philos. Trans. R. Soc. Lond. A 2014, 372, 20140101. [Google Scholar] [CrossRef] [PubMed]
- Lugiato, L.; Prati, F.; Brambilla, M. Nonlinear Optical Systems; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Pearson, J.E. Complex patterns in a simple system. Science 1993, 261, 189–192. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.J.; McCormick, W.D.; Pearson, J.E.; Swinney, H.L. Experimental observation of self-replicating spots in a reaction-diffusion system. Nature 1994, 369, 215–218. [Google Scholar] [CrossRef]
- Muñuzuri, A.P.; Pérez-Villar, V.; Markus, M. Splitting of Autowaves in an Active Medium. Phys. Rev. Lett. 1997, 79, 1941–1944. [Google Scholar] [CrossRef]
- Kaminaga, A.; Vanag, V.K.; Epstein, I.R. A reaction–diffusion memory device. Angew. Chem. Int. Ed. 2006, 45, 3087–3089. [Google Scholar] [CrossRef] [PubMed]
- Kaminaga, A.; Vanag, V.K.; Epstein, I.R. “Black spots” in a surfactant-rich Belousov–Zhabotinsky reaction dispersed in a water-in-oil microemulsion system. J. Chem. Phys. 2005, 122, 174706. [Google Scholar] [CrossRef] [PubMed]
- Kolokolnikov, T.; Tlidi, M. Spot deformation and replication in the two-dimensional Belousov–Zhabotinski reaction in a water-in-oil microemulsion. Phys. Rev. Lett. 2007, 98, 188303. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.W.; Blanchedeau, P.; Dulos, E.; Kepper, P.D. Dividing Blobs, Chemical Flowers, and Patterned Islands in a Reaction–Diffusion System. J. Phys. Chem. A 1998, 102, 8236–8244. [Google Scholar] [CrossRef]
- Meron, E.; Gilad, E.; von Hardenberg, J.; Shachak, M.; Zarmi, Y. Vegetation patterns along a rainfall gradient. Chaos Solitons Fractals 2004, 19, 367–376. [Google Scholar] [CrossRef]
- Ren, X.; Wei, J. On the spectra of three-dimensional lamellar solutions of the diblock copolymer problem. SIAM J. Math. Anal. 2003, 35, 1–32. [Google Scholar] [CrossRef]
- Nishiura, Y.; Suzuki, H. Higher Dimensional SLEP Equation and Applications to Morphological Stability in Polymer Problems. SIAM J. Math. Anal. 2005, 36, 916–966. [Google Scholar] [CrossRef]
- Tlidi, M.; Vladimirov, A.G.; Mandel, P. Curvature Instability in Passive Diffractive Resonators. Phys. Rev. Lett. 2002, 89, 233901. [Google Scholar] [CrossRef] [PubMed]
- Muratov, C.B.; Osipov, V.V. General theory of instabilities for patterns with sharp interfaces in reaction-diffusion systems. Phys. Rev. E 1996, 53, 3101–3116. [Google Scholar] [CrossRef]
- Hayase, Y.; Ohta, T. Sierpinski Gasket in a Reaction-Diffusion System. Phys. Rev. Lett. 1998, 81, 1726–1729. [Google Scholar] [CrossRef]
- Hayase, Y.; Ohta, T. Self-replicating pulses and Sierpinski gaskets in excitable media. Phys. Rev. E 2000, 62, 5998–6003. [Google Scholar] [CrossRef]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054–1057. [Google Scholar] [CrossRef] [PubMed]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.P.; Akhmediev, N. Rogue Wave Observation in a Water Wave Tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Soto-Crespo, J.; Ankiewicz, A. Extreme waves that appear from nowhere: On the nature of rogue waves. Phys. Lett. A 2009, 373, 2137–2145. [Google Scholar] [CrossRef]
- Akhmediev, N.; Dudley, J.M.; Solli, D.R.; Turitsyn, S.K. Recent progress in investigating optical rogue waves. J. Opt. 2013, 15, 060201. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photon. 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Mussot, A.; Louvergneaux, E.; Akhmediev, N.; Reynaud, F.; Delage, L.; Taki, M. Optical Fiber Systems Are Convectively Unstable. Phys. Rev. Lett. 2008, 101, 113904. [Google Scholar] [CrossRef] [PubMed]
- Odent, V.; Taki, M.; Louvergneaux, E. Experimental spatial rogue patterns in an optical feedback system. Nat. Hazards Earth Syst. Sci. 2010, 10, 2727–2732. [Google Scholar] [CrossRef] [Green Version]
- Arecchi, F.T.; Bortolozzo, U.; Montina, A.; Residori, S. Granularity and Inhomogeneity Are the Joint Generators of Optical Rogue Waves. Phys. Rev. Lett. 2011, 106, 153901. [Google Scholar] [CrossRef] [PubMed]
- Birkholz, S.; Nibbering, E.T.J.; Brée, C.; Skupin, S.; Demircan, A.; Genty, G.; Steinmeyer, G. Spatiotemporal Rogue Events in Optical Multiple Filamentation. Phys. Rev. Lett. 2013, 111, 243903. [Google Scholar] [CrossRef] [PubMed]
- Montina, A.; Bortolozzo, U.; Residori, S.; Arecchi, F.T. Non-Gaussian Statistics and Extreme Waves in a Nonlinear Optical Cavity. Phys. Rev. Lett. 2009, 103, 173901. [Google Scholar] [CrossRef] [PubMed]
- Lushnikov, P.M.; Vladimirova, N. Non-Gaussian statistics of multiple filamentation. Opt. Lett. 2010, 35, 1965–1967. [Google Scholar] [CrossRef] [PubMed]
- Marsal, N.; Caullet, V.; Wolfersberger, D.; Sciamanna, M. Spatial rogue waves in a photorefractive pattern-forming system. Opt. Lett. 2014, 39, 3690–3693. [Google Scholar] [CrossRef] [PubMed]
- Baronio, F.; Conforti, M.; Degasperis, A.; Lombardo, S.; Onorato, M.; Wabnitz, S. Vector Rogue Waves and Baseband Modulation Instability in the Defocusing Regime. Phys. Rev. Lett. 2014, 113, 034101. [Google Scholar] [CrossRef] [PubMed]
- Leonetti, M.; Conti, C. Observation of three dimensional optical rogue waves through obstacles. Appl. Phys. Lett. 2015, 106, 254103. [Google Scholar] [CrossRef]
- Pierangeli, D.; di Mei, F.; Conti, C.; Agranat, A.J.; DelRe, E. Spatial Rogue Waves in Photorefractive Ferroelectrics. Phys. Rev. Lett. 2015, 115, 093901. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.P.; Belić, M.; Zhang, Y. Second-order rogue wave breathers in the nonlinear Schrödinger equation with quadratic potential modulated by a spatially-varying diffraction coefficient. Opt. Express 2015, 23, 3708–3716. [Google Scholar] [CrossRef] [PubMed]
- Bonatto, C.; Feyereisen, M.; Barland, S.; Giudici, M.; Masoller, C.; Leite, J.R.R.; Tredicce, J.R. Deterministic Optical Rogue Waves. Phys. Rev. Lett. 2011, 107, 053901. [Google Scholar] [CrossRef] [PubMed]
- Reinoso, J.A.; Zamora-Munt, J.; Masoller, C. Extreme intensity pulses in a semiconductor laser with a short external cavity. Phys. Rev. E 2013, 87, 062913. [Google Scholar] [CrossRef] [PubMed]
- Tyson, J.J. Some further studies of nonlinear oscillations in chemical systems. J. Chem. Phys. 1973, 58, 3919–3930. [Google Scholar] [CrossRef]
- Verdasca, J.; de Wit, A.; Dewel, G.; Borckmans, P. Reentrant hexagonal Turing structures. Phys. Lett. A 1992, 168, 194–198. [Google Scholar] [CrossRef]
- Bordeu, I.; Clerc, M.G.; Lefever, R.; Tlidi, M. From localized spots to the formation of invaginated labyrinthine structures in a Swift–Hohenberg model. Commun. Nonlinear Sci. Numer. Simul. 2015, 29, 482–487. [Google Scholar] [CrossRef]
- Tlidi, M.; Sonnino, A.; Sonnino, G. Delayed feedback induces motion of localized spots in reaction-diffusion systems. Phys. Rev. E 2013, 87, 042918. [Google Scholar] [CrossRef] [PubMed]
- Gurevich, S.V.; Friedrich, R. Instabilities of Localized Structures in Dissipative Systems with Delayed Feedback. Phys. Rev. Lett. 2013, 110, 014101. [Google Scholar] [CrossRef] [PubMed]
- Gurevich, S.V. Dynamics of localized structures in reaction-diffusion systems induced by delayed feedback. Phys. Rev. E 2013, 87, 052922. [Google Scholar] [CrossRef] [PubMed]
- Tlidi, M.; Vladimirov, A.G.; Pieroux, D.; Turaev, D. Spontaneous Motion of Cavity Solitons Induced by a Delayed Feedback. Phys. Rev. Lett. 2009, 103, 103904. [Google Scholar] [CrossRef] [PubMed]
- Panajotov, K.; Tlidi, M. Spontaneous motion of cavity solitons in vertical-cavity lasers subject to optical injection and to delayed feedback. Eur. Phys. J. D 2010, 59, 67–72. [Google Scholar] [CrossRef]
- Pimenov, A.; Vladimirov, A.G.; Gurevich, S.V.; Panajotov, K.; Huyet, G.; Tlidi, M. Delayed feedback control of self-mobile cavity solitons. Phys. Rev. A 2013, 88, 053830. [Google Scholar] [CrossRef]
- Panajotov, K.; Tlidi, M. Chaotic behavior of cavity solitons induced by time delay feedback. Opt. Lett. 2014, 39, 4739–4742. [Google Scholar] [CrossRef] [PubMed]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tlidi, M.; Gandica, Y.; Sonnino, G.; Averlant, E.; Panajotov, K. Self-Replicating Spots in the Brusselator Model and Extreme Events in the One-Dimensional Case with Delay. Entropy 2016, 18, 64. https://doi.org/10.3390/e18030064
Tlidi M, Gandica Y, Sonnino G, Averlant E, Panajotov K. Self-Replicating Spots in the Brusselator Model and Extreme Events in the One-Dimensional Case with Delay. Entropy. 2016; 18(3):64. https://doi.org/10.3390/e18030064
Chicago/Turabian StyleTlidi, Mustapha, Yerali Gandica, Giorgio Sonnino, Etienne Averlant, and Krassimir Panajotov. 2016. "Self-Replicating Spots in the Brusselator Model and Extreme Events in the One-Dimensional Case with Delay" Entropy 18, no. 3: 64. https://doi.org/10.3390/e18030064
APA StyleTlidi, M., Gandica, Y., Sonnino, G., Averlant, E., & Panajotov, K. (2016). Self-Replicating Spots in the Brusselator Model and Extreme Events in the One-Dimensional Case with Delay. Entropy, 18(3), 64. https://doi.org/10.3390/e18030064







