Assessment of Nociceptive Responsiveness Levels during Sedation-Analgesia by Entropy Analysis of EEG †
Abstract
:1. Introduction
2. Experimental Section
2.1. Database
2.2. EEG Signal Preprocessing
2.3. Entropy Based Measures
2.3.1. RMSE
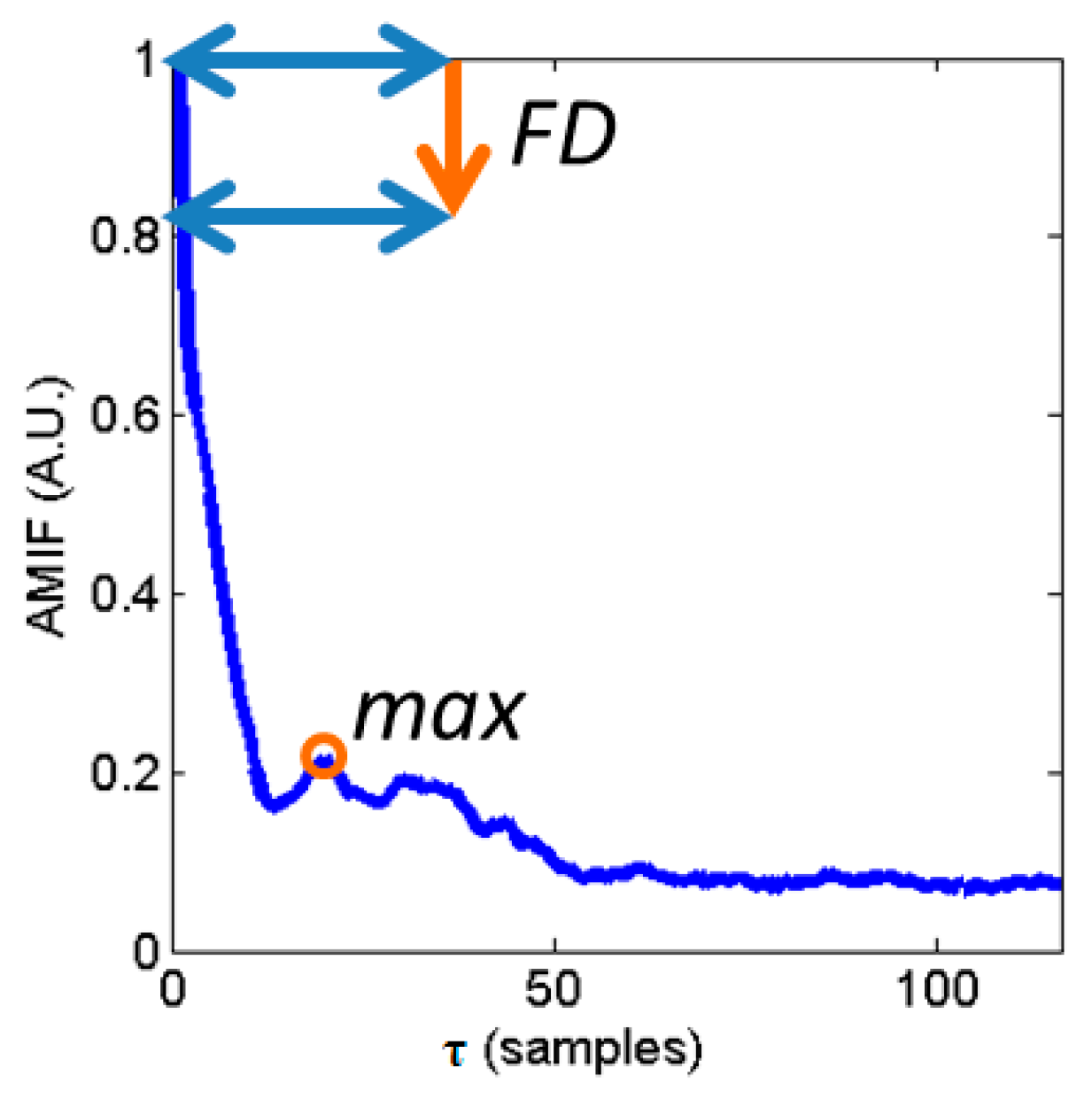
2.3.2. AMIF
2.3.3. Statistical Analysis
3. Results
3.1. CeProp, CeRemi, BIS, Time and Spectral HR Indexes
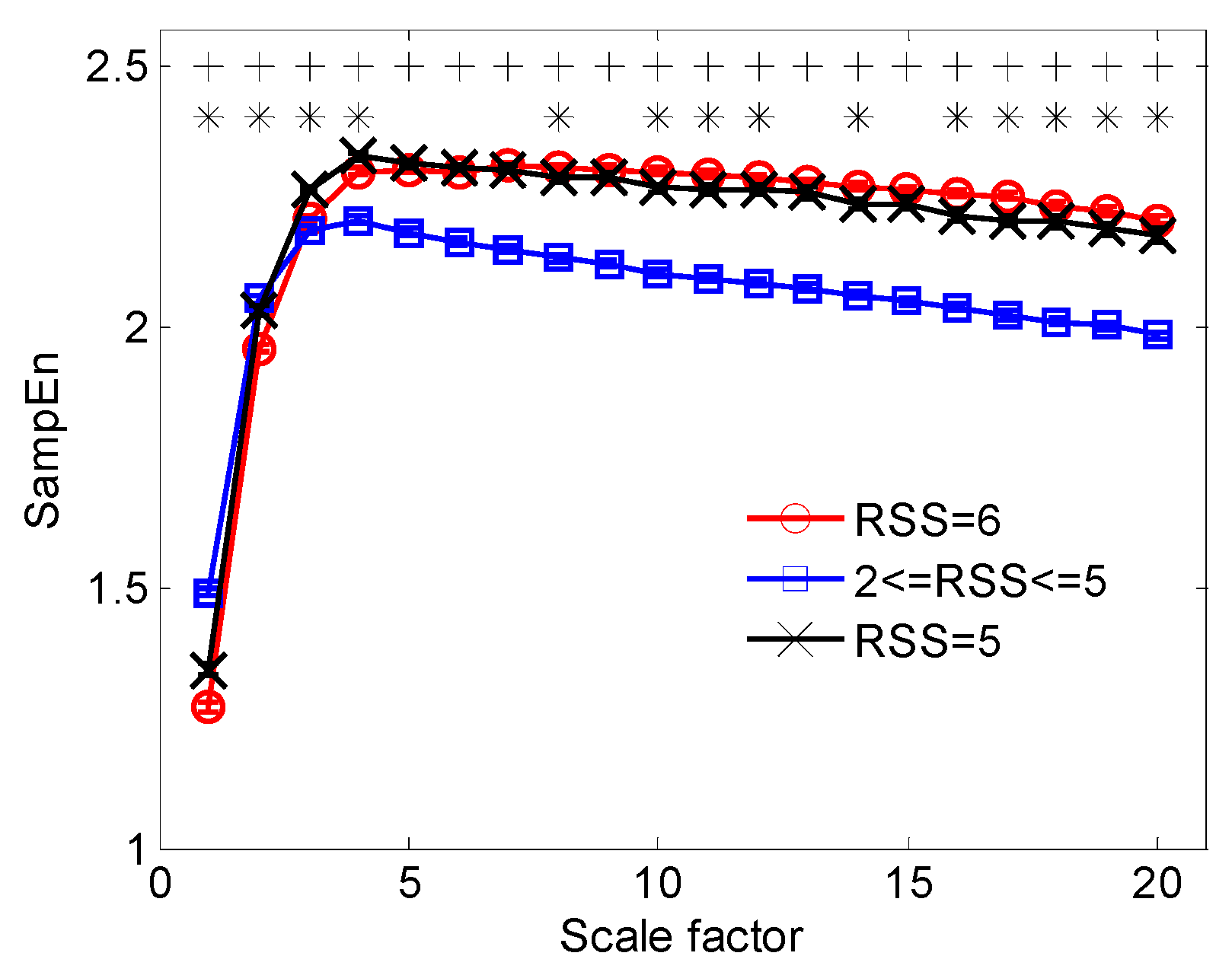
3.2. Multiscale Entropy Analysis of EEG: RMSE and AMIF
3.3. Multivariate Statistical Analysis
3.4. Validation in GAG Reflex during Endoscopy Tube Insertion
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- American Society of Anesthesiologists Task Force on Sedation and Analgesia by Non-Anesthesiologists. Practice guidelines for sedation and analgesia by non-anesthesiologists. Anesthesiology 2002, 96, 1004–1017. [Google Scholar]
- Gambús, P.L.; Jensen, E.W.; Jospin, M.; Borrat, X.; Martínez, P.G.; Fernández-Candil, J.; Valencia, J.F.; Barba, X.; Caminal, P.; Trocóniz, I.F. Modeling the effect of propofol and remifentanil combinations for sedation-analgesia in endoscopic procedures using an adaptive neuro fuzzy inference system (ANFIS). Anesth. Analg. 2011, 112, 331–339. [Google Scholar]
- Recart, A.; White, P.F.; Wang, A.; Gasanova, I.; Byerly, S.; Jones, S.B. Effect of auditory evoked potential index monitoring on anesthetic drug requirements and recovery profile after laparoscopic surgery: A clinical utility study. Anesthesiology 2003, 99, 813–818. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, Y.; Iwasaki, K.; Shibata, S.; Kato, J.; Ogawa, S.; Oi, Y. Different effects on circulatory control during volatile induction and maintenance of anesthesia and total intravenous anesthesia: autonomic nervous activity and arterial cardiac baroreflex function evaluated by blood pressure and heart rate variability. J. Clin. Anesth. 2006, 18, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Bouillon, T.W. Pharmacodynamic interaction between propofol and remifentanil regarding hypnosis, tolerance of laryngoscopy, bispectral index, and electroencephalographic approximate entropy. Anesthesiology 2004, 100, 1353–1372. [Google Scholar] [CrossRef] [PubMed]
- Ferenets, R.; Lipping, T.; Anier, A.; Jantti, V.; Melto, S.; Hovilehto, S. Comparison of entropy and complexity measures for the assessment of depth of sedation. IEEE Trans. Biomed. Eng. 2006, 53, 1067–1077. [Google Scholar] [CrossRef] [PubMed]
- Rampil, I.J. A primer for EEG signal processing in anesthesia. Anesthesiology 1998, 89, 980–1002. [Google Scholar] [CrossRef] [PubMed]
- Sigl, J.C.; Chamoun, N.G. An introduction to bispectral analysis for the EEG. J. Clin. Monit. 1994, 10, 392–404. [Google Scholar] [CrossRef] [PubMed]
- Viertiö-Oja, H.; Maja, V.; Särkelä, M.; Talja, P.; Tenkanen, N.; Tolvanen-Laakso, H.; Paloheimo, M.; Vakkuri, A.; Yli-Hankala, A.; Meriläinen, P. Description of the EntropyTM algorithm as applied in the Datex-Ohmeda S/5™ Entropy Module. Acta Anaesthesiol. Scand. 2004, 48, 154–161. [Google Scholar] [CrossRef] [PubMed]
- Jensen, E.W.; Lindholm, P.; Henneberg, S. Auto regressive modeling with exogenous input of auditory evoked potentials to produce an on-line depth of anaesthesia index. Methods Inf. Med. 1996, 35, 256–260. [Google Scholar] [PubMed]
- Litvan, H.; Jensen, E.W.; Galan, J.; Lund, J.; Rodriguez, B.E.; Henneberg, S.W.; Caminal, P.; Villar Landeira, J.M. Comparison of conventional averaged and rapid averaged, autoregressive-based extracted auditory evoked potentials for monitoring the hypnotic level during propofol induction. Anesthesiology 2002, 97, 351–358. [Google Scholar] [CrossRef] [PubMed]
- Valencia, J.F.; Borrat, X.; Gambus, P.L. Validation of a new index, qCON, for assessment of the level of consciousness during sedation. In Proceedings of the American Society of Anesthesiologists Annual Meeting, Washington, DC, USA, 13–17 October 2012.
- Jeanne, M.; Logier, R.; de Jonckheere, J.; Tavernier, B. Validation of a graphic measurement of heart rate variability to assess analgesia/nociception balance during general anesthesia. In Proceedings of the Annual International Conference of the IEEE on Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 1840–1843.
- Storm, H. Changes in skin conductance as a tool to monitor nociceptive stimulation and pain. Curr. Opin. Anaesthesiol. 2008, 21, 796–804. [Google Scholar] [CrossRef] [PubMed]
- Rantanen, M.; Yli-Hankala, A.; van Gils, M.; Yppärilä-Wolters, H.; Takala, P.; Huiku, M.; Kymäläinen, M.; Seitsonen, E.; Korhonen, I. Novel multiparameter approach for measurement of nociception at skin incision during general anaesthesia. Br. J. Anaesth. 2006, 96, 367–376. [Google Scholar] [CrossRef] [PubMed]
- Jensen, E.W.; Valencia, J.F.; López, A.; Anglada, T.; Agustí, M.; Ramos, Y.; Serra, R.; Jospin, M.; Pineda, P.; Gambus, P. Monitoring hypnotic effect and nociception with two EEG-derived indices, qCON and qNOX, during general anaesthesia. Acta Anaesthesiol. Scand. 2014, 58, 933–941. [Google Scholar] [CrossRef] [PubMed]
- Melia, U.; Vallverdu, M.; Jospin, M.; Jensen, E.W.; Valencia, J.F.; Claria, F.; Gambus, P.; Caminal, P. Prediction of nociceptive responses during sedation by time-frequency representation. In Proceedings of the Annual International Conference of the IEEE on Engineering in Medicine and Biology Society, Osaka, Japan, 3–7 July 2013; pp. 2547–2550.
- Melia, U.; Vallverdu, M.; Jospin, M.; Jensen, E.W.; Valencia, J.F.; Gambus, P.; Caminal, P. Auto-Mutual Information Function for Predicting Pain Responses in EEG Signals during Sedation. In XIII Mediterranean Conference on Medical and Biological Engineering and Computing; Springer: Berlin/Heidelberg, Germany, 2014; pp. 623–626. [Google Scholar]
- Liang, Z.; Wang, Y.; Sun, X.; Li, D.; Voss, L.J.; Sleigh, J.W.; Hagihira, S.; Li, X. EEG entropy measures in anesthesia. Front. Comput. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liang, Z.; Voss, L.J.; Sleigh, J.W.; Li, X. Multi-scale sample entropy of electroencephalography during sevoflurane anesthesia. J. Clin. Monit. Comput. 2014, 4, 409–417. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Wang, Y.; Ouyang, G.; Voss, L.J.; Sleigh, J.W.; Li, X. Permutation auto-mutual information of electroencephalogram in anesthesia. J. Neural Eng. 2013, 2, 026004. [Google Scholar] [CrossRef] [PubMed]
- Valencia, J.F.; Porta, A.; Vallverdú, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h Holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Hornero, R.; Abásolo, D.; Escudero, J.; Gómez, C. Nonlinear analysis of electroencephalogram and magnetoencephalogram recordings in patients with Alzheimer’s disease. Philos. Trans. R. Soc. Lond. A 2009, 367, 317–336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schnider, T.W.; Minto, C.F.; Shafer, S.L.; Gambus, P.L.; Andresen, C.; Goodale, D.B.; Youngs, E.J. The influence of age on propofol pharmacodynamics. Anesthesiology 1999, 90, 1502–1516. [Google Scholar] [CrossRef] [PubMed]
- Schnider, T.W.; Minto, C.F.; Gambus, P.L.; Andresen, C.; Goodale, D.B.; Shafer, S.L.; Youngs, E.J. The influence of method of administration and covariates on the pharmacokinetics of propofol in adult volunteers. Anesthesiology 1998, 88, 1170–1182. [Google Scholar] [CrossRef] [PubMed]
- Minto, C.F.; Schnider, T.W.; Egan, T.D.; Youngs, E.; Lemmens, H.J.; Gambus, P.L.; Billard, V.; Hoke, J.F.; Moore, K.H.; Hermann, D.J.; et al. Influence of age and gender on the pharmacokinetics and pharmacodynamics of remifentanil: I. Model development. Anesthesiology 1997, 86, 10–23. [Google Scholar] [CrossRef] [PubMed]
- Ramsay, M.A.; Savege, T.M.; Simpson, B.R.; Goodwin, R. Controlled sedation with alphaxalone-alphadolone. Br. Med. J. 1974, 2, 656–659. [Google Scholar] [CrossRef] [PubMed]
- Melia, U.; Clariá, F.; Vallverdú, M.; Caminal, P. Filtering and thresholding the analytic signal envelope in order to improve peak and spike noise reduction in EEG signals. Med. Eng. Phys. 2014, 36, 547–553. [Google Scholar] [CrossRef] [PubMed]
- Valencia, J.F.; Vallverdú, M.; Porta, A.; Voss, A.; Schroeder, R.; Vázquez, R.; de Luma, A.B.; Caminal, P. Ischemic risk stratification by means of multivariate analysis of the heart rate variability. Physiol. Meas. 2013, 34, 325–338. [Google Scholar] [CrossRef] [PubMed]
- Bari, V.; Valencia, J.F.; Vallverdú, M.; Girardengo, G.; Marchi, A.; Bassani, T.; Caminal, P.; Cerutti, S.; George, A.L., Jr.; Brink, P.A.; et al. Multiscale complexity analysis of the cardiac control identifies asymptomatic and symptomatic patients in long QT syndrome type 1. PLoS ONE 2014, 9, e93808. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. 2000, 278, H2039–H2049. [Google Scholar]
- Hoyer, D.; Leder, U.; Hoyer, H. Mutual information and phase dependencies: Measures of reduced nonlinear cardiorespiratory interactions after myocardial infarction. Med. Eng. Phys. 2002, 24, 33–43. [Google Scholar] [CrossRef]
- Smith, W.D.; Dutton, R.; Smith, N.T. Measuring the performance of anesthetic depth indicators. Anesthesiology 1996, 84, 38–51. [Google Scholar] [CrossRef] [PubMed]
- Brocas, E.; Dupont, H.; Paugam-Burtz, C.; Servin, F.; Mantz, J.; Desmonts, J.M. Bispectral index variations during tracheal suction in mechanically ventilated critically ill patients: Effect of an alfentanil bolus. Intensive Care Med. 2002, 28, 211–213. [Google Scholar] [CrossRef] [PubMed]
- Sato, A.; Sato, Y.; Shimada, F.; Torigata, Y. Varying changes in heart rate produced by nociceptive stimulation of the skin in rats at different temperatures. Brain Res. 1976, 110, 301–311. [Google Scholar] [CrossRef]
- Logier, R.; Jeanne, M.; Dassonneville, A.; Delecroix, M.; Tavernier, B. PhysioDoloris: A monitoring device for analgesia/nociception balance evaluation using heart rate variability analysis. In Proceedings of the Annual International Conference of the IEEE on Engineering in Medicine and Biology Society, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 1194–1197.
- Win, N.N.; Fukayama, H.; Kohase, H.; Umino, M. The different effects of intravenous propofol and midazolam sedation on hemodynamic and heart rate variability. Anesth. Analg. 2005, 101, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Eur. Heart J. 1996, 17, 354–381. [Google Scholar]
- Huhle, R.; Burghardt, M.; Zaunseder, S.; Wessel, N.; Koch, T.; Malberg, H.; Heller, A.R. Effects of awareness and nociception on heart rate variability during general anaesthesia. Physiol. Meas. 2012, 33, 207–217. [Google Scholar] [CrossRef] [PubMed]
- Jeanne, M.; Logier, R.; de Jonckheere, J.; Tavernier, B. Heart rate variability during total intravenous anesthesia: Effects of nociception and analgesia. Auton. Neurosci. 2009, 147, 91–96. [Google Scholar] [CrossRef] [PubMed]
- Jeanne, M.; Clément, C.; de Jonckheere, J.; Logier, R.; Tavernier, B. Variations of the analgesia nociception index during general anaesthesia for laparoscopic abdominal surgery. J. Clin. Monit. Comput. 2012, 26, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Gugino, L.D.; Chabot, R.J.; Prichep, L.S.; John, E.R.; Formanek, V. Quantitative EEG changes associated with loss and return of consciousness in healthy adult volunteers anaesthetized with propofol or sevoflurane. Br. J. Anaesth. 2001, 87, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Feshchenko, V.A.; Veselis, R.A.; Reinsel, R.A. Propofol-induced alpha rhythm. Neuropsychobiology 2004, 50, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Hindriks, R.; van Putten, M.J. Meanfield modeling of propofol-induced changes in spontaneous EEG rhythms. Neuroimage 2002, 60, 2323–2334. [Google Scholar] [CrossRef] [PubMed]
- Ching, S.; Cimenser, A.; Purdon, P.L.; Brown, E.N.; Kopell, N.J. Thalamocortical model for a propofol-induced alpha-rhythm associated with loss of consciousness. Proc. Natl. Acad. Sci. USA 2010, 107, 22665–22670. [Google Scholar] [CrossRef] [PubMed]
| Score | Description |
|---|---|
| 1 | Patient awake, anxious, agitated or restless |
| 2 | Patient awake, cooperative, orientated and tranquil |
| 3 | Patient drowsy with response to commands |
| 4 | Patient asleep, brisk response to glabella tap or loud auditory stimulus |
| 5 | Patient asleep, sluggish response to stimulus |
| 6 | No response to firm nail-bed pressure or other noxious stimuli. |
| Index | Groups (mean ± std) | Trial 1 | Trial 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (2 ≤ RSS ≤ 5 vs. RSS = 6) | (RSS = 5 vs. RSS = 6) | ||||||||
| 2 ≤ RSS ≤ 5 | RSS = 5 | RSS = 6 | Pk | Sen | Spe | Pk | Sen | Spe | |
| CeProp | 1.829 ± 0.907 † | 2.363 ± 0.705 | 2.382 ± 0.669 | 0.693 | 68.2 | 58.1 | 0.502 | 45.0 | 53.8 |
| CeRemi | 1.106 ± 0.815 † | 1.034 ± 0.820 † | 1.386 ± 0.598 | 0.622 | 56.9 | 56.6 | 0.642 | 58.3 | 56.8 |
| BIS | 76.1 ± 13.6 † | 65.2 ± 13.7 † | 59.4 ± 14.3 | 0.799 | 75.7 | 68.6 | 0.622 | 64.3 | 56.6 |
| mHR | 72.2 ± 13.3 † | 69.6 ± 12.4 † | 66.7 ± 11.9 | 0.616 | 54.0 | 61.2 | 0.559 | 51.0 | 55.5 |
| sdHR | 2.984 ± 3.699 † | 2.567 ± 3.490 † | 1.995 ± 2.862 | 0.627 | 37.2 | 80.3 | 0.554 | 30.8 | 78.2 |
| Pβ | 0.252 ± 0.164 † | 0.204 ± 0.125 † | 0.144 ± 0.094 | 0.721 | 52.5 | 82.2 | 0.663 | 48.2 | 77.2 |
| Pα | 0.300 ± 0.159 † | 0.400 ± 0.128 † | 0.422 ± 0.147 | 0.712 | 63.1 | 67.4 | 0.555 | 46.7 | 57.6 |
| Pθ | 0.165 ± 0.061 † | 0.179 ± 0.057 † | 0.201 ± 0.062 | 0.657 | 63.3 | 58.1 | 0.597 | 57.2 | 52.6 |
| Pδ | 0.313 ± 0.194 † | 0.250 ± 0.150 † | 0.266 ± 0.142 | 0.552 | 43.7 | 66.0 | 0.544 | 66.5 | 41 |
| Index | Groups (mean ± std) | Trial 1 | Trial 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (2 ≤ RSS ≤ 5 vs. RSS = 6) | (RSS = 5 vs. RSS = 6) | ||||||||
| 2 ≤ RSS ≤ 5 | RSS = 5 | RSS = 6 | Pk | Sen | Spe | Pk | Sen | Spe | |
| RMSE1 | 1.489 ± 0.302 | 1.342 ± 0.228 | 1.271 ± 0.235 | 0.725 | 60.1 | 74.6 | 0.599 | 53.3 | 62.4 |
| RMSE2 | 2.052 ± 0.253 | 2.029 ± 0.164 | 1.957 ± 0.192 | 0.668 | 64.9 | 62.1 | 0.617 | 58.9 | 58.6 |
| RMSE3 | 2.185 ± 0.260 | 2.262 ± 0.123 | 2.207 ± 0.175 | 0.553 | 33.5 | 61.6 | 0.625 | 66.4 | 49.7 |
| RMSE10 | 2.100 ± 0.301 | 2.265 ± 0.154 | 2.296 ± 0.174 | 0.741 | 50.7 | 86.4 | 0.577 | 47.2 | 63.7 |
| RMSE11 | 2.091 ± 0.308 | 2.261 ± 0.166 | 2.292 ± 0.178 | 0.738 | 51.6 | 85.5 | 0.563 | 45.8 | 64.7 |
| RMSE16 | 2.036 ± 0.315 | 2.213 ± 0.209 | 2.254 ± 0.202 | 0.741 | 56.2 | 80.1 | 0.563 | 46.9 | 61.4 |
| RMSE17 | 2.021 ± 0.316 | 2.202 ± 0.205 | 2.249 ± 0.207 | 0.754 | 58.0 | 80.7 | 0.572 | 48.3 | 62.9 |
| RMSEα | −0.016 ± 0.033 | −0.009 ± 0.028 | 0.002 ± 0.029 | 0.663 | 59.9 | 63.8 | 0.604 | 55.0 | 58.3 |
| max(Req = 2)δ | 0.232 ± 0.055 | 0.211 ± 0.054 | 0.191 ± 0.040 | 0.734 | 60.9 | 76.2 | 0.606 | 49.0 | 67.0 |
| max(Req = 2)α | 0.524 ± 0.027 | 0.537 ± 0.022 | 0.542 ± 0.024 | 0.686 | 62.7 | 62.6 | 0.567 | 58.4 | 52.6 |
| FD(Req = 0.5)TB | 0.862 ± 0.054 | 0.850 ± 0.039 | 0.832 ± 0.036 | 0.700 | 63.1 | 71.7 | 0.642 | 57.6 | 64.0 |
| Index | Trial 1 | Trial 2 | ||||
|---|---|---|---|---|---|---|
| (2 ≤ RSS ≤ 5 vs. RSS = 6) | (RSS = 5 vs. RSS = 6) | |||||
| Pk | Sen (%) | Spe (%) | Pk | Sen (%) | Spe (%) | |
| f1 | 0.713 | 64.8 | 68.1 | 0.718 | 63.3 | 61.6 |
| f2 | 0.732 | 65.7 | 70.2 | 0.722 | 60.3 | 65.3 |
| f3 | 0.747 | 62.4 | 74.9 | 0.660 | 59.5 | 64.1 |
| f4 | 0.802 | 68.4 | 80.1 | 0.683 | 58.4 | 69.5 |
| f5 | 0.776 | 66.2 | 76.7 | 0.701 | 60.3 | 67.3 |
| Index | Groups | – | |||
|---|---|---|---|---|---|
| GAG = 1 (mean ± std) | GAG = 0 (mean ± std) | Pk | Sen (%) | Spe (%) | |
| CeProp | 2.307 ± 0.780 | 2.415 ± 0.718 | 0.549 | 54.4 | 52.3 |
| CeRemi | 1.147 ± 0.811 † | 1.396 ± 0.646 | 0.624 | 58.4 | 54.7 |
| BIS | 80.5 ± 11.9 † | 68.3 ± 15.0 | 0.738 | 72.1 | 63.1 |
| mHR | 79.0 ± 15.4 † | 72.2 ± 13.4 | 0.637 | 57.3 | 59.9 |
| sdHR | 3.16 ± 4.56 † | 2.31 ± 3.24 | 0.615 | 36.6 | 76.6 |
| Pβ | 0.321 ± 0.199 † | 0.229 ± 0.148 | 0.642 | 52.5 | 70.3 |
| Pα | 0.215 ± 0.138 † | 0.369 ± 0.161 | 0.766 | 74.3 | 67.3 |
| Pθ | 0.138 ± 0.063 † | 0.170 ± 0.062 | 0.656 | 68.3 | 57.7 |
| Pδ | 0.350 ± 0.211 † | 0.262 ± 0.162 | 0.615 | 50.5 | 71.5 |
| RMSE1 | 1.611 ± 0.280 † | 1.407 ± 0.297 | 0.702 | 62.4 | 66.4 |
| RMSEα | −0.026 ± 0.032 † | −0.005 ± 0.031 | 0.687 | 61.6 | 66.2 |
| max(Re2)δ | 0.254 ± 0.061 † | 0.217 ± 0.054 | 0.690 | 54.5 | 70.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valencia, J.F.; Melia, U.S.P.; Vallverdú, M.; Borrat, X.; Jospin, M.; Jensen, E.W.; Porta, A.; Gambús, P.L.; Caminal, P. Assessment of Nociceptive Responsiveness Levels during Sedation-Analgesia by Entropy Analysis of EEG. Entropy 2016, 18, 103. https://doi.org/10.3390/e18030103
Valencia JF, Melia USP, Vallverdú M, Borrat X, Jospin M, Jensen EW, Porta A, Gambús PL, Caminal P. Assessment of Nociceptive Responsiveness Levels during Sedation-Analgesia by Entropy Analysis of EEG. Entropy. 2016; 18(3):103. https://doi.org/10.3390/e18030103
Chicago/Turabian StyleValencia, José F., Umberto S. P. Melia, Montserrat Vallverdú, Xavier Borrat, Mathieu Jospin, Erik W. Jensen, Alberto Porta, Pedro L. Gambús, and Pere Caminal. 2016. "Assessment of Nociceptive Responsiveness Levels during Sedation-Analgesia by Entropy Analysis of EEG" Entropy 18, no. 3: 103. https://doi.org/10.3390/e18030103







