Decision-Making Model under Risk Assessment Based on Entropy
Abstract
:1. Introduction
2. Classification of Risk Problem
3. Discussion of the Risk Assessment Model
3.1. Applicability of the R = P × C Classical Model
- The line of extra-long tunnel is designed to be of a gable slope for drainage.
- Comprehensive advanced geological forecasting, which includes conventional geological methods, comprehensive advanced geophysical exploration, and horizontal borehole advanced forecasting (five holes of every main tunnel section, and three holes of every parallel guide-pit tunnel), is applied in high-risk active fault regions and fault fracture zones.
- Comprehensive advanced geological forecasting, which includes conventional geological methods, comprehensive advanced geophysical exploration, and horizontal borehole advanced forecasting (three holes for every main tunnel section, and one hole for every parallel guide-pit tunnel), is applied in the syncline and anticline of the soluble rock region.
- According to the surrounding rock and water enrichment situation, a parallel driftway between the main tunnel and water enrichment area is excavated to reduce the water inrush hazard of the groundwater for the main tunnel.
3.2. Applicability Discussion of the Expected Utility-Entropy Model
- a:
- b:
- The expected utility and entropy model is different from the typical risk assessment model in application. The former is for the choice between different schemes. The objective of risk assessment is to provide a basis for risk disposition.
- Entropy represents the uncertainty of different outcomes in the expected utility and entropy model. However, the first step in risk assessment is hazard classification. Risk control measures correspond with risk levels. Thus, entropy in risk assessment should be used to represent the uncertainty of risk levels. In addition, the calculation of entropy should be different from that of the expected utility and entropy model.
- The value of entropy is not related to the expected value in the expected utility and entropy model. However, in this way, risk assessment does not make sense for the following reasons:
- (a)
- When the hazard is relatively small, people would not take measures to reduce the uncertainty no matter how large the uncertainty is. For example, people must choose between two ways ahead. No useful information for decision-making currently exists. People who make a wrong choice will suffer great losses. Under this circumstance, people would pay the price to obtain useful information. However, if the price of making a wrong choice is acceptable, people would not take measures to reduce the uncertainty of this state. In the expected utility and entropy model, high entropy means high risk. It does not make sense under this circumstance.
- (b)
- When the hazard is large, people would pay the price to obtain further information on uncertainty reduction. The more serious the consequences are when people make a wrong choice, the more people would spend on obtaining information.
4. Our Recommend Approach
4.1. Entropy-Hazard Risk Assessment Model
- When the hazard is relatively large, people would pay the price to reduce the uncertainty for risk control.
- No matter how large the uncertainty is, people would not take measures to reduce uncertainty when the hazard is small.
- If the hazard and uncertainty can be reduced to the same degree at the same cost, people would prefer choosing to reduce the hazard. For example, we assume that the hazard value of one incident is R1 and the uncertainty value of that is R2. When taking measures respectively, but at the same cost T, the hazard and uncertainty are reduced by 100%. People choose measures that reduce the hazard because risk is absent when the hazard value decreases to 0 regardless of the size of the uncertainty. By contrast, a risk still exists even when the entropy decreases to 0.
- When , measures should not be taken;
- When , measures can be taken.
4.2. Calculation Method of Entropy
4.2.1. Calculation of the Entropy Value
4.2.2. Calculation Method of
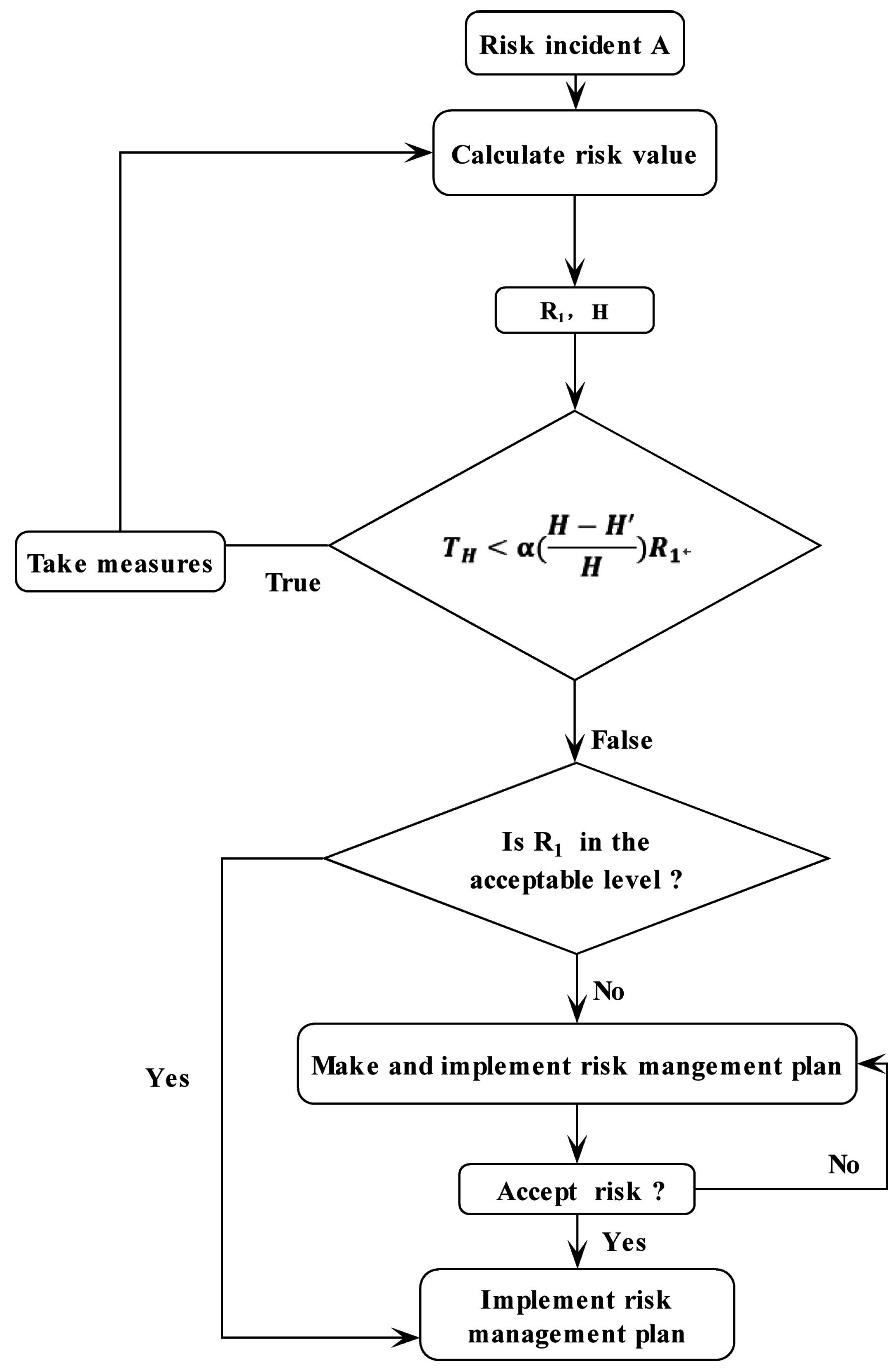
5. Assessment Process and Case Study
- Step 1: Analyze risk incidents and obtain information about risk incidents, including influencing factors and their values.
- Step 2: Enter the initial parameters: C, (the cost of ith exploration measures) and .
- Step 3: Determine the risk category to which the incident belongs and calculate P, H.If it belongs to Case 1, the probability P is calculated using formula (2), and H is calculated using formula (9);If it belongs to Case 2, the probability P is calculated using formula (3), and H is calculated using formula (12).
- Step 4: Calculate using formula (13) and calculate using formula (7). If < (the tolerance cost of i-th exploration measures), continue to step 5; otherwise, skip to step 6.
- Step 5: After taking measures, update initial parameters: , C, and . Calculate the updated probability P using formula (2) or (3).
- Step 6: Determine whether to take risk control measures according to the value and acceptance criteria. In addition, implement the next risk management plan. A simple example is made to provide a specific explanation.
- Measure 1: = 0.6743, =38.44
- Measure 2: = 0.1842, = 17,164
- Measure 3: = 0.3173, = 12,502
- Measure 4: = 0.6667, = 303
6. Conclusions and Discussion
- The occurrence of risk incidents is assumed to be determined by a certain formula and influencing factors. On the basis of this assumption, risk incidents are classified into two categories.
- Uncertainty is taken as a part of the risk assessment model, and it is expressed by entropy. Importantly, the calculation formula of entropy is given under different circumstances.
- Entropy may be used to represent uncertainty under risk. With regard to the interrelation between hazard and uncertainty, a new risk assessment model based on entropy is developed.
- Decision strategies for reducing uncertainty are based on the value of information. Specifically, the comparison between reducing hazard and reducing uncertainty is expressed in terms of cost. If the value of collecting information, namely reducing uncertainty, is larger than that of reducing hazard, then the measures taken to reduce uncertainty are tolerable and available.
- Risk assessment under uncertainty involves a decision to reduce uncertainty or reduce hazard. The general assessment process of our model is based on the criterion that uncertainty is first reduced, followed by the hazard.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Einstein, H.H. Risk and risk analysis in rock engineering. Tunn. Undergr. Space Technol. 1996, 11, 141–155. [Google Scholar] [CrossRef]
- Aven, T.; Zio, E. Foundational issues in risk assessment and risk management. Risk Anal. 2014, 34, 1164–1172. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.T. Risk assessment and management in underground rock engineering—An overview. J. Rock Mech. Geotech. Eng. 2012, 4, 193–204. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Fenton, G.A.; Griffiths, D.V. Risk Assessment in Geotechnical Engineering; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Honjo, Y.; Suzuki, M.; Hara, T.; Zhang, F. (Eds.) Geotechnical Risk and Safety; CRC Press: Leiden, The Netherlands, 2009.
- Juang, C.H.; Phoon, K.K.; Puppala, A.J.; Green, R.A.; Fenton, G.A. (Eds.) GeoRisk 2011: Geotechnical Risk Assessment and Management; ASCE: Reston, VA, USA, 2011.
- Taroun, A.; Yang, J.B. Dempster–Shafer theory of evidence: Potential usage for decision making and risk analysis in construction project management. Built Hum. Environ. Rev. 2011, 4 (Suppl. 1), 155–166. [Google Scholar]
- Jensen, F.V.; Nielsen, T.D. Bayesian Networks and Decision Graphs, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Sousa, R.L.; Einstein, H.H. Risk analysis during tunnel construction using Bayesian networks: Porto metro case study. Tunn. Undergr. Space Technol. 2012, 27, 86–100. [Google Scholar] [CrossRef]
- Sousa, R.L. Risk Analysis for Tunneling Projects. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- Choi, H.H.; Cho, H.N.; Seo, J.W. Risk assessment methodology for underground construction projects. J. Constr. Eng. Manag. 2004, 130, 258–272. [Google Scholar] [CrossRef]
- Zhou, H.B.; Zhang, H. Risk assessment methodology for a deep foundation pit construction project in Shanghai, China. J. Constr. Eng. Manag. 2011, 137, 1185–1194. [Google Scholar] [CrossRef]
- Vicari, A.; Ciraudo, A.; Del Negro, C.; Herault, A.; Fortuna, L. Lava flow simulations using discharge rates from thermal infrared satellite imagery during the 2006 Etna Eruption. Nat. Hazards 2009, 50, 539–550. [Google Scholar] [CrossRef]
- Li, S.C.; Zhou, Z.Q.; Li, L.P.; Xu, Z.H.; Zhang, Q.Q.; Shi, S.S. Risk assessment of water inrush in karst tunnels based on attribute synthetic evaluation system. Tunn. Undergr. Space Technol. 2013, 38, 50–58. [Google Scholar] [CrossRef]
- Li, L.; Lei, T.; Li, S.; Zhang, Q.; Xu, Z.; Shi, S.; Zhou, Z. Risk assessment of water inrush in karst tunnels and software development. Arab. J. Geosci. 2015, 8, 1843–1854. [Google Scholar] [CrossRef]
- Ge, Y.H.; Li, S.C.; Zhang, Q.S.; Lu, W. Risk analysis of water inrush into karst tunnel using fuzzy comprehensive evaluation method. In Proceedings of the International Workshop on Intelligent Systems and Applications (ISA 2009), Wuhan, China, 23–24 May 2009; pp. 1–4.
- Yazdani-Chamzini, A. Proposing a new methodology based on fuzzy logic for tunnelling risk assessment. J. Civ. Eng. Manag. 2014, 20, 82–94. [Google Scholar] [CrossRef]
- Li, X.; Li, Y. Research on risk assessment system for water inrush in the karst tunnel construction based on GIS: case study on the diversion tunnel groups of the Jinping II Hydropower Station. Tunn. Undergr. Space Technol. 2014, 40, 182–191. [Google Scholar] [CrossRef]
- Fouladgar, M.M.; Yazdani-Chamzini, A.; Zavadskas, E.K. Risk evaluation of tunneling projects. Arch. Civ. Mech. Eng. 2012, 12, 1–12. [Google Scholar] [CrossRef]
- Aven, T. A semi-quantitative approach to risk analysis, as an Alternative to QRAs. Reliab. Eng. Syst. Saf. 2008, 93, 790–797. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. The Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Amundrud, Ø.; Aven, T. On how to understand and acknowledge risk. Reliab. Eng. Syst. Saf. 2015, 142, 42–47. [Google Scholar] [CrossRef]
- He, Y.; Huang, R.H. Risk attributes theory: Decision making under risk. Eur. J. Oper. Res. 2008, 186, 243–260. [Google Scholar] [CrossRef]
- Tom, S.M.; Fox, C.R.; Trepel, C.; Poldrack, R.A. The neural basis of loss aversion in decision-making under risk. Science 2007, 315, 515–518. [Google Scholar] [CrossRef] [PubMed]
- Karagoz, S.; Aydin, N.; Isikli, E. Decision Making in Solid Waste Management under Fuzzy Environment. In Intelligence Systems in Environmental Management: Theory and Applications; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Paté-Cornell, M.E.; Dillon, R.L. The respective roles of risk and decision analysis in decision support. Decis. Anal. 2006, 3, 220–232. [Google Scholar] [CrossRef]
- Yang, J.; Qiu, W. A measure of risk and a decision-making model based on expected utility and entropy. Eur. J. Oper. Res. 2005, 164, 792–799. [Google Scholar] [CrossRef]
- Bell, D.E. Risk, return, and utility. Manag. Sci. 1995, 41, 23–30. [Google Scholar] [CrossRef]
- Jia, J.; Dyer, J.S.; Butler, J.C. Measures of perceived risk. Manag. Sci. 1999, 45, 519–532. [Google Scholar] [CrossRef]
- Dyer, J.S.; Jia, J. Relative risk-value models. Eur. J. Oper. Res. 1997, 103, 170–185. [Google Scholar] [CrossRef]
- Pedrycz, W.; Chen, S.M. Granular Computing and Decision-Making: Interactive and Iterative Approaches; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Peters, G.; Weber, R. DCC: A framework for dynamic granular clustering. Granul. Comput. 2016, 1, 1–11. [Google Scholar] [CrossRef]
- Livi, L.; Sadeghian, A. Granular computing, computational intelligence, and the analysis of non-geometric input spaces. Granul. Comput. 2016, 1, 13–20. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, H. Managing multi-granularity linguistic information in qualitative group decision making: An overview. Granul. Comput. 2016, 1, 21–35. [Google Scholar] [CrossRef]
- Antonelli, M.; Ducange, P.; Lazzerini, B.; Marcelloni, F. Multi-objective evolutionary design of granular rule-based classifiers. Granul. Comput. 2016, 1, 37–58. [Google Scholar] [CrossRef]
- Mendel, J.M. A comparison of three approaches for estimating (synthesizing) an interval type-2 fuzzy set model of a linguistic term for computing with words. Granul. Comput. 2016, 1, 59–69. [Google Scholar] [CrossRef]
- Lingras, P.; Haider, F.; Triff, M. Granular meta-clustering based on hierarchical, network, and temporal connections. Granul. Comput. 2016, 1, 71–92. [Google Scholar] [CrossRef]
- Skowron, A.; Jankowski, A.; Dutta, S. Interactive granular computing. Granul. Comput. 2016, 1, 95–113. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Bridging gaps between several forms of granular computing. Granul. Comput. 2016, 1, 115–126. [Google Scholar] [CrossRef]
- Loia, V.; D’Aniello, G.; Gaeta, A.; Orciuoli, F. Enforcing situation awareness with granular computing: A systematic overview and new perspectives. Granul. Comput. 2016, 1, 127–143. [Google Scholar] [CrossRef]
- Yao, Y. A triarchic theory of granular computing. Granul. Comput. 2016, 1, 145–157. [Google Scholar] [CrossRef]
- Ciucci, D. Orthopairs and granular computing. Granul. Comput. 2016, 1, 159–170. [Google Scholar] [CrossRef]
- Kreinovich, V. Solving equations (and systems of equations) under uncertainty: How different practical problems lead to different mathematical and computational formulations. Granul. Comput. 2016, 1, 171–179. [Google Scholar] [CrossRef]
- Wilke, G.; Portmann, E. Granular computing as a basis of human-data interaction: A cognitive cities use case. Granul. Comput. 2016, 1, 181–197. [Google Scholar] [CrossRef]
- Min, F.; Xu, J. Semi-greedy heuristics for feature selection with test cost constraints. Granul. Comput. 2016, 1, 199–211. [Google Scholar] [CrossRef]
- Maciel, L.; Ballini, R.; Gomide, F. Evolving granular analytics for interval time series forecasting. Granul. Comput. 2016, 1, 213–224. [Google Scholar] [CrossRef]
- Apolloni, B.; Bassis, S.; Rota, J.; Galliani, G.L.; Gioia, M.; Ferrari, L. A neuro fuzzy algorithm for learning from complex granules. Granul. Comput. 2016, 1, 225–246. [Google Scholar] [CrossRef]
- Song, M.; Wang, Y. A study of granular computing in the agenda of growth of artificial neural networks. Granul. Comput. 2016, 1, 247–257. [Google Scholar] [CrossRef]
- Liu, H.; Gegov, A.; Cocea, M. Rule-based systems: A granular computing perspective. Granul. Comput. 2016, 1, 259–274. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Renyi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1961; pp. 547–561.
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H.; Principe, J. Insights into Entropy as a Measure of Multivariate Variability. Entropy 2016, 18, 196. [Google Scholar] [CrossRef]
- Yang, J.; Qiu, W. Normalized Expected Utility-Entropy Measure of Risk. Entropy 2014, 16, 3590–3604. [Google Scholar] [CrossRef]
- Gao, B.; Wu, C.; Wu, Y.; Tang, Y. Expected Utility and Entropy-Based Decision-Making Model for Large Consumers in the Smart Grid. Entropy 2015, 17, 6560–6575. [Google Scholar] [CrossRef]
- He, D.; Xu, J.; Chen, X. Information-Theoretic-Entropy Based Weight Aggregation Method in Multiple-Attribute Group Decision-Making. Entropy 2016, 18, 171. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Fischer, K.; Kleine, A. Remarks on “A measure of risk and a decision-making model based on expected utility and entropy” by Jiping Yang and Wanhua Qiu (EJOR 164 (2005), 792–799). Eur. J. Oper. Res. 2007, 182, 469–474. [Google Scholar] [CrossRef]
- International Tunneling Association. Guidelines for tunneling risk management. Tunn. Undergr. Space Technol. 2004, 19, 617–643. [Google Scholar]
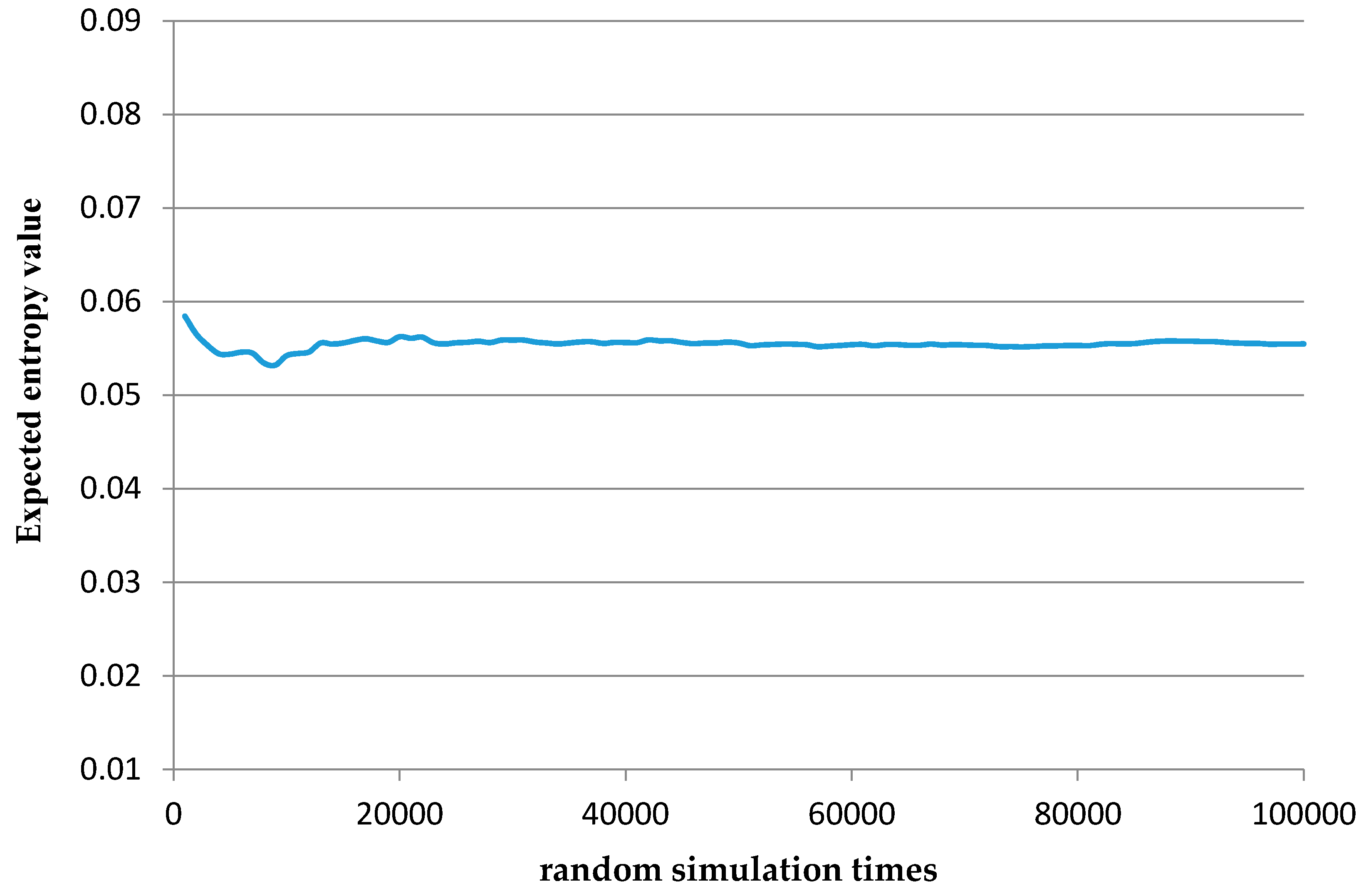
| Risk Factors | Risk Value | ||||
|---|---|---|---|---|---|
| Probability | Outcome | Risk Value | |||
| Before taking exploration measures | (0, 2) | 1 | 0.5 | C | 0.5C |
| After taking exploration measures | (0.9, 1.4) | 1 | 0.8 | C | 0.8C |
| Frequency | Consequence | ||||
|---|---|---|---|---|---|
| Disastrous | Severe | Serious | Considerable | Insignificant | |
| Very likely | Unacceptable | Unacceptable | Unacceptable | Unwanted | Unwanted |
| Likely | Unacceptable | Unacceptable | Unacceptable | Unwanted | Acceptable |
| Occasional | Unacceptable | Unwanted | Unwanted | Acceptable | Acceptable |
| Unlikely | Unwanted | Unwanted | Acceptable | Acceptable | Negligible |
| Very unlikely | Unwanted | Acceptable | Acceptable | Negligible | Negligible |
| Case 1 | Index Type | Influencing Factors | Risk | |||
| Risk Incident | Occurrence Probability | Consequence | Risk Level | |||
| Range | C | |||||
| Entropy Value | >0 | 0~−ln(0.5) | 0 | 0 | 0 | |
| Case 2 | Index Type | Influencing Factors | Risk | |||
| Risk Incident | Occurrence Probability | Consequence | Risk Level | |||
| Range | C | |||||
| Entropy Value | >0 | >0 | 0 | 0 | 0~ln(0.25) | |
| Risk Level | Scope of Risk Component R1 | Risk-Acceptable Criterion |
|---|---|---|
| >106 | Unacceptable | |
| 105~106 | Unwanted | |
| 5 × 103~105 | Acceptable | |
| <5 × 103 | Negligible |
| Number of Measure | Target Factor | Expense | Expected Precision Range |
|---|---|---|---|
| 1 | 13,000 | 0.005 | |
| 2 | 20,000 | 0.05 | |
| 3 | 10,000 | 0.1 | |
| 4 | 30,000 | 0.01 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Lu, H.; Xia, Y.; Xiong, Z. Decision-Making Model under Risk Assessment Based on Entropy. Entropy 2016, 18, 404. https://doi.org/10.3390/e18110404
Dong X, Lu H, Xia Y, Xiong Z. Decision-Making Model under Risk Assessment Based on Entropy. Entropy. 2016; 18(11):404. https://doi.org/10.3390/e18110404
Chicago/Turabian StyleDong, Xin, Hao Lu, Yuanpu Xia, and Ziming Xiong. 2016. "Decision-Making Model under Risk Assessment Based on Entropy" Entropy 18, no. 11: 404. https://doi.org/10.3390/e18110404
APA StyleDong, X., Lu, H., Xia, Y., & Xiong, Z. (2016). Decision-Making Model under Risk Assessment Based on Entropy. Entropy, 18(11), 404. https://doi.org/10.3390/e18110404






