Analysis of the Keller–Segel Model with a Fractional Derivative without Singular Kernel
Abstract
:1. Introduction
2. The Caputo and Fabrizio Fractional Order Derivative
3. Chemotaxis Model Proposed by Keller and Segel
3.1. Existence of Coupled Solutions
3.2. Uniqueness of the Coupled Solutions
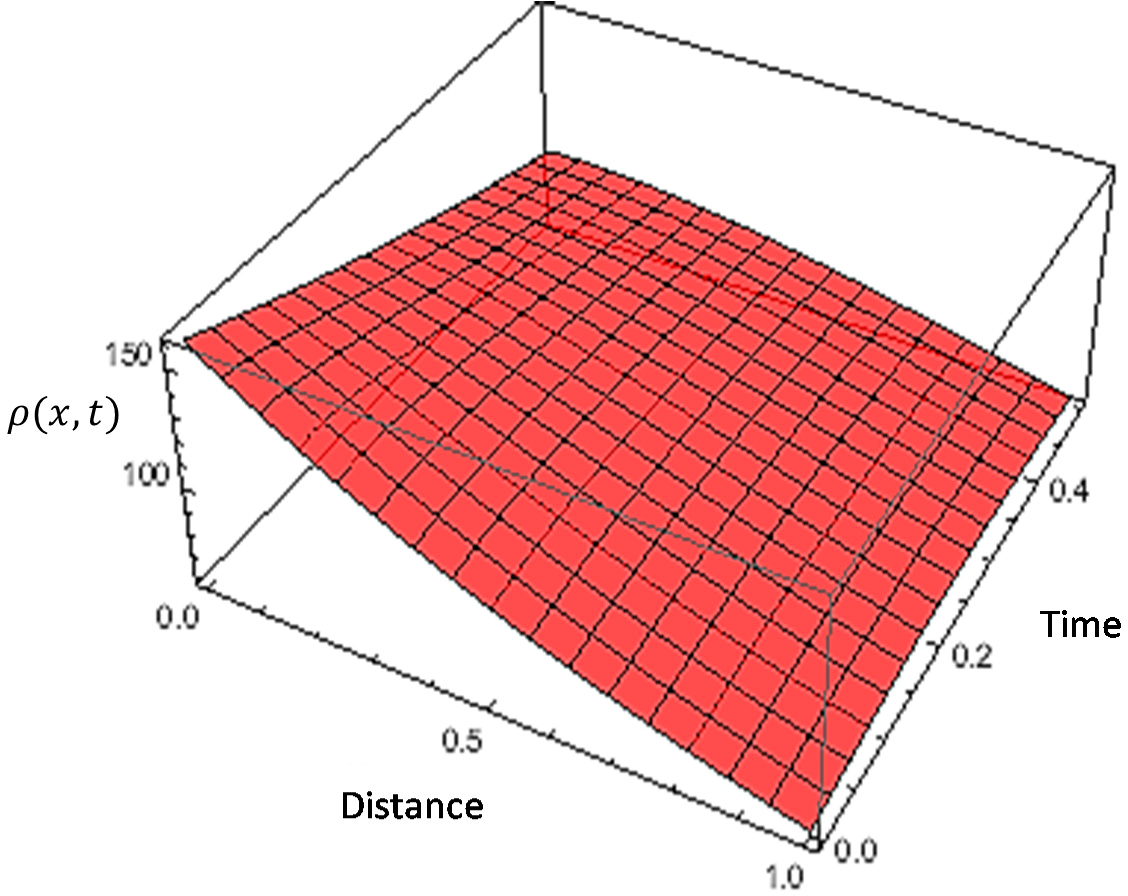
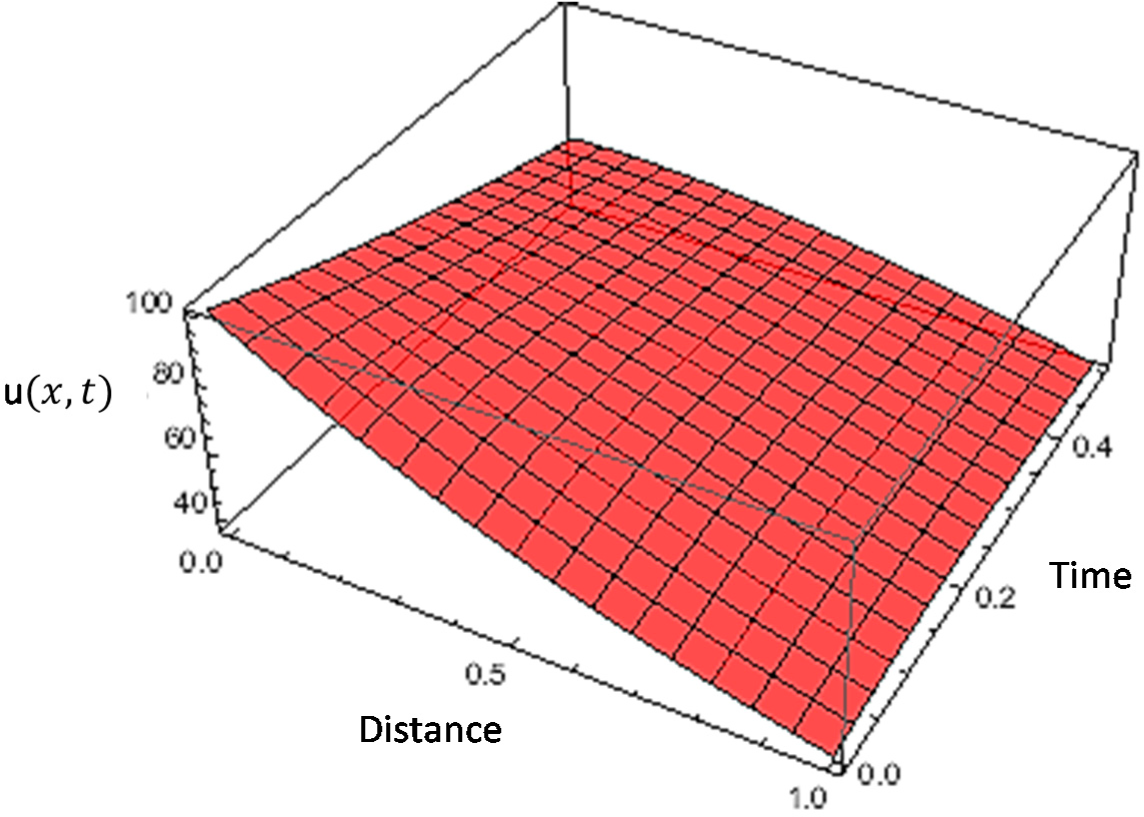
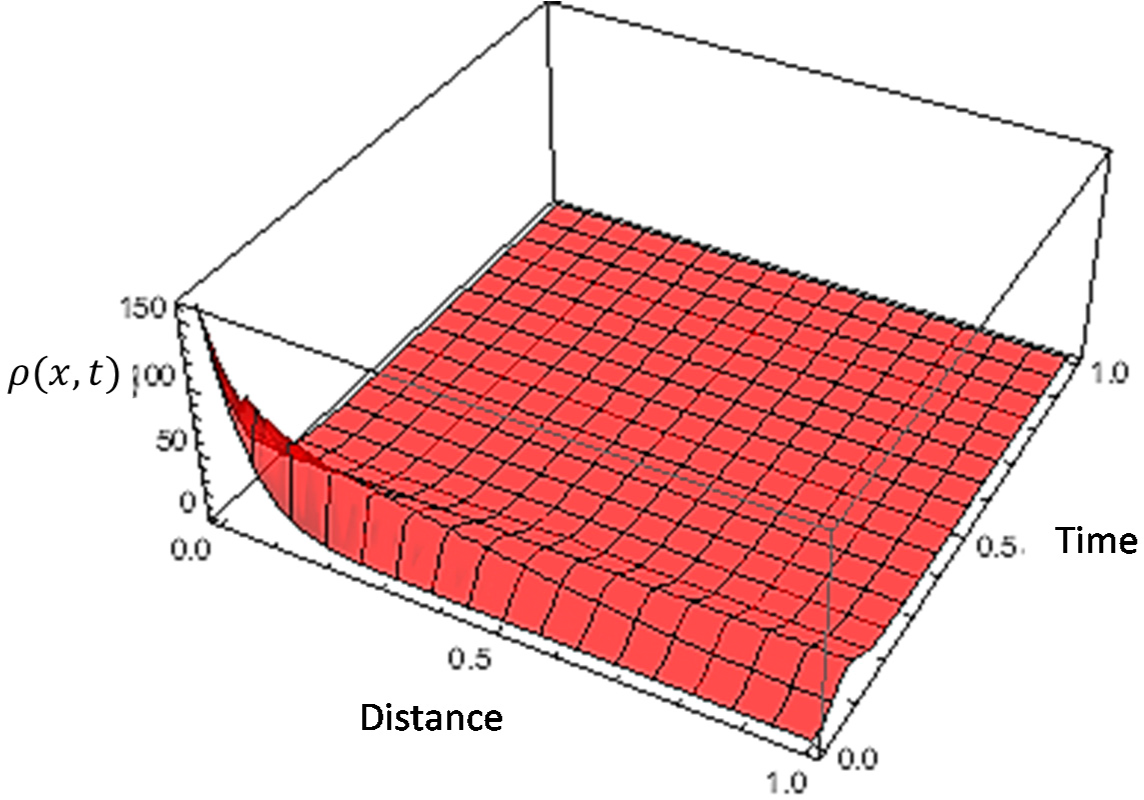
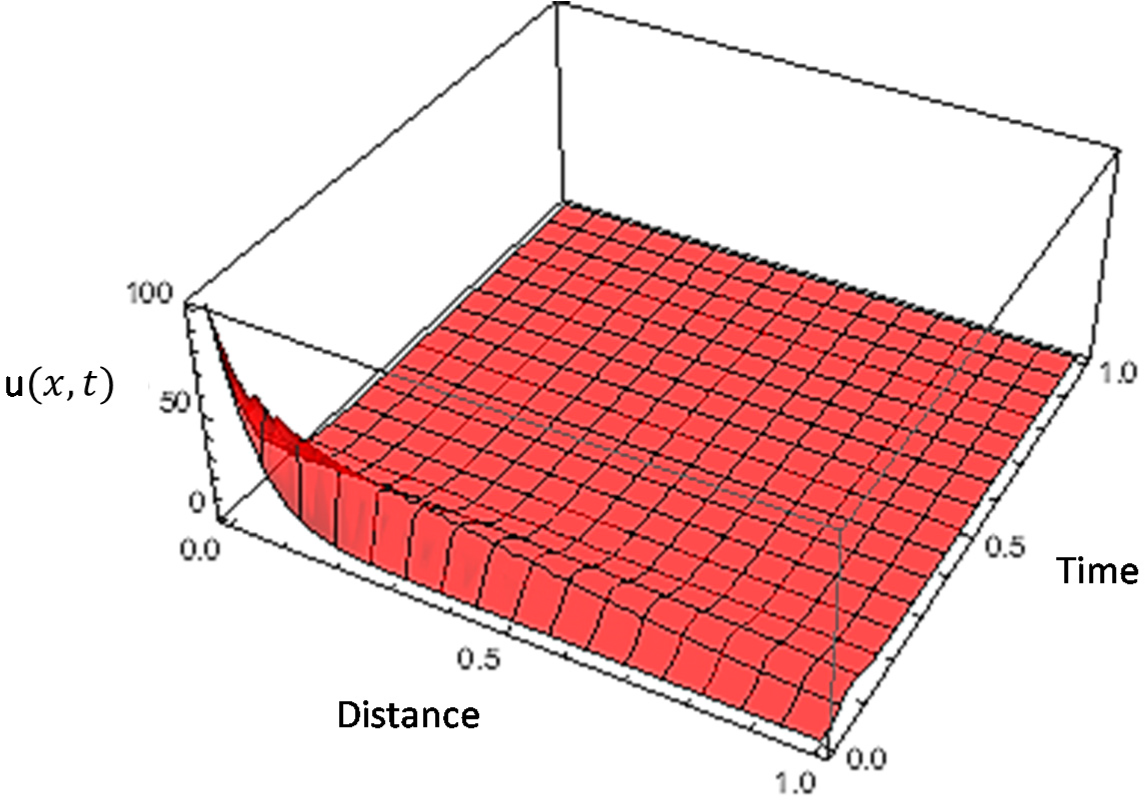
4. Derivation of Approximate Coupled-Solutions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Reference
- Herrero, M.A.; Velázquez, J.J.L. A blow-up mechanism for a chemotaxis model. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1997, 24, 633–683. [Google Scholar]
- Xia, L.; Jiang, G.; Song, Y.; Song, B. Modeling and Analyzing the Interaction between Network Rumors and Authoritative Information. Entropy 2015, 17, 471–482. [Google Scholar]
- Paolo, R. Self-Similarity in Population Dynamics: Surname Distributions and Genealogical Trees. Entropy 2015, 17, 425–437. [Google Scholar]
- Cristina, M.C.; Sebastiano, P. An 18 Moments model for dense gases: Entropy and galilean relativity principles without expansions. Entropy 2015, 17, 214–230. [Google Scholar]
- Francisco, C.; Morgan, M.; Olivier, R.; Amine, A.; Elias, C. Kinetic Theory Modeling and Efficient Numerical Simulation of Gene Regulatory Networks Based on Qualitative Descriptions. Entropy 2015, 17, 1896–1915. [Google Scholar] [Green Version]
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. Fract. Calc. Appl. Anal. 2002, 5, 367–386. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Cloot, A.; Botha, J.F. A generalized groundwater flow equation using the concept of non-integer order derivatives. Water SA 2006, 32, 55–78. [Google Scholar]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional-order governing equation of Lévy motion. Water Resour. Res. 2000, 36, 1413–1423. [Google Scholar]
- Wheatcraft, W.; Tyler, S.W. An explanation of scale-dependent dispersivity in heterogeneous aquifers using concepts of fractal geometry. Water Resour. Res. 1988, 24, 566–578. [Google Scholar]
- Cushman, J.H.; Ginn, T.R. Fractional advection-dispersion equation: A classical mass balance with convolution-Fickian flux. Water Resour. Res. 2000, 36, 3763–3766. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—part II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar]
- Wang, X.J.; Zhao, Y.; Cattani, C.; Yang, X.J. Local Fractional Variational Iteration Method for Inhomogeneous Helmholtz Equation within Local Fractional Derivative Operator. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Atangana, A.; Doungmo, G.E.F. Extension of Matched Asymptotic Method to Fractional Boundary Layers Problems. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Abu Hammad, M.; Khalil, R. Conformable fractional Heat differential equation. Int. J. Pure Appl. Math. 2014, 2, 215–221. [Google Scholar]
- Yang, X.J.; Machado, J.T.; Hristov, J. Nonlinear dynamics for local fractional Burgers’ equation arising in fractal flow. Nonlinear Dyn. 2015, 80, 1661–1664. [Google Scholar]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett. 2015, 47, 54–60. [Google Scholar]
- Yang, X.J.; Srivastava, H.M.; He, J.H.; Baleanu, D. Cantor-type cylindrical-coordinate method for differential equations with local fractional derivatives. Phys. Lett. A 2013, 377, 1696–1700. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new Definition of Fractional Derivative without Singular Kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a New Fractional Derivative without Singular Kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Atangana, A.; Badr, S.T.A. Extension of the RLC electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1–6. [Google Scholar]
- Keller, E.F.; Segel, L.A. Initiation of slime mold aggregation viewed as instability. J. Theor. Biol. 1970, 26, 399–415. [Google Scholar]
- Lapidus, R.; Levandowsky, M. Modeling chemosensory responses of swimming eukaryotes. Biol. Growth Spread 1979, 38, 388–396. [Google Scholar]
- Tindall, M.J.; Maini, P.K.; Porter, S.L.; Armitage, J.P. Overview of mathematical approaches used to model bacterial chemotaxis II: Bacterial populations. Appl. Numer. Math. 2009, 70, 1570–1607. [Google Scholar]
- Atangana, A.; Vermeulen, P.D. Modelling the Aggregation Process of Cellular Slime Mold by the Chemical Attraction. BioMed. Res. Int. 2014, 2014. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atangana, A.; Alkahtani, B.S.T. Analysis of the Keller–Segel Model with a Fractional Derivative without Singular Kernel. Entropy 2015, 17, 4439-4453. https://doi.org/10.3390/e17064439
Atangana A, Alkahtani BST. Analysis of the Keller–Segel Model with a Fractional Derivative without Singular Kernel. Entropy. 2015; 17(6):4439-4453. https://doi.org/10.3390/e17064439
Chicago/Turabian StyleAtangana, Abdon, and Badr Saad T. Alkahtani. 2015. "Analysis of the Keller–Segel Model with a Fractional Derivative without Singular Kernel" Entropy 17, no. 6: 4439-4453. https://doi.org/10.3390/e17064439





