Detecting Chronotaxic Systems from Single-Variable Time Series with Separable Amplitude and Phase
Abstract
:1. Introduction
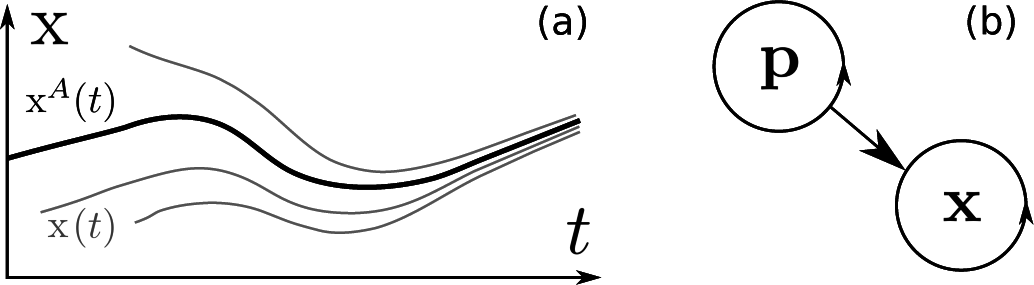
2. Chronotaxic Systems
3. Inverse Approach for Chronotaxic Systems
3.1. Inverse Approaches to Nonautonomous Dynamical Systems
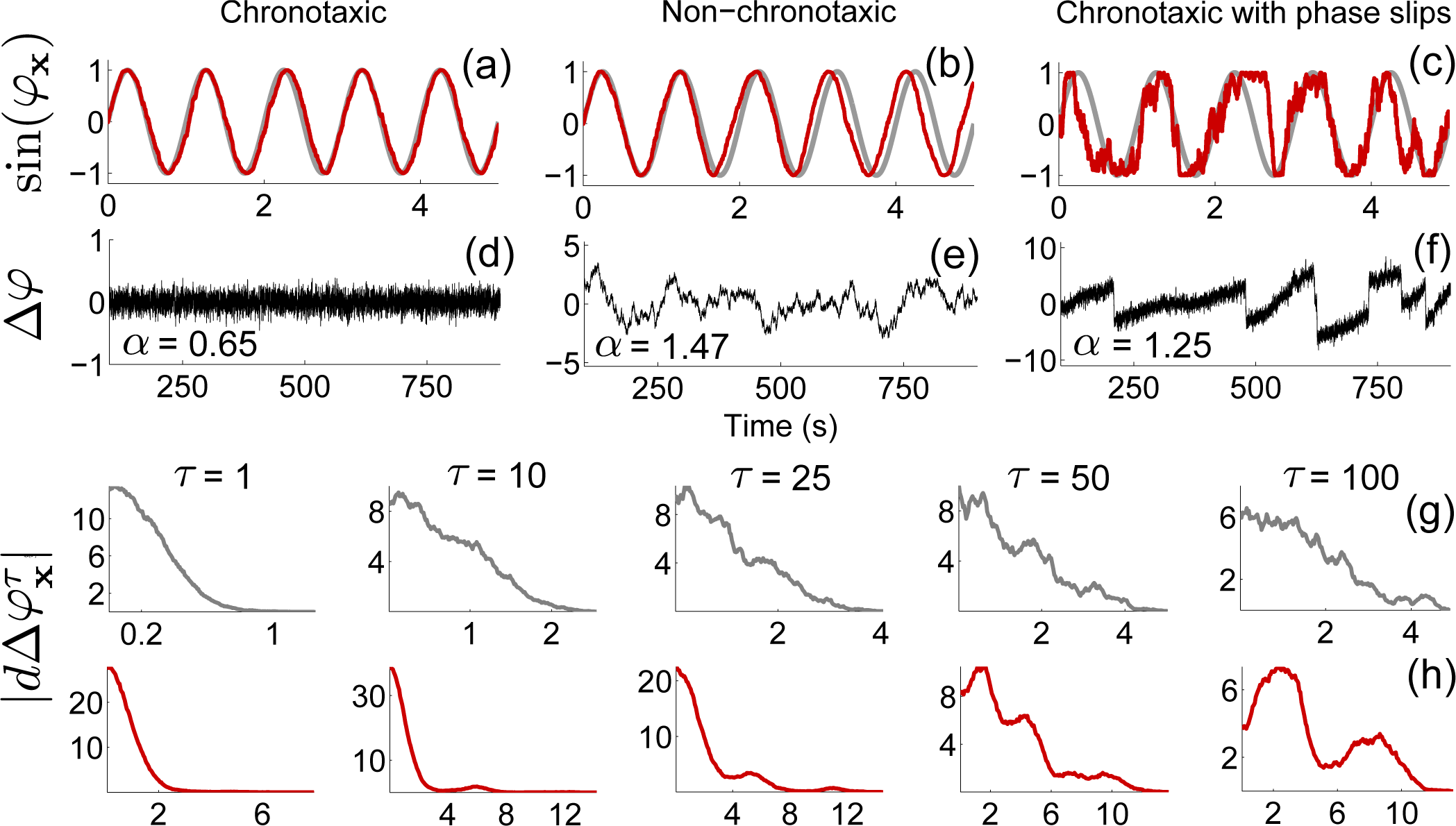
3.2. Detecting Chronotaxicity
3.3. Extracting the Perturbed and Unperturbed Phases
3.4. Dynamical Bayesian Inference
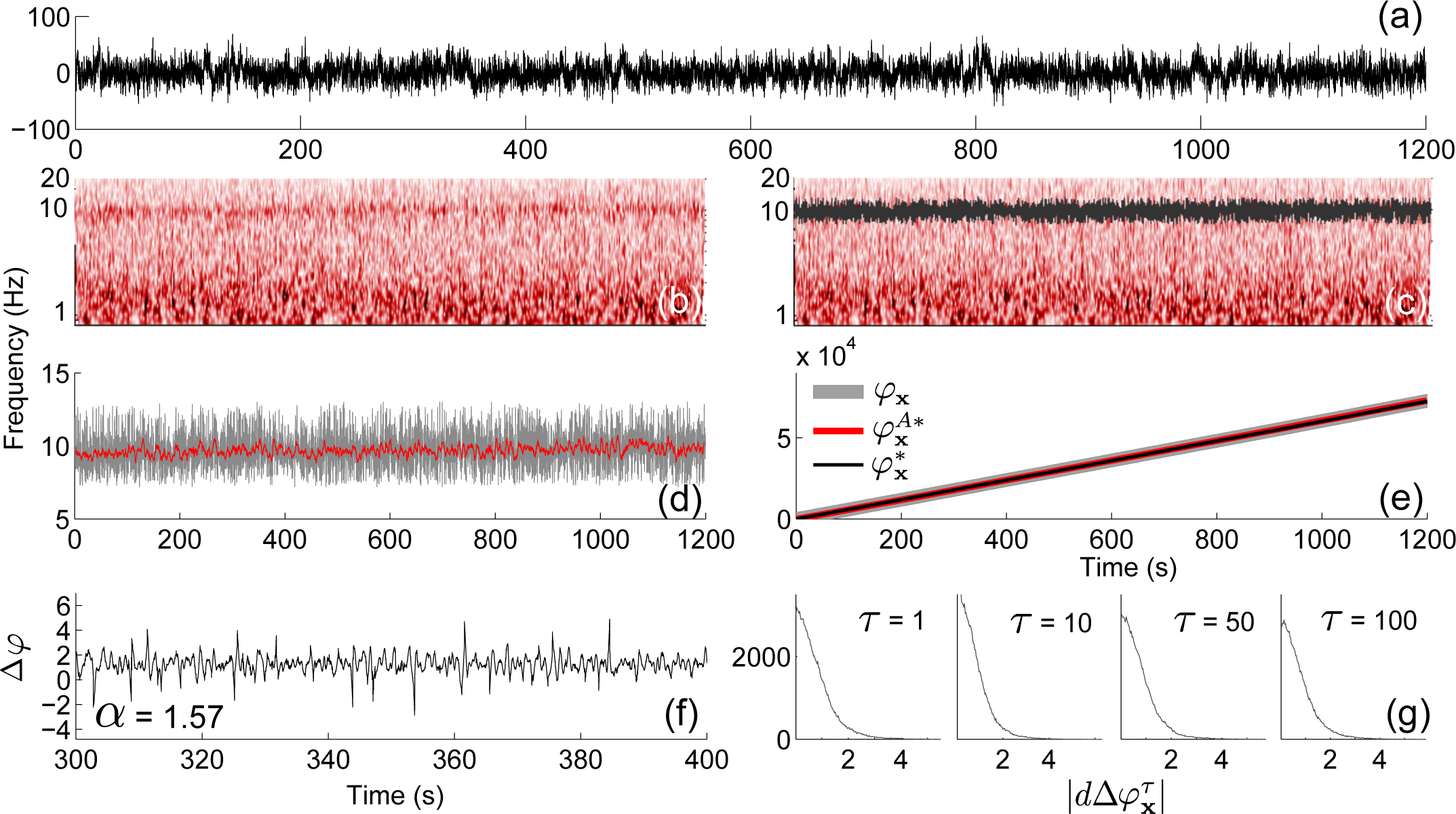
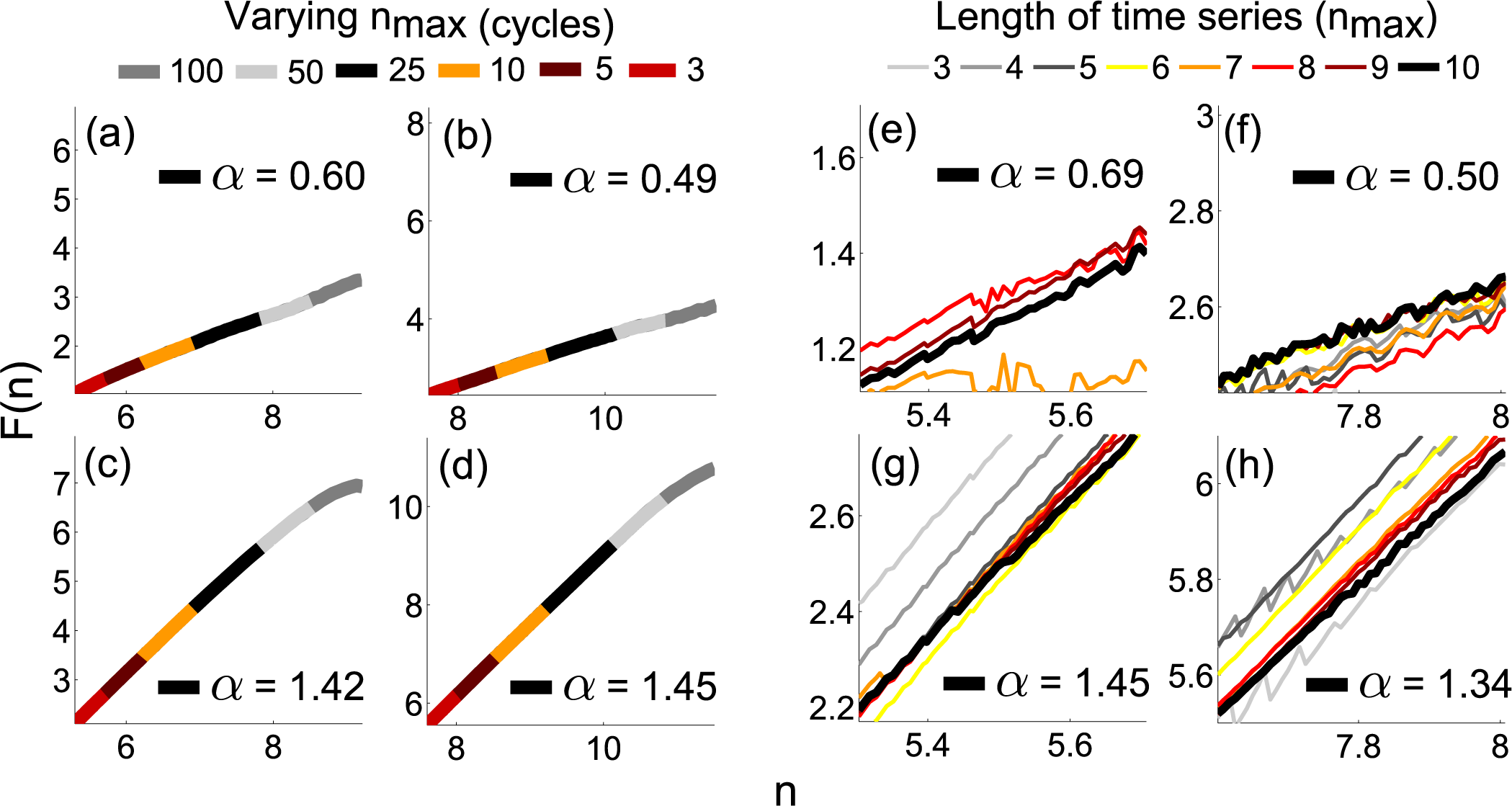
3.5. Phase Fluctuation Analysis
4. Application of Inverse Approach Methods
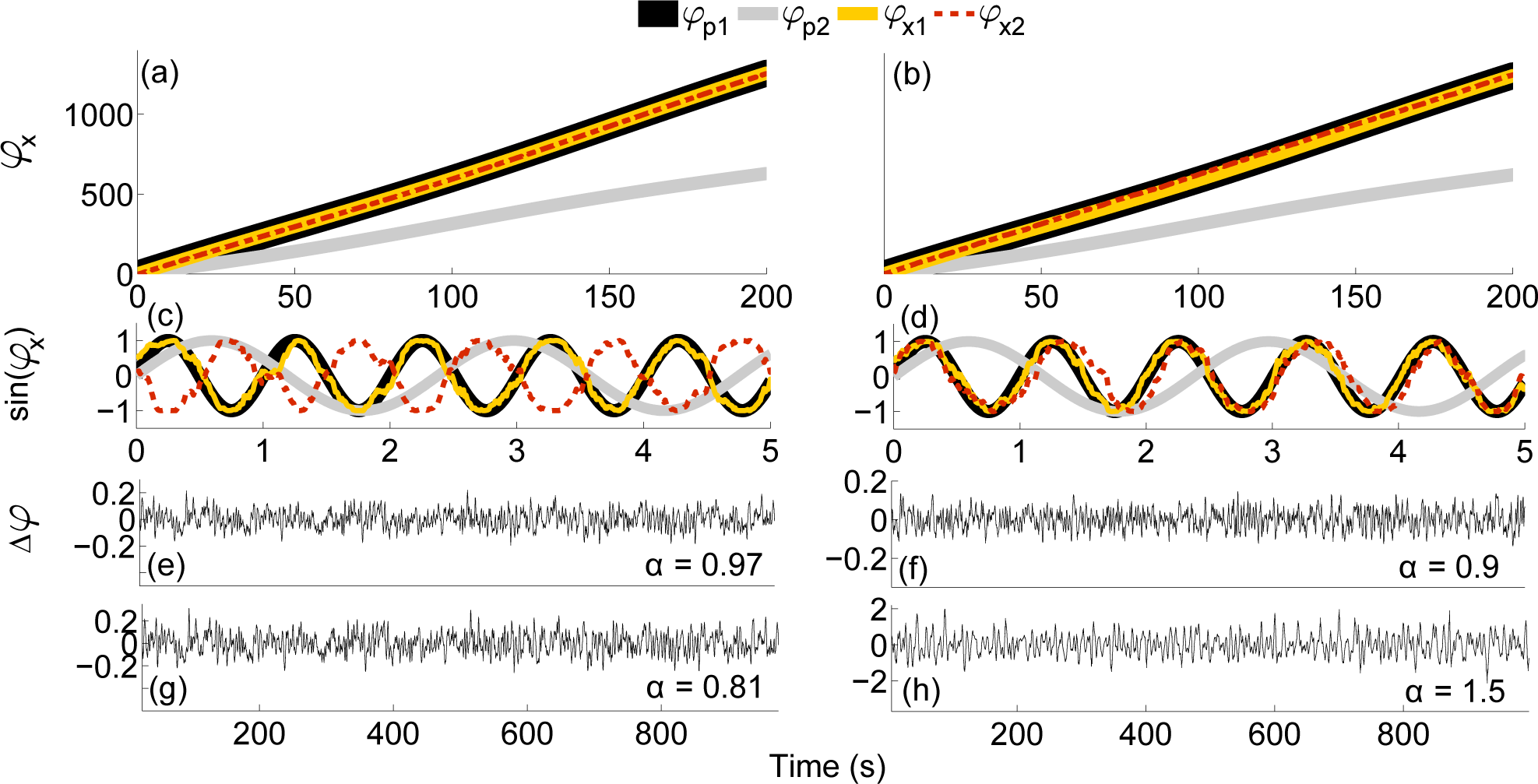
4.1. Numerical Simulations
4.2. Practical Considerations
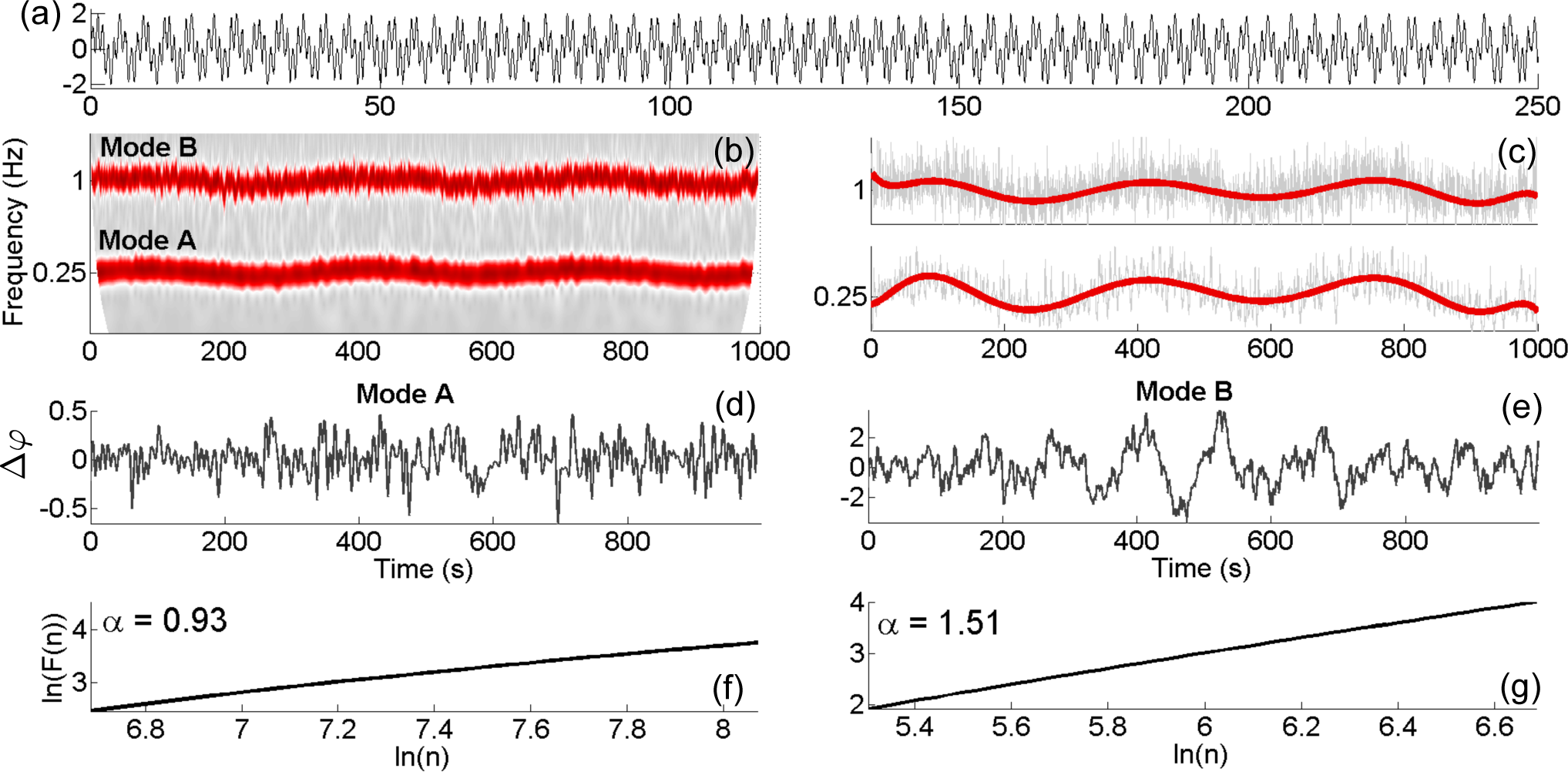
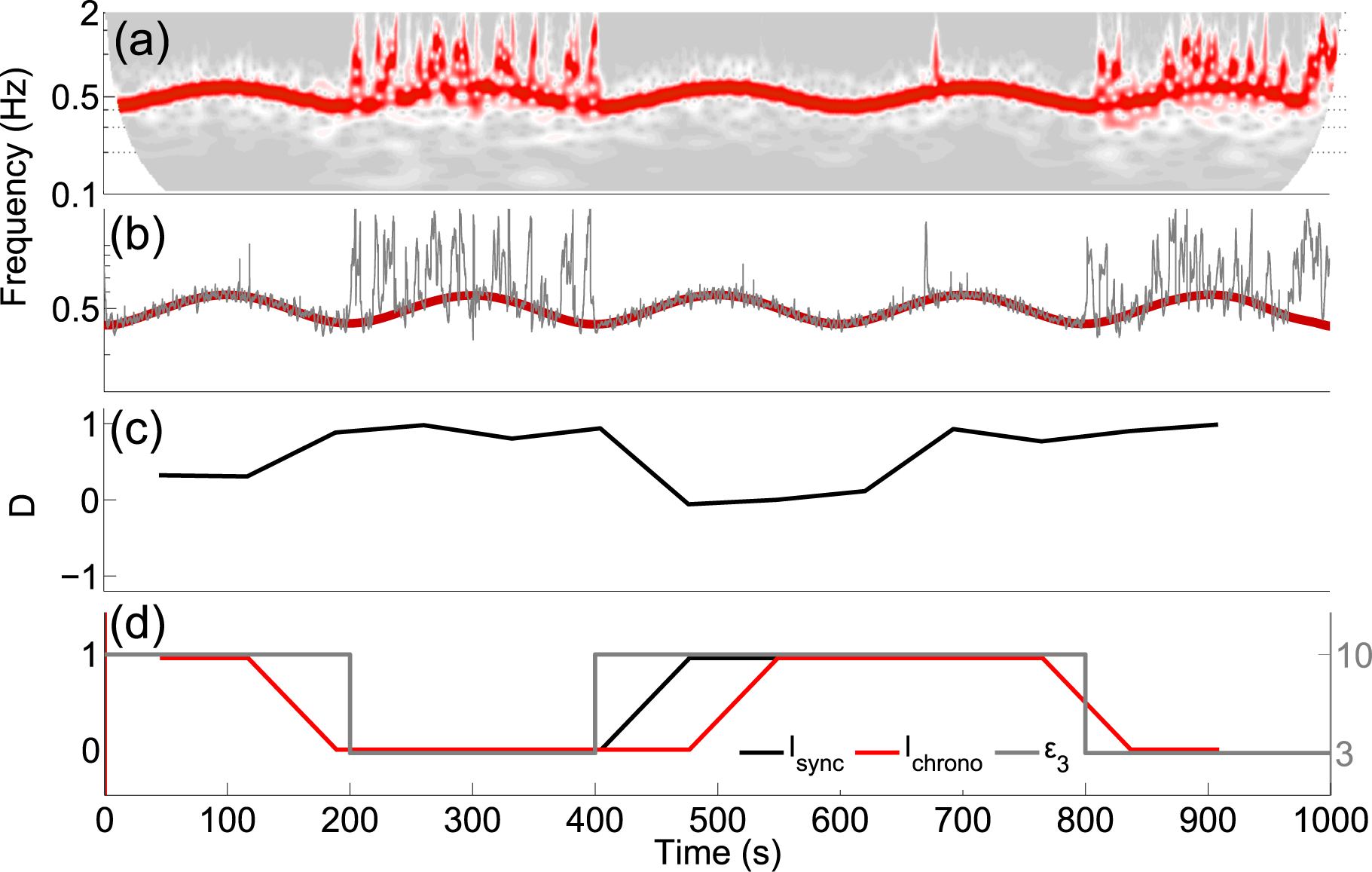
4.3. Application to Experimental Data
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kloeden, P.E.; Pöetzsche, C. (Eds.) Nonautonomous Dynamical Systems in the Life Sciences; Springer: Cham, Switzerland, 2013; pp. 3–39.
- Friedrich, R.; Peinke, J.; Sahimi, M.; Tabar, M.R.R. Approaching Complexity by Stochastic Methods: From Biological Systems to Turbulence. Phys. Rep. 2011, 506, 87–162. [Google Scholar]
- Wessel, N.; Riedl, M.; Kurths, J. Is the Normal Heart Rate “Chaotic” due to Respiration? Chaos 2009, 19, 028508. [Google Scholar]
- Friston, K. A. Free Energy Principle for Biological Systems. Entropy 2012, 14, 2100–2121. [Google Scholar]
- Kurz, F.T.; Aon, M.A.; O’Rourke, B.; Armoundas, A.A. Wavelet Analysis Reveals Heterogeneous Time-Dependent Oscillations of Individual Mitochondria. Am. J. Physiol. Heart Circ. Physiol. 2010, 299, H1736–H1740. [Google Scholar]
- Shiogai, Y.; Stefanovska, A.; McClintock, P.V.E. Nonlinear Dynamics of Cardiovascular Ageing. Phys. Rep. 2010, 488, 51–110. [Google Scholar]
- Iatsenko, D.; Bernjak, A.; Stankovski, T.; Shiogai, Y.; Owen-Lynch, P.J.; Clarkson, P.B.M.; McClintock, P.V.E.; Stefanovska, A. Evolution of Cardiorespiratory Interactions with Age. Phil. Trans. R. Soc. A 2013, 371, 20110622. [Google Scholar]
- Stam, C.J. Nonlinear Dynamical Analysis of EEG and MEG: Review of an Emerging Field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar]
- Stefanovska, A.; Bračič, M.; Kvernmo, H.D. Wavelet Analysis of Oscillations in the Peripheral Blood Circulation Measured by Laser Doppler Technique. IEEE Trans. Bio. Med. Eng. 1999, 46, 1230–1239. [Google Scholar]
- Suprunenko, Y.F.; Clemson, P.T.; Stefanovska, A. Chronotaxic Systems: A New Class of Self-sustained Non-autonomous Oscillators. Phys. Rev. Lett. 2013, 111, 024101. [Google Scholar]
- Suprunenko, Y.F.; Clemson, P.T.; Stefanovska, A. Chronotaxic Systems with Separable Amplitude and Phase Dynamics. Phys. Rev. E 2014, 89, 012922. [Google Scholar]
- Suprunenko, Y.F.; Stefanovska, A. Generalized Chronotaxic Systems: Time-Dependent Oscillatory Dynamics Stable under Continuous Perturbation. Phys. Rev. E 2014, 90, 032921. [Google Scholar]
- Bishnani, Z.; Mackay, R.S. Safety Criteria for Aperiodically Forced Systems. Dyn. Syst. 2003, 18, 107–129. [Google Scholar]
- Clemson, P.T.; Suprunenko, Y.F.; Stankovski, T.; Stefanovska, A. Inverse Approach to Chronotaxic Systems for Single-Variable Time Series. Phys. Rev. E 2014, 89, 032904. [Google Scholar]
- Clemson, P.T.; Stefanovska, A. Discerning Non-autonomous Dynamics. Phys. Rep. 2014, 542, 297–368. [Google Scholar]
- Gabor, D. Theory of Communication. J. Inst. Electr. Eng. 1946, 93, 429–457. [Google Scholar]
- Sheppard, L.W.; Vuksanović, V.; McClintock, P.V.E.; Stefanovska, A. Oscillatory Dynamics of Vasoconstriction and Vasodilation Identified by Time-Localized Phase Coherence. Phys. Med. Biol. 2011, 56, 3583–3601. [Google Scholar]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed Wavelet Transforms: An Empirical Mode Decomposition-Like Tool. Appl. Comput. Harmon. Anal 2011, 30, 243–261. [Google Scholar]
- Iatsenko, D.; McClintock, P.V.E.; Stefanovska, A. Linear and Synchrosqueezed Time-Frequency Representations Revisited: Overview, Standards of Use, Resolution, Reconstruction, Concentration and Algorithms. Digit. Signal Process. 2015, 42, 1–26. [Google Scholar]
- Stankovski, T.; Duggento, A.; McClintock, P.V.E.; Stefanovska, A. Inference of Time-Evolving Coupled Dynamical Systems in the Presence of Noise. Phys. Rev. Lett. 2012, 109, 024101. [Google Scholar]
- Duggento, A.; Stankovski, T.; McClintock, P.V.E.; Stefanovska, A. Dynamical Bayesian Inference of Time-Evolving Interactions: From a Pair of Coupled Oscillators to Networks of Oscillators. Phys. Rev. E 2012, 86, 061126. [Google Scholar]
- Jamšek, J.; Paluš, M.; Stefanovska, A. Detecting Couplings between Interacting Oscillators with Time-Varying Basic Frequencies: Instantaneous Wavelet Bispectrum and Information Theoretic Approach. Phys. Rev. E 2010, 81, 036207. [Google Scholar]
- Friston, K. Functional and Effective Connectivity: A Review. Brain Connect. 2011, 1, 13–36. [Google Scholar]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Dover: New York, NY, USA, 2003. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W.; Buck, J.R. Discrete-Time Signal Processing, 2nd ed; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Kralemann, B.; Cimponeriu, L.; Rosenblum, M.; Pikovsky, A.; Mrowka, R. Phase Dynamics of Coupled Oscillators Reconstructed from Data. Phys. Rev. E 2008, 77, 066205. [Google Scholar]
- Kaiser, G. A Friendly Guide to Wavelets; Birkhäuser Boston: Valley Stream, NY, USA, 1994. [Google Scholar]
- Morlet, J. Sampling Theory and Wave Propagation. In Issues in A coustic Signal-Image Processing and Recognition; Chen, C.H., Ed.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 233–261. [Google Scholar]
- Delprat, N.; Escudie, B.; Guillemain, P.; Kronland-Martinet, R.; Tchamitchian, P.; Torrésani, B. Asymptotic Wavelet and Gabor Analysis: Extraction of Instantaneous Frequencies. IEEE Trans. Inf. Theory 1992, 38, 644–664. [Google Scholar]
- Carmona, R.A.; Hwang, W.L.; Torrésani, B. Characterization of Signals by the Ridges of their Wavelet Transforms. IEEE Trans. Signal Process. 1997, 45, 2586–2590. [Google Scholar]
- Rosenblum, M.G.; Pikovsky, A.S. Detecting Direction of Coupling in Interacting Oscillators. Phys. Rev. E. 2001, 64, 045202. [Google Scholar]
- Stankovski, T; Duggento, A; McClintock, P.V.E.; Stefanovska, A. A Tutorial on Time-Evolving Dynamical Bayesian Inference. Eur. Phys. J. Spec. Top. 2014, 223, 2685–2703. [Google Scholar]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic Organisation of DNA Nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar]
- Kioka, H.; Kato, H.; Fujikawa, M.; Tsukamoto, O.; Suzuki, T.; Imamura, H.; Nakano, A.; Higo, S.; Yamazaki, S.; Matsuzaki, T.; et al. Evaluation of Intramitochondrial ATP Levels Identifies GO/G1 Switch Gene 2 as a Positive Regulator of Oxidative Phosphorylation. Proc. Natl. Acad. Sci. USA 2014, 111, 273–278. [Google Scholar]
- Iatsenko, D.; McClintock, P.V.E.; Stefanovska, A. Nonlinear Mode Decomposition: A Noise-Robust, Adaptive Decomposition Method. Phys. Rev. E 2015, in press. [Google Scholar]
- Vejmelka, M.; Paluš, M.; Šušmáková, K. Identification of Nonlinear Oscillatory Activity Embedded in Broadband Neural Signals. Int. J. Neural Syst. 2010, 20, 117–128. [Google Scholar]
- Paluš, M.; Novotná, D. Enhanced Monte Carlo Singular System Analysis and Detection of Period 7.8 years Oscillatory Modes in the monthly NAO Index and Temperature Records. Nonlinear Proc. Geoph. 2004, 11, 721–729. [Google Scholar]
- Hardstone, R.; Poil, S.S.; Schiavone, G.; Jansen, R.; Nikulin, V.V.; Mansvelder, H.D.; Linkenkaer-Hansen, K. Detrended Fluctuation Analysis: A Scale-Free View on Neuronal Oscillations. Front. Physiol. 2012, 3, 450. [Google Scholar]
- Klimesch, W. EEG Alpha and Theta Oscillations Reflect Cognitive and Memory Performance: A Review and Analysis. Brain Res. Rev. 1999, 29, 169–195. [Google Scholar]
- Purdon, P.L.; Pierce, E.T.; Mukamel, E.A.; Prerau, M.J.; Walsh, J.L.; Wong, K.F.K.; Salazar-Gomez, A.F.; Harrell, P.G.; Sampson, A.L.; Cimenser, A.; et al. Electroencephalogram Signatures of Loss and Recovery of Consciousness from Propofol. Proc. Natl. Acad. Sci. USA 2013, 110, E1142–E1151. [Google Scholar]
- Rudrauf, D.; Douiri, A.; Kovach, C.; Lachaux, J.P.; Cosmelli, D.; Chavez, M.; Adam, C.; Renault, B.; Martinerie, J.; Le Van Quyen, M. Frequency Flows and the Time-Frequency Dynamics of Multivariate Phase Synchronization in Brain Signals. Neuroimage 2006, 31, 209–227. [Google Scholar]
- Fell, J.; Axmacher, N. The Role of Phase Synchronization in Memory Processes. Nat. Rev. Neurosci. 2011, 12, 105–118. [Google Scholar]
- Lachaux, J.P.; Rodriguez, E.; Martinerie, J.; Varela, F.J. Measuring Phase Synchrony in Brain Signals. Hum. Brain Mapp. 1999, 8, 194–208. [Google Scholar]
- Tass, P.; Rosenblum, M.G.; Weule, J.; Kurths, J.; Pikovsky, A.; Volkmann, J.; Schnitzler, A.; Freund, H.J. Detection of n:m Phase Locking from Noisy Data: Application to Magnetoencephalography. Phys. Rev. Lett. 1998, 81, 3191–3294. [Google Scholar]
- Le Van Quyen, M.; Foucher, J.; Lachaux, J.P.; Rodriguez, E.; Lutz, A.; Martinerie, J.; Varela, F.J. Comparison of Hilbert Transform and Wavelet Methods for the Analysis of Neural Synchrony. J. Neurosci. Methods 2001, 111, 83–98. [Google Scholar]
- Sheppard, L.W.; Hale, A.C.; Petkoski, S; McClintock, P.V.E.; Stefanovska, A. Characterizing an Ensemble of Interacting Oscillators: The Mean-Field Variability Index. Phys. Rev. E 2013, 87, 012905. [Google Scholar]
- Palva, S.; Palva, J.M. New Vistas for α-Frequency Band Oscillations. Trends Neurosci. 2007, 30, 150–158. [Google Scholar]
- Stankovski, T.; Ticcinelli, V.; McClintock, P.V.E.; Stefanovska, A. Coupling Functions in Networks of Oscillators. New J. Phys. 2015, 17, 035002. [Google Scholar]
- Sauseng, P.; Klimesch, W. What does Phase Information of Oscillatory Brain Activity Tell us about Cognitive Processes? Neurosci. Biobehav. R. 2008, 32, 1001–1013. [Google Scholar]
- Darvas, F.; Miller, K.J.; Rao, R.P.N.; Ojemann, J.G. Nonlinear Phase-Phase Cross-Frequency Coupling Mediates Communication between Distant Sites in Human Neocortex. J. Neurosci. 2009, 29, 426–435. [Google Scholar]
- Tort, A.B.L.; Komorowski, R.; Eichenbaum, H.; Kopell, N. Measuring Phase-Amplitude Coupling between Neuronal Oscillations of Different Frequencies. J. Neurophysiol. 2010, 104, 1195–1210. [Google Scholar]
- Friston, K.J. Another Neural Code? Neuroimage 1997, 5, 213–220. [Google Scholar]
- Hurtado, J.M.; Rubchinsky, L.L.; Sigvardt, K.A. Statistical Method for Detection of Phase-Locking Episodes in Neural Oscillations. J. Neurophysiol. 2004, 91, 1883–1898. [Google Scholar]
- Lisman, J.E.; Jensen, O. The Theta-Gamma Neural Code. Neuron 2013, 77, 1002–1016. [Google Scholar]
- Canolty, R.T.; Knight, R.T. The Functional Role of Cross-Frequency Coupling. Trends Cogn. Sci. 2010, 14, 506–515. [Google Scholar]
- Mukamel, E.A.; Pirondini, E.; Babadi, B.; Foon Kevin Wong, K.; Pierce, E.T.; Harrell, P.G.; Walsh, J.L.; Salazar-Gomez, A.F.; Cash, S.S.; Eskandar, E.N.; et al. A Transition in Brain State during Propofol-Induced Unconsciousness. J. Neurosci. 2014, 34, 839–845. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lancaster, G.; Clemson, P.T.; Suprunenko, Y.F.; Stankovski, T.; Stefanovska, A. Detecting Chronotaxic Systems from Single-Variable Time Series with Separable Amplitude and Phase. Entropy 2015, 17, 4413-4438. https://doi.org/10.3390/e17064413
Lancaster G, Clemson PT, Suprunenko YF, Stankovski T, Stefanovska A. Detecting Chronotaxic Systems from Single-Variable Time Series with Separable Amplitude and Phase. Entropy. 2015; 17(6):4413-4438. https://doi.org/10.3390/e17064413
Chicago/Turabian StyleLancaster, Gemma, Philip T. Clemson, Yevhen F. Suprunenko, Tomislav Stankovski, and Aneta Stefanovska. 2015. "Detecting Chronotaxic Systems from Single-Variable Time Series with Separable Amplitude and Phase" Entropy 17, no. 6: 4413-4438. https://doi.org/10.3390/e17064413




