Oxygen Saturation and RR Intervals Feature Selection for Sleep Apnea Detection
Abstract
:1. Introduction
2. Materials and Methods
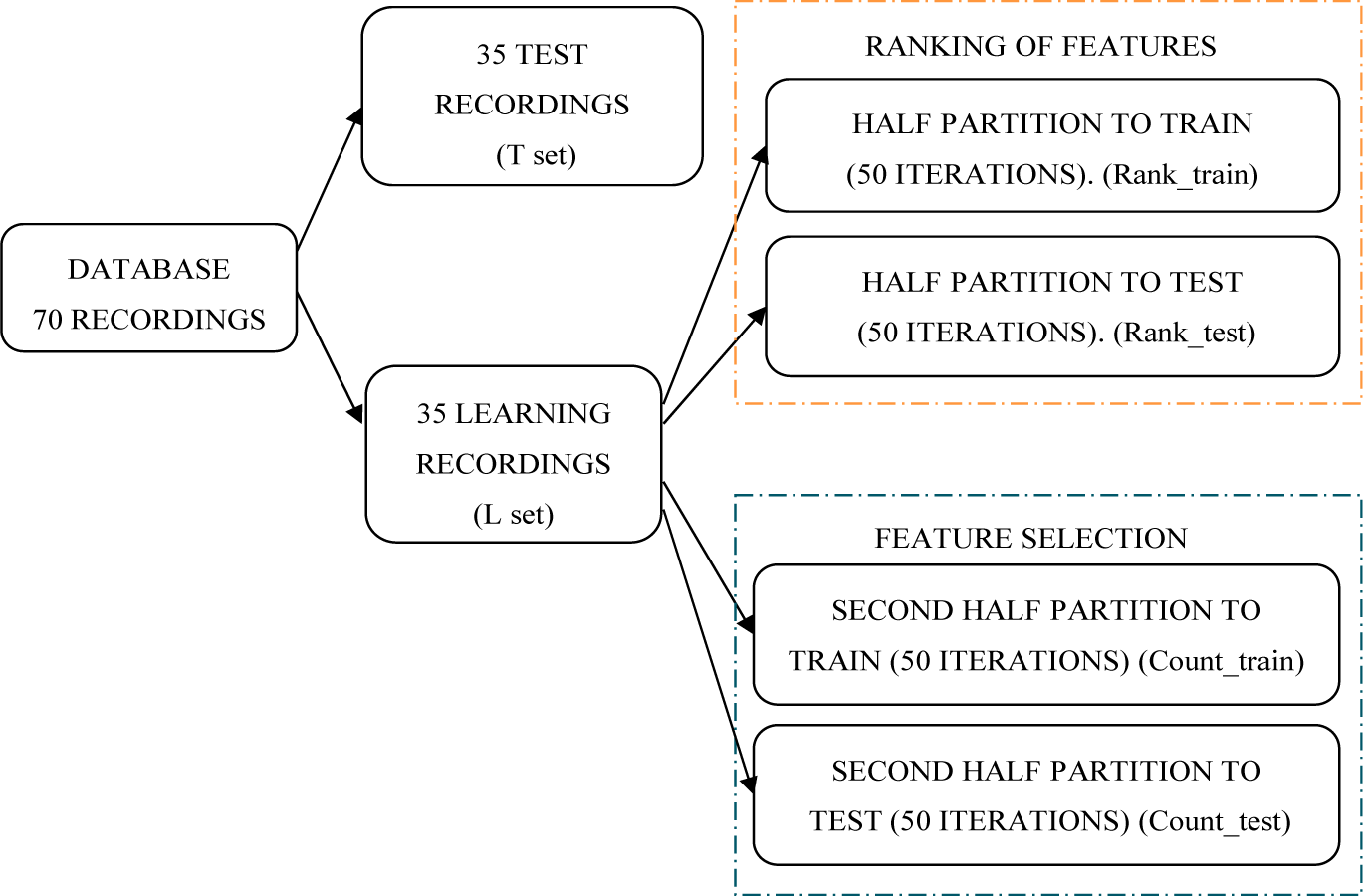
2.1. Data Sets
- Class A (46 recordings): Recordings contain AHI greater than or equal to 10 and at least 70 min with apnea. Both the L set and the T set contain 23 recordings fitting this criterion.
- Class B (4 recordings): Recordings contain AHI greater or equal to 5 and between 5 and 69 min with apnea. There are two recordings in each group (L and T set) that fit this criterion.
- Class C (20 recordings): These recordings can be considered normal since AHI is lower than 5. Both groups (L and T set) contain 10 recordings of class C.
2.2. Time Domain Oximetry Features
2.3. Frequency Domain Oximetry Features
2.4. Generation and Postprocessing of RR Intervals
2.5. Time Domain RR Interval Features
- -
- meanNN: the mean value of the NN-intervals in 5 min segments
- -
- sdNN: standard deviation of the NN-intervals in 5 min segments
- -
- cvNN: coefficient of variation of the NN-intervals (quotient of standard deviation and mean value of the filtered tachogram)
- -
- Rmssd: root mean square of successive 5 min of NN intervals:
- -
- sdaNN1: standard deviation of mean values of successive 1 min of NN-intervals:where M = 5, and N is the number of NN intervals in a one minute segment.
- -
- pNN20: Percentage of NN-interval differences greater than 20 ms
- -
- pNN30: Percentage of NN-interval differences greater than 30 ms
- -
- pNN50: Percentage of NN-interval differences greater than 50 ms
- -
- pNN100: Percentage of NN-interval differences greater than 100 ms
- -
- pNN120: Percentage of NN-interval differences greater than 120 ms
- -
- pNN150: Percentage of NN-interval differences greater than 150 ms
- -
- Shanon: The Shannon entropy in each 5 min tachogram is calculated by the following expression:where f is the probability density function estimated from histogram obtained in each 5 min tachogram frame and w is the width of the ith bin. In our particular case, the width of each bin is 20 ms leading to the total of n = 100 bins.
- -
- Renyi: Renyi entropy for a histogram of each 5 min tachogram is calculated. Expression (9) estimates the Renyi entropy:where w is the width of the ith bin. Entropies of order 2, 4 and 0.25 (Renyi2, Renyi4 and Renyi0.25) will be used.
- -
- noNNtime: Total time with artifacts in milliseconds.
2.6. Frequency Domain RR Interval Features
- -
- ULF: power in the frequency band from 0 Hz up to 0.0033 Hz.
- -
- VLF: power in the frequency band from 0.0033 Hz up to 0.04 Hz.
- -
- LF: power in the frequency band from 0.04 Hz up to 0.15 Hz.
- -
- HF power in the frequency band from 0.15 Hz up to 0.4 Hz.
- -
- LF/HF: ratio of LF and HF.
- -
- LF/P: ratio between LF and total power P.
- -
- HF/P: ratio of HF and total power P.
- -
- VLF/P: ratio between VLF and total power P.
- -
- ULF/P: ratio between ULF and total power P.
- -
- (ULF + VLF)/P: ratio of ULF + VLF and total power P.
- -
- (ULF + VLF + LF)/P: ratio of ULF + VLF + LF and total power P.
- -
- LFn: LF in normalized units, LF/(P − VLF) × 100.
- -
- HFn: HF in normalized units, HF/(P − VLF) × 100.
2.7. Measures of Non-linear Dynamics of RR Intervals
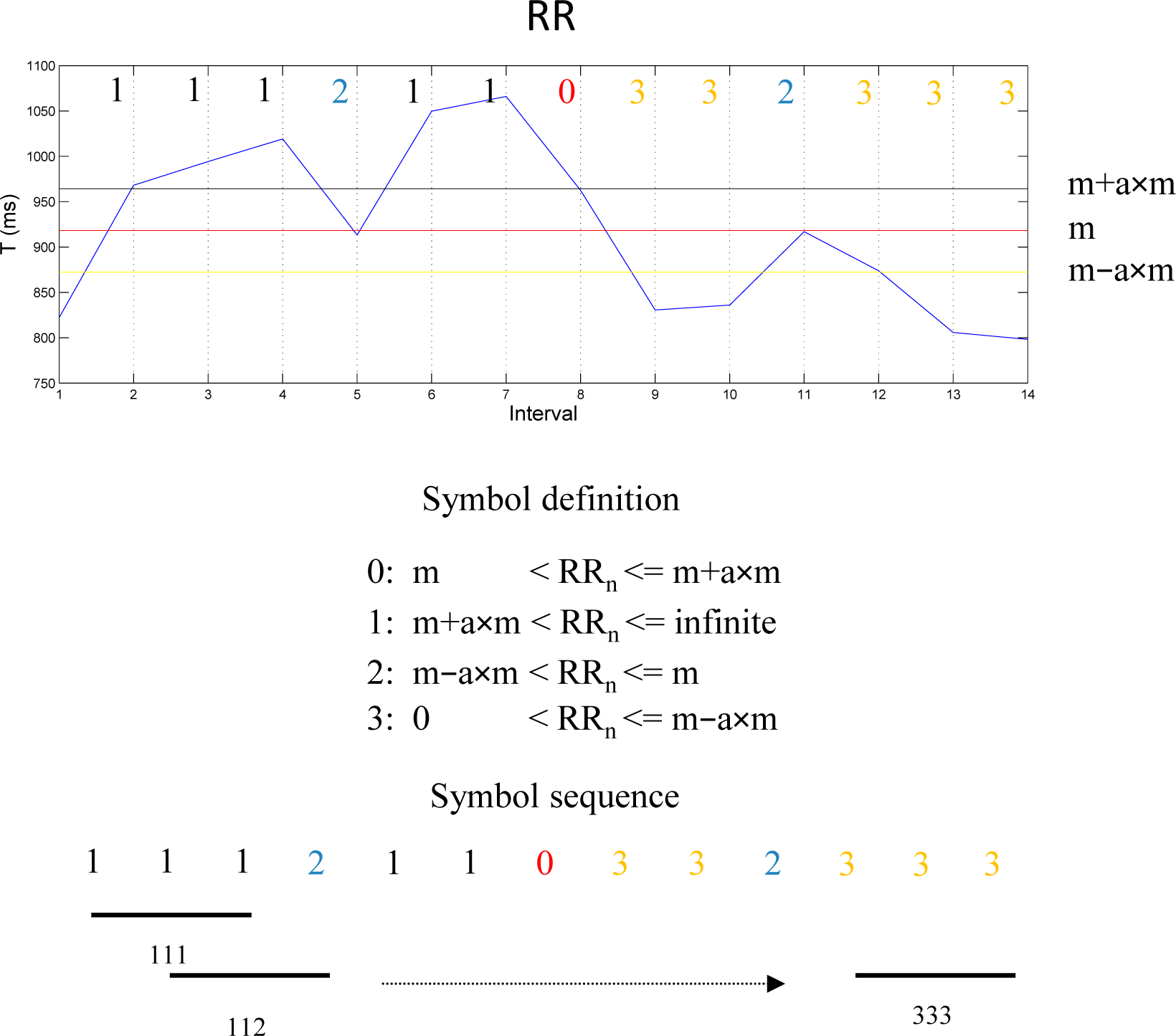
2.7.1. Symbolic Dynamic (SD)
- -
- WPSUM13: This variable quantifies the percentage of words which contain the symbols “1” and “3”. This feature is a measure of increased HRV.
- -
- WPSUM02: This variable quantifies the percentage of words which contain the symbols “0” and “2”. This feature is a measure of decreased HRV.
- -
- FWSHANNON: Shannon entropy of order k is defined on the basis of the probability distribution p of words of length k [12].where ωk denotes the set of all words of length k.
- -
- FWRENYI: This is a generalization of Shannon entropy based on the distribution of probability p of length k words and defined by the following expression:where q is a real number greater than zero. The q parameter can be adjusted to weight probabilities differently, for example if q > 1, the words of length k with large probabilities dominantly influence the Renyi entropy. On the other hand if 0 < q <1 the words with small probabilities mainly determine the value of Hk(q). In our case we have considered these two possibilities using q = 0.25 (FWRENYI0.25) and q = 4 (FWRENYI4). Starting from the word sequences it is possible to derive other sequences which can then be analyzed. The variables which we state in the following are based on this proposal.
- -
- WSDVAR: This variable is a measure of the variability of the time series calculated from the transformed sequence of words. The resulting sequence of words {ω1,ω2,ω3,…} of Figure 2 is transformed into a sequence as described in (14):where n13(ωi) represents the number of symbols corresponding to 1 or 3 in the word and s13(ωi) represents the first occurring symbol, either 1 or 3, in the word ωi. WSDVAR is defined as the standard deviation of the sequence .
- -
- FORBWORDS: This variable counts the so-called forbidden words of length 3. Specifically, the number of words that never occur or do so with very low probability (less than 0.001) is calculated. If the sequence under study is highly complex, we will find few forbidden words. A large number of forbidden words can, on the other hand, imply a much more regular behaviour.
- -
- POLVAR: These variables represent the probability that the word “000000” occurs for a specific threshold, thus describing the occurrence of low heart rate variability. We select three versions for analysis: POLVAR5, POLVAR10, POLVAR20, with thresholds of 5, 10 and 20 ms respectively.
- -
- PHVAR: Oposite to POLVAR, the PHVAR variables represent the probability of the word “111111”, so quantifying high variation in heart rate as defined by thresholds as above (5, 10 and 20 ms) resulting in the PHVAR5, PHVAR10 and PHVAR20 variables.
2.8. Classifier
2.9. Global Classification Criterion
2.10. Feature Selection
3. Results
3.1. Descriptive Statistics
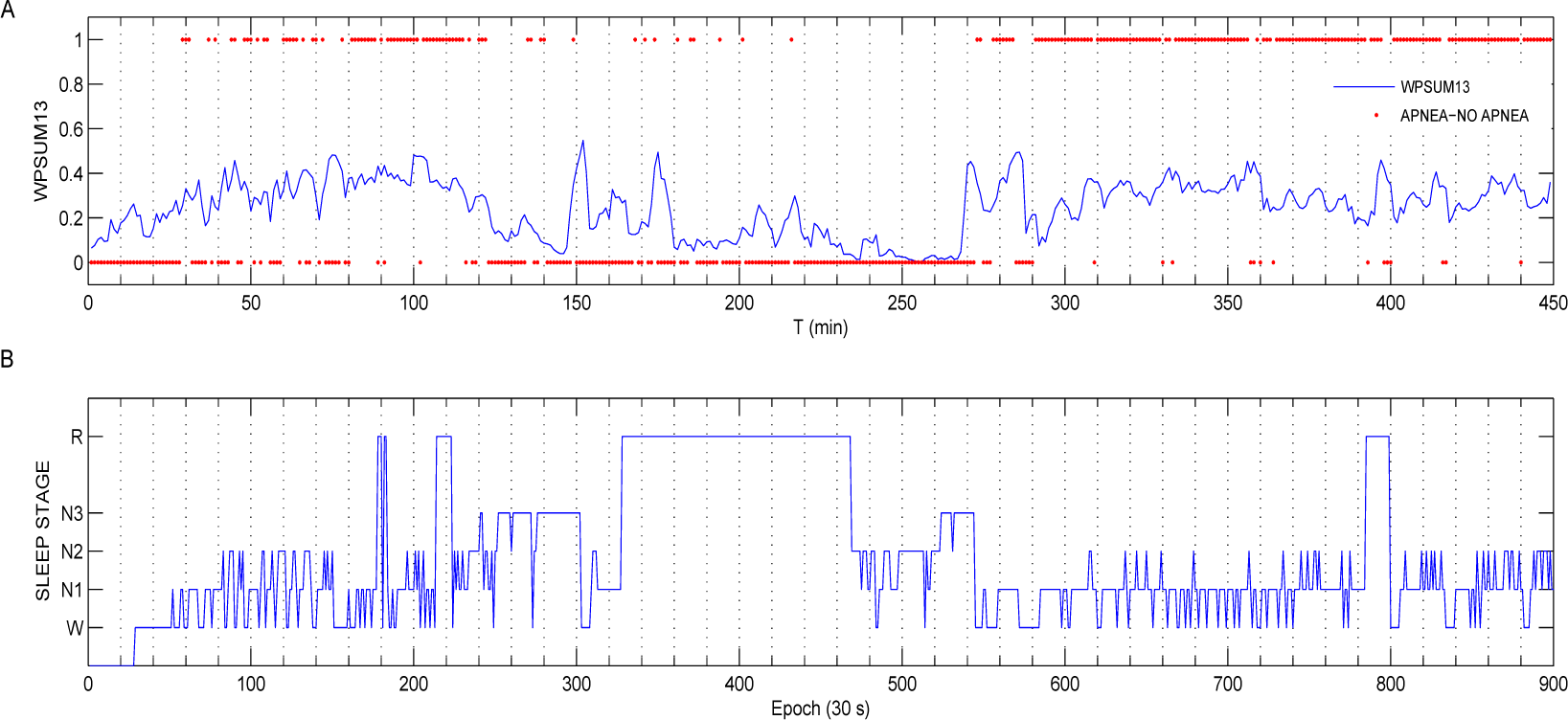
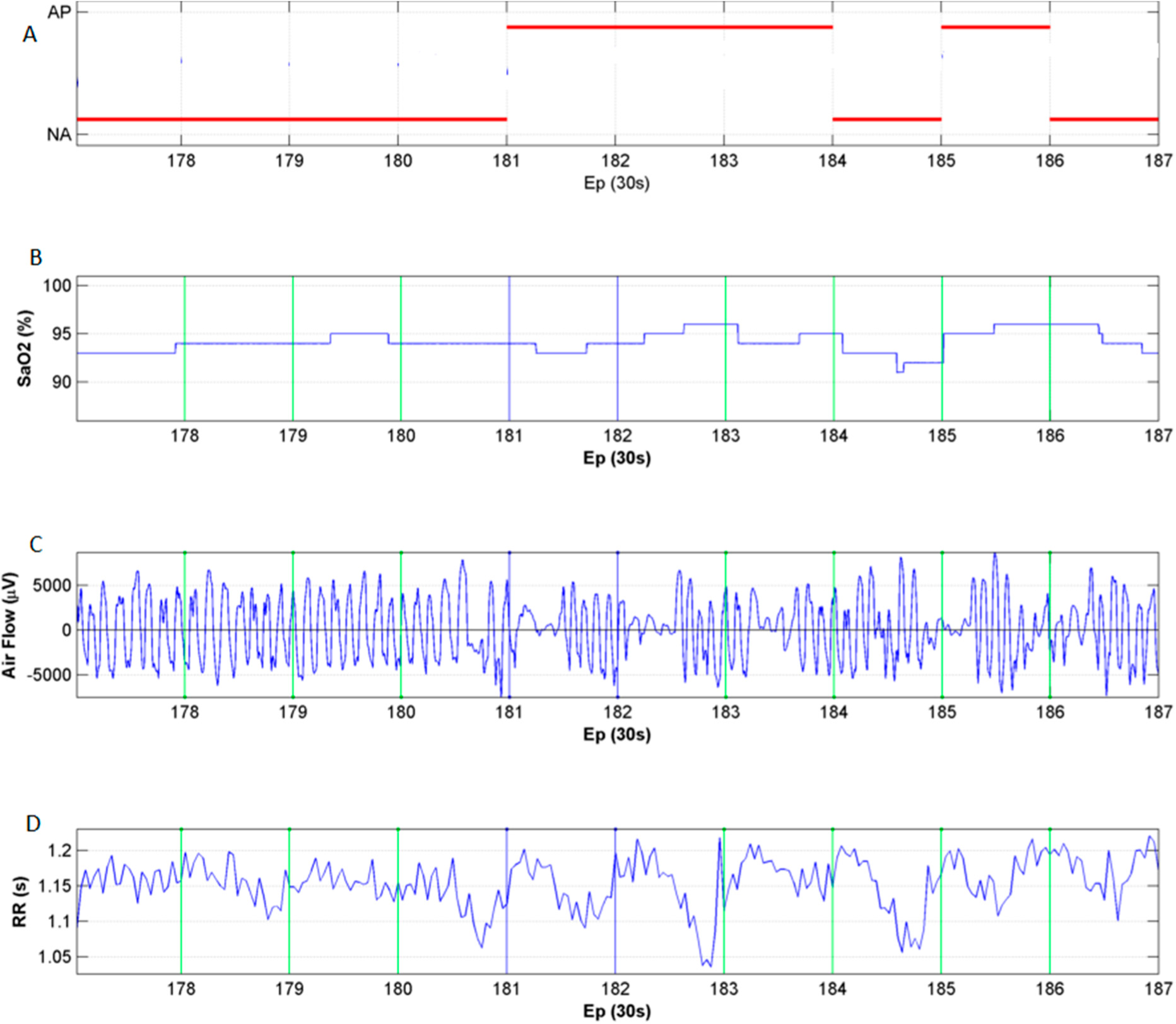
3.2. HRV and Oximetry Pattern Obtained in Presence of OSA
3.3. Results of the OSA Detection System Based on LDA Classifier
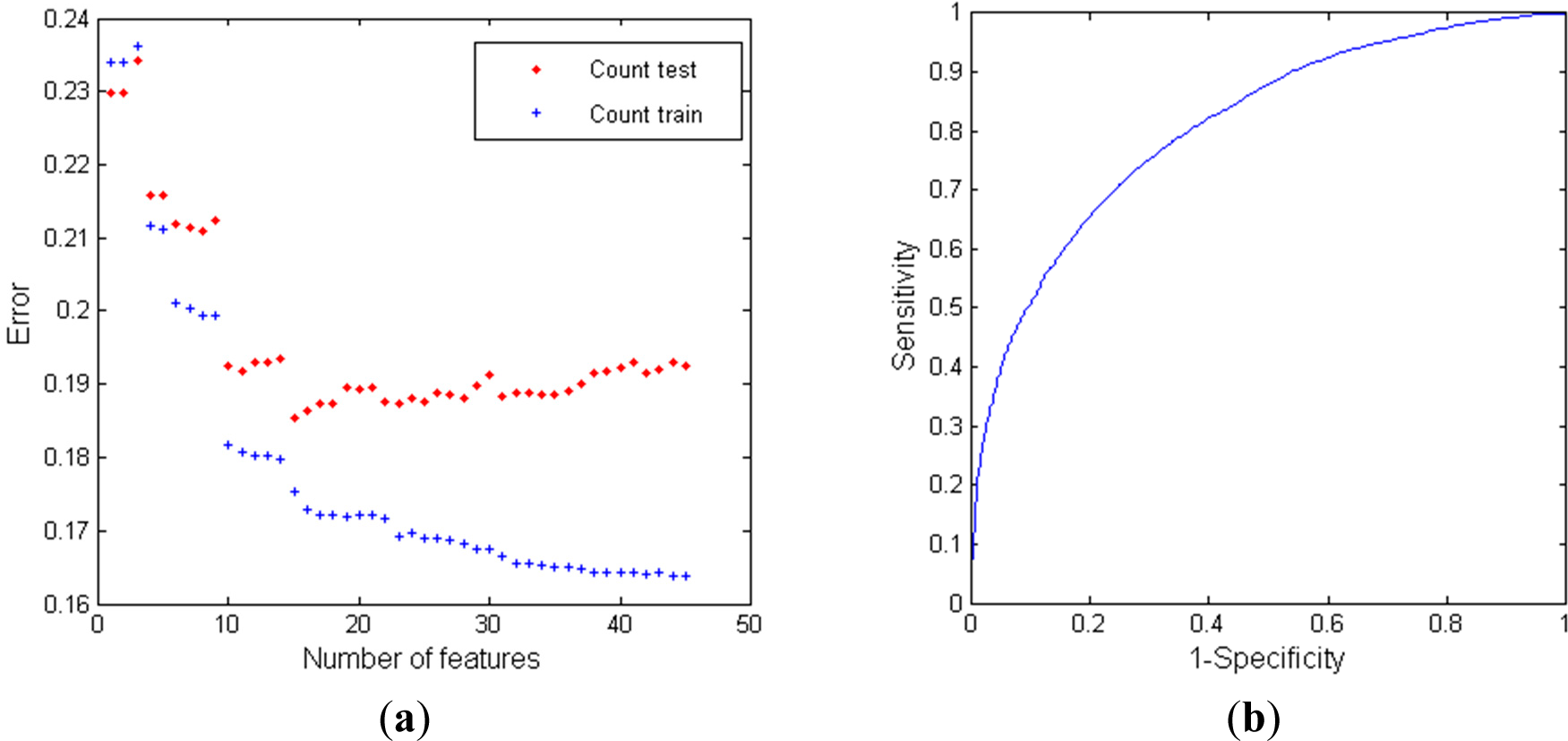
3.3.1. Classifier Performance using RR Intervals
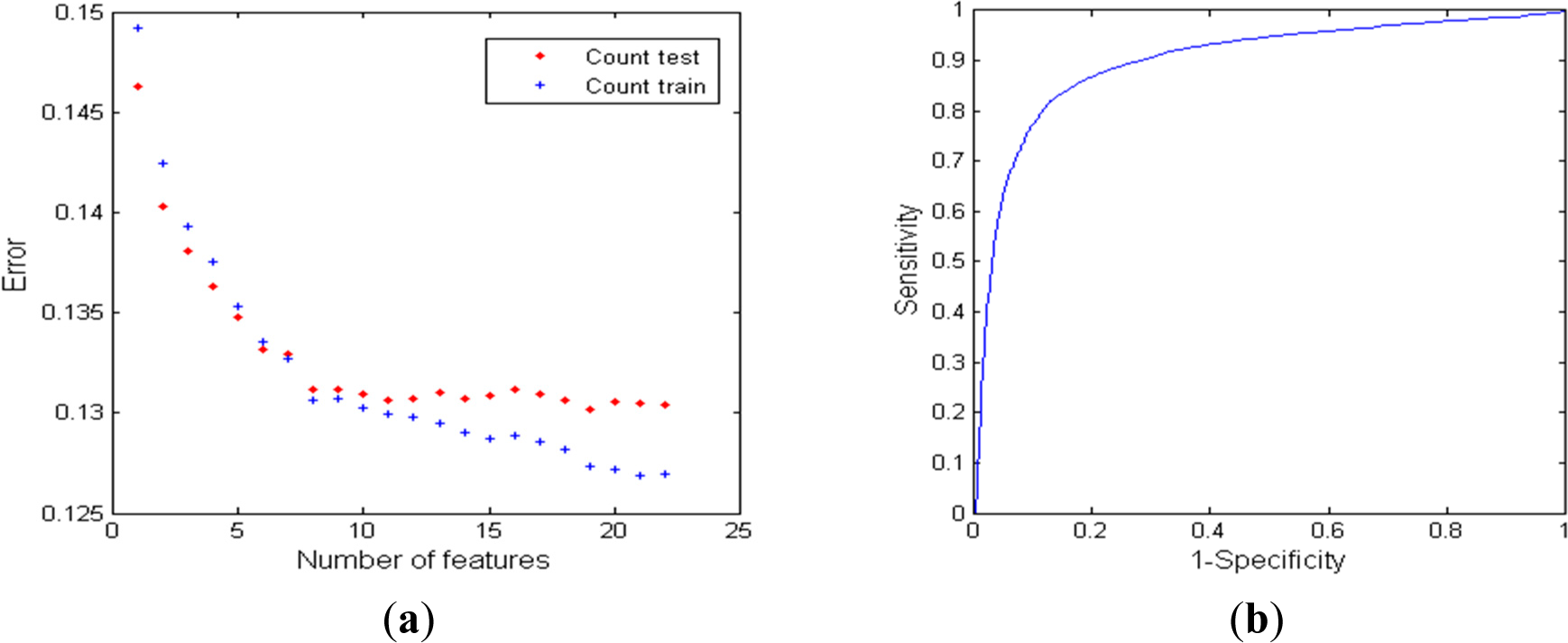
3.3.2. Classifier Performance using Oximetry
3.3.3. Classifier Performance using RR Series and Oximetry
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ravelo-Garcia, A.; Navarro-Mesa, J.; Hernádez-Pérez, E.; Martin-González, S.; Quintana-Morales, P.; Guerra-Moreno, I.; Juliá-Serdá, G. Cepstrum Feature Selection for the Classification of Sleep Apnea-Hypopnea Syndrome based on Heart Rate Variability, Proceedings of the IEEE Computing in Cardiology Conference (CinC), Zaragoza, Spain, 22–25 September 2013; pp. 959–962.
- Ravelo, A.; Travieso, C.; Lorenzo, F.; Navarro, J.; Martin, S.; Alonso, J.; Ferrer, M. Application of support vector machines and gaussian mixture models for the detection of obstructive sleep apnoea based on the RR series. WSEAS Trans. Comput. 2006, 5, 121–124. [Google Scholar]
- Park, J.G.; Ramar, K.; Olson, E.J. Updates on definition, consequences, and management of obstructive sleep apnea. Mayo Clin. Proc. 2011, 86, 549–555. [Google Scholar]
- Berry, R.B.; Budhiraja, R.; Gottlieb, D.J.; Gozal, D.; Iber, C.; Kapur, V.K.; Marcus, C.L.; Mehra, R.; Parthasarathy, S.; Quan, S.F.; et al. Rules for scoring respiratory events in sleep: Update of the 2007 AASM manual for the scoring of sleep and associated events. J. Clin. Sleep Med. 2012, 8, 597–619. [Google Scholar]
- Moser, D.; Anderer, P.; Gruber, G.; Parapatics, S.; Loretz, E.; Boeck, M.; Kloesch, G.; Heller, E.; Schmidt, A.; Danker-Hopfe, H.; et al. Sleep classification according to AASM and Rechtschaffen & Kales: Effects on sleep scoring parameters. Sleep 2009, 32, 139–149. [Google Scholar]
- Ruehland, W.R.; O’Donoghue, F.J.; Pierce, R.J.; Thornton, A.T.; Singh, P.; Copland, J.M.; Stevens, B.; Rochford, P.D. The 2007 AASM recommendations for EEG electrode placement in polysomnography: Impact on sleep and cortical arousal scoring. Sleep 2011, 34, 73–81. [Google Scholar]
- Deutsch, P.; Simmons, M.; Wallace, J. Cost-effectiveness of split-night polysomnography and home studies in the evaluation of obstructive sleep apnea syndrome. J. Clin. Sleep Med. 2006, 2, 145–153. [Google Scholar]
- Chiner, E. Approach to the cost of polysomnography in a spanish hospital. Int. J. Pulmon. Med. 2001, 2(2). [Google Scholar]
- Lévy, P.; Pépin, J.L.; Deschaux-Blanc, C.; Paramelle, B.; Brambilla, C. Accuracy of Oximetry for Detection of Respiratory Disturbances in Sleep Apnea Syndrome. Chest 1996, 109, 395–399. [Google Scholar]
- Coccagna, G.; Lugaresi, E. Arterial blood gases and pulmonary and systemic arterial pressure during sleep in chronic obstructive pulmonary disease. Sleep 1978, 1, 117–124. [Google Scholar]
- Wessel, N.; Voss, A.; Malberg, H.; Ziehmann, C.; Voss, H.U.; Schirdewan, A.; Meyerfeldt, U.; Kurths, J. Nonlinear analysis of complex phenomena in cardiological data. Herzschr. Elektrophys. 2000, 11, 159–173. [Google Scholar]
- Voss, A.; Kurths, J.; Kleiner, H.J.; Witt, A.; Wessel, N.; Saparin, P.; Osterziel, K.J.; Schumann, R.; Dietz, R. The application of methods of non-linear dynamics for the improved and predictive recognition of patients threatened by sudden cardiac death. Cardiovasc. Res. 1996, 31, 419–433. [Google Scholar]
- Penzel, T.; Moody, G.B.; Mark, R.G.; Goldberger, A.L.; Peter, J.H. The Apnea-ECG Database. Comput. Cardiol. 2000, 27, 255–258. [Google Scholar]
- Ravelo-García, A.G.; Navarro-Mesa, J.L.; Murillo-Díaz, M.J.; Julia-Serda, G. Application of RR Series and Oximetry to a Statistical Classifier for the Detection of Sleep Apnoea/Hipopnoea, Proceedings of the IEEE Computers in Cardiology Conference 2004 (CinC), Chicago, IL, USA, 19–22 September 2004; pp. 305–308.
- Trimer, R.; Cabidu, R.; Sampaio, L.L.M.; Stirbulov, R.; Poiares, D.; Guizilini, S.; Bianchi, A.M.; Costa, F.S.M.; Mendes, R.G.; Delfino, A., Jr.; et al. Heart rate variability and cardiorespiratory coupling in obstructive sleep apnea: Elderly compared with young. Sleep Med. 2014, 15, 1324–1331. [Google Scholar]
- Maeder, M.T. More on heart rate variability in obstructive sleep apnea: Confusion on a higher level or first step to unravel the cardiovascular mystery of the sleep apnea patient? Sleep Breath. 2014, 18, 233–234. [Google Scholar]
- Kleiger, R.E.; Bosner, M.S.; Rottman, J.N.; Stein, P.K. Time-domain measurements of heart rate variability. J. Ambul. Monit. 1992, 10, 487–498. [Google Scholar]
- Wessel, N.; Malberg, H.; Bauernschmitt, R.; Kurths, J. Nonlinear methods of cardiovascular physics and their clinical applicability. Int. J. Bifurcat. Chaos. 2007, 17, 3325–3371. [Google Scholar]
- Bigger, J.T.; Fleiss, J.L.; Steinman, R.C.; Rolnitzky, L.M.; Kleiger, R.E.; Rottman, J.N. Frequency domain measures of heart period variability and mortality after myocardial infarction. Circulation 1992, 85, 164–171. [Google Scholar]
- Ravelo-García, A.G.; Casanova-Blancas, U.; Martín-González, S.; Hernández-Pérez, E.; Guerra-Moreno, I.; Quintana-Morales, P.; Wessel, N.; Navarro-Mesa, J.L. An Approach to the Enhancement of Sleep Apnea Detection by means of Detrended Fluctuation Analysis of RR intervals. Comput. Cardiol. 2014, 41, 905–908. [Google Scholar]
- Hayano, J.; Barros, A.K.; Kamiya, A.; Ohte, N.; Yasuma, F. Assessment of pulse rate variability by the method of pulse frequency demodulation. BioMed. Eng. Online. 2005, 4. [Google Scholar] [CrossRef]
- Task Force of the European Society of Cardiology, the North American. Society of Pacing, and Electrophysiology. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Circulation 1996, 93, 1043–1065.
- Ravelo-García, A.G.; Saavedra-Santana, P.; Juliá-Serdá, G.; Navarro-Mesa, J.L.; Navarro-Esteva, J.; Álvarez-López, X.; Gapelyuk, A.; Penzel, T.; Wessel, N. Symbolic dynamics marker of heart rate variability combined with clinical variables enhance obstructive sleep apnea screening. Chaos 2014, 24, 024404. [Google Scholar]
- Wessel, N.; Riedl, M.; Kurths, J. Is the normal heart rate “chaotic” due to respiration? Chaos 2009, 19, 028508. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized additive models. Stat. Sci. 1986, 1, 297–310. [Google Scholar]
- Al-Angari, H.M.; Sahakian, A.V. Automated recognition of obstructive sleep apnea syndrome using support vector machine classifier. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 463–468. [Google Scholar]
- Bouckaert, RR.; Frank, E. Evaluating the replicability of significance tests for comparing learning algorithms. In Advances in Knowledge Discovery and Data Mining, Proceedings of the 8th Pacific-Asia Conference, PAKDD 2004, Sydney, Australia, 26–28 May 2004; Dai, H., Srikant, R., Zhang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; 3056, pp. 3–12. [Google Scholar]
- Marcos, J.V.; Hornero, R.; Álvarez, D.; del Campo, F.; Zamarrón, C. Assessment of four statistical pattern recognition techniques to assist in obstructive sleep apnoea diagnosis from nocturnal oximetry. Med. Eng. Phys. 2009, 31, 971–978. [Google Scholar]
- Alvarez, D.; Hornero, R.; Marcos, J.V.; del Campo, F. Multivariate analysis of blood oxygen saturation recordings in obstructive sleep apnea diagnosis. IEEE Trans. Biomed. Eng. 2010, 57, 2816–2824. [Google Scholar]
- Alvarez, D.; Hornero, R.; Marcos, J.V.; Wessel, N.; Penzel, T.; del Campo, F. Assessment of feature selection approaches to enhance information from overnight oximetry in the context of sleep apnea diagnosis. Int. J. Neural Syst. 2013, 23. [Google Scholar] [CrossRef]
- Xie, B.; Minn, H. Real-Time Sleep Apnea Detection by Classifier Combination. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 469–477. [Google Scholar]
- Burgos, A.; Goñi, A.; Illarramendi, A.; Bermúdez, J. Real-Time Detection of Apneas on a PDA. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 995–1002. [Google Scholar]
- Masa, J.F.; Corral, J.; Pereira, R.; Duran-Cantolla, J.; Cabello, M.; Hernández-Blasco, L.; Monasterio, C.; Alonso, A.; Chiner, E.; Rubio, M.; et al. Effectiveness of home respiratory polygraphy for the diagnosis of sleep apnoea and hypopnoea syndrome. Thorax 2011, 66, 567–573. [Google Scholar]
- Ravelo-García, A.G.; Navarro-Mesa, J.L.; Casanova-Blancas, U.; Martin-Gonzalez, S.; Quintana-Morales, P.; Guerra-Moreno, I.; Canino-Rodríguez, J.M.; Hernández-Pérez, E. Application of the Permutation Entropy over the Heart Rate Variability for the Improvement of Electrocardiogram-based Sleep Breathing Pause Detection. Entropy 2015, 17, 914–927. [Google Scholar]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; Gomez-Pilar, J.; del Campo, F.; Hornero, R. Assessment of Time and Frequency Domain Entropies to Detect Sleep Apnoea in Heart Rate Variability Recordings from Men and Women. Entropy 2015, 17, 123–141. [Google Scholar]




| SUBJECTS | AHI | DIPS/h | APNEA-HYPOPNEA DURATION (s) |
|---|---|---|---|
| APNEA (Group A and B) | 48.87 (11–151.9) | 53.65 (7.9–122.3) | 17.8 (10–125) |
| NORMAL (Group C) | 1.87 (0–4.8) | 1.55 (0–4.3) | 12 (0–30) |
| Features | A | NA | P |
|---|---|---|---|
| meanNN5m (ms) | 917.12 (820.97;995.03) | 913.89 (836.84;989.55) | NS |
| SdNN5m (ms) | 63.27 (42.85;89.94) | 40.35 (27.42;61.65) | <0.0001 |
| CvNN5m (ms) | 0.07 (0.05;0.1) | 0.05 (0.03;0.07) | <0.0001 |
| sdaNN1 (ms) | 20.04 (12.19;32.19) | 14.97 (8.51;27.27) | <0.001 |
| Rmssd (ms) | 31.42 (19.9;50.1) | 22.78 (14.49;37.35) | <0.0001 |
| pNN20 (%) | 0.47 (0.26;0.62) | 0.36 (0.14;0.58) | <0.01 |
| pNN30 (%) | 0.71 (0.53;0.89) | 0.84 (0.6;0.96) | <0.001 |
| pNN50 (%) | 0.1 (0.02;0.26) | 0.03 (0;0.16) | <0.0001 |
| pNN100 (%) | 0.01 (0;0.05) | 0 (0;0.02) | <0,001 |
| pNN110 (%) | 0.28 (0.2;0.44) | 0.35 (0.22;0.55) | NS |
| pNN120 (%) | 0.53 (0.38;0.74) | 0.64 (0.42;0.86) | <0.01 |
| pNN150 (%) | 0.9 (0.74;0.98) | 0.97 (0.84;1) | <0.0001 |
| Shanon | 2.47 (2.11;2.78) | 2.03 (1.68;2.41) | <0.0001 |
| Renyi025 2.7 | (2.37;2.99) | 2.34 (2.01;2.69) | <0.0001 |
| Renyi4 2.17 | (1.79;2.49) | 1.7 (1.36;2.07) | <0.0001 |
| Renyi2 | 2.31 (1.94;2.63) | 1.84 (1.5;2.23) | <0.0001 |
| ULF (s2) | 22.08 (6.39;68.77) | 15.44 (4.14;55.92) | NS |
| VLF (s2) | 935.2 (406.61;1953.83) | 270.45 (112.84;691.04) | <0.0001 |
| LF (s2) | 376.71 (165.92;877.88) | 151.93 (66.32;362.75) | <0.0001 |
| HF (s2) | 110.78 (43.41;292.77) | 63.88 (25.07;178.28) | <0.001 |
| P (s2) 1713.15 | (767.24;3471.79) | 628.22 (283.64;1478.56) | <0.0001 |
| LF/HF | 3.51 (2.04;6.34) | 2.35 (1.09;4.98) | <0.05 |
| LF/P | 0.25 (0.16;0.38) | 0.26 (0.17;0.37) | NS |
| HF/P | 0.07 (0.04;0.13) | 0.11 (0.05;0.24) | <0.001 |
| VLF/P 0.61 | (0.46;0.73) | 0.5 (0.34;0.66) | <0.001 |
| ULF/P | 0.01 (0;0.04) | 0.03 (0.01;0.07) | NS |
| (ULF+VLF+LF)/P | 0.93 (0.87;0.96) | 0.89 (0.76;0.95) | <0.001 |
| (ULF+VLF)/P | 0.65 (0.48;0.77) | 0.56 (0.38;0.73) | <0.001 |
| UVLF (s2) | 989.77 (430.6;2043.49) | 298.42 (124.49;769.25) | <0.0001 |
| LFn 0.78 | (0.67;0.86) | 0.7 (0.52;0.83) | <0.05 |
| HFn 0.22 | (0.14;0.33) | 0.3 (0.17;0.48) | <0.05 |
| NoNNtime (ms) | 1053.13 (0;3993.13) | 1050.47 (0;4400.96) | NS |
| Features | A | NA | P |
|---|---|---|---|
| FORBWORD | 30 (21;38) | 37 (25;43) | <0.0001 |
| FWSHANNON | 2.82 (2.51;3.11) | 2.65 (2.24;3.08) | <0.001 |
| FWRENYI025 | 3.33 (3.07;3.59) | 3.13 (2.86;3.5) | <0.0001 |
| FWRENYI4 | 1.95 (1.6;2.29) | 1.91 (1.52;2.38) | NS |
| WSDVAR | 1.82 (1.38;2.2) | 1.24 (0.77;1.73) | <0.0001 |
| WPSUM02 | 0.33 (0.14;0.55) | 0.59 (0.33;0.82) | <0.0001 |
| WPSUM13 | 0.26 (0.13;0.41) | 0.09 (0.03;0.21) | <0.0001 |
| POLVAR5 | 0 (0;0.01) | 0 (0;0.01) | NS |
| POLVAR10 | 0 (0;0.03) | 0 (0;0.04) | NS |
| POLVAR20 | 0.06 (0.01;0.24) | 0.11 (0.01;0.44) | NS |
| PHVAR5 | 0.42 (0.23;0.56) | 0.32 (0.14;0.53) | <0.01 |
| PHVAR10 | 0.17 (0.05;0.31) | 0.08 (0.01;0.25) | <0.001 |
| PHVAR20 0.02 | (0;0.1) | 0 (0;0.05) | <0.0001 |
| Features | A | NA | P |
|---|---|---|---|
| var Sat1m | 5.229 (2.231;12.737) | 0.251 (0.163;0.778) | <0.0001 |
| var Sat5m | 6.678 (3.135;15.376) | 0.623 (0.259;1.659) | <0.0001 |
| Fb1 | 1.7 × 10−26 (5 × 10−27;1.2 × 10−25) | 4.1 × 10−25 (6.3 × 10−26;4.3 × 10−24) | <0.0001 |
| Fb2 | 0.054 (0.02;0.121) | 0.113 (0.046;0.236) | <0.0001 |
| Fb3 | 0.04 (0.015;0.087) | 0.073 (0.032;0.144) | <0.001 |
| Fb4 | 0.041 (0.016;0.087) | 0.06 (0.025;0.116) | NS |
| Fb5 | 0.045 (0.019;0.098) | 0.055 (0.023;0.104) | NS |
| Fb6 | 0.05 (0.02;0.107) | 0.051 (0.022;0.098) | NS |
| Fb7 | 0.057 (0.021;0.123) | 0.045 (0.018;0.087) | <0.01 |
| Fb8 | 0.057 (0.022;0.129) | 0.037 (0.015;0.073) | <0.01 |
| Fb9 | 0.047 (0.018;0.109) | 0.031 (0.013;0.062) | NS |
| Fb10 | 0.032 (0.012;0.075) | 0.026 (0.01;0.052); | NS |
| Fb11 | 0.021 (0.008;0.051) | 0.021 (0.008;0.043) | NS |
| Fb12 | 0.016 (0.006;0.036) | 0.017 (0.007;0.036) | NS |
| Fb13 | 0.012 (0.005;0.026) | 0.014 (0.005;0.031) | NS |
| Fb14 | 0.009 (0.004;0.021) | 0.011 (0.004;0.025) | NS |
| Fb15 | 0.008 (0.003;0.018) | 0.01 (0.004;0.022) | NS |
| Fb16 | 0.007 (0.003;0.016) | 0.008 (0.003;0.019) | NS |
| Fb17 | 0.006 (0.002;0.014) | 0.007 (0.003;0.016) | NS |
| Fb18 | 0.005 (0.002;0.012) | 0.006 (0.002;0.014) | NS |
| Fb19 | 0.004 (0.002;0.009) | 0.005 (0.002;0.012) | <0.05 |
| Fb20 | 0.003 (0.001;0.007) | 0.004 (0.002;0.01) | NS |
| Features | Signals | n | Variables | Acc % | Se % | Sp % | AUC % | Gc % | Gc %* |
|---|---|---|---|---|---|---|---|---|---|
| TD + FD + SD | RR | 15 | meanNN5m, ULF/P, ULF, WPSUM13, sdaNN1, Renyi4, Renyi025, Shanon, LF/P, HFn, Renyi2, sdNN5m, POLVAR5, (ULF+VLF)/P, POLVAR20 | 79.4 | 42.4 | 94.3 | 80.9 | 71.4 | 81.8 |
| Var + Fbank | SpO2 | 19 | var Sat1m, Fb2, Fb9, Fb8, Fb11, Fb20, Fb7, Fb12, Fb1, Fb18, Fb4, Fb5, Fb13, Fb17, Fb14, Fb15, Fb16, Fb6, Fb10 | 86.5 | 75.6 | 91 | 89.8 | 91.4 | 97 |
| TD + FD + SD + (Var + Fbank) | SpO2 + RR | 33 | var Sat1m, Fb2, Fb9, LF/HF, Fb3, (ULF+VLF+LF)/P, Fb8, sdaNN1, Fb12, FORBWORD, Fb11, var Sat5m, Fb1, pNN120, ULF/P, POLVAR5, LF/P, FWRENYI025, POLVAR10, Fb7, Shanon, HF, Renyi2, sdNN, Fb20, cvNN5m, Fb6, noNNtime, Fb16, Renyi025, pNN30, Renyi4, pNN110 | 86.9 | 73.4 | 92.3 | 91.9 | 94.3 | 100 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ravelo-García, A.G.; Kraemer, J.F.; Navarro-Mesa, J.L.; Hernández-Pérez, E.; Navarro-Esteva, J.; Juliá-Serdá, G.; Penzel, T.; Wessel, N. Oxygen Saturation and RR Intervals Feature Selection for Sleep Apnea Detection. Entropy 2015, 17, 2932-2957. https://doi.org/10.3390/e17052932
Ravelo-García AG, Kraemer JF, Navarro-Mesa JL, Hernández-Pérez E, Navarro-Esteva J, Juliá-Serdá G, Penzel T, Wessel N. Oxygen Saturation and RR Intervals Feature Selection for Sleep Apnea Detection. Entropy. 2015; 17(5):2932-2957. https://doi.org/10.3390/e17052932
Chicago/Turabian StyleRavelo-García, Antonio G., Jan F. Kraemer, Juan L. Navarro-Mesa, Eduardo Hernández-Pérez, Javier Navarro-Esteva, Gabriel Juliá-Serdá, Thomas Penzel, and Niels Wessel. 2015. "Oxygen Saturation and RR Intervals Feature Selection for Sleep Apnea Detection" Entropy 17, no. 5: 2932-2957. https://doi.org/10.3390/e17052932










