Entropic Measures of Complexity of Short-Term Dynamics of Nocturnal Heartbeats in an Aging Population
Abstract
:1. Introduction
2. Materials and Methods
2.1. Signal Preprocessing
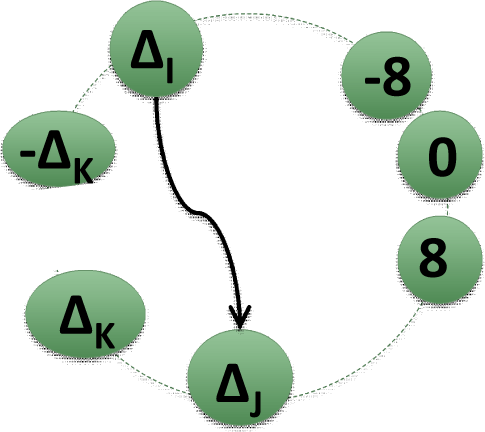
2.2. Matrices of Network Representation of RR-Increments
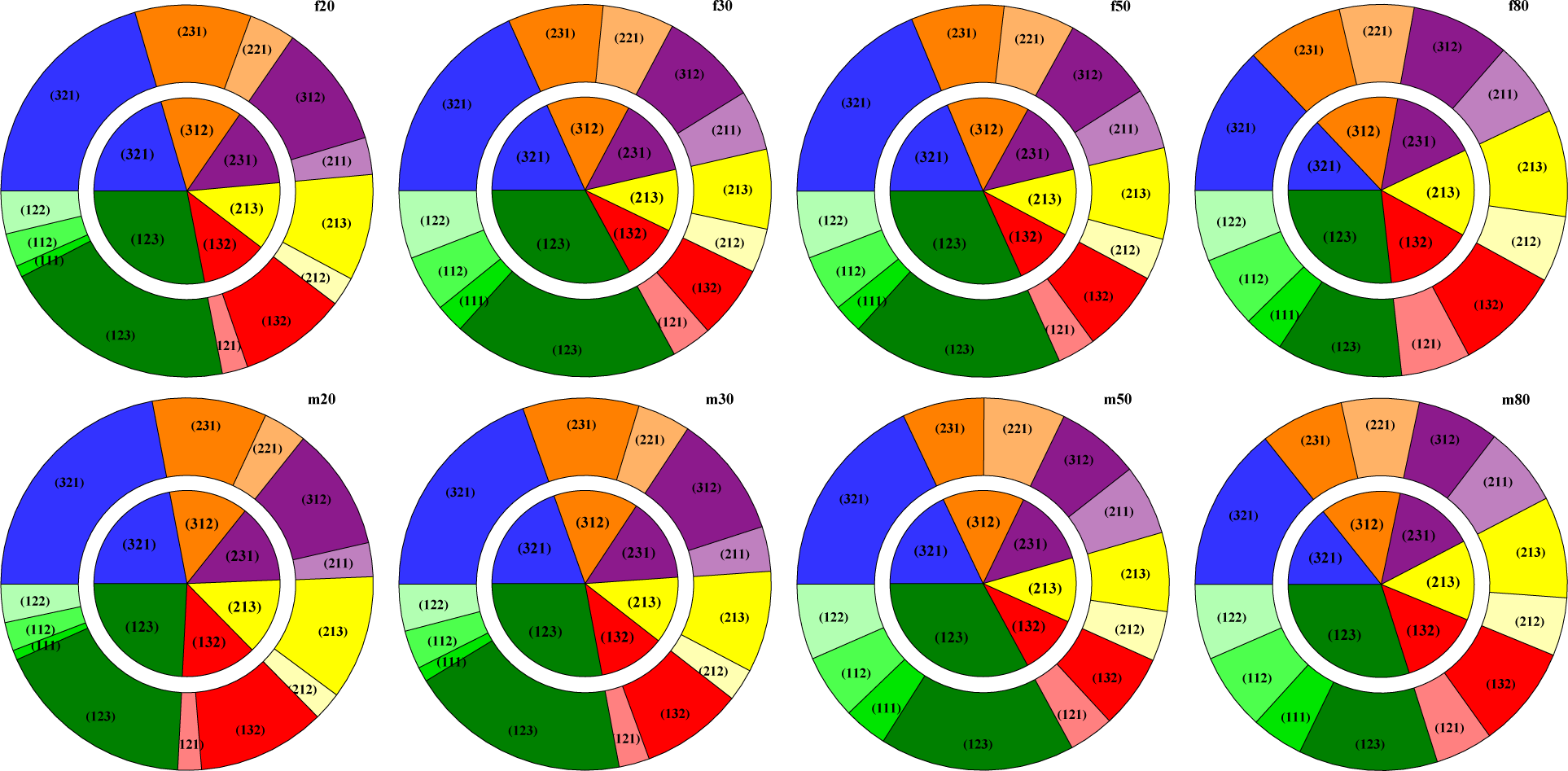
2.3. Ordinal Patterns
2.4. Statistics and Graphical Tools Used
3. Results and Discussion
3.1. Standard HRV Characteristics of the Groups Studied
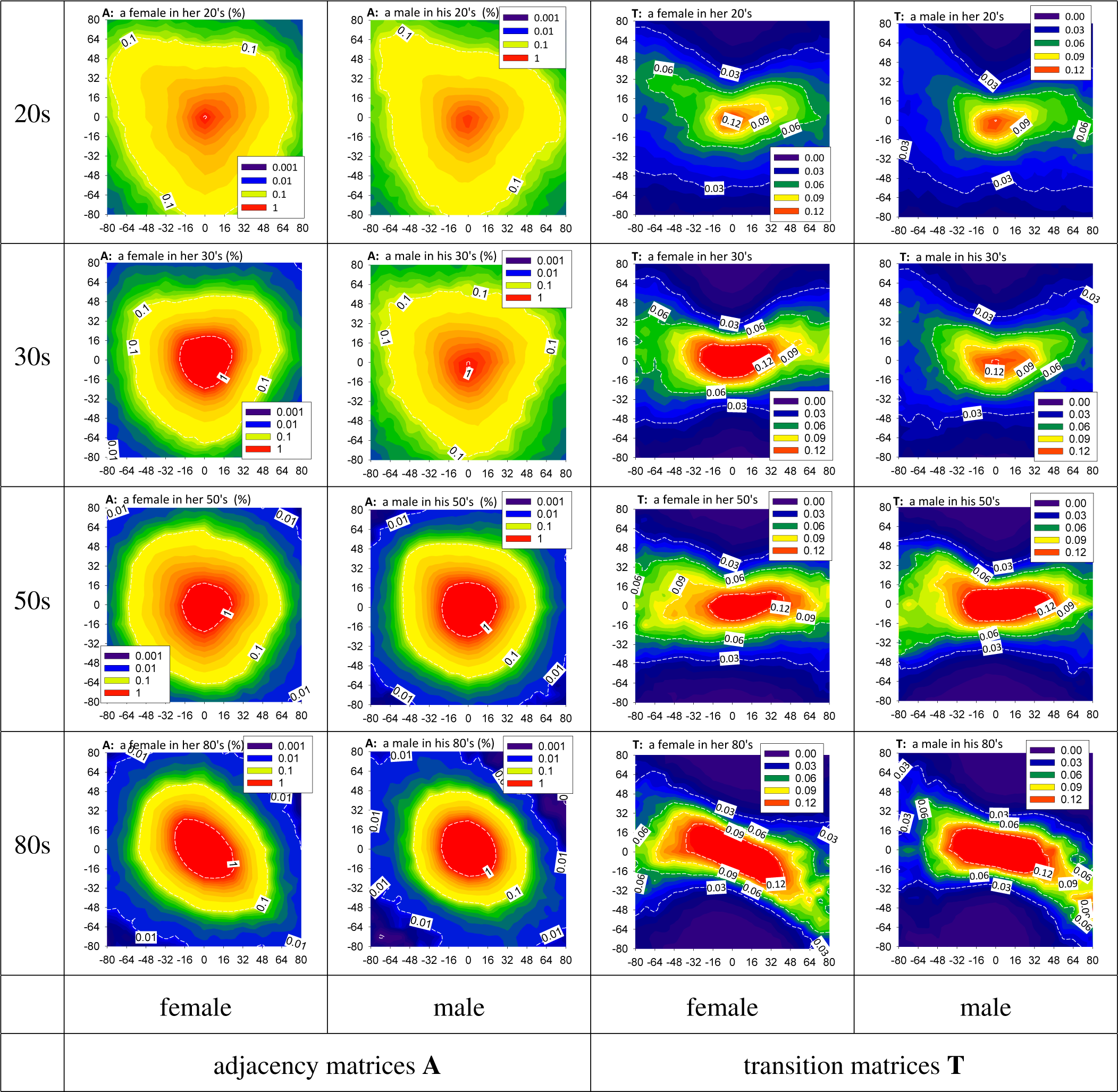
3.2. HRV by Adjacency and Transition Matrices
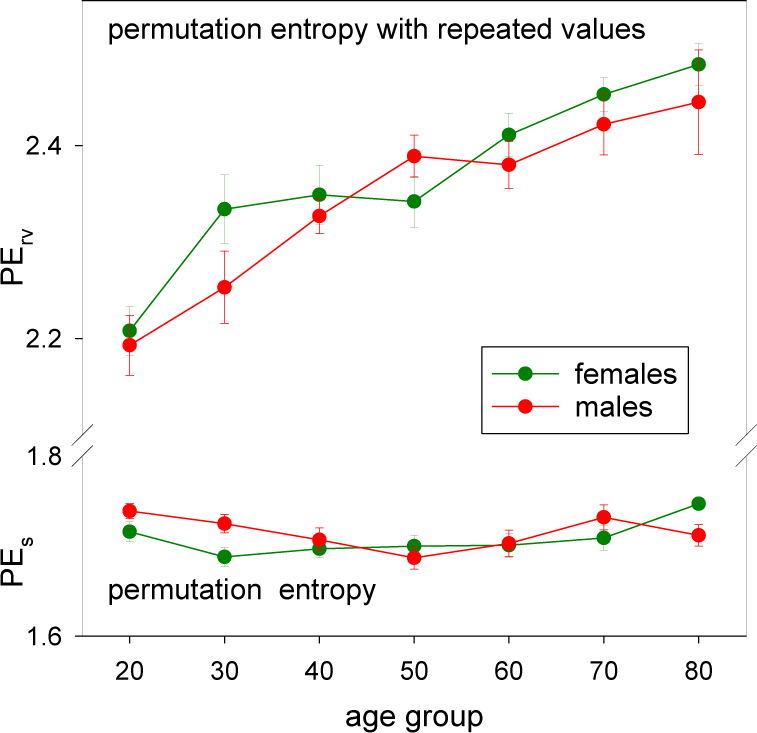
3.3. HRV by Permutation Entropy with Repeated Values
3.4. Correlations between the Measures Studied
3.5. Physiological Aspects of Healthy Aging
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar]
- Faes, L.; Nollo, G.; Jurysta, F.; Marinazzo, D. Information dynamics of brain–heart physiological networks during sleep. New J. Phys. 2014, 16. [Google Scholar] [CrossRef]
- Cirugeda-Roldan, E.; Cuesta-Frau, D.; Miro-Martinez, P.; Oltra-Crespo, S. Comparative study of entropy sensitivity to missing biosignal data. Entropy 2014, 16, 5901–5918. [Google Scholar]
- Donner, R.V.; Zou, Y.; Donges, J.F.; Marwan, N.; Kurths, J. Recurrence networks—a novel paradigm for nonlinear time series analysis. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Campanharo, A.S.L.O.; Sirer, M.I.; Malmgren, R.D.; Ramos, F.M.; Amaral, L.A.N. Duality between time series and networks. PLoS ONE 2011, 6. [Google Scholar] [CrossRef]
- Bauer, A.; Kantelhardt, J.W.; Bunde, A.; Barthel, P.; Schneider, R.; Malik, M.; Schmidt, G. Phase-rectified signal averaging detects quasi-periodicities in non-stationary data. Physica A 2006, 364, 423–434. [Google Scholar]
- Bauer, A.; Kantelhardt, J.W.; Barthel, P.; Schneider, R.; Mäkikallio, T.; Ulm, K.; Hnatkova, K.; Schömig, A.; Huikuri, H.; Bunde, A.; et al. Deceleration capacity of heart rate as a predictor of mortality after myocardial infarction: cohort study. Lancet 2006, 367, 1674–1681. [Google Scholar]
- Makowiec, D.; Struzik, Z.; Graff, B.; Żarczyńska-Buchowiecka, M.; Wdowczyk, J. Transition network entropy in characterization of complexity of heart rhythm after heart transplantation. Acta Phys. Pol. B 2014, 45, 1771–1781. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef]
- Amigó, J.M. Permutation Complexity in Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Bian, C.; Qin, C.; Ma, Q.D.Y.; Shen, Q. Modified permutation-entropy analysis of heartbeat dynamics. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Klabunde, R.E. Cardiovascular Physiology Concepts; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2012. [Google Scholar]
- Esler, M.D.; Thompson, J.M.; Kaye, D.M.; Turner, A.G.; Jennings, G.L.; Cox, H.S.; Lambert, G.W.; Seals, D.R. Effects of aging on the responsiveness of the human cardiac sympathetic nerves to stressors. Circulation 1995, 91, 351–358. [Google Scholar]
- Hotta, H.; Uchida, S. Aging of the autonomic nervous system and possible improvements in autonomic activity using somatic afferent stimulation. Geriatr. Gerontol. Int. 2010, 10, S127–S136. [Google Scholar]
- Ebert, T.J.; Morgan, B.J.; Barney, J.A.; Denahan, T.; Smith, J.J. Effects of aging on baroreflex regulation of sympathetic activity in humans. Am. J. Physiol. Heart Circ. Physiol. 1992, 263, H798–H803. [Google Scholar]
- Callegaro, C.C.; Taylor, J. Age-related effects of vagotonic atropine on cardiovagal baroreflex gain. Neurobiol. Aging. 2010, 33, 368–374. [Google Scholar]
- Task Force of the European Society of Cardiology the North American Society of Pacing. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Circulation 1996, 93, 1043–1065. [Google Scholar]
- Reardon, M.; Malik, M. Changes in Heart Rate Variability with Age. Pacing Clin. Electrophysiol. 1996, 19, 1863–1866. [Google Scholar]
- Umetani, K.; Singer, D.H.; McCraty, R.; Atkinson, M. Twenty-four hour time domain heart rate variability and heart rate: Relations to age and gender over nine decades. J. Am. Coll. Cardiol. 1998, 31, 593–601. [Google Scholar]
- Pikkujämsä, S.M.; Mäkikallio, T.H.; Sourander, L.B.; Räihä, I.J.; Puukka, P.; Skyttä, J.; Peng, C.K.; Goldberger, A.L.; Huikuri, H.V. Cardiac interbeat interval dynamics from childhood to senescence: Comparison of conventional and new measures based on fractals and chaos theory. Circulation 1999, 100, 393–399. [Google Scholar]
- Crasset, V.; Mezzetti, S.; Antoine, M.; Linkowski, P.; Degaute, J.P.; van de Borne, P. Effects of aging and cardiac denervation on heart rate variability during sleep. Circulation 2001, 103, 84–88. [Google Scholar]
- Shimazu, T.; Tamurai, N.; Antoine, M.; Linkowski, P.; Degaute, J.P.; van de Borne, P. Aging of the autonomic nervous system. Nihon Rinsho. 2005, 63, 973–977. [Google Scholar]
- Beckers, F.; Verheyden, B.; Aubert, A.E. Aging and nonlinear heart rate control in a healthy population. Am. J. Physiol. Heart Circ. Physiol. 2006, 290, H2560–H2570. [Google Scholar]
- Struzik, Z.R.; Hayano, J.; Soma, R.; Kwak, S.; Yamamoto, Y. Aging of complex heart rate dynamics. IEEE Trans. Biomed. Eng. 2006, 53, 89–94. [Google Scholar]
- Meersman, R.E.D.; Stein, P.K. Vagal modulation and aging. Biol. Psychol. 2007, 74, 165–173. [Google Scholar]
- Monahan, K.D. Effect of aging on baroreflex function in humans. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 293, R3–R12. [Google Scholar]
- Makowiec, D.; Rynkiewicz, A.; Galaska, R.; Wdowczyk-Szulc, J.; Żarczyńska-Buchowiecka, M. Reading multifractal spectra: Aging by multifractal analysis of heart rate. Europhys. Lett. 2011, 94. [Google Scholar] [CrossRef]
- Goldberger, J.J.; Cain, M.E.; Hohnloser, S.H.; Kadish, A.H.; Knight, B.P.; Lauer, M.S.; Maron, B.J.; Page, R.L.; Passman, R.S.; Siscovick, D.; et al. American Heart Association/American College of Cardiology Foundation/Heart Rhythm Society Scientific Statement on Noninvasive Risk Stratification Techniques for Identifying Patients at Risk for Sudden Cardiac Death: A Scientific Statement From the American Heart Association Council on Clinical Cardiology Committee on Electrocardiography and Arrhythmias and Council on Epidemiology and Prevention. Circulation 2008, 118, 1497–1518. [Google Scholar]
- Poirier, P. Exercise, heart rate variability, and longevity: The cocoon mystery? Circulation 2014, 129, 2085–2087. [Google Scholar]
- Schmitt, D.T.; Ivanov, P.C. Fractal scale-invariant and nonlinear properties of cardiac dynamics remain stable with advanced age: a new mechanistic picture of cardiac control in healthy elderly. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 293, R1923–R1937. [Google Scholar]
- Tobaldini, E.; Nobili, L.; Strada, S.; Casali, K.R.; Braghiroli, A.; Montano, N. Heart rate variability in normal and pathological sleep. Front. Physiol. 2013, 4. [Google Scholar] [CrossRef]
- Guyton, A.C.; Hall, J.E. Textbook of Medical Physiology; Elsevier Saunders: Philadelphia, PA, USA, 2006. [Google Scholar]
- Carskadon, M.A.; Dement, W.C. Normal human sleep : An overview. In Principles and Practice of Sleep Medicine, 5th; Kryger, M.H., Roth, T., Dement, W.C., Eds.; Elsevier Saunders: Philadelphia, PA, USA, 2011; Chapter 2; pp. 16–26. [Google Scholar]
- Monti, A.; Medigue, C.; Nedelcoux, H.; Escourrou, P. Autonomic control of the cardiovascular system during sleep in normal subjects. Eur. J. Appl. Physiol. 2002, 87, 174–181. [Google Scholar]
- Schumann, A.Y.; Bartsch, R.P.; Penzel, T.; Ivanov, P.C.; Kantelhardt, J.W. Aging effects on cardiac and respiratory dynamics in healthy subjects across sleep stages. Sleep 2010, 33, 943–955. [Google Scholar]
- Ohayon, M.M.; Carskadon, M.A.; Guilleminault, C.; Vitiello, M.V. Meta-analysis of quantitative sleep parameters from childhood to old age in healthy individuals: developing normative sleep values across the human lifespan. Sleep 2004, 27, 1255–73. [Google Scholar]
- Espiritu, J.R. Aging-related sleep changes. Clin. Geriatr. Med. 2008, 24, 1–14. [Google Scholar]
- Bartsch, R.P.; Schumann, A.Y.; Kantelhardt, J.W.; Penzel, T.; Ivanov, P.C. Phase transitions in physiologic coupling. Proc. Natl. Acad. Sci. USA 2012, 109, 10181–10186. [Google Scholar]
- Nicolini, P.; Ciula, M.M.; de Asmundus, C.; Magrini, F.; Brugada, P. The prognostic value of heart rate variability in the elderly, changing the perspective: from sympathovagal balance to chaos theory. Pacing Clin. Electrophysiol. 2012, 35, 622–638. [Google Scholar]
- Makowiec, D.; Graff, B.; Kaczkowska, A.; Graff, G.; Wejer, D.; Wdowczyk, J.; Zarczynska-Buchowiecka, M.; Gruchala, M.; Struzik, Z.R. Visualization of short-term heart period variability with network tools as a method for quantifying autonomic drive. 2014; arXiv:1407.4921v1. [Google Scholar]
- Tarvainen, M.P.; Niskanen, J.P.; Lipponen, J.A.; Ranta-aho, P.O.; Karjalainen, P.A. Kubios HRV-heart rate variability analysis software. Comput. Methods Progr. Biomed. 2014, 113, 210–220. [Google Scholar]
- Dietrich, D.F.; Schindler, C.; Schwartz, J.; Barthélémy, J.C.; Tschopp, J.M.; Roche, F.; von Eckardstein, A.; Brändli, O.; Leuenberger, P.; Gold, D.R.; et al. Heart rate variability in an ageing population and its association with lifestyle and cardiovascular risk factors: Results of the SAPALDIA study. Europace 2006, 8, 521–529. [Google Scholar]
- Schmitt, D.T.; Stain, P.K.; Ivanov, P.C. Stratification pattern of static and scale-invariant dynamic measures of heartbeat fluctuations across sleep stages in young and elderly. IEEE Trans. Biomed. Eng. 2009, 56, 1564–1573. [Google Scholar]
- Kuo, T.B.J.; Lin, T.; Yang, C.C.H.; Li, C.L.; Chen, C.F.; Chou, P. Effect of aging on gender differences in neural control of heart rate. Am. J. Physiol. Heart Circ. Physiol. 1999, 277, H2233–H2239. [Google Scholar]
- Trinder, J. Cardiovascular control during sleep: “Sleep-dependent changes in the coupling between heart period and blood pressure in human subjects,” by Silvani et al. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 294, R1684–R1685. [Google Scholar]
- Silvani, A.; Grimaldi, D.; Vandi, S.; Barletta, G.; Vetrugno, R.; Provini, F.; Pierangeli, G.; Berteotti, C.; Montagna, P.; Zoccoli, G.; Cortelli, P. Sleep-dependent changes in the coupling between heart period and blood pressure in human subjects. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 294, R1686–R1692. [Google Scholar]
- Parati, G.; Lombardi, C.; Narkiewicz, K. Sleep apnea: epidemiology, pathophysiology, and relation to cardiovascular risk. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 293, R1671–R1683. [Google Scholar]
- Martini, F.H.; Ober, W.C.; Nath, J.L. Visual Anatomy & Physiology; Pearson Education: Upper Saddle River, NJ, USA, 2011. [Google Scholar]



| Group Name | Age | Female | Male |
|---|---|---|---|
| twenties (20s) | 20–29 | 18 | 18 |
| thirties (30s) | 30–39 | 13 | 13 |
| forties (40s) | 40–49 | 16 | 20 |
| fifties (50s) | 50–59 | 13 | 19 |
| sixties (60s) | 60–69 | 11 | 13 |
| seventies (70s) | 70–79 | 10 | 12 |
| eighties (80s) | 80–89 | 11 | 7 |
| Standard Indices of HRV
| Entropic Indices of HRV
| ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Age Years | RR [ms] | SDNN [ms] | RMSSD [ ms] | pNN50 | DFA:α2 | ST | DCA | PErv | |
| females | |||||||||
| 20–29 | 962 ± 23 | 107 ± 8 | 60 ± 5 | 30 ± 4 | 0.96 ± 0.02 | 1.5 ± 0.2 | 3.1 ± 0.1 | 4.9 ± 0.4 | 2.2 ± 0.03 |
| 30–39 | 880 ± 19 | 77 ± 5 | 36 ± 5 | 12 ± 4 | 1.06 ± 0.03 | 2.5 ± 0.5 | 2.6 ± 0.1 | 2.8 ± 0.6 | 2.3 ± 0.04 |
| 40–49 | 905 ± 26 | 81 ± 6 | 34 ± 5 | 12 ± 4 | 1.06 ± 0.02 | 2.3 ± 0.4 | 2.6 ± 0.1 | 2.6 ± 0.6 | 2.3 ± 0.03 |
| 50–59 | 947 ± 18 | 74 ± 5 | 33 ± 3 | 10 ± 3 | 1.06 ± 0.03 | 1.8 ± 0.2 | 2.6 ± 0.1 | 2.6 ± 0.5 | 2.3 ± 0.03 |
| 60–69 | 944 ± 28 | 76 ± 9 | 29 ± 2 | 7 ± 2 | 1.07 ± 0.02 | 1.4 ± 0.1 | 2.5 ± 0.1 | 1.9 ± 0.4 | 2.4 ± 0.02 |
| 70–79 | 934 ± 26 | 69 ± 3 | 30 ± 5 | 8 ± 3 | 1.05 ± 0.05 | 1.8 ± 0.5 | 2.3 ± 0.2 | 1.2 ± 0.3 | 2.5 ± 0.02 |
| 80–89 | 972 ± 37 | 81 ± 8 | 33 ± 3 | 6 ± 2 | 1.08 ± 0.06 | 1.9 ± 0.5 | 2.4 ± 0.1 | 1.2 ± 0.4 | 2.5 ± 0.02 |
| males | |||||||||
| 20–29 | 1055 ± 25 | 138 ± 11 | 78 ± 9 | 38 ± 5 | 1.01 ± 0.02 | 1.6 ± 0.3 | 3.3 ± 0.1 | 4.5 ± 0.4 | 2.2 ± 0.03 |
| 30–39 | 1030 ± 27 | 124 ± 8 | 63 ± 9 | 29 ± 5 | 1.01 ± 0.03 | 2.5 ± 0.5 | 3.1 ± 0.1 | 4.4 ± 0.6 | 2.3 ± 0.04 |
| 40–49 | 977 ± 31 | 98 ± 6 | 39 ± 3 | 15 ± 3 | 0.99 ± 0.02 | 4.0 ± 0.8 | 2.7 ± 0.1 | 3.1 ± 0.4 | 2.3 ± 0.02 |
| 50–59 | 936 ± 28 | 93 ± 6 | 33 ± 4 | 7 ± 2 | 1.04 ± 0.02 | 3.8 ± 0.5 | 2.5 ± 0.1 | 1.9 ± 0.3 | 2.4 ± 0.02 |
| 60–69 | 996 ± 25 | 85 ± 6 | 31 ± 3 | 9 ± 3 | 1.07 ± 0.03 | 3.2 ± 0.5 | 2.5 ± 0.1 | 2.2 ± 0.5 | 2.4 ± 0.02 |
| 70–79 | 926 ± 31 | 85 ± 13 | 40 ± 8 | 13 ± 4 | 1.03 ± 0.03 | 2.0 ± 0.3 | 2.6 ± 0.1 | 1.2 ± 0.3 | 2.4 ± 0.03 |
| 80–89 | 876 ± 23 | 86 ± 10 | 48 ± 18 | 11 ± 7 | 0.98 ± 0.07 | 2.8 ± 0.9 | 2.4 ± 0.2 | 1.2 ± 0.4 | 2.5 ± 0.05 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makowiec, D.; Kaczkowska, A.; Wejer, D.; Żarczyńska-Buchowiecka, M.; Struzik, Z.R. Entropic Measures of Complexity of Short-Term Dynamics of Nocturnal Heartbeats in an Aging Population. Entropy 2015, 17, 1253-1272. https://doi.org/10.3390/e17031253
Makowiec D, Kaczkowska A, Wejer D, Żarczyńska-Buchowiecka M, Struzik ZR. Entropic Measures of Complexity of Short-Term Dynamics of Nocturnal Heartbeats in an Aging Population. Entropy. 2015; 17(3):1253-1272. https://doi.org/10.3390/e17031253
Chicago/Turabian StyleMakowiec, Danuta, Agnieszka Kaczkowska, Dorota Wejer, Marta Żarczyńska-Buchowiecka, and Zbigniew R. Struzik. 2015. "Entropic Measures of Complexity of Short-Term Dynamics of Nocturnal Heartbeats in an Aging Population" Entropy 17, no. 3: 1253-1272. https://doi.org/10.3390/e17031253





