1. Introduction
As highlighted by the emerging fields of systems biology and medicine, health requires the integration—across multiple time and spatial scales—of control systems, feedback loops, and regulatory processes that enable an organism to function and adapt to the demands of everyday life. Within this framework, aging and disease can be viewed as the breakdown of nonlinear feedback loops acting across multiple scales, resulting in a loss of physiological complexity [
1]. Physiologic complexity can be estimated using a number of techniques derived from the fields of nonlinear dynamics and statistical physics that quantify the moment-to-moment quality, scaling, and/or correlation properties of dynamic signals [
2,
3].
One increasingly used entropy-based metric of complexity is multiscale entropy (MSE). MSE characterizes the information content of a signal by quantifying the degree of regularity or predictability over multiple scales of time [
4]. MSE has been used to evaluate the relationship between complexity and health in a number of populations and physiological systems. For example, MSE of heart beat intervals demonstrates a clear loss of complexity with aging, is lower in patients with congestive heart failure, and is predictive of mortality [
5]. MSE has also been used to distinguish older adults with atrial fibrillation from healthy controls [
6] and differentiate healthy fetuses from fetuses with a pathological condition at birth [
7]. Additionally, it has been used in physiological processes as varied as red blood cell flickering, gait dynamics and sleep [
6,
8,
9,
10]. The use of MSE for studying center-of-pressure (COP) dynamics has received a significant amount of attention, particularly in elderly populations where falls are of greater concern [
8,
11,
12].
Despite its promise as a sensitive and novel biomarker of health and disease, few attempts have been made to outline the methodological challenges associated with the calculation of MSE. While current publications on MSE may discuss one or two methodological issues, no publication—to our knowledge—comprehensively covers all the issues presented here. For the MSE-naïve researcher, designing a protocol for the purpose of MSE analysis can be daunting, and this difficulty can be further amplified by the recognition that improper choice of parameters during MSE analysis can lead to ambiguity in complexity signatures between healthy and diseased states [
13]. In this paper, we address a number of key issues involved in study design, analysis and interpretation of MSE for physiological signals using COP as a model example. In particular we focus on five methodological issues considered critical for the proper design and analyses of an MSE study: (1) data length; (2) frequency range of analyses; (3) sampling rate; (4) point matching tolerance and sequence length; and (5) filtering. We choose COP because it is distinct from the more commonly analyzed, discrete heartbeat interval; the raw displacement COP data is continuous and potentially plagued by nonstationarities; and the physiologic basis for COP is not as well-defined as that of heart-rate and other physiological processes. A systematic review of publications using MSE to analyze COP was conducted which serves to highlight the existing methodological heterogeneity in key MSE parameters. We start with an overview of MSE since a basic understanding of the technique is required for context in the subsequent sections.
2. Overview of Multiscale Entropy
MSE quantifies the degree of irregularity within a system across multiple time scales. The entropy measure used to determine the amount of irregularity at each time scale is called sample entropy (SampEn). SampEn represents the rate of generation of new information and is precisely equal to the negative natural logarithm of the conditional probability that
m consecutive points that repeat themselves, within some tolerance,
r, will again repeat with the addition of the next (
m + 1) point [
6]. The tolerance,
r, is often derived by calculating a certain percentage of the time-series standard deviation (SD).
As described by Richman
et al. [
14], the mathematical derivation of SampEn is as follows. For a time-series of length N,
vectors,
, are formed for
, where
is the vector of
m data points from
to
. The vectors being compared against
to assess the number of “repeats” or “matches” are represented by
. A match is established once the distance between two vectors,
and
—defined as the maximum difference of their corresponding scalar components—is less than
r. The vector
is referred to as the template and in the case of a match the
is referred to as a template match. This is again repeated for
and
. This process of matching is illustrated in
Figure 1.
The probability of matches are calculated for each reference vector
and
and represented by
and
, respectively.
equals to
times the number of vectors,
, within
r of,
, and
is given by
times the number of vectors,
, within
r of,
, when
j ranges from 1 to
and
. The restriction
assures that self-matches are not counted (
i.e., vectors are not compared to themselves). SampEn can then be defined as:
where
and
.
represents the probability that two sequences will match for
m points and
represents the probability that two sequences will match for
m + 1 points across all possible comparisons.
A few points regarding SampEn bear noting. First, by nature of the calculations, SampEn for periodic, regular signals is approximately zero while SampEn is maximal with irregular, random signals. This can be understood with the fact that A and B are nearly identical in periodic signals; A/B is near unity; and thus the logarithm of A/B approximates to zero. On the other hand, irregular signals have lower probability of matches at m + 1 (A) compared to that of matches at m (B); A/B is a low-magnitude fraction; and ln (A/B) calculates to a large negative number which is made positive with the negative in Equation (1), ultimately yielding a larger SampEn.
Second, the theoretic basis of sample entropy rests on the probability of matches, and the actual calculation is an estimation based on the available samples. Much like the probability of “heads” for a coin approximated by counting the number of heads after a number of trial flips, the estimation of SampEn becomes increasingly susceptible to stochastic effects as the number of trials diminishes in quantity. The confidence in the accuracy of SampEn, thus, diminishes with smaller time series. Longer datasets are considered optimal. However, it may be incorrect to assume that the dynamics remain unchanged over the course of sampled time, particularly for longer time series.
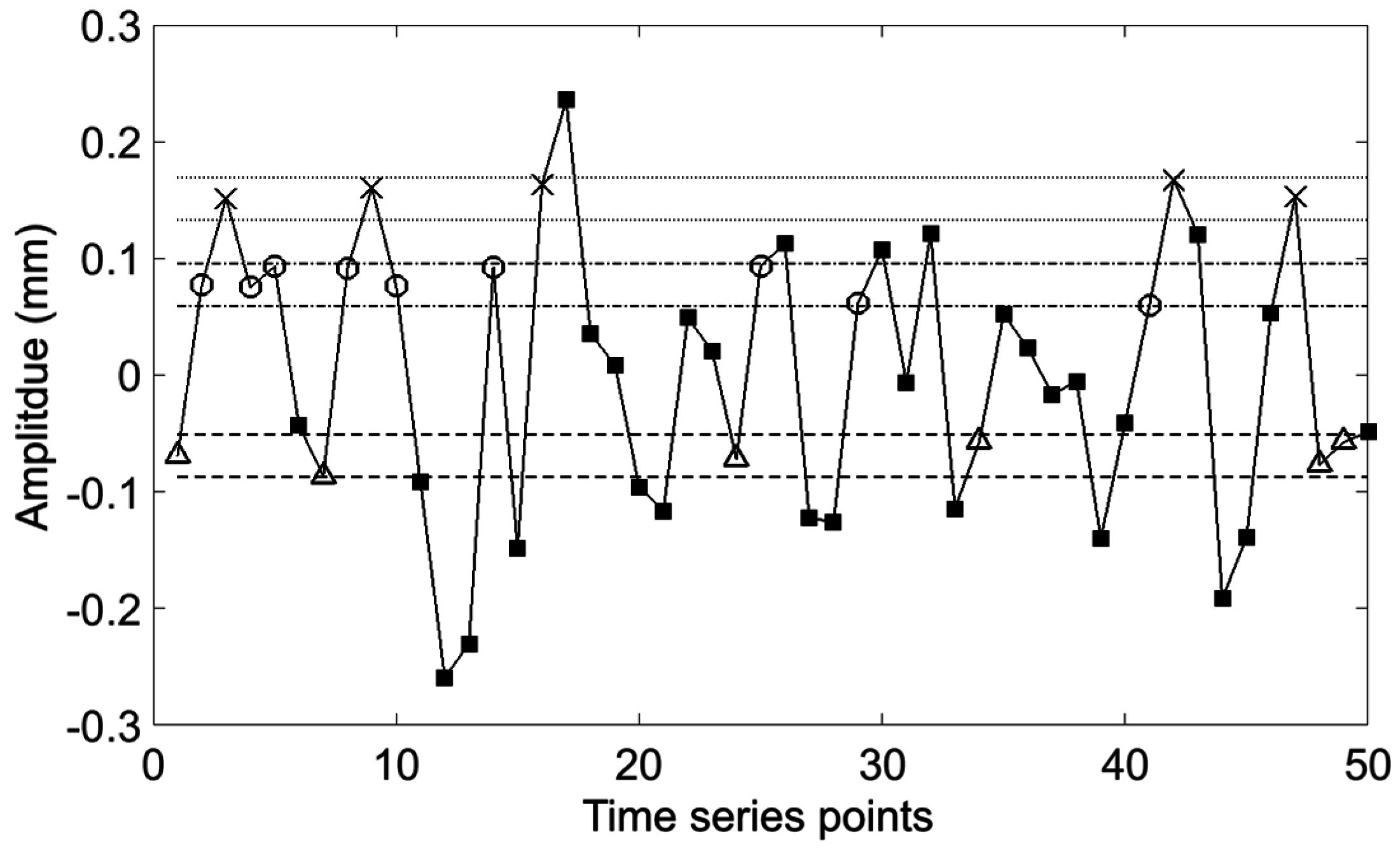
Figure 1.
Demonstration of SampEn calculation with
m = 2. The dashed line is the tolerance about the first point and highlights matching points to the first point with Δ markers. Likewise the dash-dot line and dotted line highlight matches of the second and third points with ○ and × markers respectively. Points which do not match any of the template points are marked by ■ symbols. SampEn is calculated from the ratio of sequences of length
m and length
m + 1 which match
m and
m + 1 length templates. The first templates are represented by the first 2 (
m) and 3 (
m + 1) points. We observe 2 Δ–○ template matches to the
m length template and one Δ–○–× template match to the
m + 1 length template. The template is then stepped one sample at a time and the process repeated until the end of the waveform is reached. SampEn can then be calculated from the ratio of the total number of
m + 1 to
m length template matches. Adapted from [
6].
Figure 1.
Demonstration of SampEn calculation with
m = 2. The dashed line is the tolerance about the first point and highlights matching points to the first point with Δ markers. Likewise the dash-dot line and dotted line highlight matches of the second and third points with ○ and × markers respectively. Points which do not match any of the template points are marked by ■ symbols. SampEn is calculated from the ratio of sequences of length
m and length
m + 1 which match
m and
m + 1 length templates. The first templates are represented by the first 2 (
m) and 3 (
m + 1) points. We observe 2 Δ–○ template matches to the
m length template and one Δ–○–× template match to the
m + 1 length template. The template is then stepped one sample at a time and the process repeated until the end of the waveform is reached. SampEn can then be calculated from the ratio of the total number of
m + 1 to
m length template matches. Adapted from [
6].
Third, the number of matches (
A and
B) in SampEn is determined by the
cumulative number of matches found between the possible permutations of vector comparisons. The quotient for
A and
B is subsequently entered into the logarithmic calculations to find SampEn. This approach is inherently different than that taken by approximate entropy (ApEn), the predecessor for SampEn. ApEn relies on determining the probability of matches found for each vector and then entering this probability into the logarithmic function. As a result, a time series with 100 data points would be associated with 99 such probabilities and, by extension, 99 logarithmic calculations for
m = 2 (and 98 probabilities and 98 logarithmic calculations for
m = 3). In stark contrast, SampEn has only one logarithmic calculation. To obtain ApEn, the logarithmic terms are summed respectively for
m = 2 and
m = 3, and the difference of the two sums would equal ApEn. The unintended consequence of the ApEn approach is that smaller time series and highly irregular time series may encounter zero matches which would subsequently yield an undefined ApEn since the logarithm of 0 cannot be calculated. To avoid this issue, self-matches are included to ensure that every logarithmic calculation entails a non-zero positive integer. This naturally biases the ApEn towards a lower entropy value for short and highly irregular time series [
14].
MSE is termed “multiscale” because the sample entropy (SampEn) is calculated across multiple time scales (τ). This is achieved through a coarse-graining procedure. At the first scale, the MSE algorithm evaluates SampEn for the time-series at each sampled point. At greater MSE scales, SampEn is computed on coarse-grained versions of the original time-series. The coarse-graining procedure divides the original time-series into non-overlapping windows of length, λ. Within each window the average is taken resulting in a new time-series of length N/λ. This is shown for time scales 2 and 3 in
Figure 2. The procedure is repeated until the last time scale is reached [
6].
Figure 2.
MSE coarse graining procedure example for scales two and three. Adapted from [
15].
Figure 2.
MSE coarse graining procedure example for scales two and three. Adapted from [
15].
The MSE output of SampEn
vs. Scale, τ, can be used to calculate a complexity index, C
I. The C
I is calculated by taking the area under this curve. A few important points about this composite approach are worth noting. First,
r, the tolerance for matches, remains constant for all scales of the MSE calculation. The
r is determined by the standard deviation of the time series at scale 1 (not coarse grained). Second, MSE assigns a high C
I to time-series with complex dynamics across all the time scales evaluated. For this reason,
1/f noise is associated with a high C
I because the SampEn remains relatively constant across time scales. Uncorrelated or white noise, however, is characterized by high irregularity (SampEn) at lower scales but increasingly decreased SampEn at higher scales, ultimately yielding a relatively smaller C
I. Since
1/f noise is ubiquitous in nature [
16], this technique has gained traction in the analysis of physiological signals. Third, the coarse graining procedure, itself, does not necessarily make MSE calculations immune to cross temporal scale effects. Coarse graining is a type of filter that is susceptible to aliasing. Periodicity at a specific frequency (represented by decreased SampEn) can be seen at multiples of the cycle frequency [
17].
4. Methodological Considerations
The first three subsections (4.1–4.3) listed below should be considered prior to protocol development. This ensures that the protocol for data collection is designed appropriately for MSE analysis. All subsections (4.1–4.6) herein discuss methodological considerations applicable to the actual data analysis.
4.1. Determining Required Data Length
Because SampEn is ultimately a probabilistic calculation, SampEn requires a minimum number of points to obtain an accurate estimate of matching probability. The confidence in the accuracy of SampEn is diminished greatly when the number of matches is low. This can occur with shorter data (due to short data acquisition or substantial coarse graining at higher MSE scales), highly irregular time series, tight tolerance window (small r), or data with trends or drifts. Of these factors, data length becomes a universally unavoidable issue for all finite time series since coarse graining for ascending MSE scales ultimately generates a time series too short for reliable MSE analyses.
To address this methodological issue, an important first step is to determine the minimum number of points required for SampEn. Estimates for the minimum number of SampEn points are sometimes based on theoretical calculations for ApEn which suggest that 10
m points should be sufficient, although 20
m—30
m points would be preferable for an accurate estimate [
27,
37]. However ApEn estimates based on simulated random time-series show increasing effects of self-matching bias with a smaller number of points [
14]. In comparison, due to the exclusion of self-matches, SampEn is not susceptible to such biases and is generally considered more robust to shorter time series. However, it is noted in Richman
et al. [
14] that the confidence intervals for simulated random time-series at a length of 10
m remain quite large for SampEn, therefore we recommend that between 14
m and 23
m points be present at the last MSE scale analyzed. As denoted by the N
τM column in
Table 1, the majority of the reviewed studies satisfied this criterion with 300 data points (17
m with
m = 2) used for analyses at the last scale. Determining the number of points at the last MSE scale is done by multiplying the sample rate times the data length and then dividing by the largest MSE scale,
. One outlier was the Gruber study where the acquired data totaled 7 s. Although the N
τM for this study could not be determined due to lack of reporting for f
s, it is unlikely that sufficient data points at physiologically relevant frequencies could be extracted from such a short acquisition window.
Ideally, as much data as possible should be acquired but constraints arise from a subject’s capacity to sustain such testing for long durations. For COP, fatigue can emerge generating altered dynamics and transient effects such as shifts, fidgets, or drifts. These changes can produce dynamics that no longer become the state for which the investigators were originally intending to evaluate. Duarte’s study [
22], for instance, acquired testing for 30 min in both young and older subjects, and this duration may have potentially caused transient effects (
i.e., nonstationarities as discussed below) that ultimately change the MSE results. The study, however, was interested in very low physiological frequencies and may not have had other options.
The length of testing is therefore dictated by the subject’s capacity to maintain a specific dynamic and by the lowest physiologic frequency of interest. When this lowest physiologic frequency of interest is known, the required length of the time series to be collected in a study can be determined. This should be done such that the lowest frequency component included is not clearly oversampled. To achieve this, a simple formula based on the number of points remaining at the last coarse-grained time scale, N
τM, can be used:
where f
L is the lowest frequency component of interest and
m is the sequence length. This will result in 2 × (
m + 1) samples per cycle for the lowest frequency component at the last time scale. A minimum number of oscillations are required to accurately characterize the information at some low frequency, so we use an example to check that this is reasonable when using this formula. If we take N
τM = 300,
m = 2 and f
L = 0.5 Hz, we observe that we need our time series to be 100 s in length. This would result in 50 oscillations of this low frequency component which is reasonable.
In the end, the confidence interval for a SampEn calculation may not be dictated by data length alone and can be influenced by other factors such as increased signal regularity or higher tolerance r. As a result, the extent by which an investigator can coarse grain the time series (for higher MSE scale analyses) can be determined not merely by data length alone but also by an additional stability analysis process. Stability is established by observing consistent trends in SampEn with increasing MSE scales. However, if there are significant deviations or erratic patterns (e.g., an increase with a subsequent decrease or vice versa) in consecutive SampEn values as MSE scales increase, then this would suggest that the SampEn calculations are now susceptible to stochastic effects and thus unreliable. This stability analysis can be evaluated within-subjects and across subjects to observe overall patterns. An arbitrary value of a ± 0.1 change in SampEn from scale τ-1 to τ followed by a change in the opposite direction of ± 0.1 can be used to determine the last stable scale. When this test fails analysis should stop at τ-1, the scale where the instability begins.
Of note, new variants of MSE, such as Modified MSE, have been created to overcome these limitations seen with short time-series [
38]. A review of a number of other variants on MSE, each of which has their own strengths is provided in Humeau–Heurtier [
39].
4.2. Range of Frequencies for Analysis
For continuous time series such as COP data, each MSE scale represents a time frequency: smaller scales correspond to higher frequencies while larger scales correspond to lower frequencies. For certain discrete data such as heart interbeat intervals, on the other hand, this frequential correlation is not nearly as straightforward since each MSE scale corresponds to an approximate average of vacillating interbeat periods at varying degrees of coarse graining. The MSE analyses of continuous COP data are therefore more conducive to physiological interpretations based on the frequency represented at each scale: a SampEn value for a 1 Hz time series would reveal information about the amount of irregularity of the time series at 1 Hz, and so on.
The frequency range on which to focus MSE analyses is constrained by two factors: (1) physiological considerations and (2) the limits set by the granularity and length of the data. In an ideal world, SampEn values would impart information about a well-described physiological mechanism operating at the analyzed frequency. However, unlike heart rate, the physiological basis for COP is not well understood. This lack of clarity may account for the wide range of frequencies (e.g., from 0.0056 to 60 Hz) analyzed by the studies summarized in
Table 1.
Several tactics have been adopted to deal with this issue. One approach is to recruit healthy control groups which, in the case of COP studies, have been largely composed of healthy young individuals. Comparisons are subsequently made at each frequency range to determine which frequencies differed statistically between a disordered condition and the healthy young, and these frequencies are then examined to identify the effects of a specific intervention. Jiang
et al. [
23], for instance, selected the frequencies of interest based on the dissimilarity of the C
I between elderly and young subjects at baseline. Once the intervention—vibratory insoles—were applied, the C
I in elderly were re-evaluated at those pre-identified frequencies and were found to increase making their C
I similar to the C
I in healthy young. This led to the conclusion that vibratory insoles applied to the elderly people might be able to improve their postural stability [
23]. Other studies, such as Wei
et al. [
12] and Wayne
et al. [
33], have similarly used young as healthy controls to identify the frequencies to analyze.
When statistical comparisons with a “healthy” group is not feasible, assumptions must be made about which physiological frequencies are clinically relevant. Some assumptions are based on physiological feasibility: for example, frequencies above 20 Hz are likely too rapid to affect balance-related processes or neurophysiological dynamics at the whole-body level. Other assumptions are premised on the distribution of spectral power. For instance, the preponderance of spectral power (95%) of quiet standing COP exists at frequencies lower than 1 Hz [
22]. However, the majority of the studies in our systematic review examined frequencies greater than 1 Hz and some identified statistically significant results.
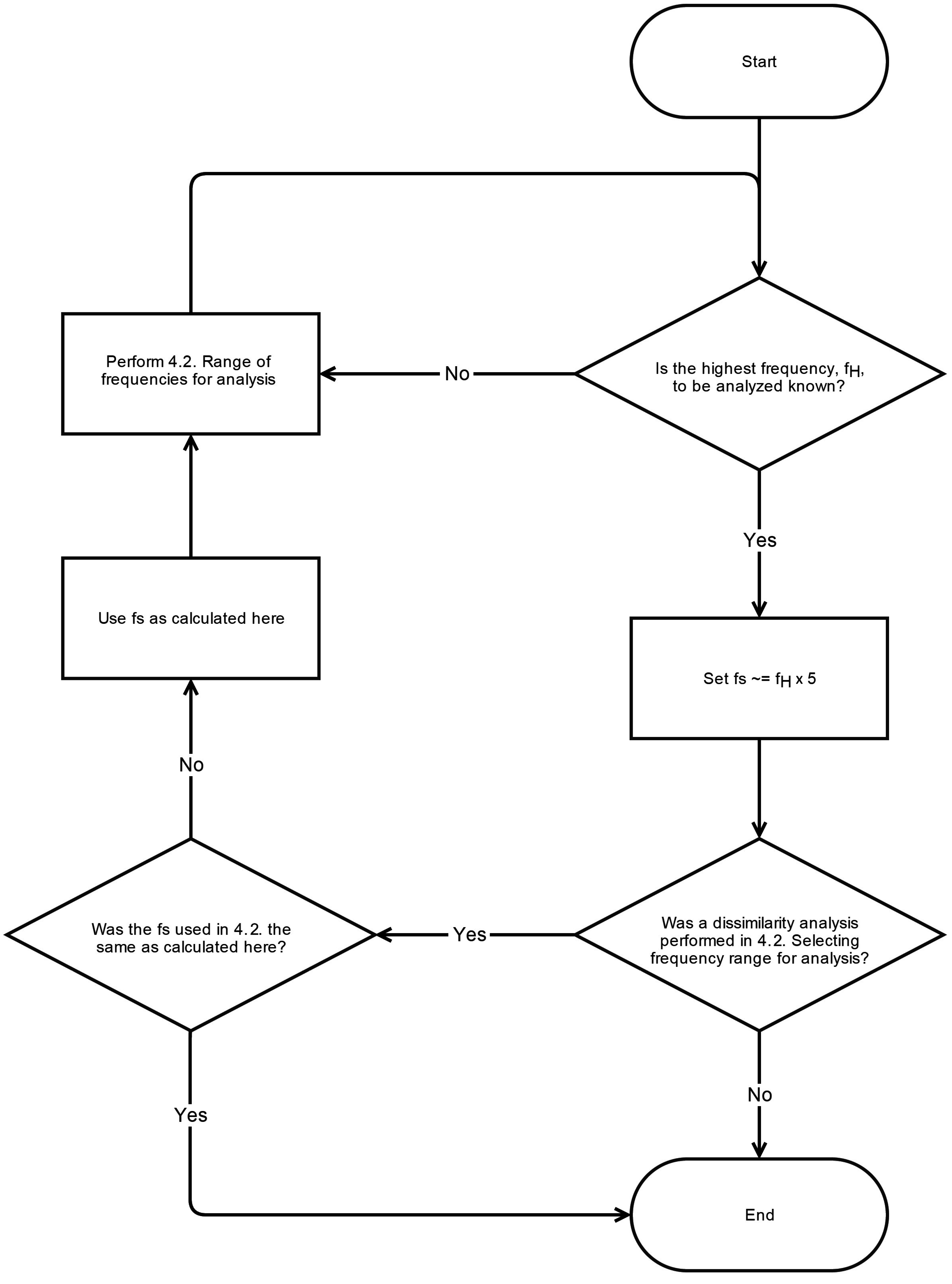
The other constraint limiting the range of analyzed frequencies is the granularity and length of data. The highest frequency, fH, feasible for analysis is set by the sample rate at which the data is collected. As discussed below, accurate characterization of a physiological process at a specific frequency requires sufficient granularity, and we recommend having at least five points per cycle for fH represented at the first MSE scale. Therefore, MSE analyses at 10 Hz frequency should be performed on data with at least a 50 Hz sampling rate (fs). When the data are acquired at very high sample rates, this guideline may permit analyses of data at frequencies that are too high to be physiologically realistic. In this case, fH should be selected based on physiologic feasibility.
The lowest frequency, f
L, feasible for analysis is limited by the length of time over which data is acquired. The shorter the time series, the less one can evaluate the lower frequencies. To determine the lowest frequency which should be included in the analysis based on the time series length one can rearrange Equation (2):
This will set the lowest frequency which should be included in the analysis (i.e., the lowest frequency IMF or the cutoff frequency of a high-pass filter) such that at the last time scale it will have 2 × (m + 1) samples per cycle. For example if we performed EMD on a time-series of length t = 40 s which resulted in one of the low frequency IMFs having a characteristic frequency of 0.5 Hz. We need to understand whether that IMF should be included in the analysis or if instead it should be eliminated since it will be oversampled even at the last time scale. Using Equation (3) with NτM = 300 we observe that the minimum fL should not be lower than 1.25 Hz. Therefore the 0.5 Hz IMF should not be included since it will always be oversampled. We include m in the denominator because for larger sequence lengths we do not want to detrend the signal to much. Since we are looking at longer sequences the relevant information (oscillations) will be prevalent at lower frequencies. We would like to emphasize that Equations (2) and (3) are merely guidelines to help setup a study and analysis such that meaningful information can be garnered from a dataset. There are a number of other important factors to consider when determining how long of a time-series to collect and which frequencies to analyze; subject fatigue, protocol limitations (inability to collect long data; BOLD-fMRI), and which frequencies are physiologically meaningful. While complexity generally persists across multiple time scales in some cases there may be a valid physiological reason for not analyzing below a particular frequency.
4.3. Appropriate Sample Rate (fs)
To adequately capture the dynamics of a specific frequency of interest, a minimum number of samples are required per cycle or period. Traditionally, in engineering, the Nyquist criterion mandates that the sampling rate be twice the frequency to be evaluated. In our systematic review, some researchers choose f
s such that the number of samples per cycle at the highest frequency, f
H, was 2 to 4. While this satisfies the Nyquist criterion for sampling, the more conservative approach would recommend at least five samples per cycle (5 × the highest frequency) since evaluation of sinusoidal waveforms with sampling at less than 5 samples per cycle results in mean amplitude errors greater than 5% [
40]. To fully capture the information contained in the highest frequency component (f
H) it is recommended to set f
s such that there are at least five samples/cycle for f
H at the first MSE scale. The counter-situation is when the sampling is obtained at a much higher rate.
As stated previously, experimental data obtained at a sampling rate much greater than that required by the Nyquist theorem could lead to analyses of processes that are not relevant to the system of interest. In this oversampled case, matching would occur at smaller time intervals and thereby fail to assess the dynamics at the frequencies of interest. For example, assuming that no physiological process in COP operates at frequencies greater than 20 Hz, sampling our signal with f
s =1 kHz and working with
m = 2 would lead MSE analyses to characterize dynamics at frequencies which are too high to be physiologically relevant. With this sampling frequency, a 20 Hz cycle would be associated with 50 samples and the MSE analyses utilizing two or three-sample sequences would deal with dynamics that are much greater than 20 Hz. There is the option to increase
m to around 50 to ultimately include data encompassing 20 Hz or lower frequencies, however, this would introduce other unintended and undesired effects—namely, decreased number of matches and diminished confidence in SampEn (to be explained in
Section 4.4). In these cases, down-sampling of the data prior to data analyses would be recommended.
4.4. Sequence Length (m), and Point Matching Tolerance (r)
The selection of
m and
r is driven by two overarching factors: (1) maximizing the accuracy and confidence in the SampEn values obtained at each MSE scale and (2) optimizing the ability to distinguish any real, salient features in the dataset. In principle, the accuracy and confidence of the entropy estimate improve as the numbers of matches of length
m and
m + 1 increase. The number of matches can be increased by choosing small
m (short templates) and large
r (wide tolerance). However, a larger
r will result in a conditional property (A/B) of 1 and thus a SampEn of zero for nearly all stationary time series, thereby limiting one’s ability to discriminate between various time series. On the other hand,
r must be large enough to avoid the influence of noise and to simultaneously increase probability of matches to ensure that confidence in SampEn is adequate [
27].
A much more quantitative approach to seeking a value of
r was advocated by Lake
et al., in 2002 [
41]. In this study, Lake derived the variance,
, of the conditional probability (CP) of A/B where CP represents the probability of a match of length
m + 1 given there is a match of length
m:
where B is again the number of template matches of length m, K
A is the number of overlapping pairs of matching templates of length
m + 1 and K
B is the number of overlapping pairs of matching templates of length m. Selection of the value
r is then determined by maximizing the following quantity:
which is the maximum of the relative error of SampEn and of the CP estimate, respectively.
To identify the optimal value for sequence length m, a number of techniques have been utilized. Selecting the appropriate value for m has its basis on the fact that m determines where the information content is being assessed. Since SampEn is essentially a marker of how much new information is generated, it is important to ensure that the template matches for m and m + 1 are within the vicinity of where the important dynamics are present.
To identify the template lengths associated with sufficient information content and thus the optimal range of m, Lake
et al. [
41] employed an autoregressive model while Chen
et al. [
42] instead utilized a mutual information method and false nearest neighbor (FNN) technique which is more appropriate for nonlinear time series. These considerations, although applicable to SampEn analyses of raw time-series, are largely negated by the process of coarse-graining and the utilization of multiple scales in MSE. As a result, the choice of
m is relatively arbitrary for MSE but becomes more a function of data logistics:
m = 2 is superior to
m = 1 since it allows more detailed reconstruction of the joint probabilistic dynamics while
m > 2 is unfavorable due to the requirement of larger data lengths [
42].
Numerous studies have taken more of an empirical approach to this issue by observing the effects of varying
m and
r on the calculated MSE results. In our systematic review, Duarte
et al. [
22] and Jiang
et al. [
23] performed such evaluations and have concluded that while absolute changes in complexity values are observed, relative changes were insignificant [
9,
22]. Indeed, according to Duarte
et al., the relative results remain generally consistent when
r is swept between 10% and 30% [
22], suggesting that this range should be sufficient for most data sets. Similarly, Pincus
et al., has found that entropy analyses produce statistically reliable and reproducible results with
m = 2 and
r = 10%–25% and an appropriate data length [
37]. Our systematic review reveals that the selection of
m and
r are relatively consistent across studies: sequence length
m is typically 2 and point matching tolerance
r is either 15% or 20%.
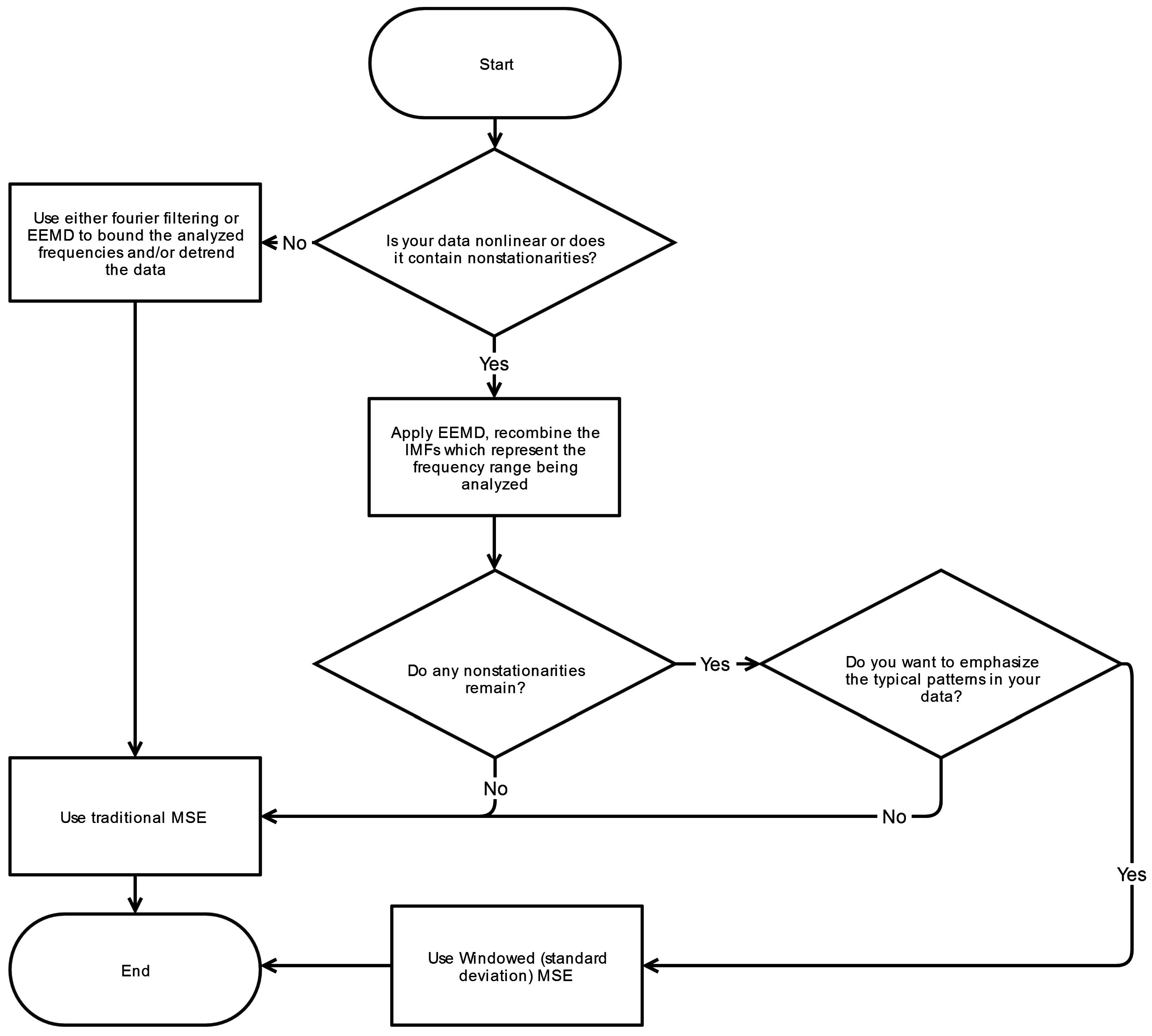
4.5. Filtering
Filtering raw data is a critical pre-processing step for MSE analysis. General trends and low frequency drifts, in particular, can lend to diminished sequence matching and incorrectly ascertained increase in irregularity manifesting as a higher SampEn. Moreover, the infrequent sequence matching corresponds to a widened confidence interval for the derived SampEn values. Nonstationarities at higher frequencies may also have unpredictable effects on the calculated SampEn values. To remove such effects, Empirical Mode Decomposition (EMD) is the technique most commonly used as demonstrated in
Table 1.
EMD is well-suited for decomposition of nonlinear, nonstationary physiologic signals and possesses advantages over Fourier and wavelet analysis because it employs a fully adaptive approach derived by means of a sifting process [
8]. Unlike Fourier or wavelet methods, there are no a priori assumptions about the nature of a signal and it does not rely on a specific basis (e.g., sinusoidal or Haar wavelet function) for decomposing the signal. Fourier based filtering of nonlinear, nonstationary signals can produce undesired artifacts in the outputted signal. After decomposition by EMD the resulting IMFs can be recombined in various permutations, representing a range of characteristic frequencies which are a subset of the original signals bandwidth. This resulting signal can then be analyzed with methods such as MSE.
EMD is not without its limitations as it is susceptible to mode-mixing and end-effect issues. Mode mixing occurs when an oscillation at a particular frequency is not fully isolated to a single IMF but rather leaked to adjacent IMFs. Ensemble Empirical Mode Decomposition (EEMD) minimizes mode mixing through the implementation of noise-assisted sifting [
24]. End effects represent errors that occur at the beginning or end of an IMF due to the EMD process. To enable proper decomposition of the edges of a time-series, values must be appended at the boundaries in an appropriate manner. Improper additions or extensions can lead to unwanted distortions. A detailed review of EEMD which addresses mode-mixing and end-effect issues can be found in Wu and Huang [
24].
Generally, removal of nonstationarities that have characteristics well outside the frequencies of interest is not difficult to accomplish through the use of EMD or other filtering methods. However sudden, transient movements, such as shifts and fidgets, can also cause nonstationarities with predominant frequencies within the frequencies of interest since they are simply larger versions of the complex postural sway adjustments seen on a regular basis. Due to this overlap in frequencies, these particular nonstationarities may commonly persist despite the filtering step. A more detailed discussion on technique (Fourier-based, wavelet, EMD) selection for the filtering of biomedical signals can be found in Fonseca-Pinto [
43].
4.5.1. Nonstationarities within Frequency Band of Interest
The presence of a single large nonstationarity can generate significant changes in the calculated tolerance window,
r. As noted previously,
r is directly proportional to the signal’s standard deviation (at Scale 1) and importantly is established thereafter for all scales. A large spike or extrema can increase
r, increase the number of template matches, and thus decrease the overall complexity index C
I. As a consequence, a lower C
I can be paradoxically construed as either increased regularity or larger presence of spurious extremas. This phenomenon is depicted in
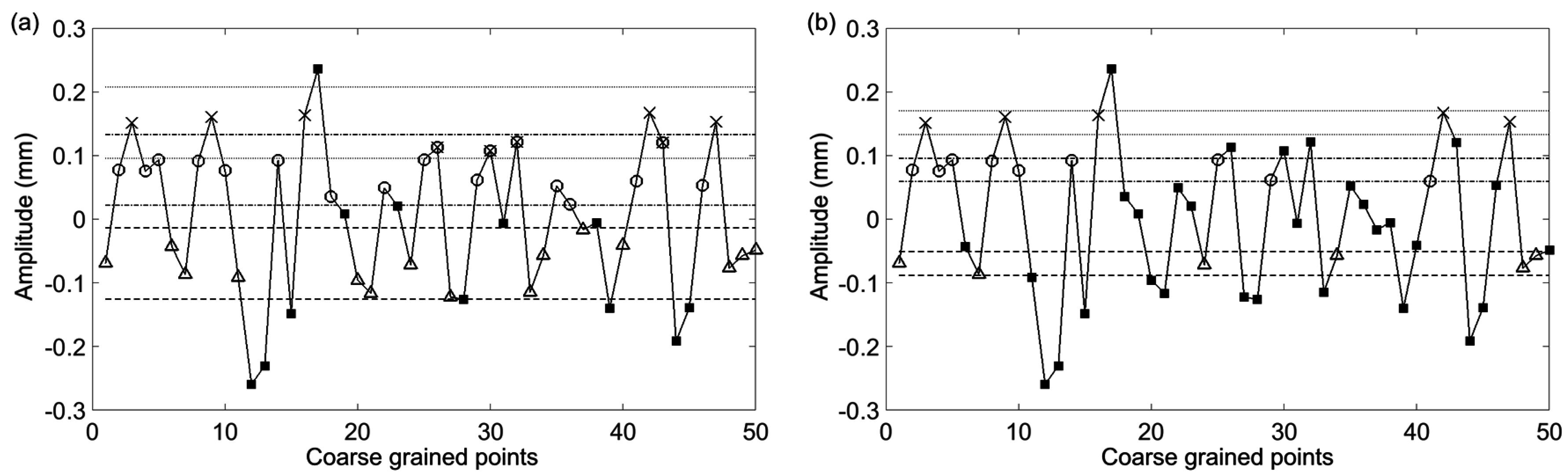
Figure 3 where the large nonstationarity starting at 34 s, potentially due to the subject shifting, greatly increases the standard deviation of the signal and therefore the value of
r. We explore how this nonstaionarity affects the SampEn calculation at scale 15. In
Figure 4a the nonstationarity is included while in
Figure 4b it is excluded. As shown, this results in more template matches in the former case and therefore lower sample entropy. The absolute difference in SampEn at this coarse grained level is substantial: |0.872–1.902| = 1.03.
Figure 3.
Center-of-Pressure waveform shown with a large nonstationarity between time 34 s and 37 s.
Figure 3.
Center-of-Pressure waveform shown with a large nonstationarity between time 34 s and 37 s.
Figure 4.
The first 50 coarse-grained points from
Figure 3 with τ = 15. The straight (dashed, dotted, dashed-dotted) lines represent the point matching tolerance,
r, based on a standard deviation which includes the nonstationarity (
a) and does not include the nonstationarity (
b). Two sequence template matches are represented by Δ–○ vectors which are comprised of matches to the first (Δ) and second (○) points from the first template. Three sequence template matches are represented by Δ–○-×, where the next point (×) matches the third point from the template. Points which do not match any template points are represented by ■ symbols. In (a) due to the large nonstationarity, the calculated standard deviation is large enough to cause overlap between the tolerance about the 2nd (dash-dot line) and 3rd points in the template sequence. This results in certain points matching both the 2nd and 3rd points as indicated by markers with both an ○ and an ×. Because of the wide tolerance the complexity index will be less than what it would be without the large nonstationarity. In (b) it is observed that exclusion of the nonstationarity results in tighter tolerance about the template sequence points. In turn this will result in a larger complexity index. Adapted from [
6].
Figure 4.
The first 50 coarse-grained points from
Figure 3 with τ = 15. The straight (dashed, dotted, dashed-dotted) lines represent the point matching tolerance,
r, based on a standard deviation which includes the nonstationarity (
a) and does not include the nonstationarity (
b). Two sequence template matches are represented by Δ–○ vectors which are comprised of matches to the first (Δ) and second (○) points from the first template. Three sequence template matches are represented by Δ–○-×, where the next point (×) matches the third point from the template. Points which do not match any template points are represented by ■ symbols. In (a) due to the large nonstationarity, the calculated standard deviation is large enough to cause overlap between the tolerance about the 2nd (dash-dot line) and 3rd points in the template sequence. This results in certain points matching both the 2nd and 3rd points as indicated by markers with both an ○ and an ×. Because of the wide tolerance the complexity index will be less than what it would be without the large nonstationarity. In (b) it is observed that exclusion of the nonstationarity results in tighter tolerance about the template sequence points. In turn this will result in a larger complexity index. Adapted from [
6].
![Entropy 17 07849 g004]()
Different approaches have been attempted to deal with this dilemma. Some researchers have used a fixed standard deviation [
22] irrespective of the time-series variability. Although this approach removes sensitivity to nonstationarities, it is also less adaptive to the variability in amplitudes seen across subjects. Subjects who exhibit larger amplitudes will generally be associated with a greater complexity, C
I, and
vice versa. Other researchers have chosen to remove the nonstationarity from the time-series [
22]. Conceptually, removal of such nonstationarities—which may occur frequently in certain cases—constitutes removal of information which may be an important aspect of the systems dynamics. For this reason, we seek to preserve the intrinsic structure of the signal as much as it is feasible. Lastly, some have used a median absolute deviation (MAD) in place the signal’s standard deviation [
44]. The MAD is computed by taking the median of the absolute deviations between the data’s median. This approach is again less sensitive to large nonstationarities but due to the inherent difference between MAD (based on median of absolute differences) and standard deviation (based on variance, which is the average of squared differences), the comparative relationship between MAD-based MSE and the traditional MSE algorithm is unclear. One possible solution to this issue of nonstationarities is proposed here.
4.5.2. Windowed Standard Deviation MSE
An alternative method for determining the point matching tolerance r is the windowed standard deviation—herein referred to as windowed-MSE or WMSE. In this approach, the standard deviation is calculated for a fixed width window as it is stepped across the time-series as opposed to calculating standard deviation for the entire time-series. The window is stepped one sample at a time until the end of the time series, and in the process generating N-n standard deviation calculations, where n is the window width. The median value for all N-n standard deviations is then determined and subsequently used to calculate the point matching tolerance r, which is subsequently applied to all scales.
The window width n should be set such that each window provides a reasonable estimate of the population standard deviation. For a normally distributed time series with no outliers, to be 95% confident that the error between the window and population standard deviation is less than 10%, the window width must be 240 samples. The confidence interval for the window standard deviation estimate of the population standard deviation, σ, can be calculated using:
where n is the window width, s is the sample (or window) standard deviation,
χ2 is the chi-squared distribution for a given significance level, α, with degrees of freedom,
n − 1 [
45]. With the estimate of 240 samples as provided by Equation (6) with an arbitrary s and α of 95%, we can be reasonably confident that each of our windows is providing an accurate estimate of the entire time-series (population) standard deviation.
For time-series without existing nonstationarities, WMSE produces results very similar to that of the traditional MSE approach, since standard deviation remains the means by which the point matching tolerance r is calculated. For time-series with sporadic nonstationarities, WMSE deemphasizes the nonstationarities and yields a larger CI relative to the traditional MSE method, as should be expected.
Figure 5.
Multiscale Entropy and Windowed Multiscale Entropy calculations for the waveform shown in
Figure 3 with a large nonstationarity.
Figure 5.
Multiscale Entropy and Windowed Multiscale Entropy calculations for the waveform shown in
Figure 3 with a large nonstationarity.
Figure 5 provides an example of the difference in the SampEn Vs τ curves for MSE and WMSE calculations using the time-series depicted in
Figure 3 with a large nonstationarity.
Table 2 highlights the details of the standard deviation result for this waveform using MSE and WMSE. It is evident that the inclusion of the nonstationarity in the time series (0–37 s) generates a much different standard deviation as compared to that seen with exclusion of the nonstationarity (0–34 s) when determined by the traditional algorithm (MSE column). However the standard deviation derived using the WMSE approach is much more robust against the effects of including the nonstationarity (WMSE column). Since the standard deviation as calculated by WMSE is smaller in the nonstationarity case, we see higher sample entropies at a given scale in
Figure 5 for the WMSE curve.
Table 2.
Differences in the standard deviation result between MSE and WMSE for the waveform shown in
Figure 3. The results are shown including the nonstationarity (with) at the end and not including it (without).
Table 2.
Differences in the standard deviation result between MSE and WMSE for the waveform shown in Figure 3. The results are shown including the nonstationarity (with) at the end and not including it (without).
| Nonstationarity | MSE | WMSE |
|---|
| With (0–37 s) | 0.3718 | 0.1214 |
| Without (0–34 s) | 0.1234 | 0.1214 |
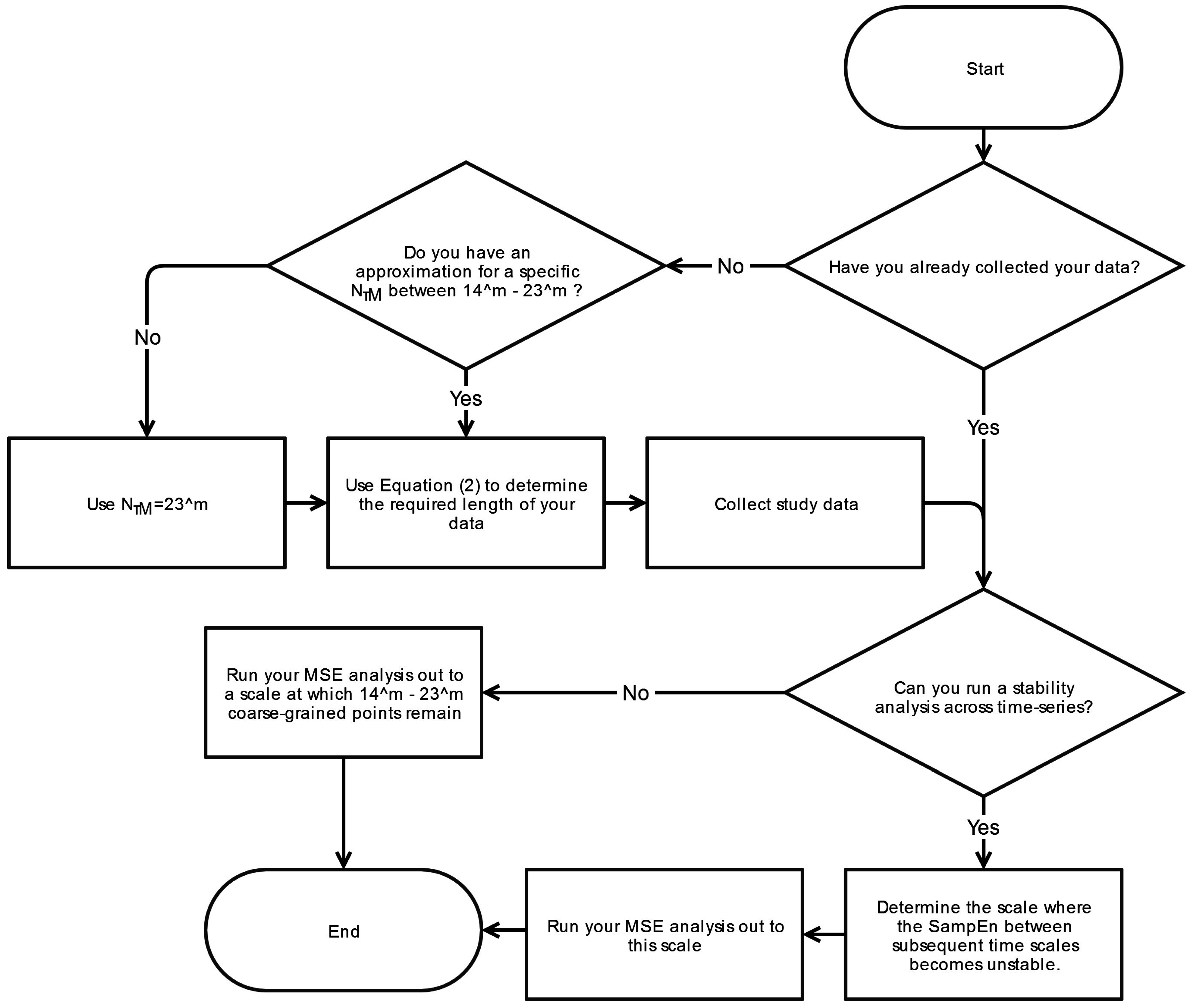
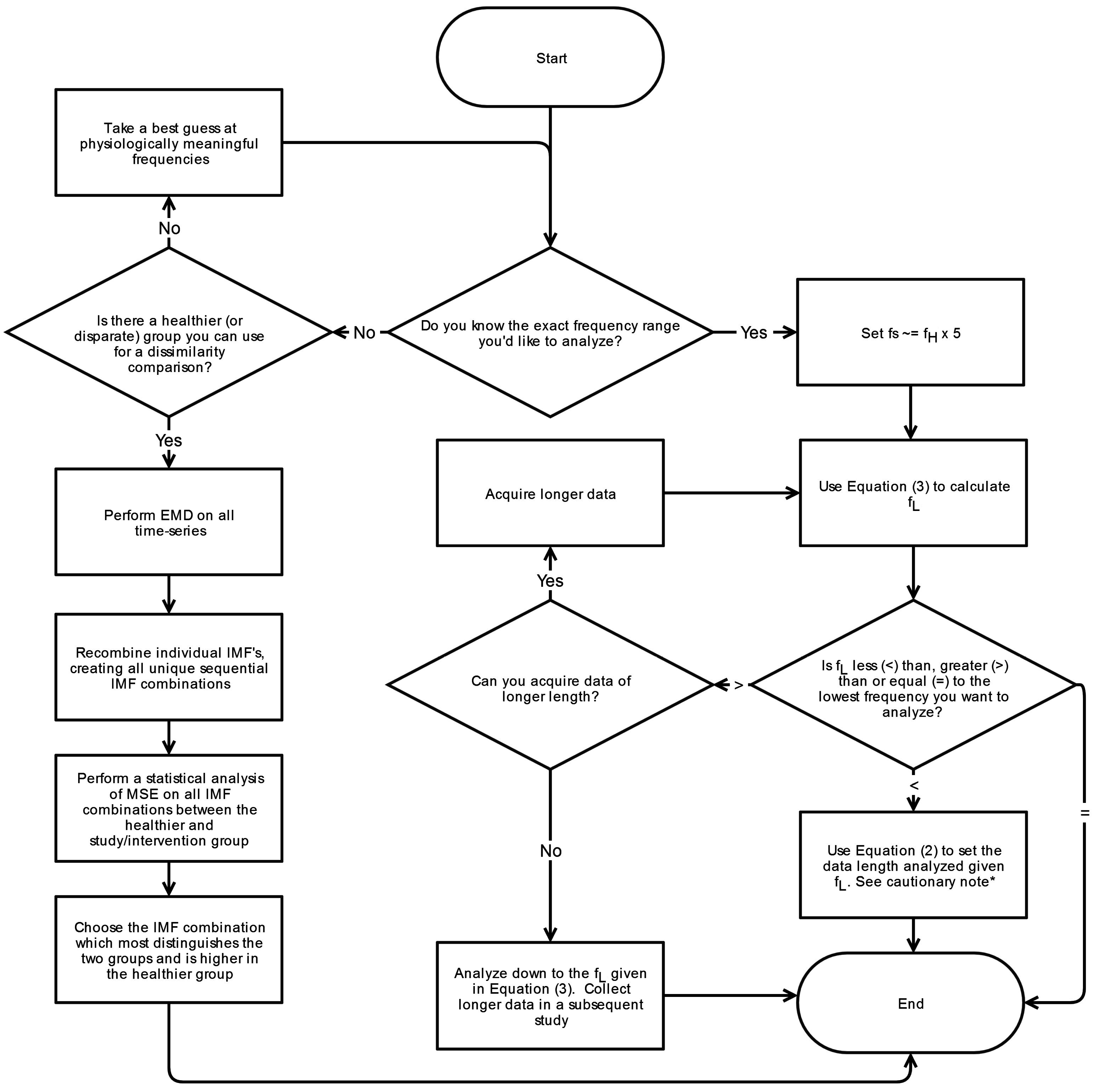
6. Conclusions
This systematic review has revealed significant heterogeneity in the way MSE is applied to COP displacement data. Part of the heterogeneity arises from the lack of clarity regarding the methodological challenges involved in MSE-based analyses. We recommend that prior to testing, future studies should consider establishing these important factors: the minimal amount of time for data collection, the physiological frequencies to evaluate, the inclusion of healthy controls, and sampling rate for data acquisition. Once the data is collected, the researchers must then decide how the data should be filtered, what values
m and
r should be assigned, and how to address the nonstationarities that persist despite the filtering process. These recommendations are summarized in flowcharts in
Appendix A.
As MSE increases in popularity, modifications of the MSE methodological algorithm will likely arise with corresponding changes in the way the parameters are assigned. Already, different variants of MSE have been published, and this review does not include them due to their sheer number, their limited employment to COP studies, and—at present—their lack of mature development. Nevertheless, many of the methodological challenges discussed here still apply, and this paper intends to help researchers understand how to properly design their studies and to analyze their data using MSE. Further discussions about these methodological issues should hopefully enhance consistency across studies in both reporting and possibly methodology for MSE analyses of COP data and other continuous real-world time series. In turn, accurate and consistent results for the MSE assessment of physiological signals will help determine whether MSE gains more traction as a clinical biomarker. The concept of complexity and health is still novel in the clinical setting but could become an important part of patient diagnoses in the future.