1. Introduction
Pattern recognition is a scientific discipline whose methods allow us to describe and classify objects. The descriptive process involves the symbolic representation of these objects through a numerical vector
:
where its
n components represent the value of the attributes of such objects. Given a set of objects (“dataset”)
X, there are two approaches to attempt the classification: (1) supervised; and (2) unsupervised.
In the unsupervised approach case, no prior class information is used. Such an approach aims at finding a hypothesis about the structure of
X based only on the similarity relationships among its elements. These relationships allow us to divide the space of
X into
k subsets, called clusters. A cluster is a collection of elements of
X, which are “similar” between them and “dissimilar” to the elements belonging to other clusters. Usually, the similarity is defined by a metric or distance function
d:
X ×
X → ℜ [
1–
3]. The process to find the appropriate clusters is typically denoted as a clustering method.
1.1. Clustering Methods
In the literature, many clustering methods have been proposed [
4,
5]. Most of them begin by defining a set of
k centroids (one for each cluster) and associating each element in
X with the nearest centroid based on a distance
d. This process is repeated, until the difference between centroids at iteration
t and iteration
t − 1 tends to zero or when some other optimality criterion is satisfied. Examples of this approach are
k-means [
6] and fuzzy
c-means [
7–
9]. Other methods not following the previous approach are: (1) hierarchical clustering methods that produce a tree or a graph in which, during the clustering process, based on some similarity measure, the nodes (which represent a possible cluster) are merged or split; in addition to the distance measure, we must also have a stopping criterion to tell us whether the distance measure is sufficient to split a node or to merge two existing nodes [
10–
12]; (2) density clustering methods, which consider clusters as dense regions of objects in the dataset that are separated by regions of low density; they assume an implicit, optimal number of clusters and make no restrictions with respect to the form or size of the distribution [
13]; and (3) meta-heuristic clustering methods that handle the clustering problem as a general optimization problem; these imply a greater flexibility of optimization algorithms, but also longer execution times [
14,
15].
We propose a numerical clustering method that lies in the group of meta-heuristic clustering methods, where the optimization criterion is based on information theory. Some methods with similar approaches have been proposed in the literature (see Section 1.6).
1.2. Determining the Optimal Value of k
In most clustering methods, the number
k of clusters must be explicitly specified. Choosing an appropriate value has important effects on the clustering results. An adequate selection of
k should consider the shape and density of the clusters desired. Although there is not a generally accepted approach to this problem, many methods attempting to solve it have been proposed [
5,
16,
17]. In some clustering methods (such as hierarchical and density clustering), there is no need to explicitly specify
k. Implicitly, its value is, nevertheless, still required: the cardinality or density of the clusters must be given. Hence, there is always the need to select a value of
k. In what follows, we assume that the value of
k is given
a priori. We do not consider the problem of finding the optimal value of
k. See, for example, [
18–
20].
1.3. Evaluating the Clustering Process
Given a dataset
X to be clustered and a value of
k, the most natural way to find the clusters is to determine the similarity among the elements of
X. As mentioned, usually, such similarity is established in terms of proximity through a metric or distance function. In the literature, there are many metrics [
21] that allow us to find a variety of clustering solutions. The problem is how to determine if a certain solution is good or not. For instance, in
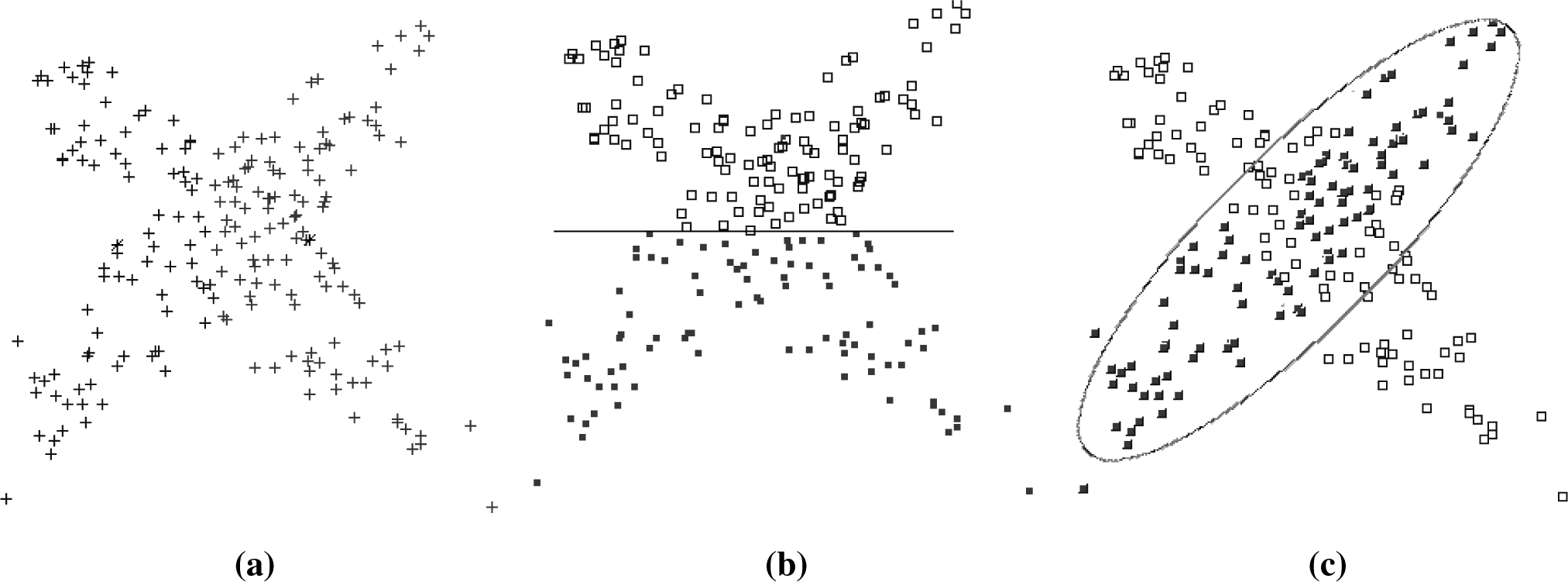
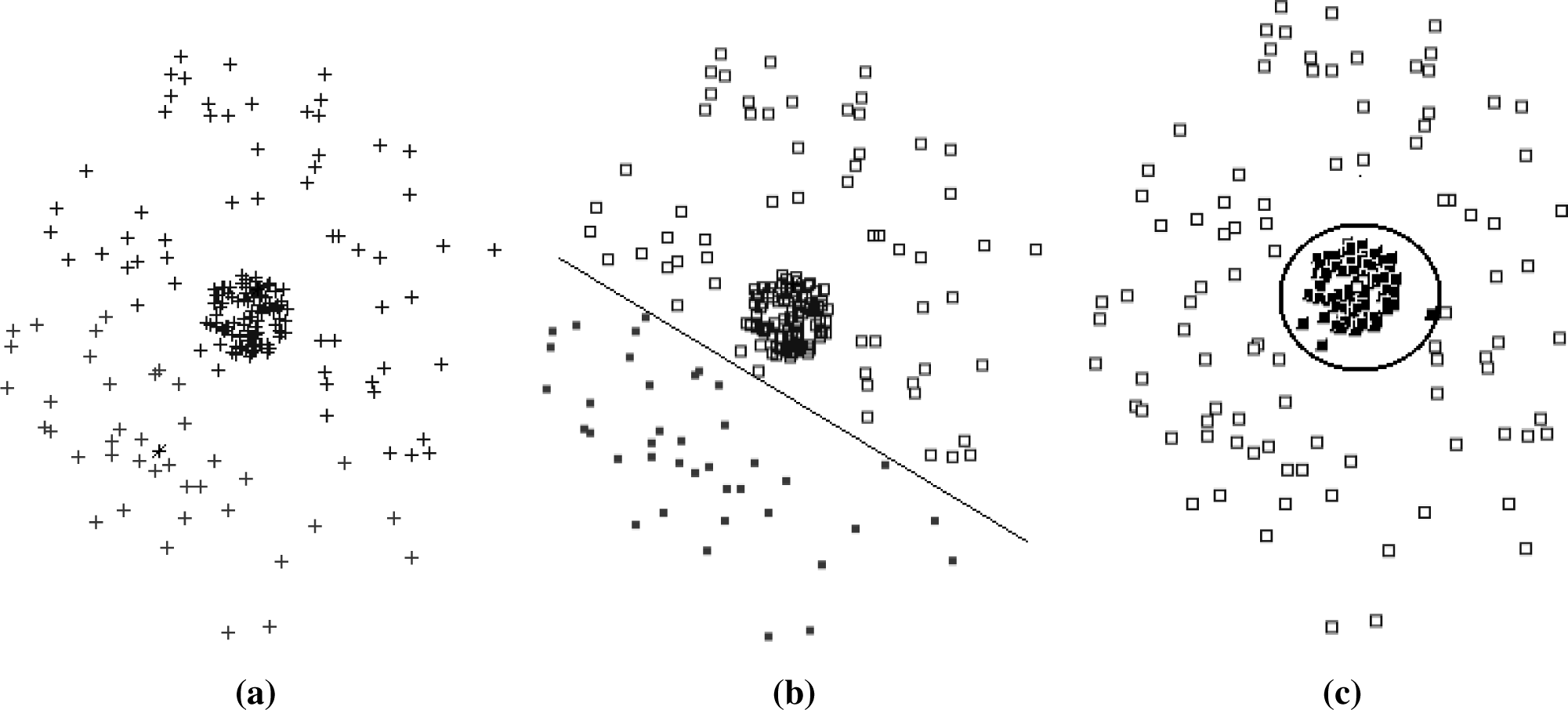
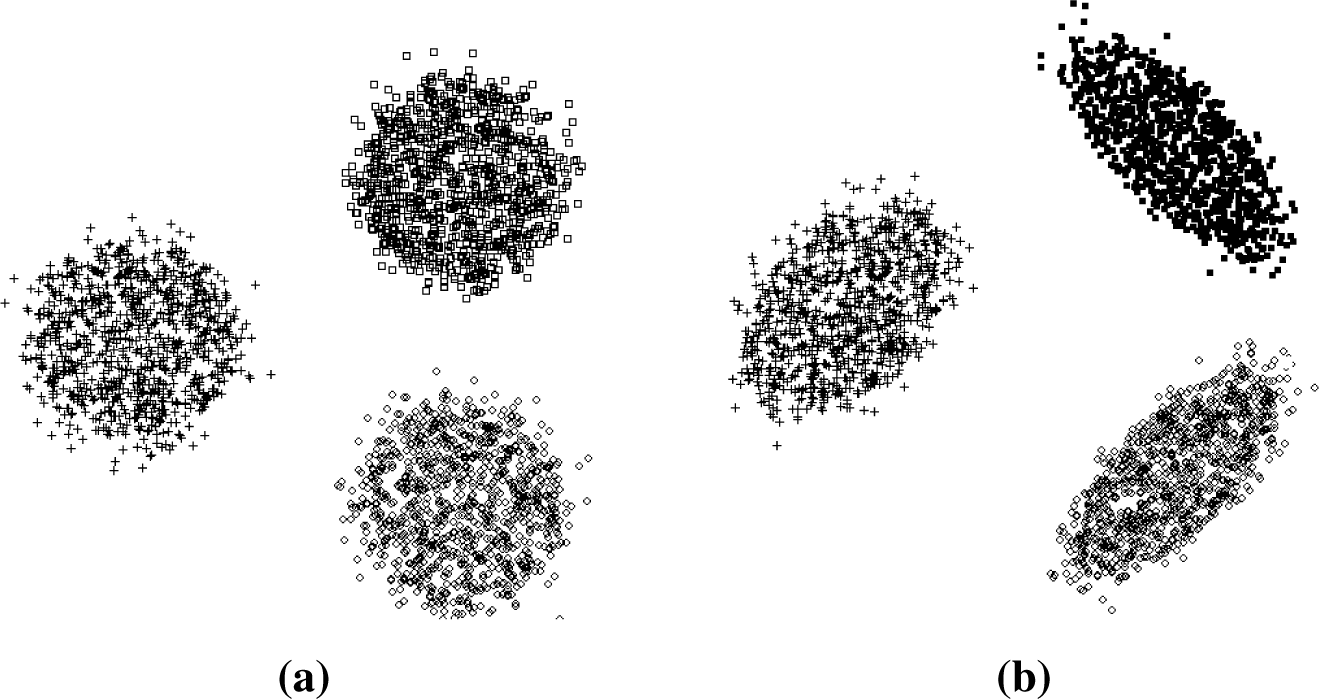
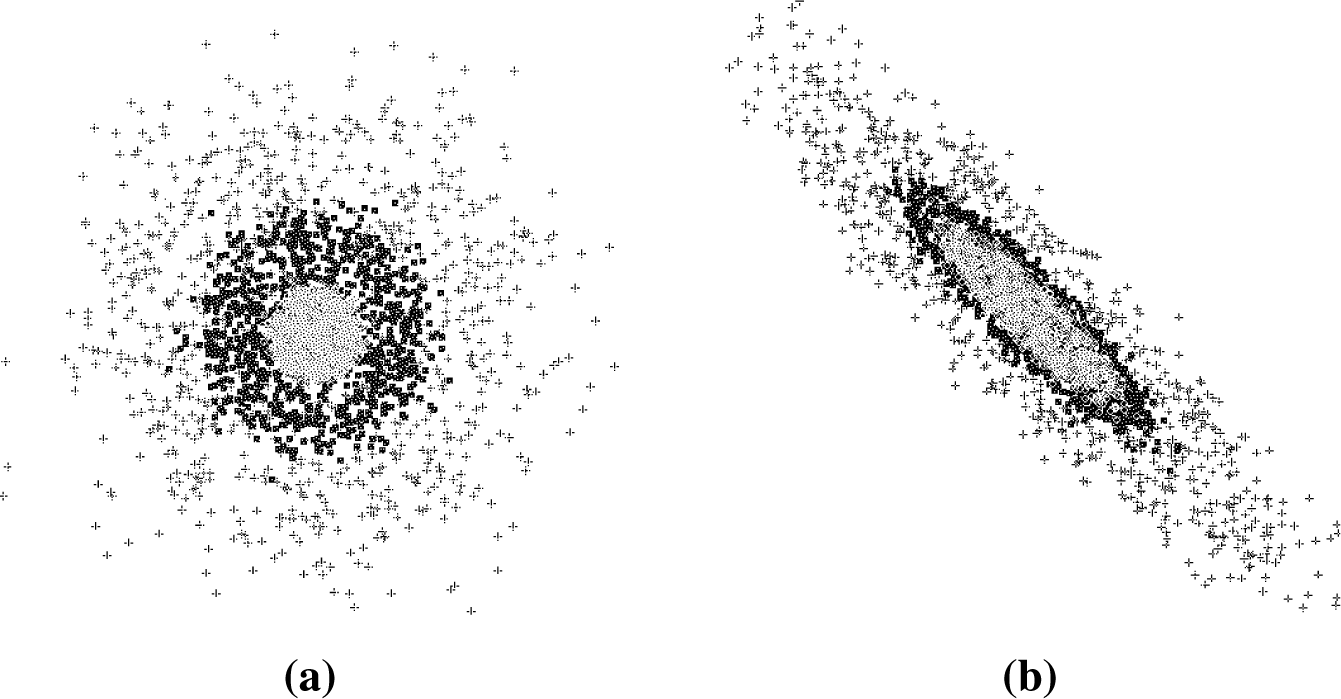
Figures 1 and
2, we can see two datasets clustered with
k = 2. For such datasets, there are several possible solutions, as shown in
Figures 1b,c and
2b,c, respectively.
Frequently, the goodness of a clustering solution is quantified through validity indices [
4,
8,
22,
23]. The indices in the literature are classified into three categories: (1) external indices that are used to measure the extent to which cluster labels match externally-supplied class labels (F-measure [
24], NMIMeasure [
25], entropy [
26], purity [
27]); (2) internal indices, which are used to measure the goodness of a clustering structure with respect to the intrinsic information of the dataset ([
8,
28–
31]); and (3) relative indices that are used to compare two different clustering solutions or particular clusters (the RAND index [
32] and adjusted RAND index [
33]).
Clusters are found and then assigned a validity index. We bypass the problem of qualifying the clusters and, rather, define a quality measure and then find the clusters that optimize it. This allows us to define the clustering process as follows:
Definition 1. Given a dataset X to be clustered and a value of k, clustering is a process that allows the partition of the space of X into k regions, such that the elements that belong to them optimize a validity index q.
Let
Ci be a partition of
X and Π = {
C1,
C2, …
Ck} the set of such partitions that represents a possible clustering solution of
X. We can define a validity index
q as a function of the partition set Π, such that the clustering problem may be reduced to an optimization problem of the form:
where
gi and
hj are constraints, likely based on prior information about the partition set Π (e.g., the desired properties of the clusters).
We want to explore the space of those feasible partition sets and find one that optimizes a validity index instead, doing an a posteriori evaluation of a partition set (obtained by any optimization criterion) through such an index. This approach allows us to find “the best clustering” within the limits of a validity index. To tightly confirm such an assertion, we resort to the statistical evaluation of our method (see Section 5).
1.4. Finding the Best Partition of X
Finding the suitable partition set Π of
X is a difficult problem. The total number of different partition sets of the form Π = {
C1,
C2, …
Ck} may be expressed by the function
S(
N,
k) associated with the Stirling number of the second kind [
34], which is given by:
where
N = |
X|. For instance, for
N = 50 and
k = 2,
S(
N,
k) ≈ 5.63 × 10
14. This number illustrates the complexity of the problem that we need to solve. Therefore, it is necessary to resort to a method that allows us to explore efficiently a large solution space. In the following section, we briefly describe some meta-heuristic searches.
1.6. Related Works
Our method is meta-heuristic (see Section 1.1). The main idea behind our method is to handle the clustering problem as a general optimization problem. There are various suitable meta-heuristic clustering methods. For instance, in [
52–
54], three different clustering methods based on differential evolution, ant colony and multi-objective programming, respectively, are proposed.
Both meta-heuristic or analytical methods (iterative, density-based, hierarchical) have objective functions, which are associated with a metric. In our method, the validity index becomes the objective function.
Our objective function is based on information theory. Several methods based on the optimization of information theoretical functions have been studied [
55–
60]. Typically, they optimize quantities, such as entropy [
26] and mutual information [
61]. These quantities involve determining the probability distribution of the dataset in a non-parametric approach, which does not make assumptions about a particular probability distribution. The term non-parametric does not imply that such methods completely lack parameters; they aim to keep the number of assumptions as weak as possible (see [
57,
60]). Non-parametric approaches involve density functions, conditional density functions, regression functions or quantile functions in order to find the suitable distribution. Typically, such functions imply tuning parameters that determine the convergence of searching for the optimal distribution.
A common clustering method based on information theory is ENCLUS (entropy clustering) [
62], which allows us to split iteratively the space of the dataset
X in order to find those subspaces that minimize the entropy. The method is motivated by the fact that a subspace with clusters typically has lower entropy than a subspace without clusters. In order to split the space of
X, the value of a resolution parameter must be defined. If such a value is too large, the method may not able to capture the differences in entropy in different regions in the space.
Our proposal differs from traditional clustering methods (those based on minimizing a proximity measure as k-means or fuzzy c-means) in that, instead of finding those clusters that optimize such a measure and then defining a validity index to evaluate its quality, our method finds the clusters that optimize a purported validity index.
As mentioned, such a validity index is an information theoretical function. In this sense, our method is similar to those mentioned methods based on information theory. However, it does not use explicitly a non-parametric approach to find the distribution of the dataset. It explores the space of all possible probability distributions to find one that optimizes our validity index. For this reason, the use of a suitable meta-heuristic is compulsory. With the exception of the parameters of such a meta-heuristic, our method does not resort to additional parameters to find the optimal distribution and, consequently, the optimal clustering solution.
Our validity index involves entropy. Usually in the methods based on information theory, the entropy is interpreted as a “disorder” measure; thus, an obvious way is to minimize such a measure. In our work, we propose to maximize it due to the maximum entropy principle.
1.7. Organization of the Paper
The rest of this work is organized as follows: In Section 2, we briefly discuss the concept of information content, entropy and the maximum entropy principle. Then, we approach such issues in the context of the clustering problem. In Section 3, we formalize the underlying ideas and describe the main line of our method (in what follows, clustering based on entropy (CBE)). In Section 4, we present a general description of the datasets. Such datasets were grouped into three categories: (1) synthetic Gaussian datasets; (2) synthetic non-Gaussian datasets; and (3) experimental datasets taken from the UCIdatabase repository. In Section 5, we present the methodology to evaluate the effectiveness of CBE regardless of a validity index. In Section 6, we show the experimental results. We use synthetically-generated Gaussian datasets and apply a Bayes classifier (BC) [
63–
65]. We use the results as a standard for comparison due to its optimal behavior. Next, we consider synthetic non-Gaussian datasets. We prove that CBE yields results comparable to those obtained by a multilayer perceptron network (MLP). We show that our (non-supervised) method’s results are comparable to those of BC and MLP, even though these are supervised. The results of other clustering methods are also presented, including an information theoretic-based method (ENCLUS). Finally, in Section 7, we present our conclusions. We have included three appendices expounding important details.
2. Maximum Entropy Principle and Clustering
The so-called entropy [
26] appeals to an evaluation of the information content of a random variable
Y with possible values {
y1,
y2, …
yn}. From a statistical viewpoint, the information of the event (
Y =
yi) is inversely proportional to its likelihood. This information is denoted by
I(
yi), which can be expressed as:
From information theory [
26,
66], the entropy of
Y is the expected value of
I. It is given by:
Typically, the log function may be taken to be log2, and then, the entropy is expressed in bits; otherwise, as ln, in which case the entropy is in nats. We will use log2 for the computations in this paper.
When
p(
yi) is uniformly distributed, the entropy of
Y is maximal. This means that
Y has the highest level of unpredictability and, thus, the maximal information content. Since entropy reflects the amount of “disorder” of a system, many methods employ some form of such a measure in the objective function of clustering. It is expected that each cluster has a low entropy, because data points in the same cluster should look similar [
56–
60].
We consider a stochastic system with a set of states S = {Π1, Π2, …, Πn} whose probabilities are unknown (recall that Πi is a likely partition set of X of the form Π = {C1, C2, …, Ck}). A possible assertion would be that the probabilities of all states are equal (p(Π1) = p(Π2) = … = p(Πn−1) = p(Πn)), and therefore, the system has the maximum entropy. However, if we have additional knowledge, then we should be able to find a probability distribution that is better in the sense that it is less uncertain. This knowledge can consist of certain average values or bounds on the probability distribution of the states, which somehow define several conditions imposed upon such distribution. Usually, there is an infinite number of probability models that satisfies these conditions.
The question is: which model should we choose? The answer lies in the maximum entropy principle, which may be stated as follows [
67]: when an inference is made on the basis of incomplete information, it should be drawn from the probability distribution that maximizes the entropy, subject to the constraints on the distribution. As mentioned, a condition is an expected value of some measure about the probability distributions. Such a measure is one for which each of the states of the system has a value denoted by
g(Π
i).
For example, let
X = {9, 10, 9, 2, 1} be a discrete dataset to be clustered with
k = 2. We assume that the “optimal” labeling of the dataset is the one that is shown in
Table 1.
Such labeling defines a partition Π* of the form Π* = {
C1 = {9, 10, 9},
C2 = {2, 1}}. The probability model of Π* is given by the conditional probabilities
p(
x|
Ci) that represent the likelihood that, when observing cluster
Ci, we can find object
x.
Table 2 shows such probabilities.
The entropy of
X conditioned on the random variable
C taking a certain value
Ci is denoted as
H(
X|
C =
Ci). Thus, we define the total entropy of Π* as:
Given the probability model of Π* and
Equation (6), the total entropy of Π* is shown in
Table 3. We may also calculate the mean and the standard deviation of the elements
x ∈
Ci denoted as
σ(
Ci) in order to define a quality index:
Alternative partition sets are shown in
Tables 4 and
5.
In terms of maximum entropy, partition H(Π2) is better than H(Π1). Indeed, we can say that H(Π2) is as good as H(Π*). If we assume that a cluster is a partition with the minimum standard deviation, then the partition set Π* is the best possible solution of the clustering problem. In this case, the minimum standard deviation represents a condition that may guide the search for the best solution. We may consider any other set of conditions depending on the desired properties of the clusters. The best solution will be the one with the maximum entropy, which complies with the selected conditions.
In the example above, we knew the labels of the optimal class and the problem became trivial. In the clustering problems, there are no such labels, and thus, it is compulsory to find the optimal solution based solely on the prior information supplied by one or more conditions. We are facing an optimization problem of the form:
where ϵ
i is the upper bound of value of the
i-th condition. We do not know the value of ϵ
i, and thus, we do not have enough elements to determine compliant values of
gi. Based on prior knowledge, we infer whether the value of
gi is required to be as small (or large) as possible. In our example, we postulated that
gi(Π) (based on the standard deviation of the clusters) should be as small as possible. Here,
gi(Π) becomes an optimization condition. Thus, we can redefine the above problem as:
which is a multi-objective optimization problem [
68].
Without loss of generality, we can reduce the problem in
Equation (9) to one of maximizing the entropy and minimizing the sum of the standard deviation of the clusters (for practical purposes, we choose the standard deviation; however, we may consider any other statistics, even higher-order statistics). The resulting optimization problem is given by:
where
g(Π) is the sum of the standard deviation of the clusters. In a
n-dimensional space, the standard deviation of the cluster
Ci is a vector of the form
, where
σj is the standard deviation of each dimension of the objects
. In general, we calculate the standard deviation of a cluster as:
Then, we define the corresponding
g(Π) as:
The entropy of the partition set Π denoted by
H(Π) is given by
Equation (6).
The problem of
Equation (10) is intractable via classical optimization methods [
69,
70]. The challenge is to simultaneously optimize all of the objectives. The tradeoff point is a Pareto-optimal solution [
71]. Genetic algorithms are popular tools used to search for Pareto-optimal solutions [
72,
73].
7. Conclusions
A new unsupervised classifier system (CBE) has been defined based on the entropy as a quality index (QI) in order to pinpoint those elements in the dataset that, collectively, optimize such an index. The effectiveness of CBE has been tested by solving a large number of synthetic problems. Since there is a large number of possible combinations of the elements in the space of the clusters, an eclectic genetic algorithm is used to iteratively find the assignments in a way that increases the intra- and inter-cluster entropy simultaneously. This algorithm is run for a fixed number of iterations and yields the best possible combination of elements given a preset number of clusters
k. That the GA will eventually reach the global optimum is guaranteed by the fact that it is elitist. That it will approach the global optimum satisfactorily in a relatively small number of iterations (800) is guaranteed by extensive tests performed elsewhere (see [
48,
49]).
We found that when compared to BC’s performance over Gaussian distributed datasets, CBE and BC have, practically, indistinguishable success ratios, thus proving that CBE is comparable to the best theoretical option. Here, we, again, stress that BC corresponds to supervised learning, whereas CBE does not. The advantage is evident. When compared to BC’s performance over non-Gaussian sets, CBE, as expected, displayed a much better success ratio. The conclusions above have been reached for a statistical p-value of 0.05. In other words, the probability of such results to persist on datasets outside our study is better than 0.95, thus ensuring the reliability of CBE.
The performance value φ was calculated by: (1) providing a method to produce an unlimited supply of data; (2) This method is able to yield Gaussian and non-Gaussian distributed data; (3) Batches of N = 36 datasets were clustered; (4) For every one of the N Gaussian sets, the difference between our algorithm’s classification and BC’s classification (φ) was calculated; (5) For every batch,
was recorded; (6) The process described in Steps 3, 4 and 5 was repeated until the
distributed normally; (7) Once the
are normal, we know the mean and standard deviation of the means; (8) Given these, we may infer the mean and standard deviation of the original pdf of the φs; (9) From Chebyshev’s theorem, we may obtain the upper bound of φ with probability 0.95. From this methodology, we may establish a worst case upper bound on the behavior of all of the analyzed algorithms. In other words, our conclusions are applicable to any clustering problem (even those outside of this study) with a probability better than 0.95.
For completeness, we also tested the effectiveness of CBE by solving a set of “real world” problems. We decided to use an MLP as the comparison criterion to measure the performance of CBE based on the nearness of its effectiveness with regard to it. Of all of the unsupervised algorithms that were evaluated, CBE achieved the best performance.
Here, two issues should be underlined: (1) Whereas BC and MLP are supervised, CBE is not. The distinct superiority of one method over the others, in this context, is evident; (2) As opposed to BC, CBE was designed not to need the previous calculation of the conditional probabilities of BC; a marked advantage of CBE over BC. It is important to mention that our experiments include tight tests comparing the behavior of other clustering methods. We compared the behavior of k-means, fuzzy c-means and ENCLUS against BC and MLP. The results of the comparison showed that CBE outperforms them (with 95% reliability).
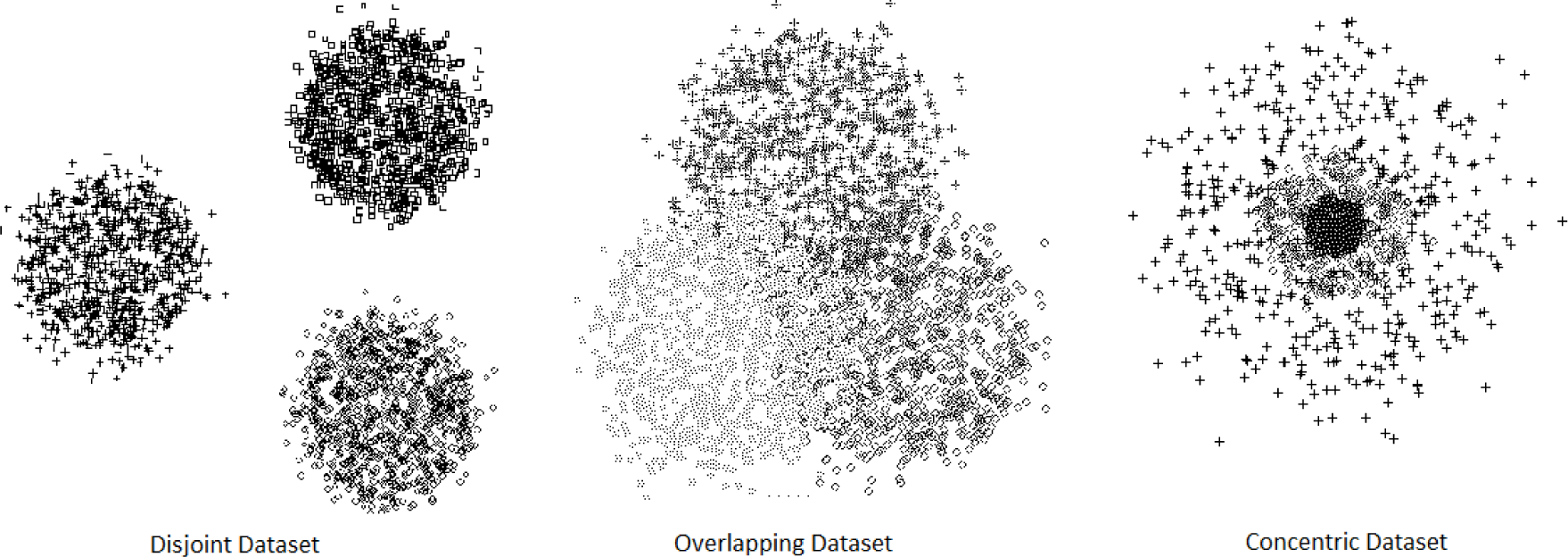
For disjoint sets, which offer no major difficulty, all four methods (k-means, fuzzy c-means, ENCLUS and CBE) perform very well relative to BC. However, when tackling partially overlapping and concentric datasets, the differences are remarkable. The information-based methods (CBE and ENCLUS) showed the best results; nevertheless, CBE was better than ENCLUS. For non-Gaussian datasets, the values of CBE and ENCLUS also outperform the other methods. When CBE is compared to ENCLUS, CBE is 62.5% better.
In conclusion, CBE is a non-supervised, highly efficient, universal (in the sense that it may be easily utilized with other quality indices) clustering technique whose effectiveness has been proven by tackling a very large number of problems (1,530,000 combined instances). It has been, in practice, used to solve complex clustering problems that other methods were not able to solve.