In online applications, where the reaction of the system is required after a few milliseconds, performance is crucial and irreducible. Closed form solutions are needed that are scalable in not only sophisticated processing systems, but in embedded environments, as well. In the following example information about the form of the posterior distribution is included. This helps to achieve a closed form analytical solution for the estimates needed, which, in turn, helps to keep iteration steps at a minimum. For example, posterior distribution can be assumed to be a Gaussian distribution or that it is known to be of this form, but the scale is not known. By applying MrE, the distribution’s mean and variance can be inferred, which represent the scaling parameters of the distribution.
2.1. Maximum Relative Entropy as a Universal Approach for Filtering Applications
Let the following be either an approximate or exact mathematical model about the behavior of the system,
where f is a mathematical model’s function, x(t) is the system state vector, u (t) is a control signal, which perturbs the system into a non-equilibrium state (this is assumed to be a known solution, but it does not take away from the generality of the approach), and δ is an unknown system parameter vector (which can be initially guessed or assumed). When the function, f, is differentiable, the same model is valid at any time moment by selecting that time moment’s (discretization interval’s) probabilistic variable xk as a mean, 〈xk〉,
where k is time index of any discretization interval. When the function arguments are not differentiable at all points of their domain, they might have discontinuities at their boundary conditions. However, often, smoothness in one state space variables causes discontinuities in the other state variables, which implicitly enforces a boundary constraint. These connections are often only seen at the macroscopic (course-grained) level. For example, the inductor’s current just before the commutation (−0) is equal to the inductor’s current right after commutation (+0) in the RL circuit. However, the inductor’s voltage has an abrupt change at the commutation moment, and its (−0) and (+0) values can be found implicitly from the boundary condition of the current signal using Kirchhoff’s circuit laws. This information becomes useful when the functional with partly differentiable functions need to be constrained. When discontinuity points exist in the function, MrE optimization on the domain that is differentiable is used. This results in unknowns at the boundary conditions or the discontinuity points. Some states, control variables or parameters will be equal at time moments (−0) and (+0). This information might be seen at the macro (course-grained) level of the system. Then, we solve every boundary condition for the unknowns and, finally, infer the parameters of the differential equations simultaneously.
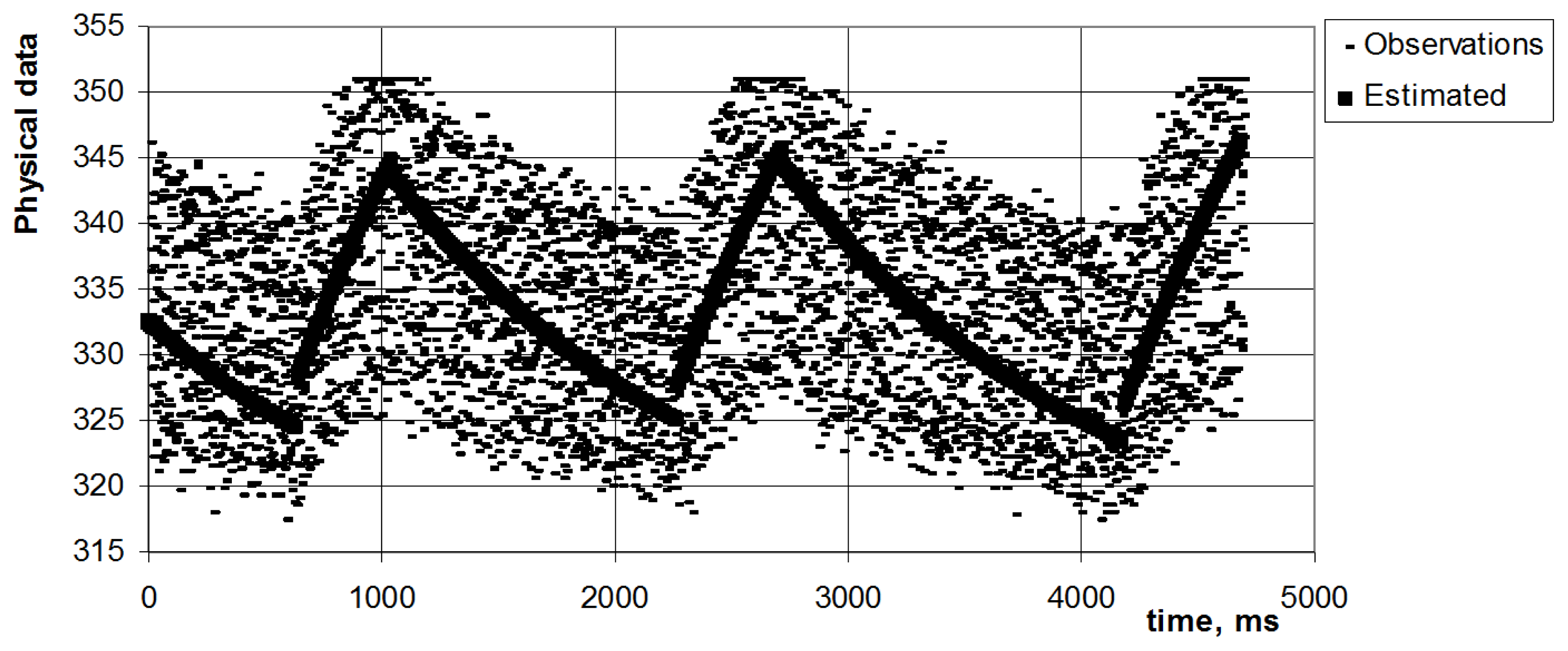
A toy numeric example with a control signal perturbing a first order nonhomogenous ordinary differential equation system by a relay control (on/off or so-called bang-bang control) is shown below. This type of control signal causes a discontinuity point in the domain of the differential equations system. Simultaneous inferring of the differential equation parameters is illustrated.
If the measured time series is in a vector form, cxk, i.e., at time moments t0, t1, ..., tn observations (data) are collected regarding the one dimensional variable x(t) as cx0, cx1, ..., cxn, then our entropy will have the form,
where the posterior distribution,
P =
P (〈
xk〉
, xk), would update the prior distribution,
Plikelihood (
cxk, xk), so that our set of estimated values for 〈
xk〉 maximizes the entropy;
Equation (3). This enforces the constraints in
Equation (2) on the posterior and produces a Lagrangian,
The integral
Equation (4) can be multidimensional. Furthermore, the exact form of the constraints may be unknown or so-called non-parametric,
i.e., their behavior is known, but the constraints’ forms or mathematical models are undefined. Integrals should be summed over time windows to establish a Lagrangian for the joint action in such cases. One should consider using the computationally feasible methods of the Monte Carlo family or similar brute force sampling approaches for these cases. In our toy example, an example with a computable solution is provided, and other complicated cases are out of the scope of the paper.
In some cases,
Equation (4) does not have a closed form solution, and one should seek a numeric iterative approach. For example, when the mathematical models are parabolic partial differential equations, applying the variational data assimilation method as in [
11] is suggested. In our toy example,
Equation (4) has a closed form solution with some unknown parameters from our mathematical model. These parameters are inferred by using boundary conditions, which are satisfied for the time series. If it is assumed that the control signal that perturbs the system is known and it is further assumed that there are two subsequent sets of time series with different perturbations, then one approach to explicitly estimate the value of the unknown parameter
δ is to find it, such that it satisfies the boundary condition between the two time series,
i.e., the last estimate of the first time series must be equal to the very first estimate of the next time series. This is illustrated in the following section, where this is accomplished by incorporating the differential equation’s boundary condition.
2.2. Example with Nonhomogenous Differential Equation Constraints
We examine a toy system below that uses a one-dimensional time series of measurements. At time moments
t0,
t1, ...,
tn observations (data) are collected regarding the one-dimensional variable
x(
t) as
cx0,
cx1, ...,
cxn. We assume the observations are represented by independent probabilistic variables
x0,
x1, ...,
xn, and their uncertainties are equal to
. Then, the probability density function of the joint prior or the likelihood [
2] for the time series variables is,
Note: It is reasonable to see the likelihood as containing “prior” information, since it represents the relationship that has already been established between observation values and probabilistic variables.
The goal here is to find a posterior distribution for the variables that will satisfy the constraints (dynamics). Frequently, the unbiased model is unknown for the variable as a function of time, because it contains unobservable nonlinearities. Further, the analytical closed form model can be more complicated than what is known a priori about the system based on experience. Yet, often, the main behavior of a system can be approximated by an exponential law. Thus, inferring the posterior distribution may be done by not incorporating the dynamic constraints, which exactly represent the physical system behavior, but by the constraints representing an exponential approximation. This type of assumption that uses an exponential approximation allows for the closed form solutions to be found for practical filtering applications and will be shown below, e.g., simultaneously approximating a time series with an exponential curve, while inferring parameters of the differential equation.
The main problem with the estimation of an exponential mathematical model is that the start and the end processes, and thus, the data from them, are equally important. Markov assumptions cannot then be explicitly assumed. In the resistance-inductance (RL) circuit, where the control signal is the voltage signal for the circuit, the parameters (R and L) of the circuit can be calculated from the transient conditions when a step control signal function is applied and the system is in a steady state. At the beginning, the rate of current increase will give information about the inertia of the system, which is represented by L. At the end of the transient process, the steady state of the system will give information about the resistance of the system R. Thus, the time series is “smoothed” with an approximate exponential law, and the estimates must be determined with a wide enough processing window that not only covers the start of the transient process, but also so that the pattern of the saturation effect is partially “seen” in the time series. This way, the estimates, which behave according to the exponential law, as well as the parameters of the differential equation are inferred. In other words, the more information that is included, the less uncertainty is left in the estimate expression after the entropy is maximized.
Again, for illustration, assume that the following approximation for the system behavior model is,
where
u (
t) is the control signal that perturbs the system variable,
x(
t), according to
Equation (6), and where
δ and
C are the parameters of the first order nonhomogenous, differential equation and
xsteady is the steady state value of the variable
x(
t) when there is no control signal
u (
t) applied, assuming that the system is in a steady state. Further, it can be assumed that the system control signal,
u(
t), is constant over the duration of all discretization intervals, Δ
t, at any time moment
k. It can also be assume that
Equation (6) is the constraint over the probabilistic variable’s mean. In this case, the constraint is,
Here, the mean of some probabilistic variable is a function of time. The inference process should not only estimate the means of the probabilistic variable at time moments
k, but also take into account the dynamics, which is given
a priori. The solution of
Equation (6) is represented by,
where
x0 represents the initial condition value at some initial time. If it is assumed that the initial conditions of the variable
x(
t) are the previous sample’s value and the current sample’s value is the final value after the discretization interval passed, then
Equation (8) can be rewritten as:
The exponential term does not depend on the actual means, so an intermediate notation will used,
, which simplifies the expression to,
The common denominator is found, and all of the terms to the left side of
Equation (10) are moved, which yields,
The entropy is maximized to find the joint distribution that is closest to
Pobs, but that also satisfies the approximate model (knowledge about the system) in
Equation (9), which is assumed is enough to mimic the behavior of the system at the a macroscopic level. Before doing so, the general shape of the posterior distribution will be assumed, but the scaling factors are unknown, so that,
where it is assumed that the variance of the means
is constant for each variable, respectively, for illustrative purposes. Then, the entropy to be maximized is,
This is maximized to derive the Lagrangian,
where dΩ = d
x0 · d
x1 · . . . · d
xk · . . . · d
xn and where λ
k are the Lagrange multipliers, which enforce the constraints (dynamics) over the means of the variables under consideration. By inserting
Equations (5) and
(12) into
Equation (14) and integrating over the variables, the Lagrangian is simplified to,
where
ε is an integration constant along with additive terms, which do not affect the Lagrangian in
Equation (15). This constant can be omitted, which yields the final Lagrangian,
It should be noted at this point that the “distance” that is mentioned in [
10] is the quadratic term in the Lagrangian.
2.3. Maximization of the Expectation
After differentiating the entropy with respect to the variables means, 〈x0〉, . . ., 〈xn〉, a system of n+1 equations is formed,
Every discretization interval constraint (which originates from
Equation (11) forms the system of
n equations,
which together with
Equation (17) form a system of 2
n + 1 linear equations that have a closed form solution.
For illustration, the solutions for the cases n = 4, n = 6 and n = 8 are provided. After this is done, the pattern of the solution will be generalized.
In the first case (n = 4), the function f is differentiable. For illustration, we assume that there are jump discontinuities at discretization points x0, x4, x8, x12, etc. It is not a necessity to strictly enforce this assumption, but it is made so that the sequence of actions necessary for this approach are clear. At the jump discontinuities in this system (control signal in the whole period of the differentiable interval is constant), the boundary conditions claim that 〈xk (−0)〉 = 〈xk (+0)〉, i.e., the boundary condition is of the Dirichlet type. Then, for every differentiable period of the function, we have two systems of equations,
and:
which results in to a system of nine equations and mine unknowns consisting of five state variables and four Lagrange multipliers,
After some manipulations, the final solution for the two state variables 〈x0〉 and 〈x4〉 is:
and:
Values 〈x0〉 and 〈x4〉 belong to the very first differentiable period of the time series when a control signal u is a constant, i.e., ufirst = const. Thus, the closed form solutions for〈x0 (+0)〉 and 〈x4 (−0)〉 values have been found.
After introducing the following coefficients for convenience,
For this first differentiable period, the coefficients effective at the jump discontinuity of the control signal from ufirst to usecond at the fourth discretization interval are introduced,
The expression of 〈x4 (−0)〉 can be rewritten as:
The next differentiable period from the fourth to eight discretization intervals, where again we have n = 4 (this is not necessary, but the same value is used for illustration purposes). This yields the closed form expressions for the state variables at the jump discontinuities,
After introducing convenience coefficients for 〈x4 (+0)〉,
the expression for 〈x4 (+0)〉 is arrived at,
From a macroscopic level, there is a Dirichlet boundary condition with jump discontinuity at the fourth discretization interval, which states that 〈x4 (−0)〉 = 〈x4 (+0)〉. The following equation is solved to determine δ,
which yields,
One might ask: if the illustrative coefficients
Afirst,
Bfirst,
Asecond and
Bsecond that were selected are all functions of
δ, then is the calculation of
Equation (38) valid? Generally not if the rate of change of
δ is of the same order as the discretization interval’s size. For this example, it is
a priori known that some external disturbances affect our system through changing the value of
δ,
i.e., it is actually a function of time,
δ (
t). However, in many physical systems, the parameters’ rate of change is much smaller than the rates of change of the state and control variables. Specifically, in a current application of this, the rate of change of
δ (
t) in our system was ten-times smaller than the duration of differentiable period. This allowed us to assume that
γ(
δ) was constant, because any change in
δ resulted in approximately a ten- to one hundred-times smaller change in
γ(
δ) compared to the change effecting
Equation (37). Therefore, the algorithm can start from a certain value of
δ, find the
δ using
Equation (38), then put it back into expressions
Equations (24)–
(31), with the recalculated estimates of the means at the boundary condition defined by discontinuity point. Normally, after 3–5 iterations, the value of
δ converges to the acceptable precision.
When δ converges to an acceptable value, the remaining estimates of, 〈x1〉, 〈x2〉 and 〈x3〉 are calculated. Thus, some information from observations is precalculated and then applied to the boundary conditions. This yields the exact values for the differentiable points, which are in between the discontinuity points.
Let us analyze the example with n = 6. Similarly to previous example, we derive our boundary solution for the system of 13 equations as,
The convenience coefficients are then redefined as:
which yields,
The
δ is determined by the same procedure with the 3–5 iterations that were used with
Equation (38) and
n = 4.
For the third example of n = 8, the convenience coefficients that are affected are only shown,
which yields,
2.4. Generalization of the Estimation Algorithm
After seeing the pattern of solutions in
Equations (47)–
(50), we generalize for any even number,
n discretization intervals of the differentiable period. The convenience coefficients are redefined for the solution pattern,
The mean estimate expressions for the boundary conditions, i.e., for the first 〈x0 (+0)〉 and the last 〈xn (−0)〉 means of the time series are as follows,
and:
The value of the parameter
γ(
δ) is not affected by the change in
δ nearly as much as the effect that
δ produces in equation
Equations (54) and
(55). This is because the discretization interval, Δ
t, is usually chosen as small as possible (typically limited by embedded hardware resources), and the total duration of the time series (the processing window of simultaneous updates or the part of
f of differentiable points) is also relatively small. Different control signals
ufirst and
usecond for two subsequent time series with jump discontinuities between,
δ, can be calculated based on the fact that the last estimated mean of the first processing window is equal to the first estimated mean of the next processing window. In other words, if
Equations (54) and
(55) can be rewritten into the form,
and:
where 〈
xn (−0)〉 = 〈
xn (+0)〉. The value for
δ is found using
Equation (38). After the estimate for
δ is determined from
Equation (38), the parameter
γ can be recalculated and then used to calculate the mean estimates according to the expression in
Equations (54) and
(55) again; and then, calculate
δ again by using
Equation (38), and so on. This algorithm usually requires 3–5 iterations to converge to the acceptable precision of
δ, regardless of the uncertainty of the input variables. Acceptable precision in our case is the situation when a new iteration changed the
δ value by 0.1%. At this point, we assume that it is no longer necessary to proceed with further iterations, because the information gain about the value would become negligible.
We present the algorithm for the calculation in pseudo code:
double Calculate Delta Coefficient (
double initial value,
double precision,
double [] observations,
double C, // inertia coefficient as constant
double u, // control signal’ s value
double x_steady, // steady state value
double dt // the size of discretization interval
{
double delta = initial_value;
double earlier_delta = undefined;
precalculate arguments of equations containing
a) observations;
b) coefficient C;
c) the size of discretization interval;
d) control signals value;
e) steady state value of variable;
while (true) // loop continuously
{
calculate alpha and beta coefficients;
calculate A_first, B_first, A_sec, B_sec;
delta = (B_sec – B_first)/(A_first – A_sec);
if ((delta – earlier_delta )ˆ2< precision)
break ; // halt the loop
earlier_delta = delta;
}
return delta;
}
Notice that there is still a singular point in
Equation (38) that has to be avoided when implementing the filtering algorithm. The coefficients
Afirst and
Asecond depend on the observation values, as shown in
Equations (54) and
(55). Thus, the size of
n needs to be such that the change in observations in the processing window is noticeable in order to avoid this singularity in a real system,
i.e., the system must be perturbed enough or its control signal is reduced so that the change of measurements of the input channel is noticeable. If this condition is satisfied, the MrE filter will be stable. Our physical system naturally satisfied this requirement. In this example, during the whole measurement and estimation process, there are no singularities.
We need to make an important theoretical note here regarding this approach as compared to exponential smoothing used in EWMA. For this, the numeric example with n = 4 is used.
After solving the systems of equations in
Equation (21), in addition to the 〈
x4〉 value in
Equation (23), also the expression for 〈
x3〉 is constructed,
From exponential smoothing [
9], the next discretization interval’s estimate is calculated using,
At this point, it is unclear what the parameters
θ and
xunknown represent in the MrE filter and how to resolve this by analyzing the equations
Equations (58) and
(23). It is clear that parameter
θ is our function
γ(
δ), and
Equation (59) can be rewritten in the form,
All
Equation (61) values are constants for a single differentiable period, as was mentioned earlier. Thus, exponential smoothing is a special case of applying the MrE filter. Because of this, the physical meaning of the coefficients in the exponential smoothing can be understood. Furthermore, because MrE is more general, when the situation changes (for example, when the control force changes, or external disturbances change the system parameter
δ), it can be adapted to our exponential filter, so that it returns unbiased estimates.