On Shannon’s Formula and Hartley’s Rule: Beyond the Mathematical Coincidence †
Abstract
:1. Introduction
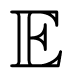 (X2) and Y = X + Z is the channel output. Here Z denotes the additive Gaussian random variable (independent of X) that models the communication noise with power N =
(X2) and Y = X + Z is the channel output. Here Z denotes the additive Gaussian random variable (independent of X) that models the communication noise with power N =
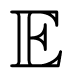 (Z2). By expanding mutual information I(X; Y ) = h(Y) − h(Y|X) as a difference of differential entropies, noting that
is constant, and choosing X Gaussian so as to maximize h(Y), Shannon arrived at his formula
.
(Z2). By expanding mutual information I(X; Y ) = h(Y) − h(Y|X) as a difference of differential entropies, noting that
is constant, and choosing X Gaussian so as to maximize h(Y), Shannon arrived at his formula
.During 1928, Hartley formulated a way to quantify information and its line rate (also known as data signalling rate R bits per second) [5]. This method, later known as Hartley’s law, became an important precursor for Shannon’s more sophisticated notion of channel capacity. (...)Hartley argued that the maximum number of distinguishable pulse levels that can be transmitted and received reliably over a communications channel is limited by the dynamic range of the signal amplitude and the precision with which the receiver can distinguish amplitude levels. Specifically, if the amplitude of the transmitted signal is restricted to the range of [−A,+A] volts, and the precision of the receiver is ±Δ volts, then the maximum number of distinct pulses M is given by. By taking information per pulse in bit/pulse to be the base-2-logarithm of the number of distinct messages M that could be sent, Hartley [5] constructed a measure of the line rate R as R = log2(M) [bits per symbol].—Wikipedia [4]
Hartley’s rate result can be viewed as the capacity of an errorless M-ary channel (...). But such an errorless channel is an idealization, and if M is chosen small enough to make the noisy channel nearly errorless, the result is necessarily less than the Shannon capacity of the noisy channel (...), which is the Hartley–Shannon result that followed later [in 1948].—Wikipedia [4]
- (1)
- Hartley did put forth his rule (2) twenty years before Shannon.
- (2)
- The fundamental tradeoff (1) between transmission rate, bandwidth, and signal-to-noise ratio came out unexpected in 1948: the time was not even ripe for this breakthrough.
- (3)
- Hartley’s rule is inexact while Shannon’s formula is characteristic of the additive white Gaussian noise (AWGN) channel (C′ ≠ C).
- (4)
- Hartley’s rule is an imprecise relation between signal magnitude, receiver accuracy and transmission rate that is not an appropriate formula for the capacity of a communication channel.
2. Hartley’s Rule is not Hartley’s
I started with information theory, inspired by Hartley’s paper, which was a good paper, but it did not take account of things like noise and best encoding and probabilistic aspects.—Claude Elwood Shannon [6]
(...) in 1928, Hartley [5] reasoned that Nyquist’s result, when coupled with a limitation on the accuracy of signal reception, implied a restriction on the amount of data that can be communicated reliably over a physical channel. Hartley’s argument may be summarized as follows. If we assume that (1) the amplitude of a transmitted pulse is confined to the voltage range [−A,A] and (2) the receiver can estimate a transmitted amplitude reliably only to an accuracy of ±Δ volts, then, as illustrated in [the] Figure (...), the maximum number of pulse amplitudes distinguishable at the receiver is (1 + A/Δ). (...)[in the Figure’s legend:] Hartley considered received pulse amplitudes to be distinguishable only if they lie in different zones of width 2Δ (...)Hartley’s formulation exhibits a simple but somewhat inexact interrelation among (...) the maximum signal magnitude A, the receiver accuracy Δ, and the allowable number of message alternatives. Communication theory is intimately concerned with the determination of more precise interrelations of this sort.—John M. Wozencraft; Irwin Mark Jacobs [7]
Although not explicitly stated in this form in his paper, Hartley [5] has implied that the quantity of information which can be transmitted in a frequency band of width B and time T is proportional to the product: 2BT logM, where M is the number of “distinguishable amplitude levels.” [...] He approximates the waveform by a series of steps, each one representing a selection of an amplitude level. [...] For example, consider a waveform to be traced out on a rectangular grid [...], the horizontal mesh-width representing units of time (equal to 1/2B in order to give the necessary 2BT data in a time T), and the vertical the “smallest distinguishable” amplitude change; in practice this smallest step may be taken to equal the noise level n. Then the quantity of information transmitted may be shown to be proportional to BT log(1 + a/n) where a is the maximum signal amplitude, an expression given by Tuller [8], being based upon Hartley’s definition of information.—E. Colin Cherry [9]
3. Independent 1948 Derivations of Shannon’s Formula
With many profound scientific discoveries (for example Einstein’s discovery in 1905 of the special theory of relativity) it is possible with the aid of hindsight to see that the times were ripe for a breakthrough. Not so with information theory. While of course Shannon was not working in the vacuum in the 1940’s, his results were so breathtakingly original that even the communication specialists of the day were at a loss to understand their significance.—Robert McEliece [10]
In the end, [1] and the book based on it came as a bomb, and something of a delayed-action bomb.—John R. Pierce [11]
(...) two important papers (...) were almost concurrent to [1].The first subsequent paper was [12], whose coauthors were B. R. Oliver and J. R. Pierce. This is a very simple paper compared to [1], but it had a tremendous impact by clarifying a major advantage of digital communication. (...) It is probable that this paper had a greater impact on actual communication practice at the time than [1].The second major paper written at about the same time as [1] is [2]. This is a more tutorial amplification of the AWGN channel results of [1]. (...) This was the paper that introduced many communication researchers to the ideas of information theory.—Robert Gallager [13]
Formulas similar to (1) for the white noise case have been developed independently by several other writers, although with somewhat different interpretations. We may mention the work of N. Wiener [17], W. G. Tuller [8], and H. Sullivan in this connection.—Claude Elwood Shannon [1]
By 1948 the need for a theory of communication encompassing the fundamental tradeoffs of transmission rate, reliability, bandwidth, and signal-to-noise ratio was recognized by various researchers. Several theories and principles were put forth in the space of a few months by A. Clavier [18], C. Earp [19], S. Goldman [20], J. Laplume [21], C. Shannon [1], W. Tuller [8], and N. Wiener [17]. One of those theories would prove to be everlasting.—Sergio Verdú [14]
(...) this result [Shannon’s formula] was discovered independently by several researchers, and serves as an illustration of a scientific concept whose time had come.—Lars Lundheim [22]
This idea occurred at about the same time to several writers, among them the statistician R. A. Fisher, Dr. Shannon of the Bell Telephone Laboratories, and the author. Fisher’s motive in studying this subject is to be found in classical statistical theory; that of Shannon in the problem of coding information; and that of the author in the problem of noise and message in electrical filters. Let it be remarked parenthetically that some of my speculations in this direction attach themselves to the earlier work of Kolmogoroff in Russia, although a considerable part of my work was done before my attention was called to the work of the Russian school.—Norbert Wiener[17]
Information theory has been identified in the public mind to denote the theory of information by bits, as developed by C. E. Shannon and myself.—Norbert Wiener[23]
Wiener’s head was full of his own work and an independent derivation of (1) (...) Competent people have told me that Wiener, under the misapprehension that he already knew what Shannon had done, never actually found out.—John R. Pierce [11]
A symposium on “Recent Advances in the Theory of Communication” was presented at the November 12, 1947, meeting of the New York section of the Institute of Radio Engineers. Four papers were presented by A. G. Clavier (...); B.D. Loughlin (...); and J. R. Pierce and C. E. Shannon, both of Bell Telephone Laboratories.—C.W. Earp [19]
Let S be the rms amplitude of the maximum signal that may delivered by the communication system. Let us assume, a fact very close to the truth, that a signal amplitude change less than noise amplitude cannot be recognized, but a signal amplitude change equal to noise is instantly recognizable. Then, if N is the rms amplitude of the noise mixed with the signal, there are 1 + S/N significant values of signal that may be determined. (...) the quantity of information available at the output of the system [is = log(1 + S/N)].—William G. Tuller [8]
The existence of [Shannon’s] work was learned by the author in the spring of 1946, when the basic work underlying this paper had just been completed. Details were not known by the author until the summer of 1948, at which time the work reported here had been complete for about eight months.—William G. Tuller [8]
(...) much of the early reaction to Shannon’s work was either uninformed or a diversion from his aim and accomplishment. (...) In 1949, William G. Tuller published a paper giving his justification of (1) [8].—John R. Pierce [11]
How many different signals can be distinguished at the receiving point in spite of the perturbations due to noise? A crude estimate can be obtained as follows. If the signal has a power P, then the perturbed signal will have a power P + N. The number of amplitudes that can be reasonably well distinguished is where K is a small constant in the neighborhood of unity depending on how the phrase “reasonably well” is interpreted. (...) The number of bits that can be sent in this time is.—Claude Elwood Shannon [2]
(...) Hodges cites a Shannon manuscript date 1940, which is, in fact, a typographical error.(...) First submission of this work for formal publication occurred soon after World War ll.—Claude Elwood Shannon [6]
4. Hartley’s Rule yields Shannon’s Formula: C′ = C
5. Hartley’s Rule as a Capacity Formula
Theorem 1
Proof
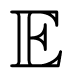 (X2) and additivity results from the fact that X and Z are uncorrelated; and in the uniform case, Φ(X) = |X| and additivity is simply a consequence of the inequality |X + Z| ≤ |X| + |Z|. Also in both cases, the noise Z = Z* maximizes the differential entropy h(Z) under the constraint Φ(Z) ≤ c′, and the input X = X* that maximizes mutual information I(X; Y ) = I(X;X + Z*) is such that the corresponding output Y * = X* + Z* also maximizes the differential entropy h(Y ) under the constraint Φ(Y ) ≤ c + c′. When Φ(X) =
(X2) and additivity results from the fact that X and Z are uncorrelated; and in the uniform case, Φ(X) = |X| and additivity is simply a consequence of the inequality |X + Z| ≤ |X| + |Z|. Also in both cases, the noise Z = Z* maximizes the differential entropy h(Z) under the constraint Φ(Z) ≤ c′, and the input X = X* that maximizes mutual information I(X; Y ) = I(X;X + Z*) is such that the corresponding output Y * = X* + Z* also maximizes the differential entropy h(Y ) under the constraint Φ(Y ) ≤ c + c′. When Φ(X) =
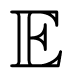 (X2) (power limitation), both Y * and Z* are Gaussian while for Φ(X) = |X| (amplitude limitation), both Y* and Z* have a uniform distribution.
(X2) (power limitation), both Y * and Z* are Gaussian while for Φ(X) = |X| (amplitude limitation), both Y* and Z* have a uniform distribution.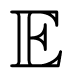 (X2) to show that under limited power, Gaussian noise is the worst possible noise that one can inflict in the channel (in terms of its capacity). To show this, he considered an arbitrary additive noise Z and defined Z̃ as a random variable of the same distribution type as Z* but with the same differential entropy as Z. Thus for Φ(X) =
(X2) to show that under limited power, Gaussian noise is the worst possible noise that one can inflict in the channel (in terms of its capacity). To show this, he considered an arbitrary additive noise Z and defined Z̃ as a random variable of the same distribution type as Z* but with the same differential entropy as Z. Thus for Φ(X) =
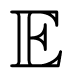 (X2), Z̃ is a zero-mean Gaussian variable of average power Ñ = 22h(Z)/2π e, which is referred to as the entropy power [1] of Z. He then established that the capacity associated with the noise Z satisfies [1]
(X2), Z̃ is a zero-mean Gaussian variable of average power Ñ = 22h(Z)/2π e, which is referred to as the entropy power [1] of Z. He then established that the capacity associated with the noise Z satisfies [1]Definition 2 (Entropic Amplitude).
Theorem 3
Proof
6. A Mathematical Analysis
6.1. Conditions for Shannon’s Formula to Hold
- the probability density function (pdf) pZ of the zero-mean noise Z, which is assumed independent of X;
- a constraint set C on the possible distributions of X. The channel capacity is computed under this constraint as
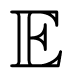 (X*2) and N =
(X*2) and N =
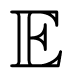 (Z2) so that P/N denotes the signal-to-noise ratio at the optimum.
(Z2) so that P/N denotes the signal-to-noise ratio at the optimum.Lemma 4
Proof
Example 1 (Gaussian channel).
Example 2 (uniform channel).
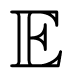 (eiωX), the characteristic function of any random variable X.
(eiωX), the characteristic function of any random variable X.Lemma 5
Proof
Example 3 (Gaussian channel (continued)).
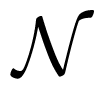 (0, P).
(0, P).Example 4 (uniform channel (continued)).
Example 5 (Cauchian channel).
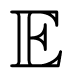 (X*2) = +∞ and N =
(X*2) = +∞ and N =
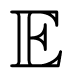 (Z2) = +∞ so that the signal-to-noise ratio is not defined.
(Z2) = +∞ so that the signal-to-noise ratio is not defined.Lemma 6
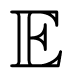 (b(X)) ≤ C, where
(b(X)) ≤ C, whereProof
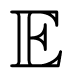 (b(X)) should be equal to the capacity C. The assertion follows.
(b(X)) should be equal to the capacity C. The assertion follows.Example 6 (Gaussian channel (continued)).
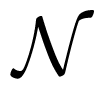 (0,N) and Y * ~
(0,N) and Y * ~ 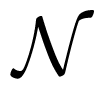 (0, P + N). Therefore,
(0, P + N). Therefore,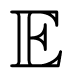 (b(X)) ≤ C is now equivalent to
(b(X)) ≤ C is now equivalent to 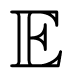 (X2) ≤ P as expected.
(X2) ≤ P as expected.Example 7 (uniform channel (continued)).
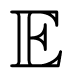 (b(X)) ≤ C is equivalent to |X| ≤ A a.e. as expected.
(b(X)) ≤ C is equivalent to |X| ≤ A a.e. as expected.Theorem 7
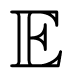 (b(X)) ≤ C where
(b(X)) ≤ C whereProof
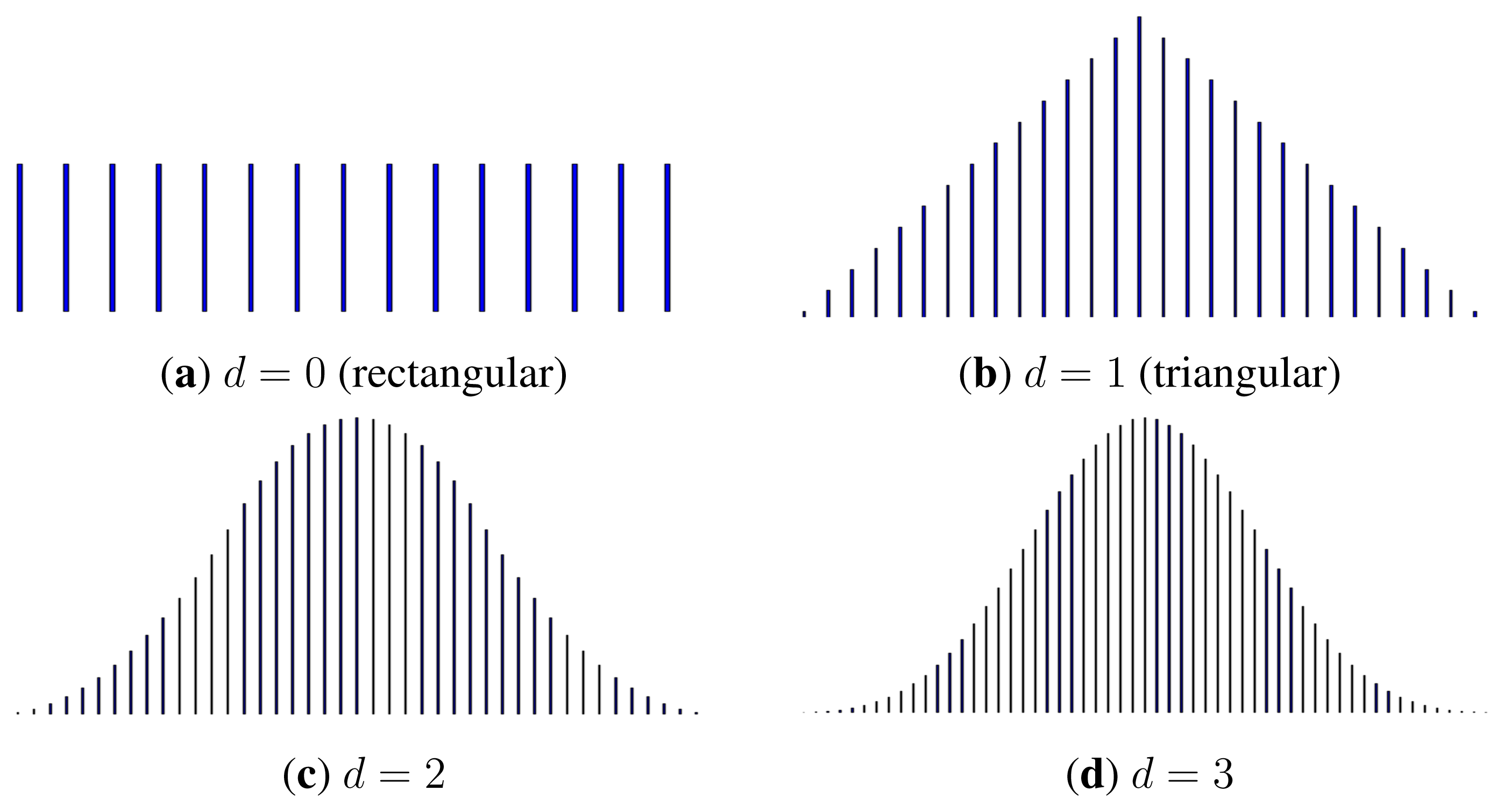
6.2. B-Spline Channels of Any Degree
Definition 8 (B-spline Channel).
Theorem 9
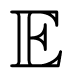 (bd(X)) ≤ Cd where
(bd(X)) ≤ Cd whereProof
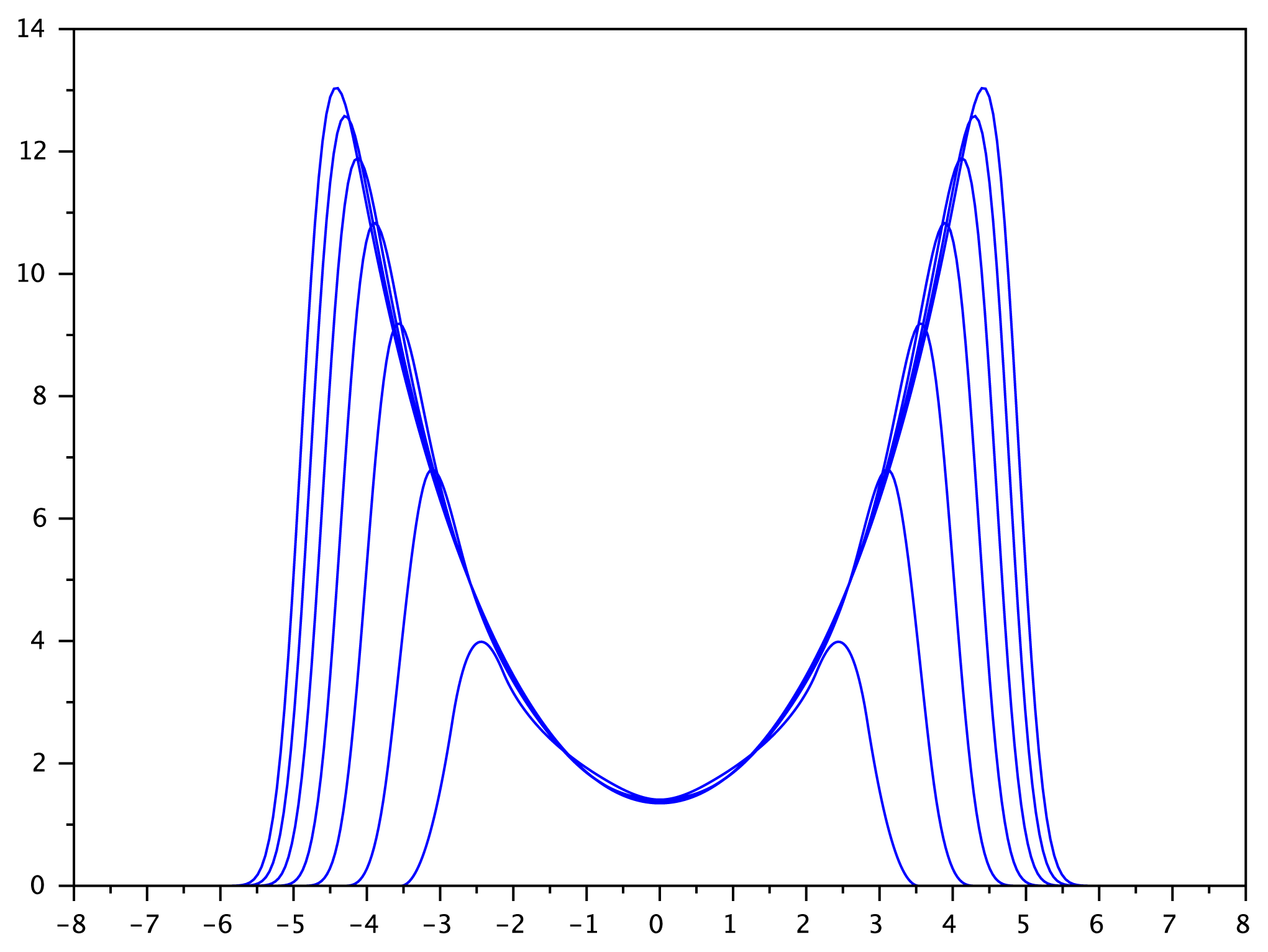
6.3. Convergence as d → +∞
Theorem 10
Proof
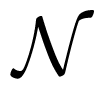 (0,N) (in fact, the B-spline pdf converges uniformly to the Gaussian pdf) [27]. Since Yd has the same distribution as M · Zd, it also converges in distribution to the Gaussian Y ~
(0,N) (in fact, the B-spline pdf converges uniformly to the Gaussian pdf) [27]. Since Yd has the same distribution as M · Zd, it also converges in distribution to the Gaussian Y ~ 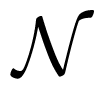 (0, P + N). Again by the central limit theorem,
(0, P + N). Again by the central limit theorem,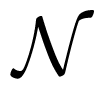 (0, P). Finally, we can write
(0, P). Finally, we can writeAcknowledgments
Author Contributions
Conflicts of Interest
- †This paper is an extended version of our paper published in Proceedings of the MaxEnt 2014 Conference on Bayesian Inference and Maximum Entropy Methods in Science and Engineering.
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27. [Google Scholar]
- Shannon, C.E. Communication in the presence of noise. Proc. Inst. Radio Eng 1949, 37, 10–21. [Google Scholar]
- Butzer, P.; Dodson, M.; Ferreira, P.; Higgins, J.; Lange, O.; Seidler, P.; Stens, R. Multiplex signal transmission and the development of sampling techniques: The work of Herbert Raabe in contrast to that of Claude Shannon. Appl. Anal 2011, 90, 643–688. [Google Scholar]
- Wikipedia. Shannon–Hartley theorem. Available online: http://en.wikipedia.org/wiki/Shannon-Hartley_theorem accessed on 28 August 2014.
- Hartley, R.V.L. Transmission of information. Bell Syst. Tech. J 1928, 7, 535–563. [Google Scholar]
- Ellersick, F.W. A conversation with Claude Shannon. IEEE Commun. Mag 1984, 22, 123–126. [Google Scholar]
- Wozencraft, J.M.; Jacobs, I.M. Principles of Communication Engineering; John Wiley & Sons: New York, NY, USA, 1965; pp. 2–5. [Google Scholar]
- Tuller, W.G. Theoretical limitations on the rate of transmission of information. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1948. [Google Scholar]
- Cherry, E.C. A history of information theory. Proc. Inst. Elect. Eng 1951, 98, 383–393. [Google Scholar]
- McEliece, R.J. The Theory of Information and Coding, 2nd ed; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Pierce, J.R. The early days of information theory. IEEE Trans. Inf. Theory 1973, 19, 3–8. [Google Scholar]
- Oliver, B.; Pierce, J.; Shannon, C.E. The Philosophy of PCM. Proc. Inst. Radio Eng 1948, 36, 1324–1331. [Google Scholar]
- Gallager, R.; Claude, E. Shannon: A retrospective on his life, work, and impact. IEEE Trans. Inf. Theory 2001, 47, 2681–2695. [Google Scholar]
- Verdú, S. Fifty years of Shannon theory. IEEE Trans. Inf. Theory 1998, 44, 2057–2078. [Google Scholar]
- Golay, M.J.E. Note on the theoretical efficiency of information reception with PPM. Proc. Inst. Radio Eng 1949, 37, 1031. [Google Scholar]
- Slepian, D. Information theory in the fifties. IEEE Trans. Inf. Theory 1973, 19, 145–148. [Google Scholar]
- Wiener, N. Time series, Information and Communication. In Cybernetics; John Wiley & Sons: New York, NY, USA, 1948; Volume Chapter III, pp. 10–11. [Google Scholar]
- Clavier, A.G. Evaluation of transmission efficiency according to Hartley’s expression of information content. Electron. Commun. ITT Tech. J 1948, 25, 414–420. [Google Scholar]
- Earp, C.W. Relationship between rate of transmission of information, frequency bandwidth, and signal-to-noise ratio. Electron. Commun. ITT Tech. J 1948, 25, 178–195. [Google Scholar]
- Goldman, S. Some fundamental considerations concerning noise reduction and range in radar and communication. Proc. Inst. Radio Eng 1948, 36, 584–594. [Google Scholar]
- Laplume, J. Sur le nombre de signaux discernables en présence du bruit erratique dans un système de transmission à bande passante limitée. Comptes rendus de l’Académie des Sciences de Paris 1948, 226, 1348–1349. (In French) [Google Scholar]
- Lundheim, L. On Shannon and “Shannon’s Formula”. Telektronikk 2002, 98, 20–29. [Google Scholar]
- Wiener, N. What is information theory? IRE Trans. Inf. Theory 1956, 2, 48. [Google Scholar]
- Hodges, A. Alan Turing: The Enigma; Simon and Schuster: New York, NY, USA, 1983; p. 552. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Rioul, O. Information theoretic proofs of entropy power inequalities. IEEE Trans. Inf. Theory 2011, 57, 33–55. [Google Scholar]
- Unser, M.; Aldroubi, A.; Eden, M. On the asymptotic convergence of B-spline wavelets to Gabor functions. IEEE Trans. Inf. Theory 1992, 38, 864–872. [Google Scholar]
- Barron, A.R. Entropy and the central limit theorem. Ann. Probab 1986, 14, 336–342. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rioul, O.; Magossi, J.C. On Shannon’s Formula and Hartley’s Rule: Beyond the Mathematical Coincidence. Entropy 2014, 16, 4892-4910. https://doi.org/10.3390/e16094892
Rioul O, Magossi JC. On Shannon’s Formula and Hartley’s Rule: Beyond the Mathematical Coincidence. Entropy. 2014; 16(9):4892-4910. https://doi.org/10.3390/e16094892
Chicago/Turabian StyleRioul, Olivier, and José Carlos Magossi. 2014. "On Shannon’s Formula and Hartley’s Rule: Beyond the Mathematical Coincidence" Entropy 16, no. 9: 4892-4910. https://doi.org/10.3390/e16094892




