Exclusion-Zone Dynamics Explored with Microfluidics and Optical Tweezers
Abstract
:1. Introduction
2. Results and Discussion
2.1. Formation of the Exclusion Zone
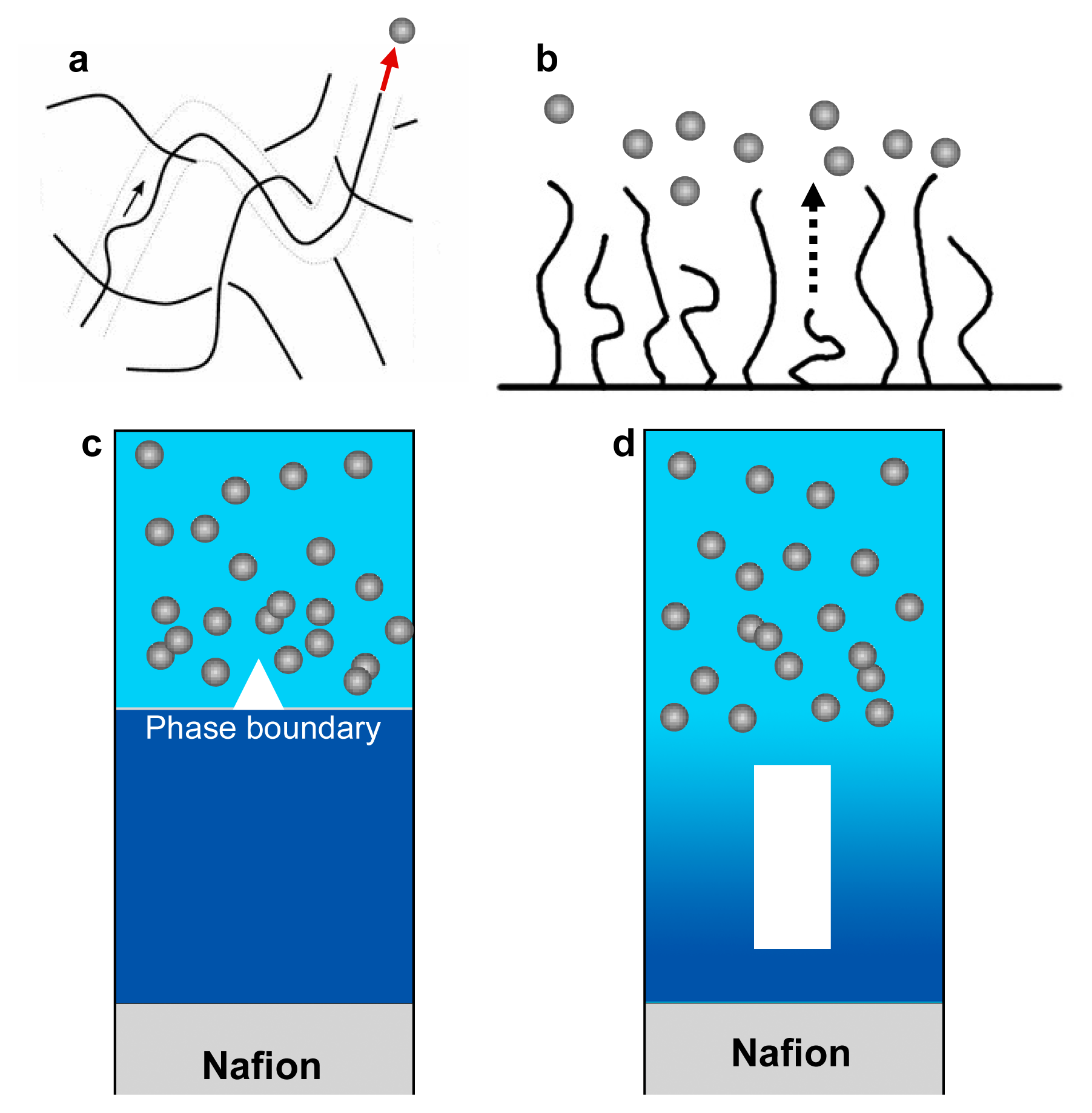
2.2. Possible Mechanisms of Exclusion Zone Formation
2.3. Kinetics of Exclusion Zone Formation
3. Experimental Section
3.1. General Information
3.2. Parafilm-Based Microfluidic Device
3.3. PDMS-Based Microfluidic Device
3.4. Microfluidic Experiment and Exclusion-Zone Observation
3.5. Optical Tweezers
3.6. Atomic Force Microscopy and Force Spectroscopy
3.7. Data Analysis
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zheng, J.M.; Pollack, G.H. Long-range forces extending from polymer-gel surfaces. Phys. Rev. E 2003, 68, 031408. [Google Scholar]
- Pollack, G. The Fourth Phase of Water; Ebner and Sons Publishers: Seattle, WA, USA, 2013. [Google Scholar]
- Schurr, J.M.; Fujimoto, B.S.; Huynh, L.; Chiu, D.T. A Theory of Macromolecular Chemotaxis. J. Phys. Chem. B 2013, 117, 7626–7652. [Google Scholar]
- Schurr, J.M. Phenomena associated with gel-water interfaces. Analyses and alternatives to the long-range ordered water hypothesis. J. Phys. Chem. B 2013, 117, 7653–7674. [Google Scholar]
- Pollack, G.H. Comment on “A theory of macromolecular chemotaxis” and “Phenomena associated with gel-water interfaces. Analyses and alternatives to the long-range ordered water hypothesis”. J. Phys. Chem. B 2013, 117, 7843–7846. [Google Scholar]
- Tanchak, O.M.; Yager, K.G.; Fritzsche, H.; Harroun, T.; Katsaras, J.; Barrett, C.J. Water distribution in multilayers of weak polyelectrolytes. Langmuir 2006, 22, 5137–5143. [Google Scholar]
- Zheng, J.M.; Chin, W.C.; Khijniak, E.; Khijniak, E.; Pollack, G.H. Surfaces and interfacial water: evidence that hydrophilic surfaces have long-range impact. Adv. Colloid Interface Sci 2006, 127, 19–27. [Google Scholar]
- Klimov, A.; Pollack, G.H. Visualization of charge-carrier propagation in water. Langmuir 2007, 23, 11890–11895. [Google Scholar]
- Zhao, Q.; Zheng, J.; Chai, B.; Pollack, G.H. Unexpected effect of light on colloidal crystal spacing. Langmuir 2008, 24, 1750–1755. [Google Scholar]
- Chai, B.H.; Zheng, J.M.; Zhao, Q.; Pollack, G.H. Spectroscopic studies of solutes in aqueous solution. J. Phys. Chem. A 2008, 112, 2242–2247. [Google Scholar]
- Zheng, J.M.; Wexler, A.; Pollack, G.H. Effect of buffers on aqueous solute-exclusion zones around ion-exchange resins. J. Colloid Interface Sci 2009, 332, 511–514. [Google Scholar]
- Chai, B.; Yoo, H.; Pollack, G.H. Effect of radiant energy on near-surface water. J. Phys. Chem. B 2009, 113, 13953–13958. [Google Scholar]
- Chai, B.; Pollack, G.H. Solute-free interfacial zones in polar liquids. J. Phys. Chem. B 2010, 114, 5371–5375. [Google Scholar]
- Yoo, H.; Paranji, R.; Pollack, G.H. Impact of Hydrophilic Surfaces on Interfacial Water Dynamics Probed with NMR Spectroscopy. J. Phys. Chem. Lett 2011, 2, 532–536. [Google Scholar]
- O’Rourke, C.; Klyuzhin, I.; Park, J.S.; Pollack, G.H. Unexpected water flow through Nafion-tube punctures. Phys. Rev. E 2011, 83, 056305. [Google Scholar]
- Figueroa, X.A.; Pollack, G.H. Exclusion-Zone Formation From Discontinuous Nafion Surfaces. Int. J. Des. Nat. Ecodyn 2011, 6, 286–296. [Google Scholar]
- Chai, B.; Mahtani, A.G.; Pollack, G.H. Unexpected Presence of Solute-Free Zones at Metal-Water Interfaces. Contemp. Mater 2012, 3, 1–12. [Google Scholar]
- Das, R.; Pollack, G.H. Charge-based forces at the Nafion-water interface. Langmuir 2013, 29, 2651–2658. [Google Scholar]
- Phillips, R.; Kondev, J.; Theriot, J. Physical Biology of the Cell; Garland Science: New York, NY, USA, 2009. [Google Scholar]
- Chen, C.S.; Chung, W.J.; Hsu, I.C.; Wu, C.M.; Chin, W.C. Force field measurements within the exclusion zone of water. J. Biol. Phys 2012, 38, 113–120. [Google Scholar]
- Bianco, P.; Nagy, A.; Kengyel, A.; Szatmári, D.; Mártonfalvi, Z.; Huber, T.; Kellermayer, M.S. Interaction forces between F-actin and titin PEVK domain measured with optical tweezers. Biophys. J 2007, 93, 2102–2109. [Google Scholar]
- Kellermayer, M.S.; Smith, S.B.; Granzier, H.L.; Bustamante, C. Folding-unfolding transitions in single titin molecules characterized with laser tweezers. Science 1997, 276, 1112–1116. [Google Scholar]
- Mártonfalvi, Z.; Bianco, P.; Linari, M.; Caremani, M.; Nagy, A.; Lombardi, V.; Kellermayer, M. Low-force transitions in single titin molecules reflect a memory of contractile history. J. Cell Sci 2014, 127, 858–870. [Google Scholar]
- Huszár, I.; Mártonfalvi, Z.; Kellermayer, M. Effect of Hofmeister-series salts on the dynamics of exclusion-zone formation. 2014. manuscript in preparation. [Google Scholar]
- Mortimer, R.G.; Eyring, H. Elementary transition state theory of the Soret and Dufour effects. Proc. Natl. Acad. Sci. USA 1980, 77, 1728–1731. [Google Scholar]
- Howard, J. Mechanics of Motor Proteins and the Cytoskeleton; Sinauer Associates, Inc: Sunderland, MA, USA, 2001. [Google Scholar]
- Duffy, D.C.; McDonald, J.C.; Schueller, O.J.; Whitesides, G.M. Rapid Prototyping of Microfluidic Systems in Poly (dimethylsiloxane). Anal. Chem 1998, 70, 4974–4984. [Google Scholar]
- McDonald, J.C.; Whitesides, G.M. Poly (dimethylsiloxane) as a material for fabricating microfluidic devices. Acc. Chem. Res 2002, 35, 491–499. [Google Scholar]
- Hutter, J.; Bechhoefer, J. Calibration of atomic-force microscope tips. Rev. Sci. Instrum 1993, 64, 1868–1873. [Google Scholar]







© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huszár, I.N.; Mártonfalvi, Z.; Laki, A.J.; Iván, K.; Kellermayer, M. Exclusion-Zone Dynamics Explored with Microfluidics and Optical Tweezers. Entropy 2014, 16, 4322-4337. https://doi.org/10.3390/e16084322
Huszár IN, Mártonfalvi Z, Laki AJ, Iván K, Kellermayer M. Exclusion-Zone Dynamics Explored with Microfluidics and Optical Tweezers. Entropy. 2014; 16(8):4322-4337. https://doi.org/10.3390/e16084322
Chicago/Turabian StyleHuszár, István N., Zsolt Mártonfalvi, András József Laki, Kristóf Iván, and Miklós Kellermayer. 2014. "Exclusion-Zone Dynamics Explored with Microfluidics and Optical Tweezers" Entropy 16, no. 8: 4322-4337. https://doi.org/10.3390/e16084322




