Human Brain Networks: Spiking Neuron Models, Multistability, Synchronization, Thermodynamics, Maximum Entropy Production, and Anesthetic Cascade Mechanisms

Abstract

Advances in neuroscience have been closely linked to mathematical modeling beginning with the integrate-and-fire model of Lapicque and proceeding through the modeling of the action potential by Hodgkin and Huxley to the current era. The fundamental building block of the central nervous system, the neuron, may be thought of as a dynamic element that is “excitable”, and can generate a pulse or spike whenever the electrochemical potential across the cell membrane of the neuron exceeds a threshold. A key application of nonlinear dynamical systems theory to the neurosciences is to study phenomena of the central nervous system that exhibit nearly discontinuous transitions between macroscopic states. A very challenging and clinically important problem exhibiting this phenomenon is the induction of general anesthesia. In any specific patient, the transition from consciousness to unconsciousness as the concentration of anesthetic drugs increases is very sharp, resembling a thermodynamic phase transition. This paper focuses on multistability theory for continuous and discontinuous dynamical systems having a set of multiple isolated equilibria and/or a continuum of equilibria. Multistability is the property whereby the solutions of a dynamical system can alternate between two or more mutually exclusive Lyapunov stable and convergent equilibrium states under asymptotically slowly changing inputs or system parameters. In this paper, we extend the theory of multistability to continuous, discontinuous, and stochastic nonlinear dynamical systems. In particular, Lyapunov-based tests for multistability and synchronization of dynamical systems with continuously differentiable and absolutely continuous flows are established. The results are then applied to excitatory and inhibitory biological neuronal networks to explain the underlying mechanism of action for anesthesia and consciousness from a multistable dynamical system perspective, thereby providing a theoretical foundation for general anesthesia using the network properties of the brain. Finally, we present some key emergent properties from the fields of thermodynamics and electromagnetic field theory to qualitatively explain the underlying neuronal mechanisms of action for anesthesia and consciousness.

1. Introduction

Advances in neuroscience have been closely linked to mathematical modeling beginning with the integrate-and-fire model of Lapicque [1] and proceeding through the modeling of the action potential by Hodgkin and Huxley [2] to the current era of mathematical neuroscience; see [3,4] and the numerous references therein. Neuroscience has always had models to interpret experimental results from a high-level complex systems perspective; however, expressing these models with dynamic equations rather than words fosters precision, completeness, and self-consistency. Nonlinear dynamical system theory, in particular, can provide a framework for a rigorous description of the behavior of large-scale networks of neurons. A particularly interesting application of nonlinear dynamical systems theory to the neurosciences is to study phenomena of the central nervous system that exhibit nearly discontinuous transitions between macroscopic states. One such example exhibiting this phenomenon is the induction of general anesthesia [5–9].

The rational, safe, and effective utilization of any drug in the practice of medicine is grounded in an understanding of the pharmacodynamics of the drug, loosely defined as what the drug does to the body [10]. A very important measure of the pharmacodynamics of any drug is the drug concentration parameter EC₅₀, which reflects the drug dose at which the therapeutic effect is achieved in 50% of the cases. This concept is certainly applicable for the administration of general inhalational anesthetics, where the potency of the drug is defined by the minimum alveolar concentration (MAC) of the drug needed to prevent a response to noxious stimuli in 50% of administrations [11].

The MAC concept is intrinsically embedded in a probabilistic framework [10]. It is the concentration at which the probability of a response to a noxious stimulus is 0.5. Typically the MAC of a particular anesthetic is determined by administering various doses of the agent to a population of patients and determining the dose at which there is a 0.5 chance of responding to a noxious stimulus. (Technically, we identify the concentration in the alveoli, the fundamental functional gas exchange units of the lung, at which the chance of response is 0.5.) It has been possible, however, to conduct studies of single subjects, varying the anesthetic concentration and determining responsiveness. When this has been done, it has been noted that the transition from responsiveness to non-responsiveness in the individual patient is very sharp, almost an all-or-none transition [12]. This simply confirms the observations of generations of clinicians. And this raises the question of how to account for such a transition in terms of the known molecular properties of the anesthetic agent.

The mechanism of general anesthesia is still under considerable investigation. Theories range from a nonspecific perturbation of the lipid bilayer membrane of neurons, the cells responsible for the “information” function of the central nervous system, to the interaction of the anesthetic agent with specific protein receptors [13]. It is certainly possible that if the mechanism of general anesthesia is the binding of the anesthetic agent to a specific receptor protein, then the nearly all-or-none transition or bifurcation from the awake state to the anesthetized state could be explained by a highly cooperative binding of the anesthetic to the receptor. In fact, it has been common to mathematically model the probability of responsiveness to drug concentration using the Hill equation, a simplified static equation originally derived in 1909 to describe the cooperative binding of oxygen to the hemoglobin molecule [14]. However, an alternative explanation could be sought in the dynamic network properties of the brain.

The human central nervous system involves a complex large-scale interconnected neural network involving feedforward and feedback (or recurrent) networks, with the brain serving as the central element of this network system. The brain is interconnected to receptors that transmit sensory information to the brain, and in turn the brain delivers action commands to effectors. The neural network of the brain consists of approximately 10¹¹ neurons (nerve cells) with each having 10⁴ to 10⁵ connections interconnected through subnetworks or nuclei. The nuclei in turn consist of clusters of neurons each of which performs a specific and defined function.

The most basic characteristic of the neurons that comprise the central nervous system is the electrochemical potential gradient across the cell membrane. All cells of the human body maintain an electrochemical potential gradient between the inside of the cell and the surrounding milieu. Neurons have the capacity of excitability. If stimulated beyond a threshold, then the neuron will “fire” and produce a large voltage spike (the action potential) before returning to the resting potential [3,4]. The neurons of the brain are connected in a complex network in which the firing of one neuron can be the stimulus for the firing of another neuron.

A major focus of theoretical neuroscience has been describing neuronal behavior in terms of this electrochemical potential, both at the single neuron level but more ambitiously, at the level of multi-neuron networks. In this type of analysis the specific properties of the single neuron that are most relevant are how the spike of a one neuron alters the electrochemical potential of another neuron, and how this change in the potential results in a neuronal spike. The physical connection between neurons occurs in the synapse, a small gap between the axon, the extension of the cell body of the transmitting neuron, and the dendrite, the extension of the receiving neuron. The signal is transmitted by the release of a neurotransmitter from the axon into the synapse. This neurotransmitter diffuses across the synapse, binds to a postsynaptic receptor membrane protein on the dendrite, and alters the electrochemical potential of the receiving neuron.

It is possible that the anesthetic bifurcation to unconsciousness or the nearly all-or-none characteristic induction of anesthesia is a type of phase transition of the neural network. This possibility was first considered by Steyn-Ross et al. (see [15] and the references therein). Their focus was on the mean voltage of the soma, or cell body, of neurons. Specifically, the authors in [15] show that the biological change of state to anesthetic unconsciousness is analogous to a thermodynamic phase change involving a liquid to solid phase transition. For certain ranges of anesthetic concentrations, their first-order model predicts the existence of multiple steady states for brain activity leading to a transition from normal levels of cerebral cortical activity to a quiescent, low-firing state.

In this paper, we develope an alternative approach to the possibility of neuronal network phase transition in terms of neuronal firing rates, using the concept of multistability for dynamical systems. Multistability is the property whereby the solutions of a dynamical system can alternate between two or more mutually exclusive Lyapunov stable and convergent states under asymptotically slowly changing inputs or system parameters. In particular, multistable systems give rise to the existence of multiple (isolated and/or a continuum of) Lyapunov stable equilibria involving a quasistatic-like behavior between these multiple semistable steady states [16–18]. Semistability is the property whereby the solutions of a dynamical system converge to Lyapunov stable equilibrium points determined by the system initial conditions [19,20].

Multistability is ubiquitous in biological systems ranging from biochemical networks to ecosystems to gene regulation and cell replication [21–23]. Since molecular studies suggest that one possible mechanism of action of anesthetics is the inhibition of synaptic transmission in cortical neurons [24,25], this suggests that general anesthesia is a phenomenon in which different equilibria can be attained with changing anesthetic agent concentrations. Hence, multistability theory can potentially provide a theoretical foundation for describing general anesthesia.

Although general anesthesia has been used in the clinical practice of medicine for over 150 years, the mechanism of action is still not fully understood [13] and is still under considerable investigation [5–9]. Early theories postulated that anesthesia is produced by disturbance of the physical properties of cell membranes. The work of Meyer and Overton [26,27] demonstrated that for some anesthetics there was a correlation between anesthetic potency and solubility in fat-like solvents. This led to a theory that anesthesia resulted from a nonspecific perturbation of the lipid bilayer membrane of neurons [9,28]. Subsequent research then found that membrane proteins performed functions of excitability and this led to a focus on anesthetic binding and perturbation of hydrophobic regions of membrane proteins [29]. Further research also revealed that some anesthetic gases follow the Meyer-Overton correlation but do not produce anesthesia and some Meyer-Overton gases are excitatory and can cause seizures [30,31]. These results led to the more common modern focus on the interaction of the anesthetic agent with specific protein receptors [13].

In particular, there has been extensive investigation of the influence of anesthetic agents on the binding of neurotransmitters to their postsynaptic receptors [7–9]. A plethora of receptors have been investigated, including receptors for glycine, serotonin type 2 and 3, N-methyl-d-aspartate (NMDA), α-2 adrenoreceptors, α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA), histamine, acetylcholine, and γ-aminobutyric acid (GABA). One attractive aspect of this focus on postsynaptic receptors is it facilitates mathematical analysis on the basis of the effect of receptor binding on the postsynaptic potential. This is in marked contrast to the Meyer-Overton hypothesis, which failed to explicitly detail how a nonspecific perturbation of the lipid membrane would result in the anesthetic state.

In parallel with the investigation of the molecular interactions of general anesthetic agents, there has also been active investigation of the anatomic pathways involved in the transition from consciousness to anesthesia [5]. There is compelling evidence that the immobility created by some anesthetics is mediated at the level of the spinal cord. In contrast, functional imaging and electroencephalograph analysis has suggested that the site of suppression of consciousness is the thalamus, and thalamocortical tracts may play a critical role in the suppression of consciousness [9].

Despite these advances in our understanding of the molecular interactions of anesthetic agents and of specific anatomic loci for the action of anesthetic agents, there has been less development of a mathematical framework to understand this fascinating and clinically important phenomenon. It is certainly possible that if the mechanism of general anesthesia is the binding of the anesthetic agent to a specific receptor protein, then the nearly all-or-none transition from the awake state to the anesthetized state could be explained by a highly cooperative binding of the anesthetic to the receptor. In fact, as noted above, it has been common to mathematically model the probability of responsiveness to drug concentration using the Hill equation [14]. However, to date, no single unifying receptor mediating general anesthesia has been identified.

Rather, the most likely explanation for the mechanisms of action of anesthetics lies in the network properties of the brain. It is well established that there are two general types of neurons in the central nervous system—excitatory and inhibitory—interconnected in a complex dynamic network. The action potential of a spiking neuron is propagated along the axon to synapses where chemical neurotransmitters are released that generate a postsynaptic potential on the dendrites of connected neurons. Excitatory neurons generate a depolarizing postsynaptic potential on the dendrite of the connected neuron and if the depolarization is of sufficient magnitude, then a spike will be induced in the connected neuron. In contrast, inhibitory neurons generate a hyperpolarizing postsynaptic potential; an effect that acts to maintain a quiescent state.

There is considerable evidence that general anesthetics alter postsynaptic potentials [24,25]. An interesting example of how changes in the postsynaptic potential may be applied to the analysis of the induction of anesthesia is the view of anesthesia as a phase transition proposed by Steyn-Ross et al. (see [15] and the references therein). While their analysis was highly informative, in this paper we use a dynamical system theory framework in terms of neuronal firing rates, using the concepts of network thermodynamics [32] and multistability, for explaining the mechanisms of action for general anesthesia. This facilitates a focus on the network properties of the central nervous system. The firing rate models used for network analysis must have sufficient generality and include parameters that can account for such relevant physiological changes at the single neuron level. The synaptic drive firing model, introduced by Ermentrout and his collaborators [4,32], and the system thermodynamic framework, introduced in [32], is the underlying framework for this paper.

In this paper, the fundamental building block of the central nervous system, the neuron, is represented as a dynamic element that is “excitable”, and can generate a pulse or spike whenever the electrochemical potential across the cell membrane of the neuron exceeds a threshold value. More specifically, a nonlinear discontinuous system framework is developed in Sections 2 and 3 for describing the relationship between the synaptic voltage and firing rates of excitatory and inhibitory neural networks. To establish convergence and semistability for discontinuous dynamical systems we introduce the notion of nontangency between a discontinuous vector field and a weakly invariant or weakly negatively invariant subset of level or sublevel sets of Lyapunov functions in Section 5. Specifically, to capture the notion of nontangency we introduce the direction cone of a discontinuous vector field. Then, using positive limit sets, restricted prolongations, and nontangency we develop Lyapunov analysis for convergence and semistability to establish multistability for discontinuous dynamical systems. Here, the restricted prolongation of a point is a subset of its positive prolongation as defined in [33]. In addition, using nontangency, we present Lyapunov results for convergence and semistability to develop sufficient conditions for multistability for discontinuous dynamical systems.

While previous treatments of nontangency-based Lyapunov tests for convergence and semistability for dynamical systems with continuous vector fields are given in [19], our results involve dynamical systems with discontinuous vector fields for capturing plasticity (i.e., dynamic network connections) in our neural network model generating absolutely continuous solutions necessitating stability analysis via nonsmooth Lyapunov stability theory involving Clarke generalized gradients and set-valued Lie derivatives. Using the aforementioned dynamical system framework, we apply the results of Sections 4 and 5 to excitatory-inhibitory firing neural models in an attempt to understand the mechanisms of action of anesthetics. While there is ongoing debate as to whether information is encoded by the firing rates (i.e., rate coding) of spiking neurons or by precise timing of single neuron spikes (i.e., temporal coding) [34], it is evident that firing rates do characterize central nervous system activity. Firing rates are nonnegative entities and the nonnegativity constraint for neural network activity can be easily incorporated within nonlinear dynamical system theory using solutions of differential equations and differential inclusions evolving in cones [35].

There is extensive experimental verification that collections of neurons may function as oscillators and the synchronization of oscillators may play a key role in the transmission of information within the central nervous system. This may be particularly relevant to understand the mechanism of action for general anesthesia. In Section 7, we provide sufficient conditions for global asymptotic and exponential synchronization for our excitatory and inhibitory cortical neuronal network.

To avoid the complexity of large-scale and high connectivity models of the neural network of the brain, the scale and connectivity of the network can be simplified using mean field theories. Early mean field theories assumed that the brain is organized into a limited number of pools of identical spiking neurons [36]. However, more commonly mean field theories assume that the strength of connection between neurons is normally distributed around some mean value. Mean field theories can impose self-consistency on field variables; for example, if postsynaptic potentials are assumed to be a function of some mean firing rate, then those postsynaptic potentials should lead to a consistent predicted mean firing rate. The idea of applying mean field theories, drawn from the study of condensed matter, originated with [37]. Subsequently, Sompolinsky et al. [38] developed a mean field theory for neural networks analogous to the equations developed for spin glasses with randomly symmetric bonds [39]. The authors in [40] investigated the stability of system states for a network of integrate-and-fire neurons, whereas the authors in [41] extended this theoretical model to the analysis of oscillations. Gerstner et al. [42,43] subsequently developed a mean field theory using a spike response model and demonstrated that the integrate-and-fire model was a special case of the spike response model.

In Section 8 of the paper, we extend our results further by demonstrating multistability in the mean when the coefficients of the neuronal connectivity matrix are random variables. Specifically, we use a stochastic multiplicative uncertainty model to include modeling of a priori uncertainty in the coefficients of the neuronal connectivity matrix by means of state-dependent noise. Our stochastic multiplicative uncertainty model uses state-dependent Gaussian white noise to represent parameter uncertainty by defining a measure of ignorance, in terms of an information-theoretic entropy, and then determining the probability distribution which maximizes this measure subjected to agreement with a given model. To account for time delay and memory effects in inhibitory and excitatory networks, in Sections 9 and 10 we extend the results of Section 8 to a large-scale excitatory and inhibitory synaptic drive firing rate model with time-varying delays and stochastic input uncertainty, and global mean-square synchronization of this model is investigated.

Finally, in Sections 11 and 12 we discuss key emergent properties from the fields of thermodynamics and electromagnetic field theory for developing plausible mechanisms of action for general anesthesia. Specifically, in Section 11, we highlight how the supreme law of nature—the second law of thermodynamics—can be used to arrive at mechanistic models for the anesthetic cascade using the principle of maximum entropy production and thermodynamics as applied to the human brain. In Section 12, we use the idea of anesthetics disrupting the inflow of free energy to the brain as electrical signals that generate electromagnetic fields causing a shielding effect leading to the emergence of unconsciousness.

2. Biological Neural Networks: A Dynamical Systems Approach

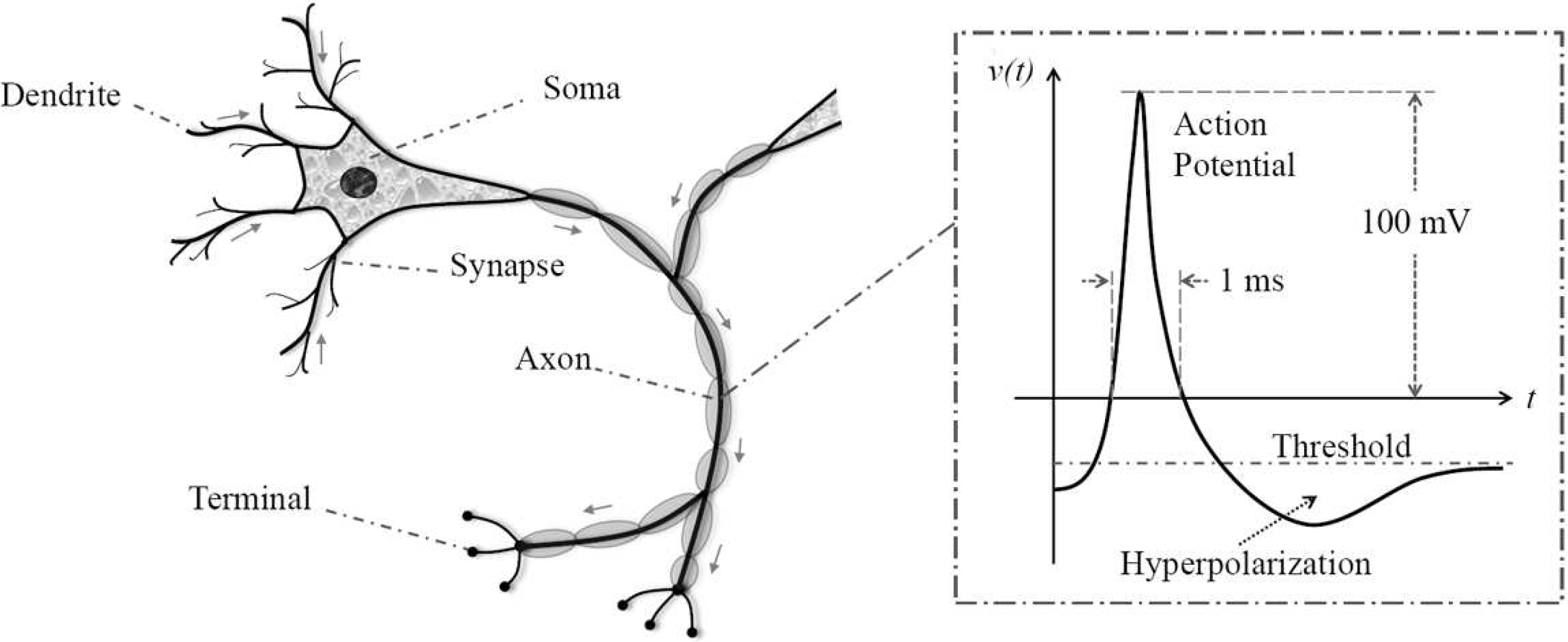
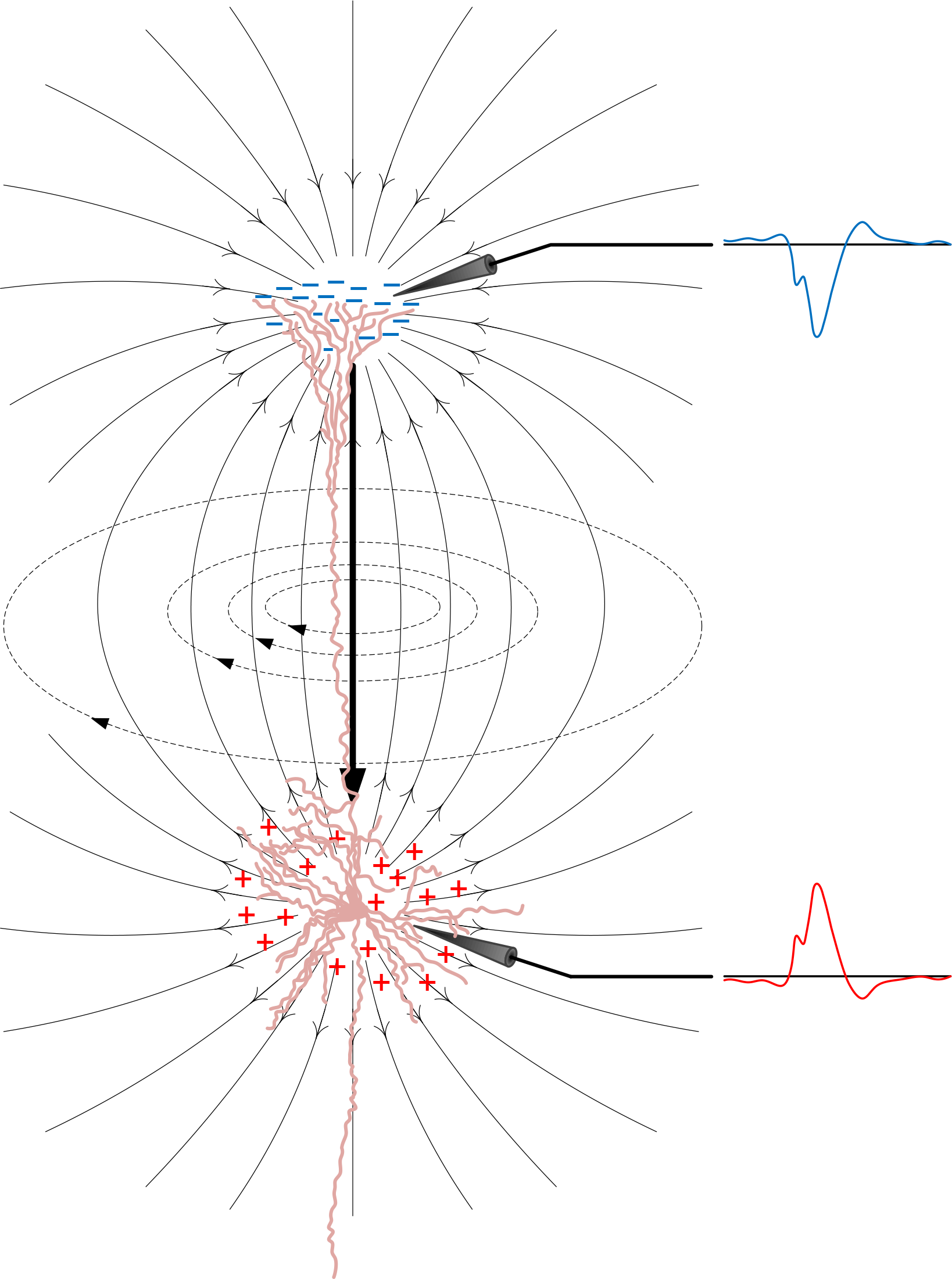
The fundamental building block of the central nervous system, the neuron, can be divided into three functionally distinct parts, namely, the dendrites, soma (or cell body), and axon (see Figure 1). The dendrites play the role of input devices that collect signals from other neurons and transmit them to the soma; whereas the soma generates a signal that is transmitted to other neurons by the axon. The axons of other neurons connect to the dendrites and soma surfaces by means of connectors called synapses. The behavior of the neuron is best described in terms of the electrochemical potential gradient across the cell membrane. If the voltage gradient across the membrane increases to a critical threshold value, then there is a subsequent abrupt step-like increase in the potential gradient, the action potential. This action potential is transmitted from the soma along the axon to a dendrite of a receiving neuron. The action potential elicits the release of neurotransmitter molecules that diffuse to the dendrite of a “receiving” neuron. This alters the voltage gradient across the receiving neuron.

The electrochemical potential for a neuron can be described by a nonlinear four-state system [32]. Coupling these system equations for each neuron in a large neural population is computationally prohibitive. To simplify the mathematical modeling, it has been common to use phenomenological firing rate models for studying neural coding, memory, and network dynamics [4]. Firing rate models involve the averaged behavior of the spiking rates of groups of neurons rather than tracking the spike rate of each individual neuron cell. In such population models, the activity of a neuron, that is, the rate at which the neuron generates an action potential (i.e., “fires”) is modeled as a function of the voltage (across the membrane). The “firing” of a neuron evokes voltage changes, postsynaptic potentials on receiving neurons; that is, neurons electrically connected to the firing neurons via axon-dendrite connections.

In general, neurons are either excitatory or inhibitory depending on whether the postsynaptic potential increases or decreases the potential of the receiving neuron. In particular, excitatory neurotransmitters depolarize postsynaptic membranes by increasing membrane potentials and can collectively generate an action potential. Inhibitory neurotransmitters hyperpolarize the postsynaptic membrane by decreasing membrane potentials, thereby nullifying the actions of excitatory neurotransmitters and in certain cases prevent the generation of action potentials.

Biological neural network models predict a voltage in the receiving or postsynaptic neuron given by

$$v_i^{\text{X}}(t)=\sum _{j=1}^{n_{\text{E}}}{A}_{ij}^{\text{XE}}\sum _k{\alpha }_j^{\text{E}}(t-t_k)+\sum _{j^{\prime }=1}^{n_{\text{I}}}{A}_{i{j}^{\prime }}^{\text{XI}}\sum _{k^{\prime }}{\alpha }_{j^{\prime }}^{\text{I}}(t-t_{k^{\prime }}),$$

(1)

where $v_i^{\text{X}}(\cdot )$, X ∈ {E, I}, i = 1, ..., n_E + n_I, is the excitatory (X = E) and inhibitory (X = I) voltage in the ith receiving neuron, $A_{ij}^{\text{XY}}$, X, Y ∈{E, I}, are constants representing the coupling strengths (in volts) of the jth neuron on the ith neuron, k, k′ = 1,..., enumerate the action potential or firings of the excitatory and inhibitory transmitting (presynaptic) neurons at firing times t_k and t_k′, respectively, and ${\alpha }_j^{\text{E}}(\cdot )$ and ${\alpha }_{j^{\prime }}^{\text{I}}(\cdot )$ are dimensionless functions describing the evolution of the excitatory and inhibitory postsynaptic potentials, respectively. Using a (possibly discontinuous) function f_i(·) to represent the firing rate (in Hz) of the ith neuron and assuming that the firing rate is a function of the voltage $v_i^{\text{E}}(\cdot )$ (resp., $v_i^{\text{I}}(\cdot )$) across the membrane of the ith neuron given by $f_i\left(v_i^{\text{E}}\right)$ (resp., $f_i\left(v_i^I\right)$), it follows that

$$\begin{array}{r}\hfill v_i^{\text{E}}(t)=\sum _{j=1,j\ne i}^{n_{\text{E}}}{A}_{ij}^{\text{EE}}{\int }_{-\infty }^t{\alpha }_j^{\text{E}}(t-\tau )f_j(v_j^{\text{E}}(\tau ))\text{d}\tau +\sum _{j^{\prime }=1}^{n_{\text{I}}}{A}_{i{j}^{\prime }}^{\text{EI}}{\int }_{-\infty }^t{\alpha }_{j^{\prime }}^{\text{I}}(t-\tau )f_{j^{\prime }}(v_{j^{\prime }}^{\text{I}}(\tau ))\text{d}\tau +v_{{\text{th}}_i}^{\text{E}}(t),\\ \hfill i=1,\dots ,n_{\text{E}},\end{array}$$

(2)

$$\begin{array}{r}\hfill v_i^{\text{I}}(t)=\sum _{j=1,j\ne i}^{n_{\text{E}}}{A}_{ij}^{\text{IE}}{\int }_{-\infty }^t{\alpha }_j^{\text{E}}(t-\tau )f_j(v_j^{\text{E}}(\tau ))\text{d}\tau +\sum _{j^{\prime }=1,j^{\prime }\ne i}^{n_{\text{I}}}{A}_{i{j}^{\prime }}^{\text{II}}{\int }_{-\infty }^t{\alpha }_{j^{\prime }}^{\text{I}}(t-\tau )f_{j^{\prime }}(v_{j^{\prime }}^{\text{I}}(\tau ))\text{d}\tau +v_{{\text{th}}_i}^{\text{I}}(t),\\ \hfill i=1,\dots ,n_{\text{I}},\end{array}$$

(3)

where the neuronal connectivity matrix A^XY, with units of volts, contains entries $A_{ij}^{\text{XY}}$, X, Y ∈{E, I}, representing the coupling strength of the jth neuron on the ith neuron such that $A_{ij}^{\text{XE}}>0$ and $A_{ij}^{\text{XI}}<0$, X ∈{E, I}, if the jth neuron is connected (i.e., contributes a postsynaptic potential) to the ith neuron, and $A_{ij}^{\text{XY}}=0$, otherwise. Furthermore, $v_{{\text{th}}_i}^{\text{E}}(\cdot )$ and $v_{{\text{th}}_i}^{\text{I}}(\cdot )$ are continuous input voltages characterizing nerve impulses from sensory (pain) receptors, sensorimotor (temperature sensing) receptors, or proprioceptive (motion sensing) receptors. Alternatively, $v_{{\text{th}}_i}^{\text{E}}(\cdot )$ and $v_{{\text{th}}_i}^{\text{I}}(\cdot )$ can be thought of as inputs from the reticular activating system within the brainstem responsible for regulating arousal and sleep-wake transitions. Note that $A_{ii}^{\text{EE}}\triangleq A_{ii}^{\text{II}}\triangleq 0$ by definition.

Next, defining the synaptic drive—a dimensionless quantity—of each (excitatory or inhibitory) neuron by

$$S_i^{(\text{E},\text{I})}(t)\triangleq {\int }_{-\infty }^t{\alpha }_i^{(\text{E},\text{I})}(t-\tau )f_i\left(v_i^{(\text{E},\text{I})}(\tau )\right)\text{d}\tau ,$$

(4)

and assuming an exponential decay of the synaptic voltages of the form ([4,44])

$${\alpha }_i^{(\text{E},\text{I})}(t)=B_i^{(\text{E},\text{I})}{e}^{-\frac{t}{{\lambda }_i^{(\text{E},\text{I})}}},$$

(5)

where the dimensionless gain $B_i^{(\text{E},\text{I})}$ is equal to $B_i^{\text{E}}$ if the ith neuron is excitatory and $B_i^{\text{I}}$ if the ith neuron is inhibitory, and similarly for $S_i^{(\text{E},\text{I})}$, $v_i^{(\text{E},\text{I})}$, ${\alpha }_i^{(\text{E},\text{I})}$, and ${\lambda }_i^{(\text{E},\text{I})}$, it follows from Equations (4) and (5) that

$$\frac{\text{d}{S}_i^{(\text{E},\text{I})}(t)}{\text{d}t}=-\frac{1}{{\lambda }_i^{(\text{E},\text{I})}}{S}_i^{(\text{E},\text{I})}(t)+B_i^{(\text{E},\text{I})}{f}_i\left(v_i^{(\text{E},\text{I})}(t)\right).$$

(6)

Now, using the expressions for the excitatory and inhibitory voltage given by Equations (2) and (3), respectively, it follows that

$$\frac{\text{d}{S}_i^{\text{E}}(t)}{\text{d}t}=-\frac{1}{{\lambda }_i^{\text{E}}}{S}_i^{\text{E}}(t)+B_i^{\text{E}}{f}_i\left(\sum _{j=1,j\ne i}^{n_{\text{E}}}{A}_{ij}^{\text{EE}}{S}_j^{\text{E}}(t)+\sum _{j^{\prime }=1}^{n_{\text{I}}}{A}_{i{j}^{\prime }}^{\text{EI}}{S}_{j^{\prime }}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{E}}(t)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n_{\text{E}},$$

(7)

$$\frac{\text{d}{S}_i^{\text{I}}(t)}{\text{d}t}=-\frac{1}{{\lambda }_i^{\text{I}}}{S}_i^{\text{I}}(t)+B_i^{\text{I}}{f}_i\left(\sum _{j=1}^{n_{\text{E}}}{A}_{ij}^{\text{IE}}{S}_j^{\text{E}}(t)+\sum _{j^{\prime }=1,j^{\prime }\ne i}^{n_{\text{I}}}{A}_{i{j}^{\prime }}^{\text{II}}{S}_{j^{\prime }}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{I}}(t)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n_{\text{I}}.$$

(8)

The above analysis reveals that a form for capturing the neuroelectic behavior of biological excitatory and inhibitory neuronal networks can be written as

$$\frac{\text{d}{S}_i(t)}{\text{d}t}=-\frac{1}{{\tau }_i}{S}_i(t)+B_i{f}_i\left(\sum _{j=1}^n{A}_{ij}{S}_j(t)+v_{{\text{th}}_i}(t)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_i(0)=S_{i0},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n,$$

(9)

where S_i(t) ∈ $𝒟$ ⊆ ℝ, t ≥ 0, is the ith synaptic drive, v_thi(t) ∈ ℝ, t ≥ 0, denotes the input voltage to the ith neuron, A_ij is a constant representing the coupling strength of the jth neuron on the ith neuron, τ_i is a time constant, B_i is a constant gain for the firing rate of the ith neuron, and f_i(·) is a nonlinear activation function describing the relationship between the synaptic drive and the firing rate of the ith neuron.

In this paper, we will explore different activation functions including discontinuous hard-limiter activation functions, and continuous half-wave rectification, saturation, and sigmoidal functions. Specifically, for a typical neuron ([3])

$$f_i(x)={[x]}_{+},$$

(10)

where i ∈ {1,..., n} and [x]₊ = x if x ≥ 0, and [x]₊ = 0, otherwise. Alternatively, we can approximate f_i(x) by the smooth (i.e., infinitely differentiable) half-wave rectification function

$$f_i(x)=\frac{x{e}^{\gamma x}}{1+e^{\gamma x}},$$

(11)

where i ∈ {1,..., n} and γ ≫ 0. Note that f′_i(x) ≈ 1 for x > 0 and f″_i(x) ≈ 0, x ≠ 0. In addition, note that Equations (10) and (11) reflect the fact that as the voltage increases across the membrane of the ith neuron, the firing rate increases as well. Often, the membrane potential-firing rate curve exhibits a linear characteristic for a given range of voltages. At higher voltages, however, a saturation phenomenon appears, indicating that the full effect of the firing rate has been reached. To capture this effect, f_i(·) can be modeled as

$$f_i(x)=\frac{f_{\text{max}}(e^{\gamma x}-1)}{1+e^{\gamma x}},$$

(12)

where i ∈ {1,..., n}, γ ≫ 0, and f_max = lim_γ→∞ f_i(x) denotes the maximum firing rate.

3. Connections to Mean Field Excitatory and Inhibitory Synaptic Drive Models

The excitatory and inhibitory neural network model given by Equations (7) and (8) can possess multiple equilibria. For certain values of the model parameters it can be shown that as the inhibitory time constants ${\lambda }_i^{\text{I}}$, i = 1, ..., n_I, get larger, multiple stable and unstable state equilibria can appear [45]. Since molecular studies suggest that one possible mechanism of action of anesthetics is the prolongation of the time constants of inhibitory neurons [24,25], this suggests that general anesthesia is a phenomenon in which different equilibria can be attained with changing anesthetic agent concentrations. To explore this multistability phenomenon, in [45,46] we developed a simplified scale and connectivity neural network model using a mean field theory. As noted in the Introduction, mean field theories assume that the brain is organized into limited number of pools of identical spiking neurons [36]. However, more commonly, mean field theories assume that the strength of the connection between neurons is normally distributed around some mean value.

To see how our general excitatory and inhibitory synaptic drive model given by Equations (7) and (8) can be reduced to a mean excitatory and mean inhibitory model, consider Equations (7) and (8) with continuously differentiable f_i(·) = f(·), $B_i^{\text{E}}=B_i^{\text{I}}=1$, ${\lambda }_i^{\text{E}}={\lambda }^{\text{E}}$, and ${\lambda }_i^{\text{I}}={\lambda }^{\text{I}}$. In this case, Equations (7) and (8) become

$$\frac{\text{d}{S}_i^{\text{E}}(t)}{\text{d}t}=f\left(\sum _{j=1}^{n_{\text{E}}}{A}_{ij}^{\text{EE}}{S}_j^{\text{E}}(t)+\sum _{k=1}^{n_{\text{I}}}{A}_{ik}^{\text{EI}}{S}_k^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{E}}(t)\right)-\frac{1}{{\lambda }^{\text{E}}}{S}_i^{\text{E}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n_{\text{E}},$$

(13)

$$\frac{\text{d}{S}_i^{\text{I}}(t)}{\text{d}t}=f\left(\sum _{j=1}^{n_{\text{E}}}{A}_{ij}^{\text{IE}}{S}_j^{\text{E}}(t)+\sum _{k=1}^{n_{\text{I}}}{A}_{ik}^{\text{II}}{S}_k^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{I}}(t)\right)-\frac{1}{{\lambda }^{\text{I}}}{S}_i^{\text{I}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n_{\text{I}},$$

(14)

where f(·) is given by either Equation (11) or Equation (12) and $A_{ii}^{\text{EE}}=A_{ii}^{\text{II}}=0$. Next, let $A_{jj}^{\text{EE}}={\overline{A}}^{\text{EE}}+{\Delta }_{ij}^{\text{EE}}$, $A_{ij}^{\text{EI}}={\overline{A}}^{\text{EI}}+{\Delta }_{ij}^{\text{EI}}$, $A_{ij}^{\text{IE}}={\overline{A}}^{\text{IE}}+{\Delta }_{ij}^{\text{IE}}$, and $A_{ij}^{\text{II}}={\overline{A}}^{\text{II}}+{\Delta }_{ij}^{\text{II}}$, where ${\overline{A}}^{\text{XY}}\triangleq \frac{1}{n_{\text{X}}{n}_{\text{Y}}}{\sum }_{i=1}^{n_{\text{X}}}{\sum }_{j=1}^{n_{\text{Y}}}{A}_{ij}^{\text{XY}}$, X, Y ∈{E, I}, denote mean and ${\Delta }_{ij}^{\text{XY}}$, X, Y ∈ {E, I}, are deviations from the mean. In this case, it follows that

$$\sum _{i=1}^{n_{\text{E}}}\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{EE}}=\sum _{i=1}^{n_{\text{E}}}\sum _{j=1}^{n_{\text{I}}}{\Delta }_{ij}^{\text{EI}}=\sum _{i=1}^{n_{\text{I}}}\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{IE}}=\sum _{i=1}^{n_{\text{I}}}\sum _{j=1}^{n_{\text{I}}}{\Delta }_{ij}^{\text{II}}=0.$$

(15)

Using the average and perturbed expression for $A_{ij}^{\text{XY}}$, X, Y ∈{E, I}, Equations (13) and (14) can be rewritten as

$$\begin{array}{r}\hfill \frac{\text{d}{S}_i^{\text{E}}(t)}{\text{d}t}=f\left(n_{\text{E}}{\overline{A}}^{\text{EE}}{\overline{S}}^{\text{E}}(t)+\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{EE}}{S}_j^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{EI}}{\overline{S}}^{\text{I}}(t)+\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{EI}}{S}_k^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{E}}(t)\right)-\frac{1}{{\lambda }^{\text{E}}}{S}_i^{\text{E}}(t),\\ \hfill i=1,\dots ,n_{\text{E}},\end{array}$$

(16)

$$\begin{array}{r}\hfill \frac{\text{d}{S}_i^{\text{I}}(t)}{\text{d}t}=f\left(n_{\text{E}}{\overline{A}}^{\text{IE}}{\overline{S}}^{\text{E}}(t)+\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{IE}}{S}_j^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{II}}{\overline{S}}^{\text{I}}(t)+\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{II}}{S}_k^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{I}}(t)\right)-\frac{1}{{\lambda }^{\text{I}}}{S}_i^{\text{I}}(t),\\ \hfill i=1,\dots ,n_{\text{I}},\end{array}$$

(17)

where ${\overline{S}}^{\text{E}}(t)\triangleq \frac{1}{n_{\text{E}}}{\sum }_{j=1}^{n_{\text{E}}}{S}_j^{\text{E}}(t)$ and ${\overline{S}}^{\text{I}}(t)\triangleq \frac{1}{n_{\text{I}}}{\sum }_{j=1}^{n_{\text{I}}}{S}_j^{\text{I}}(t)$ denote the mean excitatory synaptic drive and mean inhibitory synaptic drive in dimensionless units, respectively. Now, defining ${\delta }_i^{\text{E}}(t)\triangleq S_i^{\text{E}}(t)-{\overline{S}}^{\text{E}}(t)$ and ${\delta }_i^{\text{I}}(t)\triangleq S_i^{\text{I}}(t)-{\overline{S}}^{\text{I}}(t)$, where ${\delta }_i^{\text{E}}(t)$ and ${\delta }_i^{\text{I}}(t)$ are deviations from the mean, Equations (16) and (17) become

$$\begin{array}{lll}\frac{\text{d}{S}_i^{\text{E}}(t)}{\text{d}t}\hfill & =\hfill & f(n_{\text{E}}{\overline{A}}^{\text{EE}}{\overline{S}}^{\text{E}}(t)+{\overline{S}}^{\text{E}}(t)\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{EE}}+n_{\text{I}}{\overline{A}}^{\text{EI}}{\overline{S}}^{\text{I}}(t)+{\overline{S}}^{\text{I}}(t)\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{EI}}+\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{EE}}{\delta }_j^{\text{E}}(t)\hfill \\ \hfill & \hfill & +\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{EI}}{\delta }_k^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{E}}(t))-\frac{1}{{\lambda }^{\text{E}}}{S}_i^{\text{E}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n_{\text{E}},\hfill \end{array}$$

(18)

$$\begin{array}{lll}\frac{\text{d}{S}_i^{\text{I}}(t)}{\text{d}t}\hfill & =\hfill & f(n_{\text{E}}{\overline{A}}^{\text{IE}}{\overline{S}}^{\text{E}}(t)+{\overline{S}}^{\text{E}}(t)\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{IE}}+n_{\text{I}}{\overline{A}}^{\text{II}}{\overline{S}}^{\text{I}}(t)+{\overline{S}}^{\text{I}}(t)\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{II}}+\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{IE}}{\delta }_j^{\text{E}}(t)\hfill \\ \hfill & \hfill & +\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{II}}{\delta }_k^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{I}}(t))-\frac{1}{{\lambda }^{\text{I}}}{S}_i^{\text{I}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n_{\text{I}}.\hfill \end{array}$$

(19)

Next, assume that all terms with a factor ${\Delta }_{ij}^{\text{XY}}$, X, Y ∈ {E, I}, i = 1,..., n_X and j = 1,..., n_Y, in Equations (18) and (19) are small relative to the remaining terms in f(·). Then, a first-order expansion of Equations (18) and (19) gives

$$\begin{array}{rr}\hfill \frac{\text{d}{S}_i^{\text{E}}(t)}{\text{d}t}& \hfill =f\left(n_{\text{E}}{\overline{A}}^{\text{EE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{EI}}{\overline{S}}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{E}}(t)\right)+f^{\prime }\left(n_{\text{E}}{\overline{A}}^{\text{EE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{EI}}{\overline{S}}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{E}}(t)\right)\\ \hfill & \hfill \times \left[{\overline{S}}^{\text{E}}(t)\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{EE}}+{\overline{S}}^{\text{I}}(t)\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{EI}}+\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{EE}}{\delta }_j^{\text{E}}(t)+\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{EI}}{\delta }_k^{\text{I}}(t)\right]-\frac{1}{{\lambda }^{\text{E}}}{S}_i^{\text{E}}(t),\\ \hfill & \hfill i=1,\dots ,n_{\text{E}},\end{array}$$

(20)

$$\begin{array}{rr}\hfill \frac{\text{d}{S}_i^{\text{I}}(t)}{\text{d}t}& \hfill =f\left(n_{\text{E}}{\overline{A}}^{\text{IE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{II}}{\overline{S}}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{I}}(t)\right)+f^{\prime }\left(n_{\text{E}}{\overline{A}}^{\text{IE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{II}}{\overline{S}}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{I}}(t)\right)\\ \hfill & \hfill \times \left[{\overline{S}}^{\text{E}}(t)\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{IE}}+{\overline{S}}^{\text{I}}(t)\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{II}}+\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{IE}}{\delta }_j^{\text{E}}(t)+\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{II}}{\delta }_k^{\text{I}}(t)\right]-\frac{1}{{\lambda }^{\text{I}}}{S}_i^{\text{I}}(t),\\ \hfill & \hfill i=1,\dots ,n_{\text{I}}.\end{array}$$

(21)

Now, assuming that the higher-order terms can be ignored, Equations (20) and (21) become

$$\begin{array}{ll}\frac{\text{d}{S}_i^{\text{E}}(t)}{\text{d}t}\hfill & =f\left(n_{\text{E}}{\overline{A}}^{\text{EE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{EI}}{\overline{S}}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{E}}(t)\right)+f^{\prime }\left(n_{\text{E}}{\overline{A}}^{\text{EE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{EI}}{\overline{S}}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{E}}(t)\right)\hfill \\ \hfill & \times \left[{\overline{S}}^{\text{E}}(t)\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{EE}}+{\overline{S}}^{\text{I}}(t)\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{EI}}\right]-\frac{1}{{\lambda }^{\text{E}}}{S}_i^{\text{E}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n_{\text{E}},\hfill \end{array}$$

(22)

$$\begin{array}{ll}\frac{\text{d}{S}_i^{\text{I}}(t)}{\text{d}t}\hfill & =f\left(n_{\text{E}}{\overline{A}}^{\text{IE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{II}}{\overline{S}}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{I}}(t)\right)+f^{\prime }\left(n_{\text{E}}{\overline{A}}^{\text{IE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{II}}{\overline{S}}^{\text{I}}(t)+v_{{\text{th}}_i}^{\text{I}}(t)\right)\hfill \\ \hfill & \times \left[{\overline{S}}^{\text{E}}(t)\sum _{j=1}^{n_{\text{E}}}{\Delta }_{ij}^{\text{IE}}+{\overline{S}}^{\text{I}}(t)\sum _{k=1}^{n_{\text{I}}}{\Delta }_{ik}^{\text{II}}\right]-\frac{1}{{\lambda }^{\text{I}}}{S}_i^{\text{I}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n_{\text{I}}.\hfill \end{array}$$

(23)

Finally, summing Equations (22) and (23) over i = 1, ..., n_E and i = 1, ..., n_I, dividing by n_E and n_I, respectively, using Equation (15), and assuming $v_{{\text{th}}_1}^{\text{E}}(t)=v_{{\text{th}}_2}^{\text{E}}(t)=\cdots v_{{\text{th}}_{n_{\text{E}}}}^{\text{E}}(t)=v_{\text{th}}^{\text{E}}$ and $v_{{\text{th}}_1}^{\text{I}}(t)=v_{{\text{th}}_2}^{\text{I}}(t)=\cdots v_{{\text{th}}_{n_{\text{I}}}}^{\text{I}}(t)=v_{\text{th}}^{\text{I}}$, t ≥ 0, it follows that the average excitatory synaptic drive and the average inhibitory synaptic drive are given by

$$\frac{\text{d}{\overline{S}}^{\text{E}}(t)}{\text{d}t}=f\left(n_{\text{E}}{\overline{A}}^{\text{EE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{EI}}{\overline{S}}^{\text{I}}(t)+v_{\text{th}}^{\text{E}}\right)-\frac{1}{{\lambda }^{\text{E}}}{\overline{S}}^{\text{E}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{S}}^{\text{E}}(0)={\overline{S}}_0^{\text{E}},\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(24)

$$\frac{\text{d}{\overline{S}}^{\text{I}}(t)}{\text{d}t}=f\left(n_{\text{E}}{\overline{A}}^{\text{IE}}{\overline{S}}^{\text{E}}(t)+n_{\text{I}}{\overline{A}}^{\text{II}}{\overline{S}}^{\text{I}}(t)+v_{\text{th}}^{\text{I}}\right)-\frac{1}{{\lambda }^{\text{I}}}{\overline{S}}^{\text{I}}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{S}}^{\text{I}}(0)={\overline{S}}_0^{\text{I}}.$$

(25)

Equations (24) and (25) represent the spatial average (mean) dynamics of the system given by Equations (13) and (14), and are predicated on a mean field assumption that reduces the complex (approximately 10¹¹ × 10¹¹) neuronal connectivity matrix to a 2×2 excitatory–inhibitory system. This is a drastic assumption, but one which has been commonly used in theoretical neuroscience going back to the pioneering work of Wilson and Cowan [36]. Preliminary results using the simplified two-state mean excitatory and inhibitory synaptic drive model given by Equations (24) and (25) for connecting notions of general anesthesia to multistability and bifurcations are given in [45,46].

4. Multistability Theory and Discontinuous Spiking Neuron Models

Multistability is the property whereby the solutions of a dynamical system can alternate between two or more mutually exclusive semistable states under asymptotically slowly changing inputs or system parameters. In particular, the state of a multistable system converges to Lyapunov stable equilibria that belong to an equilibrium set that has a multivalued hybrid topological structure consisting of isolated points and closed sets homeomorphic to intervals on the real line. To develop the notion of multistability, consider the autonomous differential equation given by

$$\dot{x}(t)=f(x(t)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x(0)=x_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{a}.\text{e}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(26)

where, for every t ≥ 0, x(t) ∈ $𝒟$ ⊆ ℝⁿ, f : ℝⁿ → ℝⁿ is Lebesgue measurable and locally essentially bounded [47], that is, f is bounded on a bounded neighborhood of every point x, excluding sets of measure zero. Furthermore, let $ℰ$_e ≜ {x ∈ ℝⁿ : f(x) = 0} denote the set of equilibria for Equation (26).

Definition 1 ([47,48]) An absolutely continuous function x : [0, τ] → ℝⁿ is said to be a Filippov solution of Equation (26) on the interval [0, τ] with initial condition x(0) = x₀, if x(t) satisfies

$$\frac{\text{d}}{\text{d}t}x(t)\in 𝒦[f](x(t)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{a}.\text{e}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\in [0,\tau ],$$

(27)

where the Filippov set-valued map $𝒦$[f]: ℝⁿ → 2^ℝn is defined by

$$𝒦[f](x)\triangleq \underset{\delta >0}{\cap }\underset{\mu (𝒮)=0}{\cap }\overline{\text{co}}\left\{f\left({ℬ}_{\delta }(x)\backslash 𝒮\right)\right\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\in {ℝ}^n,$$

and where $ℬ$_δ(x) denotes the open ball centered at x with radius δ, 2^ℝn denotes the collection of all subsets of ℝⁿ, μ(·) denotes the Lebesgue measure in ℝⁿ, “$\overline{\text{co}}$” denotes the convex closure, and ∩_{μ($𝒮$) = 0} denotes the intersection over all sets $𝒮$ of Lebesgue measure zero [49].

Note that since f is locally essentially bounded, $𝒦$[f](·) is upper semicontinuous and has nonempty, compact, and convex values. Thus, Filippov solutions are limits of solutions to Equation (26) with f averaged over progressively smaller neighborhoods around the solution point, and hence, allow solutions to be defined at points where f itself is not defined. Hence, the tangent vector to a Filippov solution, when it exists, lies in the convex closure of the limiting values of the system vector field f(·) in progressively smaller neighborhoods around the solution point. Note that $𝒦$[f]: ℝⁿ → 2^ℝn is a map that assigns sets to points.

Dynamical systems of the form given by Equation (27) are called differential inclusions [50] and for each state x ∈ ℝⁿ, they specify a set of possible evolutions rather than a single one. It follows from 1) of Theorem 1 of [51] that there exists a set $𝒩$_f ⊂ ℝⁿ of measure zero such that, for every set $𝒲$ ⊂ ℝⁿ of measure zero,

$$𝒦[f](x)=\overline{\text{co}}\left\{\underset{i\to \infty }{\text{lim}}f(x_i):x_i\to x,\hspace{0.17em}\hspace{0.17em}{x}_i\notin {𝒩}_f\cup 𝒲\right\},$$

(28)

where {x_i}_i∈ℤ̄+ ⊂ ℝⁿ converges to x ∈ ℝⁿ.

Differential inclusions include piecewise continuous dynamical systems as well as switched dynamical systems as special cases. For example, if f(·) is piecewise continuous, then Equation (26) can be represented as a differential inclusion involving the Filippov set-valued map of piecewise continuous vector fields given by $𝒦[f](x)=\overline{\text{co}}\left\{{\text{lim}}_{i\to \infty }f(x_i):x_i\to x,\hspace{0.17em}{x}_i\notin {𝒮}_f\right\}$, where $𝒮$_f has measure zero and denotes the set of points where f is discontinuous [52]. Similarly, differential inclusions can include, as a special case, switched dynamical systems of the form

$$\dot{x}(t)=f_p(x(t)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x(0)=x_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(29)

where x(t) ∈ $𝒟$ ⊆ ℝⁿ, f_p : ℝⁿ → ℝⁿ is locally Lipschitz continuous, and p ∈ $𝒫$ = {1,..., d} is a finite index set.

To see how the state-dependent switched dynamical system given by Equation (29) can be represented as a differential inclusion involving Filippov set-valued maps, define the switched system (29) with a piecewise linear partitioned state space as the triple ($𝒟$, $𝒬$, $𝒱$), where $𝒟$ = ℝⁿ or $𝒟$ is a polytope in ℝⁿ of dimension dim($𝒟$) = n, $𝒬$ = {$𝒟$_p}_p∈$𝒫$ is a piecewise linear partition of $𝒟$ with index set $𝒫$, and $𝒱$ = {f_p}_{p∈$𝒫$ⁿ}, and where f_p : $𝒰$_p → ℝⁿ, $𝒰$_p is an open neighborhood of $𝒟$_p, and $𝒫$ⁿ = {p ∈ $𝒫$ : dim($𝒟$_p) = n}. Specifically, ${\cup }_{p=1}^d{𝒟}_p=𝒟\subseteq {ℝ}^n$, where $𝒟$ is a polytope (i.e., the convex hull of finitely many points, and hence, compact) and $𝒟$_p, p = 1,..., d, is a family of polyhedral sets in ℝⁿ with nonempty interiors. Furthermore, for every i, j ∈ {1,..., d}, i ≠ j, let $𝒟$̄_i ∩ $𝒟$̄_j = ∅ or $𝒟$̄ⁱ ∩ $𝒟$̄_j is a (n − 1)-dimensional manifold included in the boundaries ∂$𝒟$_i and ∂$𝒟$_j. Finally, since each vector field f_i is Lipschitz continuous in the state x, it defines a continuously differentiable flow ψ_i(t, x) within every open set $𝒰$_i ⊃ $𝒟$_i. In particular, each flow ψ_i(t, x) is well defined on both sides of the boundary ∂$𝒟$_j. Thus, in the interior of each operating region $𝒟$_p, the global dynamics of Equation (29) is completely described by the local dynamics characterized by a particular vector field f_p, and hence, there exists a unique classical (i.e., continuously differentiable) solution to Equation (29). However, for a point x ∈ $\mathscr{H}$_p ∩ $𝒟$_p, where $\mathscr{H}$_p is some supporting hyperplane of $𝒟$_p, nonuniqueness and nonexistence of solutions to Equation (29) can occur.

To address the problem of existence and extendability of solutions for Equation (29), let the global dynamics of Equation (29) be characterized by one of the following differential inclusions

$$\dot{x}(t)\in ℱ(x(t))\triangleq \{\begin{array}{lll}\begin{array}{cc}{f}_1(x(t)),& x(t)\in {𝒟}_1,\\ f_2(x(t)),& x(t)\in {𝒟}_2,\\ ⋮& ⋮\\ f_d(x(t)),& x(t)\in {𝒟}_d,\end{array}\hfill & x(0)=x_0,\hfill & \text{a}.\text{e}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,\hfill \end{array}$$

(30)

$$\dot{x}(t)\in \overline{\text{co}}ℱ(x(t)).$$

(31)

Note that $ℱ$ : ℝⁿ → 2^ℝn is nonempty and finite, and hence, compact. Moreover, since each f_p : $𝒰$_p → ℝⁿ is continuous, the set-valued map $ℱ$(·) is upper semicontinuous, that is, for every x ∈ ℝⁿ and neighborhood $𝒩$ of $ℱ$(x), there exists a neighborhood $ℳ$ of x such that $ℱ$($ℳ$) ⊂ $𝒩$. However, it is important to note that $ℱ$(x) is not convex. Alternatively, ${ℱ}^{\text{c}}(x)\triangleq \overline{\text{co}}ℱ(x)$ is convex, and hence, $ℱ$^c : ℝⁿ → 2^ℝn is an upper semicontinuous set-valued map with nonempty, convex, and compact values. That is, for every x ∈ $𝒟$ and every ε > 0, there exists δ > 0 such that, for all z ∈ ℝⁿ satisfing ‖z − x‖ ≤ δ, $ℱ$^c(z) ⊆ $ℱ$^c(x)+ ε$ℬ$̄₁(0). In this case, it can be shown that there exists a Filippov solution to the differential inclusion given by Equation (30) at all interior points x ∈ $𝒟$ ⊆ ℝⁿ [47,53]. In addition, if for each unbounded cell $𝒟$_p, p ∈ $𝒫$ⁿ, f_p($𝒟$_p) is bounded and $ℱ$^c(x) ∩ T_x$𝒟$ ≠ ∅, x ∈ $𝒟$, where T_x$𝒟$ denotes the tangent cone to $𝒟$ at x (see Definition 5) [54], then there exists a Filippov solution x :[0, ∞) → ℝⁿ to Equation (30) for every x₀ ∈ $𝒟$ ⊆ ℝⁿ ([50], p. 180).

Switched dynamical systems are essential in modeling the plasticity of the central nervous system. In particular, recent neuroimaging findings have shown that the loss of top-down (feedback) processing in association with anesthetic-induced unconsciousness observed in electroencephalographic (EEG) and functional magnetic resonance imaging (fMRI) is associated with functional disconnections between anterior and posterior brain structures [55–57]. These studies show that topological rather than network connection strength of functional networks correlate with states of consciousness. Hence, changes in network topology are essential in capturing the mechanism of action for consciousness rather than network connectivity strength during general anesthesia. Dynamic neural network topologies capturing link separation or creation, which can be modeled by switched systems and differential inclusions, can provide a mechanism for the objective selective inhibition of feedback connectivity in association with anesthetic-induced unconsciousness.

Since the Filippov set-valued map $𝒦$[f](x) is upper semicontinuous with nonempty, convex, and compact values, and $𝒦$[f](x) is also locally bounded ([47](p. 85)), it follows that Filippov solutions to Equation (26) exist ([47] (Theorem 1, p. 77)). Recall that the Filippov solution t ↦ x(t) to Equation (26) is a right maximal solution if it cannot be extended (either uniquely or nonuniquely) forward in time. We assume that all right maximal Filippov solutions to Equation (26) exist on [0, ∞), and hence, we assume that Equation (26) is forward complete. Recall that Equation (26) is forward complete if and only if the Filippov solutions to Equation (26) are uniformly globally sliding time stable ([58](Lemma 1, p. 182)).

We say that a set $ℳ$ is weakly positively invariant (resp., strongly positively invariant) with respect to Equation (26) if, for every x₀ ∈ $ℳ$, $ℳ$ contains a right maximal solution (resp., all right maximal solutions) of Equation (26)[48,59]. The set $ℳ$ ⊆ ℝⁿ is weakly negatively invariant if, for every x ∈ $ℳ$ and t ≥ 0, there exist z ∈ $ℳ$ and a Filippov solution ψ(·) to Equation (26) with ψ(0) = z such that ψ(t) = x and ψ(τ) ∈ $ℳ$ for all τ ∈ [0, t]. The set $ℳ$⊆ ℝⁿ is weakly invariant if $ℳ$ is weakly positively invariant as well as weakly negatively invariant. Finally, an equilibrium point of Equation (26) is a point x_e ∈ ℝⁿ such that 0 ∈ $𝒦$[f](x_e). It is easy to see that x_e is an equilibrium point of Equation (26) if and only if the constant function x(·) = x_e is a Filippov solution of Equation (26). We denote the set of equilibrium points of Equation (26) by $ℰ$. Since the set-valued map $𝒦$[f] is upper semicontinuous, it follows that $ℰ$ is closed.

To develop Lyapunov theory for nonsmooth dynamical systems of the form given by Equation (26), we need the notion of generalized derivatives and gradients. In this paper, we focus on Clarke generalized derivatives and gradients [52,60].

Definition 2 ([48,60]) Let V : ℝⁿ → ℝ be a locally Lipschitz continuous function. The Clarke upper generalized derivative of V (·) at x in the direction of v ∈ ℝⁿ is defined by

$$V^o(x,v)\triangleq \underset{y\to x,h\to 0^{+}}{\text{limsup}}\frac{V(y+hv)-V(y)}{h}.$$

(32)

The Clarke generalized gradient ∂V : ℝⁿ → 2^ℝ1×n of V (·) at x is the set

$$\partial V(x)\triangleq \text{co}\left\{\underset{i\to \infty }{\text{lim}}\nabla V(x_i):x_i\to x,\hspace{0.17em}\hspace{0.17em}{x}_i\notin 𝒩\cup 𝒮\right\},$$

(33)

where co denotes the convex hull, ∇ denotes the nabla operator, $𝒩$ is the set of measure zero of points where ∇V does not exist, $𝒮$ is any subset of ℝⁿ of measure zero, and the increasing unbounded sequence {x_i}_i∈ℤ̄+ ⊂ ℝⁿ converges to x ∈ ℝⁿ.

Note that Equation (32) always exists. Furthermore, note that it follows from Definition 2 that the generalized gradient of V at x consists of all convex combinations of all the possible limits of the gradient at neighboring points where V is differentiable. In addition, note that since V (·) is Lipschitz continuous, it follows from Rademacher’s theorem ([61](Theorem 6, p. 281)) that the gradient ∇V (·) of V (·) exists almost everywhere, and hence, ∇V (·) is bounded. Specifically, for every x ∈ ℝⁿ, every ε > 0, and every Lipschitz constant L for V on $ℬ$̄_ε(x), ∂V (x) ⊆ $ℬ$̄_L(0). Thus, since for every x ∈ ℝⁿ, ∂V (x) is convex, closed, and bounded, it follows that ∂V (x) is compact.

In order to state the results of this paper, we need some additional notation and definitions. Given a locally Lipschitz continuous function V : ℝⁿ → ℝ, the set-valued Lie derivative $ℒ$_f V : ℝⁿ → 2^ℝ of V with respect to f at x [48,62] is defined as

$$\begin{array}{lll}{ℒ}_{f}V(x)\hfill & \triangleq \hfill & \left\{a\in ℝ:\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}v\in 𝒦[f](x)\hspace{0.17em}\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{p}^{\text{T}}v=a\hspace{0.17em}\text{for}\hspace{0.17em}\text{all}\hspace{0.17em}{p}^T\in \partial V(x)\right\}\hfill \\ \hfill & \subseteq \hfill & \underset{p^{\text{T}}\in \partial V(x)}{\cap }{p}^{\text{T}}𝒦[f](x).\hfill \end{array}$$

(34)

If $𝒦$[f](x) is convex with compact values, then $ℒ$_f V (x), x ∈ ℝⁿ, is a closed and bounded, possibly empty, interval in ℝ. If V (·) is continuously differentiable at x, then $ℒ$_f V (x) = {∇V (x) · v : v ∈ $𝒦$[f](x)}. In the case where $ℒ$_f V (x) is nonempty, we use the notation max $ℒ$_f V (x) (resp., min $ℒ$_f V (x)) to denote the largest (resp., smallest) element of $ℒ$_f V (x). Furthermore, we adopt the convention max ∅ = −∞. Finally, recall that a function V : ℝⁿ → ℝ is regular at x ∈ ℝⁿ ([60](Definition 2.3.4)) if, for all v ∈ ℝⁿ, the right directional derivative $V_{+}^{\prime }(x,v)\triangleq {\text{lim}}_{h\to 0^{+}}\frac{1}{h}[V(x+hv)-V(x)]$ exists and V′₊(x, v) = V^o(x, v). V is called regular on ℝⁿ if it is regular at every x ∈ ℝⁿ.

The next definition introduces the notion of semistability for discontinuous dynamical systems. This stability notion is necessary for systems having a continuum of equilibria. Specifically, since every neighborhood of a nonisolated equilibrium contains another equilibrium, a nonisolated equilibrium cannot be asymptotically stable. Hence, asymptotic stability is not the appropriate notion of stability for systems having a continuum of equilibria. Two notions that are of particular relevant to such systems are convergence and semistability. Convergence is the property whereby every system solution converges to a limit point that may depend on the system initial condition (i.e., initial anesthetic concentrations). Semistability is the additional requirement that all solutions converge to limit points that are Lyapunov stable. Semistability for an equilibrium thus implies Lyapunov stability, and is implied by asymptotic stability. Thus, semistability guarantees that small perturbations from the limiting state of unconsciousness will lead to only small transient excursions from that state of unconsciousness. It is important to note that semistability is not merely equivalent to asymptotic stability of the set of equilibria. Indeed, it is possible for a trajectory to converge to the set of equilibria without converging to any one equilibrium point as examples in [19] show. For further details, see [20].

Definition 3 Let $𝒟$ ⊆ ℝⁿ be an open strongly positively invariant set with respect to Equation (26). An equilibrium point z ∈ $𝒟$ of Equation (26) is Lyapunov stable if, for every ε > 0, there exists δ = δ(ε) > 0 such that, for every initial condition x₀ ∈ $ℬ$_δ(z) and every Filippov solution x(t) with the initial condition x(0) = x₀, x(t) ∈ $ℬ$_ε(z) for all t ≥ 0. An equilibrium point z ∈ $𝒟$ of Equation (26) is semistable if z is Lyapunov stable and there exists an open subset $𝒟$₀ of $𝒟$ containing z such that, for all initial conditions in $𝒟$₀, the Filippov solutions of Equation (26) converge to a Lyapunov stable equilibrium point. The system given by Equation (26) is semistable with respect to $𝒟$ if every Filippov solution with initial condition in $𝒟$ converges to a Lyapunov stable equilibrium. Finally, the system given by Equation (26) is said to be globally semistable if the system given by Equation (26) is semistable with respect to ℝⁿ.

Finally, we introduce the definition of multistability of the dynamical system given by Equation (26).

Definition 4 Consider the nonlinear dynamical system given by Equation (26). We say that the dynamical system given by Equation (26) is multistable if (i) there exists more than one equilibrium point of Equation (26) in ℝⁿ; (ii) all Filippov solutions to Equation (26) converge to one of these equilibrium points; and (iii) almost all Filippov solutions to Equations (26) converge to Lyapunov stable equilibria; that is, the set of initial conditions driving the Filippov solutions of Equation (26) to unstable equilibria has Lebesgue measure zero.

It is important to note that our definition of multistability is different from the definition given in [18]. Specifically, pertaining to condition (iii), the definition of multistability given in [18] requires that almost all Filippov solutions to Equation (26) converge to asymptotically stable equilibria. This key difference between the two definitions allows for the dynamical system given by Equation (26) to possess a continuum of equilibria, rather than merely isolated equilibria. As we see later, if f_i is of the form given by Equation (10), then Equation (9) has a continuum of equilibria under certain conditions, and hence, Equation (26) is semistable in the sense of (iii) [63]. Hence, in this case, it is appropriate to use Definition 4 to characterize multistability.

Almost all of the existing results on multistability theory rely on linearization techniques based on the Hartman-Grobman theorem [64,65] involving the fact that the linearized system has the same topological property as the original system around a hyperbolic fixed point. When the system fixed point is not hyperbolic, however, these techniques fail to predict multistability. In this case, checking multistability becomes a daunting task. Rather than checking the transversality condition for hyperbolicity, we propose a new approach for guaranteeing multistability using equilibria-independent, semidefinite Lyapunov function methods. In particular, using the geometric structure of the vector field f for a given dynamical system, we develop nontangency-based Lyapunov tests for verifying conditions (ii) and (iii) in Definition 4 involving convergence and Lyapunov stability almost everywhere.

5. Direction Cones, Nontangency, Restricted Prolongations, and Nonsmooth Multistability Theory

To develop multistability theory for discontinuous dynamical systems of the form given by Equation (26) we use the notions of direction cones, nontangency, and restricted prolongations. In particular, to show condition (ii) in Definition 4 holds for dynamical systems of the form given by Equation (26), we adopt the notion of nontangency [19,63] to develop nontangency-based Lyapunov tests for convergence. Specifically, the authors in [19] develop a general framework for nontangency-based Lyapunov tests for the convergence of dynamical systems described by ordinary differential equations with continuous vector fields. In [63], the authors extend some of the results of [19] to nonsmooth dynamical systems, that is, systems described by ordinary differential equations with the discontinuous right-hand sides. Since the vector field f characterizing biological neural networks can involve either continuous (e.g., half-wave rectification functions) or discontinuous (e.g., hard-limiter activation functions) vector fields, and, more importantly, the fact that anesthetics reconfigure the topological structure of functional brain networks [55–57] by suppressing midbrain/pontine areas involved with regulatory arousal leading to a dynamic network topology, we use the more general definition for nontangency presented in [63].

Intuitively, a vector field is nontangent to a set at a point if the vector field at the point is not contained in the tangent space to the set at that point. We use this intuitive idea for the case where the vector field describing the system dynamics is discontinuous and the set is the set of equilibria of the system. However, this notion presents two key difficulties when the set under consideration is the set of singular points of the vector field, that is, the set of equilibria of the system. In particular, the vector field at an equilibrium point is zero, and hence, it is always contained in the tangent space to the set of equilibria. In this case, in order to capture the notion of nontangency, we introduce the direction cone of a vector field.

Alternatively, the set of equilibria may not be sufficiently regular to possess a tangent space at the equilibrium point under consideration and may have corners or self-intersections. For example, in firing rate population models appearing in neuroscience, the firing rate is a nonnegative quantity representing the probability of the firing action potential by the neuron and can be interpreted as a measure of the neuron’s activity. Since the firing rate of the excitatory-inhibitory network is nonnegative, all solutions of physical interest always take values in the nonnegative orthant ${\overline{ℝ}}_{+}^n$ of the state space for nonnegative initial conditions. For such systems, which evolve on possibly closed positively invariant subsets of ℝⁿ, it is natural to consider the nonnegative orthant as their state space. Hence, the dynamical system evolves on the nonnegative orthant and can have the boundary of the orthant as its set of equilibria. In this case, the set of equilibria has a corner at the origin. We overcome this difficulty by considering the tangent cone [66,67], which extends the notion of a tangent space to a nonsmooth setting.

To introduce the notions of direction cone and tangent cone, some notation and definitions are required. A set $ℰ$ ⊆ ℝⁿ is connected if and only if every pair of open sets $𝒰$_i ⊆ ℝⁿ, i = 1, 2, satisfying $ℰ$ ⊆ $𝒰$₁ ∪ $𝒰$₂ and $𝒰$_i ∩ $ℰ$ ≠ ∅, i = 1, 2, has a nonempty intersection. A connected component of the set $ℰ$ ⊆ ℝⁿ is a connected subset of $ℰ$ that is not properly contained in any connected subset of $ℰ$. Given a set $ℰ$ ⊆ ℝⁿ, let coco $ℰ$ denote the convex cone generated by $ℰ$.

Definition 5 Given x ∈ ℝⁿ, the direction cone $ℱ$_x of the vector field f at x is the intersection of closed convex cones of the form$\overline{{\cap }_{\mu (𝒮)=0}\text{coco}\{f(𝒰\backslash 𝒮)\}}$, where $𝒰$ ⊆ ℝⁿ is an open neighborhood of x and $𝒬$̄ denotes the closure of the set $𝒬$. Let $ℰ$ ⊆ ℝⁿ. A vector v ∈ ℝⁿ is tangent to $ℰ$ at z ∈ $ℰ$ if there exist a sequence${\left\{z_i\right\}}_{i=1}^{\infty }$ in $ℰ$ converging to z and a sequence${\left\{h_i\right\}}_{i=1}^{\infty }$ of positive real numbers converging to zero such that${\text{lim}}_{i\to \infty }\frac{1}{h_i}(z_i-z)=v$. The tangent cone to $ℰ$ at z is the closed cone T_z$ℰ$ of all vectors tangent to $ℰ$ at z. Finally, the vector field f is nontangent to the set $ℰ$ at the point z ∈ $ℰ$ if T_z$ℰ$ ∩ $ℱ$_z ⊆{0}.

The notion of nontangency introduced in Definition 5 is different from the well-known notion of transversality [68]. Transversality between a vector field and a set is possible only at a point in the set where the vector field is not zero and the set is locally a differentiable submanifold of codimension one. Alternatively, nontangency is possible even if the vector field is zero and the set is not a differentiable submanifold of codimension one.

Definition 5 formalizes the notion of nontangency by defining nontangency of a discontinuous vector field to a set at a point to be the condition that the tangent cone to the set at the point and the direction cone of the vector field at that point have no nonzero vector in common. Using the notion of nontangency, in [63] we developed necessary and sufficient conditions for convergence of discontinuous dynamical systems. Specifically, convergence of system trajectories are guaranteed if and only if the vector field is nontangent to the positive limit set of the point at some positive limit point. However, this result cannot be applied directly in practice since it is not generally possible to find the positive limit set of system solution trajectories. Since nontangency to any outer estimate of the positive limit set implies nontangency to the positive limit set itself, we use nontangency-based Lyapunov tests for convergence. In particular, if the vector field f is nontangent to the largest invariant subset of the zero-level set of the derivative of a Lyapunov function that is nonincreasing along the solutions of Equation (26), then every bounded solution converges to a limit.

Since the application of the convergence results discussed above depends on verifying the boundedness of trajectories, the well-known results for boundedness involving proper (that is, radially unbounded in the case where the state space is ℝⁿ) Lyapunov functions [69,70] by introducing the notion of a weakly proper function need to be extended. Specifically, in [63] we consider Lyapunov functions whose connected components of their sublevel sets are compact. In this case, the existence of a weakly proper Lyapunov function that is nonincreasing along the system trajectories implies that the trajectories are bounded.

Using the notion of nontangency we then developed Lyapunov measures for almost everywhere semistability to arrive at multistability theory for discontinuous dynamical systems [63]. Here, prolongations [33,71] play a role analogous to that played by positive limit sets in the aforementioned discussion. In particular, the notion of a restricted prolongation of a point is used to show that an equilibrium point of Equation (26) is Lyapunov stable if and only if the discontinuous vector field is nontangent at the equilibrium to its restricted prolongation. The restricted prolongation of a point is a subset of its positive prolongation [33,71] and is defined as follows.

Definition 6 Given a point x ∈ ℝⁿ and a bounded open neighborhood $𝒰$ ⊂ ℝⁿ of x, the restricted prolongation of x with respect to $𝒰$ is the set${ℛ}_x^{𝒰}\subseteq \overline{𝒰}$ of all subsequential limits of sequences of the form${\{{\psi }_i(t_i)\}}_{i=1}^{\infty }$, where${\left\{t_i\right\}}_{i=1}^{\infty }$ is a sequence in [0, ∞), ψ_i(·) is a solution to Equation (26) with ψ_i(0) = x_i, i = 1, 2,..., and${\left\{x_i\right\}}_{i=1}^{\infty }$ is a sequence in $𝒰$ converging to x such that the set {z ∈ ℝⁿ : z = ψ_i(t), t ∈ [0, t_i]} is contained in $𝒰$̄ for every i = 1, 2,....

The utility of prolongations in stability analysis follows from the fact that an equilibrium point is Lyapunov stable if and only if the positive prolongation of the equilibrium consists only of the equilibrium point. See, ([71], Proposition 7.3) and ([33](Theorem V.1.12)). For systems with continuous vector fields this was first shown in [19]. Since the restricted prolongation of a point is a subset of the positive prolongation of the point, such a result provides a sharper version of the results ([71] (Proposition 7.3)) and ([33](Theorem V.1.12)).

As in the case for positive limit sets discussed above, since it is not generally possible to find the restricted prolongation of an equilibrium point in practice and since nontangency to any outer estimate of the restricted prolongation implies nontangency to the restricted prolongation itself, we use outer estimates of restricted prolongations in terms of connected components of invariant and negatively invariant subsets of level and sublevel sets of Lyapunov functions and their derivatives. By assuming nontangency of the vector field to invariant or negatively invariant subsets of the level set of the Lyapunov function containing the equilibrium we can trap the restricted prolongation and the positive limit set, respectively, in the level sets of the Lyapunov function and its derivative.

The following theorem establishes sufficient conditions for convergence and Lyapunov stability almost everywhere for the system given by Equation (26). This result follows from the fact that ${ℛ}_x^{𝒰}$ is connected and the fact that if $𝒩$ is composed of isolated equilibria of Equation (26) or f is nontangent to $𝒩$ at every point in $𝒩$, then the solution to Equation (26) is convergent. For details of these facts; see [45]. For the statement of the next result, V̇ denotes the set-valued Lie derivative for the Filippov solutions to Equation (26) and V⁻¹(0) ≜ {x ∈ ℝⁿ : V (x) = 0}.

Theorem 1 ([45]) Assume there exists a locally Lipschitz continuous and regular function V : ℝⁿ → ℝ such that V̇ is defined almost everywhere on ℝⁿ and satisfies V̇ (x) ≤ 0 for almost all x ∈ ℝⁿ. Let x ∈ ℝⁿ be such that the solution of Equation (26) is bounded and let $𝒩$ denote the largest weakly invariant set contained in V̇⁻¹(0). If either every point in $𝒩$ is Lyapunov stable or f is nontangent to $𝒩$ at every point in $𝒩$, then almost all solutions of Equation (26) converge to Lyapunov stable equilibria.

Example 1 Consider the two-class mean excitatory and mean inhibitory synaptic drive network characterized by a discontinuous vector field for modeling plasticity in the network given by

$${\dot{S}}^{\text{E}}(t)=-0.5S^{\text{E}}(t)+f_1\left(S^{\text{E}}(t),S^{\text{I}}(t)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}^{\text{E}}(0)=S_0^{\text{E}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(35)

$${\dot{S}}^{\text{I}}(t)=-S^{\text{I}}(t)+f_2\left(S^{\text{E}}(t),S^{\text{I}}(t)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}^{\text{I}}(0)=S_0^{\text{I}},$$

(36)

where$S_0^{\text{E}}\ge 0$, $S_0^{\text{I}}\ge 0$, and f_i(·), i = 1, 2, are given by

$$f_1(S^{\text{E}},S^{\text{I}})={\left[\text{step}(S^{\text{I}}-S^{\text{E}})(S^{\text{E}}-0.5S^{\text{I}})\right]}_{+},$$

(37)

$$f_2(S^{\text{E}},S^{\text{I}})={\left[\text{step}(S^{\text{I}}-S^{\text{E}})(2S^{\text{E}}-S^{\text{I}})\right]}_{+},$$

(38)

where step(y) = 1 for y ≥ 0 and step(y) = 0, otherwise. For this system, the set of equilibria in${\overline{ℝ}}_{+}^2$ are given by$ℰ\triangleq \left\{(S^{\text{E}},S^{\text{I}})\in {\overline{ℝ}}_{+}^2:S^{\text{E}}=S^{\text{I}}\right\}$.

Next, we show that for almost all the initial conditions$\left(S_0^{\text{E}},S_0^{\text{I}}\right)\in {\overline{ℝ}}_{+}^2$, the equilibrium set $ℰ$ is attractive. To see this, consider the function V : ℝ² → ℝ given by$V\left(S^{\text{E}},S^{\text{I}}\right)=\frac{1}{2}\left[{(S^{\text{E}})}^2+{(S^{\text{I}})}^2\right]$. Now, it follows that the set-valued Lie derivative V̇ (S^E, S^I) satisfies

$$\dot{V}(S^{\text{E}},S^{\text{I}})=\{\begin{array}{ll}\left\{-\frac{1}{2}{\left(S^{\text{E}}\right)}^2-{\left(S^{\text{I}}\right)}^2\right\},\hfill & S^{\text{E}}>S^{\text{I}}\ge 0\hspace{0.17em}\hspace{0.17em}\text{or}\hspace{0.17em}\hspace{0.17em}{S}^I>2S^{\text{E}}\ge 0,\hfill \\ \left\{\frac{1}{2}\left(S^{\text{E}}-S^{\text{I}}\right)\left(S^{\text{E}}+4S^{\text{I}}\right)\right\},\hfill & 0\le S^{\text{E}}<S^{\text{I}}<2S^{\text{E}},\hfill \\ \overline{\text{co}}\left\{-\frac{1}{2}{\left(S^{\text{E}}\right)}^2-{\left(S^{\text{I}}\right)}^2,\frac{1}{2}\left(S^{\text{E}}-S^{\text{I}}\right)\left(S^{\text{E}}+4S^{\text{I}}\right)\right\},\hfill & \text{otherwise},\hspace{0.17em}\hspace{0.17em}\left(S^{\text{E}},S^{\text{I}}\right)\in {\overline{ℝ}}_{+}^2.\hfill \end{array}$$

It can be verified that V̇ (S^E, S^I) ≤ 0 for almost all$(S^{\text{E}},S^{\text{I}})\in {\overline{ℝ}}_{+}^2$ and V̇⁻¹(0) = $ℰ$.

Next, we show that the vector field f of the system given by Equations (35) and (36) is nontangent to $ℰ$. Let (S^E, S^I) ∈ $ℰ$ and note that it follows from the expression of f that the direction cone $ℱ$_{(S^E, S^I)} of the vector field f at (S^E, S^I) ∈ $ℰ$ is given by

$${ℱ}_{\left(S^{\text{E}},S^{\text{I}}\right)}=\left\{k{[1,2]}^{\text{T}}:k\in ℝ\right\}.$$

(39)

In addition, the tangent cone to $ℰ$ at (S^E, S^I) ∈ $ℰ$ is given by

$$T_{\left(S^{\text{E}},S^{\text{I}}\right)}ℰ=\left\{k{[1,1]}^{\text{T}}:k\in ℝ\right\}.$$

(40)

Now, it follows from Equations (39) and (40) that T_{(S^E, S^I)}$ℰ$ ∩ $ℱ$_{(S^E, S^I)} = {0}, and hence, for every (S^E, S^I) ∈ $ℰ$, f is nontangent to $ℰ$ at (S^E, S^I).

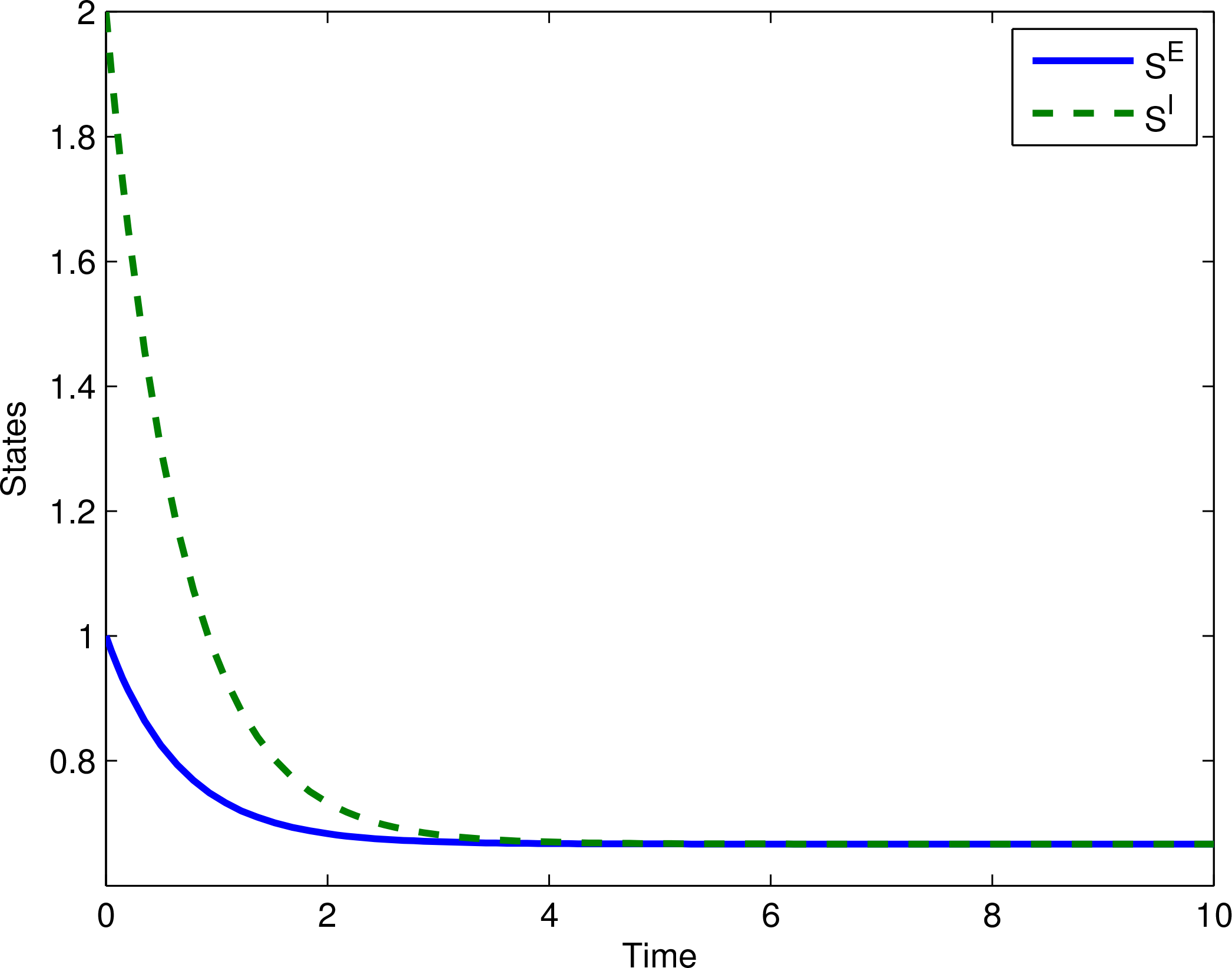
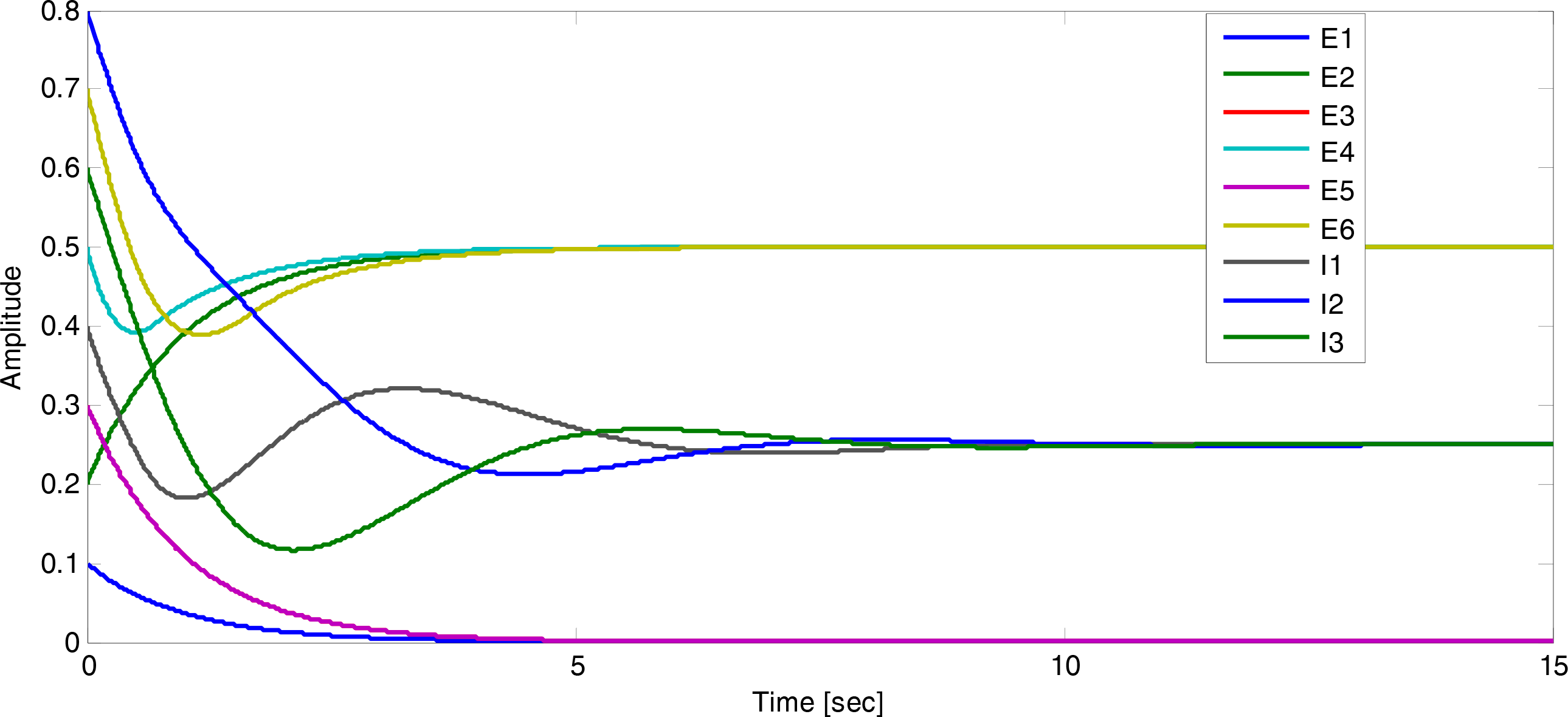
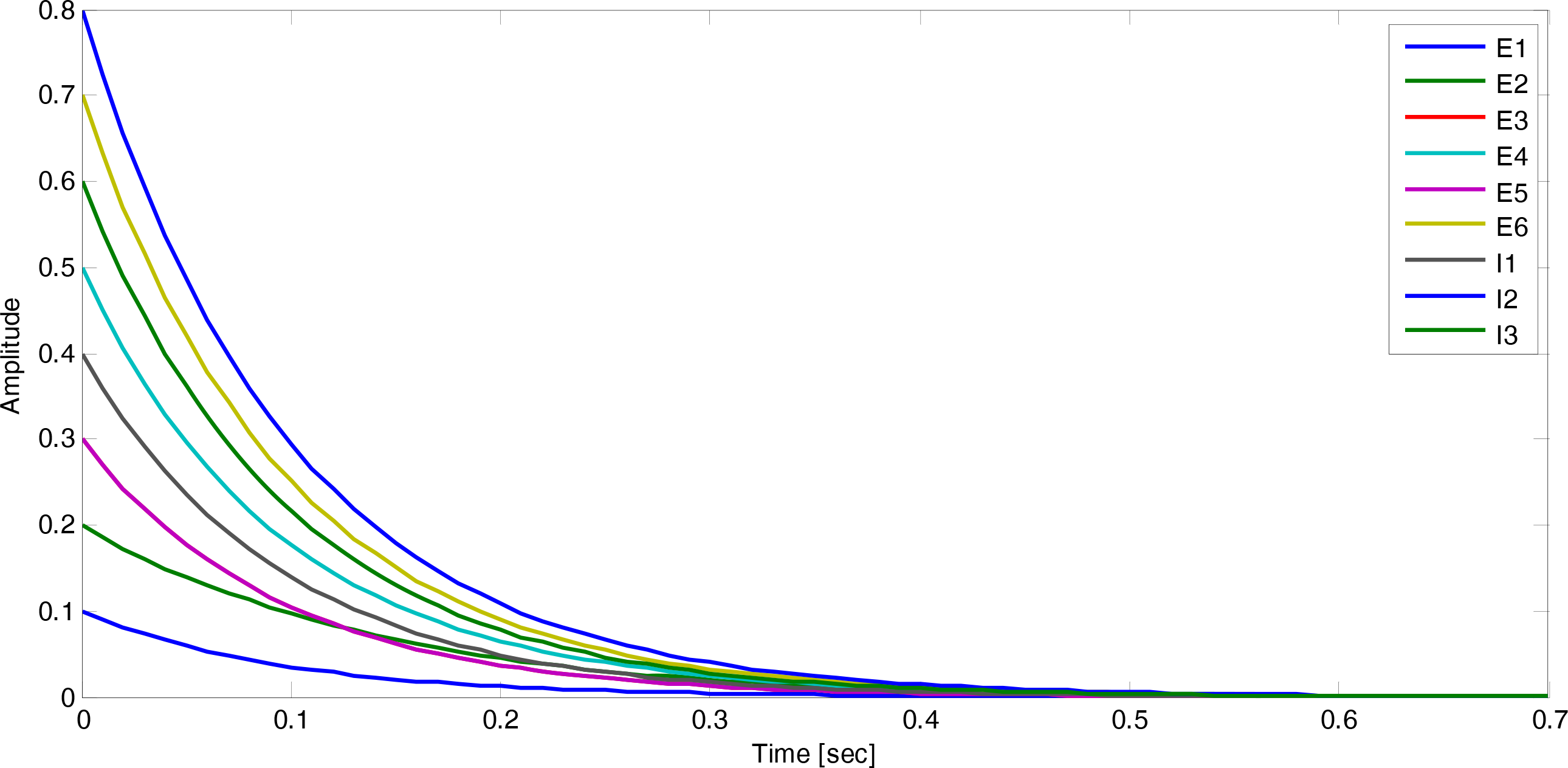
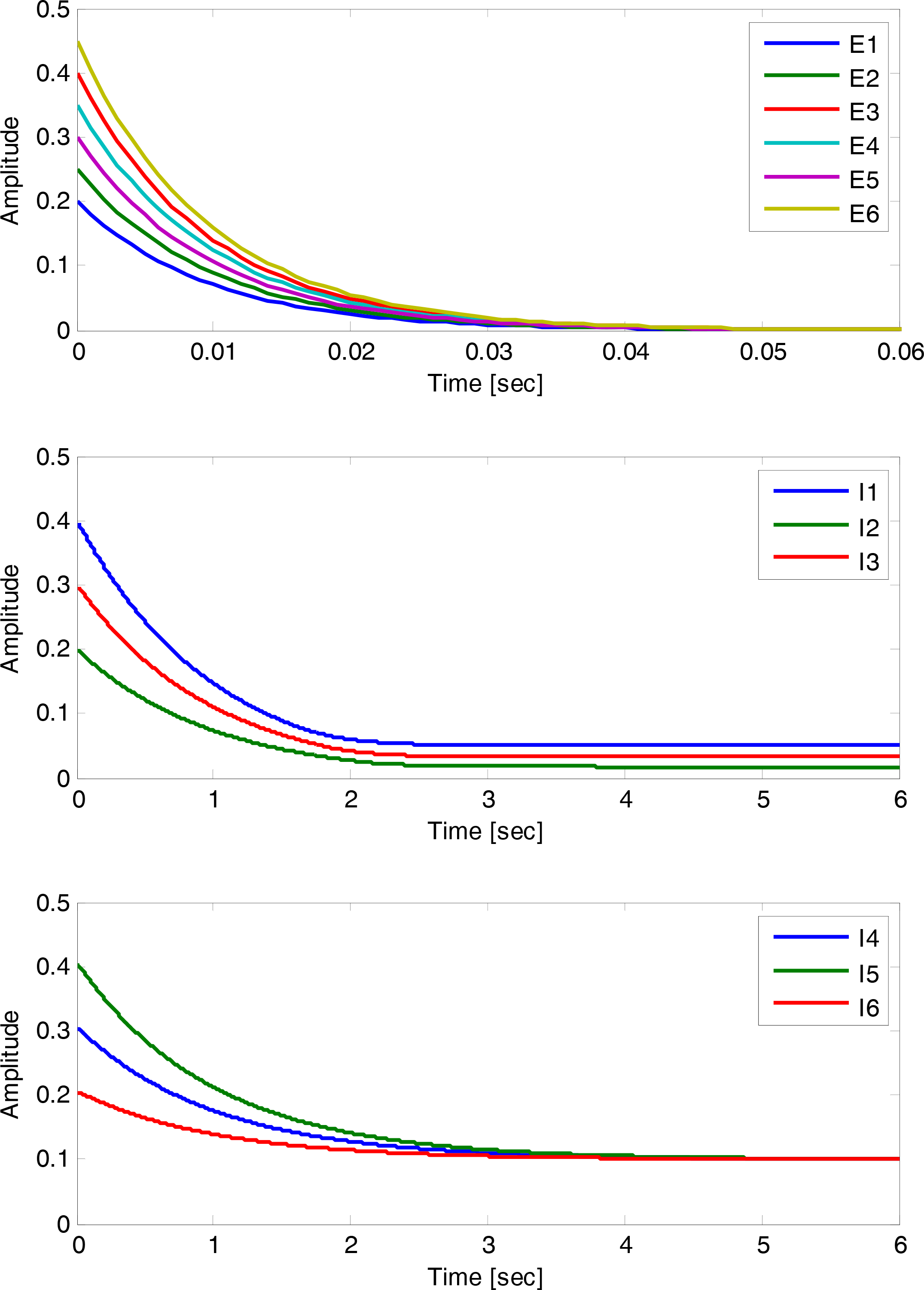
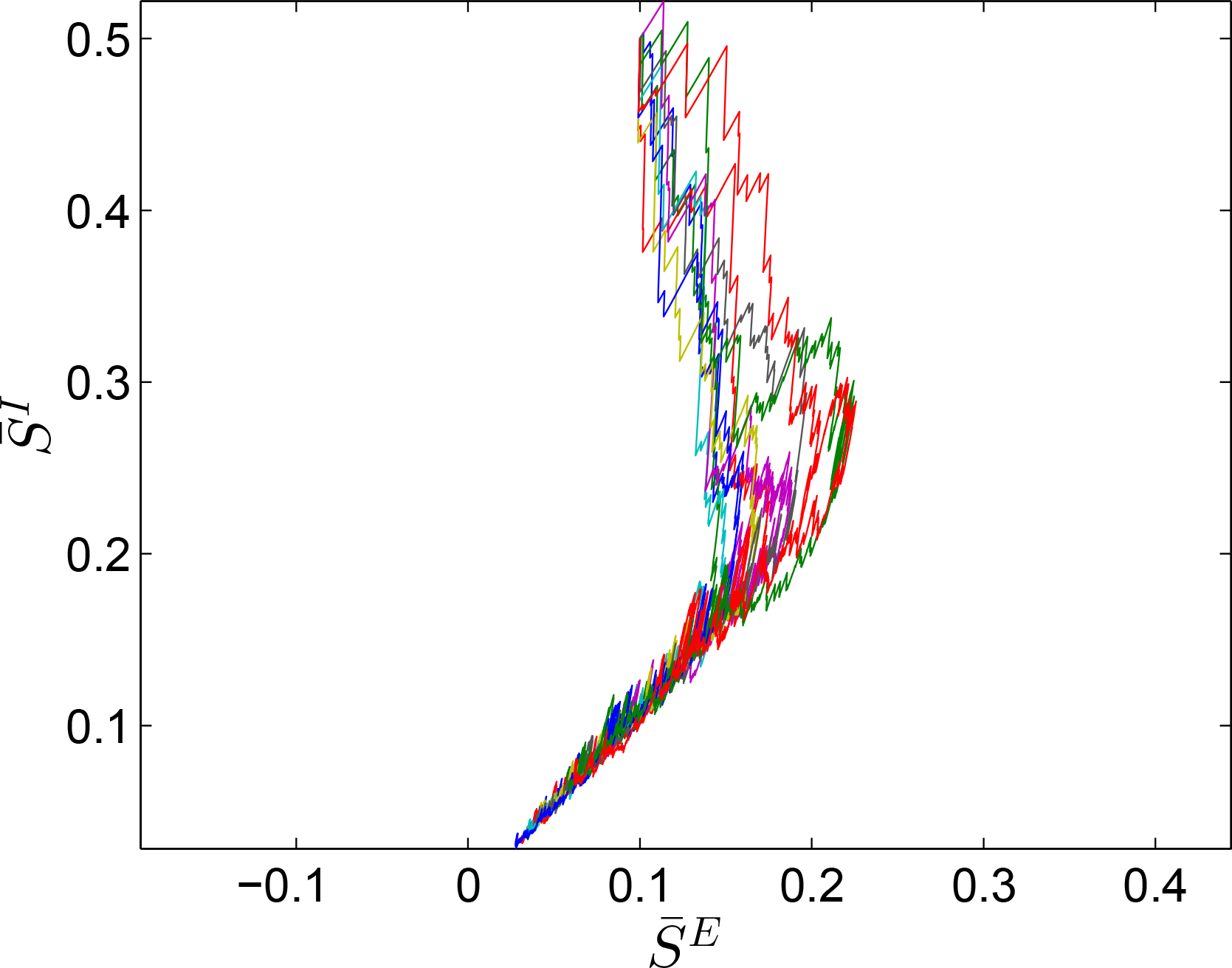
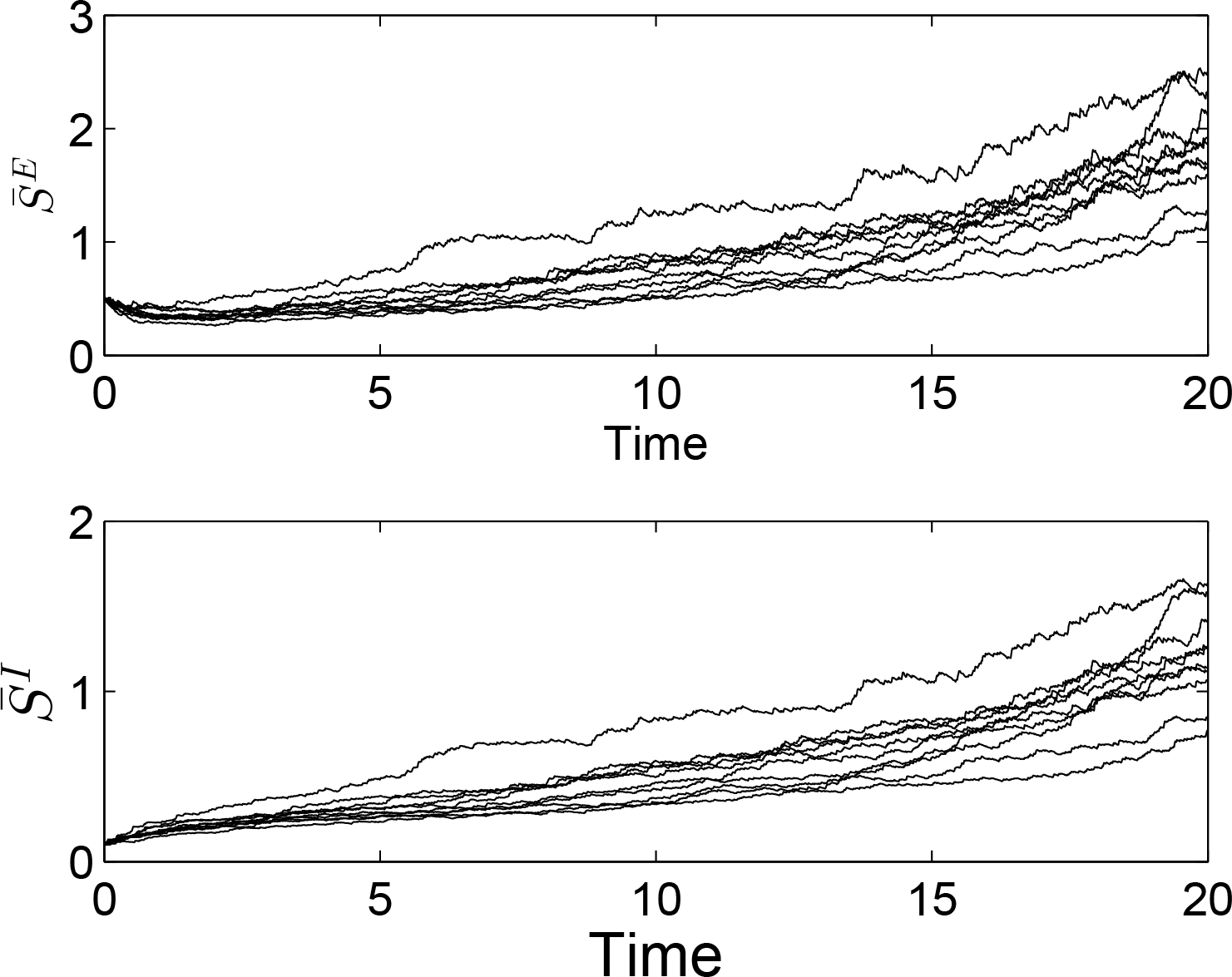
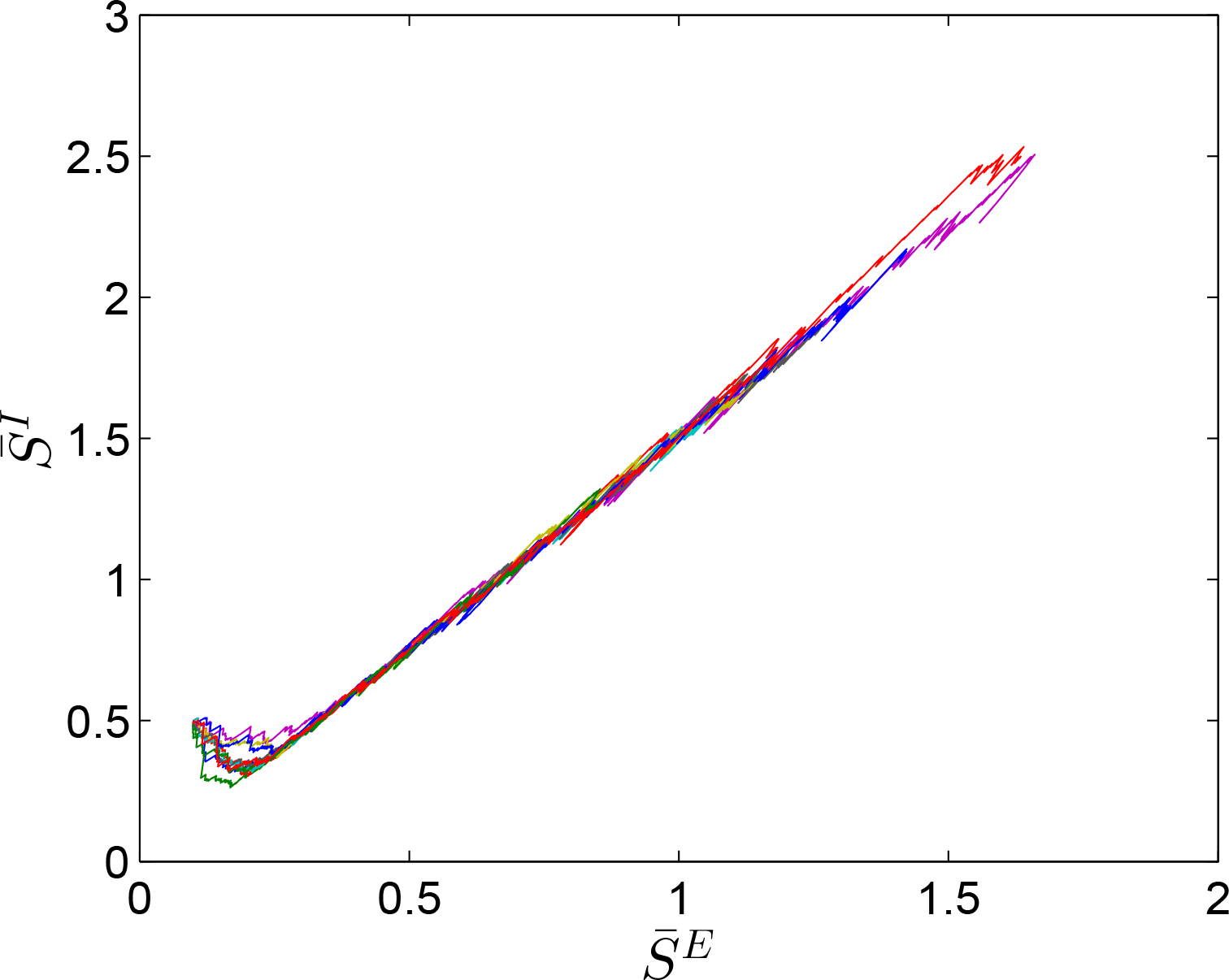
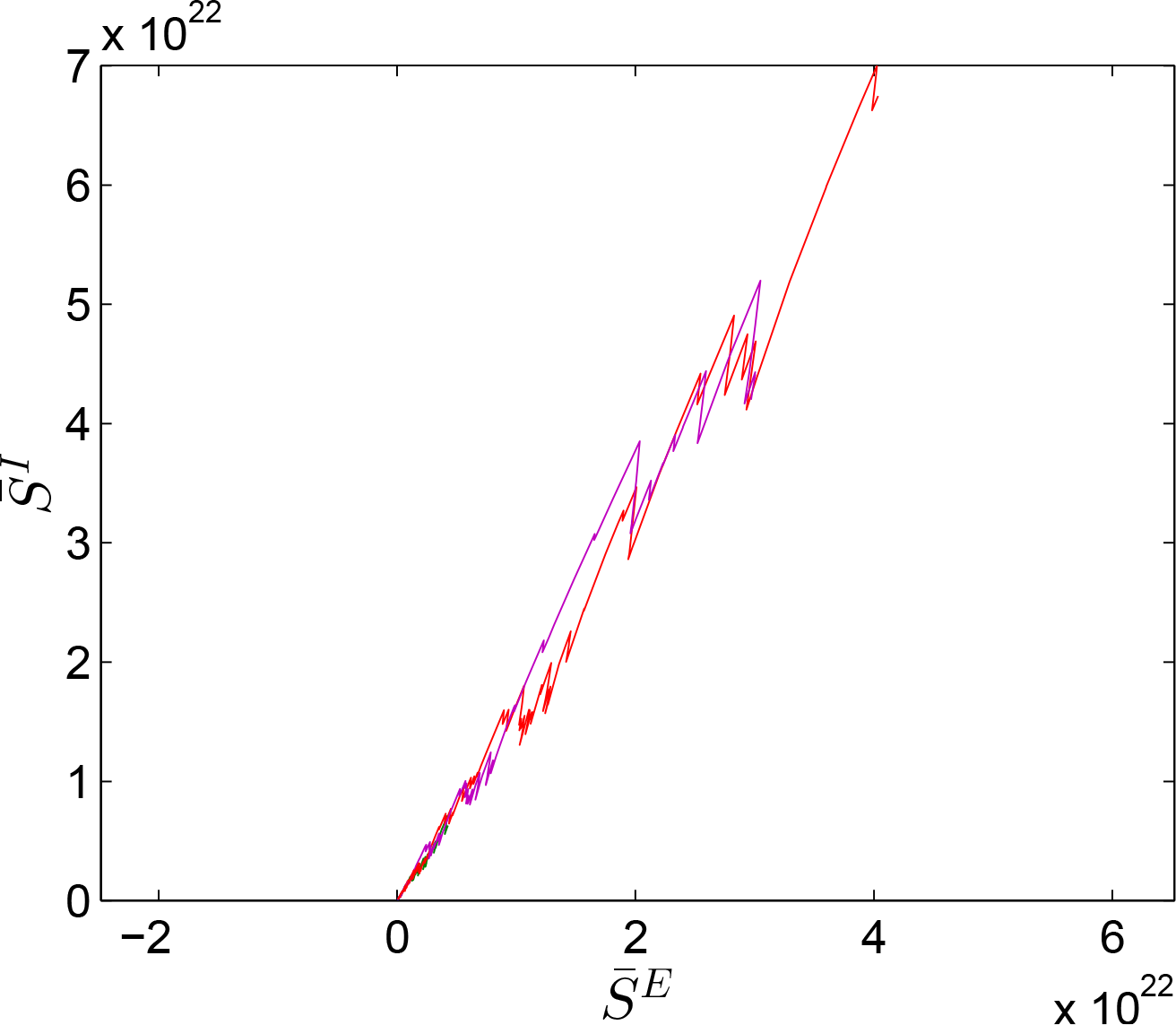
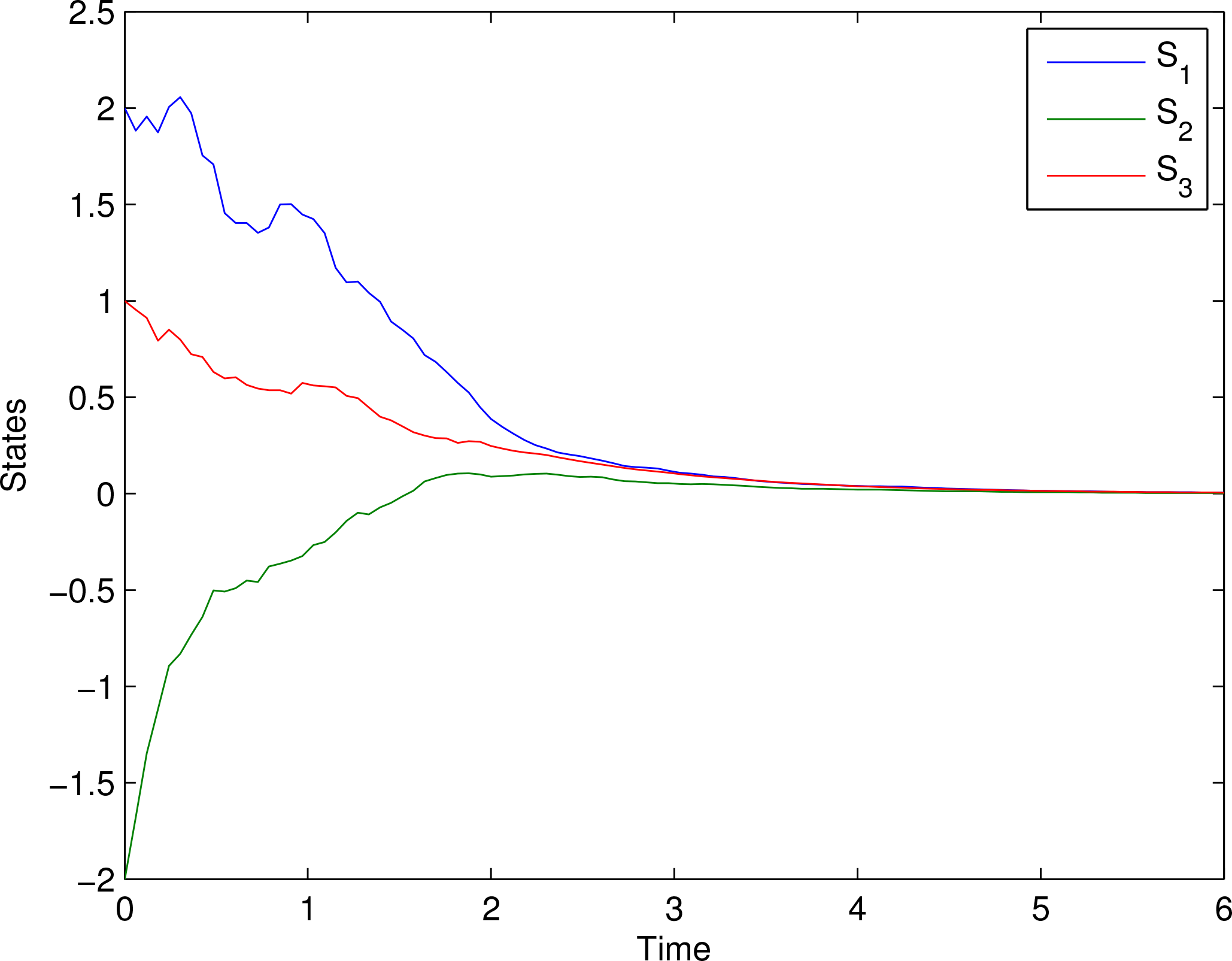
Finally, it follows from Theorem 5.1 that almost all solutions of the system converge to Lyapunov stable equilibria in $ℰ$, and hence, by definition, the system given by Equations (35) and (36) is multistable. Figure 2 shows the state trajectories versus time for the initial condition $\left[S_0^{\text{E}},S_0^{\text{I}}\right]=[1,2]$. This system is additionally synchronized; a notion that we discuss in Section 7.

6. Multistability of Excitatory-Inhibitory Biological Networks

Having developed multistability theory for discontinuous dynamical systems, in this section we apply the results of Section 5 to the excitatory-inhibitory neural firing rate model given by Equation (9). The form of biological neural network models given by Equation (9) represents a wide range of firing rate population models appearing in neuroscience [3,4]. The firing rate is a nonnegative quantity representing the probability of the firing action potential by the neuron and can be interpreted as a measure of the neuron’s activity. Since the firing rate of the excitatory-inhibitory network is nonnegative, all solutions of physical interest always take values in the nonnegative orthant of the state space for nonnegative initial conditions. For such systems, which evolve on possibly closed positively invariant subsets of ℝⁿ, it is natural to consider the nonnegative orthant ${\overline{ℝ}}_{+}^n$ as their state space, and hence, these systems are nonnegative dynamical systems [35]. In this case, the stability and convergence result developed in Section 5 holds with respect to ${\overline{ℝ}}_{+}^n$ by replacing ℝⁿ with ${\overline{ℝ}}_{+}^n$. For related details, see [35].

The following result, which follows from Proposition 2.1 of [35], gives necessary and sufficient conditions for the firing rates S_i(t), i = 1,..., n, to remain in the nonnegative orthant of the state space. For the statement of the next result recall that f is nonnegative [35] if and only if f(x) ≥≥ 0, $x\in {\overline{ℝ}}_{+}^n$, where “≥≥” denotes a component-wise inequality.

Proposition 1 Consider the excitatory-inhibitory network given by Equation (9). The firing rate vector S(t) ≜ [S₁(t),...,S_n(t)]^T ∈ ℝⁿ remains in the nonnegative orthant of the state space${\overline{ℝ}}_{+}^n$ for all t ≥ 0 if and only if, for every S_i ≥ 0 and v_thi ≥ 0, i = 1,..., n, the function$\tilde{f}={\left[f_1\left({\sum }_{j=1}^n{A}_{1j}{S}_j+v_{{\text{th}}_1}\right),\dots ,f_n\left({\sum }_{j=1}^n{A}_{nj}{S}_j+v_{{\text{th}}_n}\right)\right]}^{\text{T}}:{ℝ}^n\to {ℝ}^n$ is nonnegative.

Consider the excitatory-inhibitory network given by Equation (9) where f_i(·) is given by Equation (10), and note that f̃ : ℝⁿ → ℝⁿ is nonnegative. Thus, it follows from Proposition 1 that if $S_0\in {\overline{ℝ}}_{+}^n$, then $S(t)\in {\overline{ℝ}}_{+}^n$ for all t ≥ 0. Next, assume v_thi(t) ≡ 0, so that the vector-matrix form of Equation (9) can be written as

$$\dot{S}(t)=-LS(t)+\tilde{f}\left(AS(t)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S(0)=S_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(41)

where $L\triangleq \text{diag}\left[\frac{1}{{\tau }_1},\dots ,\frac{1}{{\tau }_n}\right]\in {ℝ}^{n\times n}$ is a time constant matrix, A ≜ [A_ij] ∈ ℝ^n×n is a matrix representing the strength of the synaptic interconnections, and $\tilde{f}(S)\triangleq {\left[f_1\left({\sum }_{j=1}^m{A}_{1j}{S}_j\right),\dots ,f_n\left({\sum }_{j=1}^m{A}_{nj}{S}_j\right)\right]}^{\text{T}}:{ℝ}^n\to {ℝ}^n$ is a vector activation function describing the relationship between the synaptic drives and the firing rates of the neurons, where S = [S₁,...,S_n]^T and f_i(·) is defined in Equation (10). Finally, assume that the set ${ℰ}_{\text{e}}=\left\{S\in {\overline{ℝ}}_{+}^n:\tilde{f}(\mathit{AS})-\mathit{LS}=0\right\}\subset {\overline{ℝ}}_{+}^n$ has a nonzero element, that is, $ℰ$_e has a nonzero solution for $S\in {\overline{ℝ}}_{+}^n$. For the statement of the next theorem, $𝒩$ (X) denotes the nullspace of the matrix X.

Theorem 2 Consider the excitatory-inhibitory network given by Equation (41) with f_i(·), i = 1,..., n, given by Equation (10) and$S\in {\overline{ℝ}}_{+}^n$. Let Ω₁ ≥ 0 and Ω₂ ≥≥ 0, where

$${\Omega }_1\triangleq \frac{1}{2}\left[\left(HL-\tilde{H}\tilde{A}\right)+{\left(HL-\tilde{H}\tilde{A}\right)}^{\text{T}}\right],$$

(42)

$${\Omega }_2\triangleq (I-H)L+(\tilde{H}-I)\tilde{A},$$

(43)

H = H^T, rank H = n, and H̃ and à are n × n matrices whose entries are given by H̃_ij = [H_ij]₊ and Ã_ij = [A_ij]₊, and satisfy (HL − H̃Ã) ≥ 0. Furthermore, assume that every point$S\in 𝒩({\Omega }_1)\cap {\overline{ℝ}}_{+}^n$ is Lyapunov stable with respect to Equation (41). Then Equation (41) is multistable.

Proof. Consider the function $V(S)=\frac{1}{2}{S}^{\text{T}}HS$, $S\in {\overline{ℝ}}_{+}^n$, and note that the derivative of V (S) along the trajectories of Equation (41) with f_i(·), i = 1 ..., n, given by Equation (10) is given by

$$\begin{array}{lll}\dot{V}(S)\hfill & =\hfill & S^{\text{T}}H\left(-LS+\tilde{f}(AS)\right)\hfill \\ \hfill & =\hfill & -\sum _{i=1}^n\sum _{j=1}^n\frac{1}{{\tau }_i}{H}_{ij}{S}_i{S}_j+\sum _{i=1}^n\sum _{j=1}^n{H}_{ij}{S}_j{\left[\sum _{k=1,k\ne i}^n{A}_{ik}{S}_k\right]}_{+},\hfill \end{array}$$

(44)

where [ · ]₊ is defined as in Equation (10). Now, since $S\in {\overline{ℝ}}_{+}^n$, [x]₊ ≥ 0 and [x + y]₊ ≤ [x]₊ +[y]₊ for all x, y ∈ ℝ, it follows that

$$\begin{array}{lll}\dot{V}(S)\hfill & \le \hfill & -\sum _{i=1}^n\sum _{j=1}^n\frac{1}{{\tau }_i}{H}_{ij}{S}_i{S}_j+\sum _{i=1}^n\sum _{j=1}^n{[H_{ij}]}_{+}{S}_j{\left[\sum _{k=1,k\ne i}^n{A}_{ik}{S}_k\right]}_{+}\hfill \\ \hfill & \le \hfill & -\sum _{i=1}^n\sum _{j=1}^n\frac{1}{{\tau }_i}{H}_{ij}{S}_i{S}_j+\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1,k\ne i}^n{[H_{ij}]}_{+}{[A_{ik}]}_{+}{S}_j{S}_k\hfill \\ \hfill & =\hfill & -S^{\text{T}}HLS+S^{\text{T}}\tilde{H}\tilde{A}S\hfill \\ \hfill & =\hfill & -S^{\text{T}}{\Omega }_{1}S,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.\hfill \end{array}$$

(45)

Next, since H is such that (HL− H̃Ã) ≥ 0, it follows from Equation (45) that V̇ (S) ≤ 0 for all $S\in {\overline{ℝ}}_{+}^n$, and hence, V̇⁻¹(0) ⊆ $𝒩$ (Ω₁).

Since Ω₁ ≥ 0, the dynamical system

$$\dot{x}(t)=-(HL-\tilde{H}\tilde{A})x(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x(0)=S_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(46)

where $S_0\in {\overline{ℝ}}_{+}^n$, is Lyapunov stable. Next, for every $S\in {\overline{ℝ}}_{+}^n$, it follows that Ṡ = −LS + f̃(AS) ≤≤ −LS + ÃS. Now, since H is chosen such that all the entries of Ω₂ are nonnegative, it follows that

$$\dot{S}\le \le -LS+\tilde{A}S\le \le -LS+\tilde{A}S+{\Omega }_{2}S=-(HL-\tilde{H}\tilde{A})S,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.$$

(47)

In this case, S(t) ≤≤ x(t), t ≥ 0, where x(t), t ≥ 0, is the solution to Equation (46). In addition, since $S(t)\in {\overline{ℝ}}_{+}^n$, t ≥ 0, $S_0\in {\overline{ℝ}}_{+}^n$, and Equation (46) is Lyapunov stable, it follows that $S(t)\in {\overline{ℝ}}_{+}^n$ is bounded for all t ≥ 0.

Finally, let $𝒲$ be the largest weakly invariant set contained in V̇⁻¹(0) and note that since $S(t)\in {ℝ}_{+}^n$, t ≥ 0, $𝒲\subseteq 𝒩({\Omega }_1)\cap {\overline{ℝ}}_{+}^n$. Now, since $S\in 𝒩({\Omega }_1)\cap {\overline{ℝ}}_{+}^n$ is Lyapunov stable with respect to Equation (41), it follows from Corollary 4.2 of [45] that all the solutions of the excitatory-inhibitory network given by Equation (41) converge to one of the Lyapunov stable equilibria in $𝒩({\Omega }_1)\cap {\overline{ℝ}}_{+}^n$ for Equation (41) with $S_0\in {\overline{ℝ}}_{+}^n$. Hence, it follows from Theorem 1 that Equation (41) is multistable.

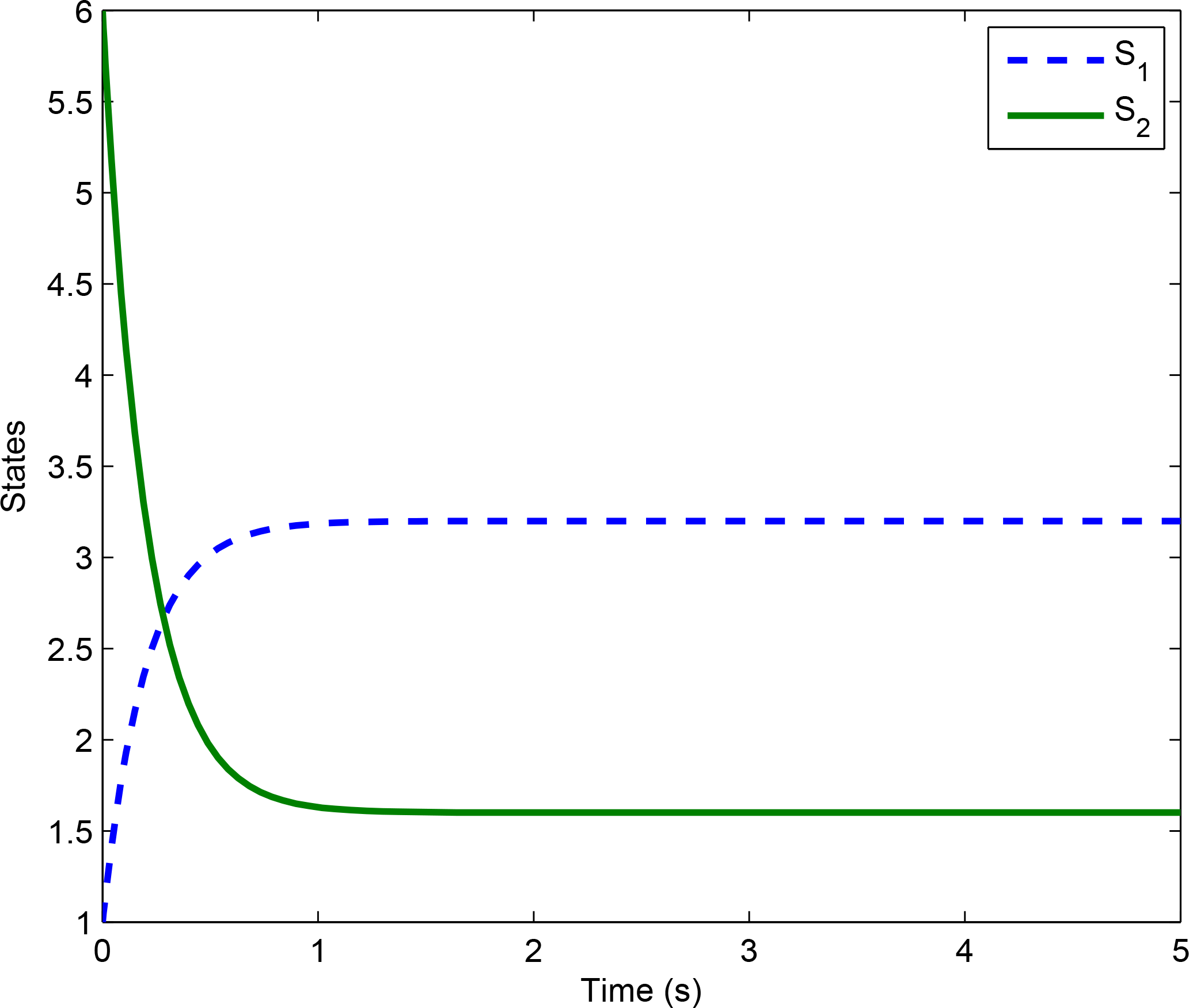
Example 2 Consider the excitatory-inhibitory network characterized by the dynamics

$${\dot{S}}_1(t)=-S_1(t)+f_1(2S_2(t)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_1(0)=S_{01},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(48)

$${\dot{S}}_2(t)=-4S_2(t)+f_2\left(2S_1(t)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_2(0)=S_{02},$$

(49)

where S₀₁ ≥ 0, S₀₂ ≥ 0, and, f_i(·), i = 1, 2, are defined by Equation (10), and note that Equations (48) and (49) can be written in the form of Equation (41) with

$$L=\left[\begin{array}{cc}1& 0\\ 0& 4\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}A=\left[\begin{array}{cc}0& 2\\ 2& 0\end{array}\right].$$

Let H = I₂ and define H̃ and à by H̃_ij = [H_ij]₊ and Ã_ij = [A_ij]₊ so that

$${\Omega }_1=\frac{1}{2}\left(\left(HL-\tilde{H}\tilde{A}\right)+{\left(HL-\tilde{H}\tilde{A}\right)}^{\text{T}}\right)=\left[\begin{array}{cc}1& -2\\ -2& 4\end{array}\right]\ge 0$$

and

$${\Omega }_2=(I-H)L+(\tilde{H}-I)\tilde{A}=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right],$$

which contains nonnegative entries.

Next, it follows from Proposition 1 that S(t) ≥≥ 0, t ≥ 0, for all$(S_{10},S_{20})\in {\overline{ℝ}}_{+}^2$, and hence, Equations (48) and (49) collapse to the linear model given by

$${\dot{S}}_1(t)=-S_1(t)+2S_2(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_1(0)=S_{01},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(50)

$${\dot{S}}_2(t)=-4S_2(t)+2S_1(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_2(0)=S_{02}.$$

(51)

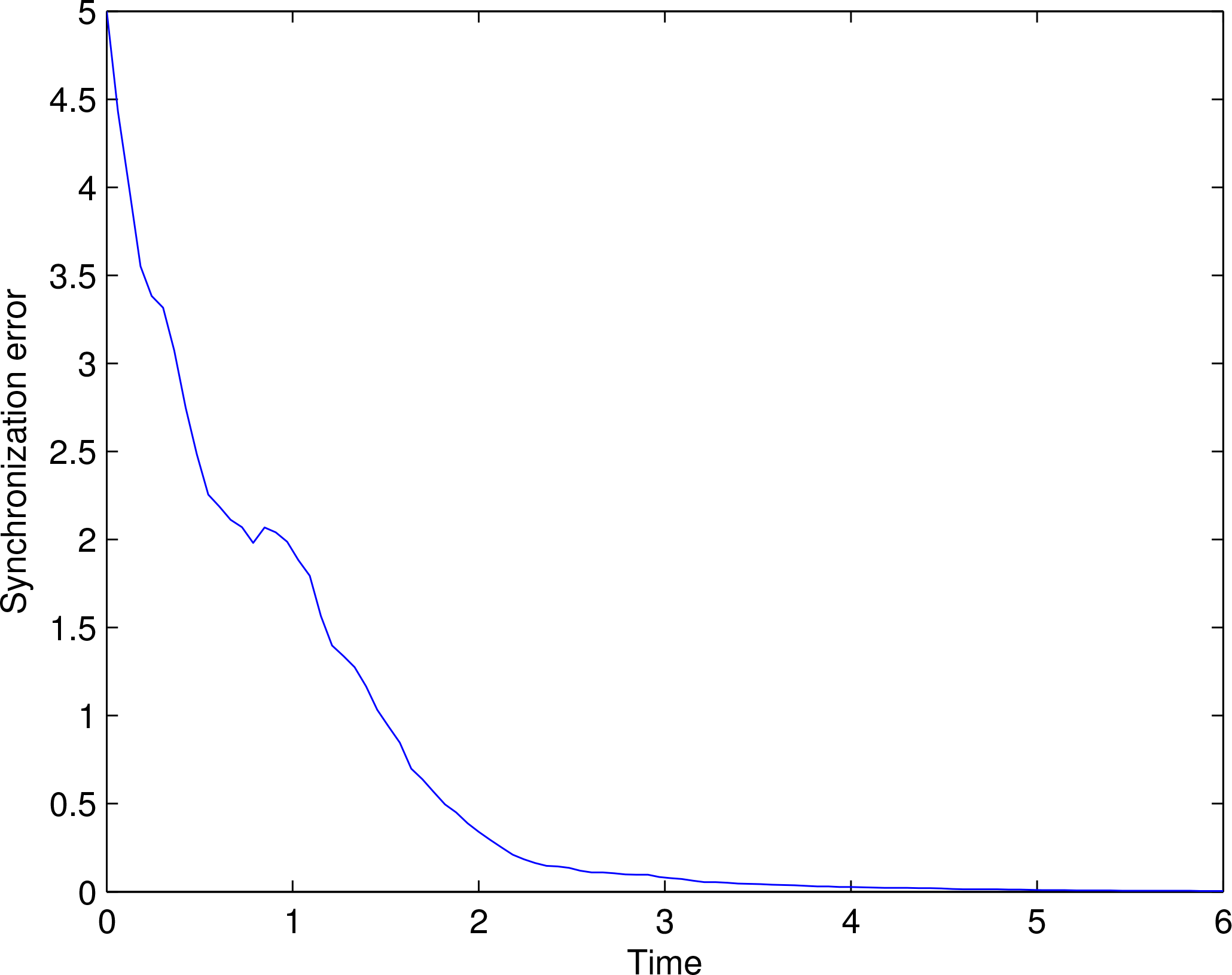
Clearly, the system given by Equations (50) and (51) is Lyapunov stable, and hence, every$S\in 𝒩({\Omega }_1)\cap {\overline{ℝ}}_{+}^n$ is Lyapunov stable with respect to Equations (48) and (49). Now, it follows from Theorem 2 that the system given by Equations (48) and (49) is mutistable. For the initial conditions S₀₁ = 3 and S₀₂ = 1 the trajectories of the state variables with respect to time is shown in Figure 3.

7. Synchronization of Biological Neural Networks

Numerous complex large-scale dynamical networks often demonstrate a degree of synchronization. System synchronization typically involves coordination of events that allows a dynamical system to operate in unison resulting in system self-organization. The onset of synchronization in populations of coupled dynamical networks have been studied for various complex networks including network models for mathematical biology, statistical physics, kinetic theory, bifurcation theory, as well as plasma physics [72]. Synchronization of firing neural oscillator populations using probabilistic analysis has also been addressed in the neuroscience literature [73]. One of the most important questions in neuroscience is how do neurons, or collections of neurons, communicate. In other words, what is the neural code? There is extensive experimental verification that collections of neurons may function as oscillators [74–76] and the synchronization of oscillators may play a key role in the transmission of information within the central nervous system. This may be particularly relevant to understanding the mechanism of action for general anesthesia [45].

It has been known for a long time that general anesthesia has profound effects on the spectrum of oscillations in the electroencephalograph [77,78]. More recently, the authors in [79] have suggested that thalamocortical circuits function as neural pacemakers and that alterations in the thalamic oscillations are associated with the induction of general anesthesia. Furthermore, it is well known that anesthetic drugs frequently induce epileptiform activity as part of the progression to the state of unconsciousness [31].

Multiple lines of evidence indicate that anesthetic agents impact neural oscillators. In addition, epileptiform activity implies synchronization of oscillators. This leads to the possibility that synchronization of these oscillators is involved in the transition to the anesthetic state. To develop global synchronization properties for the biological neural network system given by Equation (41) we introduce the notions of asymptotic synchronization and exponential synchronization.

Definition 7 The biological neural network given by Equation (41) is said to be globally asymptotically synchronized if

$$\underset{t\to \infty }{\text{lim}}\left|S_i(t)-S_j(t)\right|=0$$

(52)

for all$S_0\in {\overline{ℝ}}_{+}^n$ and i, j = 1, 2,..., n, i ≠ j.

Definition 8 The biological neural network given by Equation (41) is said to be globally exponentially synchronized if there exist constants ρ > 0 and p > 0 such that

$$\left|S_i(t)-S_j(t)\right|\le \rho e^{-pt}\left|S_{0i}-S_{0j}\right|,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(53)

for all$S_0={\left[S_{01},\dots ,S_{0n}\right]}^{\text{T}}\in {\overline{ℝ}}_{+}^n$ and i, j = 1, 2,..., n, i ≠ j.

The following theorems provide sufficient conditions for global asymptotic synchronization and global exponentially synchronization of the biological neural network system given by Equation (41). For the statement of the theorems we define the ones vector of order n by e_n ≜ [1,..., 1]^T.

Theorem 3 Consider the biological neural network given by Equation (41) with f_i(·), i = 1, 2, ..., n, given by Equation (10). If there exist positive definite matrices P, Q ∈ ℝ^n×n and a diagonal positive-definite matrix R ∈ ℝ^n×n such that

$$\left[\begin{array}{cc}Q& -P\\ -P& R\end{array}\right]\ge 0,$$

(54)

and either Ω₃ < 0 or both Ω₃ ≤ 0 and $𝒩$ (Ω₃) = span(e_n) hold, where

$${\Omega }_3\triangleq -PL-LP+Q+A^{\text{T}}RA,$$

(55)

then Equation (41) is globally asymptotically synchronized.

Proof. Consider the Lyapunov function candidate $V:{\overline{ℝ}}_{+}^n\to ℝ$ given by V (S) = S^TPS. It follows that the derivative of V (S) along the trajectories of Equation (41) is given by

$$\dot{V}(S)=2S^{\text{T}}P\left(-LS+\tilde{f}(AS)\right)=-2S^{\text{T}}PLS+2S^{\text{T}}P\tilde{f}(AS).$$

Next, it follows from Equation (54) that V̇ (S) satisfies

$$\begin{array}{ll}\dot{V}(S)\hfill & \le -2S^{\text{T}}PLS+S^{\text{T}}QS+{\tilde{f}}^{\text{T}}(AS)R\tilde{f}(AS)\hfill \\ \hfill & =S^{\text{T}}(-PL-LP+Q)S+{\tilde{f}}^{\text{T}}(AS)R\tilde{f}(AS),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.\hfill \end{array}$$

(56)

Since $f_i^2(x)\le x^2$, x ∈ ℝ, for f_i(·), i = 1, ..., n, given by Equation (10) and R ∈ ℝ^n×n is a positive-definite diagonal matrix, it follows that

$${\tilde{f}}^{\text{T}}(AS)R\tilde{f}(AS)\le S^{\text{T}}{A}^{\text{T}}RAS,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.$$

(57)

Now, it follows from Equations (56) and (57) that

$$\dot{V}(S)\le S^{\text{T}}{\Omega }_{3}S,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.$$

(58)

If Ω₃ < 0, then V̇ (S) ≤ 0, $S\in {\overline{ℝ}}_{+}^n$, and V̇ (S) = 0 if and only if S = 0. Hence, the zero solution S(t) ≡ 0 to Equation (41) is asymptotically stable, which implies that lim_t→∞ |S_i(t) − S_j(t)| = 0 for all S₀ ∈ ℝⁿ and i, j = 1, 2, ..., n, i ≠ j. Hence, Equation (41) is globally asymptotically synchronized. Alternatively, if Ω₃ ≤ 0 and $𝒩$ (Ω₃) = span(e_n) holds, then V̇ (S(t)) ≤ 0, t ≥ 0, and hence, V (S(t)) ≤ V (S₀) for all t ≥ 0. Next, since P is positive definite and V̇ (S(t)) is a nonincreasing function of time, it follows that V (S(t)) is bounded for all t ≥ 0, and hence, S(t) is bounded for all t ≥ 0, which further implies that V̈ (S(t)) is bounded for all t ≥ 0. Thus, V̇ (S(t)) is uniformly continuous in t. Now, it follows from Barbalat’s lemma ([20](p. 221)) that V̇ (S(t)) → 0 as t → ∞, which, since $𝒩$ (Ω₃) = span(e_n), implies that Equation (41) is globally asymptotically synchronized.

Theorem 4 Consider the biological neural network given by Equation (41) with f_i(·), i = 1, 2, ..., n, given by Equation (10). If there exist positive definite matrices P, Q ∈ ℝ^n×n, a diagonal positive-definite matrix R ∈ ℝ^n×n and a scalar ε > 0 such that Equation (54) holds, and either Ω₄ < 0 or both Ω₄ ≤ 0 and $𝒩$ (Ω₄) = span(e_n) hold, where

$${\Omega }_4\triangleq 2\epsilon P-PL-LP+Q+A^{\text{T}}RA,$$

(59)

then Equation (41) is globally exponentially synchronized.

Proof. The proof is similar to the proof of Theorem 3 using the function $V:\left[0,\infty \right)\times {\overline{ℝ}}_{+}^n\to ℝ$ given by V (t, S) = e^2εtS^TPS and, hence, is omitted.

Definition 9 ([80]) Let ($ℛ$, +, ·) be a ring with the two binary operations of addition (+) and multiplication (·) connected by distributive laws, and let $𝒯$ ($ℛ$, K) be the set of matrices with entries in $ℛ$ such that the sum of the entries in each row is equal to K for some K ∈ $ℛ$.

Lemma 1 ([81]) Let G be an n × n matrix such that G ∈ $𝒯$ ($ℛ$, K). Then there exists a matrix Ḡ ∈ ℝ^{(n−1)×(n−1)} given by Ḡ = MGJ such that MG = ḠM, where M and J are given by

$$M=\left[\begin{array}{ccccc}1& -1& 0& \cdots & 0\\ 0& 1& -1& \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & 0\\ 0& \cdots & 0& 1& -1\end{array}\right]\in {ℝ}^{(n-1)\times n},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}J=\left[\begin{array}{cccc}1& 1& \cdots & 1\\ 0& 1& \ddots & ⋮\\ 0& \ddots & \ddots & 1\\ 0& \cdots & 0& 1\\ 0& \cdots & 0& 0\end{array}\right]\in {ℝ}^{n\times (n-1)}.$$

(60)

Next, we analyze the synchronization properties of a special class of biological neural network given by Equation (41) where L, A ∈ $𝒯$ ($ℛ$, K) and f_i(·), i = 1, ..., n, satisfies

$$f_i(x)=\{\begin{array}{ll}0,\hfill & x<0,\hfill \\ x,\hfill & 0\le x\le f_{\text{max}},\hfill \\ f_{\text{max}},\hfill & x>f_{\text{max}},\hfill \end{array}$$

(61)

where f_max denotes the maximum firing rate.

Lemma 2 Consider the biological neural network given by Equation (41) and assume that f_i(·), i = 1, ..., n, is given by Equation (61). Then S(t) is bounded for all t ≥ 0.

Proof. Consider the function V (S) = S^TS and note that the derivative of V (S) along the trajectories of Equation (41) satisfies

$$\dot{V}(S)=2S^{\text{T}}\left(-LS+\tilde{f}(AS)\right)=-2S^{\text{T}}LS+2S^{\text{T}}\tilde{f}(AS).$$

(62)

Note that since $2x^{\text{T}}y\le r{x}^{\text{T}}x+\frac{1}{r}{y}^{\text{T}}y$ for all x, y ∈ ℝⁿ and r > 0, it follows that

$$\dot{V}(S)\le -2S^{\text{T}}LS+{\lambda }_{\text{min}}(L)S^{\text{T}}S+\frac{1}{{\lambda }_{\text{min}}(L)}{\tilde{f}}^{\text{T}}(AS)\tilde{f}(AS),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.$$

(63)

Now, since 0 ≤ f_i(x) ≤ f_max for all x ∈ ℝ and S^TLS ≥ λ_min(L)S^TS, it follows that

$$\begin{array}{ll}\dot{V}(S)\hfill & \le -2{\lambda }_{\text{min}}(L)S^{\text{T}}S+{\lambda }_{\text{min}}(L)S^{\text{T}}S+\frac{n}{{\lambda }_{\text{min}}(L)}{f}_{\text{max}}^2\hfill \\ \hfill & =-{\lambda }_{\text{min}}(L)S^{\text{T}}S+\frac{n}{{\lambda }_{\text{min}}(L)}{f}_{\text{max}}^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.\hfill \end{array}$$

(64)

Next, we show that if ‖S₀‖² = c < m, where $m=\frac{n}{{\lambda }_{\text{min}}^2(L)}{f}_{\text{max}}^2$, then V (S(t)) ≤ m for all t ≥ 0. To see this, assume, ad absurdum, that V (S(t)) > m for some t > 0, which holds since V (S(t)) is continuous in t, and note that there exists τ ∈ (0, t) such that V (S(τ)) = m and V̇ (S(τ)) > 0. Now, using Equation (64) it follows that V̇ (S(τ)) ≤ 0 for all τ > 0 such that V (S(τ)) = m, which contradicts V̇ (S(τ)) > 0. Alternately, if ‖S₀‖² = c ≥ m, then using a similar argument it can be shown that V (S(t)) ≤ c for all t ≥ 0. Hence, ‖S(t)‖² is bounded for all t ≥ 0, and hence, the solution S(t) is bounded for all t ≥ 0.

Theorem 5 Consider the biological neural network given by Equation (41) where L, A ∈ $𝒯$ ($ℛ$, K) and f_i(·), i = 1, 2, ..., n, is given by Equation (61). If there exist positive definite matrices P, Q ∈ ℝ^{(n−1)×(n−1)}, a diagonal positive-definite matrix R ∈ ℝ^{(n−1)×(n−1)} such that Equation (54) holds, and

$${\Omega }_5\triangleq -P\overline{L}-\overline{L}P+Q+{\overline{A}}^{\text{T}}R\overline{A}<0,$$

(65)

where L̄ and Ā are generated from L and A using Lemma 1, then Equation (41) is globally asymptotically synchronized.

Proof. Consider the function $V:{\overline{ℝ}}_{+}^n\to ℝ$ given by V (S) = S^TM^TPMS, where M is given by Equation (60). It follows that the derivative of V (S) along the trajectories of Equation (41) is given by

$$\dot{V}(S)=2S^{\text{T}}{M}^{\text{T}}PM\left(-LS+\tilde{f}(AS)\right)=-2S^{\text{T}}{M}^{\text{T}}PMLS+2S^{\text{T}}{M}^{\text{T}}PM\tilde{f}(AS).$$

(66)

Next, it follows from Equation (54) that

$$\dot{V}(S)\le -2S^{\text{T}}{M}^{\text{T}}PMLS+S^{\text{T}}{M}^{\text{T}}QMS+{\tilde{f}}^{\text{T}}(AS)M^{\text{T}}RM\tilde{f}(AS),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.$$

(67)

Note that since R ∈ ℝ^{(n−1)×(n−1)} is a diagonal positive-definite matrix and f_i(·), i = 1, 2, ..., n, given by Equation (61) satisfies (f_i(x) − f_j(y))² ≤ (x − y)² for all x, y ∈ ℝ, it follows that f̃^T(AS)M^TRM f̃(AS) ≤ S^TA^TM^TRMAS, $S\in {\overline{ℝ}}_{+}^n$. Hence,

$$\begin{array}{lll}\dot{V}(S)\hfill & \le \hfill & -2S^{\text{T}}{M}^{\text{T}}PMLS+S^{\text{T}}{M}^{\text{T}}QMS+S^{\text{T}}{A}^{\text{T}}{M}^{\text{T}}RMAS\hfill \\ \hfill & =\hfill & S^{\text{T}}{M}^{\text{T}}\left(-P\overline{L}-\overline{L}P+Q\right)S+S^{\text{T}}{M}^{\text{T}}{\overline{A}}^{\text{T}}R\overline{A}MS\hfill \\ \hfill & =\hfill & S^{\text{T}}{M}^{\text{T}}{\Omega }_{5}MS,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {\overline{ℝ}}_{+}^n.\hfill \end{array}$$

(68)

Since Ω₅ < 0, V̇ (S) ≤ 0, $S\in {\overline{ℝ}}_{+}^n$, and hence, V (S(t)) ≤ V (S₀) for all t ≥ 0. Next, since P is positive definite and V̇ (S(t)) is a non-increasing function of time, it follows that V (S(t)) is bounded for all t ≥ 0. Since, by Lemma 2, S(t) is bounded for all t, it follows that V̈ (S(t)) is bounded for all t ≥ 0, and hence, V̇ (S(t)) is uniformly continuous in t. Now, it follows from Barbalat’s lemma ([20](p. 221)) that V̇ (S(t)) → 0 as t → ∞, which implies that lim_t→∞ MS(t) = 0. Hence, Equation (41) is globally asymptotically synchronized.

Theorem 6 Consider the biological neural network given by Equation (41) where L, A ∈ $𝒯$ ($ℛ$, K) and f_i(·), i = 1, 2, ..., n, is given by Equation (61). If there exist positive definite matrices P, Q ∈ ℝ^{(n−1)×(n−1)}, a diagonal positive-definite matrix R ∈ ℝ^{(n−1)×(n−1)}, a scalar ε > 0 such that Equation (54) holds, and

$${\Omega }_6\triangleq 2\epsilon P-P\overline{L}-\overline{L}P+Q+{\overline{A}}^{\text{T}}R\overline{A}<0,$$

(69)

where L̄ and Ā are generated from L and A using Lemma 1, then Equation (41) is globally exponentially synchronized.

Proof. The proof is similar to the proof of Theorem 5 using the function $V:\left[0,\infty \right)\times {\overline{ℝ}}_{+}^n\to ℝ$ given by

$$V(t,S)=e^{2\epsilon t}{S}^{\text{T}}{M}^{\text{T}}\mathit{PMS}$$

and, hence, is omitted.

Example 3 Consider the biological neural network given by Equation (41) consisting of a netwok of six excitatory and three inhibitory neurons shown in Figure 4. The neural connectivity matrix A for this network is given by

$$A=\left[\begin{array}{ccccccccc}0& 0& 0& 0& 2& 0& 0& 0& -1\\ 0& 0& 0& 0& 0& 2& 0& 0& -1\\ 2& 0& 0& 0& 0& 0& -1& 0& 0\\ 0& 2& 0& 0& 0& 0& -1& 0& 0\\ 0& 0& 2& 0& 0& 0& 0& -1& 0\\ 0& 0& 0& 2& 0& 0& 0& -1& 0\\ 1& 1& 0& 0& 0& 0& 0& 0& -1\\ 0& 0& 1& 1& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 1& 1& 0& -1& 0\end{array}\right]$$

Here, we assume that the time constant of all nine neurons are the same, and hence,$L=\frac{1}{\tau }{I}_9$. Furthermore, we assume the functions f_i(·), i = 1, 2, ..., 9, are given by Equation (61) with the same maximum firing rate f_max = 0.5.

Next, we construct Ā and L̄ using Lemma 1 and solve the Linear Matrix Inequalities (LMIs) given by Equations (54) and (65) for the neuron time constants τ = 10, 1, and 0.1. We use the MATLAB toolbox YALMIP for solving the LMIs. For τ = 10, there is no feasible solution to Equations (54) and (65), and, as shown in Figure 5, the synaptic drive of the inhibitory neurons oscillate whereas the synaptic drive of the excitatory neurons converge to a steady-state. For τ = 1, Equations (54) and (65) are also not satisfied and as shown in Figure 6, the synaptic drive of all the neurons converge to different steady state values, which implies that the network is not synchronized. Finally, for τ = 0.1, Equations (54) and (65) are satisfied with P, Q, and R, given by

$$P=\left[\begin{array}{cccccccc}25.85& 11.25& 9.479& 4.939& 4.977& 0& -1.008& 0.7254\\ 11.25& 32.11& 14.01& 5.302& 5.223& 0& -3.626& 3.375\\ 9.479& 14.01& 3.06& 8.948& 7.178& 0& -3.037& 1.77\\ 4.939& 5.302& 8.948& 18.92& 8.76& 0& -6.062& -2.118\\ 4.977& 5.223& 7.178& 8.76& 24.36& 0& -4.475& -2.172\\ 0& 0& 0& 0& 0& 7.104& 0& 0\\ -1.008& -3.626& -3.037& -6.062& -4.475& 0& 13.32& 2.425\\ 0.7254& 3.375& 1.77& -2.118& -2.172& 0& 2.425& 10.53\end{array}\right],$$

$$Q=\left[\begin{array}{cccccccc}65.66& 19.39& 15.22& 7.273& 7.601& 0& -5.527& 2.403\\ 19.39& 92.92& 25.48& 13.29& 12.26& 0& -5.246& 1.426\\ 15.22& 25.48& 74.49& 9.073& 11.16& 0& -6.843& 0.72\\ 7.273& 13.29& 9.073& 67.94& 5.833& 0& -0.2344& 1.604\\ 7.601& 12.26& 11.16& 5.833& 62.91& 0& -4.261& 1.016\\ 0& 0& 0& 0& 0& 72.06& 0& 0\\ -5.527& -5.246& -6.843& -0.2344& -4.261& 0& 65.52& -3.424\\ 2.403& 1.426& 0.72& 1.604& 1.016& 0& -3.424& 66.32\end{array}\right],$$

$$R=\text{diag}\left[\begin{array}{cccccccc}60.65& 23.27& 63.18& 45.2& 55.94& 24.87& 33.43& 40.61\end{array}\right].$$

Hence, the biological neural network is asymptotically synchronized. See Figure 7.

Example 4 When patients lose consciousness some parts of the brain are still functional (e.g., cardiac function) whereas other parts are suppressed. This can be captured by biological neural network models that exhibit partial synchronization wherein part of the system’s state in synchronized and the other parts fire at normal levels. In addition, the administration of increasing anesthetic doses can lead to a paradoxical state of excitement in the patient prior to decreases in the level of consciousness. This paradoxical boost in brain activity prior to hypnotic induction is known as drug biphasic response [82]. There is also a second biphasic surge in the EEG power as the patient emerges from unconsciousness. Models that predict the aforementioned characteristics are of great clinical importance in providing the phenomenological trends of the anesthetic cascade.

To demonstrate partial synchronization of the model presented in Section 2, consider the biological neural network given by Equation (41) consisting of a population of neurons with six excitatory neurons E₁ – E₆ and six inhibitory neurons I₁ – I₆. The neural connectivity matrix A for this network is given by

$$A=\left[\begin{array}{cccccccccccc}0& 1& 1& 1& 1& 1& -1& 0& -1& 0& -1& 0\\ 1& 0& 1& 1& 1& 1& 0& -1& -1& -1& 0& 0\\ 1& 1& 0& 1& 1& 1& -1& 0& 0& 0& -1& -1\\ 1& 1& 1& 0& 1& 1& 0& -1& 0& -1& 0& -1\\ 1& 1& 1& 1& 0& 1& -1& 0& -1& 0& -1& 0\\ 1& 1& 1& 1& 1& 0& 0& -1& 0& -1& 0& -1\\ 1& 0& 1& 0& 1& 0& 0& -1& -1& 0& 0& 0\\ 0& 1& 0& 1& 0& 1& -1& 0& -1& 0& 0& 0\\ 0& 0& 1& 1& 1& 0& -1& -1& 0& 0& 0& 0\\ 0& 1& 0& 0& 1& 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& 1& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0\end{array}\right],$$

which implies that the three inhibitory neurons I₄, I₅, and I₆ do not receive any inhibitory inputs. Here we assume that the excitatory neurons have a time constant λ^E = 0.01 s and the inhibitory neurons have a prolonged time constant λ^I = 1s. Furthermore, we assume$v_{\text{th}}^{\text{E}}=v_{\text{th}}^{\text{I}}=0.1\text{V}$ for all neurons, and the functions f_i(·), i = 1, 2, ..., 12, are given by Equation (61) with the same maximum firing rate f_max = 0.5. Figure 8 shows that as λ^I increases, the excitatory neurons that are coupled to inhibitory neurons all go to a zero synaptic drive, whereas the inhibitory neurons that themselves are not coupled to inhibitory neurons synchronize to some finite value.

8. Stochastic Multistability for a Mean Field Synaptic Drive Firing Neuronal Model

Since the neurocortex contains on the order of 10¹¹ neurons, each supporting up to 10⁵ synaptic contacts, we extend our dynamical system framework to a stochastic setting. Specifically, a large population of spiking neurons can be reduced to a distribution function describing their probabilistic evolution; that is, a function that captures the distribution of neuronal states at a given time [83]. In this section, we develop a stochastic field theory as in [84] for capturing neural activity in order to analyze system multistability. In the next section, we extend the results of this section to additionally address time delay functional models [85] in order to account for time delay and memory effects in inhibitory and excitatory networks.

In Sections 4 and 5 we developed deterministic multistability theory to explain the underlying mechanism of action for anesthesia and consciousness using a synaptic drive firing model framework [3]. In this section, we extend these results further by demonstrating multistability in the mean when the coefficients of the neuronal connectivity matrix are random variables. Specifically, we use a stochastic multiplicative uncertainty model to include modeling of a priori uncertainty in the coefficients of the neuronal connectivity matrix by means of state-dependent noise. The philosophy of representing uncertain parameters by means of multiplicative white noise is motivated by the Maximum Entropy Principle of Jaynes [86,87] and statistical analysis [88].

Maximum entropy modeling is a form of stochastic modeling wherein stochastic integration is interpreted in the sense of Itô to provide a model for system parameter uncertainty. The use of stochastic theory to model system parameter uncertainty has been used within a modern information-theoretic interpretation of probability theory [86,87,89]. In particular, rather than regarding the probability of an event as an objective quantity such as the limiting frequency of outcomes of numerous repetitions, maximum entropy modeling adopts the view that the probability of an event is a subjective quantity which reflects the observer’s certainty to a particular event occurring. This quantity corresponds to a measure of information. The validity of a stochastic model for a biological neural network does not rely on the existence of an ensemble model but rather in the interpretation that it expresses modeling certainty or uncertainty regarding the coefficients of the neuronal connectivity matrix. Hence, a stochastic multiplicative uncertainty model utilizes state-dependent Gaussian white noise to represent parameter uncertainty by defining a measure of ignorance, in terms of an information-theoretic entropy, and then determining the probability distribution which maximizes this measure subject to agreement with a given model.

To develop stochastic multistability synaptic drive model, consider for simplicity of exposition the simplified mean field synaptic drive model where the coefficients of Equations (24) and (25), with f_i(·) given by Equation (10), are randomly disturbed. Specifically, we assume that the initial value S(0) ≜ [S̄^E(0), S̄^I(0)]^T is deterministic and contained in the nonnegative orthant of the state space, and consider the stochastic differential mean field synaptic drive model given by

$$\text{d}S(t)=-LS(t)\left(\text{d}t+\nu \text{d}w(t)\right)+{\left[AS(t)\left(\text{d}t+\nu \text{d}w(t)\right)\right]}_{+},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S(0)=S_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(70)

where

$$L=\left[\begin{array}{cc}\frac{1}{{\lambda }^{\text{E}}}& 0\\ 0& \frac{1}{{\lambda }^{\text{I}}}\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}A=\left[\begin{array}{cc}{n}_{\text{E}}{\overline{A}}^{\text{EE}}& n_{\text{I}}{\overline{A}}^{\text{EI}}\\ n_{\text{E}}{\overline{A}}^{\text{IE}}& n_{\text{I}}{\overline{A}}^{\text{II}}\end{array}\right],$$

w(t) represents Brownian motion, that is, a Wiener process, ν ∈ ℝ indicates the intensity of the Gaussian white noise dw(t), and [x]₊ ≜ [[x₁]₊, [x₂]₊]^T for x = [x₁, x₂]^T ∈ ℝ². Here, we assume that every entry of the matrices A and L of the mean dynamics given by Equations (24) and (25) (with $v_{\text{th}}^{\text{E}}=v_{\text{th}}^{\text{I}}=0$) is synchronously perturbed.

For the statement of the results in this section, we require some additional notation and definitions. Specifically, let (Ω, $ℱ$, 𝕇) be the probability space associated with Equation (70), where Ω denotes the sample space, $ℱ$ denotes a σ-algebra, and 𝕇 defines a probability measure on the σ-algebra $ℱ$, that is, 𝕇 is a nonnegative countably additive set function on $ℱ$ such that 𝕇(Ω) = 1 [90]. Note that Equation (70) is a Markov process, and hence, there exists a filtration {$ℱ$_t} satisfying $ℱ$_τ ⊂ $ℱ$_t ⊂ $ℱ$, 0 ≤ τ < t, such that {ω ∈ Ω: S(t) ∈ B} ∈ $ℱ$_t, t ≥ 0, for all Borel sets B ⊂ ℝ² contained in the Borel σ-algebra $ℬ$. Finally, spec(X) denotes the spectrum of the square matrix X including multiplicity and $ℛ$(Y) denotes the range space of the matrix Y.

When every component of the vector AS(t)(dt + νdw(t)), t ≥ 0, is nonnegative, the stochastic dynamical system given by Equation (70) can be written as

$$\text{d}S(t)=\tilde{A}S(t)\text{d}t+{\tilde{A}}_{\text{s}}S(t)\text{d}w(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S(0)=S_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(71)

where à ≜ A − L and Ã_s ≜ ν(A − L). The multiplicative white noise model given by Equation (71) can be regarded as a parameter uncertainty model where dw(t) corresponds to an uncertain parameter whose pattern and magnitude are given by Ã_s/‖Ã‖ and ‖Ã_s‖, respectively. Note that if rank(A − L) < 2, then every point α ∈ $𝒩$ (Ã) is an equilibrium point of Equation (71). With a slight abuse of notation, we use $ℰ$ to denote the equilibrium set of Equation (70) or Equation (71). First, motivated by the definition of stochastic Lyapunov stability in [90], we have the following definition of stochastic semistability. For the statement of the next result, define dist(x, $ℰ$) ≜ inf_y∈$ℰ$ ‖x − y‖. For a similar definition of stochastic semistability, see [91].

Definition 10 An equilibrium solution S(t) ≡ α ∈$ℰ$ of Equation (70) is stochastically semistable if the following statements hold.

• For every ε > 0, lim_S(0)→α 𝕇[sup_0≤t<∞ ‖S(t) − α‖ ≥ ε] = 0.
• lim_S(0)→$ℰ$ 𝕇 [lim_t→∞ dist(S(t), $ℰ$) = 0] = 1.

The dynamical system given by Equation (70) is stochastically semistable if every equilibrium solution of Equation (70) is stochastically semistable. Finally, the system given by Equation (70) is globally stochastically semistable if it is stochastically semistable and 𝕇[lim_t→∞ dist(S(t), $ℰ$) = 0] = 1 for every initial condition S(0) ∈ ℝ². If, alternatively, S(t) ≡ α ∈ $ℰ$ only satisfies i), then the equilibrium solution S(t) ≡ α ∈$ℰ$ of Equation (70) is stochastically Lyapunov stable.

Definition 10 is a stability notion for the stochastic dynamical system given by Equation (70) having a continuum of equilibria and is a generalization of the notion of semistability from deterministic dynamical systems [63,92] to stochastic dynamical systems. It is noted in [92] that existing methods for analyzing the stability of deterministic dynamical systems with isolated equilibria cannot be used for deterministic dynamical systems with nonisolated equilibria due to the connectedness property of equilibrium sets. Hence, Definition 10 is essential for analyzing the stability of stochastic dynamical systems with nonisolated equilibria. Note that (i) in Definition 10 implies stochastic Lyapunov stability of an equilibrium, whereas (ii) implies almost sure convergence of trajectories to the equilibrium manifold.

Next, we extend the notion of multistability for deterministic dynamical systems defined in Section 4 to that of stochastic multistability for stochastic dynamical systems.

Definition 11 Consider the dynamical system given by Equation (70) and let μ(·) denote the Lebesgue measure in ℝ². We say that the system given by Equation (70) is stochastically multistable if the following statements hold.

• $ℰ$\{(0, 0)} ≠ ∅.
• For every S(0) ∈ ℝ², there exists α(ω) ∈ $ℰ$, ω ∈ Ω, such that 𝕇 [lim_t→∞ S(t) = α(ω)] = 1.
• There exists a subset $ℳ$ ⊂ ℝ² satisfying μ($ℳ$) = 0 such that, for every S(0) ∈ ℝ²\$ℳ$, 𝕇[lim_t→∞ dist(S(t), $ℰ$) = 0] = 1.

Stochastic multistability is a global stability notion for the stochastic dynamical system given by Equation (70) having isolated equilibria and/or a continuum of equilibria, whereas stochastic semistability is a local stability notion for the stochastic dynamical system given by Equation (70) having a continuum of equilibria. Hence, stochastic multistability is a stronger notion than stochastic semistability. The next result states a relationship between stochastic multistability and global stochastic semistability.

Proposition 2 Consider the dynamical system given by Equation (70). If Equation (70) is globally stochastically semistable, then Equation (70) is stochastically multistable.

Proof. Suppose that the dynamical system given by Equation (70) is globally stochastically semistable. Then, by definition, 𝕇[lim_t→∞ dist(S(t), $ℰ$) = 0] = 1 for every initial condition S(0) ∈ ℝ². Next, we show that for every S(0) ∈ ℝ², there exists α = α(ω) ∈ $ℰ$, ω ∈ Ω, such that 𝕇[lim_t→∞ S(t) = α(ω)] = 1. Let

• Γ(S) ≜ {x ∈ ℝ² : there exists a divergent sequence ${\left\{t_i\right\}}_{i=1}^{\infty }$ such that $𝕇\left[\underset{i\to \infty }{\text{lim}}S(t_i)=x\right]=1$}

and $ℬ$_δ(z) ≜ {x ∈ ℝ² : ‖x − z‖ < δ}.

Suppose z ∈ Γ(S) is stochastically Lyapunov stable and let ε₁, ε₂ > 0. Since z is stochastically Lyapunov stable there exists an open neighborhood $ℬ$_δ(z), where δ = δ(ε₁, ε₂) > 0, such that, for every S(0) ∈ $ℬ$_δ(z), 𝕇[sup_t≥0 ‖S(t) − z‖ ≥ ε₁] < ε₂, and hence, 𝕇[sup_t≥0 ‖S(t) − z‖ < ε₁] ≥ 1 − ε₂. Now, since z ∈ Γ(S), it follows that there exists a divergent sequence ${\left\{t_i\right\}}_{i=1}^{\infty }$ in [0, ∞) such that 𝕇[lim_i→∞ S(t_i) = z] = 1, and hence, for every ε₃, ε₄ > 0, there exists k = k(ε₃) ≥ 1 such that 𝕇[sup_i≥k ‖S(t_i) − z‖ >ε₃] < ε₄ or, equivalently, 𝕇[sup_i≥k ‖S(t_i) − z‖ < ε₃] ≥ 1 − ε₄.

Next, note that 𝕇[sup_t≥tk ‖S(t) − z‖ < ε₁] ≥ 𝕇[sup_t≥0 ‖S(t) − z‖ < ε₁]. It now follows that

$$\begin{array}{c}𝕇\left[\underset{t\ge t_k}{\text{sup}}\Vert S(t)-z\Vert <{\epsilon }_1\right]\ge 𝕇\left[\underset{t\ge t_k}{\text{sup}}\Vert S(t)-z\Vert <{\epsilon }_1|\underset{i\ge k}{\text{sup}}\Vert S(t_i)-z\Vert <{\epsilon }_3\right]\\ \times 𝕇\left[\underset{i\ge k}{\text{sup}}\Vert S(t_i)-z\Vert <{\epsilon }_3\right]\\ \ge (1-{\epsilon }_2)(1-{\epsilon }_4),\end{array}$$

where 𝕇[·|·] denotes conditional probability. Since ε₁, ε₂, and ε₄ were chosen arbitrarily, it follows that 𝕇[z = lim_t→∞ S(t)] = 1. Thus, 𝕇[lim_n→∞ S(t_n) = z] = 1 for every divergent sequence ${\left\{t_n\right\}}_{n=1}^{\infty }$, and hence, Γ(S) = {z}; that is, for every S(0) ∈ ℝ², there exists α = α(ω) ∈$ℰ$, ω ∈ Ω, such that 𝕇[lim_t→∞ S(t) = α(ω)] = 1.

Next, recall from [93] that a matrix à ∈ ℝ^n×n is semistable if and only if lim_t→∞ e^Ãt exists. In other words, à is semistable if and only if for every λ ∈ spec(Ã), λ = 0 or Re λ < 0 and if λ = 0, then 0 is semisimple. Furthermore, if à is semistable, then the index of à is zero or one, and hence, à is group invertible. The group inverse Ã^# of à is a special case of the Drazin inverse Ã^D in the case where à has index zero or one [93]. In this case, lim_t→∞ e^Ãt = I_q − ÃÃ^# [93].

Proposition 3 If à is semistable, then, for sufficiently small |ν|, the dynamical system given by Equation (71) is globally stochastically semistable.

Proof. First, note that the solution to Equation (71) is given by

$$S(t)=e^{\tilde{A}t}S(0)+{\int }_0^t{e}^{\tilde{A}(t-s)}{\tilde{A}}_{\text{s}}S(s)\text{d}w(s),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0.$$

(72)

Since à is semistable, it follows that lim_t→∞ e^ÃtS(0) exists. In this case, let S_∞ = lim_t→∞ e^ÃtS(0). Furthermore, note that S_∞ = (I₂ − ÃÃ^#)S(0) ∈ $𝒩$ (Ã) [93], where Ã^# denotes the group inverse of Ã. Next, note that ${\int }_0^t{e}^{\tilde{A}(t-s)}{\tilde{A}}_{\text{s}}S(s)\text{d}w(s)$ is an Itô integral and let ‖·‖ denote the Euclidean norm on ℝ². Then, it follows from Property e) of Theorem 4.4.14 of ([90](p. 73)) that

$$\begin{array}{ll}𝔼\left[{\Vert {\int }_0^t{e}^{\tilde{A}(t-s)}{\tilde{A}}_{\text{s}}S(s)\text{d}w(s)\Vert }^2\right]\hfill & ={\int }_0^t𝔼\left[{\Vert e^{\tilde{A}(t-s)}{\tilde{A}}_{\text{s}}S(s)\Vert }^2\right]\hspace{0.17em}\text{d}s\hfill \\ \hfill & ={\nu }^2{\int }_0^t𝔼\left[{\Vert e^{\tilde{A}(t-s)}\tilde{A}S(s)\Vert }^2\right]\hspace{0.17em}\text{d}s\hfill \\ \hfill & ={\nu }^2{\int }_0^t𝔼\left[{\Vert \left(e^{\tilde{A}(t-s)}-\left(I_2-\tilde{A}{\tilde{A}}^{\#}\right)\right)\tilde{A}S(s)\Vert }^2\right]\hspace{0.17em}\text{d}s\hfill \\ \hfill & ={\nu }^2{\int }_0^t𝔼\left[{\Vert \left(e^{\tilde{A}(t-s)}-\left(I_2-\tilde{A}{\tilde{A}}^{\#}\right)\right)\tilde{A}\left(S(s)-S_{\infty }\right)\Vert }^2\right]\hspace{0.17em}\text{d}s,\hfill \end{array}$$

(73)

where 𝔼[ · ] denotes expectation with respect to the probability space (Ω, $ℱ$, 𝕇).

Next, define e(t) ≜ e^ÃtS(0) − (I₂ − ÃÃ^#)S(0) = e^ÃtS(0) − S_∞. Then it follows from the semistability of à that lim_t→∞ e(t) = 0. Since ė(t) = Ãe(t) for every t ≥ 0, it follows from the equivalence of (uniform) asymptotic stability and (uniform) exponential stability for linear time-invariant systems [94] that there exist real scalars σ, r > 0 such that ‖e(t)‖ ≤ σe^−rt ‖e(0)‖, t ≥ 0, or, equivalently, ‖[e^Ãt − (I₂ − ÃÃ^#)]S(0)‖ ≤ σe^−rt ‖ÃÃ^#S(0)‖, t ≥ 0. Hence,

$$\begin{array}{ll}{\Vert e^{\tilde{A}t}-\left(I_2-\tilde{A}{\tilde{A}}^{\#}\right)\Vert }^{\prime }\hfill & =\underset{S(0)\in {ℝ}^2\backslash \left\{0\right\}}{\text{max}}\frac{\Vert \left[e^{\tilde{A}t}-(I_2-\tilde{A}{\tilde{A}}^{\#})\right]S(0)\Vert }{\Vert S(0)\Vert }\hfill \\ \hfill & \le \sigma e^{-rt}\underset{S(0)\in {ℝ}^2\backslash \left\{0\right\}}{\text{max}}\frac{\Vert \tilde{A}{\tilde{A}}^{\#}S(0)\Vert }{\Vert S(0)\Vert }\hfill \\ \hfill & =\sigma e^{-rt}{\Vert \tilde{A}{\tilde{A}}^{\#}\Vert }^{\prime },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,\hfill \end{array}$$

(74)

where ‖·‖^′ =σ_max(·) and σ_max(·) denotes the maximum singular value. Thus, Equation (74) implies

$${\Vert e^{\tilde{A}t}-\left(I_2-\tilde{A}{\tilde{A}}^{\#}\right)\Vert }^{\prime }\le \rho e^{-rt},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(75)

where ρ ≜ σ‖ÃÃ^#‖.

Next, it follows from Equations (73) and (75) that

$${\int }_0^t𝔼\left[{\Vert e^{\tilde{A}(t-s)}{\tilde{A}}_{\text{s}}(s)S(s)\Vert }^2\right]\hspace{0.17em}\text{d}s\le {\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}{\int }_0^t{e}^{-2r(t-s)}𝔼\left[{\Vert S(s)-S_{\infty }\Vert }^2\right]\hspace{0.17em}\text{d}s,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0.$$

(76)

Now, it follows from Equations (72), (76), and the triangle inequality that

$$\begin{array}{ll}𝔼\left[{\Vert S(t)-S_{\infty }\Vert }^2\right]\hfill & \le {\Vert e^{\tilde{A}t}S(0)-S_{\infty }\Vert }^2+{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}{\int }_0^t{e}^{-2r(t-s)}𝔼\left[{\Vert S(s)-S_{\infty }\Vert }^2\right]\text{d}s\hfill \\ \hfill & \le {\Vert e^{\tilde{A}t}S(0)-S_{\infty }\Vert }^2+{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}{e}^{-2rt}{\int }_0^t{e}^{2rs}𝔼\left[{\Vert S(s)-S_{\infty }\Vert }^2\right]\text{d}s,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,\hfill \end{array}$$

and hence,

$$\begin{array}{c}{e}^{2rt}𝔼\left[{\Vert S(t)-S_{\infty }\Vert }^2\right]\le e^{2rt}{\Vert e^{\tilde{A}t}S(0)-S_{\infty }\Vert }^2+{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}\\ \times {\int }_0^t{e}^{2rs}𝔼\left[{\Vert S(s)-S_{\infty }\Vert }^2\right]\text{d}s,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0.\end{array}$$

Hence, it follows from the Gronwall-Bellman lemma ([20](p. 125)) that

$$\begin{array}{l}{e}^{2rt}𝔼\left[{\Vert S(t)-S_{\infty }\Vert }^2\right]\le e^{2rt}{\Vert e^{\tilde{A}t}S(0)-S_{\infty }\Vert }^2+{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}{\int }_0^t{e}^{2rs}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times {\Vert e^{\tilde{A}s}S(0)-S_{\infty }\Vert }^2{e}^{{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}(t-s)}\text{d}s,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,\end{array}$$

or, equivalently, for ν ≠ 0,

$$\begin{array}{ll}𝔼\left[{\Vert S(t)-S_{\infty }\Vert }^2\right]\hfill & \le {\Vert e^{\tilde{A}t}S(0)-S_{\infty }\Vert }^2+{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}{\int }_0^t{e}^{-2r(t-s)}{\Vert e^{\tilde{A}s}S(0)-S_{\infty }\Vert }^2{e}^{{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}(t-s)}\text{d}s\hfill \\ \hfill & \le {\Vert e^{\tilde{A}t}S(0)-S_{\infty }\Vert }^2+{\nu }^2{\rho }^4{\Vert \tilde{A}\Vert }^{\prime 2}{\Vert S(0)\Vert }^2{\int }_0^t{e}^{-2r}{e}^{{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}(t-s)}\text{d}s\hfill \\ \hfill & ={\Vert e^{\tilde{A}t}S(0)-S_{\infty }\Vert }^2+{\nu }^2{\rho }^4{\Vert \tilde{A}\Vert }^{\prime 2}{\Vert S(0)\Vert }^2{e}^{-\left(2r-{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}\right)t}{\int }_0^t{e}^{-{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}s}\text{d}s\hfill \\ \hfill & {\Vert e^{\tilde{A}t}S(0)-S_{\infty }\Vert }^2+{\rho }^2{\Vert S(0)\Vert }^2{e}^{-\left(2r-{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}\right)t}\left(1-e^{-{\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}t}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0.\hfill \end{array}$$

Taking |ν| to be such that

$${\nu }^2{\rho }^2{\Vert \tilde{A}\Vert }^{\prime 2}<2r,$$

(77)

it follows that lim_t→∞ e^{−(2r−ν2ρ2‖Ã‖′2)t} = 0. In this case, lim_t→∞ 𝔼[‖S(t) − S_∞‖²] = 0, that is, S(t), t ≥ 0, converges to S_∞ in the mean square.

Finally, by Theorem 7.6.10 of [95] or ([90](p. 187)) (Khasminskiy’s theorem), for every initial condition S(0) ∈ ℝ² and every ε > 0, we have

$$𝕇\left[\underset{0\le t<\infty }{\text{sup}}\Vert S(t)-S_{\infty }\Vert \ge \epsilon \right]\le \frac{1}{{\epsilon }^2}𝔼\left[{\Vert S(0)-S_{\infty }\Vert }^2\right]$$

and 𝕇[lim_t→∞ S(t) exists] = 1. Thus, the dynamical system given by Equation (71) is globally stochastically semistable.

Remark 1 If à is semistable, then there exists an invertible transformation matrix T ∈ ℝ^2×2 such that TÃT⁻¹ = diag[−λ, 0], where λ ∈ spec(Ã) and λ > 0. In this case, defining the new coordinates [Ŝ₁(t), Ŝ₂(t)]^T ≜ TS(t), Equation (71) yields the two decoupled stochastic differential equations given by

$$\text{d}{\widehat{S}}_1(t)=-\lambda {\widehat{S}}_1(t)\text{d}t-\nu \lambda {\widehat{S}}_1(t)\text{d}w(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{S}}_1(0)={\widehat{S}}_{10},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(78)

$$\text{d}{\widehat{S}}_2(t)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{S}}_2(0)={\widehat{S}}_{20}(0).$$

(79)

Since the analytical solution to Equation (78) is given by${\widehat{S}}_1(t)={\widehat{S}}_1(0)e^{-\lambda \left(1+\frac{1}{2}\lambda {\nu }^2\right)t-\nu \lambda w(t)}$, it follows that

$$S(t)=T^{-1}\widehat{S}(t)=T^{-1}\left[\begin{array}{l}{\widehat{S}}_1(0)e^{-\lambda \left(1+\frac{1}{2}\lambda {\nu }^2\right)t-\nu \lambda w(t)}\hfill \\ {\widehat{S}}_2(0)\hfill \end{array}\right].$$

Finally, we provide a sufficient condition for stochastic multistability for the dynamical system given by Equation (71). For this result, the following lemma is first needed.

Lemma 3 Let à ∈ ℝ^n×n. If there exist n × n matrices P = P^T ≥ 0 and R = R^T ≥ 0, and a nonnegative integer k such that

$$0={\left({\tilde{A}}^k\right)}^{\text{T}}\left({\tilde{A}}^{\text{T}}P+P\tilde{A}+R\right){\tilde{A}}^k,$$

(80)

$$k=\text{min}\left\{l\in {\overline{\mathbb{Z}}}_{+}:\underset{i=1}{\overset{n}{\cap }}𝒩\left(R{\tilde{A}}^{i+l-1}\right)=𝒩(\tilde{A})\right\},$$

(81)

then (i) $𝒩$ (PÃ^k) ⊆ $𝒩$ (Ã) ⊆ $𝒩$ (RÃ^k) and (ii) $𝒩$ (Ã) ∩ $ℛ$(Ã) = {0}.

Proof. The proof is similar to that of Lemma 4.5 of [96] and, hence, is omitted.

Theorem 7 Consider the dynamical system given by Equation (71). Suppose there exist 2 × 2 matrices P = P^T ≥ 0 and R = R^T ≥ 0, and a nonnegative integer k such that Equations (80) and (81) hold with n = 2. If $𝒩$ (A − L)\{(0, 0)} ≠ ∅ and |ν| is sufficiently small, then the dynamical system given by Equation (71) is stochastically multistable.

Proof. By Proposition 3 it suffices to show that à ≜ A − L is semistable. Consider the deterministic dynamical system given by

$$\dot{x}(t)=\tilde{A}x(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x(0)=x_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(82)

where x(t) ∈ ℝ². Note that à is semistable if and only if Equation (82) is semistable [93], and hence, it suffices to show that Equation (82) is semistable. Since, by Lemma 3, $𝒩$ (Ã) ∩ $ℛ$(Ã) = {0}, it follows from ([97](p. 119)) that à is group invertible. Thus, let L ≜ I₂ − ÃÃ^# and note that L² = L. Hence, L is the unique 2 × 2 matrix satisfying $𝒩$ (L) = $ℛ$(Ã), $ℛ$(L) = $𝒩$ (Ã), and Lx = x for all x ∈ $𝒩$ (Ã).

Next, consider the nonnegative function

$$𝕍(x)=x^{\text{T}}{\left({\tilde{A}}^k\right)}^{\text{T}}P{\tilde{A}}^{k}x+x^{\text{T}}{L}^{\text{T}}Lx.$$

If 𝕍(x) = 0 for some x ∈ ℝ², then PÃ^kx = 0 and Lx = 0. Now, it follows from Lemma 3 that x ∈ $𝒩$ (Ã), whereas Lx = 0 implies x ∈ $ℛ$(Ã), and hence, 𝕍(x) = 0 only if x = 0. Hence, 𝕍(·) is positive definite. Next, since LÃ = Ã − ÃÃ^# Ã = 0, it follows that the time derivative along the trajectories of Equation (82) is given by

$$\begin{array}{ll}\dot{𝕍}(x(t))\hfill & =-x^{\text{T}}(t){\left({\tilde{A}}^k\right)}^{\text{T}}R{\tilde{A}}^{k}x(t)+x^{\text{T}}(t){\tilde{A}}^{\text{T}}{L}^{\text{T}}Lx(t)+x^{\text{T}}(t)L^{\text{T}}L\tilde{A}x(t)\hfill \\ \hfill & =-x^{\text{T}}(t){\left({\tilde{A}}^k\right)}^{\text{T}}R{\tilde{A}}^{k}x(t)\hfill \\ \hfill & \le 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0.\hfill \end{array}$$

Note that 𝕍̇⁻¹(0) = $𝒩$ (RÃ^k).

To find the largest invariant set $ℳ$ contained in $𝒩$ (RÃ^k), consider a solution x(·) of Equation (82) such that RÃ^kx(t) = 0 for all t ≥ 0. Then, $R{\tilde{A}}^k\frac{{\text{d}}^{i-1}}{\text{d}{t}^{i-1}}x(t)=0$ for every i ∈ {1, 2,...} and t ≥ 0, that is, RÃ^kÃⁱ⁻¹x(t) = RÃ^k+i−1x(t) = 0 for every i ∈ {1, 2,...} and t ≥ 0. Equation (81) now implies that x(t) ∈ $𝒩$ (Ã) for all t ≥ 0. Thus, $ℳ$ ⊆ $𝒩$ (Ã). However, $𝒩$ (Ã) consists of only equilibrium points, and hence, is invariant. Hence, $ℳ$ = $𝒩$ (Ã).

Finally, let x_e ∈$𝒩$ (Ã) be an equilibrium point of Equation (82) and consider the Lyapunov function candidate 𝕌(x) = 𝕍(x − x_e), which is positive definite with respect to x_e. Then it follows that the Lyapunov derivative along the trajectories of Equation (82) is given by

$$\dot{𝕌}(x(t))=-{\left(x(t)-x_{\text{e}}\right)}^{\text{T}}{\left({\tilde{A}}^k\right)}^{\text{T}}R{\tilde{A}}^k\left(x(t)-x_{\text{e}}\right)\le 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0.$$

Thus, it follows that x_e is Lyapunov stable. Now, it follows from Theorem 3.1 of [63] that Equation (82) is semistable, that is, A is semistable. Finally, it follows from Proposition 3 that Equation (71) is stochastically multistable.

Example 5 In this example, we illustrate the stochastic multistability properties of the two-state nonlinear synaptic drive neuronal firing model given by Equation (70). Specifically, consider the mean field synaptic drive model given by Equation (70) with n_EĀ^EE = 1 V, n_IĀ^EI = −1 V, n_EĀ^IE = 1 V, n_IĀ^II = 0 V, and λ^E = 10 ms, and let λ^I vary. In this case, the system matrices in Equation (71) are given by

$$A=\left[\begin{array}{cc}1& -1\\ 1& 0\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}L=\left[\begin{array}{cc}0.1& 0\\ 0& \frac{1}{{\lambda }^{\text{I}}}\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}A-L=\left[\begin{array}{cc}0.9& -1\\ 1& -\frac{1}{{\lambda }^{\text{I}}}\end{array}\right].$$

Figure 9 shows the eigenvalues of A − L as a function of λ^I.

Note that for λ^I < 0.9 ms or λ^I > 0.93 ms, (A − L) is unstable, whereas for 0.9 ms < λ^I < 0.93 ms, (A − L) is asymptotically stable. Clearly, rank (A − L) < 2 for λ^I = 0.9 ms. Hence, it follows from Theorem 7 that the stochastic dynamical system given by Equation (71) exhibits multistability for λ^I = 0.9 ms. In this case, A − L is semistable and the $𝒩$ (A − L) is characterized by the direction vector [1, 0.9]^T.

For our simulation, we use the initial condition S(0) = [0.1, 0.5]^T. Figures 10 and 11 show the time response for the average excitatory and inhibitory synaptic drives, and the phase portrait for λ^I = 0.9 ms with ν = 0.2. Furthermore, for λ^I = 0.9 ms with ν = 0.2, Figure 12 shows a histogram of the limit points of log_e S^E (or, equivalently, log_e 0.9S^I) over 10, 000 samples. Note that the mean and variance of log_e S^E is −1.6135 and 0.3152, respectively. Similar plots shown in Figures 10 and 11 are shown for λ^I = 0.78 ms and λ^I = 1.20 ms with ν = 0.2 in Figures 13 and 16. Finally, Figures 17 and 18 show similar simulations for the case where λ^I = 0.9 ms (i.e., (A − L) is semistable) and ν = 1. However, note that in this case the condition given by Equation (77) of Proposition 3 is not satisfied, and hence, the model exhibits instability.

The trajectories of Equations (24) and (25) can exhibit unstable and multistable behaviors for different values of the parameters, which are similar to the simulation results for Equation (70). Moreover, its averaging dynamics will be analogous to the results of the deterministic model given in [98].

9. A Synaptic Drive Firing Model with Time-Varying Delays and Stochastic Multiplicative Uncertainty

In this section, we extend the synaptic drive model developed in Section 2 to investigate the conditions that would lead to synchronization or neutral oscillators. In particular, we extend the biological neural network model of Section 2 to include time-varying delays and stochastic input uncertainty. The system uncertainty model involves a Markov process wherein stochastic integration is interpreted in the sense of Itô.

For the statement of the results of this section, we require some additional notation and definitions. Specifically, $𝒞$([−τ, 0], ℝⁿ) with τ > 0 denotes a Banach space of continuous vector-valued functions mapping the interval [−τ, 0] into ℝⁿ with topology of uniform convergence and designated operator norm given by ‖|ψ‖| = sup_{−τ≤θ≤0} ‖ψ(θ)‖ for ψ ∈ $𝒞$([−τ, 0], ℝⁿ). Furthermore, let S_t ∈$𝒞$((−∞, +∞), ℝⁿ) defined by S_t(θ) ≜ S(t + θ), θ ∈ (−∞, 0], t ≥ 0, denote an (infinite dimensional) state at time t corresponding to the piece of trajectories S between −∞ and t, and assume v_thi(t) ≡ 0. To capture communication delays in our biological neural network model given by Equation (9), define S(t) ≜ [S₁(t), S₂(t),..., S_n(t)]^T, f(S) ≜ [f₁(S₁), f₂(S₂),..., f_n(S_n)]^T, where f_i(·) is defined by Equation (11) or Equation (12), $L\triangleq \text{diag}\left[\frac{1}{{\tau }_1},\frac{1}{{\tau }_2},\dots ,\frac{1}{{\tau }_n}\right]$, and B ≜ diag[B₁, B₂,..., B_n]. Furthermore, define

$$\begin{array}{l}\widehat{S}(t)\triangleq \left[\begin{array}{c}{\sum }_{j=2}^n{A}_{1j}{S}_j(t-{\delta }_{1j}(t))\\ 0\\ ⋮\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ {\sum }_{j=1,j\ne 2}^n{A}_{2j}{S}_j(t-{\delta }_{2j}(t))\\ ⋮\\ 0\end{array}\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\cdots +\left[\begin{array}{c}0\\ ⋮\\ 0\\ {\sum }_{j=1}^{n-1}{A}_{nj}{S}_j(t-{\delta }_{nj}(t))\end{array}\right],\end{array}$$

(83)

where δ_ij(t) denotes the continuous, time-varying time delay of the transmission signal from the jth neuron to the ith neuron at time t, δ_ij(t) ≥ 0, t ≥ 0, and S_j(t) denotes the jth component of S(t). The system delays δ_ij(t) correspond to the times of the spike hitting the synapse and t is the time after the spike, and hence, these delays account for the distance traveled by the voltage spikes down the axon.

We modify the biological neural network system given by Equation (9) to include the effects of stochastic perturbations as well as time delays. Specifically, we consider the model

$$\text{d}S(t)=\left(-LS(t)+Bf\left(\widehat{S}(t)\right)\right)\text{d}t+\sigma (S(t))\text{d}w(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S(\theta )=\varphi (\theta ),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\infty <\theta \le 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(84)

where ϕ(·) ∈ $𝒞$ ≜ $𝒞$((−∞, 0], ℝⁿ) is a continuous vector-valued function specifying the initial state of the system given by Equation (84)w(t) = [w₁(t), w₂(t),..., w_n(t)]^T captures noise in the input voltage and is represented by Brownian motion, that is, an n-dimensional mutually independent standard Wiener process, and σ(S) = diag[σ₁(S), σ₂(S),..., σ_n(S)] represents the state-dependent noise intensity matrix for the Gaussian white noise process dw(t). Henceforth, we consider Equation (84) as the model of the perturbed biological neural network.

Next, since Ŝ(t) defined by Equation (83) contains n(n−1) terms with different time delays, each term can be written as the product of an n × n-dimensional matrix and an n-dimensional vector. Specifically, for i′ 1, 2,..., n, j = 1, 2,..., n, i′ ≠ j, define i ≜ i′ (n−1) +j, i′ > j, and i ≜ i′(n−1) +j−1, i′ < j, where i = 1, 2,..., n(n − 1), define δ_i(t) ≜ δ_i′j (t), and define the matrix A_i ∈ ℝ^n×n whose (i′, j)th entry is A_i′j and all the other entries are 0. Thus, the ith term in Equation (83) can be replaced by A_iS(t − δ_i(t)), i ∈{1, 2,..., n(n − 1)}. Hence, setting N = n(n − 1), Ŝ(t) can be written as

$$\widehat{S}(t)=\sum _{i=1}^N{A}_{i}S(t-{\delta }_i(t)).$$

(85)

For the statement of the results in this section, we define the infinitesimal operator $ℒ$ :[0, ∞) × $𝒞$((−∞, 0], ℝⁿ) → ℝ associated with the stochastic process given by Equation (84), acting on the functional V : ℝ × $𝒞$ → ℝ, by

$$ℒV(t,S_t)\triangleq \underset{h\to 0^{+}}{\text{limsup}}\frac{𝔼\left[V(t+h,S_{t+h})|S_t\right]-V(t,S_t)}{h}.$$

(86)

For a two-times continuously differentiable function V :[0, ∞) × ℝⁿ → ℝ of the random variable S, the infinitesimal operator $ℒ$V (t, S) is defined as [90]

$$\begin{array}{lll}ℒV(t,S)\hfill & \triangleq \hfill & \underset{h\to 0^{+}}{\text{lim}}\frac{𝔼\left[V(t+h,S(t+h))\right]-V(t,S)}{h}\hfill \\ \hfill & =\hfill & \frac{\partial V(t,S)}{\partial t}+V^{\prime }(t,S)\left(-LS+Bf(\widehat{S})\right)+\frac{1}{2}{\sigma }^{\text{T}}(S)V^{″}(t,S)\sigma (S),\hfill \end{array}$$

(87)

where V′ (t, S) denotes the Fréchet derivative of V and V″ (t, S) denotes the Hessian matrix of V with respect to S at (t, S). The following lemma provides an explicit formula for the infinitesimal operator on two kinds of functionals using the ideas from Lemma 3.1 of [99].

Lemma 4 Consider the biological neural network given by Equation (84) and let

$$V_1(t,\psi )={\int }_{-d(t)}^0{\psi }^{\text{T}}(\theta )H\psi (\theta )\text{d}\theta ,$$

(88)

$$V_2(t,\psi )={\int }_{-d(t)}^0{\text{e}}^{\epsilon (t+\theta )}{\psi }^{\text{T}}(\theta )H\psi (\theta )\text{d}\theta ,$$

(89)

where t ≥ 0, ψ ∈ $𝒞$((−∞, 0], ℝⁿ), ε > 0, H ∈ ℝ^n×n, d : ℝ → ℝ is differentiable, and d(t) ≥ 0, t ≥ 0. Then, the infinitesimal operator acting on V₁ : [0, ∞) × $𝒞$ → ℝ and V₂ : [0, ∞) × $𝒞$ → ℝ are given by

$$ℒV_1(t,S_t)=S^{\text{T}}(t)HS(t)-(1-\dot{d}(t))S^{\text{T}}(t-d(t))HS(t-d(t)),$$

(90)

$$ℒV_2(t,S_t)={\text{e}}^{\epsilon t}{S}^{\text{T}}(t)HS(t)-{\text{e}}^{\epsilon (t-d(t))}(1-\dot{d}(t))S^{\text{T}}(t-d(t))HS(t-d(t)).$$

(91)

Proof. For sufficiently small h > 0,

$$\begin{array}{lll}𝔼\left[V_1(t+h,S_{t+h})|S_t\right]\hfill & =\hfill & 𝔼\left[{\int }_{-d(t+h)}^0{S}^{\text{T}}(t+h+\theta )HS(t+h+\theta )\text{d}\theta |S_t\right]\hfill \\ \hfill & =\hfill & 𝔼\left[{\int }_{h-d(t+h)}^h{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta |S_t\right]\hfill \\ \hfill & =\hfill & 𝔼\left[{\int }_0^h{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta |S_t\right]\hfill \\ \hfill & \hfill & +{\int }_{-d(t)}^0{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta \hfill \\ \hfill & \hfill & +𝔼\left[{\int }_{d(t+h)}^{-d(t)}{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta |S_t\right]\hfill \\ \hfill & \hfill & +𝔼\left[{\int }_{h-d(t+h)}^{-d(t+h)}{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta |S_t\right]\hfill \\ \hfill & =\hfill & 𝔼\left[{\int }_0^h{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta |S_t\right]\hfill \\ \hfill & \hfill & +{\int }_{-d(t)}^0{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta \hfill \\ \hfill & \hfill & -𝔼\left[{\int }_{-d(t)}^{-\left(d(t)+h\dot{d}(t)+O(h)\right)}{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta |S_t\right]\hfill \\ \hfill & \hfill & -𝔼\left[{\int }_{-d(t+h)}^{-h-d(t+h)}{S}^{\text{T}}(t+\theta )HS(t+\theta )\text{d}\theta |S_t\right]\hfill \\ \hfill & =\hfill & h{S}^{\text{T}}(t)HS(t)+V_1(t,S_t)\hfill \\ \hfill & \hfill & -h\left(1-\dot{d}(t)\right)S^{\text{T}}(t-d(t))HS(t-d(t))+O(h),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,\hfill \end{array}$$

(92)

where O(h) denotes higher-order terms in h. Substituting Equation (92) into Equation (86) yields Equation (90). The proof of Equation (91) is similar to the proof of Equation (90) and, hence, is omitted.

To develop a global synchronization property for the biological neural network system given by Equation (84), we introduce the notion of stochastic synchronization. Here, we focus on mean-square synchronization.

Definition 12 The biological neural network given by Equation (84) is said to be globally asymptotically mean-square synchronized if

$$\underset{t\to \infty }{\text{lim}}𝔼\left[{\left|\Vert S_{it}-S_{jt}\Vert \right|}^2\right]=0$$

(93)

for all ϕ(·) ∈ $𝒞$((−∞, 0], ℝⁿ) and i, j = 1, 2,..., n, i ≠ j, where S_it ≜ S_i(t + θ), θ ∈ (−∞, 0], t ≥ 0, and ‖|S_it − S_jt‖| = sup_{−τ≤θ≤0} |S_i(t + θ) − S_j(t + θ)|, τ > 0.

Definition 13 The biological neural network given by Equation (84) is said to be globally exponentially mean-square synchronized if there exist constants ρ > 0 and p > 0 such that

$$𝔼\left[{\left|\Vert S_{it}-S_{jt}\Vert \right|}^2\right]\le \rho e^{-pt}{\int }_{-\infty }^0{\left|{\varphi }_i(\theta )-{\varphi }_j(\theta )\right|}^2\text{d}\theta ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}p>0,$$

(94)

for all ϕ(·) = [ϕ₁(·),..., ϕ_n(·)]^T ∈ $𝒞$((−∞, 0], ℝⁿ) and i, j = 1, 2,..., n, i ≠ j.

10. Synchronization of Stochastic Biological Neural Networks

In this section, we develop sufficient conditions for global mean-square synchronization for the biological neural network given by Equation (84) with differentiable time delays using Barbalat’s lemma and linear matrix inequalities (LMIs). Here, we assume that the noise intensity matrix function σ(S) has a linear growth rate; that is, there exists r > 0 such that

$$\text{tr}[{\sigma }^2(S)]\le r{S}^{\text{T}}{M}^{\text{T}}MS,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {ℝ}^n,$$

(95)

where M is defined in Equation (60).

The following theorem provides sufficient conditions for global mean-square asymptotic synchronization of the biological neural network system given by Equation (84).

Theorem 8 Consider the biological neural network given by Equation (84) with f_i(·), i = 1, 2,..., n, given by either Equation (11) or Equation (12), and assume that δ̇_i(t) ≤ h₁ < 1, and δ_i(t) ≥ 0, t ≥ 0, i = 1, 2,..., N, hold. If there exist a positive-definite matrix P ∈ ℝ^n×n, nonnegative definite matrices Q_i ∈ ℝ^n×n, i = 1, 2,..., N, and R ∈ ℝ^n×n, and a nonnegative-definite diagonal matrix Λ ∈ ℝ^n×n such that

$$\left[\begin{array}{cc}R& -PB\\ -BP& \Lambda \end{array}\right]\ge 0,$$

(96)

$${\Omega }_7\triangleq \left[\begin{array}{cccc}-(1-h_1)Q_1+A_1^{\text{T}}\Lambda A_1& A_1^{\text{T}}\Lambda A_2& \cdots & A_1^{\text{T}}\Lambda A_N\\ A_2^{\text{T}}\Lambda A_1& -(1-h_1)Q_2+A_2^{\text{T}}\Lambda A_2& \ddots & ⋮\\ ⋮& \ddots & \ddots & A_{N-1}^{\text{T}}\Lambda A_N\\ A_N^{\text{T}}\lambda A_1& \cdots & A_N^{\text{T}}\Lambda A_{N-1}& -(1-h_1)Q_N+A_N^{\text{T}}\Lambda A_N\end{array}\right]\le 0,$$

(97)

and either Ω₈ < 0 or both Ω₈ ≤ 0 and $𝒩$ (Ω₈) = span(e_n) hold, where

$${\Omega }_8\triangleq -PL-LP+k_{1}r{M}^{\text{T}}M+R+\sum _{i=1}^N{Q}_i,$$

(98)

k₁ ≜ λ_max(P), r is such that Equation (95) holds, M is given by Equation (60), and A_i, i = 1,..., N, is defined in Equation (85), then Equation (84) is globally asymptotically mean-square synchronized.

Proof. Consider the functional V : [0, ∞) × $𝒞$ → ℝ given by V (t, ψ) = V₁(ψ(0)) + V₂(t, ψ), where V₁(ψ(0)) = ψ^T(0)Pψ(0) and $V_2(t,\psi )={\sum }_{i=1}^N{\int }_{-{\delta }_i(t)}^0{\psi }^{\text{T}}(\theta )Q_i\psi (\theta )\text{d}\theta$. It follows from Equation (87) and Lemma 4 that the infinitesimal operator $ℒ$V (t, S_t) associated with the stochastic process given by Equation (84) is given by

$$ℒV(t,S_t)=ℒV_1(S(t))+ℒV_2(t,S_t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(99)

where

$$ℒV_1(S(t))=2S^{\text{T}}(t)P\left(-LS(t)+Bf(\widehat{S}(t))\right)+\text{tr}\left[\sigma (S(t))P\sigma (S(t))\right],$$

(100)

$$ℒV_2(t,S_t)=\sum _{i=1}^N\left[S^{\text{T}}(t)Q_{i}S(t)-\left(1-{\dot{\delta }}_i(t)\right)S^{\text{T}}(t-{\delta }_i(t))Q_{i}S(t-{\delta }_i(t))\right],$$

(101)

and Ŝ(t) ∈ ℝⁿ is defined by Equation (85). Next, since $𝔼[V(t,S_t)]=V(0,S_0)+𝔼\left[{\int }_0^tℒV(u,S_u)\text{d}u\right]$, it follows that 𝔼[dV (t, S_t)] = 𝔼[$ℒ$V₁(S(t)) + $ℒ$V₂(t, S_t)] dt.

To complete the proof, we show that $ℒ$V₁(S(t)) + $ℒ$V₂(t, S_t) ≤ 0, t ≥ 0, and $ℒ$V₁(S(t)) + $ℒ$V₂(t, S_t) ≡ 0 implies MS(t) ≡ 0. To see this, note that Equation (95) implies

$$\text{tr}\left[\sigma (S)P\sigma (S)\right]\le k_1\text{tr}[\sigma (S)\sigma (S)]\le k_{1}r{S}^{\text{T}}{M}^{\text{T}}MS,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\in {ℝ}^n.$$

(102)

Furthermore, note that for every diagonal matrix Λ ∈ ℝ^n×n such that Λ ≥ 0, it follows that for f_i(·), i = 1,..., n, given by Equation (11) or Equation (12),

$$f^{\text{T}}\left(\widehat{S}(t)\Lambda f\left(\widehat{S}(t)\right)\right)\le {\widehat{S}}^{\text{T}}(t)\Lambda \widehat{S}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0.$$

(103)

Now, using Equations (96), (102), and (103), it follows from Equation (100) that

$$\begin{array}{lll}ℒV_1(S(t))\hfill & \le \hfill & 2S^{\text{T}}(t)P\left(-LS(t)+Bf\left(\widehat{S}(t)\right)\right)+k_{1}r{S}^{\text{T}}(t)M^{\text{T}}MS(t)\hfill \\ \hfill & \le \hfill & -2S^{\text{T}}(t)PLS(t)+S^{\text{T}}(t)RS(t)+f^{\text{T}}\left(\widehat{S}(t)\right)\Lambda \widehat{f}(S(t))+k_{1}r{S}^{\text{T}}(t)M^{\text{T}}MS(t)\hfill \\ \hfill & \le \hfill & S^{\text{T}}(t)\left(-2PL+k_{1}r{M}^{\text{T}}M+R\right)S(t)+{\widehat{S}}^{\text{T}}(t)\Lambda \widehat{S}(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0.\hfill \end{array}$$

(104)

Hence, since δ̇_i(t) ≤ h₁ < 1, t > 0, it follows from Equations (101) and (104) that

$$\begin{array}{ccc}ℒV_1\left(S(t)\right)+ℒV_2(t,S_t)& \le & S^{\text{T}}(t)\left[-2PL+k_{1}r{M}^{\text{T}}M+R+\sum _{i=1}^N{Q}_i\right]\hspace{0.17em}S(t)\\ & & +\sum _{i=1}^N\sum _{j=1}^N{S}^{\text{T}}(t-{\delta }_i(t))A_i^{\text{T}}\Lambda A_{j}S(t-{\delta }_j(t))\\ & & -\sum _{i=1}^N(1-h_1)S^{\text{T}}(t-{\delta }_i(t))Q_{i}S(t-{\delta }_i(t))\\ & =& {\eta }^{\text{T}}(t){\Omega }_7\eta (t)+S^{\text{T}}(t){\Omega }_{8}S(t)\\ & \le & S^{\text{T}}(t){\Omega }_{8}S(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,\end{array}$$

where η(t) ≜ [S^T(t − δ₁(t)),..., S^T(t − δ_N (t))]^T.

Finally, if Ω₇ ≤ 0 and Ω₈ < 0, it follows that 𝔼[dV (t, S_t)] = 𝔼[$ℒ$V₁(S(t)) + $ℒ$V₂(t, S_t)]dt ≤ 0, t ≥ 0, and 𝔼[V (t, S_t)] ≤ 𝔼[V (0, S₀)]. Note that since P is positive definite and 𝔼[V (t, S_t)] is a non-increasing function of time, it follows that 𝔼[‖S(t)‖²] is bounded for all t ≥ 0. Since $ℒ$[S^T(t)Ω₈S(t)] = 2S^T(t)Ω₈[−LS(t)+ Bf(Ŝ(t))] + tr[σ(S(t))Ω₈σ(S(t))], t ≥ 0, and 𝔼[‖S(t)‖²], t ≥ 0, is bounded, it follows that 𝔼[$ℒ$[S^T(t)Ω₂S(t)]], t ≥ 0, is bounded. Since 𝔼 [d[S^T(t)Ω₂S(t)]] = 𝔼[$ℒ$[S^T(t)Ω₈S(t)]] dt, t ≥ 0, and 𝔼[$ℒ$[S^T(t)Ω₈S(t)]] is bounded, it follows that 𝔼[S^T(t)Ω₈S(t)] is uniformly continuous in t. Note that since 𝔼[V (t, S_t)] ≥ 0, t ≥ 0, and 𝔼[S^T(t)Ω₈S(t)] is uniformly continuous in t, it follows from Barbalat’s lemma ([20](p. 221)) that 𝔼[S^T(t)Ω₈S(t)] → 0 as t →∞. Since Ω₈ < 0, it follows that 𝔼[‖S(t)‖²] → 0 as t →∞. Thus, 𝔼[‖MS(t)‖²] ≤ ‖M‖²𝔼[‖S(t)‖²] → 0 as t → ∞. Hence, 𝔼[‖|MS_t‖|²] → 0 as t → ∞, that is, Equation (84) is globally asymptotically mean-square synchronized.

Alternately, if Ω₇ ≤ 0, $𝒩$ (Ω₈) = span(e_n), and Ω₈ ≤ 0, then a similar argument shows that 𝔼[S^T(t)Ω₈S(t)] → 0 as t →∞, which, since $𝒩$ (Ω₈) = span(e_n), implies that Equation (84) is globally asymptotically mean-square synchronized.

The next theorem establishes a sufficient condition for global exponential mean-square synchronization of the network system given by Equation (84).

Theorem 9 Consider the biological neural network given by Equation (84) with f_i(·), i = 1, 2,..., n, given by either Equation (11) or Equation (12), and assume that δ̇_i(t) ≤ h₁ < 1, and h₂ ≥ δ_i(t) ≥ 0, t ≥ 0, i = 1, 2,...,N, hold. If there exist a positive-definite matrix P ∈ ℝ^n×n, nonnegative definite matrices Q_i ∈ ℝ^n×n, i = 1, 2,...,N, and R ∈ ℝ^n×n, a nonnegative-definite diagonal matrix Λ ∈ ℝ^n×n, and a scalar ε> 0 such that Equation (96) holds,

$$\begin{array}{c}{\Omega }_9\triangleq [\begin{array}{cc}-(1-h_1)e^{-2\epsilon h_2}{Q}_1+A_1^{\text{T}}\Lambda A_1& A_1^{\text{T}}\Lambda A_2\\ A_2^{\text{T}}\Lambda A_1& -(1-h_1)e^{-2\epsilon h_2}{Q}_2+A_2^{\text{T}}\Lambda A_2\\ ⋮& \ddots \\ A_N^{\text{T}}\Lambda A_1& \cdots \end{array}\\ \begin{array}{cc}\cdots & A_1^{\text{T}}\Lambda A_N\\ \ddots & ⋮\\ \ddots & A_{N-1}^{\text{T}}\Lambda A_N\\ \cdots & -(1-h_1)e^{-2\epsilon h_2}{Q}_N+A_N^{\text{T}}\Lambda A_N\end{array}]\le 0,\end{array}$$

(105)

and either Ω₁₀ < 0 or both Ω₁₀ ≤ 0 and $𝒩$ (Ω₁₀) = span(e_n) hold, where

$${\Omega }_{10}\triangleq -PL-LP+k_{1}r{M}^{\text{T}}M+R+\sum _{i=1}^N{Q}_i+2\epsilon P,$$

(106)

k₁ ≜ λ_max(P), r is such that Equation (95) holds, M is given by Equation (60), and A_i, i = 1,...,N, is defined in Equation (85), then Equation (84) is globally exponentially mean-square synchronized.

Proof. The proof is similar to the proof of Theorem 8 using the functional V :[0, ∞) ×$𝒞$ → ℝ given by

$$V(t,\psi )=e^{2\omega t}{\psi }^{\text{T}}(0)P\psi (0)+\sum _{i=1}^N{\int }_{-{\delta }_i(t)}^0{e}^{2\epsilon (t+\theta )}{\psi }^{\text{T}}(\theta )Q_i\psi (\theta )\text{d}\theta$$

and, hence, is omitted.

The following corollary to Theorem 9 is immediate.

Corollary 1 Consider the biological neural network given by Equation (84) with f_i(·), i = 1, 2,..., n, given by either Equation (11) or Equation (12), and assume that δ̇_i(t) ≤ h₁ < 1, and h₂ ≥ δ_i(t) ≥ 0, t ≥ 0, i = 1, 2,...,N, hold. If there exist a positive-definite matrix P ∈ ℝ^n×n, nonnegative definite matrices Q_i ∈ ℝ^n×n, i = 1, 2,...,N, and R ∈ ℝ^n×n, and a nonnegative-definite diagonal matrix Λ ∈ ℝ^n×n such that Equation (96) holds, and Ω₇ < 0 and Ω₈ < 0, where Ω₇ and Ω₈ are given by Equations (97) and (98) with k₁ ≜ λ_max(P), r is such that Equation (95) holds, M is given by Equation (60), A_i, i = 1,...,N, is defined in Equation (85), then Equation (84) is globally exponentially mean-square synchronized.

Proof. The result is a direct consequence of Theorem 9 by noting that if Ω₇ < 0 and Ω₈ < 0 hold, then there exists a sufficiently small ε> 0 such that Ω₉ ≤ 0 and Ω₁₀ < 0 hold, where Ω₉ and Ω₁₀ are given by Equations (105) and (106).

Remark 2 Note that Theorem 8 does not require that the time delays be bounded, whereas Theorem 9 and Corollary 1 hold for the case where the time delays are bounded.

Remark 3 It is important to note that if f_i(·), i = 1, 2,..., n, in Equation (84) is replaced by Equation (10), then the results of Theorems 8 and 9 as well as Corollary 1 still hold.

Example 6 Consider the stochastic network system characterized by

$$\begin{array}{lll}\text{d}{S}_1(t)\hfill & =\hfill & \left(-S_1(t)+0.2f_1(0.3S_2(t-{\delta }_1(t))-0.5S_3(t-{\delta }_2(t)))\right)\text{d}t\hfill \\ \hfill & \hfill & +0.1\left(S_1(t)-S_2(t)\right)\text{d}{w}_1(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_1(\theta )=2+\text{sin}\theta ,\hfill \end{array}$$

(107)

$$\begin{array}{lll}\text{d}{S}_2(t)\hfill & =\hfill & \left(-1.1S_2(t)+0.3f_2(0.4S_1(t-{\delta }_3(t))-0.3S_3(t-{\delta }_4(t)))\right)\text{d}t\hfill \\ \hfill & \hfill & +0.1\left(S_2(t)-S_3(t)\right)\text{d}{w}_2(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_2(\theta )=-3+\text{cos}\theta ,\hfill \end{array}$$

(108)

$$\begin{array}{lll}\text{d}{S}_3(t)\hfill & =\hfill & \left(-1.4S_3(t)+0.5f_3(0.4S_1(t-{\delta }_5(t))+0.3S_2(t-{\delta }_6(t)))\right)\text{d}t\hfill \\ \hfill & \hfill & +0.1\left(S_3(t)-S_1(t)\right)\text{d}{w}_3(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_3(\theta )=1-\theta ,\hfill \end{array}$$

(109)

where θ ∈ [−1, 0], δ₁(t) = 1 + 0.1 sin t, δ₂(t) = 1 + 0.1t, δ₃(t) = 0.5, δ₄(t) = 0.1t, δ₅(t) = 0.3, δ₆(t) = 0.4, t ≥ 0, f_i(·), i = 1, 2, 3, are defined by either Equation (11) or Equation (12), and dw_i, i = 1, 2, 3, are standard Gaussian white noise processes.

Using the MATLAB LMI Toolbox^®, it can be shown that

$$\begin{array}{ccc}P=\left[\begin{array}{ccc}205& -2.69& 0.13\\ -2.69& 169& -1.96\\ 0.13& -1.96& 122\end{array}\right],& R=\left[\begin{array}{ccc}101& -1.85& 0.12\\ -1.85& 107& -2.00\\ 0.12& -2.00& 118\end{array}\right],& \Lambda =\left[\begin{array}{ccc}81.2& 0& 0\\ 0& 114& 0\\ 0& 0& 114\end{array}\right],\end{array}$$

$$\begin{array}{ccc}{Q}_1=\left[\begin{array}{ccc}34.3& 0.37& 0.02\\ 0.37& 49.7& 0.49\\ 0.02& 0.49& 25.8\end{array}\right],& Q_2=\left[\begin{array}{ccc}34.3& 0.33& 0.02\\ 0.33& 30.7& 0.52\\ 0.02& 0.52& 54.0\end{array}\right],& Q_3=\left[\begin{array}{ccc}66.3& 0.37& 0.03\\ 0.37& 30.7& 0.46\\ 0.03& 0.46& 25.8\end{array}\right],\end{array}$$

$$\begin{array}{ccc}{Q}_4=\left[\begin{array}{ccc}34.3& 0.33& 0.02\\ 0.3& 30.7& 0.52\\ 0.02& 0.52& 45.9\end{array}\right],& Q_5=\left[\begin{array}{ccc}76.9& 0.38& 0.03\\ 0.38& 30.7& 0.46\\ 0.03& 0.46& 25.8\end{array}\right],& Q_6=\left[\begin{array}{ccc}34.3& 0.39& 0.02\\ 0.39& 60.8& 0.52\\ 0.02& 0.52& 25.8\end{array}\right],\end{array}$$

satisfy Equations (96)–(98), with r = 0.03 and A_i, i ∈ 1, 2,..., 6, defined as in Equation (85), and hence, the conditions of Theorem 8 are satisfied. Next, define the synchronization error$e(t)\triangleq {\left[{\left(S_1(t)-S_2(t)\right)}^2+{\left(S_2(t)-S_3(t)\right)}^2\right]}^{\frac{1}{2}}$. The trajectories of the state variables and the synchronization error with respect to time are shown in Figures 19 and 20, respectively. Note that even though some of the delays in this example are not bounded, that is, δ_i(t) → ∞ as t → ∞ for i ∈{2, 4}, the system is globally mean-square asymptotically synchronized.

11. Thermodynamics, Neuroscience, Consciousness, and the Entropic Arrow of Time

In this and the next section, we present some qualitative insights from the fields of thermodynamics and electromagnetic field theory that can potentially be useful in developing mechanistic models [100] that can explain the underlying mechanisms of action for general anesthesia and consciousness. Specifically, by merging the two universalisms of thermodynamics and dynamical systems theory with neuroscience, one can provide key insights into the theoretical foundation for understanding the network properties of the brain by rigorously addressing large-scale interconnected biological neuronal network models that govern the neuroelectric behavior of biological excitatory and inhibitory neuronal networks. In addition, electrical signals in the brain can generate electromagnetic fields that can cause a shielding effect between the thalamus and frontal cortex, which in turn can lead to the emergence of unconsciousness. Both these paradigms are the subject of ongoing research.

In current clinical practice of general anesthesia, potent drugs are administered which profoundly influence levels of consciousness and vital respiratory (ventilation and oxygenation) and cardiovascular (heart rate, blood pressure, and cardiac output) functions. These variation patterns of the physiologic parameters (i.e., ventilation, oxygenation, heart rate variability, blood pressure, and cardiac output) and their alteration with levels of consciousness can provide scale-invariant fractal temporal structures to characterize the degree of consciousness [101] in sedated patients. Here, we hypothesize that the degree of consciousness reflects the adaptability of the central nervous system and is proportional to the maximum work output under a fully conscious state divided by the work output of a given anesthetized state. A reduction in maximum work output (and cerebral oxygen consumption) or elevation in the anesthetized work output (or cerebral oxygen consumption) will thus reduce the degree of consciousness. Hence, the fractal nature (i.e., complexity) of conscious variability is a self-organizing emergent property of the large-scale interconnected biological neuronal network since it enables the central nervous system to maximize entropy production and dissipate energy gradients. Within the context of aging and complexity in acute illnesses, variation of physiologic parameters and their relationship to system complexity and system thermodynamics have been explored in [102–107].

Complex dynamical systems involving self-organizing components forming spatio-temporal evolving structures that exhibit a hierarchy of emergent system properties form the underpinning of the central nervous system. These complex dynamical systems are ubiquitous in nature and are not limited to the central nervous system. Such systems include, for example, biological systems, immune systems, ecological systems, quantum particle systems, chemical reaction systems, economic systems, cellular systems, and galaxies, to cite but a few examples. The connection between the local subsystem interactions and the globally complex system behavior is often elusive. These systems are known as dissipative systems [108,109] and consume energy and matter while maintaining their stable structure by dissipating entropy to the environment.

In the central nervous system billions of neurons interact to form self-organizing dissipative nonequilibrium structures [108–110]. The fundamental common phenomenon among these systems are that they evolve in accordance to the laws of (nonequilibrium) thermodynamics, which are among the most firmly established laws of nature. System thermodynamics, in the sense of [110], involves open interconnected dynamical systems that exchange matter and energy with their environment in accordance with the first law (conservation of energy) and the second law (nonconservation of entropy) of thermodynamics. Self-organization can spontaneously occur in such systems by invoking the two fundamental axioms of the science of heat. Namely, (i) if the energies in the connected subsystems of an interconnected system are equal, then energy exchange between these subsystems is not possible, and (ii) energy flows from more energetic subsystems to less energetic subsystems. These axioms establish the existence of a system entropy function as well as equipartition of energy [110–112] in system thermodynamics and synchronization [73] in neuronal networks; an emergent behavior in thermodynamic systems as well as neuroscience. Hence, in complex interconnected dynamical systems, self-organization is not a property of the systems parts but rather emerges as a result of the nonlinear subsystem interactions.

In recent research the authors in [110–114] combined the two universalisms of thermodynamics and dynamical systems theory under a single umbrella to develop a dynamical system formalism for classical thermodynamics so as to harmonize it with classical mechanics. While it seems impossible to reduce thermodynamics to a mechanistic world picture due to microscopic reversibility and Poincaré recurrence [110,115], the system thermodynamic formulation in [110,112] provides a harmonization of classical thermodynamics with classical mechanics. In particular, our dynamical system formalism captures all of the key aspects of thermodynamics, including its fundamental laws, while providing a mathematically rigorous formulation for thermodynamical systems out of equilibrium by unifying the theory of heat transfer with that of classical thermodynamics. In addition, the concept of entropy for a nonequilibrium state of a dynamical process is defined, and its global existence and uniqueness is established. This state space formalism of thermodynamics shows that the behavior of heat, as described by the conservation equations of thermal transport and as described by classical thermodynamics, can be derived from the same basic principles and is part of the same scientific discipline. Connections between irreversibility, the second law of thermodynamics, and the entropic arrow of time are also established in [110,112,113].

Building on the results of this paper, we propose to merge system thermodynamics with neuroscience to develop a theoretical foundation for the mechanisms of action of general anesthesia using the network properties of the brain by rigorously addressing the large-scale interconnected biological neuronal network model given by Equations (7) and (8). Even though simplified mean field models of the form given by Equations (24) and (25) have been extensively used in mathematical neuroscience literature to describe large neural populations, the complex large-scale interconnected system given by Equations (7) and (8) is essential in indentifying the mechanisms of action for general anesthesia. We postulate that unconsciousness is associated with reduced physiologic parameter variability, reflecting the inability of the central nervous system to adapt. The degree of consciousness is a function of the numerous coupling in the network properties of the brain that form a complex large-scale, interconnected system. Complexity here refers to the quality of a system wherein interacting subsystems self-organize to form hierarchical evolving structures exhibiting emergent system properties, and hence, a complex dynamical system is a system that is greater than the sum of its subsystems or parts. This complex system—involving numerous nonlinear dynamical subsystem interactions making up the system—has inherent emergent properties that depend on the integrity of the entire dynamical system and not merely a mean field simplified reduced-order model.

As in thermodynamics, neuroscience is a theory of large-scale systems wherein graph theory [116] can be used in capturing the (possibly dynamic) connectivity properties of network interconnections, with neurons represented by nodes, synapses represented by edges or arcs, and synaptic efficacy captured by edge weighting giving rise to a weighted adjacency matrix governing the underlying directed dynamic graph network topology. However, unlike thermodynamics, wherein energy spontaneously flows from a state of higher temperature to a state of lower temperature, neuron membrane potential variations occur due to ion species exchanges which evolve from regions of higher chemical potentials to regions of lower chemical potentials (i.e., Gibbs’ chemical potential [114]). And this evolution does not occur spontaneously but rather requires a hierarchical (i.e., hybrid) continuous-discrete architecture for the opening and closing of specific gates within specific ion channels.

Merging our proposed dynamical neuroscience framework developed in Sections 2 and 3 with system thermodynamics [110,112,114] by embedding thermodynamic state notions (i.e., entropy, energy, free energy, chemical potential, etc.) within our dynamical system framework can allow us to directly address the otherwise mathematically complex and computationally prohibitive large-scale dynamical model given by Equations (7) and (8). In particular, a thermodynamically consistent neuroscience model would emulate the clinically observed self-organizing, spatio-temporal fractal structures that optimally dissipate energy and optimize entropy production in thalamocortical circuits of fully conscious patients. This thermodynamically consistent neuroscience framework can provide the necessary tools involving multistability, synaptic drive equipartitioning (i.e., synchronization across time scales), energy dispersal, and entropy production for connecting biophysical findings to psychophysical phenomena for general anesthesia. In particular, we hypothsize that as the model dynamics transition to an anesthetized state, the system will involve a reduction in system complexity—defined as a reduction in the degree of irregularity across time scales—exhibiting partial synchronization of neural oscillators (i.e., thermodynamic energy equipartitioning). This would result in a decrease in system energy consumption (myocardial depression, respiratory depression, hypoxia, ischemia, hypothension, venodialtion), and hence, a decrease in the rate of entropy production. In other words, unconsciousness is characterized by system decomplexification, which is manifested in the failure to develop efficient mechanisms to dissipate energy thereby pathologically retaining higher internal (or local) entropy levels.

The human brain is isothermal and isobaric, that is, the temperatures of the subnetworks of the brain are equal and remain constant, and the pressure in each subnetwork also remains constant. The human brain network is also constantly supplied with a source of (Gibbs) free energy provided by chemical nourishment of the blood to ensure adequate cerebral blood flow and oxygenation, which involves a blood concentration of oxygen to ensure proper brain function. Information-gathering channels of the blood also serve as a constant source of free energy for the brain. If these sources of free energy are degraded, then internal (local) entropy is produced.

In the transition to an anesthetic state, complex physiologic work cycles (cardiac respiratory pressure-volume loops, mithochondrial ATP production) necessary for homeostasis follow regressive diffusion and chemical reaction paths that degrade energy production and decrease the rate of entropy production. Hence, in an isolated large-scale network (i.e., a network with no energy exchange between the internal and external environment) all the energy, though always conserved, will eventually be degraded to the point where it cannot produce any useful work (oxygenation, ventilation, heart rate stability, organ function). Hence, all motion would cease leading the brain network to a state of unconsciousness (semistability) wherein all or partial [117] subnetworks will possess identical energies (energy equipartition or synchronization) and, hence, internal entropy will approach a local maximum or, more precisely, a saddle surface in the state space of the process state variables. Thus, the transition to a state of anesthetic unconsciousness involves an evolution from an initial state of high (external) entropy production (consciousness) to a temporary saddle state characterized by a series of fluctuations corresponding to a state of significantly reduced (external) entropy production (unconsciousness).

In contrast, in a healthy conscious human entropy dissipation occurs spontaneously and, in accordance with Jaynes’ maximum entropy production principle [86,118], energy dispersal is optimal leading to a maximum entropy production rate. Hence, low entropy in (healthy) human brain networks is synonymous with consciousness and the creation of order (negative entropy) reflects a rich fractal spatio-temporal variability which, since the brain controls key physiological processes such as ventilation and cardiovascular function, is critical for delivering oxygen and anabolic substances as well as clearing the products of catabolism to maintain healthy organ function. And in accordance with the second law of thermodynamics, the creation and maintenance of consciousness (internal order—negative entropy) is balanced by the external production of a greater degree of (positive) entropy. This is consistent with the maxim of the second law of thermodynamics as well as the writings of Kelvin [119], Gibbs [120,121], and Schrödinger [122] in that the creation of a certain degree of life and order in the universe is inevitably coupled by an even greater degree of death and disorder [110].

In a network thermodynamic model of the human brain, consciousness can be equated to the brain dynamic states corresponding to a low internal system entropy. In recent research [112], the author shows that the second law of thermodynamics provides a physical foundation for the arrow of time. In particular, the author shows that the existence of a global strictly increasing entropy function on every nontrivial network thermodynamic system trajectory establishes the existence of a completely ordered time set that has a topological structure involving a closed set homeomorphic to real line, which establishes the emergence of the direction of time flow. Thus, awareness of the passage of time is a direct consequence of regressive changes in the continuous rate of entropy production taking place in the brain and eventually leading (in finite time) to a state of no entropy production (i.e., death). Since these universal regressive changes in the rate of entropy production are spontaneous, continuous, and decreasing in time, human experience perceives time flow as unidirectional. However, since the rate of time flow and the rate of system entropy regression (i.e., free energy consumption) are bijective (i.e., one-to-one and onto), the human experience of time flow is subjective.

During the transition to an anesthetized state, the external and internal free energy sources are substantially reduced or completely severed in part of the brain leading the human brain network to a semistable state corresponding to a state of local saddle (stationary) entropy. Since all motion in the state variables (synaptic drives) ceases in this unconscious (synchronized) state, our index for the passage of time vanishes until the anesthetic wears off allowing for an immediate increase of the flow of free energy back into the brain and other parts of the body. This, in turn, gives rise to a state of consciousness wherein system entropy production is spontaneously resumed. Merging system thermodynamics with multistability theory and mathematical neuroscience with the goal of providing a mathematical framework for describing the anesthetic cascade mechanism is the subject of current research. In addition, connections between thermodynamics, neuroscience, and the arrow of time [110,112,113] are also being explored to develop an understanding on how the arrow of time is built into the very fabric of our conscious brain.

12. An Electromagnetic Field Theory of Consciousness

The cerebral cortex can be modeled by a columnar topology, where thousands of 0.3–0.6 mm-wide cortical macrocolumns are compactly organized in a parallel configuration to create the approximately 4mm-thick cerebral cortex [123]. Macrocolumns are bundles of approximately 100, 000 neurons which are arranged in six distinguishable layers and create a six-layered structure of the cortex; see Figure 21. Layers I, II, III, V, and VI are mainly composed of excitatory pyramidal cells, whereas Layer IV is almost free of pyramidal cells and is mainly composed of stellate cells. The apical dendrites of pyramidal cells perpendicularly extend towards the cortex superficial layer (Layer I), where they receive inputs from other parts of the brain.

Information is communicated inside the brain by electrical signals, or more specifically, by the creation and transmission of ions. The electrical signal received by dendrites at synapses travels along the dendrites to the cell body, and the resulting cell-generated signal travels to another cell along the axon. Thus, the spatial topology of the cortex dictates the paths along which the ions can flow through and the locations where they can reside. Based on the specific columnar topology of the cerebral cortex described above, the major portion of the electric current inside the cortex, which is conducted by pyramidal cells, flows radially through the cortex.

The almost evenly distributed short-range current flow through stellate cells in Layer IV do not significantly contribute to the global orientation of the current flow through the cortex. When apical dendrites of pyramidal cells receive excitatory inputs through synapses in Layer I, positive ions flow through them from synaptic clefts toward cell bodies, creating a deficit of positive ions at the synaptic clefts. The positive ions flowing through apical dendrites generate a transient radial current and, due to the capacitive characteristics of the cell membrane, accumulate around the cell membrane. As a result, macroscopic electrical activities in cerebral cortex possess four global behaviors (see Figures 21 and 22). Namely, (i) at Layer I, the potential transition due to the activity of neurons is negative; (ii) at layers II, III, V, and VI, the potential transition due to the activity of neurons is positive; (iii) no significant potential transition is observed in Layer IV; and (iv) transient currents due to neuron activity flows radially inside the cortex.

Sparse activities of neurons in a region of the cortex do not generate significant electromagnetic effect in the cortex. However, when a large portion of neurons in a column or adjacent columns are hyperactivated, that is, fire synchronously, the resulting electromagnetic field due to the structured movement and ion configuration described above is strong enough to create significant electromagnetic interference inside the cortex; see Figure 22.

The state of unconsciousness due to the induction of general anesthesia can potentially be due to the strong electromagnetic pattern formation in the cerebral cortex. Available physiological evidence strongly suggests that the excitatory input signals received from the reticular activating system [123] are crucial in maintaining the conscious state of cerebral activities. Anesthetics are believed to prolong the post synaptic potential of inhibitory neurons, which mainly reside in Layer IV of the cortex [123]. Inhibitory neurons provide negative feedback signals for the population of neurons of cortical columns, and hence, can play an essential role in the stability of the highly interconnected network of neurons as well as the global behavior of these neurons. In particular, anesthetics can reduce the inflow of free energy to the brain leading to global or partial [117] synchronization of neuron firing.

Synchronization in the population of neurons present in Layers II, III, V, and VI of the cortex can create a strong electromagnetic pattern. The resulting electromagnetic field can affect the reception of signals from the reticular activating system by reducing the conduction velocity, partially or totally blocking, or even reflecting the incoming signals. Consequently, the cortex loses a large amount of its crucial background wash of input signals, which can result in loss of consciousness [15].

Even though electromagnetic field models have been proposed to explain consciousness (see [124] and the references therein), these models are largely based on emperical observation and lack precise mathematical formulations. A mathematical framework for fostering precision, completeness, and self-consistency in understanding the anesthetic cascade in the human brain using system thermodynamics and electromagnetic field theories are the subject of current research by the authors.

13. Conclusions

With advances in biochemistry, molecular biology, and neurochemistry there has been impressive progress in the understanding of the function of single neurons. Using the example of the mechanism of action of general anesthesia, the past decade has seen a remarkable explosion of our understanding of how anesthetic agents affect the properties of neurons. However, despite this advance, we still do not understand how molecular mechanisms translate into the induction of general anesthesia at the macroscopic level. In particular, there has been little focus on how the molecular properties of anesthetic agents lead to the observed macroscopic property that defines the anesthetic state, that is, lack of responsiveness to noxious stimuli. This clinical property leads to consideration of anesthesia as a nearly binary (on-or-off) variable, and the relationship between the concentration of an anesthetic agent in the central nervous system and the anesthetic state is described in terms of the probability of responsiveness as a function of anesthetic concentration [10]. In clinical studies, the typical observation is that at low concentrations of anesthetic agent the probability of responsiveness (to noxious stimuli) is high, possibly unity. Then as the anesthetic concentration increases there is a sharp transition to a probability of responsiveness that is low and possibly zero.

In this paper, we developed a synaptic drive firing rate model to model the central nervous system as a (possibly discontinuous) autonomous dynamical system and showed that the transition to the anesthetic state exhibits multistability; that is, the system exhibits multiple attracting equilibria under asymptotically slowly changing system parameters directly affected by anesthetic concentrations. In future research we plan to merge system thermodynamics, multistability theory, and dynamic network graph-theoretic notions to develop a framework for understanding central nervous system behavior characterized by abrupt transitions between mutually exclusive conscious and unconscious states.

Such phenomena are not limited to general anesthesia and can be seen in biochemical systems, ecosystems, gene regulation and cell replication, as well as numerous medical conditions (e.g., seizures, epilepsy, schizophrenia, hallucinations, etc.) and are obviously of great clinical importance but have been lacking rigorous theoretical frameworks. The primary impact of such frameworks will be to allow for the development of models that go beyond words to dynamic equations, leading to mathematical models with greater precision and self-consistency. Mathematical formulations enforce self-consistency and while “self-consistency is not necessarily truth, self-inconsistency is certainly falsehood.” And within the context of general anesthesia, a dynamical system formulation for neuroscience can foster the development of new frameworks that will allow us to interpret experimental and clinical results, connect biophysical findings to psychophysical phenomena, explore new hypothesis based on the cognitive neuroscience of consciousness and develop new assertions, and improve the reliability of general anesthesia. In addition, such a framework can establish a scientific basis for new metrics of anesthetic depth by making the assessment of consciousness a mechanistically grounded tool.