Effects of Anticipation in Individually Motivated Behaviour on Survival and Control in a Multi-Agent Scenario with Resource Constraints
Abstract
: Self-organization and survival are inextricably bound to an agent’s ability to control and anticipate its environment. Here we assess both skills when multiple agents compete for a scarce resource. Drawing on insights from psychology, microsociology and control theory, we examine how different assumptions about the behaviour of an agent’s peers in the anticipation process affect subjective control and survival strategies. To quantify control and drive behaviour, we use the recently developed information-theoretic quantity of empowerment with the principle of empowerment maximization. In two experiments involving extensive simulations, we show that agents develop risk-seeking, risk-averse and mixed strategies, which correspond to greedy, parsimonious and mixed behaviour. Although the principle of empowerment maximization is highly generic, the emerging strategies are consistent with what one would expect from rational individuals with dedicated utility models. Our results support empowerment maximization as a universal drive for guided self-organization in collective agent systems.1. Introduction
Homoeostasis, i.e., the maintenance of “internal conditions”, is essential to any dynamic system capable of self-organization [1]. In particular, living beings, ranging from unicellular organisms to complex plants and animals, have to keep quantities, such as body temperature, sugar- and pH-level, within certain ranges. This regulation requires animals to interact with their environment, e.g. to eat in order to increase their sugar level. As a consequence, successful self-organization and thus survival depends on an individual’s potential to perform actions that lead to a desired outcome with high certainty. In other words, survival is inextricably bound to an individual’s control over the environment. This control can only be established and increased over the long term by anticipating the outcome of the individual’s actions. Anticipation is not restricted to mammals [2] and allows living beings to adapt to an ecological niche, i.e., to environmental constraints that affect survival. Recent experimental evidence [3,4] not only suggests that anticipatory behaviour dramatically enhances the chances of survival [2,5,6], but also identifies it as key to increasingly complex cognitive functions, ranging from short-term sensorimotor interaction to higher-level social abilities [7]. It requires the individual to learn and maintain internal predictive models to forecast changes in the environment, as well as the impact of its own actions [8]. Most real-world scenarios also demand forecasting the behaviour of others with similar interests. In the struggle for life, such interests may be reflected in shared resources essential for homoeostasis, e.g. food as a source of energy.
Observations from biology [9,10] and ecological theories drawn from psychology [11–13] suggest that living beings not favour situations with high subjective control. Motivated by these observations, the information-theoretic quantity of “empowerment” [9,14] has recently been developed as a domain-independent measure of control. Furthermore, empowerment maximization, i.e., seeking states with higher empowerment, has been hypothesized as one possible candidate of an intrinsic motivation mechanism driving the behaviour of biological or artificial agents.
In the present paper, we examine how different assumptions about the behaviour of an individual’s peers in the anticipation process affect subjective control and survival strategies. Our analysis is based on simulations of the interactions of multiple artificial agents with a shared and possibly scarce resource. In order to quantify subjective control and drive behaviour, we use empowerment and the principle of empowerment maximization. As a broader goal, we investigate whether this principle can trigger efficient behaviour under different resource constraints.
Section 2 clarifies the notion of control and outlines how research in psychology and control theory laid the foundations for the development of empowerment. Of further importance within this section, we define what we understand by “anticipatory behaviour” and identify key theoretical research. In Section 3, we introduce a comprehensive model accounting for the interaction and anticipation of multiple agents in a resource-centric environment. In Section 4, we conduct two experiments to investigate our research questions. This is followed by a discussion and remarks on future work in Section 5.
2. Background
In this section, we not only want to give an informal understanding of control in terms of the information-theoretic quantity of empowerment, we also want to insinuate that this mathematical characterization may converge with the psychological understanding of what would constitute control. To probe how far this analogy can be pushed, we will later investigate in our experiments how our formalized approach may be able to give rise to, in fact, psychologically plausible effects.
The Oxford Dictionary defines control as a means of “maintaining influence or authority over something”. We adopt findings from psychology as a starting point towards the quantification of subjective control. In his “Locus of Control of Reinforcement” theory [11], Rotter distinguishes between an action, a reaction, an expectation and external influences that affect the sensation of control. He situates an individual’s belief in control between the two extremes of external vs. internal control. In the case of external control, a subject attributes a mismatch between the expectation and the observed outcome of an action entirely to external forces. In the case of internal control, control is explained entirely by the individual’s own actions invoking the observed outcome.
As a reaction to Rotter’s rather informal notions, Oesterreich proposed the “Objective Control and Control Competence” theory [12]. In this probabilistic framework, he associates chains of actions with potential perceptual follow-up states via transition probabilities. Oesterreich characterizes such a state by its “Efficiency Divergence”, representing the likelihood of different actions leading to distinct follow-up states. As a precursor to the empowerment maximization principle, he suggests selecting states with maximum efficiency divergence as a heuristic to reach a desired goal state. Von Foerster seems to refer to this idea when stating in his essays on cybernetics and cognition “I shall act always so as to increase the total number of choices” [15].
Oesterreich bases his theory entirely on actions and potential follow-up-states, i.e., perceptions. He thus implicitly uses the concept of a “perception-action loop” to which Gibson contributed significantly with his “Theory of Affordances” [13]. Gibson suggests that animals and humans view the world and their ecological niche in terms of what they can perceive and do; for better or worse. He therefore develops an agent-centric perspective, in which the concept of the environment is a by-product of its embodiment, i.e., “the interplay between the agent’s sensors and actuators” [14]. He states that man has changed the environment in order to make more available what benefits and less what injures him. Gibson thus implicitly supports Oesterreich’s heuristic to select states with maximum efficiency divergence.
Touchette and Lloyd formulate control in information-theoretic terms. They consider control problems where systems evolve from states of high to states of low entropy through the intervention of an agent [16]. In a subsequent paper [17], they implemented the perception-action loop via causal Bayesian networks by modelling an agent’s controller as a communication channel between his actuator and sensors. In order to model the evolution of an agent’s controller in an information acquisition task, Klyubin et al. extend the formalism by Touchette and Lloyd and unroll the perception-action loop in time [18]. This is later used as a prerequisite to introduce empowerment [9,14] as an information-theoretic, universal measure for subjective control. Empowerment is based solely on an agent’s embodiment and measures the amount of Shannon information “an agent could potentially ‘inject’ into the environment via its actuator and later capture via its sensor” [14]. Akin to efficiency divergence, the empowerment of a state is low if any choice of action would lead to the same follow-up state and high if different actions would lead to different states, which, in addition, would be clearly distinguished by the agent’s sensor. Analogous to Gibson and Oesterreich, and inspired by common behavioural patterns in nature, the authors hypothesize that living beings follow a principle of empowerment maximization: namely, striving towards situations where, in the long term, they could potentially do more different things if they wanted to. A recent empirical study supports this claim for humans, observing that participants in a control task became frustrated in conditions of low empowerment and tend to be more efficient in situations with high empowerment [19].
Currently, there is little research examining the use of empowerment in the challenging scenario of multi-agent systems. In a 2007 paper, Capdepuy et al. [20] examined how the sharing of information influences empowerment as a trigger for complex collective behaviour. Later [21], they used the notion of multiple-access channels to model simultaneous interaction and relate coordination to information-theoretic limits of control.
To clarify the notion of an “anticipatory system”, we adopt the popular definition of Rosen: an anticipatory system creates and maintains “a predictive model of itself and/or its environment, which allows it to change state at an instant in accord with the model’s predictions pertaining to a later instant” [8]. Anticipatory behaviour reverses traditional causality, in that current decisions are influenced by their potential future outcome [22]. It therefore represents an extension of pure embodied intelligence [23]. Anticipation is not synonymous with prediction, but considers the impact of prediction on current behaviour [24,25].
Research on anticipatory behaviour dates back to the formulation of the ideomotor principle in the early 19th century [26]. This introspective theory was denied by behaviourism in the early 20th century, but the pioneering work of Rosen and discoveries in cognitive science, namely mirror neurons and the simulation hypothesis [27], caused a rise in scientific interest. Nevertheless, explicit research in a large number of disciplines, like physics, biology, sociology, psychology, engineering and artificial intelligence [2], only emerged during the last decade [22,26]. Current research focusses mainly on techniques for learning predictive models and on the definition of anticipation frameworks. Recurrent neural networks, Kalman filters and Bayesian predictors were successfully used to learn action-effect rules [7]. Capdepuy et al. [28] proposed an information-theoretic mechanism to create an internal representation of the agent’s environment, and subsequently, they developed an information-theoretic anticipation framework to identify relevant relationships between events [29]. They also evaluated an active exploration strategy, in which an agent gradually collects samples of the interaction with the environment, such that the prediction accuracy becomes maximized [30].
Only a few studies focus on anticipation in a multi-agent scenario. Paul Davidsson first investigated how anticipation affects cooperative and competitive behaviour [31]. However, cooperation and competition were most prominently examined in the iterated prisoner’s dilemma [24,32–34]. Other researchers studied the effect of anticipation on cooperation in Robot Soccer [35,36] or on the success of agents in a thief-guard game [37]. To our knowledge, the effect of anticipation on the behaviour of multiple agents in the context of empowerment has not been investigated yet.
In our experiments, we address several important questions present in current research on anticipation. Hoffmann noted that “perhaps most important, the processes by which anticipations are transformed into actions are not yet appropriately understood” [26]. We address this question by using empowerment to drive decision-making and examining the consequences. Furthermore, we investigate how an agent can benefit from simulating the behaviour of its peers [5]. Finally, we study how the extent of prediction influences the success of anticipation in terms of survival [38].
3. Formal Model
We first define the perception-action loop, as well as empowerment in the case of a single agent and then extend it to the multi-agent case. We assume the system to be discrete in terms of time t ∈ ℕ and states. Random variables, sets and functions are written in capital letters, while tuples, constants and literals are distinguished by the use of small letters. The set of values that a random variable X can take will be denoted by . The probability that X assumes a value x is denoted by p(x).
3.1. The Perception-Action Loop and Empowerment for a Single Agent
As in the related work, we define the perception-action loop by means of a causal Bayesian network. In this notation, every entity under consideration is represented by a random variable, while arrows indicate causal dependencies between them. Figure 1 shows a partial section from the perception-action loop for a single agent, unrolled in time. The environment, comprising the agent’s state Xt and the shared resource Rt, is only affected by the prior environment state and the agent’s action, performed via its actuator At. The agent can perceive the environment via its sensor St, which provides information to the actuator and, thus, closes the interaction loop.
We assume the generic case that the agent not only performs once, but h times, resulting in possible action sequences . We will call h the agent’s “mental horizon”. From Gibson’s agent-centric perspective [13], the system dynamics then induce the agent’s embodiment as a conditional probability distribution between the current state at time t, a sequence of actions and the resulting perception.
The central idea of empowerment [9] is to interpret the agent’s embodiment as a discrete, memoryless communication channel. In information theory, a communication channel transmits a signal X from a sender to a receiver. In the discrete case, the correspondence of signals can be described via a conditional probability distribution p(Y | X). In the classic communication problem, a receiver might receive a potentially different signal Y due to noise in the channel. A channel is called memoryless if the output-distribution p(X) only depends on the inputs at that time. The channel capacity represents the maximum mutual information between the receiver and the sender over all possible input distributions. It is thus “the maximum amount of information the received signal can contain about the transmitted signal” [14]. One efficient means to calculate the capacity of a discrete channel is the algorithm by Blahut [39]. By interpreting the system dynamics as a communication channel, empowerment measures how much information an agent can potentially inject into its environment via its actuator and then perceive via its sensor [9]:
Definition 1. Empowerment
This corresponds to the agent’s subjective control over the environment, given the current sensor state st. In case of deterministic state transitions, i.e., “one-to-one transitions” [17], the entropy of an action is preserved and empowerment is simplified to the logarithm of the number of potential follow-up states. The simplest way to include empowerment maximization into decision-making is to greedily select the first action of a potential sequence, which leads to a state with maximum empowerment. This choice is immediate if the transition rule is deterministic, but different choices are possible in the stochastic case. We choose the “expected empowerment” of an action as a basis for action selection, defined as:
Definition 2. Expected Empowerment
In our experiments, we will let agents greedily choose the actions with the highest expected empowerment.
3.2. Embracing Multiple Agents and Anticipation
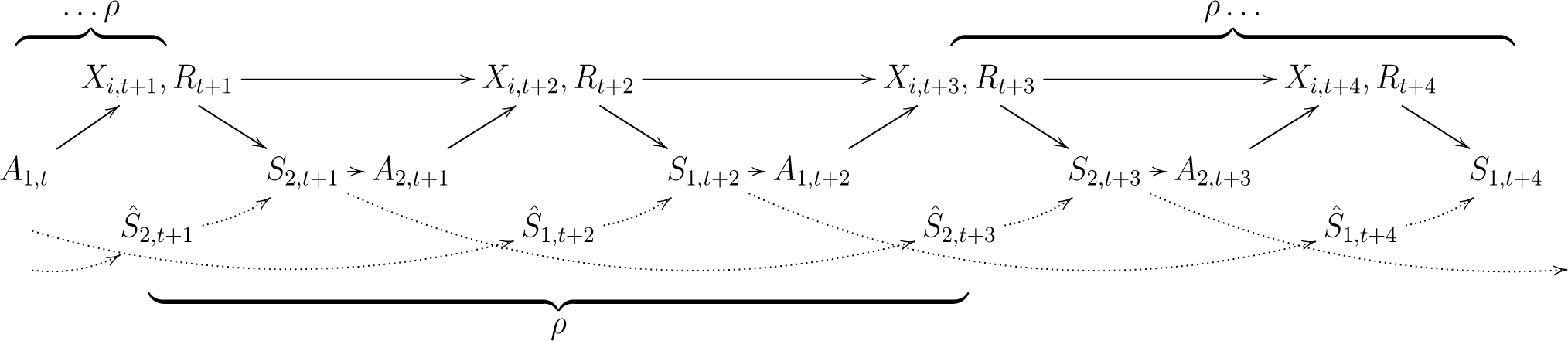
In order to account for multiple agents, we have to extend the perception-action loop and empowerment. As opposed to Capdepuy et al. [21], we assume a round-based, sequential interaction of agents to foster a thorough analysis of their behaviour and to make the anticipation process less complex. We formalize this assumption by decomposing the loop into a sequence of atomic perception-action loops. Each of these represents one “round” ρ = (X1,…, XN), in which each agent performs once. Although the sequentiality implies an implicit pseudo-hierarchy, it does not affect our investigation, since we only analyse the global behaviour of agents. Figure 2 shows a partial section from a perception-action loop in which each round comprises the interaction of two agents X1, X2.
Here, a particular agent does not immediately perceive the effect of its actions, but the environment state after other agents have also acted, i.e., N time steps later. This stresses the need for anticipation: if the environment were static, it would be sufficient for the agent to have a local representation of the system dynamics, which covers exclusively the impact of its actions on the shared resource. Nevertheless, anticipation in the multi-agent case also involves predicting the intentions and survival strategies of others, at least implicitly [40]. This learning process can be very complex in a real environment and is beyond the scope of this paper. Instead, we will select representative models of extreme behaviour implied by the system dynamics and analyse their effect on the agents’ perceived control and survival strategies.
In terms of the taxonomy introduced by Butz et al. [5], we perform “state anticipations”, which directly influence the current decision-making. We implement anticipation by means of a forward model [2,7], i.e., we generate predictions about the next sensed stimuli, given the actual state and a potential action. Predicting changes in the environment for an h-step lookahead thus provides the agents with the h-step embodiment . The calculation of this distribution is accomplished by involving h successive repetitions of two estimation steps, illustrated by the dotted lines in Figure 2:
- (1)
Empty-world estimation: The agent estimates intermediate, follow-up sensor states from a fixed and initially provided distribution . This comes with the assumption that the environment is static and only accounts for the impact of the agent’s own actions, as if no other agents were present.
- (2)
Anticipatory estimation: The previous estimation is refined by including the effect of the other agents’ actions on the environment and, therefore, on the sensor state Si,t+N. This also accounts for intrinsic changes in the environment, e.g. due to the growth of the shared resource. A conditional probability distribution is used as a behavioural model to map from the intermediate to the finally estimated states.
This approach, as with many predictive models [5,6], suffers from a combinatorial explosion when the state space or the number of available actions increases or the transitions become stochastic. We will keep this “naive” model for the sake of precision, but want to remark that only recently, several approximative optimizations were proposed [10,41].
The behavioural model represents an initial guess of the other agents’ collective behaviour and the resource dynamics. In the course of a simulation, agents might behave differently than expected or even die, resulting in an inaccurate behavioural model and misguiding anticipation. We thus applied a simple unsupervised algorithm to adapt the behavioural model to such unexpected events. This compares expectations with real action outcomes, a strategy present in several anticipation frameworks [26,42]. In detail, the algorithm stores all estimated, intermediate, follow-up states when an agent performs. After perceiving the de facto sensor state st+N in the next round, an update of the behavioural model is invoked. If the estimated sensor state does not correspond to the perceived state, the conditional probability of the estimated state, given the intermediate follow-up states, is decreased, while the conditional probability of the perceived state is increased. In our simulations, we only change probabilities by 0.1 per time step. This slow adaptation is intended in order to not alter the effect of different behavioural models too much. One crucial consequence of this learning algorithm is that the behavioural model becomes time-variant, as the estimated system dynamics. Consequently, any calculation based on these dynamics will be transient. This also applies to empowerment, which translates from the single-agent case using simple time-shifts according to the number of agents per round N:
Definition 3. Empowerment for Multiple Agents
Definition 4. Expected Empowerment for Multiple Agents
4. Experiments
We conducted two experiments to investigate the effect of anticipation on subjective control and survival strategies in the given scenario. For a thorough analysis, we chose a minimal model for the agents and the shared resource, which will be outlined first.
4.1. The Testbed
We restrict our simulations to three agents with equal properties. This decision is motivated by the research of Simmel, who demonstrated that a group of three individuals is sufficient to examine a broad range of complex behaviours [43] and thus introduced the triad as a prominent model in microsociology. The shared resource represents the crucial factor in the struggle for survival and is therefore at the centre of the experiments. We assume the resource to grow linearly by rgrowth ∈ ℕ at each time step. Most real resources are finite, so we bound our resource from above via the parameter rmax ∈ ℕ. We decided for a maximum size of rmax = 12 to allow for complex behaviour, while keeping the agent’s sensor state space sufficiently small for a thorough analysis. Thus, the resource takes values rvalue in = {0, 1,…, 12}. In our experiments, agents can only perceive and affect each other implicitly via the shared resource. This assumption allows us to evaluate whether the agents are able to deal with entities even when they are not among the currently attended stimuli, representing one ability for autonomous mental life [7]. We thus have a limited sensor with states. We perform simulations for eight rounds, i.e., , of fixed order. Separate simulations are run for mental horizons up to ten, i.e., h ∈ {1,…, 10}.
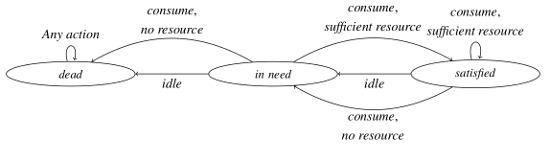
An agent can either be “dead”, “in need of resource” or “satisfied”, represented by states Xt = {0, 1, 2}. As action alternatives, it can either consume or idle, i.e., . For the sake of simplicity, we assume that the system dynamics are known to the agents. However in a real environment, they must be learned. Our fixed empty-world system dynamics are illustrated in the finite state machine in Figure 3. All agents are initially “in need”. In this situation, agents can only escape death by consuming the resource immediately. Successful consumption will lower the resource by two units, i.e., rcon = 2, and the agent will become satisfied. If there is not enough resource available, i.e., R < rcon, or the agent decides to idle instead, it will die. Once it is satisfied, an agent can only remain in this state if it continues to consume further resource. Analogous to the previous case, a lack of resource or deliberate idling will result in a fall-back to the inferior state “in need”.
These constraints provide us with a minimal model for the phenomena that we wish to capture. More specifically, forcing an agent to consume at least every second round in order to escape death allows us to formulate two kinds of extreme behaviour: an agent performs “greedily” if it consumes non-stop, and it acts “parsimoniously” if it alternates between consumption and idling and, thus, only consumes as often as necessary. We use these extremes to construct two opposed predictive models for “greedy” and “parsimonious” behaviour and use them as initial assumptions in the anticipation process. To predict the alteration inherent in parsimonious behaviour, we assume a probability of 0.5 that agents either consume or idle. The underlying conditional probability distribution is therefore stochastic, while greedy behaviour can be modelled deterministically.
4.2. Scarcity
In order to simulate a struggle for survival and analyse emerging strategies, we must make the shared resource not only finite, but also scarce with respect to the number of agents in the system and their needs. We define the scarcity (T) ∈ ℝ of a resource as the ratio of the produced resource and the resource units , which would be consumed if all agents behaved greedily for rounds:
Definition 5. Scarcity
Here, N denotes the number of agents in the system and rvalue(0) is given explicitly or defaults to zero. Making scarcity dependent on N ensures the compatibility of results across runs with different agent numbers. We assume the following constraints:
Assumptions 1. Constraints to scarcity
The constraints in Equation (8) express that resource growth is always positive and that consumption involves at least one unit. It implies that , hence scarcity is well defined. Equation (9) denies any abundance of resources and fixes the co-domain of scarcity to . Scarcity is zero if the shared resource exactly meets the requirements of greedy agents. It is one if agents cannot survive for a single time step. We parametrize our experiments by the scarcity of the resource to implicitly determine the resource parameters rvalue(0) and rgrowth. The testbed settings cover a wide range of scarcity configurations, as listed in Table 1. This table can be used to conveniently look-up which experimental parameters correspond to which scarcities.
As scarcity increases, the survival of all agents becomes impossible if they behave greedily. Values highlighted in grey indicate high degrees of scarcity for which only a subset of agents can survive, even when behaving parsimoniously from the very beginning on.
4.3. Experiment: The Impact of Anticipation on Subjective Control and Survival Strategies
The calculation of empowerment is inextricably bound to a particular behavioural model. In the first experiment, we want to examine how initial assumptions about the behaviour of its peers influence an agent’s empowerment and therefore shape its decisions and survival strategies. We calculated the empowerment for the possible sensor states, given either the assumption of greedy or parsimonious behaviour of all other agents. The calculation is done for mental horizons up to h = 10. The behavioural models cover the resource growth and its consumption by the other agents. Given that the consumption rate is fixed, the models are only affected by changes of rgrowth, and we can thus limit our simulations to the scarcity values , 0.25 and 0.75 (cf. Table 1).
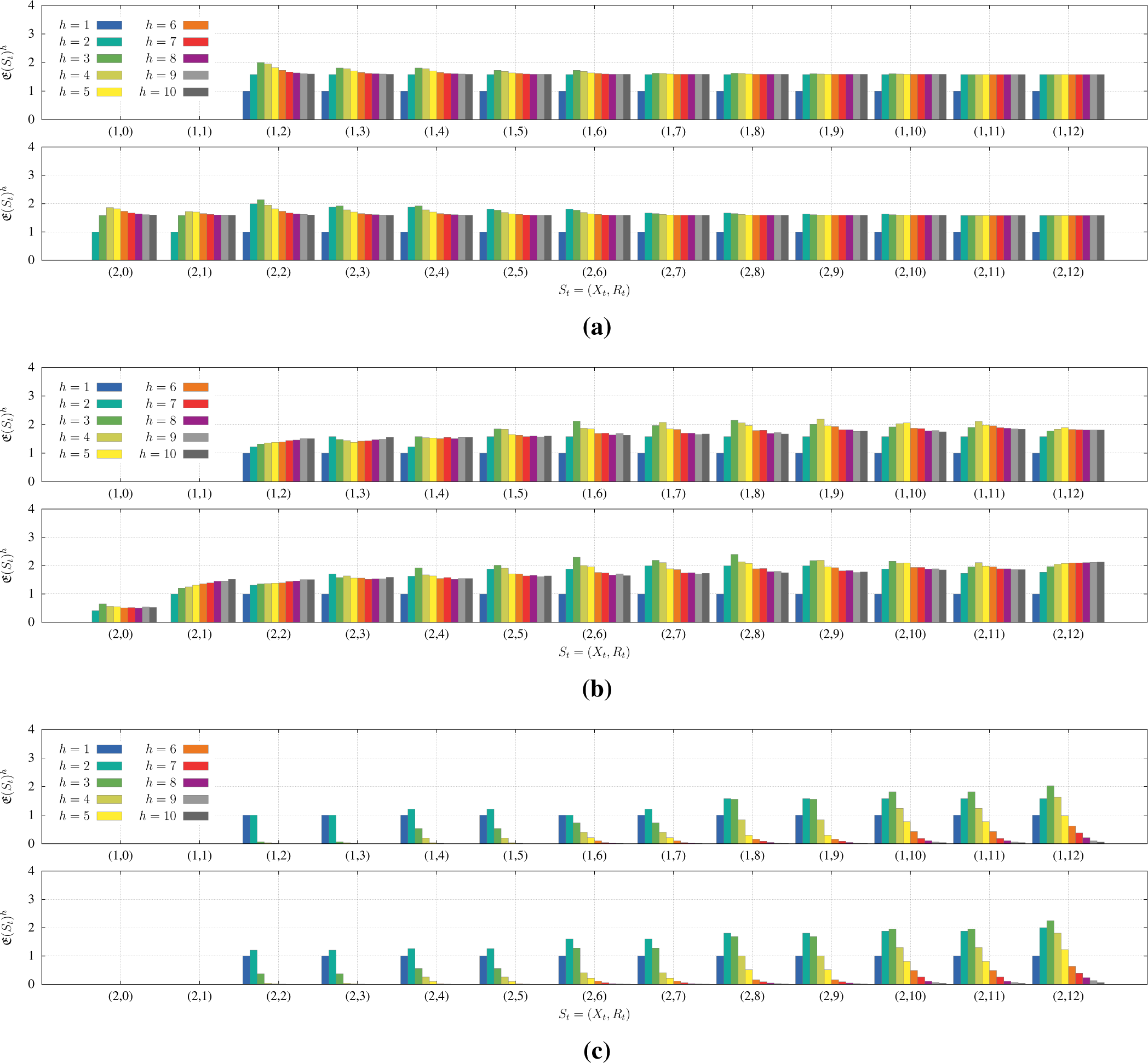
Figures 4 and 6 show an agent’s empowerment over all sensor states for different, colour-coded mental horizons. While in Figure 4, the agent initially assumes that its peers perform greedily, Figure 6 illustrates how assuming the others to act parsimoniously affects subjective control. In both cases, the diagrams show empowerment for increasing degrees of scarcity. In each sub-figure, the top row comprises the sensor states an agent perceives when it is “in need” of the resource. The bottom row, in turn, represents the sensor states when an agent is “satisfied”. From left to right, resource values increase from zero to 12. Note that the model evolution makes empowerment time-variant, thus both figures only represent a snapshot of empowerment at t = 0.
Some characteristics are independent of anticipatory estimation: The empty-world system dynamics imply that, once an agent is “dead”, no action can change its situation. This makes the agent’s subjective control drop to zero for the sensor states To not unnecessarily bloat the plot, these states were omitted from the diagrams. Empowerment is also always zero for the states St = (1,0), (1,1), because there are insufficient resources to consume and any action will thus lead to death. These states illustrate Seligman’s concept of “helplessness”: “A person or animal is helpless with respect to some outcome when the outcome occurs independently of all his voluntary responses” [44].
4.3.1. Greedy Peers
We now examine an agent’s empowerment for different degrees of scarcity if the peers are initially considered to behave greedily. In this deterministic case, as noted in Section 3.1, empowerment simplifies to the logarithm of the number of potential follow-up states.
For (Figure 4a), i.e., a situation in which there is plenty for everyone, empowerment decreases for increasing resource values, i.e., for sensor states St ∈ {(1, 2), (1, 3),…, (1, 12)} and St ∈ {(2, 2), (2, 3),…, (2, 12)}. This shape is due to the abundance of resources, which covers all of the agents’ needs, even if they consume greedily. Thus, idling in a particular state will increase the shared resource and make lower resource states unavailable to the agent.
Larger mental horizons allow extended exploration. Nevertheless, the upper boundary on the resource limits the exploration space to a finite number of potentially accessible states. This space is further confined due to the inaccessibility of lower resource values. Consequently, empowerment increases for larger mental horizons, but also saturates for larger resource values. The more resource is available to an agent, the less meaningful becomes its ability to anticipate.
For the present deterministic behavioural model, different actions will unambiguously lead to a single follow-up state with possibly unequal empowerment. By comparing the empowerment of the states a particular action will lead to, we can directly infer the agent’s behaviour: if the empowerment is the same for the follow-up states or both actions lead to the same state, the agent is indecisive. Otherwise, it will stick to the principle of empowerment maximization and choose the action leading to the state with higher empowerment. For a scarcity of , agents will be indecisive between idling and consuming for a low mental horizon of h = 1. For larger horizons h > 1, they will clearly prefer consuming, because idling would lead to higher resource states and thus less control. Assuming the peers to behave greedily makes the agent favour states with lower resource values. Unfortunately, a flaw in prediction, e.g. an underestimation of the peers’ consumption, could lead to predicting a sufficiently high resource value, although it will turn out to be too low to consume. As this might cause the agent to fall to an inferior state, we label this survival strategy “risk-seeking”. These rather theoretical observations are visualized more clearly in Figure 5, showing the agents’ and resource’s state changes with time for one sample drawn from simulations. The “risk-seeking” behaviour is represented in blue.
The empowerment of an agent changes dramatically if the resource becomes slightly scarce, i.e., . From Figure 4b, we can see that the agent lacks any control in state St = (2,0), because the resource recovers too slowly to allow for consumption. Furthermore, empowerment now increases for increasing resource values and sensor states St ∈ {(1, 2), (1, 3),…, (1, 12)}, as well as St ∈ {(2, 2), (2, 3),…, (2, 12)}. In contrast to the zero-scarcity case, the greedy consumption of other agents denies an agent the possibility to get back to sensor states with high resource values once the resource is used up. With increasing scarcity, we can thus observe a turn from a risk-seeking to a risk-averse survival strategy. We label it “risk-averse”, because the agent strives towards states with higher resource values, for which the consequences of misconceptions in prediction are less tragic. Any scarcity value will compromise the survival of the agents if they perform greedily. The longer the action sequences are that an agent can handle in prediction, the sooner it will recognize this threat. With an increasing mental horizon, an agent will thus predict a gradual collapse of alternatives and thus a drop in empowerment. Nonetheless, empowerment does not drop to zero here, but to a non-vanishing plateau, expressing that any action sequence can reach several alternative states. This is the case, because anticipation is optimized for the immediate future: any state transition in which at least one agent fails to consume would result in its death, triggering an update of the other agents’ behavioural models. By using a transitory model for estimating more distant sensor states, the agent gets an unrealistic estimate represented by such artefacts.
The agents’ helplessness is even stronger given higher scarcity values. A scarcity of does not allow all agents to survive, even when they behave strictly parsimoniously. The empowerment distribution (Figure 4c) shows considerably more spots with zero empowerment than previously observed. This can be interpreted as “helplessness over the long term”: the agents recognise sooner that any action sequence will lead to the same miserable outcome. Thus, they already become indecisive between life- and death-states and exhibit suicidal behaviour for a mental horizon of h = 1 and resource values Rt < 7. A risk-averse strategy is only partially preserved for high resource values and low mental horizons. Note that this distribution reflects an agents’ empowerment at t = 0. The death of other agents at a later time and the following update of the behavioural model might lead to a rise in empowerment.
4.3.2. Parsimonious Peers
Next, we will analyse how the agent’s empowerment and the induced behaviour changes if the peers are assumed to behave parsimoniously. The behavioural model is now stochastic, i.e., it expresses “one-to-many transitions” [17], which increase entropy in the distribution of potential follow-up sensor states. One consequence is that empowerment is less pronounced throughout (Figure 6).
The first empowerment distribution (Figure 6a) was calculated for a scarcity of zero and shares some characteristics with the outcome from assuming greedy behaviour. However, the explanation for the shape of this distribution is more complicated than in the deterministic case: as before, higher resource states cause action sequences to collapse into single states close to the upper resource boundary. This has two opposed effects on the entropy of the follow-up state distribution: on the one hand, the entropy is decreased, because the transitions become deterministic; on the other hand, it is increased, because the action sequences, representing inputs to the corresponding communication channel, cannot be clearly distinguished by their output, i.e., their follow-up states. Here, the first tendency is stronger, resulting in a decrease of channel capacity, i.e., empowerment. Compared to the greedy case, behaviour almost approximates to a risk-seeking survival strategy; however, agents become indecisive in their action choice for high resource values. This implies that agents might prefer idling to consuming, although there is sufficient resources available for constant satisfaction.
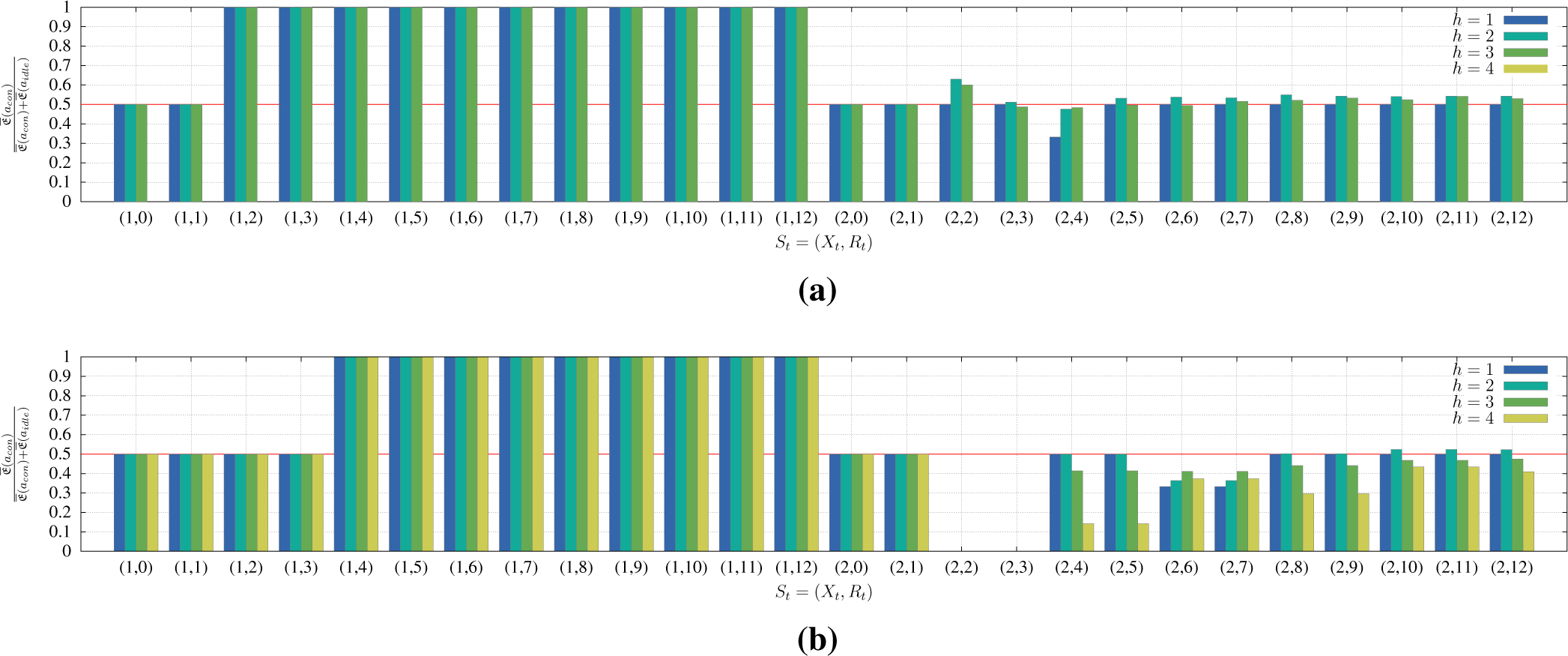
For a low scarcity of , assuming parsimonious behaviour results in an as yet unfamiliar distribution, represented by Figure 6b: for sensor states St ∈ {(1, 2), (1, 3),…, (1, 12)} and St ∈ {(2, 0), (2, 1),…, (2, 12)} and for a particular mental horizon, empowerment first increases to a maximum and then decreases again. For larger mental horizons, this maximum shifts to higher resource values. Thus, larger mental horizons provide the agents with more subjective control in states with higher resource values. To interpret the behaviour induced by a stochastic behavioural model, we calculated the decision bias towards consumption for all sensor states St and mental horizons h (Figure 7) by means of expected empowerment. In detail, we calculated the fraction of expected empowerment with respect to the action acon. Since there are only two actions to choose from, a value >0.5 indicates a definitive choice of consumption, while a value <0.5 means that the agent will favour idling. We label the novel survival strategy implied by Figure 7a “mixed”: for higher resource states, an agent puts more weight on consuming, but prefers to idle in lower resource states. In other words, agents strictly consume when there is sufficient resource available, but start saving when it falls below a certain threshold. With larger mental horizons, agents choose to idle even for high resource values. The ability to predict future threats earlier thus allows one to take preventive actions sooner. A realization of this “mixed” behaviour is visualized by the purple line in Figure 5.
The empowerment distribution for a high scarcity of (Figure 6c) only resembles the results from the greedy model at first sight. Here, empowerment does not completely vanish for high mental horizons, but converges smoothly to zero. The distribution detects a difference between empowerment for the states of being “in need” and “satisfied” and thus implies a lower risk for indecisiveness and suicidal behaviour. Observing the decision bias in Figure 7b, one can infer that agents will instantly begin to behave parsimoniously for mental horizons h > 3.
4.4. Experiment: The Impact of Anticipation on Survival
We have demonstrated that initial assumptions about an agent’s peers have a strong effect on individual behaviour and lead to a diverse set of survival strategies. We will now switch to a global perspective and address the question of which of the emerging survival strategies is most efficient under different degrees of scarcity. In other words, we analyse which behaviours of the other agents should be assumed in order to survive as long as possible. We define the global survival rate as the ratio of all agents that are still alive after rounds, formally:
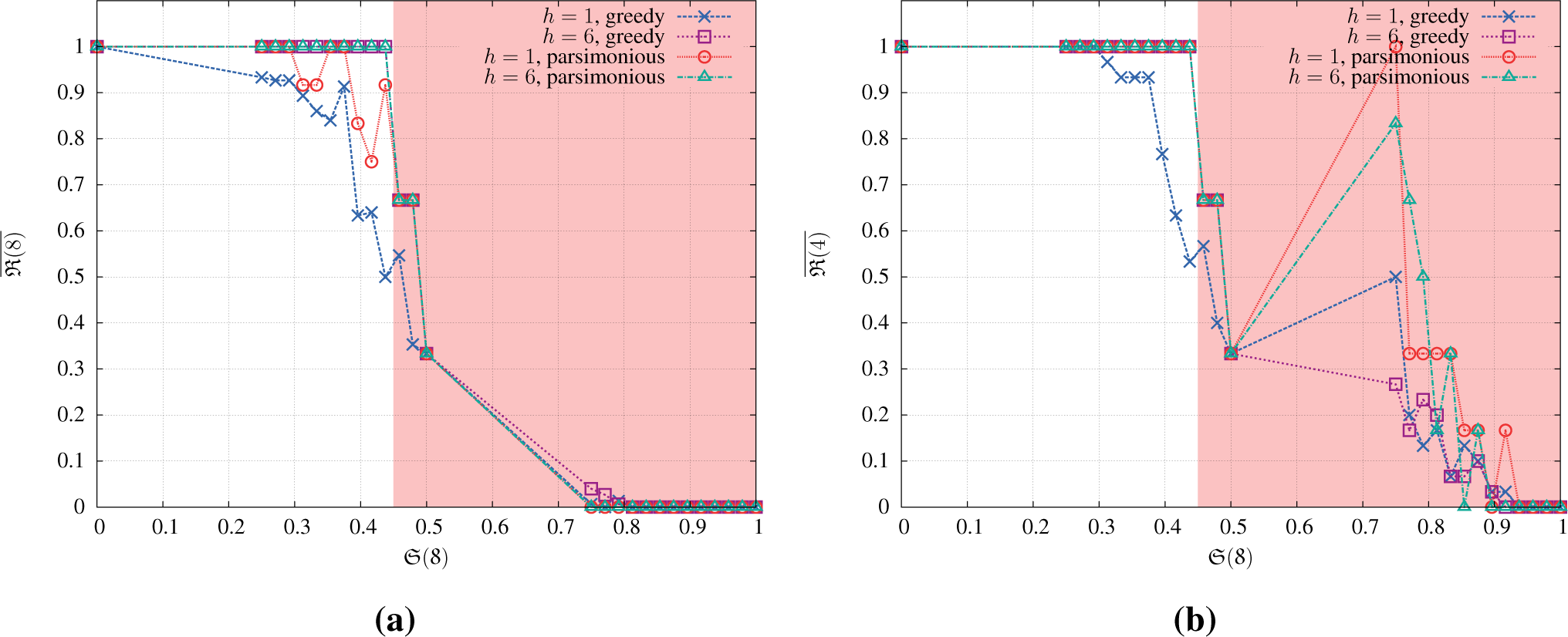
We simulated the agents’ interactions (cf. Figure 5) for each degree of scarcity (cf. Table 1) and mental horizons up to h = 8. To cope with the effects of indecisiveness, we calculated 50 samples and averaged the survival rate, resulting in 21,600 individual simulations. In Figure 8, we compare the average survival rates for a subset of mental horizons over increasing degrees of scarcity. The left diagram shows the survival rate after the whole and the right diagram the results after only half of the simulation.
The survival rate after the complete simulation (Figure 8a) shows a sudden drop at scarcity , because an initial resource value of rvalue(0) = 2 at this degree of scarcity makes it impossible for all agents to survive, even when performing parsimoniously. The red line in Figure 5 illustrates this effect. The diagram shows only minor differences in survival rate between both behavioural models. At first sight, it thus seems to refute our prior impression that assuming other agents to behave parsimoniously constitutes an advantage for higher degrees of scarcity. At closer inspection, however, not necessarily surviving for the duration of the whole experiment, but rather for as long as possible would seem to be a more realistic goal. Thus, we revisit the survival rate after only half of the simulation, i.e., . From Figure 8b, we can see that a parsimonious behavioural model leads to much higher “half time” survival rates for critical scarcity values . However, survival is equally bad at , because the resource constraints are too hard, even when behaving parsimoniously. The induced behaviour even lets all agents survive at for a mental horizon as low as one. Furthermore, the survival rate decreases slower for extreme degrees of scarcity.
This also illustrates that the effect of our scarcity measure on the survival of agents is slightly non-monotonic for the whole simulation duration and strongly non-monotonic for shorter intervals. This is caused by the dependency of the measure on both the initial resource value and its growth.
5. Discussion
The survival strategies emerging in the simulations seem plausible in respect to rational individuals with dedicated utility models: if there were no scarcity, we would expect them to consume greedily in order to stay “satisfied”. Nevertheless, as soon as the resource starts to become scarce, an individual should better start consuming less and finally refrain from consuming more than absolutely necessary if scarcity rises even more. In accordance with empowerment maximization, the strategies promising the longest lifetime were triggered by those behavioural models leading to the highest subjective control (Table 2).
We can infer several rather generic findings from our experimental results: given the constraints posed by our model, agents seem to develop the most efficient behaviour locally if they assume their peers to act in a way that would be indeed the most efficient on a global level. Furthermore, driven by empowerment maximization, multiple agents with equal limitations to their perceptual apparatus and actions are capable of surviving in a flat hierarchy without direct communication, even when being threatened by high degrees of scarcity. Finally, we observed that different mental horizons, which determine the extent of anticipation, have a strong impact on subjective control and behaviour. We found that large mental horizons are not necessarily of benefit, because they can create a too pessimistic view of the distant past, given only present information. As a result, agents may consider themselves “helpless over the long term”, which causes them to be undecided and, sometimes, suicidal. Johannson and Balkenius report similar findings from their research on anticipation in multi-agent environments and conclude that “prediction time must be set depending on the task” [37]. In our case, this would imply that one should align the mental horizon with the possible survival time. Furthermore, we hypothesize that there may be alternative, shorter lookahead horizons, which could foster survival by means of a more optimistic prediction of the future and at the same time lower the risk of imprecise predictions. Put differently, not only focussing on distant goals, but also “appreciating the moment” seems to be essential to respond to an uncertain, but dismal-looking future in order to achieve biologically plausible behaviour.
6. Conclusions and Future Work
In the present paper, we examined the effect of anticipation on subjective control and survival strategies in a multi-agent, resource-centric environment. We used the information-theoretic quantity of empowerment as a measure for an agent’s subjective control of its environment and evaluated empowerment maximization as a principle, which may underlie biologically plausible behaviour. In order to simulate a struggle for survival, we developed a minimal model based on insights from psychology, as well as microsociology and introduced a scarce resource on which all agents depended.
Our experimental results show that the generic principle of empowerment maximization can trigger biologically plausible behaviour in different scenarios: agents developed risk-seeking, risk-averse and mixed strategies, which, in turn, correspond to greedy, parsimonious and mixed behaviour. The efficiency of these strategies under resource scarcity turns out to be very sensitive to an agent’s assumptions about the behaviour of its peers.
From these results, we can see that empowerment maximization for action selection in an anticipatory process fulfils the requirements for decision-making in self-organizing systems. More specifically, the information-theoretic nature of empowerment makes it a highly generic quantity not restricted to specific agent structures. It allows agents to increase organization over time. It not only guided our agents with respect to the crucial task of survival, but also with regard to the secondary objective of satisfaction. Different initial assumptions in the anticipation process produce qualitatively different behavioural patterns and can thus be used for guiding agent behaviour.
The model used in our simulations is at this stage minimal, but highly extensible. As an immediate next step in research, we can allows agents to perceive and affect each other and investigate the effects of selfishness, altruism and global survival. Furthermore, having the agents learn the others’ strategies might contribute to this research goal. The model suggests differentiating between agent roles to create explicit hierarchies. It also allows one to consider sensor and actuator evolution as ways of incorporating new modalities into the interaction. Furthermore, it supports the seamless integration and investigation of further means of explicit guidance, e.g. the recently proposed goal-weighted empowerment [45].
Acknowledgments
The authors would like to thank the reviewers for their detailed and very useful feedback. In particular, they want to give sincere thanks to Martin Greaves for his excellent proofreading.
Author Contributions
Christian Guckelsberger and Daniel Polani developed the model and mathematical framework. Christian Guckelsberger carried out the experiments. Christian Guckelsberger and Daniel Polani discussed the results. Christian Guckelsberger wrote the paper and Daniel Polani provided feedback on the write-up.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ashby, W.R. An Introdution to Cybernetics; Chapman & Hall Ltd: London, UK, 1956. [Google Scholar]
- Poli, R. The Many Aspects of Anticipation. Foresight 2010, 12, 7–17. [Google Scholar]
- Fleischer, J.G. Neural Correlates of Anticipation in Cerebellum, Basal Ganglia and Hippocampus. In Anticipatory Behavior in Adaptive Learning Systems: From Brains to Individual and Social Behavior; Butz, M.V., Sigaud, O., Baldessare, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 19–34. [Google Scholar]
- Butz, M.V.; Sigaud, O.; Pezzulo, G.; Baldessare, G. Anticipations, Brains, Individual and Social Behavior: An Introduction to Anticipatory Systems. In Anticipatory Behavior in Adaptive Learning Systems. From Brains to Individual and Social Behavior; Butz, M.V., Sigaud, O., Pezzulo, G., Baldessare, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–18. [Google Scholar]
- Butz, M.V.; Sigaud, O.; Gérard, P. Internal Models and Anticipation in Adaptive Learning Systems. In Anticipatory Behaviour in Adaptive Learning Systems; Butz, M.V., Sigaud, O., Gérard, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 86–109. [Google Scholar]
- Broekens, J. Internal Simulation of Behavior Has an Adaptive Advantage, Proceedings of the Cognitive Science Society, Stresa, Italy, 21–23 July 2005; pp. 342–347.
- Pezzulo, G. Anticipation and Future-Oriented Capabilities in Natural and Artificial Cognition. In 50 Years of Artificial Intelligence; Lungarella, M., Iida, F., Bongard, J., Pfeifer, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 257–270. [Google Scholar]
- Rosen, R. Anticipatory Systems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Klyubin, A.S.; Polani, D.; Nehaniv, C.L. Keep your options open: An information-based driving principle for sensorimotor systems. PLoS One 2008, 3, e4018. [Google Scholar]
- Salge, C.; Glackin, C.; Polani, D. Changing the Environment based on Empowerment as Intrinsic Motivation. Entropy 2014, 16, 2789–2819. [Google Scholar]
- Rotter, J.B. Generalized expectancies for internal vs. external control of reinforcement. Psychol. Monogr 1966, 80, 1–28. [Google Scholar]
- Oesterreich, R. Entwicklung Eines Konzepts der Objektiven Kontrolle und Kontrollkompetenz. Ein Handlungstheoretischer Ansatz. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 1979. (In German). [Google Scholar]
- Gibson, J.J. The Theory of Affordances. In The Ecological Approach to Visual Perception; Routledge: London, UK, 1986; pp. 127–138. [Google Scholar]
- Klyubin, A.S.; Polani, D.; Nehaniv, C.L. All else being equal be empowered. In Advances in Artificial Life; Springer: Berlin/Heidelberg, Germany, 2005; pp. 744–753. [Google Scholar]
- Von Foerster, H. Disorder/Order: Discovery or Invention? In Understanding Understanding; Springer: Berlin/Heidelberg, Germany, 2003; pp. 273–282. [Google Scholar]
- Touchette, H.; Lloyd, S. Information-Theoretic Limits of Control. Phys. Rev. Lett 2000, 84, 1156–1159. [Google Scholar]
- Touchette, H.; Lloyd, S. Information-Theoretic Approach to the Study of Control Systems. Phys. Stat. Mech. Appl 2004, 331, 140–172. [Google Scholar]
- Klyubin, A.S.; Polani, D.; Nehaniv, C.L. Organization of the Information Flow in the Perception-Action Loop of Evolved Agents, Proceedings of 2004 NASA/DoD Conference on Evolvable Hardware, Seattle, WA, USA, 24–26 June 2004; pp. 1–4.
- Trendafilov, D.; Murray-Smith, R. Information-Theoretic Characterization of Uncertainty in Manual Control, Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Lausanne, Switzerland, 13–15 June 2013; pp. 4913–4918.
- Capdepuy, P.; Polani, D.; Nehaniv, C.L. Maximization of Potential Information Flow as a Universal Utility for Collective Behaviour, Proceedings of the 2007 IEEE Symposium on Artificial Life, Honolulu, HI, USA, 1–5 April 2007; pp. 207–213.
- Capdepuy, P.; Polani, D.; Nehaniv, C.L. Perception-action loops of multiple agents: informational aspects and the impact of coordination. Theor. Biosci 2011, 131, 149–159. [Google Scholar]
- Butz, M.V.; Sigaud, O.; Gérard, P. Anticipatory Behavior: Exploiting Knowledge About the Future to Improve Current Behavior; Anticipatory Behaviour in Adaptive Learning Systems, Butz, M.V., Sigaud, O., Gérard, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 1–10. [Google Scholar]
- Nadin, M. Not everything we know we learned. In Anticipatory Behaviour in Adaptive Learning Systems; Butz, M.V., Sigaud, O., Gérard, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 23–43. [Google Scholar]
- Pezzulo, G., Butz, M.V., Castelfranchi, C., Falcone, R., Eds.; The Challenge of Anticipation. A Unifying Framework for the Analysis and Design of Artificial Cognitive Systems; Springer: Berlin/Heidelberg, Germany, 2008.
- Nahodil, P.; Vitku, J. Novel Theory and Simulations of Anticipatory Behaviour in Artificial Life Domain. In Advances in Intelligent Modelling and Simulation; Byrski, A., Oplatková, Z., Carvalho, M., Kisiel-Dorohinicki, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 131–164. [Google Scholar]
- Hoffmann, J. Anticipatory Behavioral Control. In Anticipatory Behaviour in Adaptive Learning Systems; Butz, M.V., Sigaud, O., Gérard, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 44–65. [Google Scholar]
- Hesslow, G. Conscious thought as simulation of behaviour and perception. Trends Cognit. Sci 2002, 6, 242–247. [Google Scholar]
- Capdepuy, P.; Polani, D.; Nehaniv, C.L. Constructing the basic Umwelt of artificial agents: An information-theoretic approach. In Advances in Artificial Life; Springer: Berlin/Heidelberg, Germany, 2007; pp. 375–383. [Google Scholar]
- Capdepuy, P.; Polani, D.; Nehaniv, C.L. Grounding action-selection in event-based anticipation. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 253–262. [Google Scholar]
- Capdepuy, P.; Polani, D.; Nehaniv, C.L. Adaptation of the Perception-Action Loop Using Active Channel Sampling, Proceedings of the 2008 NASA/ESA Conference on Adaptive Hardware and Systems, Noordwijk, The Netherlands, 22–25 June; 2008; pp. 443–450.
- Davidsson, P. Learning by linear anticipation in multi-agent systems. In Distributed Artificial Intelligence Meets Machine Learning Learning in Multi-Agent Environments; Springer: Berlin/Heidelberg, Germany, 1997; pp. 62–72. [Google Scholar]
- Gmytrasiewicz, P.; Durfee, E. Rational coordination in multi-agent environments. Autonom. Agents Multi-Agent Syst 2000, 3, 319–350. [Google Scholar]
- Colman, A. Cooperation, psychological game theory, and limitations of rationality in social interaction. Behav. Brain. Sci 2003, 26, 139–198. [Google Scholar]
- Grinberg, M.; Lalev, E. The Role of Anticipation on Cooperation and Coordination in Simulated Prisoner’s Dilemma Game Playing. In Anticipatory Behavior in Adaptive Learning Systems. From Psychological Theories to Artificial Cognitive Systems; Pezzulo, G., Butz, M.V., Sigaud, O., Baldassarre, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 209–228. [Google Scholar]
- Veloso, M.; Stone, P.; Bowling, M. Anticipation: A key for collaboration in a team of agents, Proceedings of the SPIE Sensor Fusion and Decentralized Control in Robotic Systems II, Boston, MA, USA, 19–20 September 1999; pp. 134–143.
- Sharifi, M.; Mousavian, H.; Aavani, A. Predicting the Future State of the Robocup Simulation Environment: Heuristic and Neural Networks Approaches, Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Washington, DC, USA, 5–8 October 2003; pp. 32–37.
- Johansson, B.; Balkenius, C. Prediction time in anticipatory systems. In Anticipatory Behavior in Adaptive Learning Systems. From Psychological Theories to Artificial Cognitive Systems; Pezzulo, G., Butz, M.V., Sigaud, O., Baldassarre, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 283–300. [Google Scholar]
- Sjölander, S. Some cognitive breakthroughs in the evolution of cognition and consciousness, and their impact on the biology of language. Evol. Cognit 1995, 1, 3–11. [Google Scholar]
- Blahut, R. Computation of channel capacity and rate-distortion functions. IEEE Trans. Inform. Theor 1972, 18, 460–473. [Google Scholar]
- Nehaniv, C.L.; Polani, D.; Dautenhahn, K. Meaningful Information, Sensor Evolution, and the Temporal Horizon of Embodied Organisms. Artif. Life 2002, 8, 345–349. [Google Scholar]
- Anthony, T.; Polani, D.; Nehaniv, C.L. General Self-Motivation and Strategy Identification: Case Studies based on Sokoban and Pac-Man. IEEE Trans. Comput. Intell. AI Games 2014, 6, 1–17. [Google Scholar]
- Martinho, C.; Paiva, A. Using Anticipation to Create Believable Behaviour, Proceedings of the National Conference on Artificial Intelligence, Boston, MA, USA, 16–20 July 2006; pp. 175–180.
- Wolff, K. The Sociology of Georg Simmel; Simon and Schuster: New York, NY, USA, 1950. [Google Scholar]
- Seligman, M.E.P. Helplessness: On Depression, Development, and Death; WH Freeman/Times Books/Henry Holt & Co.: New York, NY, USA, 1975. [Google Scholar]
- Edge, R. Predicting Player Churn in Multiplayer Games using Goal-Weighted Empowerment; Technical Report 13-024; University of Minnesota: St. Paul, MN, USA, 2013. [Google Scholar]




| rvalue(0) | rgrowth | rvalue(0) | rgrowth | rvalue(0) | rgrowth | |||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 0.42 | 4 | 1 | 0.83 | 8 | 0 |
| 0.25 | 12 | 1 | 0.44 | 3 | 1 | 0.85 | 7 | 0 |
| 0.27 | 11 | 1 | 0.47 | 2 | 1 | 0.88 | 6 | 0 |
| 0.29 | 10 | 1 | 0.48 | 1 | 1 | 0.9 | 5 | 0 |
| 0.31 | 9 | 1 | 0.5 | 0 | 1 | 0.92 | 4 | 0 |
| 0.33 | 8 | 1 | 0.75 | 12 | 0 | 0.94 | 3 | 0 |
| 0.35 | 7 | 1 | 0.77 | 11 | 0 | 0.96 | 2 | 0 |
| 0.38 | 6 | 1 | 0.79 | 10 | 0 | 0.98 | 1 | 0 |
| 0.40 | 5 | 1 | 0.81 | 9 | 0 | 1 | 0 | 0 |
| Scarcity | h | (Greedy) | (Parsimonious) |
|---|---|---|---|
| 0 | 4 | 3 | 1.95 |
| 0 | 6 | 3.46 | 1.73 |
| 0.25 | 4 | 3.32 | 2.14 |
| 0.25 | 6 | 3 | 2.1 |
| 0.75 | 4 | 1 | 1.81 |
| 0.75 | 6 | 0 | 0.64 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Guckelsberger, C.; Polani, D. Effects of Anticipation in Individually Motivated Behaviour on Survival and Control in a Multi-Agent Scenario with Resource Constraints. Entropy 2014, 16, 3357-3378. https://doi.org/10.3390/e16063357
Guckelsberger C, Polani D. Effects of Anticipation in Individually Motivated Behaviour on Survival and Control in a Multi-Agent Scenario with Resource Constraints. Entropy. 2014; 16(6):3357-3378. https://doi.org/10.3390/e16063357
Chicago/Turabian StyleGuckelsberger, Christian, and Daniel Polani. 2014. "Effects of Anticipation in Individually Motivated Behaviour on Survival and Control in a Multi-Agent Scenario with Resource Constraints" Entropy 16, no. 6: 3357-3378. https://doi.org/10.3390/e16063357