1. Introduction
One of the main efforts in physics is modeling and predicting natural phenomena using relevant information about the system under consideration. Theoretical physics has had a general measure of the uncertainty associated with the behavior of a probabilistic process for more than 100 years: the Shannon entropy [
1]. The Shannon information theory was applied to dynamical systems and became successful in describing their unpredictability [
2].
Along a similar avenue we may set Entropic Dynamics [
3] which makes use of inductive inference (Maximum Entropy Methods [
4]) and Information Geometry [
5]. This is clearly remarkable given that microscopic dynamics can be far removed from the phenomena of interest, such as in complex biological or ecological systems. Extension of ED to temporally-complex dynamical systems on curved statistical manifolds led to relevant measures of chaoticity [
6]. In particular, an information geometric approach to chaos (IGAC) has been pursued studying chaos in informational geodesic flows describing physical, biological or chemical systems. It is the information geometric analogue of conventional geometrodynamical approaches [
7] where the classical configuration space is being replaced by a statistical manifold with the additional possibility of considering chaotic dynamics arising from non conformally flat metrics. Within this framework, it seems natural to consider as a complexity measure the (time average) statistical volume explored by geodesic flows, namely an Information Geometry Complexity (IGC).
This quantity might help uncover connections between microscopic dynamics and experimentally observable macroscopic dynamics which is a fundamental issue in physics [
8]. An interesting manifestation of such a relationship appears in the study of the effects of microscopic external noise (noise imposed on the microscopic variables of the system) on the observed collective motion (macroscopic variables) of a globally coupled map [
9]. These effects are quantified in terms of the complexity of the collective motion. Furthermore, it turns out that noise at a microscopic level reduces the complexity of the macroscopic motion, which in turn is characterized by the number of effective degrees of freedom of the system.
The investigation of the macroscopic behavior of complex systems in terms of the underlying statistical structure of its microscopic degrees of freedom also reveals effects due to the presence of microcorrelations [
10]. In this article we first show which macro-states should be considered in a Gaussian statistical model in order to have a reduction in time of the Information Geometry Complexity. Then, dealing with correlated bivariate and trivariate Gaussian statistical models, the ratio between the IGC in the presence and in the absence of microcorrelations is explicitly computed, finding an intriguing, even though non yet deep understood, connection with the phenomenon of geometric frustration [
11].
The layout of the article is as follows. In
Section 2 we introduce a general statistical model discussing its geometry and describing both its dynamics and information geometry complexity. In
Section 3, Gaussian statistical models (up to a trivariate model) are considered. There, we compute the asymptotic temporal behaviors of their IGCs. Finally, in
Section 4 we draw our conclusions by outlining our findings and proposing possible further investigations.
2. Statistical Models and Information Geometry Complexity
Given
n real-valued random variables
defined on the sample space Ω with joint probability density
satisfying the conditions
let us consider a family
of such distributions and suppose that they can be parametrized using
m real-valued variables
so that
where
is the parameter space and the mapping
is injective. In such a way,
is an
m-dimensional statistical model on
.
The mapping
defined by
allows us to consider
as a coordinate system for
. Assuming parametrizations which are
, we can turn
into a
differentiable manifold (thus,
is called statistical manifold) [
5].
The values taken by the random variables define the micro-state of the system, while the values taken by parameters define the macro-state of the system.
Let
be an
m-dimensional statistical model. Given a point
θ, the Fisher information matrix of
in
θ is the
matrix
, where the
entry is defined by
with
standing for
. The matrix
is symmetric, positive semidefinite and determines a Riemannian metric on the parameter space Θ [
5]. Hence, it is possible to define a Riemannian statistical manifold
, where
is the metric whose components
are given by Equation (
3) (throughout the paper we use the Einstein sum convention).
Given the Riemannian manifold
, it is well known that there exists only one linear connection ∇(the Levi–Civita connection) on
that is compatible with the metric
g and symmetric [
12]. We remark that the manifold
has one chart, being Θ an open set of
, and the Levi-Civita connection is uniquely defined by means of the Christoffel coefficients
where
is the
entry of the inverse of the Fisher matrix
.
The idea of curvature is the fundamental tool to understand the geometry of the manifold
. Actually, it is the basic geometric invariant and the intrinsic way to obtain it is by means of geodesics. It is well-known, that given any point
and any vector
v tangent to
at
θ, there is a unique geodesic starting at
θ with initial tangent vector
v. Indeed, within the considered coordinate system, the geodesics are solutions of the following nonlinear second order coupled ordinary differential equations [
12]
with
τ denoting the time.
The recipe to compute some curvatures at a point
is the following: first, select a 2-dimensional subspace Π of the tangent space to
at
θ; second, follow the geodesics through
θ whose initial tangent vectors lie in Π and consider the 2-dimensional submanifolds
swiped out by them inheriting a Riemannian metric from
; finally, compute the Gaussian curvature of
at
θ, which can be obtained from its Riemannian metric as stated in the
Theorema Egregium [
13]. The number
found in such manner is called the
sectional curvature of
at
θ associated with the plane Π. In terms of local coordinates, to compute the sectional curvature we need the curvature tensor,
For any basis
for a 2-plane
, the sectional curvature at
is given by [
12]
where
R is the Riemann curvature tensor which is written in coordinates as
with
and
is the inner product defined by the metric
g.
The sectional curvature is directly related to the topology of the manifold; along this direction the
Cartan-Hadamard Theorem [
13] is enlightening by stating that any complete, simply connected
n-dimensional manifold with non positive sectional curvature is diffeomorphic to
.
We can consider upon the statistical manifold
the macro-variables
θ as accessible information and then derive the information dynamical Equation (
5) from a standard principle of least action of Jacobi type [
3]. The geodesic Equations (
5) describe a reversible dynamics whose solution is the trajectory between an initial and a final macrostate
and
, respectively. The trajectory can be equally traversed in both directions [
10]. Actually, an equation relating instability with geometry exists and it makes hope that some global information about the average degree of instability (chaos) of the dynamics is encoded in global properties of the statistical manifolds [
7]. The fact that this might happen is proved by the special case of constant-curvature manifolds, for which the Jacobi-Levi-Civita equation simplifies to [
7]
where
K is the constant sectional curvature of the manifold (see Equation (
7)) and
J is the geodesic deviation vector field. On a positively curved manifold, the norm of the separating vector
J does not grow, whereas on a negatively curved manifold, the norm of
J grows exponentially in time, and if the manifold is compact, so that its geodesic are sooner or later obliged to fold, this provide an example of chaotic geodesic motion [
14].
Taking into consideration these facts, we single out as suitable indicator of dynamical (temporal) complexity, the information geometric complexity defined as the average dynamical statistical volume [
15]
where
with
the information matrix whose components are given by Equation (
3). The integration space
is defined as follows
where
with
such that
satisfies (
5). The quantity
is the volume of the effective parameter space explored by the system at time
. The temporal average has been introduced in order to average out the possibly very complex fine details of the entropic dynamical description of the system’s complexity dynamics.
Relevant properties, concerning complexity of geodesic paths on curved statistical manifolds, of the quantity (
10) compared to the Jacobi vector field are discussed in [
16].
3. The Gaussian Statistical Model
In the following we devote our attention to a Gaussian statistical model
whose element are multivariate normal joint distributions for
n real-valued variables
given by
where
is the
n-dimensional mean vector and
C denotes the
covariance matrix with entries
,
. Since
μ is a
n-dimensional real vector and
C is a
symmetric matrix, the parameters involved in this model should be
. Moreover
C is a symmetric, positive definite matrix, hence we have the parameter space given by
Hereafter we consider the statistical model given by Equation (
12) when the covariance matrix
C has only variances
as parameters. In fact we assume that the non diagonal entry
of the covariance matrix
C equals
with
quantifying the degree of correlation.
We may further notice that the function
, when
is given by Equation (
12), is a polynomial in the variables
(
) whose degree is not grater than four. Indeed, we have that
and, therefore, the differentiation does not affect variables
. With this in mind, in order to compute the integral in (
3), we can use the following formula [
17]
where the exponential denotes the power series over its argument (the differential operator).
3.1. The monovariate Gaussian Statistical Model
We now start to apply the concepts of the previous section to a Gaussian statistical model of Equation (
12) for
. In this case, the dimension of the statistical Riemannian manifold
is at most two. Indeed, to describe elements of the statistical model
given by Equation (
12), we basically need the mean
and variance
. We deal separately with the cases when the monovariate model has only
μ as macro-variable (Case 1), when
σ is the unique macro-variable (Case 2), and finally when both
μ and
σ are macro-variables (Case 3).
3.1.1. Case 1
Consider the monovariate model with only
μ as macro-variable by setting
. In this case the manifold
is trivially the real
flat straight line, since
. Indeed, the integral in (
3) is equal to 1 when the distribution
reads as
; so the metric is
. Furthermore, from Equations (
4) and (
5) the information dynamics is described by the geodesic
, where
. Hence, the volume of Equation (
10) results
; since this quantity must be positive we assume
. Finally, the asymptotic behavior of the IGC (
9) is
This shows that the complexity linearly increases in time meaning that acquiring information about
μ and updating it, is not enough to increase our knowledge about the micro state of the system.
3.1.2. Case 2
Consider now the monovariate Gaussian statistical model of Equation(
12) when
and the macro-variable is only
σ. In this case the probability distribution function reads
while the Fisher–Rao metric becomes
. Emphasizing that also in this case the manifold is flat as well, we derive the information dynamics by means of Equations (
4) and (
5) and we obtain the geodesic
. The volume in Equation (
10) then results
Again, to have positive volume we have to assume
. Finally, the (asymptotic) IGC (
9) becomes
This shows that also in this case the complexity linearly increases in time meaning that acquiring information about
σ and updating it, is not enough to increase our knowledge about the micro-state of the system.
3.1.3. Case 3
The take home message of the previous cases is that we have to account for both mean
μ and variance
σ as macro-variables to look for possible non increasing complexity. Hence, consider the probability distribution function is given by,
The dimension of the Riemannian manifold
is two, where the parameter space Θ is given by
and the Fisher–Rao metric reads as
. Here, the sectional curvature given by Equation (
7) is a negative function and despite the fact that is not constant, we expect a decreasing behavior in time of the IGC. Thanks to Equation (
4), we find that the only non negative Christoffel coefficients are
,
and
. Substituting them into Equation (
5) we derive the following geodesic equations
The integration of the above coupled differential equations is non-trivial. We follow the method described in [
10] and arrive at
where
and
are real constants. Then, using (
21), the volume of Equation (
10) results
Since the last quantity must be positive, we assume
. Finally, employing the above expression into Equation (
9) we arrive at
We can now see a reduction in time of the complexity meaning that acquiring information about both
μ and
σ and updating them allows us to increase our knowledge about the micro state of the system.
Hence, comparing Equations (
16), (
18) and (
23) we conclude that the entropic inferences on a Gaussian distributed micro-variable is carried out in a more efficient manner when both its mean and the variance in the form of information constraints are available. Macroscopic predictions when only one of these pieces of information are available are more complex.
3.2. Bivariate Gaussian Statistical Model
Consider now the Gaussian statistical model
of the Equation (
12) when
. In this case the dimension of the Riemannian manifold
is at most four. From the analysis of the monovariate Gaussian model in
Section 3.1 we have understood that both mean and variance should be considered. Hence the minimal assumption is to consider
and
. Furthermore, in this case we have also to take into account the possible presence of (micro) correlations, which appear at the level of macro-states as off-diagonal terms in the covariance matrix. In short, this implies considering the following probability distribution function
where
.
Thanks to Equation (
15) we compute the Fisher-Information matrix
G and find
with,
The only non trivial Christoffel coefficients (
4) are
,
and
. In this case as well, the sectional curvature (Equation (
7)) of the manifold
is a negative function and so we may expect a decreasing asymptotic behavior for the IGC. From Equation (
5) it follows that the geodesic equations are,
whose solutions are,
Using (
27) in Equation (
10) gives the volume,
To have it positive we have to assume
. Finally, employing (
28) in (
9) leads to the IGC,
with
. We may compare the asymptotic expression of the ICGs in the presence and in the absence of correlations, obtaining
where “strong” stands for the fully connected lattice underlying the micro-variables. The ratio
results a
monotonic increasing function of
ρ.
While the temporal behavior of the IGC (
29) is similar to the IGC in (
23), here correlations play a fundamental role. From Equation (
30), we conclude that entropic inferences on two Gaussian distributed micro-variables on a fully connected lattice is carried out in a more efficient manner when the two micro-variables are negatively correlated. Instead, when such micro-variables are positively correlated, macroscopic predictions become more complex than in the absence of correlations.
Intuitively, this is due to the fact that for anticorrelated variables, an increase in one variable implies a decrease in the other one (different directional change): variables become more distant, thus more distinguishable in the Fisher–Rao information metric sense. Similarly, for positively correlated variables, an increase or decrease in one variable always predicts the same directional change for the second variable: variables do not become more distant, thus more distinguishable in the Fisher–Rao information metric sense. This may lead us to guess that in the presence of anticorrelations, motion on curved statistical manifolds via the Maximum Entropy updating methods becomes less complex.
3.3. Trivariate Gaussian Statistical Model
In this section we consider a Gaussian statistical model
of the Equation (
12) when
. In this case as well, in order to understand the asymptotic behavior of the IGC in the presence of correlations between the micro-states, we make the minimal assumption that, given the random vector
distributed according to a trivariate Gaussian, then
and
. Therefore, the space of the parameters of
is given by
.
The manifold
changes its metric structure depending on the number of correlations between micro-variables, namely, one, two, or three . The covariance matrices corresponding to these cases read, modulo the congruence via a permutation matrix [
17],
3.3.1. Case 1
First, we consider the trivariate Gaussian statistical model of Equation (
12) when
. Then proceeding like in
Section 3.2 we have
, where
and
. Also in this case we find that the sectional curvature of Equation (
7) is a negative function. Hence, as we state in
Section 2, we may expect a decreasing (in time) behavior of the information geometry complexity. Furthermore, we obtain the geodesics
where
and
. We remark that
for all
. Then, the volume (
10) becomes
requiring
for its positivity. Finally, using (
33) in (
9) we arrive at the asymptotic behavior of the IGC
Comparing (
34) in the presence and in the absence of correlations yields
where “weak” stands for low degree of connection in the lattice underlying the micro-variables
Notice that is a monotonic increasing function of the argument .
3.3.2. Case 2
When the trivariate Gaussian statistical model of Equation (
12) has
, the condition
constraints the correlation coefficient to be
. Proceeding again like in
Section 3.2 we have
, where
and
. The sectional curvature of Equation (
7) is a negative function as well and so we may apply the arguments of
Section 2 expecting a decreasing in time of the complexity. Furthermore, we obtain the geodesics
where
and
. We remark that
for all
. Then, the volume (
10) becomes
We have to set
for the positivity of the volume (
37), and using it in (
9) we arrive at the asymptotic behavior of the IGC
Then, comparing (
38) in the presence and in the absence of correlations yields
where “mildly weak” stands for a lattice (underlying micro-variables) neither fully connected nor with minimal connection.
This is a function of the argument that attains the maximum at , while in the extrema of the interval it tends to zero.
3.3.3. Case 3
Last, we consider the trivariate Gaussian statistical model of the Equation (
12) when
. In this case, the condition
requires the correlation coefficient to be
. Proceeding again like in
Section 3.2 we have
, where
and
. We find that the sectional curvature of Equation (
7) is a negative function; hence, we may expect a decreasing (in time) behavior of the complexity. It follows the geodesics
where
and
. We note that
for all
. Using (
40), we compute
Also in this case we need to assume
to have positive volume. Finally, substituting Equation (
41) into Equation (
9), the asymptotic behavior of the IGC results
The comparison of (
42) in the presence and in the absence of correlations yields
where “strong” stands for a fully connected lattice underlying the (three) micro-variables. We remark the latter ratio is a monotonically increasing function of the argument
.
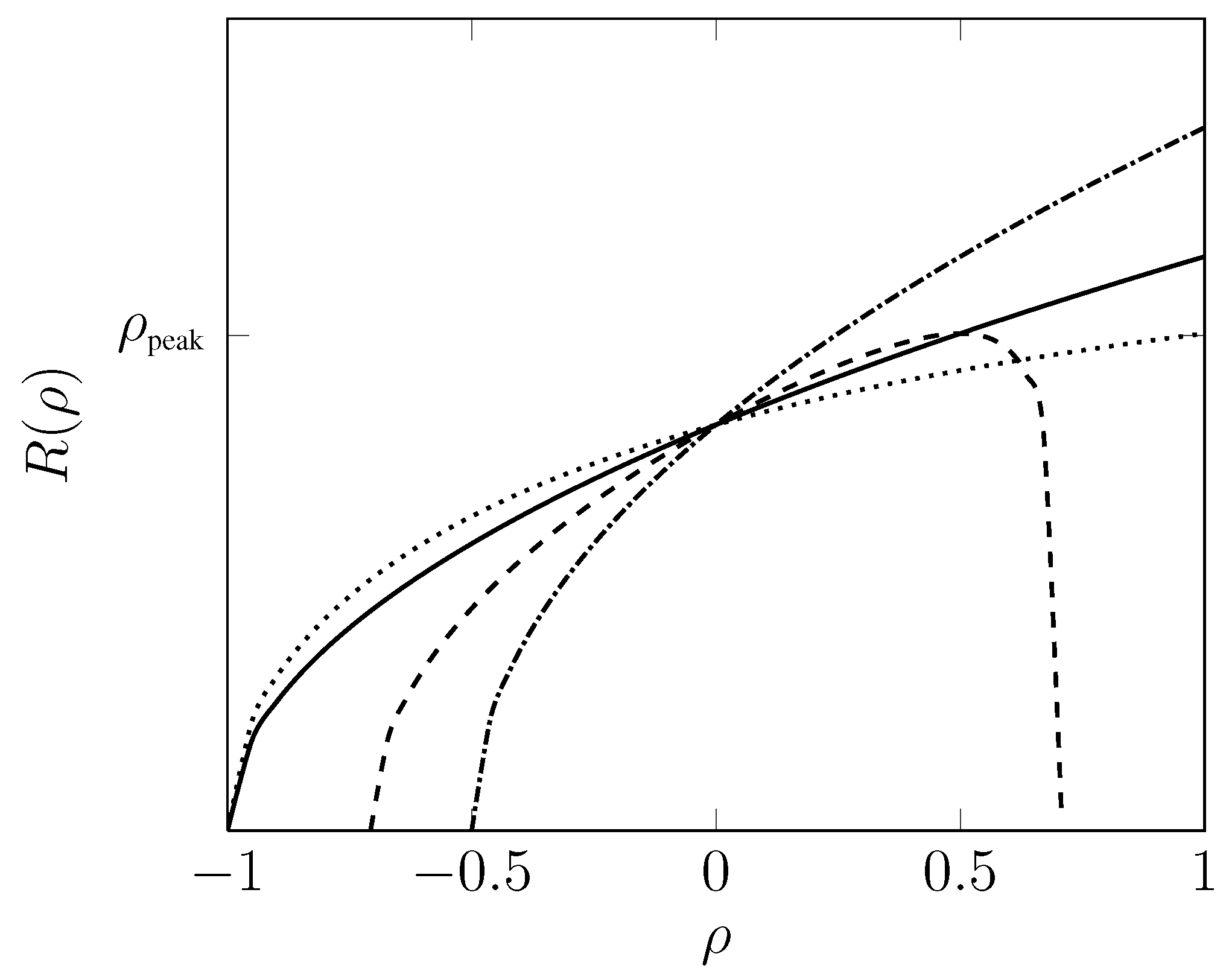
The behaviors of
of Equations (
30), (
35), (
39) and (
43) are reported in
Figure 1.
Figure 1.
Ratio of volumes vs. degree of correlations ρ. Solid line refers to ; Dotted line refers to ; Dashed line referes to ; Dash-dotted refers to .
Figure 1.
Ratio of volumes vs. degree of correlations ρ. Solid line refers to ; Dotted line refers to ; Dashed line referes to ; Dash-dotted refers to .
The
non-monotonic behavior of the ratio
in Equation (
39) corresponds to the information geometric complexities for the mildly weak connected three-dimensional lattice. Interestingly, the growth stops at a critical value
at which
. From Equation (
30), we conclude that entropic inferences on three Gaussian distributed micro-variables on a fully connected lattice is carried out in a more efficient manner when the two micro-variables are negatively correlated. Instead, when such micro-variables are positively correlated, macroscopic predictions become more complex that in the absence of correlations. Furthermore, the ratio
of the information geometric complexities for this fully connected three-dimensional lattice increases in a
monotonic fashion. These conclusions are similar to those presented for the bivariate case. However, there is a key-feature of the IGC to emphasize when passing from the two-dimensional to the three-dimensional manifolds associated with fully connected lattices: the effects of negative-correlations and positive-correlations are
amplified with respect to the respective absence of correlations scenarios,
where
.
Specifically, carrying out entropic inferences on the higher-dimensional manifold in the presence of anti-correlations, that is for
, is less complex than on the lower-dimensional manifold as evident form Equation (
44). The vice-versa is true in the presence of positive-correlations, that is for
.
4. Concluding Remarks
In summary, we considered low dimensional Gaussian statistical models (up to a trivariate model) and have investigated their dynamical (temporal) complexity. This has been quantified by the volume of geodesics for parameters characterizing the probability distribution functions. To the best of our knowledge, there is no
dynamic measure of complexity of geodesic paths on curved statistical manifolds that could be compared to our IGC. However, it could be worthwhile to understand the connection, if any, between our IGC and the complexity of paths of dynamic systems introduced in [
20]. Specifically, according to the Alekseev-Brudno theorem in the algorithmic theory of dynamical systems [
21], a way to predict each new segment of chaotic trajectory is obtained by adding information proportional to the length of this segment and independent of the full previous length of trajectory. This means that this information cannot be extracted from observation of the previous motion, even an infinitely long one! If the instability is a power law, then the required information per unit time is inversely proportional to the full previous length of the trajectory and, asymptotically, the prediction becomes possible.
For the sake of completeness, we also point out that the relevance of volumes in quantifying the
static model complexity of statistical models was already pointed out in [
22] and [
23]: complexity is related to the volume of a model in the space of distributions regarded as a Riemannian manifold of distributions with a natural metric defined by the Fisher–Rao metric tensor. Finally, we would like to point out that two of the Authors have recently associated Gaussian statistical models to networks [
17]. Specifically, it is assumed that random variables are located on the vertices of the network while correlations between random variables are regarded as weighted edges of the network. Within this framework, a static network complexity measure has been proposed as the volume of the corresponding statistical manifold. We emphasize that such a static measure could be, in principle, applied to time-dependent networks by accommodating time-varying weights on the edges [
24]. This requires the consideration of a time-sequence of different statistical manifolds. Thus, we could follow the time-evolution of a network complexity through the time evolution of the volumes of the associated manifolds.
In this work we uncover that in order to have a reduction in time of the complexity one has to consider both mean and variance as macro-variables. This leads to different topological structures of the parameter space in (
13); in particular, we have to consider at least a 2-dimensional manifold in order to have effects such as a power law decay of the complexity. Hence, the minimal hypothesis in a multivariate Gaussian model consists in considering all mean values equal and all covariances equal. In such a case, however, the complexity shows interesting features depending on the correlation among micro-variables (as summarized in
Figure 1). For a trivariate model with only two correlations the information geometric complexity ratio exhibits a non monotonic behavior in
ρ (correlation parameter) taking zero value at the extrema of the range of
ρ. In contrast to closed configurations (bivariate and trivariate models with all micro-variables correlated each other) the complexity ratio exhibits a monotonic behavior in terms of the correlation parameter. The fact that in such a case this ratio cannot be zero at the extrema of the range of
ρ is reminiscent of the geometric frustration phenomena that occurs in the presence of loops [
11].
Specifically, recall that a geometrically frustrated system cannot simultaneously minimize all interactions because of geometric constraints [
11,
18]. For example, geometric frustration can occur in an Ising model which is an array of spins (for instance, atoms that can take states
) that are magnetically coupled to each other. If one spin is, say, in the
state then it is energetically favorable for its immediate neighbors to be in the same state in the case of a ferromagnetic model. On the contrary, in antiferromagnetic systems, nearest neighbor spins want to align in opposite directions. This rule can be easily satisfied on a square. However, due to geometrical frustration, it is not possible to satisfy it on a triangle: for an antiferromagnetic triangular Ising model, any three neighboring spins are frustrated. Geometric frustration in triangular Ising models can be observed by considering spin configurations with total spin
and analyzing the fluctuations in energy of the spin system as a function of temperature. There is no peak at all in the standard deviation of the energy in the case
, and a monotonic behavior is recorded. This indicates that the antiferromagnetic system does not have a phase transition to a state with long-range order. Instead, in the case
, a peak in the energy fluctuations emerges. This significant change in the behavior of energy fluctuations as a function of temperature in triangular configurations of spin systems is a signature of the presence of frustrated interactions in the system [
19].
In this article, we observe a significant change in the behavior of the information geometric complexity ratios as a function of the correlation coefficient in the trivariate Gaussian statistical models. Specifically, in the fully connected trivariate case, no peak arises and a monotonic behavior in ρ of the information geometric complexity ratio is observed. In the mildly weak connected trivariate case, instead, a peak in the information geometric complexity ratio is recorded at . This dramatic disparity of behavior can be ascribed to the fact that when carrying out statistical inferences with positively correlated Gaussian random variables, the maximum entropy favorable scenario is incompatible with these working hypothesis. Thus, the system appears frustrated.
These considerations lead us to conclude that we have uncovered a very interesting information geometric resemblance of the more standard geometric frustration effect in Ising spin models. However, for a conclusive claim of the existence of an information geometric analog of the frustration effect, we feel we have to further deepen our understanding. A forthcoming research project along these lines will be a detailed investigation of both arbitrary triangular and square configurations of correlated Gaussian random variables where we take into consideration both the presence of different intensities and signs of pairwise interactions ( if , ).