A Probabilistic Description of the Configurational Entropy of Mixing
Abstract
: This work presents a formalism to calculate the configurational entropy of mixing based on the identification of non-interacting atomic complexes in the mixture and the calculation of their respective probabilities, instead of computing the number of atomic configurations in a lattice. The methodology is applied in order to develop a general analytical expression for the configurational entropy of mixing of interstitial solutions. The expression is valid for any interstitial concentration, is suitable for the treatment of interstitial short-range order (SRO) and can be applied to tetrahedral or octahedral interstitial solutions in any crystal lattice. The effect of the SRO of H on the structural properties of the Nb-H and bcc Zr-H solid solutions is studied using an accurate description of the configurational entropy. The methodology can also be applied to systems with no translational symmetry, such as liquids and amorphous materials. An expression for the configurational entropy of a granular system composed by equal sized hard spheres is deduced.1. Introduction
For a long time, configurational entropy has been calculated using the same formalism, i.e., computing the number of atomic configurations using the lattice gas model. Different expressions were deduced to solve specific problems as the ideal entropy of mixing is a crude approach for almost all applications, except very dilute solutions and high temperatures. All previous models compute the number of configurations under the following assumptions: (i) athermal mixture or non-interacting atoms, atomic complexes, molecules, or associated chemical species, leaving their internal properties unaffected, and (ii) no superposition among chemical species, (iii) the equivalence of all N lattice sites, and (iv) a rigid lattice with no distortion and constant volume is assumed. This methodology has been successfully applied in a number of completely different systems. Indeed, the analytically derived models are able to provide a good physical description in systems like linear polymers [1,2] or with different shapes [3], and interstitial solutions [4,5]. It has also been implemented to describe the glassy state [6]. In addition, it was applied in material science for developing general methodologies to study order-disorder in solid solutions and phase diagrams. Very precise methods were developed, such as the Cluster Variation Method (CVM) [7], with its well-known increasing complexity in multicomponent alloys or big maximum clusters, and the Cluster Site Approximation method (CSA) [8], more suitable for applications in such systems at the cost of introducing extra parameters. Unfortunately, an analytical expression can not be derived directly from these methods.
The traditional methodology, however, has encountered severe restrictions in the development of expressions in multicomponent complex systems such as interstitial solid solutions or liquids and amorphous materials. Although a huge amount of works has been carried out in both fields of research, the deduction of accurate analytical expressions for the configurational entropy of mixing has been very elusive due to the complicated underlying physics. While the difficulties with interstitial solutions arise in the blocking effects, the difficulties with liquids, amorphous materials and glasses are derived from the almost insurmountable task of computing the number of configurations in a system without lattice periodicity. In addition, the number of configurations will depend on the characteristics of the interactions between the chemical elements in each particular system, thus adding more difficulties in multicomponent systems.
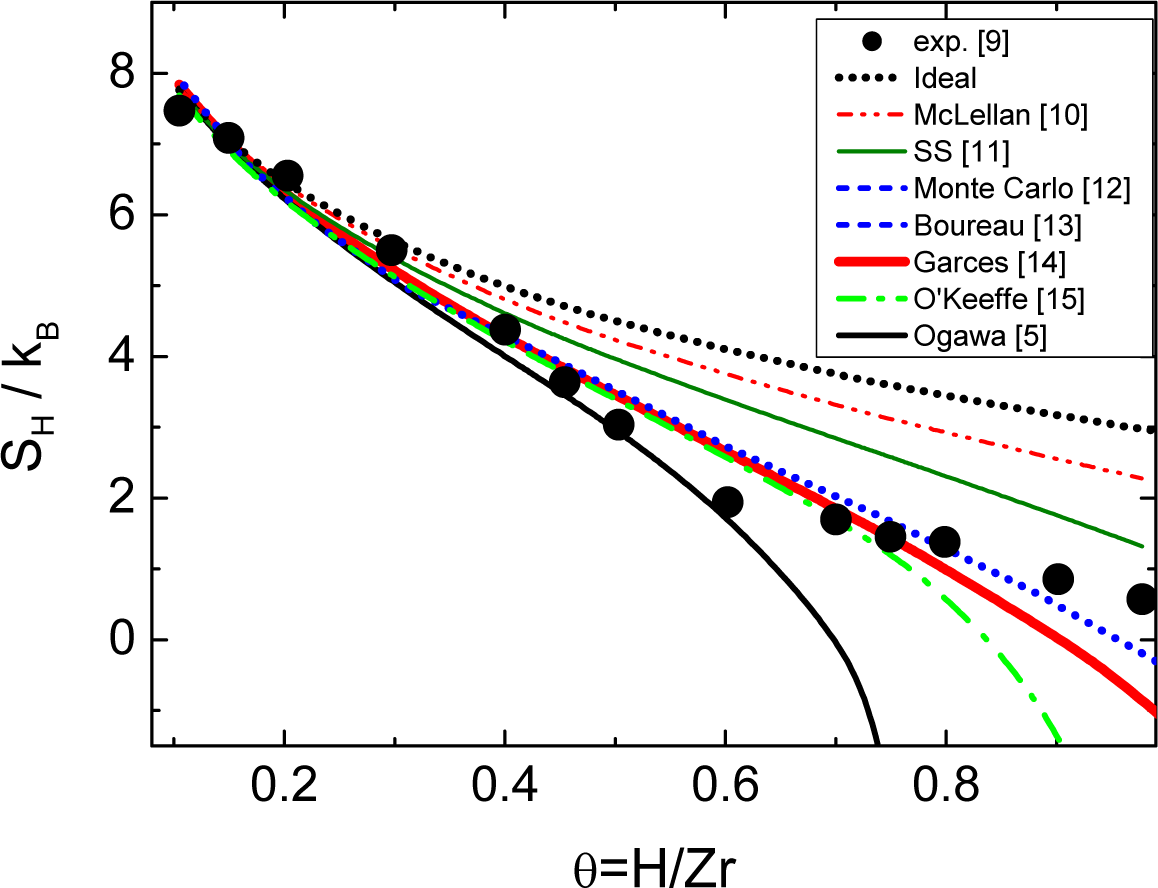
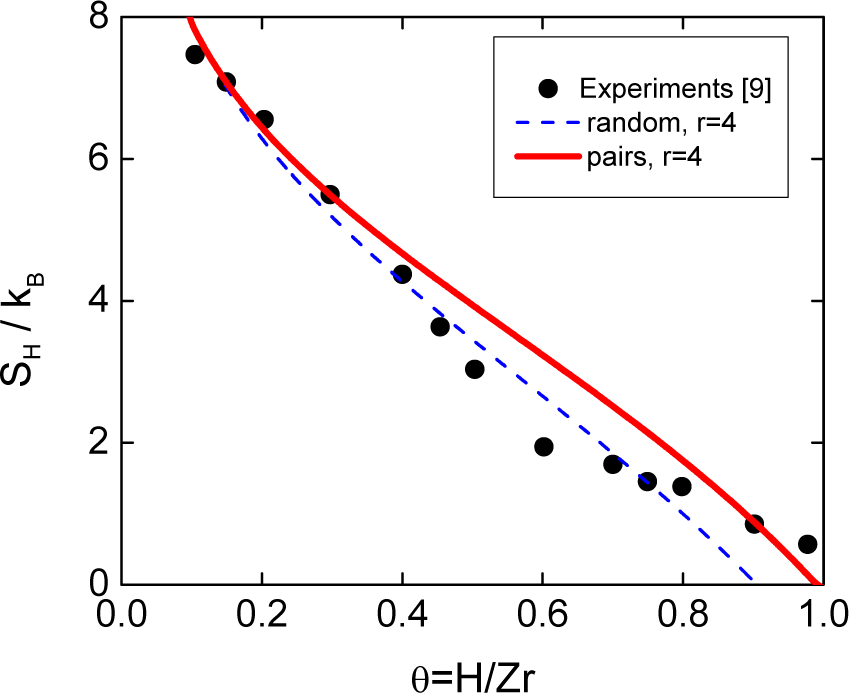
Although there are several expressions which can be used to compute the entropy of mixing in interstitial solid solutions, as Figure 1 shows for the bcc Zr-H system, they are all approximated or limited to low or medium solute concentration. The interactions between defects are not considered in previous analytical models for interstitial solutions due to the difficulty of including long-range interactions in the methodology used to compute the configurational entropy. The difficulties in this kind of system arises from site blocking effects, where the occupation of an interstitial site is prevented by the prior occupation of a neighboring interstitial site, i.e., there is an effective repulsion or SRO between interstitial atoms which may be chemical and/or strain in origin. Moreover, a given site may be blocked simultaneously by more than one interstitial atom and, consequently, not all lattice sites are equivalent. The main consequence of the SRO is to produce a dramatic decrease in the number of configurations to be considered with the consequent difficulties in computing their number correctly, e.g., the number of configurations decreases from 2 × 1019 to 2 × 107 in Ti-O according to Boureau and Tetot [4]. There is experimental and theoretical evidence that the random behavior model assumed in this kind of solid solutions is not appropriate in a number of systems, such as hcp R-H (R = Sc, Y, Lu) [16–18] and bcc Nb-H [19]. Unfortunately, the expressions available in the literature are not able to include the clustering or SRO. However, a simple, general expression overcoming the previous cited limitation has recently been deduced [19].
A similar situation to that in interstitial solutions, as regards the encoding of structural information into a compact expression, is found in liquids, amorphous materials and glasses. In these systems, the lack of periodicity of the atomic arrangements makes the deduction of a universal and unique structural description a very difficult task, leaving many open questions unanswered. Consequently, the deduction of an analytical expression for the configurational entropy of mixing of multicomponent systems, valid for any non-crystalline state of the matter, remains a largely unsolved problem.
There are numerous systems where the ideal entropy describes the experimental data sufficiently well. However, is the physics of these systems described correctly or is it just a model at hand fitting the configurational entropy data? The research on interstitial and amorphous systems shows that previous to the calculation of the configurational entropy, a detailed knowledge of the main physical features of the system is necessary. Nevertheless, this information will not be so useful unless an adequate theoretical tool is available. There are many examples of this issue in the scientific literature. The main purpose of this work is to present an alternative formalism for the calculation of the configurational entropy of mixing overcoming the previous limitation, and useful for application in complex systems even with no translational symmetry, such as liquids and amorphous materials. The methodology is based on the identification of the energy independent complexes in the mixture and the calculation of their corresponding probabilities.
This work is organized as follows: Section 2 presents a brief description of the methodology. The example of a linear polymer mixture is used to deduce the expressions due to Flory and to Huggins, and to illustrate the use of the current formalism once the main physical features of the system are identified. The method is applied to develop a general expression suitable for the study of SRO in interstitial solid solutions in Section 3. The final expression is implemented in the Fe-C system, and is also used to describe the SRO of H in bcc elements, such as Nb and Zr. Finally, in Section 4, the method is applied to an equal sized hard spheres system. Section 5 presents the Conclusions.
2. Probabilistic Description of the Configurational Entropy of Mixing
2.1. The Model
The entropy of a classical system with a discrete set of microstates is given by the Gibbs’ expression: . The index i labels all the microstate with energy Ei (i = 1,…,W) and Pi is the probability of finding a particular configuration of the ensemble consistent with a given energy value. If all microstates are equivalent with the same probability Pi = P = 1/W, the Boltzmann’s expression for the configurational entropy is deduced: S=−k ln(P)=k ln(W). Thus, the configurational entropy has been usually calculated by computing the number of configurations W. Nevertheless, it was shown that this property can also be deduced by computing probabilities through the inverse problem: S=−k ln(P) [14]. The probability P is a conditional one and its analytical determination is usually a very difficult task. However, if the assumption of energy independent complexes in the mixture is used, the conditional probability can be written as a product of independent probabilities. Therefore, if the complexes in the mixture can be identified, the configurational entropy is written as:
where ni and pi are the numbers and probabilities of each independent complex i in the mixture, respectively. Thus, Equation (1) could be a complement to the traditional method of computing the configurational entropy, helping in the understanding and identification of the representative physical features in complicated systems, such as interstitial solutions or amorphous materials.
2.2. Linear Polymer Solutions: Expressions of Flory and Huggins
The formidable problem of enumerating all the possible configurations available to the polymers on the lattice has been discussed by several authors. [1–3,20–27]. In this section, the procedure explained above is applied to a polymer solution composed of n linear polymers of size r and no monomers in order to deduce the Flory and Huggins expressions.
The approximations used by Flory to derive his well-known expression are the following:
- (1)
The lattice is rigid: independence of lattice constant on composition,
- (2)
Interchangeability of polymer segments,
- (3)
All polymers are of the same size,
- (4)
Average concentration of segments equal to overall average concentration.
To apply Equation (1) in a mixture of n polymer and n0 solvent molecules in a lattice of N = n0 + rn cells, it is only necessary to compute the probability of finding each kind of species under the above assumptions. The probabilities of finding any segment of the n polymer or a monomer are:
where φi is the volumetric fraction of each component. Replacing these expressions in Equation (1), Flory’s expression is obtained:
The computed probability of finding a polymer is an approximation in Flory’s model, but their number is correctly counted. It is important to note that Equation (3) is also valid, as a first approximation to the real problem, for polymers with different shapes as only volumetric effects are taken into account in the deduction.
A better approximation for the probability of finding a polymer was computed by Huggins, which also takes the surface fraction σ into account. In this way the size and number of bonds of the polymer are included in the description, but not its shape, e.g., numbers of kinks. For Huggins, the probability of finding a polymer is computed by:
where σi is the surface fraction of each component in the mixture. This expression means that the probability of finding a polymer is a conditional one. The condition to be fulfilled for each bond, assuming they are all independent, is to find the correct surface fraction with the right volumetric fraction. It is possible to include linear polymers with kinks in the previous expression taking into account only the number of independent free bond.
3. Analytical Expression for Interstitial Solutions
3.1. Configurational Entropy of Mixing and Interstitial SRO
The probabilistic approach of Equation (1) is applied in this section in order to develop a general analytical expression valid for any interstitial solid solution, suitable for describing clustering and SRO effects, based on the blocking model [11]. This approach will be called the SRO blocking model to distinguish it from the conventional random blocking model.
Due to interstitial repulsion, the set of vacancies is divided into two different species: free vacancies and blocked vacancies associated with each interstitial atom. The blocked vacancies do not participate in the mixing process as they are excluded for occupancy by other interstitial atoms. Therefore, it can be assumed that an interstitial complex of size , called basic complex in this work, is formed in the solid solution. It is important to note that interactions between the basic complexes can be developed for low temperature or high interstitial concentrations, giving rise to SRO with the formation of new interstitial complexes of size r times the number of interstitial atoms inside them. The complexes are energy independent entities, i.e., no interactions or correlations are assumed between them.
Therefore, the original problem could be re-interpreted as a random mixture of independent complexes of different sizes: free vacancies of one lattice site size and ni interstitial complexes of sizes ri formed by the interstitial atom and their respective blocked vacancies, fulfilling the following relation:
where β is the number of interstitial sites per metal atoms and βN the total number of interstitial lattice sites. Thus, the total number of independent complexes in the mixture is:
These complexes could be free vacancies, individual interstitials, pairs and double pairs of interstitial atoms, among others. The probability of finding each one is computed by:
where the indices i and j label all the interstitial clusters and free vacancies in the mixture. The simplest and most general expression deducible in the context of Equation (1), valid for any interstitial solutions including clustering and SRO effects, is:
where θi=ni/N is the composition of each independent complex in the solid solution.
The partial entropy of mixing for a random mixture of vacancies and one kind of interstitial atom I, computed from Equation (8) is:
Equation (8) takes into account only volumetric effects through the size r of the blocking sphere. The number of blocked vacancies is (r − 1) if there is no overlap between interstitial complexes. However, if soft blocking is present in the solid solution, the number of vacancies to be included in the size r depends on the number n of interstitials sharing the same vacancy. In this case, the number of blocked vacancies associated with each interstitial is (r − 1)/n. It is important to mention here that Equation (8) has only one parameter, the size r of each interstitial complex which can be computed knowing the solubility limit of the solid solution. Consequently, and at variance with previous models, it is not an adjustable empirical parameter. The size r could remain constant for all compositions, as in the examples presented in this work, or could change with the temperature and composition if there are different ordered phases in the solid solutions, as it is observed in the α-phase of the Zr-O system [28]. Equation (8) shows an easy way to introduce both dependencies into the present model.
The unknown variables in Equation (8) are the number of independent interstitial complexes for each interstitial concentration. These quantities are computed in this work using a phenomenological model with as few parameters as possible fitted to experimental data. They are modeled by the following functions:
- (i)
a linear function:
- (ii)
a quadratic function:
- (iii)
a sigmoid function:
In these functions, θI is the interstitial concentration. Whereas the first two functions model the compositional dependence of the clusters starting at θI = 0, the last one began at a critical composition θc described by the parameter C. The parameters A and B are related to the number of clusters in the mixture and the growth rate of clusters vs. interstitial concentration, respectively.
3.2. The Ti-O System
One interesting example to illustrate the methodology outlined in Section 3.1 is the hcp Ti-O solid solution. In the hcp structure, there is only one octahedral interstitial site per metal atom, thus β = 1. The compound Ti2O is the solubility limit of the solid solution. Thus, the occupancy of one site excludes two near neighboring sites with a soft blocking character. Consequently, the number of blocking sites per interstitial atom is (r − 1) = 1. The expression for the partial configurational entropy deduced by applying Equation (9) is:
Equation (10) is the same as the one deduced in the early work of Moon [29] and, independently, by Boureau and Campserveux [30]. Equation (10) gives the same results as the quasichemical model with infinite interaction energy and a blocking size r = 2, as was pointed out by Moon. For other size r, Equation (10) is only approximated.
3.3. The Austenitic Fe-C System
The Fe-C in the austenitic phase is another useful system to apply Equation (9). Several expressions were proposed in the past to study this system. All of these were based on a random mixture of isolated C atoms located in the octahedral sites of the fcc structure. A reasonable agreement with experimental information is achieved because the models have adjustable parameters and, mainly, due to the data to be described are restricted to dilute solutions. Hillert [31] proposed an empirical analytical expression to describe the activity of C atoms for a composition ranging from pure Fe metal to the hypothetical ordered compound Fe4C. This author found that, although the expression has no rational grounds, the model gave a satisfactory, result close to the values used to fit the experimental data [31].
It is necessary to identify the structure of the compound corresponding to the solubility limit of the solid solution in order to apply Equation (9). Following Hillert, the Fe4C compound with the Pm3m space group is assumed. For this system, β = 1 as there is only one octahedral interstitial site per iron atom. The C atoms occupy the octahedral sites and block all their twelve near neighbors belonging to the interstitial lattice. The structural analysis reveals that the blocking effect has a soft character. Indeed, each blocked site is shared by four C atoms located in the second coordination sphere of the interstitial lattice. Consequently, the number of blocked sites per interstitial atoms is (r − 1)= 12/4 = 3 and the blocking sphere has a size r = 4, constant for all C concentrations. If Equation (9) is now applied, the expression for the partial configurational entropy is:
where x is the C molar fraction. The final expression for the C activity computed from Equation (11) is the same as that deduced by Hillert, providing a rational basis for the empirical expression.
One important issue to be noted here is that the Fe4C compound was selected as the solubility limit of the austenitic phase. This compound could not be a correct model for the real solubility limit and, consequently, the blocking model and the expression for the configurational entropy should be revisited once more experimental information is obtained. Previous modeling effort [32] shows that a small number of C-C pairs, below 5%, is compatible with the experimental Mössbauer data. However, a quantity below 5% of pairs cannot be detected by this experimental technique. Consequently, the controversies regarding the solubility limit of the austenitic phase and the existence or not of pairs still remain unresolved. The next section will show the procedure for including pairs in the current method for computing the configurational entropy of mixing.
3.4. The Nb-H System
The H-Nb system is an amazing system due to the still unsolved controversies relating to the experimental results, such as: (1) inconsistencies between the solubility limit and the size of the basic complex, i.e., the size of the blocking sphere, (2) the models for the configurational entropy, (3) the critical composition of the miscibility gap, (4) the length of the H-H interaction, (5) the nature of the α- and α′-phases and (6) the structural relation between the disordered and the ordered phases observed at low temperature and compositions θ = H/Nb > 0.75.
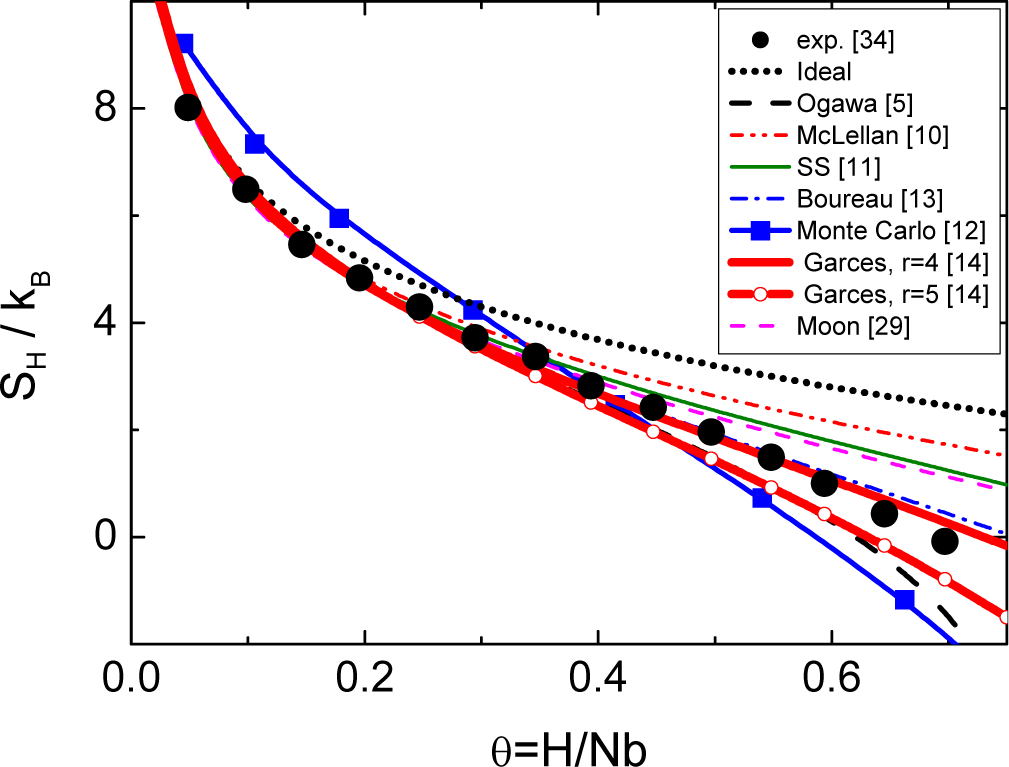
Although various models have been proposed in the past for Nb-H, the most precise analytical expression for the partial configurational entropy using the RBM is due to Boureau, as was shown by Oates et al. using the Monte Carlo method [33]. However, none of these are able to explain the experimental results for all H concentrations within the same structural model. This fact shows that the underlying physics of this system was not properly identified. Figure 2 shows a comparison between the different models for the partial configurational entropy available in the literature for Nb-H and the experimental data from Veleckis and Edwards [34]. All these models assume a random mixture of vacancies and isolated H atoms, leading to the question of whether the H-Nb system is properly described by the RBM.
It is clear from a comparison of the models shown in Figure 2 that the basic source of the controversies related to the Nb-H system is the size r of the basic complex and its change with the H concentration [5,10–15]. A structural model for Nb-H has recently been presented in [19] based on the identification of the main structural features of the solid solutions: the size r0 = 5 of the basic complex and the existence of SRO for all H concentrations. Based on this model, it is possible to solve the previously cited controversies.
3.4.1. Solubility Limit, Size of the Basic Complex and the Model for the Configurational Entropy
The experimental solubility limit of the solid solution is H/Nb = 1.21 ± 0.04 [15]. This limit can only be described if a basic complex of size r0 = 5 is assumed (see Figure 3a) but it is incompatible with the experimental data for the configurational entropy (see Figure 2). However, a combination of basic complexes, arising from statistical correlations and SRO, can also describe this limit. The simplest complex fulfilling the previous condition is a pair of H atoms with size r = 10, as it is shown in Figure 3b.
The configurational entropy derived from Equation (8) for a mixture of vacancies, isolated H atoms and pairs is:
In this expression β = 6 is the number of tetrahedral interstitial sites per metal atom in a bcc lattice, θ1 is the composition of isolated interstitial atoms and θ2 the H pairs concentration, verifying the relation θI = θ1 + 2θ2.
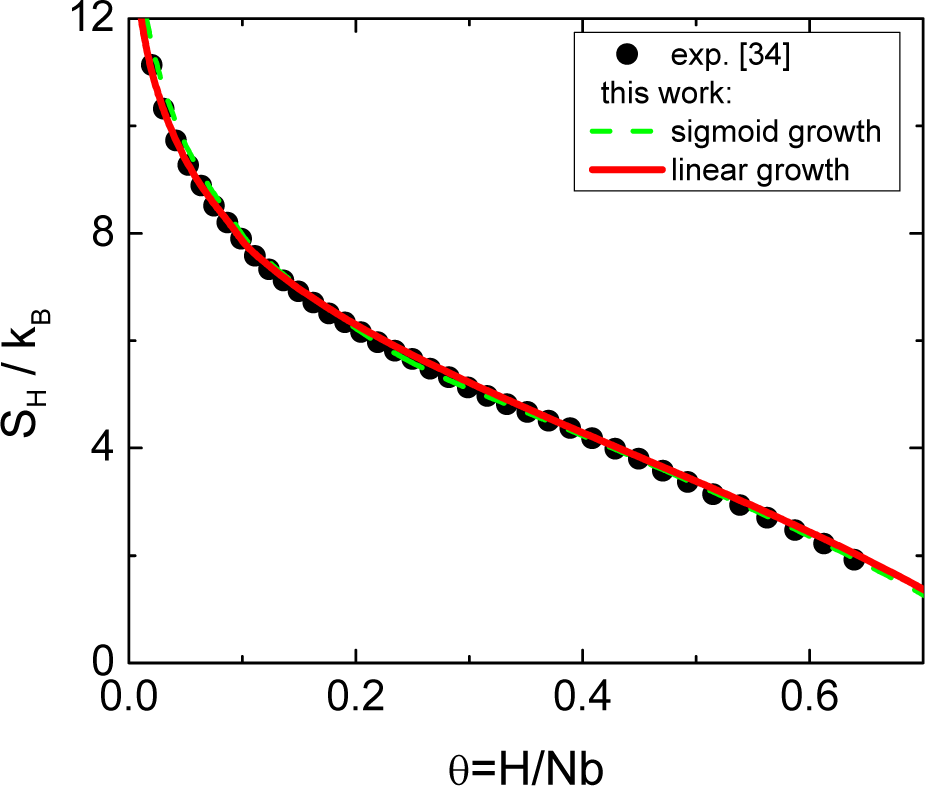
The dependence of the number of pairs vs. interstitial concentration has been modeled by three different functions. The values of the parameters adjusted to the experimental data are: (i) linear: A = 0.125, (ii) quadratic: A = 0.125 and (iii) sigmoid: A = 0.10, B = 20 and C = 0.21. The sigmoid function with A = 0.10 means that 18% of the H interstitial atoms are located in pairs. The results of the three models for the partial configurational entropy, computed numerically and plotted in Figure 4, show that the experimental data can be described better than previous models, with any of the three functions. However, the linear function with only one parameter shows the best agreement for all H concentrations.
These results highlight that it is possible to solve the controversies between the size of the basic complex, i.e., blocking sphere, and the experimental solubility limit using a hard blocking size for the basic complex of r0 = 5 and a solid solution composed of vacancies, isolated interstitial atoms and pairs. Moreover, the existence of pairs in the dilute solid solution, given by the three models, is compatible with the experimental evidence showing SRO for H concentrations lower than 1 at.% [35].
3.4.2. The Critical Composition of the Miscibility Gap and the Nature of the α- and α′-Phases
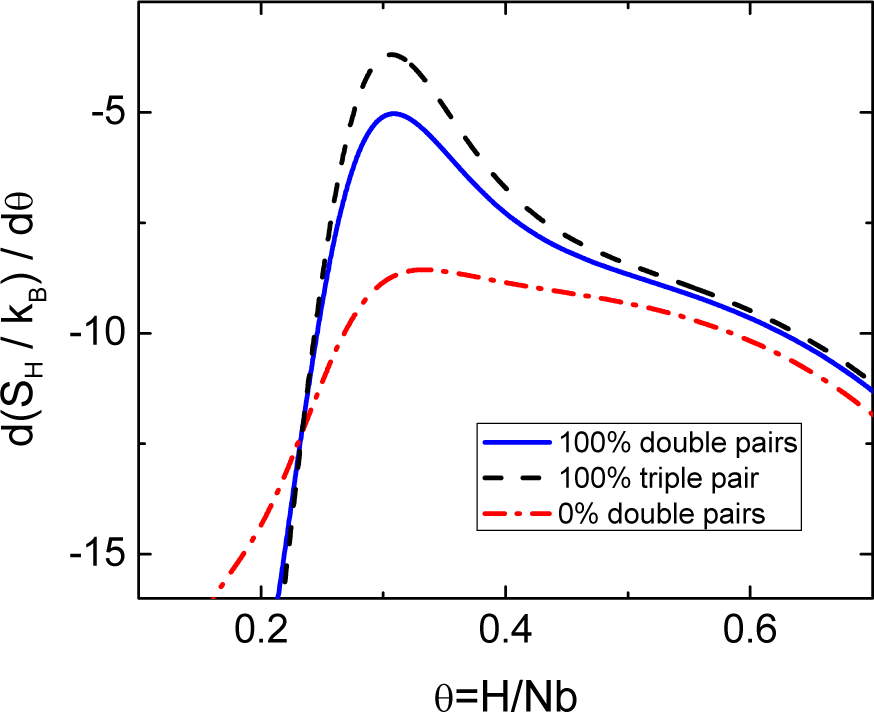
The good description of the partial configuration entropy achieved by including H pairs in the solid solution gives enough confidence in the model to compute the critical composition of the miscibility gap located at θc = 0.31 in the phase diagram. Previous models give a critical composition above θ = 0.4. The only exception is the sigmoid function, giving a critical composition at θc = 0.33. The last result, very close to the experimental critical composition, suggests that the miscibility gap could be related to an additional structural process, e.g., the clustering or ordering of pairs, characterized by a sigmoid growth beginning at a critical composition θc > 0. The present methodology can be applied easily to model the SRO of pairs if all the pairs in the mixture are assumed to form double or triple pairs. The configurational entropy expression for a mixture of vacancies of size r = 1, isolated H atoms with size r0 = 5 and double pairs with size r = 20 fulfilling the relation θI = θ1 + 4θ4 is:
Figure 5 shows the location of the partial configurational entropy maximum with the amount of double or triple pairs in the mixture giving a critical composition for the miscibility gap of θc = 0.307, in remarkable agreement with the experimental data. This result could resolve the controversies regarding the nature of the disordered phases. Whereas the α-phase could be formed by a random mixture of isolated H atoms and pairs, double and triple pairs could characterize the α′-phase.
It is also proposed that the double pair configuration could be interpreted as the seed for the ordered phases observed experimentally for H compositions greater than θ = 0.75. This work is focused on the structural properties of the solid solution; however, the interested reader can find details of the relation between pairs and the ordered phases in [19].
3.5. The bcc Zr-H System
Zr-H is another very interesting system with some unexplained results and unsolved controversies regarding the behavior of the H atoms in the bcc phase. It is currently assumed that the H atoms are located randomly in tetrahedral positions [9,36,37]. However, there is experimental evidence regarding precipitates of the γ-phase observed in the β-phase of Zr as a planar arrangement fulfilling the relation between these structures [38–41].
There are several models [5,10–15] which describe the interstitial solid solution in the bcc Zr-H system. However, they were all deduced based on a random mixture of H atoms with no statistical correlations and an assumed solubility limit of θ = 1.5. This limit is obtained within the present model by a basic complex of size r0 = 4 composed by 4 near-neighbor and 2 next-nearest-neighbor vacancies with soft blocking. Figure 1 shows that previous models fail to give a reasonable description of the experimental data. In addition, the unusual shape of the curve remains unexplained raising the question of whether the physics of this system is well modeled by a random mixture of H atoms.
The same methodology applied in Nb-H will be used in this system to look for a phenomenology different to the accepted RBM behavior. The first step is to apply Equation (12) to a solid solution composed of vacancies, isolated interstitial atoms and pairs. If this assumption is valid, the model should explain the shape of the data measured by Douglas. However, Figure 6 shows that the experimental data are well described only for a composition lower than θ = 0.4.
It is clear from Figure 6 that the existence of pairs in the solid solution is not enough to describe the shape of the partial configurational entropy and, consequently, the physics of this system for all H concentrations. Therefore, a phenomenon in addition to pair formation should exist for compositions beyond θ = 0.4. This work proposes that this phenomenon is related to the formation of double pairs in the solid solution. It is possible to compute them within the framework of the present formalism by considering a mixture composed by vacancies, isolated interstitial atoms, pairs and double pairs. The number of double pairs is modeled by a sigmoid function with parameters A = 0.06, B = 17 and C = 0.52 and the number of pairs beyond the critical composition θ = 0.4 will diminish according to the full interstitial concentration θI.
Figure 7a shows the behavior of the number of pairs and double pairs versus H concentration. Figure 7b shows a comparison between the experimental data for the partial configurational entropy and the theoretical result of this work. The agreement is noteworthy if the simplicity of the approach presented here, based on a random mixture of H clusters of different size, is taken into account. This is the first time that it is possible to visualize the effect of H clustering in such a straightforward way.
4. Non-crystalline State of Matter
The examples in Section 3 show the difficulties arising in counting the number of configurations if the assumption of no superposition between chemical species is abandoned. One solution has been proposed in this work using a methodology different from the traditional one.
The example of this section highlights the difficulties encountered in computing the configurational entropy of mixing when there is no periodicity of the lattice. The model of Section 2 can be applied as there is no reference to any lattice in the deduction of Equation (1). However, it is necessary to identify the energy independent complexes in the mixture and compute their probabilities. In addition, it is important to mention here that the reference states corresponding to the pure elements should be described with the same level of approximations used to describe the multicomponent amorphous system. For this purpose, as the first step in this research, the hard spheres system will be used, as it is a very simple model for fluids in general. Indeed, the current scientific literature reports that the equal sized hard spheres system has been used as a model for liquids, crystals, colloidal systems and, in particular, was very successful in modeling granular systems and powders. See [42–44], and references therein, for reviews in this field.
The quantitative morphological description of local structure is a requirement when studying amorphous systems, such as granular matter or glasses. While granular structures are disordered, metallic glasses displays various degrees of structural ordering beyond the short range. This means that a unique ideal structure where all the grains positions are uniquely assigned does not exist. There are a very large number of structures that have equivalent global properties (packing fraction, mechanical properties, etc.) but differ in the way the grains are locally arranged. The identification of the basic motif or structures is fundamental in order to apply the current methodology to compute the configurational entropy. However, how can different forms of disordered configurations with the same energy in systems with no translational symmetry be characterized?
There is a huge amount of research being carried out trying to answer that question. Of these, the results of Aste et al. [45–48] are relevant to this work. These authors found a universal relation fulfilled by all idealized granular materials. The same approach is adopted in this work to find an analytical expression for the configurational entropy of a system composed by equal sized hard spheres.
The Aste et al. model is based on a subdivision of the total volume in cells using the Voronoi partition. The authors showed that the local volume distributions of granular packings of monodisperse spherical grains are described very well by a universal distribution function, i.e., k-Gamma distributions. In addition, the volume distribution collapses on the same curve when the data are plotted vs (v − Vmin)/(<v> − Vmin) instead of v. The distribution was deduced using statistical mechanics and a very simple hypothesis that the Voronoi cells in the systems have k degrees of freedom associated with their volumes. k is a structure parameter which depends on the system phase. The main advantage of this model is that the parameter k describes all the crystalline states of the hard spheres system, i.e., from dilute gases to a jammed state. There is a simple dependence of k vs ρ (ρ is the packing fraction) with a sharp transition at the random close packing limit ρ → 0.645.
The formalism of Section 2 is applied in this work to this idealized system. The identification of the basic complex or motif is fundamental to the application of the current methodology to compute the configurational entropy. For this system such structures are the Voronoi cells with k degrees of freedom and volume v. Therefore, the original problem could be reinterpreted as a random mixture of independent complexes of different volume. We need only to find the number of each complex with a given cell volume and their probability as a function of the total volume VT. Consequently, in the present approach, only volumetric effects are taken into account.
The volume distribution of the Voronoi cells for a given k is the k-gamma function in the variable v − Vmin. In this model, the probability pi of a cell with volume vi is:
The k-gamma function is characterized by a shape parameter k and a scale parameter (<V> − Vmin)/k, where Vmin is the minimum available volume. The total number of complexes is N, equal to the number of hard spheres in the system. The number of each one of the complexes with volume vi is Npi. Finally, the expression for the configurational entropy of N hard spheres system is:
This expression should be put in a compact form in order to get a useful expression to compare with previous expressions and to deduce the equation of state of this idealized system. In any case, the hard spheres system is a nice example showing the benefit of using Equation (1) once the physics and the energy independent entities in the mixture are identified.
5. Conclusions
This work presents a formalism to calculate the configurational entropy of mixing alternative to the usual method of counting the number of atomic configurations. The traditional methodology found important restrictions to encode the physical information into compact expressions in complex systems such as interstitial solid solutions or liquids and amorphous materials. The methodology presented in this work is based on the identification, through a careful analysis of the main physical features of the system, of the energy independent complexes in the mixture and the calculation of their corresponding probabilities. The examples presented in this work, related to interstitial solutions and equal sized hard spheres fluid, show that accurate and general expressions for the configurational entropy of mixing can be developed, even in systems with no translational symmetry.
The effects of H SRO on the structural properties of the bcc-H solid solutions, such as Nb-H and Zr-H, are analyzed using an accurate description of the configurational entropy developed in this work. This expression, suitable for the treatment of interstitial clustering and SRO, can be applied to tetrahedral or octahedral interstitial solutions in any crystal lattice. The structural model for the Nb-H solid solution presented in this work is based on the existence of H pairs in the α–phase and double pairs in α′-phase. The model explains unsolved controversies in this system related to the length of the H-H interaction, the critical composition of the miscibility gap and the relation between the disordered and the ordered phases. The same expression is applied to the bcc Zr-H system. The unusual shape of the partial configurational entropy measured in this system can be accurately described if pairs and a small amount of double pairs are included in the model. The expression deduced in this work, by including the effect of SRO, opens up new possibilities in the calculations of phase diagrams and the thermodynamic modeling based on an accurate physical description of the alloy.
Regarding blocking effects, it is important to note here the distinction between chemical and elastic blocking and their influence on the configurational entropy. The difference between these kinds of interaction cannot be distinguished with previous models, i.e., the analytical expression of all previous models can only account for blocking effects through the RBM with no SRO description. In addition, all the earlier analytical models and Monte Carlo simulations are computed for constant volume and rigid lattices. However, the elastic interactions and lattice distortions can introduce changes in the configurational entropy through the formation of new complexes. Indeed, the importance of elastic interactions on the phase transition in Metals-H systems was discussed by several authors [49,50].
In some systems, such as Nb-H, it is not easy to distinguish between both kinds of blocking effects. Indeed, the chemical and elastic interactions between basic complexes result in a new kind of complex, e.g., double and triple pairs. However, a clear distinction between the blocking effects can be found in hcp TM-H solid solutions (TM = Sc, Y, Lu). In these systems, the behavior of H atoms at intermediate temperatures is not well described by a random distribution of H atoms over tetrahedral sites. Instead, a random distribution of pair H-TM-H along the c-axis of the cell, where a TM is located in the middle of the pair, is more appropriate for intermediate temperatures. These pairs are formed due to the chemical interactions between H atoms. In addition to chemical blocking effects, there is another one related to the relaxation of the host metal around the H-TM-H pairs providing support for the existence of a coherent stress field whose consequence is a chain formation along the c-axis of the hcp cell, observed only in Sc, Y and Lu but not in Ti and Zr [16–18]. The methodology presented in this work is able to describe the contribution to the configurational entropy arising from lattice distortions by using Equation (8), i.e., the pair and chains with different lengths can be modeled taking each of them as non-interacting complexes.
If there is no formation of new complexes, Equation (8) is also suitable for treating the expansion of the host lattice and, consequently, the quantity of interstitial atoms as a function of T and composition. It is only necessary to make the size of the complexes a function of T. This effect can be found in Nb-H. There is experimental and theoretical evidence showing a change from 3-shell to 2-shell blocking as temperature is increased [51], a result easily modeled with the present formalism. In contrast to previous methods, Equation (8) does not require the variation of r with the interstitial concentration but the solubility limit as a function of T should be correctly described. The energy interaction arising from small lattice distortion which is not able to form a new complex should be accounted for in the remaining part of the free energy (energy or enthalpy).
A similar situation to that of interstitial solutions in terms of deducing a general analytical expression for the configurational entropy of mixing is found in liquid, amorphous materials and glasses, due to the lack of lattice periodicity. In this work, an analytical expression based on the model of Aste et al, is derived for a system composed of equal sized hard spheres. This system will be used as the reference state of the pure elements in order to compute the configurational entropy of mixing in multicomponent glasses, a work that is in current development.
Conflicts of Interest
The author declares no conflict of interest.
PACS Codes: 82.60.Lf; 65.40.gd; 61.72.jj; 61.66.Dk
References
- Flory, P. Thermodynamics of High Polymer Solutions. J. Chem. Phys 1942, 10, 51–61. [Google Scholar]
- Huggins, M.L. Some Properties of Solutions of Long-chain Compounds. J. Phys. Chem 1942, 46, 151–158. [Google Scholar]
- Tompa, H. The athermal entropy of mixing of polymer solutions. Trans. Faraday Soc 1952, 48, 363–367. [Google Scholar]
- Boureau, G.; Tetot, R. Statistical thermodynamics of highly defective compounds. Phys. Rev. B 1989, 40, 2304–2310. [Google Scholar]
- Ogawa, H. A statistical-mechanical method to evaluate hydrogen solubility in metal. J. Phys. Chem. C 2010, 114, 2134–2143. [Google Scholar]
- Gibbs, J.; DiMarzio, A. Nature of the glass transition and the glassy state. J. Chem. Phys 1958, 28, 373–383. [Google Scholar]
- Kikuchi, R. A Theory of Cooperative Phenomena. Phys. Rev 1951, 81, 988–1003. [Google Scholar]
- Oates, W.A.; Zhang, F.; Chen, S.; Chang, Y. Improved cluster-site approximation for the entropy of mixing in multicomponent solid solutions. Phys. Rev. B 1999, 59, 11221–11225. [Google Scholar]
- Douglas, T. Statistical Model for the beta zirconium hydrides. J. Chem. Phys 1964, 40, 2248–2257. [Google Scholar]
- McLellan, R.B.; Garrard, T.L.; Horowitz, S.J.; Sprague, J.A. A model for concentrated interstitial solid solutions; Its application to solutions of Carbon in Gamma Iron. Trans. Metall. Soc. AIME 1967, 239, 528–535. [Google Scholar]
- Speiser, R.; Spretnak, J. Thermodynamics of binary interstitial solid solutions. Trans. Am. Soc. Met 1955, 47, 493–507. [Google Scholar]
- Oates, W.A.; Lambert, A.; Gallagher, P. Monte Carlo calculations of configurational entropies in interstitial solid solutions. Trans. Metall. Soc. AIME 1969, 245, 47–54. [Google Scholar]
- Boureau, G. A simple method of calculation of the configurational entropy for interstitial solutions with short range repulsive interactions. J. Phys. Chem. Solids 1981, 42, 743–748. [Google Scholar]
- Garcés, J. The configurational entropy of mixing of interstitials solid solutions. Appl. Phys. Lett 2010, 96, 161904. [Google Scholar]
- O’Keeffe, M.; Steward, S. Analysis of the thermodynamics behavior of H in body-centered-cubic metals with applications to Nb-H. Ber. Bunsenges. Phys. Chem 1972, 76, 1278–1282. [Google Scholar]
- Vajda, P. Hydrogen in rare-earth metals, including RH2+x phase. In Handbook on the Physics and Chemistry of Rare Earth; Gschneidner, K., Eyring, L., Eds.; North-Holland: Amsterdam, The Netherlands, 1995; Volume 20, pp. 207–291. [Google Scholar]
- Garcés, J.; González, R.; Vajda, P. First-principles study of H ordering in the α phase of M-H systems (M = Sc, Y, Ti, Zr). Phys. Rev. B 2009, 79, 054113. [Google Scholar]
- Garcés, J.; Vajda, P. H ordering in hcp M-H systems (M = Sc, Y; Ti, Zr). Int. J. Hydrog. Energy 2010, 35, 6025. [Google Scholar]
- Garcés, J. Short-range of H in the Nb-H solid solution. Int. J. Hydrog. Energy 2014, 39, 8852–8860. [Google Scholar]
- Guggenheim, E. Statistical thermodynamics of mixtures with zero energies of mixing. Proc. R. Soc. Lond. A 1944, 183, 203–212. [Google Scholar]
- Fowler, R.; Rushbrooke, G. An attempt to extend the statistical theory of perfect solutions. Trans. Faraday Soc 1937, 33, 1272–1294. [Google Scholar]
- Chang, T. The number of configurations in an assembly and cooperative phenomena. Proc. Camb. R. Soc 1939, 35, 265–292. [Google Scholar]
- Hildebrand, J. The entropy of solution of molecules of different size. J. Chem. Phys 1947, 15, 225–231. [Google Scholar]
- Staverman, J. The entropy of high polymer solutions. Generalization of formulae. Recl. Trav. Chim. Pays-Bas 1950, 69, 163–174. [Google Scholar]
- Kurata, M.; Tamura, M.; Watari, T. Statistical mechanics of polymer solutions. Parts I and II. J. Chem. Phys 1955, 23, 991–1003. [Google Scholar]
- Donohue, M.; Prausnitz, J. Combinatorial entropy of mixing molecules that differ in size and shape. A simpe approximations for binary and multicomponent mixtures. Can. J. Chem 1975, 53, 1586–1592. [Google Scholar]
- Freed, K.; Bawendi, M. Lattice theories of polimeric fluids. J. Phys. Chem 1989, 93, 2194–2203. [Google Scholar]
- Abriata, J.; Garcés, J.; Versaci, R. The O-Zr (Oxygen-Zirconium) system. Bull. Alloy Phase Diagr 1986, 7, 116–124. [Google Scholar]
- Moon, K.A. Thermmodynamics of interstitial solid solutions with repulsive solute-solute interactions. Trans TMS-AIME 1963, 227, 1116–1122. [Google Scholar]
- Boureau, G.; Campserveux, J. Contribution to the statistical treatment of interstitial solid solutions in the case of repulsive interactions. Philos. Mag 1977, 36, 9–17. [Google Scholar]
- Hillert, M. Analytical interstitial solution models. Zeitschrift für Metallkunde 1999, 90, 60–63. [Google Scholar]
- Laneri, K.; Desimoni, J.; Zarragoicoechea, G.; Fernández-Guillermet, A. Distribution of interstitials in fcc iron-carbon austenite: Monte Carlo simulations versus Mössbauer analysis. Phys. Rev. B 2002, 66, 134201. [Google Scholar]
- Meuffels, P.; Oates, W.A. Comparison of analytical approximations for hydrogen in b.c.c. metals with Monte Carlo calculations. J. Less Common Metals 1987, 130, 403–413. [Google Scholar]
- Veleckis, E.; Edwards, R. Thermodynamic properties in the systems vanadium-hydrogen, niobium-hydrogen, and tantalum-hydrogen. J. Phys. Chem 1969, 73, 683–692. [Google Scholar]
- Magerl, A.; Rush, A.; Rowe, J. Local modes in dilute metal-hydrogen alloys. Phys. Rev. B 1986, 33, 2093–2097. [Google Scholar]
- Zuzek, E.; Abriata, J.; San-Martin, A.; Manchester, F. The H-Zr (hydrogen-zirconium) System. Bull. Alloy Phase Diagr 1990, 11, 385–395. [Google Scholar]
- Fukai, Y.J. Site preference of interstitial hydrogen in metals. J. Less Common Metals 1984, 101, 1–16. [Google Scholar]
- Dey, G.; Banerjee, S. Decomposition of the β-Phase in Zr-20%Nb. J. Nucl. Mater 1984, 125, 219–227. [Google Scholar]
- Tewari, R.; Srivastava, D.; Dey, G.; Chakravarty, J.; Banerjee, S. Microstructural evolution in zirconium baseds alloys. J. Nucl. Mater 2008, 383, 153–171. [Google Scholar]
- Dey, G.; Banerjee, S.; Mukhopadhyay, P. Formation of gamma hydride in alpha and beta zircon ium alloys. J. Phys 1982, 43, 327–332. [Google Scholar]
- Flewitt, P.; Ash, P.; Crocker, A. Spontaneous hydride formation in β-phase niobium zirconium alloys. Acta Metall 1976, 24, 669–676. [Google Scholar]
- Cheng, Y.; Ma, E. Atomic-level structure and structure-property relationship in metallic glasses. Prog. Mater. Sci 2011, 56, 379–473. [Google Scholar]
- Parisi, G.; Zamponi, F. Mean field theory of hard sphere glasses and jamming. Rev. Mod. Phys 2010, 82, 789–845. [Google Scholar]
- Torquato, S.; Stillinger, F. Jammed hard-particle packings: From Kepler to Bernal and beyond. Rev. Mod. Phys 2010, 82, 2633–2672. [Google Scholar]
- Aste, T.; Di Matteo, T. Emergence of Gamma distributions in granular materials and packing models. Phys. Rev. E 2008, 77, 021309. [Google Scholar]
- Aste, T.; Di Matteo, T. Structural transitions in granular packs: Statistical mechanics and statistical geometricy investigations. Eur. Phys. J. B 2008, 64, 511–517. [Google Scholar]
- Anikeenko, A.; Medvedev, N.; Aste, T. Structural and entropic insights into the nature of the random-close-packing limit. Phys. Rev. E 2008, 77, 031101. [Google Scholar]
- Aste, T.; Delaney, G.; Di Matteo, T. k-Gamma distributions in granular packs. AIP Conf. Proc 2010, 1227. [Google Scholar] [CrossRef]
- Alefeld, G. Phase transitions of hydrogen in metals due to elastic interactions. Ber. Bunsenges. Phys. Chem 1972, 76, 746–755. [Google Scholar]
- Wagner, H.; Horner, H. Elastic interactions and the phase transition in coherent metal-hydrogen systems. Adv. Phys 1974, 23, 588–636. [Google Scholar]
- Oates, W.A.; Hasebe, M.; Meuffels, P.; Wenzl, H. Computer experiments on the thermodynamic properties of the primary solid solutions of Group Vb: Metal-Hydrogen systems. Z. Phys. Chem 1985, 146, 201–212. [Google Scholar]


© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Garcés, J. A Probabilistic Description of the Configurational Entropy of Mixing. Entropy 2014, 16, 2850-2868. https://doi.org/10.3390/e16052850
Garcés J. A Probabilistic Description of the Configurational Entropy of Mixing. Entropy. 2014; 16(5):2850-2868. https://doi.org/10.3390/e16052850
Chicago/Turabian StyleGarcés, Jorge. 2014. "A Probabilistic Description of the Configurational Entropy of Mixing" Entropy 16, no. 5: 2850-2868. https://doi.org/10.3390/e16052850



