Transitional Intermittency Exponents Through Deterministic Boundary-Layer Structures and Empirical Entropic Indices
Abstract
: A computational procedure is developed to determine initial instabilities within a three-dimensional laminar boundary layer and to follow these instabilities in the streamwise direction through to the resulting intermittency exponents within a fully developed turbulent flow. The fluctuating velocity wave vector component equations are arranged into a Lorenz-type system of equations. The nonlinear time series solution of these equations at the fifth station downstream of the initial instabilities indicates a sequential outward burst process, while the results for the eleventh station predict a strong sequential inward sweep process. The results for the thirteenth station indicate a return to the original instability autogeneration process. The nonlinear time series solutions indicate regions of order and disorder within the solutions. Empirical entropies are defined from decomposition modes obtained from singular value decomposition techniques applied to the nonlinear time series solutions. Empirical entropic indices are obtained from the empirical entropies for two streamwise stations. The intermittency exponents are then obtained from the entropic indices for these streamwise stations that indicate the burst and autogeneration processes.1. Introduction
Considerable progress has been made in understanding the basic physical processes underlying the transition of a laminar boundary layer into the turbulent state. Recently, a new approach has been introduced which uses dynamical systems theory in which the system’s trajectory traverses among mutually repelling flow states. Some of these flow states exist on the boundaries between laminar and turbulent states within the flow environment. These boundaries are assumed to be on the edge of the turbulent state, and are therefore called “edge states.” Cherubini, et al. [1] and Blau [2], have recently extended the concept of the edge of turbulence to a spatially developing flat plate boundary-layer flow. Their results indicate the presence of ordered structures, such as hairpin vortices and streamwise streaks. In the implementation of this approach, it is necessary to assume the presence of an initial disturbance to the flow. Cherubini, et al [3], presents results concerning the optimal disturbance that yields the largest energy growth rate for the disturbances. A “minimal seed,” is introduced that is considered to be the smallest flow structure for which the energy growth is maximized over short times.
However, this model does not indicate the occurrence of boundary layer flow “ejections,” which are abrupt outward flows of shear layer fluctuations or motions described as “sweeps,” which are associated with streamwise fluctuations moving toward the wall. Adrian [4] has presented an extensive review of the literature concerning the existence of these processes in the transition of the laminar boundary layer into the turbulent boundary layer. The flow structures discussed in this review [4] are single hairpin vortices with the formation of hairpin vortices into packets, which apparently evolve from a velocity field consisting of three-dimensional eddy structures. Adrian [4] indicates that at this point there is no definitive explanation for the processes involved in the formation of new packets within the flow field. Essentially, all that is known is that in fully developed turbulent flow, hairpin vortex packets are triggered continuously and in large numbers.
In this article, we present a nonlinear, low-dimensional computational model for an incompressible, laminar, three-dimensional boundary layer that should provide both the inherent unstable flow structures as input for the “edge states” studies and the prediction of both “ejections” or bursts outward from the region near the wall together with the sweep process of motion toward the wall. The spectral entropy of the time series solution of the computational model clarifies the ordered regions within the nonlinear time series solution, while the computation of the empirical entropy with the singular value decomposition method provides information concerning the nature of the distribution of kinetic energy over the empirical modes of the decomposition. The introduction of the empirical entropic index, and the subsequent evaluation of the intermittency exponent provide a connecting link within the computational procedure with the fully developed turbulent environment.
This article is organized in the following sections: In Section 2, we discuss the boundary layer flow environment that forms the basis for the evaluation of boundary layer deterministic structures. We also list the thermo-transport properties that are used throughout the computational scenario. In Section 3, we assume that our flow environment is a three-dimensional laminar flow over a flat plate with a constant velocity in the streamwise (along the x-axis) direction, with no pressure gradient, and that the flow is incompressible. We compute the laminar boundary layer development from the starting point of the plate, providing a priori the three-dimensional boundary layer velocity profiles at various stations in the streamwise direction (Cebeci and Bradshaw [5], Isaacson [6], Hansen [7]). In Section 4, the Townsend equations [8] are written for all three fluctuating velocity components within the given three-dimensional boundary layer flow. These equations are Fourier transformed into a set of deterministic equations (Hellberg and Orszag [9], Isaacson [10]) from which the time-dependent behavior of the both the Fourier components of the wave number vectors and the Fourier components of the fluctuating velocity wave vectors are obtained. The nonlinear transfer process between the streamwise fluctuating velocity wave component and the normal and spanwise velocity wave components is maintained through the inclusion of an internal feedback factor (Pyragas [11], Cuomo and Oppenheim [12]). This set of equations describing the spectral behavior of the fluctuating wave number components and the fluctuating velocity wave number components is specified as the “modified Townsend equations.” Section 5 presents the nonlinear time series solutions for the fluctuating velocity wave components at several streamwise stations. In Section 6, the spectral entropy rates for the nonlinear time series solutions are also computed at several streamwise stations. Ordered and disordered regions are indicated within the nonlinear time series solutions. The results for the singular value decomposition of selected regions of the nonlinear time series solutions are presented in Section 7. From these results, empirical entropy is defined for each of the empirical modes obtained in the computation (Isaacson [13]). In Section 8, the empirical entropic index (Tsallis [14]) is computed from the empirical entropy value for each empirical mode. Section 9 presents the intermittency exponent (Arimitsu and Arimitsu [15]) from the associated empirical entropic index for each empirical mode of the singular value decomposition process. The article closes with a discussion of the results and final conclusions.
2. Boundary-Layer Flow Environment
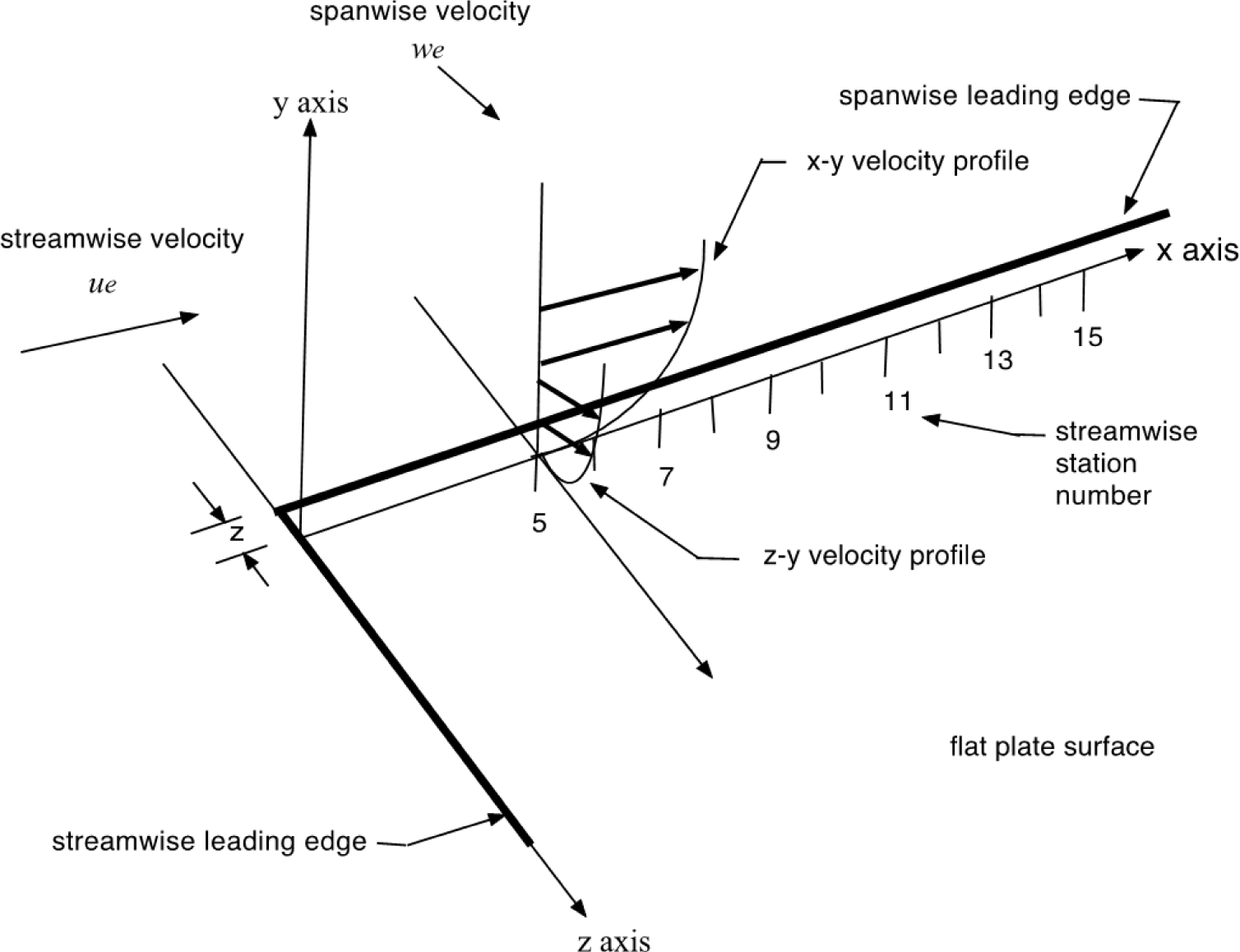
The fundamental three-dimensional laminar boundary layer flow environment that provides the control parameters for the study of the generation of nonlinear deterministic boundary layer structures is shown in Figure 1. Laminar boundary layer velocity profiles are computed for both the x–y plane and the z-y plane. The essential element of the study reported here is that these laminar (Blasius) boundary layer profiles are computed at thirteen downstream stations, from x = 0.08 (dimensionless units) to x = 0.32. These computations provide the numerical values for the velocity gradients for each of the boundary layer profiles at each of the streamwise stations.
These numerical velocity gradient values then serve as input control parameters for the computation of unstable nonlinear deterministic boundary layer structures for each of the streamwise stations. Our objective here is to gain some understanding of how the instabilities are initially generated, and how the developing laminar boundary layer characteristics affect the streamwise unstable deterministic structures along the boundary layer. We are not aware of previously published work delineating these processes.
The computational results for the laminar boundary-layer profiles and the initiation of nonlinear deterministic structures are dependent on the particular value of the kinematic viscosity chosen for the overall computational scenario. It has been found that the adiabatic combustion process of methane with 300 percent theoretical air at atmospheric pressure yields the composition and temperature for this pressure provides the value of kinematic viscosity that yields a prediction of strong deterministic structures. The process of finding these particular values of kinematic viscosity is trial and error and we have not discovered a systematic method for finding these values.
Table 1 provides the thermodynamic and transport property values used throughout the computational scenario. The thermodynamic values were obtained through the computation of the adiabatic flame temperature for the given fuel and air mixture and the transport properties were evaluated by the methods of Dorrance [16], which includes the Wilke approximation for the computation of the properties of mixtures of polyatomic molecules.
3. Laminar Boundary-Layer Development in the Downstream Direction
The three-dimensional flat plate boundary layer is approximated by assuming a spatially developing Blasius boundary layer in the downstream direction, yielding the mean velocity profiles in the x–y plane and an imposed spanwise Blasius boundary layer yielding velocity profiles in the z-y plane. The computer programs developed by Cebeci and Bradshaw [5] yielded numerical solutions for both the streamwise and the spanwise boundary layer velocity profiles. Isaacson [6] has presented the equations required for the laminar boundary-layer mean velocity gradients for each of the streamwise stations.
Hansen [7] has shown that the laminar boundary layers along the starting planes for the x–y and z–y planes are similar in nature. This similarity allows the computation of the laminar velocity profiles in the x–y and z–y planes at each of the downstream stations. The laminar velocity profiles in the z–y plane are computed at the spanwise station, z = 0.003, for each of the streamwise stations. These boundary layer velocity gradient profiles at each of the downstream stations provide the control parameters for the calculations of the nonlinear time series solutions for each corresponding station.
The computational results from the evaluation of both the spatially developing boundary layer and the spanwise boundary layer provide a three-dimensional field of mean values for the three boundary layer velocity component gradients. These gradients serve as control parameters for the modified Townsend equations which are then used to obtain the time-dependent solutions for the fluctuating velocity wave components at each streamwise station along the spatially developing boundary layer. It may be helpful to visualize the three-dimensional field of mean boundary layer velocity gradients as a computational container in which the fluctuating velocity field is placed. The time-dependent fluctuating velocity field then responds to the control parameters provided by the three-dimensional mean field of boundary layer velocity gradients at each downstream station of the spatially developing boundary layer.
4. Deterministic Equations for the Fluctuating Spectral Fields
We wish to obtain a set of coupled, nonlinear differential equations that will describe the time development of the fluctuating spectral components of velocity within the laminar boundary layer environment. This set of differential equations should be coupled and should retain the nonlinear terms that we anticipate will lead to the time-dependent development of unstable velocity fluctuations. The equations of motion for the boundary layer flow may be separated into steady plus fluctuating values of the velocity components. The equations for the velocity fluctuations may then be written as [8]:
In these equations, ρ is the density and ν is the kinematic viscosity. Taking the divergence of Equation (1) and invoking incompressibility, the pressure term may be transformed to:
In these expressions, Ui, represent the mean velocity components with i = 1,2,3 indicating the x, y, and z components, and xj, with j = 1,2,3, designates the x, y and z directions. The computational solutions for the three-dimensional laminar boundary layer flow provide the three mean velocity components and the nine gradients in the mean boundary layer velocities across the boundary-layer flow.
The fluctuating velocity and pressure fields are expanded in terms of sums of Fourier components [17]:
and
Substituting these expressions into Equation (1) yields an expression for the variations of the wave vector components with time, and also contains the pressure component, b. The pressure component is then transformed into a function of fluctuating velocity components and boundary layer velocity gradients through Equation (2) and substituted back into Equation (1). The time dependent solution for each of the velocity wave vector component amplitudes, ai(k), is then found from the equations:
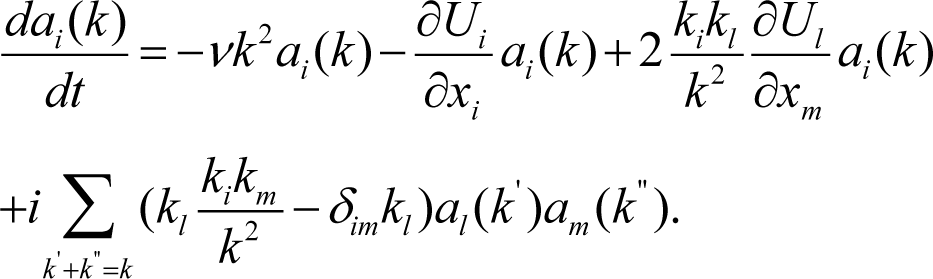
From the general equation for the balance of a transferable property, the rate of change of the wave numbers, ki may be written:
These two sets of equations will now be written in forms that incorporate the mean boundary layer velocity gradients from the steady state laminar boundary layer solution. Including the gradients of the mean velocities in the x–y and z–y boundary layers in the set of equations for the time-dependent wave number components yields the following set of equations:
We next include the mean laminar boundary layer velocity gradients in the transformed equations for the fluctuating velocity wave components. In addition, we introduce an internal feedback parameter for the coefficients of the nonlinear velocity wave components in Equations (5). The introduction of the feedback parameter will allow us to transform Equations (5) into a Lorenz-type format.
Mathieu and Scott [17] and Sagaut and Cambon [18] characterize the coefficients of the nonlinear products of the fluctuating velocity wave components in Equations (5):
as a projection matrix, with a given velocity wave vector component, ai, projected normal to the direction of the corresponding wave number component, ki. This matrix may then be interpreted as a nonlinear interactive transfer operator transferring kinetic energy at low wavenumber components toward higher wavenumber components. The projection matrix is heuristically replaced with an appropriate model equation of the form:
K is a weighting amplitude factor [11,12] and k(t) is the magnitude of the time-dependent streamwise wave number component given by:
Manneville [19] has used this form of weighting factor to describe pattern formations for different simple configurations. The feedback parameter, F, is defined as:
In this expression, the value of K is determined as the value that yields unstable solutions for the fluctuating velocity wave components within the laminar boundary layer. For the results presented in this article, we have found that K = 0.17992 for the kinematic viscosity given in Table 1.
Including the expressions for the mean boundary layer velocity gradients in Equations (5), and keeping the low order terms in the Fourier expansion process, including a feedback parameter for the nonlinear coupling terms, we arrive at the “modified Townsend equations.” These equations may then be arranged into a Lorenz form with the mean boundary-layer velocity gradients, the gas mixture kinematic viscosity and the feedback factor as the control parameters applied to the resulting Lorenz equations.
The mean boundary layer velocity gradients are computed for each streamwise station and reflect the changing nature of the boundary layer in the downstream direction. The nonlinear time series solutions of the modified Townsend equations are then obtained for each downstream station reflecting the effects of the changing boundary-layer flow. The nonlinear time series for a particular streamwise boundary layer station yield the time dependent values of the local wave number components and the fluctuating velocity wave components at that location. Each of the length parameters is non-dimensionalized by the corresponding plate length that is taken as one meter. The spatially developing boundary layer is computed for downstream locations in increments of 0.02 (2 cm), with the initial location at 0.02 (2 cm) downstream of the leading edge in the x-direction. Thirteen downstream stations are considered, beginning at the x location of 0.08, denoted as station one, through station thirteen, at a location of x = 0.32 from the origin of the boundary-layer flow. Station one at the location of 0.08 in the x direction is denoted as the transmitter station.
The nonlinear equations for the time-dependent velocity wave components are written for the initial (transmitter) station as [10]:
These equations are written in a Lorenz format. However, the coefficients are dependent on both the time-dependent wave number components and the steady boundary-layer velocity gradients for the initial transmitter station. The coefficients are written in the following form [10]:
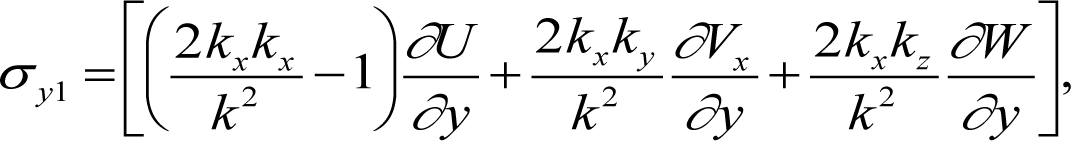
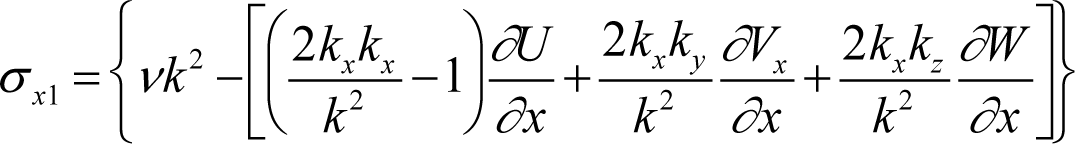
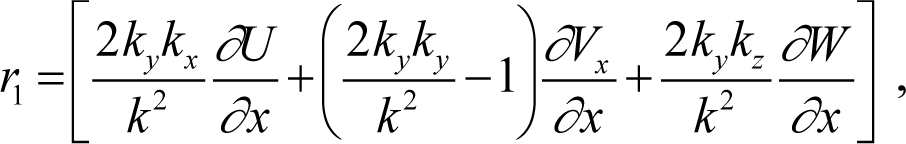
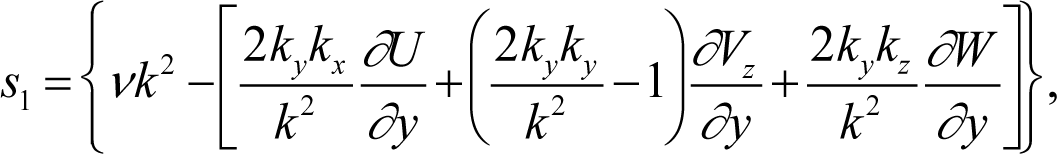
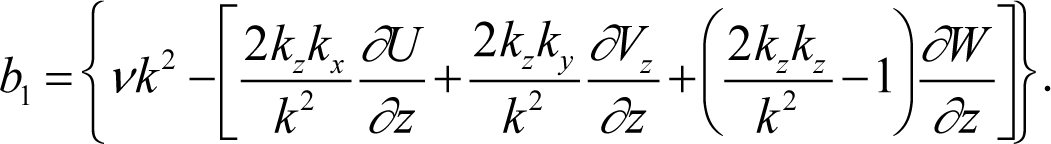
In our development, the nonlinear coupling for the normal and spanwise velocity wave components is modified by the internal feedback parameter (1–F). This factor is applied to the nonlinear terms, rather than to one of the individual variable terms.
The Lorenz system of equations has been shown to possess the characteristic of enhancing meaningful signals from a time series masked by chaotic signals [11]. Perez and Cerdeira [20] and Cuomo and Oppenheim [12] also discuss methods for extracting meaningful signals from nonlinear time series data. Feng and Tse [21] present a review of recent work in the application of the synchronization characteristics of the Lorenz equations in the field of chaos-based communications. We are applying the Lorenz form of the spectral equations for the fluctuating wave number and velocity fields at each of a number of downstream boundary-layer stations. The synchronization characteristics of the Lorenz equations are incorporated into the computational procedure at each of these downstream stations to take advantage of the enhancing process for the deterministic structures in our computational scenario.
The nonlinear equations for the time-dependent velocity wave components are applied at the initial station, denoted as the transmitter station, and to each of the downstream stations. Each of these downstream stations is denoted as a receiver station, following the nomenclature of communications theory. The time-dependent wave number components and the various boundary layer coefficients are computed for each of the receiver stations in the same manner as for the transmitter station. The output for the streamwise velocity wave vector component from the transmitter station is used as input for the streamwise velocity wave component in the nonlinear terms in the equation set at the first downstream receiver station. The input to the nonlinear coupled terms at the next downstream receiver station consists of the sum of the streamwise velocity wave component signal from the transmitter station plus the streamwise velocity wave component signal from the previous receiver station. The sum of the streamwise velocity wave components from each of the previous stations then serves as the input for the nonlinear terms in each of the subsequent station solutions.
For the nth receiver station, the nonlinear equations for the time-dependent velocity wave components are written as:
In these expressions, the input signal carrying the information from the initial transmitter station and the subsequent receiver stations to the r-th station is given by:
The computational scenario includes the solution of six simultaneous first-order differential equations, solved at each streamwise station distributed along the x-axis. The three equations for the wave number components, Equations (6), (7) and (8) are solved first, given the necessary control parameters for the mean velocity gradients from the boundary layer solution. The solutions for these equations are then stored to disc for input into the solution of the time-dependent velocity wave component equations, Equations (13), (14) and (15) at the first, or transmitter, station.
The solution of the equations for the velocity fluctuations yields the fluctuating velocity wave components for the given normal distance from the surface at the each of the streamwise stations along the x-axis. The spanwise station of z = 0.003, is held constant for each streamwise station. The Falkner-Skan transformation for the laminar boundary layer normal distance is defined as [5]:
It has been found that boundary-layer instabilities occur primarily within the boundary layer at a normal distance of η = 3.20. We have examined the prediction of boundary layer instabilities at vertical locations both above and below the value of η = 3.20, and have found negligible instabilities for those normal locations. The outer edge of the boundary layer is taken as ηe = 8.00. The initial conditions for the wave number components are kx1[1] = 0.04, ky1[1] = 0.02 and kz1[1] = 0.02. The initial values for the velocity wave components are ax1[1] = 0.20, ay1[1] = 0.01 and az1[1] = 0.001. The weighting factor has been found to be K = 0.17992 for the given kinematic viscosity.
Press [23] presents computer source codes for the integration of the equations using a fifth-order Runge-Kutta technique. The integration process uses a time step of 0.0001 s over 12,288 time steps included in the integration process. The time series solution for each velocity wave vector component is then processed to extract the characteristics of the deterministic structures represented in the time series solution.
5. Computational Results for the Deterministic Nonlinear Equations
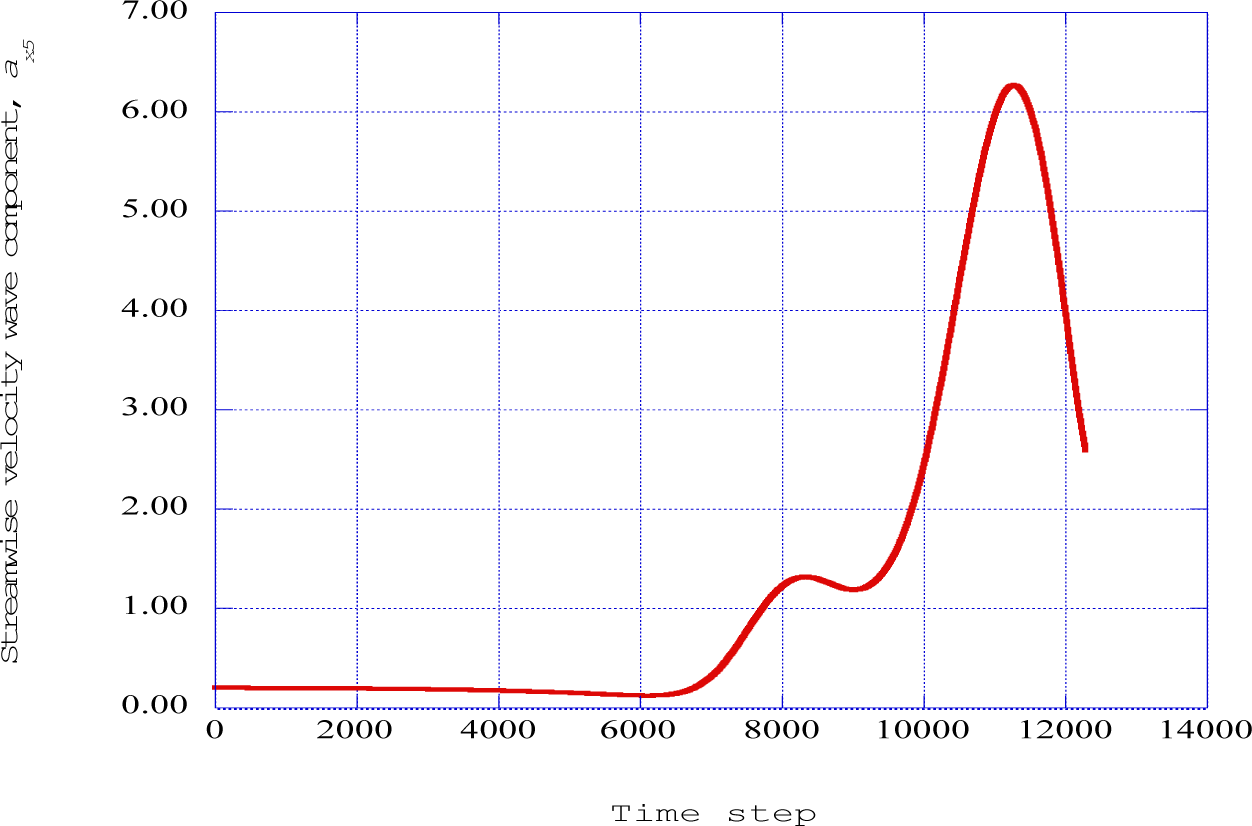
Figure 2 presents the fluctuating streamwise wave component for the fifth station over the range of the integration time step. The individual velocity gradients, obtained from the solution of the three-dimensional boundary layer equations, and the time-dependent values of the wave number components provide the necessary control parameters for the entire set of six deterministic equations.
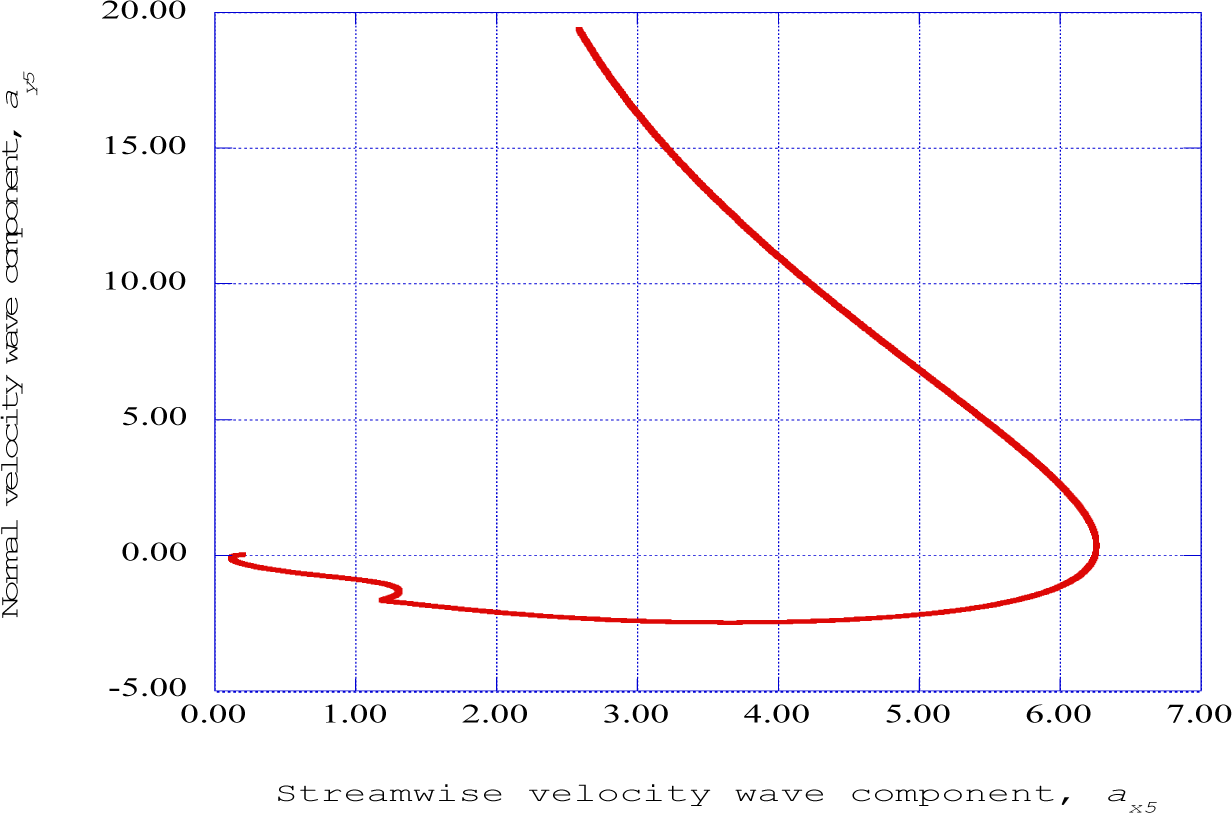
Figure 3 presents the streamwise velocity wave component the normal velocity wave component at the fifth streamwise station (x = 0.16). These results indicate that as the normal velocity wave component increases, the streamwise velocity component decreases. This indicates an outward “ejection” of flow that approaches a near vertical configuration.
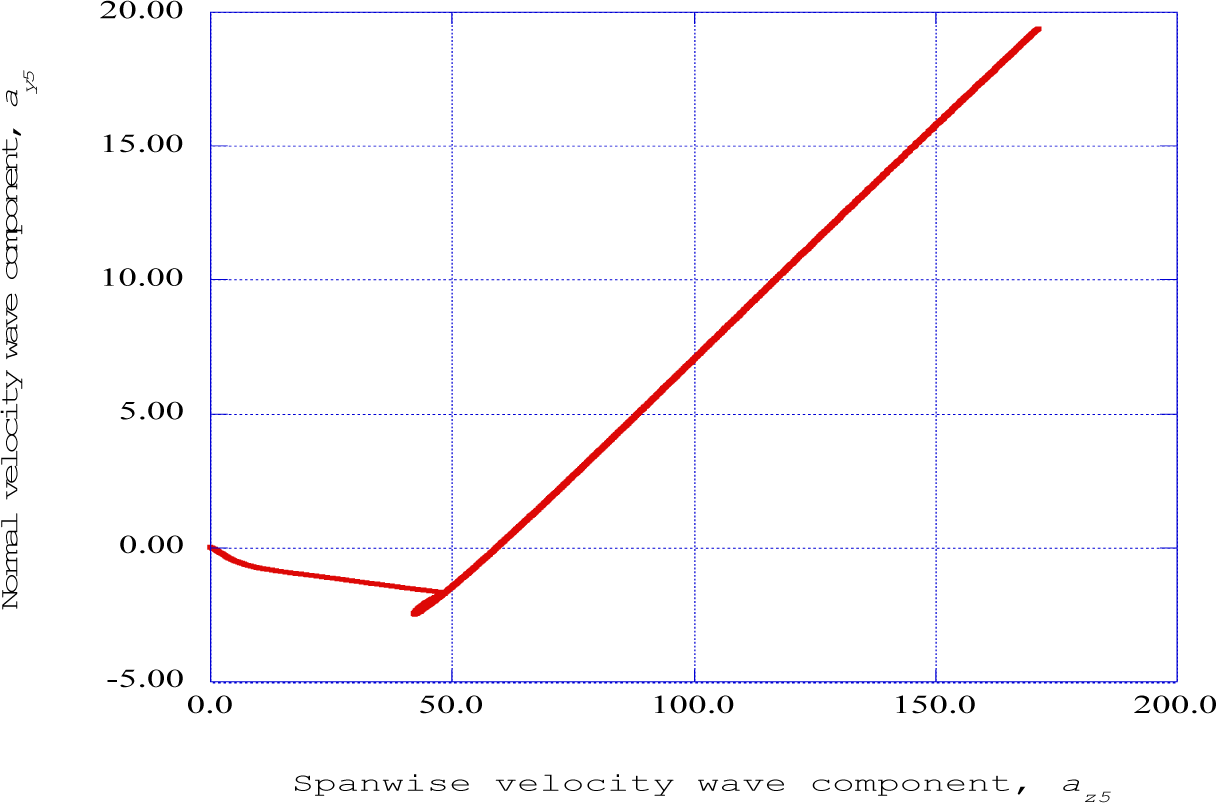
Figure 4 shows the fluctuating normal velocity wave component as a function of the fluctuating spanwise velocity component at the fifth streamwise station (x = 0.16). Apparently, the initiation of the “ejection” process includes a significant spanwise velocity wave component.
The computational procedure is initiated at the first or transmitter station, and then repeated for each subsequent streamwise or receiver station in the downstream direction. As indicated in Figures 2, 3 and 4, an “ejection” process is computed at station five in the streamwise direction. These “ejection” processes are predicted at stations six and seven, increasing in intensity. Hence, the “burst” process consists of a “sequence” of ejection processes, spread over several streamwise stations.
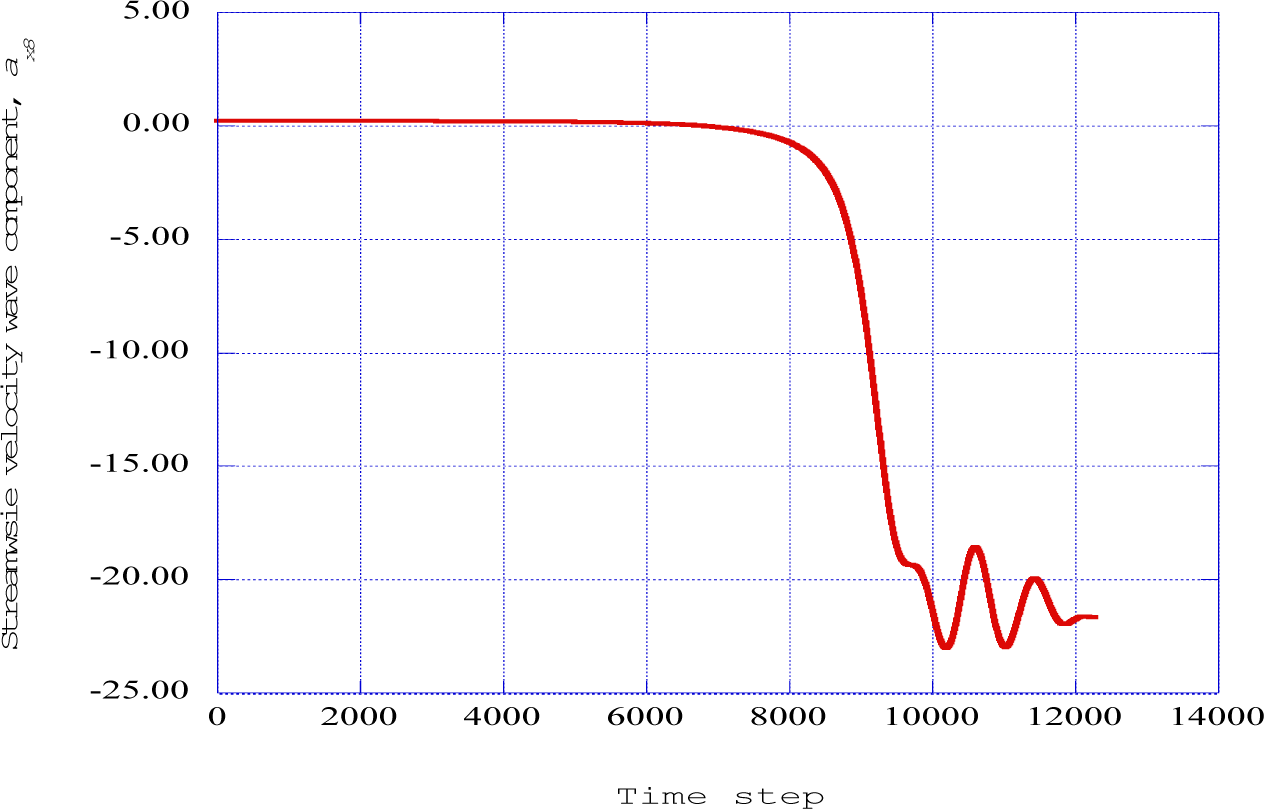
The streamwise velocity wave component produced by the receiver station at streamwise station eight (x = 0.22) is shown in Figure 5. A significant negative streamwise velocity wave component indicates a significant “sweep” process.
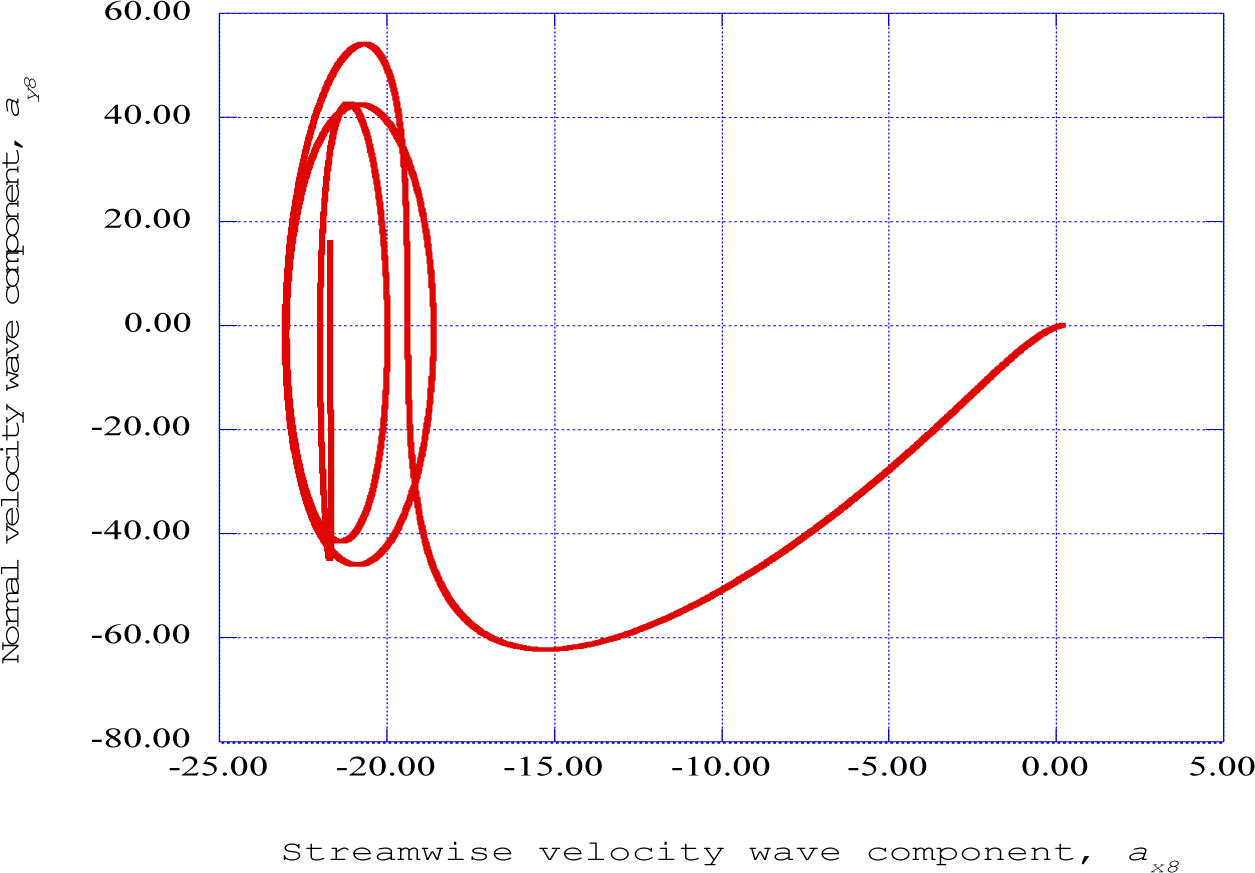
Figure 6 presents the streamwise velocity wave component versus the normal velocity wave component at streamwise station eight. The control parameters for this station are the wave number component values, the boundary-layer mean velocity gradients at this station, and the sum of the streamwise velocity wave components as indicated in Equation (25). These results indicate a negative streamwise velocity wave component moving in a downward normal direction, resulting in an oscillatory motion in the x–y plane. This flow configuration corresponds to the “sweep” phase of the overall process. This process is repeated at streamwise stations nine and ten, resulting in a “sequence” of downward processes over several stations, constituting the overall “sweep” process described in [4].
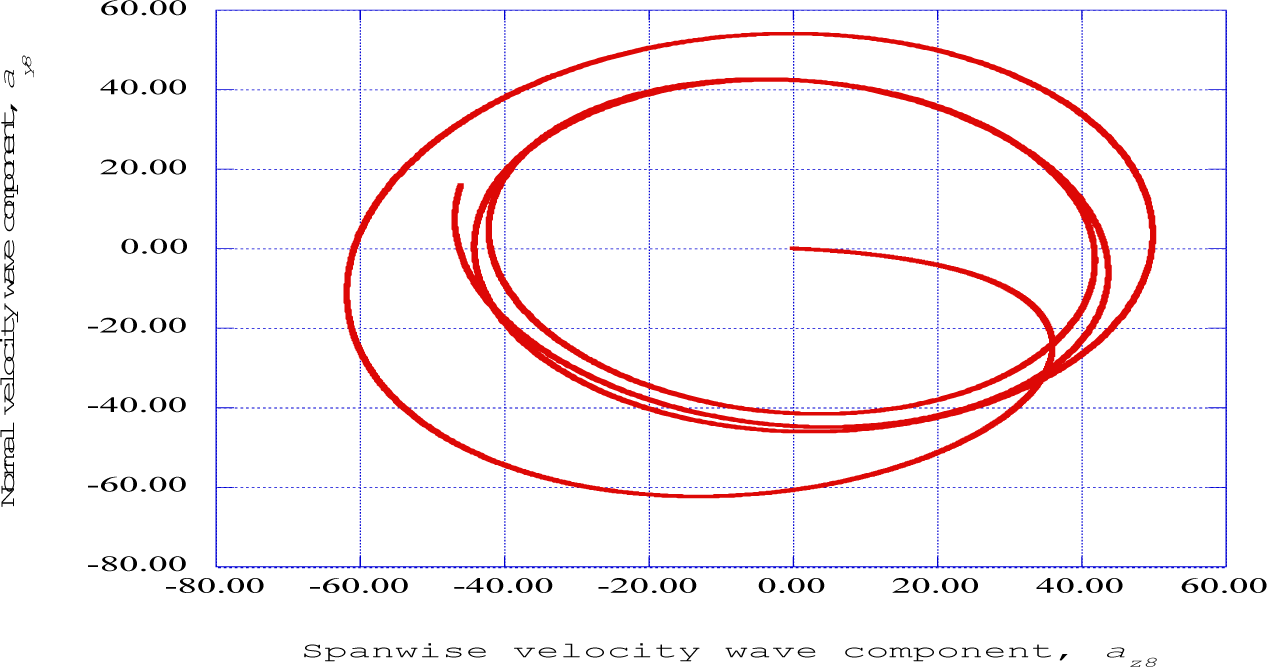
Figure 7 shows the phase plane, az8-ay8, for the output at streamwise station eight. These results indicate an oscillatory motion in the normal-spanwise plane, again, demonstrating that the normal-spanwise flow configuration plays a significant role in the “burst” and “sweep” phases of the transition of the laminar boundary layer state to the turbulent state.
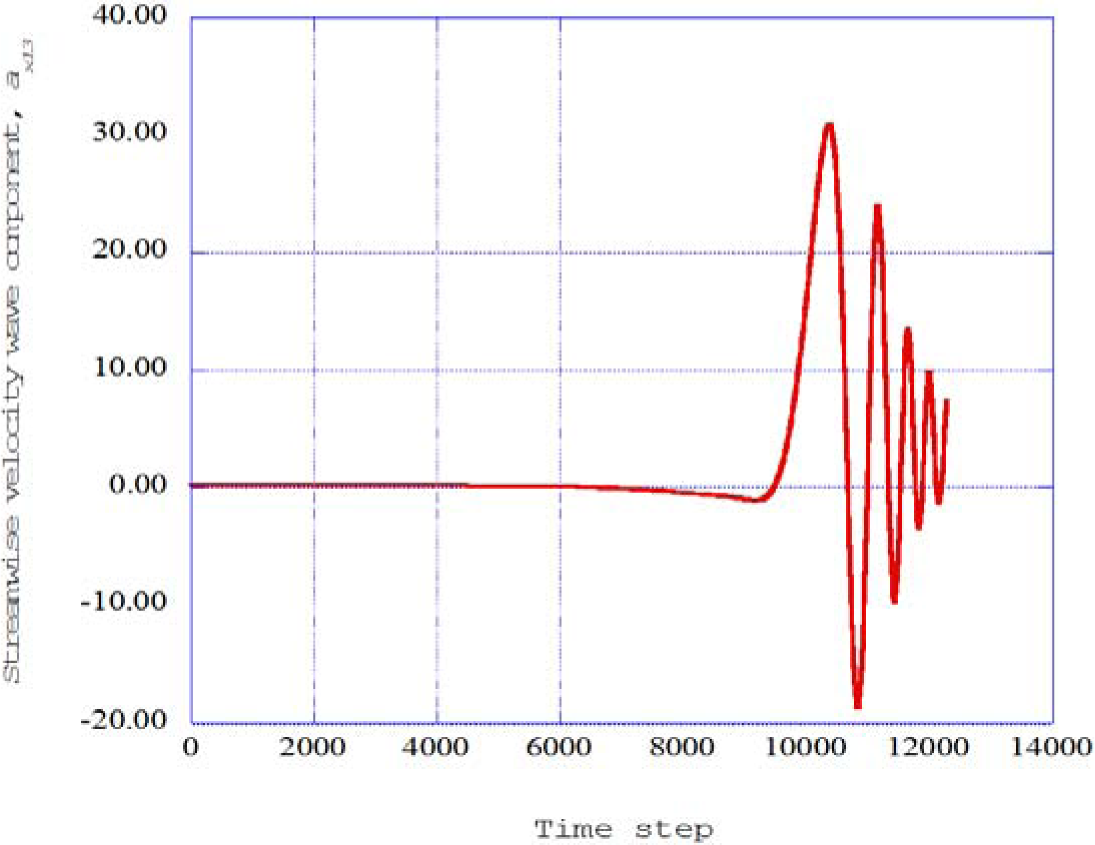
The streamwise velocity wave component at the streamwise receiver station thirteen is shown in Figure 8 as a function of the integration time step. These results indicate that the flow configuration has returned to the fundamental instability process that initiates the production of deterministic structures within the boundary layer. This is the initiation of the “autogeneration” process [4] in which the basic “burst” and “sweep” processes are regenerated.
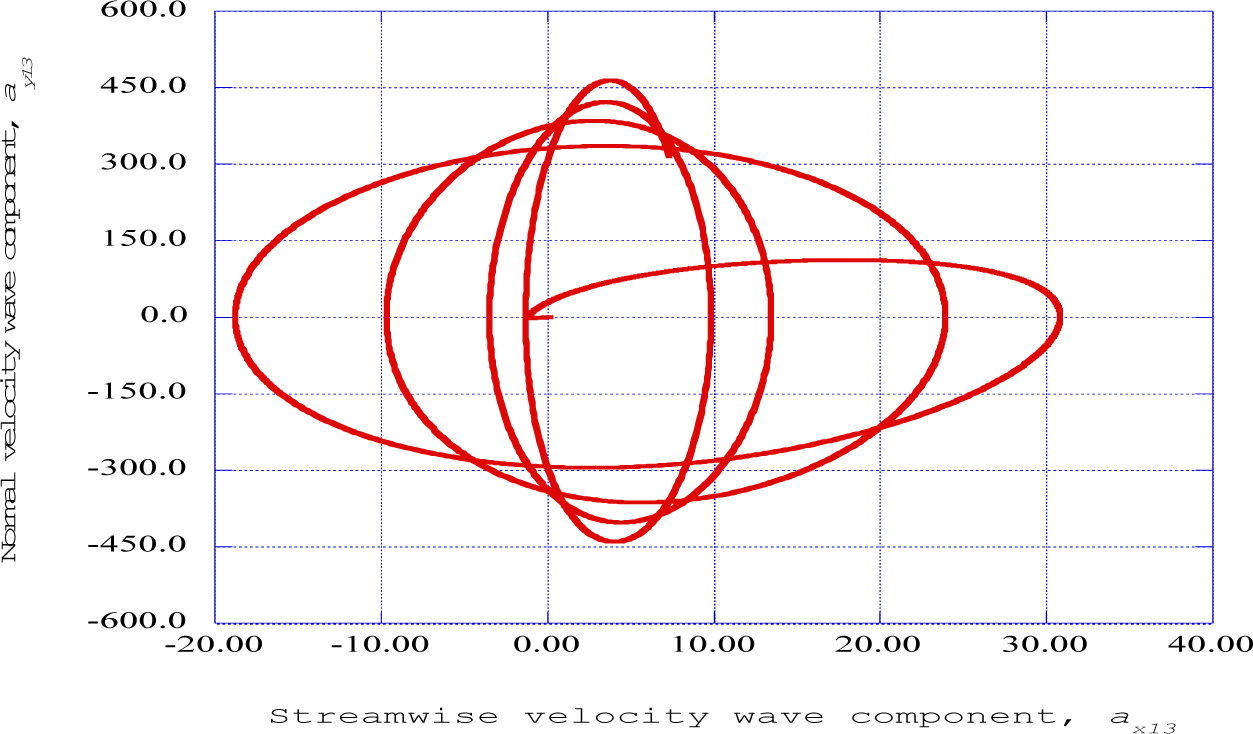
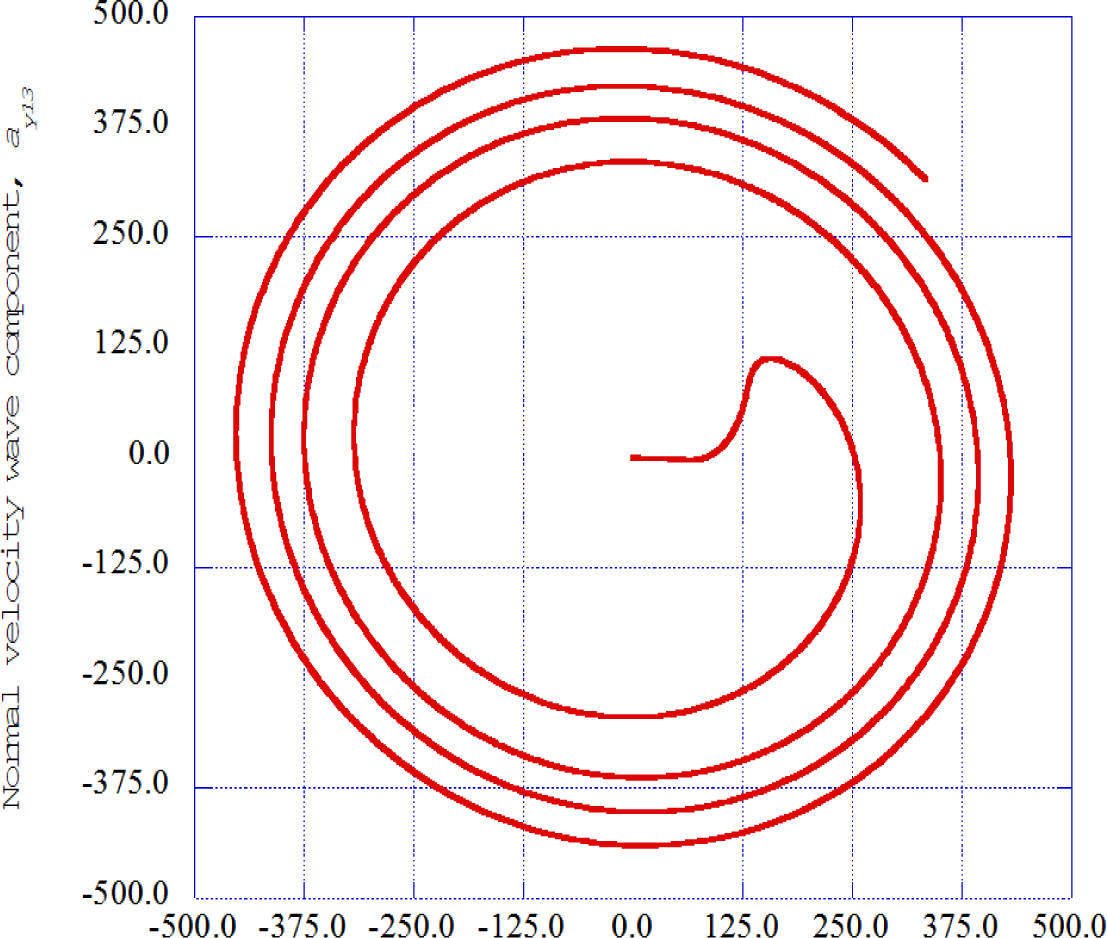
Figure 9 presents the streamwise velocity wave component versus the normal velocity wave component at streamwise receiver station thirteen. The autogeneration process involves an oscillatory motion in the spanwise and normal velocity planes, indicating the initiation of unstable boundary layer behavior. Thus, the overall process of the transition from the laminar to the turbulent state of the boundary layer consists of the continuous production of these burst, sweep and autogeneration processes.
As a concluding figure for the nonlinear time series solutions for the spatially developing boundary layer, Figure 10 presents the spanwise velocity wave component versus the normal velocity wave component at streamwise receiver station thirteen. The periodic nature of the flow configuration in the normal-spanwise plane during the autogeneration process indicates considerable order within the process. The autogeneration processes as indicated in Figures 8, 9 and 10 are repeated over the next several streamwise stations.
6. Spectral Entropy Rates for the Deterministic Structures
One of the specific objectives for this study has been to begin to understand the fundamental thermodynamic characteristics of the deterministic structures predicted within the solutions of the coupled, nonlinear Lorenz-type spectral equations [10]. The power spectral density of a segment of the nonlinear time series solution is first computed. These results then allow the computation of the spectral entropy rates for the specified segment of time series data. These spectral entropy rates provide an indication of whether ordered or disordered regions exist within the specified segment of time series data.
We wish to extract the detailed power spectral density over a specified range of the output series data from the nonlinear time series solutions for the fluctuating velocity wave components. Burg developed the maximum entropy method for extracting information contained within seismic data, with one of the first computer programs presented by Chen [22]. Burg’s method provides sharp spectral peaks in the power spectral density distribution for the specified segment of the time series solution data.
The computational methods presented by Press et al. [23] (pp. 566–575) for Burg’s maximum entropy method are included in our computational scenario to obtain the power spectrum of a specified segment of the nonlinear time series solution at each streamwise receiver station. The specified data segment for the streamwise velocity wave component time series includes 4,096 time step data samples from the time step of 8,192 to time step 12,288. Burg’s method yields the power spectral density of the streamwise velocity wave vector component, fr, for the specified data segment.
Powell and Percival [24] and Grassberger and Procaccia [25] developed methods for computing the spectral entropy rates from the power spectral density for a specified time data segment. The probability values for a particular power spectral density distribution for a given time segment are first computed from . The spectral entropy rate (1/s) is then computed for the j-th time segment as:
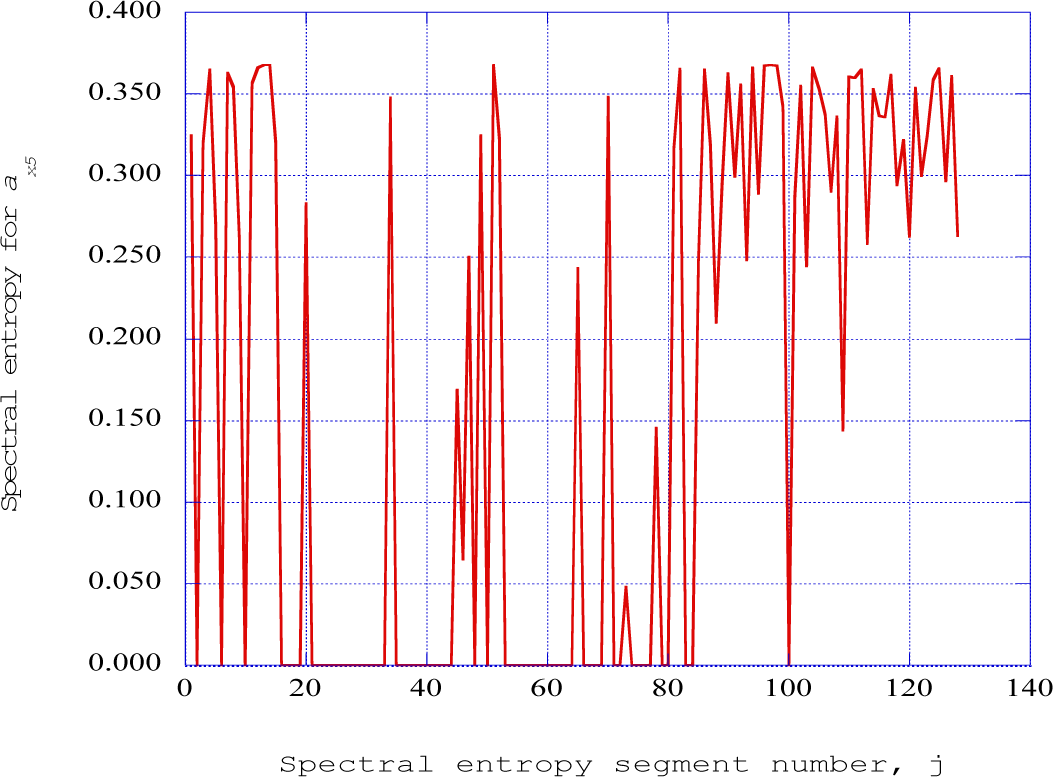
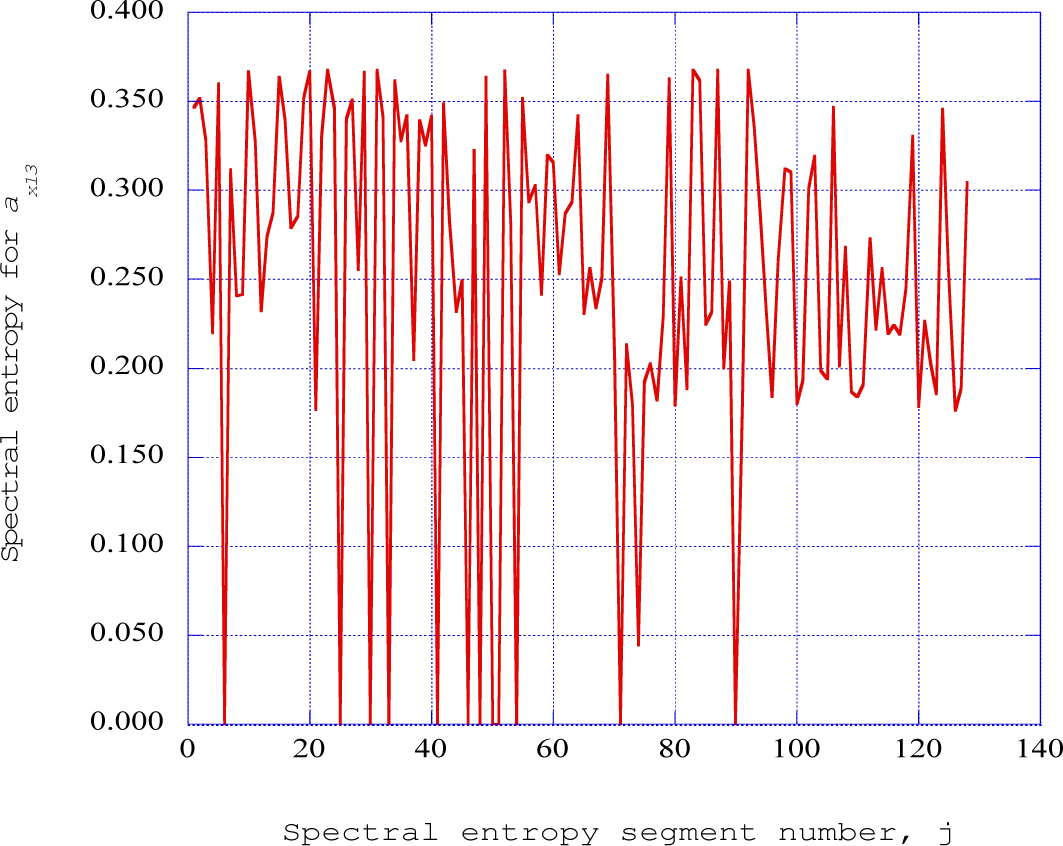
Figure 11 presents the spectral entropy rates for the specified data segment of the nonlinear time series solution at downstream receiver station five (x = 0.16). From Figures 2, 3 and 4, we note that at station five, an “ejection” or burst of boundary layer flow away from the wall region is indicated. The important observation is that in Figure 11 there are several regions of continuous spectral entropy rates of zero value, indicating ordered structures over several time segments in the nonlinear time series solution. At station thirteen, (x = 0.32), Figures 8, 9 and 10 indicate a return to the generation of relatively low level instabilities, with numerous downward spikes indicating the continuous production of more sharply defined ordered structures. In Figure 12, spectral entropy rates for station thirteen indicate a return to the process of the nonlinear production of initial disturbances within the laminar boundary layer flow. This region coincides with the process Adrian [4] describes as “autogeneration.”
7. Singular Value Decomposition and Empirical Entropy
Further thermodynamic insight is needed concerning the distribution of fluctuation kinetic energy across the ordered structures identified by the spectral entropy rates for each of the streamwise stations as the boundary layer develops in the downstream direction. Holmes et al. [26] have developed the method of proper orthogonal decomposition, or singular value decomposition, that provides additional understanding of deterministic structures that occur in turbulent flows. Given the results from a direct numerical simulation of flow field structures, these methods yield useful information concerning the distribution of fluctuating kinetic energy across the structures. Press et al. [23] (pp. 59–70) present computer source code, under the term “singular value decomposition,” that is appropriate for use in our computational procedure.
The application of the singular value decomposition procedure to a specified segment of the nonlinear time-series solution for the streamwise velocity wave component yields the distribution of the component eigenvalues λj across the empirical modes, j, for each of the streamwise stations. Here, we wish to heuristically introduce our second thermodynamic parameter [13], namely the empirical entropy, Sempj, which may be defined by the expression (Rissanen [27,28])
The application of the singular value decomposition procedure to the specified segment of the nonlinear time-series solution yields the various eigenvalues λj across the empirical modes, j for that segment [13]. The particular empirical entropy of a particular mode j provides an indication of the nature of the directed kinetic energy that exists within that particular mode.
The computational procedure for the empirical entropy by the singular value decomposition method is made up of two parts, the computation of the autocorrelation matrix and the singular value decomposition of that matrix [13]. The computer source code presented by Press et al. [23] (pp. 545–546)for the computation of the autocorrelation of the fluctuating streamwise velocity wave components and the source code for the computation of the singular value decomposition procedure, (Press pp. 66–70 [23]), are included in the overall computational scenario. This computational procedure yields the empirical eigenvalues for each of the empirical eigenfunctions for the specified time series data segment, applied at each downstream station.
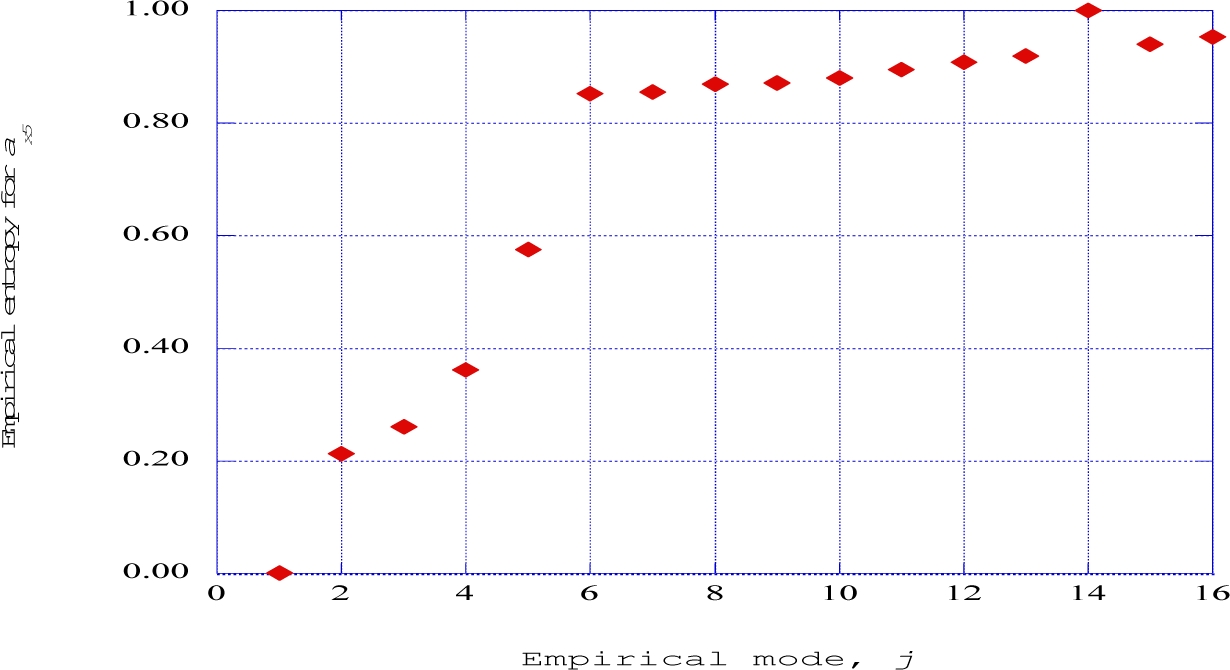
The empirical entropies for each of the empirical modes from one to sixteen for streamwise station five are shown in Figure 13. From Figure 2, this station indicates the first of the “ejection” processes. The distribution of the empirical entropy over the empirical modes indicates three different characteristics for the nature of kinetic energy within the modes. The initial four eigenmodes contain low levels of empirical entropy, indicating highly ordered directed kinetic energy. The following two modes indicate a steep increase in value, indicating a sharp increase in disorder within the kinetic energy environment. The following ten modes indicate disordered kinetic energy, with the empirical entropy approaching the maximum of unity in value.
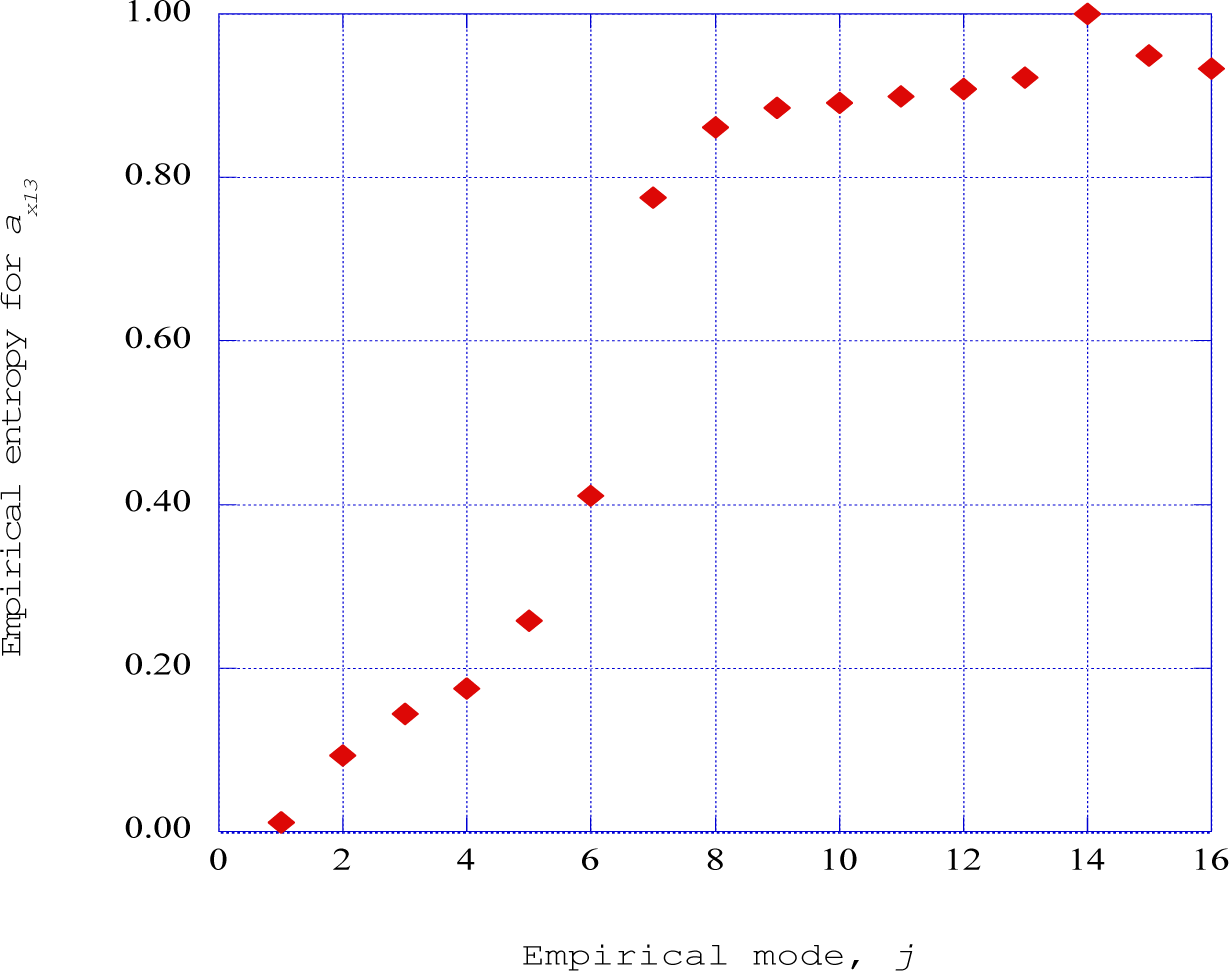
The empirical entropy is shown as a function of empirical mode number in Figure 14 for streamwise station thirteen (x = 0.32). From Figure 8, this station indicates a return of the flow configuration to the “autogeneration” process. The first four modes indicate very low levels of empirical entropy, indicating highly ordered kinetic energy. The steep increase in entropy from modes five through eight reflects an apparent change in the dynamics of the kinetic energy in these modes. The almost level range of high empirical entropy from modes eight through sixteen indicates a low level of ordered structures in the kinetic energy and an apparent high dissipation rate into background thermodynamic entropy. The significantly lower empirical entropy values for the first four modes at station thirteen are indicative of the low intensity of the instabilities generated in the “autogeneration” process.
The interpretation we make for the eigenvalues λj is that they represent twice the kinetic energy within each eigenmode distributed across j values [26]. These eigenmodes are obtained from the streamwise velocity wave components across a specified set of time series data, taken as a total ensemble of data values, and not as a sequence of values. Thus, these empirical entropy values exist as a collection of values within the nonlinear time series, and not as a cascade from low entropy modes to high entropy modes. The computation of the empirical entropy has thus provided additional insight into the thermodynamic nature of our nonlinear time series solutions.
We have, thus far, demonstrated the production of instabilities at a particular vertical station within a three-dimensional laminar boundary layer as a result of nonlinear interactions within the boundary layer. The effects of the downstream developing laminar boundary layer on the characteristics of these instabilities indicate the prediction of the burst, sweep, and autogeneration processes. The spectral entropy rates at downstream station five indicate significant ordered regions at the burst process and at downstream station thirteen the generation of a broader range of lower intensity ordered regions in the autogeneration process. The empirical entropy further characterizes the nonlinear time series into regions of low empirical entropy, a transition region, and an extensive region of high empirical entropy, coexisting simultaneously within the time series solutions.
We wish to now explore some speculative thermodynamic concepts which may allow us to extend our computational procedure through the deterministic structures produced by the instability process to a connection with the final stages of dissipation within a fully turbulent flow environment. These two exploratory concepts are the empirical entropic index and the empirical intermittency exponent.
8. Empirical Entropic Index
The empirical entropy for the fluctuating streamwise velocity wave component time series indicates different characteristics for the various deterministic regions within the time series. These results indicate that the majority of the kinetic energy in the deterministic structures is contained within the first four or five empirical modes of the singular value decompositions, with low empirical entropy. These structures have been classified as coherent [4] with well-defined structural boundaries. To characterize these structures, Tsallis [14] postulated a generalized entropic form
In this expression, k is a positive constant, pi is the probability of the subsystem to be in the state i, and W is the total number of microscopic possibilities of the system. The Tsallis entropic index, q, would be found from this expression for an ensemble of accessible subsystems.
It is tempting to apply this expression for the ordered structures as calculated in the previous section on empirical entropy. However, the Tsallis entropic form is applicable to an ensemble of microscopic subsystems, while we are working with a set of individual macroscopic systems spread over a limited number of empirical modes, j. In fact, the premise of the computation of the empirical entropy, Sempj is that this is the entropy of an ordered region described by the empirical eigenvalue, λj, for the singular value decomposition empirical mode, j. Hence, we simply adopt, in an ad hoc fashion, an expression from which we may extract an empirical index, qj, from the empirical entropy. This expression may be written as:
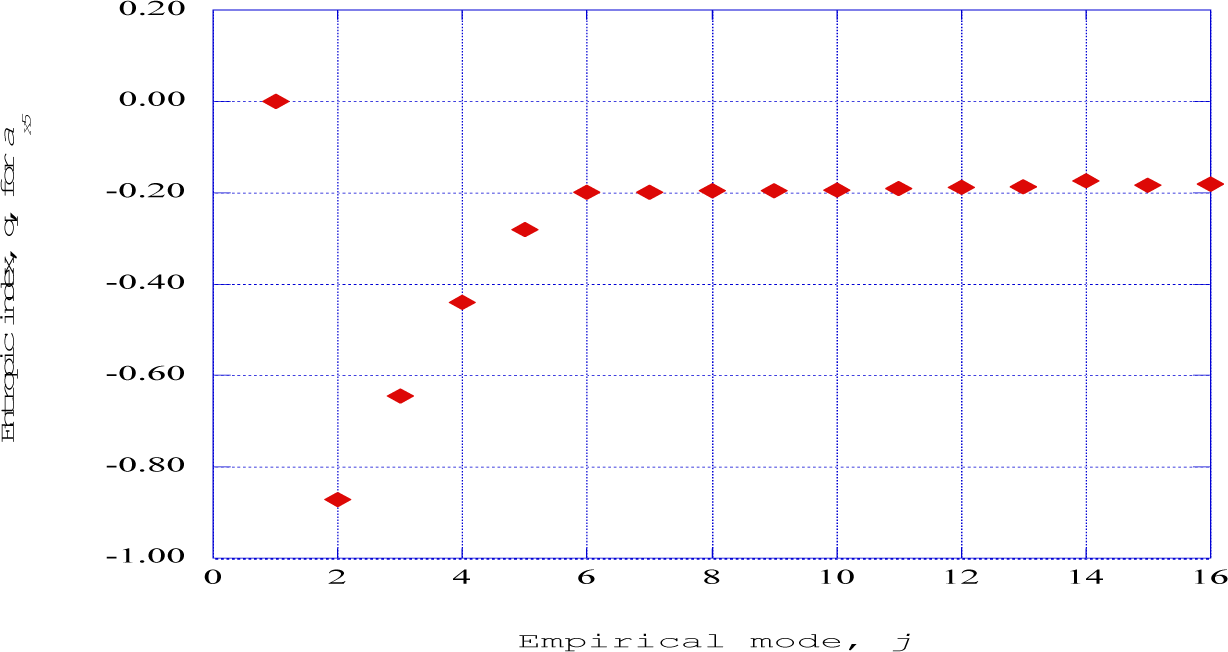
We have to keep in mind that this parameter does not have a mathematical basis in non-extensive thermo-statistics but is simply an artifact that allows us to include the effects of the nonlinear, non-equilibrium nature of the deterministic structures that we are following. The expression has the format of entropic index; hence, we simply call it an empirical entropic index or simply an entropic index. We have used this expression to extract the empirical entropic index, qj, from the empirical entropy for streamwise stations five and thirteen along the boundary layer environment. Figure 15 shows the empirical entropic index for the streamwise velocity wave components at the fifth station as a function of the empirical mode. The empirical entropic index for the empirical mode one at the streamwise station five, the streamwise velocity wave component indicates an initial value of zero. The eigenvalue for mode one contains a high fraction of directed kinetic energy, not organized into a deterministic structure, simply flowing in the streamwise direction in a reversible and adiabatic process. Hence, according to Mariz [29], dSempj / dt = 0, and the entropy for this mode does not change with time.
According to the general evolution criterion for non-equilibrium dissipative processes (Glandsdorff and Prigogine [30]), the rate of entropy change for such structures is negative, dSempj / dt < 0. Again, according to the results found by Mariz [29] for the case when dSempj / dt < 0, the Tsallis entropic index indicates a negative value. For the deterministic structures predicted in the computational results in this study, the spectral entropy results indicate that significant deterministic structures exist within a specified segment of the nonlinear time series solutions. We are therefore justified in classifying these regions as ordered, dissipative structures. Therefore, the significant negative nature for the extracted empirical entropic indices from empirical mode two to empirical mode sixteen at streamwise station five is in agreement with both the Prigogine criterion and the Mariz results for the Tsallis entropic index. This result provides a measure of confidence that our ad hoc empirical entropy index may represent the nonlinear, non-equilibrium structures in a significant way.
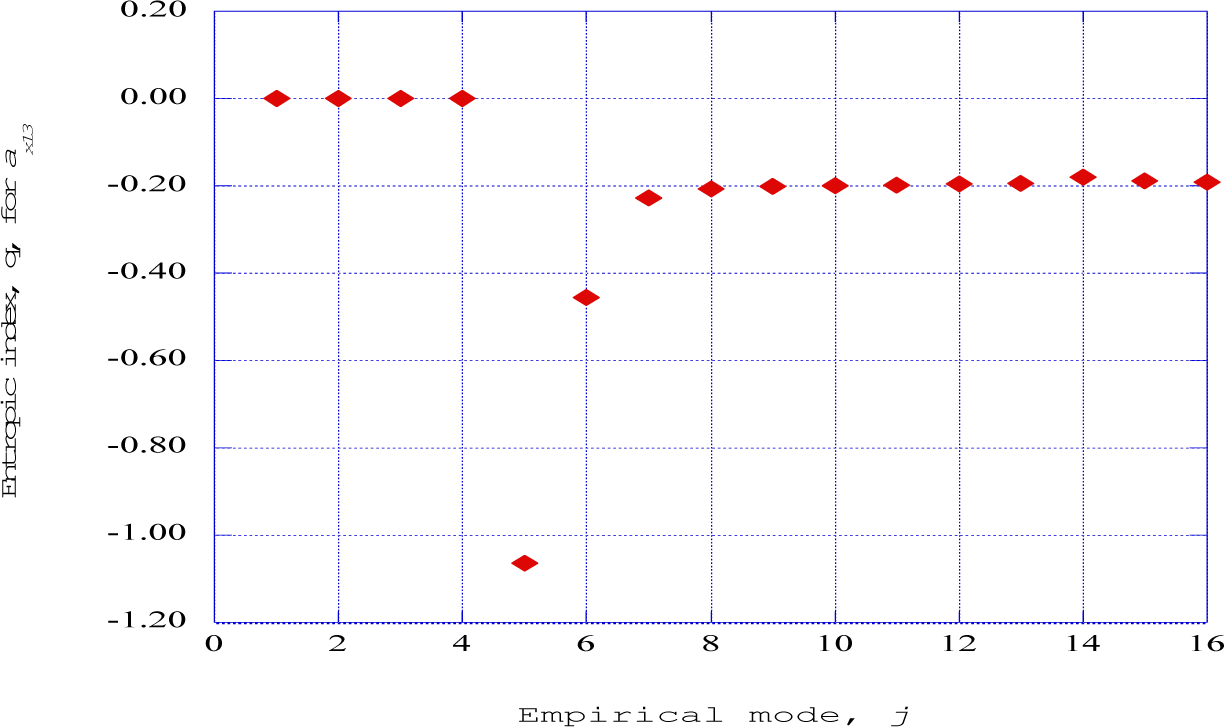
Figure 16 shows the empirical entropic index for the streamwise velocity wave component for each of the empirical modes, j, at streamwise station thirteen. This station indicates a return of the system to the autogeneration phase of the overall process, and indicates a low level of aperiodic oscillations. At this station, empirical modes one through four indicate a value of zero for the entropic index, indicating a smooth flow of streamwise kinetic energy, with negative values of entropic index from modes five through sixteen. These results indicate that dissipative structures are produced in the nonlinear time series solutions of the Lorenz form of the nonlinear differential equations describing the fluctuating velocity fields across the boundary layer.
9. Intermittency Exponents
In the preceding sections of the paper, we have focused primarily on the extraction of thermo-statistic properties from the nonlinear time series solution for the fluctuating velocity wave components in a developing laminar boundary layer along a flat plate surface in a three-dimensional configuration. In this section, we introduce a speculative method to connect the deterministic results for the entropic indices with the turbulent dissipation processes occurring in the downstream fully developed turbulent flow. We explore this computational connection through the concept of turbulent intermittency.
The concept of intermittency arises in the observation that within a fully developed turbulent flow, regions of the dissipation of kinetic energy are interspersed with regions in which the dissipation rate is very low, with the regions separated by distinct boundary surfaces. This observation led to the characterization of the dissipation of turbulent kinetic energy in the inertial range as fractal in nature (Tsallis [14]). Mathieu and Scott [17] also present a thorough discussion of intermittency in the dissipation of turbulent kinetic energy within fully developed turbulent flows.
The deterministic structures discussed in previous sections are of a macroscopic nature embedded within the nonlinear time series solution of the nonlinear equations for the fluctuating velocity field. We have found, through the singular value decomposition method, that the four lowest empirical modes contain nearly 99 per cent of the kinetic energy. We have also found that the empirical modes obtained from the singular value decomposition indicate empirical entropic indices. We will therefore, heuristically, apply a relationship, found by Arimitsu and Arimitsu [15], between the entropic index of Tsallis and the intermittency exponent required to account for the fractal nature of turbulent energy dissipation. We will substitute the absolute value of the empirical entropic indices discussed in the previous section for the empirical entropic index into the original derivation by Arimitsu and Arimitsu [15]. This expression is written as:
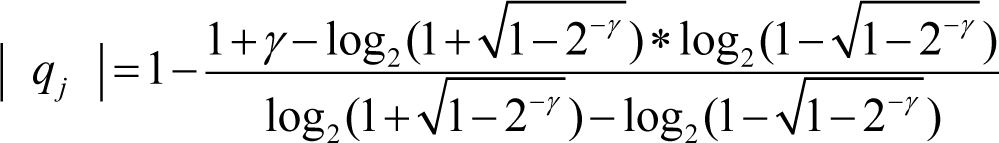
Given the absolute value of the empirical entropic index, qj, the intermittency exponent, γ, is extracted from this expression by the use of Brent’s method (pp. 397–405 [23]). Arimitsu and Arimitsu [14] derived the intermittency exponents for turbulent eddies within a fully turbulent flow that dissipates turbulent kinetic energy into thermal energy within the flow. Figure 17 shows the intermittency exponent for the ejection process at station five. A significant exponent is indicated for the third empirical mode, indicating the possible presence of “spikes”, (as discussed by Schmid and Henningson [31]), while the remaining intermittency exponents approach the values predicted for the eddies of fully developed turbulent flows.
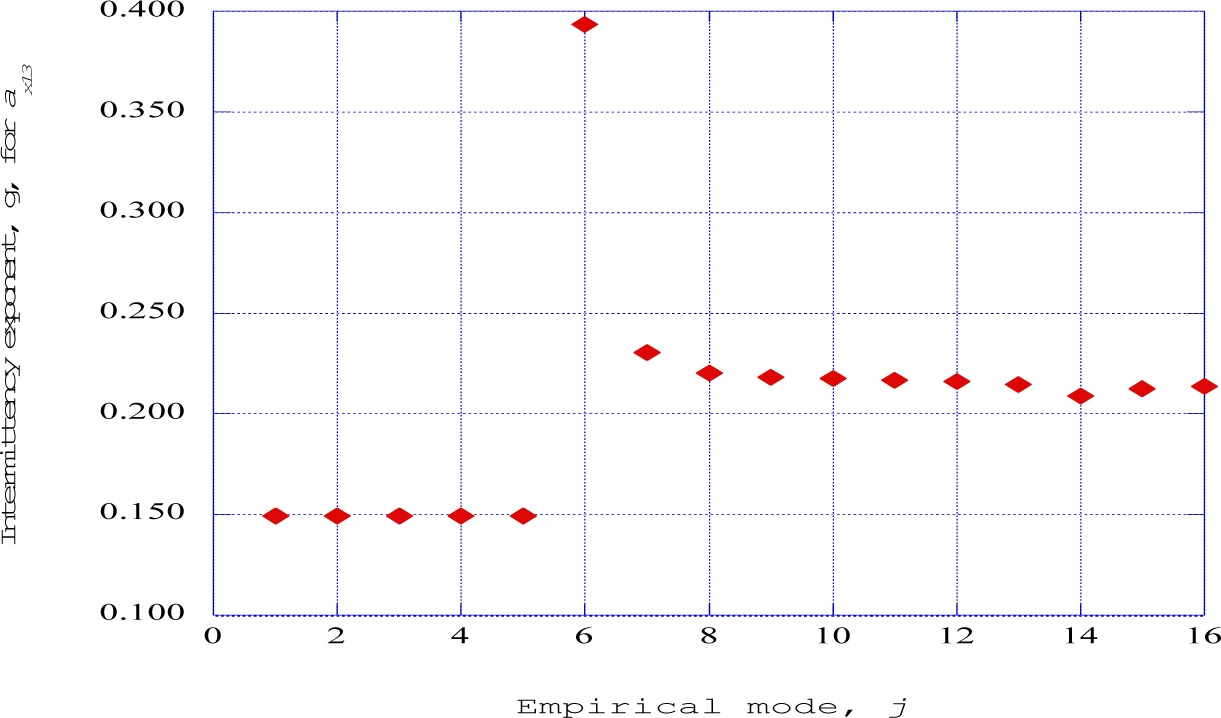
Figure 18 presents the intermittency exponents for streamwise station thirteen, which reflects the autogeneration process discussed in [4]. These results indicate that the first five empirical modes make no contributions to the intermittency exponent. Again, however, the higher empirical modes in which the directed kinetic energy does not appear, essentially with the highest entropy levels, contribute intermittency exponents corresponding to the values indicated for the dissipative eddies in fully developed turbulent flows.
10. Discussion
The objective of this article has been to present the results of a computational scenario applied to the spatial development of the fluctuating velocity wave field embedded in a developing laminar boundary layer. These results indicate the production of deterministic structures within the boundary layer consisting of burst, sweep and autogeneration processes. The computational scenario also yields the spectral entropy rates indicating ordered and disordered regions within the time series solutions, the empirical entropy values indicating different characteristics of the deterministic structures within the time series solutions, and the empirical entropic indices for those empirical entropies, together with the resulting intermittency exponents for the respective entropic indices. These deterministic structure characteristics have been computed for a number of streamwise stations in the spatially developing boundary layer.
The equations for the fluctuating velocity components within the boundary layer have been Fourier transformed into a set of three time dependent simultaneous equations for the wave number components and a set of three coupled, nonlinear time dependent equations for the velocity wave components within the boundary layer. The mean velocity gradients computed for the laminar boundary layer at each streamwise station serve as control parameters for the solution of each set of equations at each corresponding streamwise station. The computational procedure yields deterministic ordered regions within the resulting solutions for each streamwise station. The synchronization properties of the Lorenz-type equations are exploited in the computational procedures as we progress from station to station. The initial station is characterized as a transmitter station, with the streamwise velocity wave component output transmitted to the next station, called a receiver station. The sum of the streamwise velocity wave component signals from the transmitter station and the first receiver station then serve as similar input to the next receiver station. This process is repeated for each of the receiver stations in the streamwise direction.
Resulting solutions for the three velocity wave components are presented for several streamwise stations. The transmitter station shows several large-scale aperiodic oscillating patterns for each of the three velocity wave components. The autogeneration process is indicated at station three with an upward flow following at station five. These upward flows, or “ejections,” continue to be produced over the next three stations, indicating that the burst process is a “sequence” of processes spread over a length of streamwise distance. At station eight, a strong downward flow of the streamwise velocity wave component is indicated, representing a “sweep” process. These inward flow processes are indicated over the next three streamwise stations, indicating that the boundary layer “sweep” process is also a “sequence” of flow events spread over several streamwise stations in the spatially developing direction. The flow returns to the autogeneration process at station thirteen, with a return to the relatively low-level production of aperiodic oscillatory fluctuating flow motion.
A central theme of our computational scenario is to clarify certain thermodynamic aspects of the deterministic structures occurring within the fluctuating velocity field. The power spectrum of the final portion of the overall time series solutions has been computed using Burg’s maximum entropy method. The spectral entropy rates are then computed for that portion of the solution. Applying the computational technique to the initial burst process at streamwise station five, it has been found that a considerable portion of the spectral entropy rate indicates a significant region of ordered structures within the burst process. A similar computation for the autogeneration process at station thirteen indicates a continuous production of sharply ordered structures.
Application of the singular value decomposition technique to the latter portion of the nonlinear time series solutions provides values for the distribution of eigenvalues over a series of empirical decomposition modes. The empirical entropy, defined as the negative natural logarithm of the eigenvalue for each empirical mode, yields a distribution of empirical entropies as a function of the distribution of empirical modes. These results show that for the initial mode numbers, the empirical entropies are near zero, indicating closely ordered behavior. These results also indicate that for a significant range of empirical modes over the high mode numbers, the empirical entropy is near the maximum value.
To further clarify the nature of the ordered and disordered structures, the empirical entropic index is computed from the given values of empirical entropy for each empirical mode at streamwise stations five and thirteen. The empirical entropic index has a value of zero for the initial empirical mode for each of the streamwise stations. We interpret a zero value for the entropic index to indicate an ordered flow with a significant level of directed kinetic energy. This type of flow structure is simply a directed kinetic energy corresponding to a mean streamwise flow component, not of a vortex or similar motion. However, the strong negative entropic indices at empirical mode two for station five and empirical mode five at station thirteen indicate the prediction of significantly ordered structures of a dynamic nature. These structures may appear as deterministic dissipative vortices with negative absolute temperature, which eventually decay to background internal energy with high entropy.
To complete our computational scenario, we compute the intermittency exponents associated with the particular empirical entropic indices across the empirical mode numbers for streamwise stations five and thirteen. These stations indicate the first burst process and the autogeneration process following the burst and sweep processes. For both stations, a peak of intermittency exponent is indicated for empirical modes three at both stations five and thirteen. These sharp values of intermittency could be associated with the “spikes” observed in early studies of the transition process. It is of particular interest for us to observe that both the empirical entropic indices and the intermittency exponents for empirical modes six through sixteen reproduce the values determined for fully developed turbulent flow.
11. Conclusions
This article has presented the results of a computational scenario for the fluctuating velocity field embedded in a streamwise laminar boundary layer that yields the prediction of deterministic structures developing within the boundary layer flow. The time integration of the set of time dependent spectral wave number components and the set of time dependent spectral velocity wave components at the fifth streamwise station indicates an outward burst process, while the results for the eleventh station predict a strong inward sweep process. The results for the thirteenth station indicate a return to the original instability autogeneration process. The computational procedure has thus evaluated the initiating boundary layer instabilities, and sequentially predicted the bursting process, the sweep process and the return of the flow to the generation of internal boundary layer instabilities. Spectral entropy rates, obtained by the application of Burg’s maximum entropy method, indicate regions of significant ordered structures ahead of the initial bursting process. When the flow returns to the autogeneration region, the spectral entropy rates indicate the continuous generation of low intensity ordered and disordered regions. The singular value decomposition technique applied to specified segments of the solutions yields empirical entropies over decomposition modes. Empirical entropic indices are obtained from the empirical entropies for two streamwise stations. The entropic indices extracted from the empirical entropies indicate zero values for the first empirical modes and then negative values over the remaining modes. These results indicate that the deterministic structures are non-equilibrium and dissipative in nature. The intermittency exponents are obtained from the entropic indices for the streamwise burst and autogeneration stations. These intermittency exponents closely match the corresponding exponents for the dissipation of kinetic energy in the fully developed regions of turbulent flow. We thus have a computational scenario that evaluates the initiation of instabilities through nonlinear interactions within a three-dimensional laminar boundary layer and then follows the process through to the evaluation of the connecting link to the dissipation of kinetic energy within the fully developed turbulent flow.
Acknowledgments
The author would like to thank the editor and referees for their timely and helpful suggestions. The editorial assistance of the editors in improving the manuscript is very much appreciated. The comments and observations of the reviewers have clarified several technical aspects of this exploratory study for which the author expresses his thanks and appreciation.
Conflicts of Interest
The author declares no conflicts of interest.
PACS Codes: 47.15.Fe (Stability of boundary-layers); 47.27.De (Ordered regions)
| Nomenclature | |
|---|---|
| ai | Fluctuating i-th component of velocity wave vector |
| b | Fluctuating Fourier component of the static pressure |
| b1 | Coefficient in modified Townsend equations defined by Equation (21) |
| bn | Coefficient in modified Townsend equations at station n |
| F | Time-dependent feedback factor |
| fr | Power spectral density of the r_th time series segment |
| j | Mode number empirical eigenvalue |
| j | Spectral entropy segment number |
| k | Time-dependent wave number magnitude |
| k | Dimensional constant, Equation (29) |
| ki | Fluctuating i-th wave number of Fourier expansion |
| K | Adjustable weighting factor |
| n | Time step number |
| p | Local static pressure |
| p1 | Static pressure in the boundary layer channel |
| pi | Probability of being in a state i, Equation (29) |
| Pr | Probability value for the power spectral density of the r_th segment |
| q | Tsallis nonextensive entropic index |
| qj | Empirical entropic index for the empirical entropy of mode, j |
| r1 | Coefficient in modified Townsend equations defined by Equation (19) |
| rn | Coefficient in modified Townsend equations at station n |
| s1 | Coefficient in modified Townsend equations defined by Equation (20) |
| sn | Coefficient in modified Townsend equations at station n |
| Sempj | Empirical entropy for empirical mode, j |
| sj_spent | Spectral entropy rate for the j-th spectral entropy segment |
| Sq | Tsallis entropy, Equation (29) |
| t | Time |
| t1 | Combustion process input temperature |
| Taft | Adiabatic flame temperature |
| ue | Streamwise velocity at the outer edge of the x-y plane boundary layer |
| ui | The i-th component of the fluctuating velocity |
| Ui | Mean velocity in the i-th direction in the modified Townsend equations |
| Vx | Mean normal velocity in the x-y plane in the modified Townsend equations |
| Vz | Mean normal velocity in the z-y plane |
| we | Spanwise velocity at the outer edge of the z-y plane boundary layer |
| W | Mean velocity in the spanwise direction |
| W | Total number of microscopic states in a system, Equation (29) |
| x | Streamwise distance |
| xi | i-th direction |
| xj | j-th direction |
| y | Normal distance |
| z | Spanwise distance |
| Greek Letters | |
|---|---|
| γ | Intermittency exponent |
| δlm | Kronecker delta |
| η | Transformed normal distance parameter |
| λj | Eigenvalue for the empirical mode, j |
| ν1 | Kinematic viscosity of the gas mixture |
| ρ | Density |
| σy1 | Coefficient in modified Townsend equations defined by Equation (17) |
| σx1 | Coefficient in modified Townsend equations defined by Equation (18) |
| Subscripts | |
|---|---|
| e | Outer edge of the x-y plane boundary layer |
| i, j, l, m | Tensor indices |
| x | Component in the x-direction |
| y | Component in the y-direction |
| z | Component in the z-direction |
References
- Cherubini, S.; de Palma, P.; Robinet, J-Ch.; Bottaro, A. Edge states in a boundary layer. Phys. Fluids 2011, 23, 051705. [Google Scholar]
- Blau, B. Laminar-turbulent separatrix in a boundary layer flow. Phys. Fluids 2012, 24, 034107. [Google Scholar]
- Cherubini, S.; de Palma, P.; Robinet, J-Ch.; Bottaro, A. The minimal seed of turbulent transition in the boundary layer. J. Fluid Mech 2011, 689, 221–253. [Google Scholar]
- Adrian, R. Hairpin vortex organization in wall turbulence. Phys. Fluids 2007, 19, 041301. [Google Scholar]
- Cebeci, T.; Bradshaw, P. Momentum Transfer in Boundary Layers; Hemisphere: Washington, DC, USA, 1977. [Google Scholar]
- Isaacson, L.K. Spectral Entropy in a Boundary Layer Flow. Entropy 2011, 13, 402–421. [Google Scholar]
- Hansen, A.G. Similarity Analyses of Boundary Value Problems in Engineering; Prentice-Hall, Inc: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Townsend, A.A. The Structure of Turbulent Shear Flow, 2nd ed.; Cambridge University Press: Cambridge, UK, 1976. [Google Scholar]
- Hellberg, C.S.; Orszag, S.A. Chaotic behavior of interacting elliptical instability modes. Phys. Fluids 1988, 31, 6–8. [Google Scholar]
- Isaacson, L.K. Ordered Regions within a Nonlinear Time Series Solution of a Lorenz Form of the Townsend Equations for a Boundary-Layer Flow. Entropy 2013, 15, 53–79. [Google Scholar]
- Pyragas, K. Continuous control of chaos by self-controlling feedback. In Controlling Chaos: Theoretical and Practical Methods in Non-linear Dynamics; Kapitaniak, T., Ed.; Academic Press Inc: San Diego, CA, USA, 1996; pp. 118–123. [Google Scholar]
- Cuomo, K.M.; Oppenheim, A.V. Circuit implementation of synchronized chaos with applications to communications. In Controlling Chaos: Theoretical and Practical Methods in Non-linear Dynamics; Kapitaniak, T., Ed.; Academic Press Inc: San Diego, CA, USA, 1996; pp. 153–156. [Google Scholar]
- Isaacson, L.K. Spectral Entropy, Empirical Entropy and Empirical Exergy for Deterministic Boundary-Layer Structures. Entropy 2013, 15, 4134–4158. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009; pp. 37–43. [Google Scholar]
- Arimitsu, T.; Arimitsu, N. Analysis of fully developed turbulence in terms of Tsallis statistics. Phys. Rev. E 2000, 61, 3237–3240. [Google Scholar]
- Dorrance, W.H. Viscous Hypersonic Flow; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1962; pp. 276–278. [Google Scholar]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow; Cambridge University Press: New York, NY, USA, 2000; pp. 251–261. [Google Scholar]
- Sagaut, P.; Cambon, C. Homogeneous Turbulence Dynamics; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Manneville, P. Dissipative Structures and Weak Turbulence; Academic Press Inc.: San Diego, CA, USA, 1990. [Google Scholar]
- Pérez, G.; Cerdeiral, H.A. Extracting messages masked by chaos. In Controlling Chaos: Theoretical and Practical Methods in Non-linear Dynamics; Kapitaniak, T., Ed.; Academic Press Inc: San Diego, CA, USA, 1996; pp. 157–160. [Google Scholar]
- Feng, J.C.; Tse, C.K. Reconstruction of Chaotic Signals with Applications to Chaos-Based Communications; World Scientific Publishing Co Pte. Ltd.: Hackensack, NJ, USA, 2008; pp. 165–213. [Google Scholar]
- Chen, C.H. Digital Waveform Processing and Recognition; CRC Press Inc.: Boca Raton, FL, USA, 1982; pp. 131–158. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Powell, G.E.; Percival, I.C. A spectral entropy method for distinguishing regular and irregular motion for Hamiltonian systems. J. Phys. Math. Gen 1979, 12, 2053–2071. [Google Scholar]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Stations and Symmetry, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Rissanen, J. Complexity and Information in Data. In Entropy; Greven, A., Keller, G., Warnecke, G., Eds.; Princeton University Press: Princeton, NJ, USA, 2003; pp. 299–327. [Google Scholar]
- Rissanen, J. Information and Complexity in Statistical Modeling; Springer: New York, NY, USA, 2007. [Google Scholar]
- Mariz, A.M. On the irreversible nature of the Tsallis and Renyi entropies. Phys. Lett. A 1992, 165, 409–411. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; John Wiley & Sons Ltd: London, UK, 1971. [Google Scholar]
- Schmid, P.J.; Henningson, D.S. Stability and Transition in Shear Flows; Springer-Verlag New York, Inc: New York, NY, USA, 2001. [Google Scholar]

| Title | Title |
|---|---|
| Inlet temperature, t1: | 298.15 K |
| Adiabatic flame temperature, Taft: | 1140.0 K |
| Static pressure, p1: | 1.013 × 105 N/m2 |
| Kinematic viscosity, v1: | 1.523 × 10−4 m2/s |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Isaacson, L.K. Transitional Intermittency Exponents Through Deterministic Boundary-Layer Structures and Empirical Entropic Indices. Entropy 2014, 16, 2729-2755. https://doi.org/10.3390/e16052729
Isaacson LK. Transitional Intermittency Exponents Through Deterministic Boundary-Layer Structures and Empirical Entropic Indices. Entropy. 2014; 16(5):2729-2755. https://doi.org/10.3390/e16052729
Chicago/Turabian StyleIsaacson, LaVar King. 2014. "Transitional Intermittency Exponents Through Deterministic Boundary-Layer Structures and Empirical Entropic Indices" Entropy 16, no. 5: 2729-2755. https://doi.org/10.3390/e16052729




